Design and Implementation of a Path Finding Robot using Modified

Trémaux Algorithm

Semuil Tjiharjadi

a

Department of Computer System, Maranatha Christian University, Jl. Surya Sumantri 65, Bandung, Indonesia

Keywords: Trémaux Algorithm, Maze, Pathfinding, Manhattan Distance

Abstract: Using a robot to find a path to achieve a target location in an unknown maze requires a robot that can explore

the maze and determine the direction of the intersection in the maze. The robot must map the maze, determine

a route and try to reach its destination as fast as possible through the closest path. Trémaux algorithm is one

of the maze solver algorithms that is used to explore a maze and its use to find a way out of the maze, meaning

that this algorithm is designed for purposes that are on the edge of a maze and not in the middle of a maze.

For this reason, Trémaux algorithm was modified by adding the Manhattan Distance algorithm to improve

the ability of the robot to find targets in the middle of the maze. Using the Manhattan Distance algorithm

made able to make better decisions compare to Trémaux random decision at branch position. The application

of a combination of these algorithms enables the ability to search for paths in an unknown maze environment.

The success rate to explore, map the maze, and find the shortest path to the destination is dramatically

increased using a modified Trémaux algorithm.

1 INTRODUCTION

The development of an autonomous mobile robot that

can find itself and reach its destination without being

controlled has been growing rapidly. The ability of a

mobile robot to move automatically from a place to a

destination without the assistance of an operator is an

important part of the capability of a mobile robot

which is continuously being developed. This is an

application that is often used in the gaming industry.

Its use in warehouse, search and rescue applications,

its development in the era of automatic vehicles, is

one of the developing researches. Various researches,

methods, and algorithms have been developed to

support autonomous mobile robots. These methods

and algorithms are unique along with their respective

advantages and disadvantages.

Various studies on the development of maze

pathfinding have been carried out, Flood Fill

Algorithm (Chu et al., 2019; Jabbar, 2016; S.

Tjiharjadi & Setiawan, 2016), Fisher-Yates Shuffle

algorithm (Hoetama et al., 2019), A-Star (Downey &

Charles, 2015; Kumar & Kaur, 2019; S. Tjiharjadi et

al., 2017; Zikky, 2016), Pledge Algorithms (S.

a

https://orcid.org/0000-0003-0424-2122

Tjiharjadi, 2019), Modified A-Star (Kang et al.,

2018), Hybrid approach (Ansari et al., 2015),

Artificial Bee (Faridi et al., 2018), Dijkstra algorithm

(Reddy, 2013), and also Trémaux (Yew et al., 2011).

In this paper, it is reported that research using the

Trémaux algorithm is applied to a mobile robot that

has a job to find the route from the start position to

the target position automatically, it finds a path in an

unknown maze. For this need, the algorithm is

modified so that it can reach the target in the middle

of the maze. This research focuses on implementing

a small mobile robot designed to solve a maze using

the Trémaux algorithm.

Robot maze problems are based on decision-

making algorithms that are a very important field of

robotics. The mobile robot has the task of finding the

way to resolve a maze in the least amount of time and

using the shortest way (Elshamarka & Bakar Sayuti

Saman, 2012). It needs to navigate from a maze

corner to the center as quickly as possible (Semuil

Tjiharjadi, 2020).

The robot knows where the starting point is and

where the target is, but it needs to look for all the

information on the obstacles to reach the target. The

maze is made up of 25 square cells, each of which is

Tjiharjadi, S.

Design and Implementation of a Path Finding Robot using Modiﬁed Trémaux Algorithm.

DOI: 10.5220/0010744100003113

In Proceedings of the 1st International Conference on Emerging Issues in Technology, Engineering and Science (ICE-TES 2021), pages 39-48

ISBN: 978-989-758-601-9

Copyright

c

39

approximately 18 cm x 18 cm in size. The cells are

set up to form a labyrinth of 5 rows x 5 columns. A

cell at its angles is a starting location and the target

location is in the middle of the maze. Only one cell is

open to get past. Requirements for maze walls and

support platforms are given in the IEEE standard.

2 METHODS (AND MATERIALS)

The Trémaux algorithm, created by Charles Pierre

Trémaux, is a method invented to find a way out of a

maze. The way it works is to draw a line on the floor

to mark a path, being able to find an existing exit.

Only the path found by this algorithm is not

necessarily the closest route.

2.1 Trémaux Algorithm

Trémaux algorithm works according to the following

rules:

1. Every time the robot passes through the path, the

robot marks the path that is being traversed, so

that it is visible from both ends of the fork.

2. Check each lane when entering the lane, do not

enter the road that has been marked twice.

3. The robot can choose which path at a random

fork that does not have a mark.

4. When the Robot hits a dead end, it will turn back

through the road and re-mark the road so that the

road has two signs which means it doesn't need

to be crossed again.

5. The robot will always choose the path that has

the least marks.

There are three types of paths to the Trémaux

algorithm in total:

• Unmarked, which means the section has not been

explored,

• Marked once, which indicates that the line has

been crossed once,

• Marked twice, the robot has passed and is forced

to return because there is no way.

This algorithm is effective in finding a way out of

the maze, but it has several problems, such as

difficulty in drawing a line to mark a path in real life,

and then the path found to exit is not necessarily the

closest path.

To improve the Trémaux algorithm, researchers

added the Manhattan distance algorithm when path

selection was made. So that the selected path at the

branch is no longer chosen randomly, but is selected

based on the calculation of the Manhattan distance. In

simple terms, Manhattan Distance calculates the

distance by simplifying the distance between two

points as the sum of the absolute values of the two

coordinate distances (Shen et al., 2021).

𝑑1



𝑝,𝑞



=





|

𝑝𝑖 −𝑞𝑖

|

(1)

The use of the Manhattan distance helps the Robot

determine which branch to take, although it does not

mean that the branch is the closest path to the target,

at least it helps as a reference in choosing a path.

2.2 Robot Design

The robot in this study was designed to use a miniQ

2WD robot frame. The robot chassis is 122mm in

diameter, using a pair of wheels driven by a pair of

Direct Current (DC) motors as the main drive.

Figure 1: Robot chassis.

This robot can count the number of wheel

rotations because it is equipped with several rotary

encoders that are mounted on a DC motor.

Figure 2: Robot design.

ICE-TES 2021 - International Conference on Emerging Issues in Technology, Engineering, and Science

40

Figure 3: Robot system block diagram.

This robot can control the speed of movement and

is equipped with 3 infrared sensors to detect the

position of the front, right, and left of the labyrinth

wall. By using the AT Mega 324 microcontroller as a

control center to respond to input signals, it can run

the actuator based on the algorithm that has been

programmed. The flowchart of the main program is

shown in Figure 6.

2.3 Maze Layout

For testing purposes, a maze was designed that has a

cell size of 5 × 5 with a side length of 1.32 m2. Each

cell can be placed in a barrier that serves as a wall that

the robot needs to detect in its quest to find a path to

the target (Figure 4).

Figure 4: Maze arena.

The use of the Trémaux algorithm, which requires

marking line by line, is difficult in actual conditions.

Therefore, tagging is done by mapping using a two-

dimensional memory array with a size of 5x5. For this

purpose, two 5x5 memory arrays are designed, the

first array is used to store information on each cell

wall of the maze, while the second array stores the

tagging in each cell. The position of the robot

expressed in coordinates (row, column) is used to

calculate the Manhattan distance from the target

destination.

3 RESULTS AND DISCUSSION

The real robot was tested on an arena maze (no

software simulation) with a layout as shown in Figure

6. The robot started walking and marked the path by

updating the information on the cells in the memory

array. The robot started moving from the initial cell

(row 4, column 0) to the target cell (row 2, column 2)

and then returned to the starting cell. The robot's

initial orientation was facing North.

0,0 0,1 0,2 0,3 0,4

1,0 1,1 1,2 1,3 1,4

2,0 2,1 2,2 2,3 2,4

3,0 3,1 3,2 3,3 3,4

4,0 4,1 4,2 4,3 4,4 1

Figure 5: Coordinate Cell and Maze Arena Layout.

The following was one of the experiments carried out

by the robot from the starting point to the target point,

using the Trémaux algorithm and the Manhattan

distance. The robot position was marked as Yellow

and the destination was marked as Orange. Figure 6

shows the Labyrinth coordinates and a schematic of

the Robot's starting position (4,0). Whenever the

robot moves to a new cell, it would update the value

cell in the robot's memory. Cell value = 1 means that

the robot had only visited once.

Design and Implementation of a Path Finding Robot using Modiﬁed Trémaux Algorithm

41

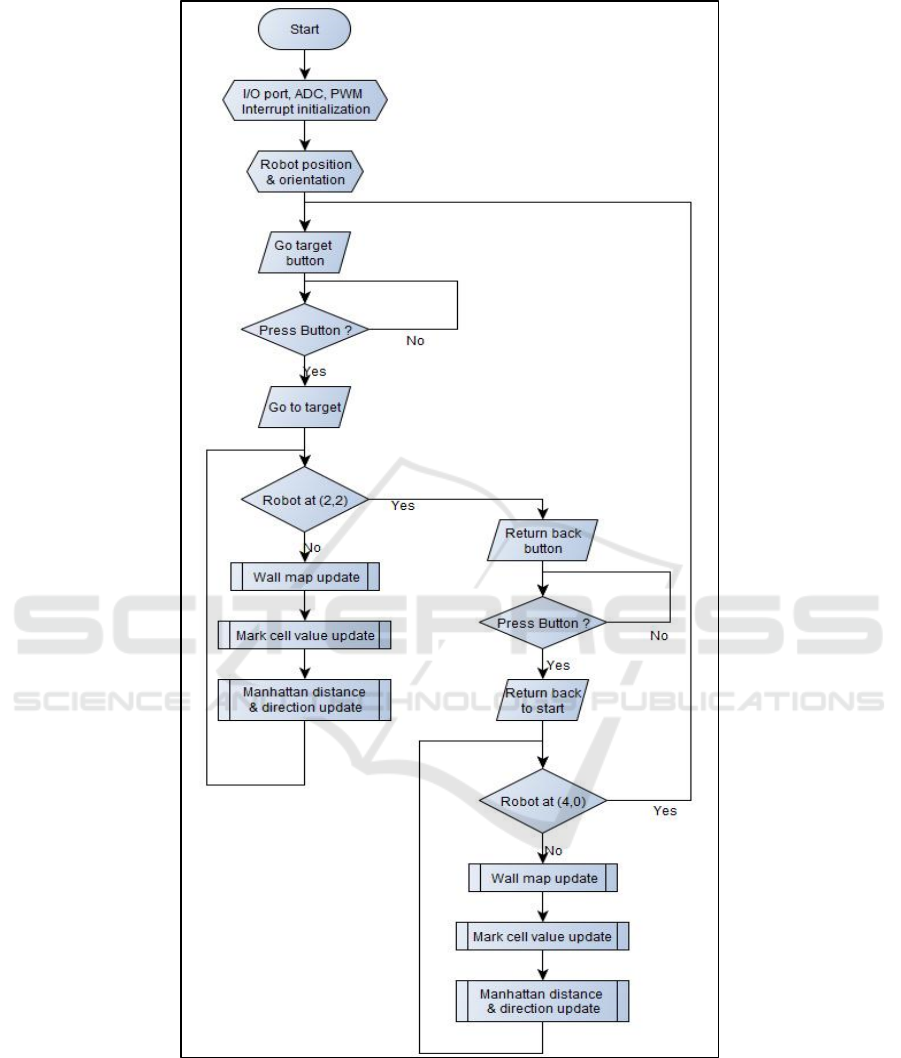
Figure 6: Flowchart of the main program.

When the robot arrives at an intersection, the robot

will compare the Trémaux cell value which marks

whether the route has been taken or not. The main

option is to choose a road that has never been traveled

(smaller Trémaux cell value), then if both cell update

values are the same, the smallest Manhattan distance

value will be selected from the available options.

Manhattan distance is the distance from a position to

a destination as a straight line.

ICE-TES 2021 - International Conference on Emerging Issues in Technology, Engineering, and Science

42

1

Figure 7: The Robot had only 1 choice and moved to (3,0)

and updated Trémaux cell value.

1 1

1

Figure 8: The Robot moved to (3,1) because the Manhattan

distance value of (3,1) was smaller than (2,0). Both have the

same Trémaux cell value.

1

1 1

1

Figure 9: The Robot moved to (2,1) because the Manhattan

distance value of (2,1) was smaller than (4,1). Both have the

same Trémaux cell value.

1

1 1

1

Figure 10: The Robot had only 1 choice and moved to (1,1)

and updated Trémaux cell value.

1 1

1

1 1

1

Figure 11: The Robot moved to (1,2) because the

Manhattan distance value of (1,2) was smaller than (1,0).

1

1 1

1

1 1

1

Figure 12: The Robot had only 1 choice and moved to (0,2).

1 1

1

1 1

1

Figure 13: The Robot had only 1 choice and moved to (0,1).

1 1 1

1 1

1

1 1

1

Figure 14: The Robot had only 1 choice and moved to (0,0).

Design and Implementation of a Path Finding Robot using Modiﬁed Trémaux Algorithm

43

2 2 1

1 1

1

1 1

1

Figure 15: The Robot found a dead end and returned to the

previous path and marked it with the value Trémaux +1 =

2. This means that it had been visited twice.

2 2 2

1 1

1

1 1

1

Figure 16: The Robot only had 1 choice and moved to (0,2).

2 2 2

1 2

1

1 1

1

Figure 17: The Robot only had 1 choice and moved to (1,2).

2 2 2

2 2

1

1 1

1

Figure 18: The Robot only had 1 choice and moved to (1,1).

2 2 2

1 2 2

1

1 1

1

Figure 19: The Robot moved (1,0) that never been visited.

2 2 2

1 2 2

1 1

1

Figure 20: The Robot moved to (2,0).

2 2 2

1 2 2

1 1

2 1

1

Figure 21: The Robot moved to (3,0) and marked it as 2.

2 2 2

1 2 2

1 1

1 2

1

Figure 22: The Robot moved to (3,1) because it had a

smaller Manhattan Distance value.

ICE-TES 2021 - International Conference on Emerging Issues in Technology, Engineering, and Science

44

2 2

1 2 2

1 1

1 2

1 1

Figure 23: The robot moved to (4,1), it had a smaller

Manhattan Distance value.

2 2 2

1 2 2

1 1

1 2

1 1 1

Figure 24: The Robot moved to (4,2) and updated Trémaux

value.

2 2 2

1 2 2

1 1

2 2 1

1 1 1

Figure 25: The Robot moved to (3,2) and updated Trémaux

value.

2 2 2

1 2 2

1 1 1

2 2 1

1 1 1

Figure 26: The Robot arrived at its destination (2,2) in 20

steps.

Figure 7 to Figure 26 shows the experiment of the

robot's journey using the Trémaux algorithm and

Manhattan Distance to reach the target point while

updating the Trémaux cell value. Each time the robot

is in a new cell, the robot updates the cell value

incremented by one. After the robot arrived at the

destination, then that point became the starting point,

and the starting point turned into the destination point

on the robot's return journey.

1

Figure 27: The Robot moved to (3,2) that had a smaller

Manhattan distance.

1

Figure 28: The Robot moved to (4,2) that had a smaller

Manhattan distance.

1

1 1

Figure 29: The Robot moved to (4,1) based on Trémaux

value.

1

1 1

Figure 30: The Robot moved to (3,2) that had a smaller

Manhattan distance.

Design and Implementation of a Path Finding Robot using Modiﬁed Trémaux Algorithm

45

1

1 1 1

1 1

Figure 31: The Robot moved to (3,0) that had a smaller

Manhattan distance than (2,1).

1

1 1 1

Figure 32: The Robot arrived at its destination in 6 steps.

Figures 27 to 32 show the robot returning to its

starting point. The destination point becomes the

starting point and the starting point becomes the

destination point on the robot's return journey. This

layout was also tested using the original Trémaux

algorithm without using the Manhattan distance

value. This experiment can be seen in table 1.

Table 1: Maze Exploration using only the Trémaux

algorithm.

Exp Status Routes

Number

of ste

p

s

1

Run

(4,0) → (3,0) → (2,0) →

(1,0) → (1,1) → (1,2) →

(0,2) → (0,1) → (0,0) →

(0,1) → (0,2) → (1,2) →

(1,1) → (2,1) → (3,1) →

(4,1) → (4,2) → (3,2) →

(

2,2

)

18

Return

back

(2,2) → (2,3) → (1,3) →

(1,4) → (0,4) → (0,3) →

(0,4) → (1,4) → (2,4) →

(3,4) → (4,4) → (4,3) →

(3,3) → (3,2) → (4,2) →

(4,1) → (3,1) → (2,1) →

(1,1) → (1,0) → (2,0) →

(3,0) → (4,0)

18

2 Run

(4,0) → (3,0) → (3,1) →

(4,1) → (4,2) → (3,2) →

(3,3) → (4,3) → (4,4) →

(3,4) → (2,4) → (1,4) →

(0,4) → (0,3) → (0,4) →

18

Exp Status Routes

Number

of ste

p

s

(1,4) → (1,3) → (2,3) →

(

2,2

)

Return

back

(2,2) → (2,3) → (1,3) →

(1,4) → (0,4) → (0,3) →

(0,4) → (1,4) → (2,4) →

(3,4) → (4,4) → (4,3) →

(3,3) → (3,2) → (4,2) →

(4,1) → (3,1) → (2,1) →

(1,1) → (1,2) → (0,2) →

(0,1) → (0,0) → (0,1) →

(0,2) → (1,2) → (1,1) →

(1,0) → (2,0) → (3,0) →

(4,0)

30

3

Run

(4,0) → (3,0) → (3,1) →

(4,1) → (4,2) → (3,2) →

(

2,2

)

6

Return

back

(2,2) → (3,2) → (3,3) →

(4,3) → (4,4) → (3,4) →

(2,4) → (1,4) → (0,4) →

(0,3) → (0,4) → (1,4) →

(1,3) → (2,3) → (2,2) →

(3,2) → (4,2) → (4,1) →

(3,1) → (3,0) → (4,0)

20

Table 1 shows that the use of the Trémaux

algorithm in maze exploration did not have the same

results, this is because the Trémaux algorithm was

developed from the Depth First Search algorithm.

Because it is more towards trial error, the Trémaux

algorithm will find a destination but not the shortest

path.

Figure 33: Another maze for the second experiment.

0,0 0,1 0,2 0,3 0,4

1,0 1,1 1,2 1,3 1,4

2,0 2,1 2,2 2,3 2,4

3,0 3,1 3,2 3,3 3,4

4,0 4,1 4,2 4,3 4,4

Figure 34: Coordinate cell and maze arena layout.

ICE-TES 2021 - International Conference on Emerging Issues in Technology, Engineering, and Science

46

The other experiment journey of this robot using

another layout can see table 2. Figure 33 shows

another maze for the second experiment and figure 34

shows the coordinate and maze layout. The robot

journey from starting point to the destination point

has been shown in table 2.

The robot in the second experiment still

prioritized the smallest Trémaux value and if the

Trémaux value was the same, the closest Manhattan

distance value would be used. The results of the

second experiment showed that the robot can choose

the closest route using a combination of the Trémaux

algorithm and the Manhattan distance value.

Combining the Trémaux algorithm with the

Manhattan distance has proven to be better than using

the Trémaux algorithm alone.

Table 2: Second Robot Experiment with another maze

layout.

Routes

Number

of steps

Run

(4,0) → (3,0) → (3,1) → (3,2) →

(3,3) → (2,3) → (2,2)

6

Return

back

(2,2) → (2,3) → (3,3) → (3,2) →

(3,1) → (3,0) → (4,0)

6

This experiment was carried out using a real robot

with a design as shown in Figure 2. Based on all

experiments, the use of infrared sensors has proven to

be effective in detecting obstacles. So, the robot can

explore the maze without any problems.

4 CONCLUSIONS

The design and implementation of robots using the

Trémaux algorithm can run a mobile robot to explore

the maze and map the existing paths. The use of the

Manhattan Distance algorithm can improve the

performance of the Trémaux algorithm to determine

the direction of travel, compared to only using the

Trémaux algorithm.

For further research, the use of the Trémaux

method can be improved by a combination of more

algorithms and also applications in larger mazes. This

research is expected to produce an effective algorithm

to operate in a wide unknown environment.

REFERENCES

Ansari, A., Sayyed, M. A., Ratlamwala, K., & Shaikh, P.

(2015). An Optimized Hybrid Approach for Path

Finding. International Journal in Foundations of

Computer Science & Technology, 5(2), 47–58.

https://doi.org/10.5121/ijfcst.2015.5205

Chu, P. M., Cho, S., Huang, K., & Cho, K. (2019). Flood-

fill-based object segmentation and tracking for

intelligent vehicles. International Journal of Advanced

Robotic Systems, 16(6), 1–11.

https://doi.org/10.1177/1729881419885206

Downey, S., & Charles, D. (2015). Distribution of artificial

intelligence in digital games. International Journal of

Intelligent Information Technologies, 11(3), 1–14.

https://doi.org/10.4018/IJIIT.2015070101

Elshamarka, I., & Bakar Sayuti Saman, A. (2012). Design

and Implementation of a Robot for Maze-Solving using

Flood-Fill Algorithm. International Journal of

Computer Applications, 56(5), 8–13.

https://doi.org/10.5120/8885-2882

Faridi, A. Q., Sharma, S., Shukla, A., Tiwari, R., & Dhar,

J. (2018). Multi-robot multi-target dynamic path

planning using artificial bee colony and evolutionary

programming in unknown environment. Intelligent

Service Robotics, 11(2), 171–186.

https://doi.org/10.1007/s11370-017-0244-7

Hoetama, D. J. O., Putri, F. P., & Winarno, P. M. (2019).

Algoritma Fisher-Yates Shuffle dan Flood Fill sebagai

Maze Generator pada Game Labirin. ULTIMA

Computing, 10(2), 59–64. https://doi.org/10.31937/

sk.v10i2.1064

Jabbar, A. (2016). Autonomous Navigation of Mobile

Robot Based on Flood Fill Algorithm. Iraqi Journal for

Electrical and Electronic Engineering, 12(1), 79–84.

https://doi.org/10.37917/ijeee.12.1.8

Kang, N. K., Son, H. J., & Lee, S. H. (2018). Modified A-

star algorithm for modular plant land transportation.

Journal of Mechanical Science and Technology.

https://doi.org/10.1007/s12206-018-1102-z

Kumar, N., & Kaur, S. (2019). A Review of Various Maze

Solving Algorithms Based on Graph Theory.

International Journal for Scientific Research &

Development, 6(12), 2–6. https://www.researchgate.net/

publication/331481380_A_Review_of_Various_Maze_

Solving_Algorithms_Based_on_Graph_Theory

Reddy, H. (2013). PATH FINDING - Dijkstra’s and A*

Algorithm’s. International Journal in IT and

Engineering, 1–15.

Shen, X., Yi, H., & Wang, J. (2021). Optimization of

picking in the warehouse. Journal of Physics:

Conference Series, 1861(1), 012100.

https://doi.org/10.1088/1742-6596/1861/1/012100

Tjiharjadi, S. (2019). Design and implementation of flood

fill and pledge algorithm for Maze Robot. International

Journal of Mechanical Engineering and Robotics

Research, 8

(4).

https://doi.org/10.18178/ijmerr.8.4.632-638

Tjiharjadi, S., & Setiawan, E. (2016). Design and

implementation of a path finding robot using flood fill

algorithm. International Journal of Mechanical

Engineering and Robotics Research, 5(3).

https://doi.org/10.18178/ijmerr.5.3.180-185

Tjiharjadi, S., Wijaya, M. C., & Setiawan, E. (2017).

Optimization maze robot using A* and flood fill

Design and Implementation of a Path Finding Robot using Modiﬁed Trémaux Algorithm

47

algorithm. International Journal of Mechanical

Engineering and Robotics Research, 6(5).

https://doi.org/10.18178/ijmerr.6.5.366-372

Tjiharjadi, Semuil. (2020). Performance comparison robot

path finding uses flood fill - Wall follower algorithm

and flood fill - Pledge algorithm. International Journal

of Mechanical Engineering and Robotics Research,

9(6), 857–864. https://doi.org/10.18178/ijmerr.9.6.857-

864

Yew, N. Z., Tiong, K. M., & Yong, S. T. (2011). Recursive

Path-finding in a Dynamic Maze with Modified

Trémaux Algorithm. Proceedings of International

Conference on Applied Mathematics and Engineering

Mathematics (ICAMEM), 5(12), 845–847.

Zikky, M. (2016). Review of A* (A Star) Navigation Mesh

Pathfinding as the Alternative of Artificial Intelligent

for Ghosts Agent on the Pacman Game. EMITTER

International Journal of Engineering Technology.

https://doi.org/10.24003/emitter.v4i1.117

ICE-TES 2021 - International Conference on Emerging Issues in Technology, Engineering, and Science

48