Decision Support System for Exported Grade Coffee Selection using

AHP and TOPSIS

Putu Indah Ciptayani

, Ni Gusti Ayu Putu Harry Saptarini

and Putu Manik Prihatini

Electrical Engineering Department, Politeknik Negeri Bali, Jalan Kampus Bukit Jimbaran, Badung, Indonesia

Keywords: Decision Support System, DSS, AHP, TOPSIS, Coffee Quality, Export Coffee.

Abstract: Coffee is one of the most famous commodities in the world. Indonesia is one of the largest coffee exporting

countries in the world. Determination of the quality of coffee for export follows the Indonesian National

Standard (SNI). In the SNI there are several criteria for determining the quality of export coffee. Each criterion

has its own nature and importance according to the preferences of the decision maker. This study aims to

apply the AHP and TOPSIS methods to build a decision support system (DSS) in selecting export coffee.

AHP was succeed in determine the weight of each criterion by building a pairwise comparison matrix between

criteria according to the preferences of the decision maker. The combination with TOPSIS was used to deal

with benefit and cost criteria. On the last step, TOPSIS was succeed in rank all the alternatives by determine

the closeness score of each alternative.

1 INTRODUCTION

Coffee is one of the most consumed beverages in the

world (Neves et al., 2011). The website

http://www.ico.org reported that coffee traded in the

world is mostly Arabica dan Robusta (ICO, 2021). By

October 2020 – May 2021, total Robusta traded

worldwide was 31.435.000 bags (36%), while

Arabica was 55.864.000 bags (64%). Based on the

report of production in each country, Indonesia is one

of the largest coffee producers after Brazil, Colombia

and Vietnam.

Indonesia has a national standard for coffee bean

quality. The assessment of the coffee beans takes

quite a long time. The decision-making process to

decide which coffee has better quality is also a

complex process. The challenge in decision-making

process is the subjective judgment. One of the

alternatives to simplify the process of multi criteria

decision making is to use the decision support system

(DSS). DSS was widely used to help the decision

maker (Belaid & Razmak, 2013).

There are many decision support system methods

that widely used recently. Simple Additive Weighting

(SAW)(Tanjung & Adawiyah, 2019), Analytic

https://orcid.org/0000-0002-6923-3852

https://orcid.org/0000-0002-4007-929X

https://orcid.org/0000-0001-7538-3235

Hierarchy Process (AHP)(Liu, 2017), Technique for

Order of Preference by Similarity to Ideal Solution

(TOPSIS)(Panda & Jagadev, 2018) and Promethee

(Taillandier et al., 2013) were the DSS method that

already implemented in real-life case. Most of DSS

use one method, but there was the study to combine

AHP and SAW conducted by Ciptayani et al.

(Ciptayani et al., 2018).

This study aims to build the decision support to

help the decision maker in deciding the Robusta

coffee quality to be exported. The coffee quality

assessment based on general and specific criteria

listed in SNI-01-2907-2008. The decision-making

process can be a complex and time consuming

because it involves multi criteria and alternatives.

Some criteria may have sub criteria, while each

criterion has their own weight based on the decision

maker preferences. Besides that, the criteria in coffee

quality assessment consists of two type, benefit and

cost. The selection of DSS method plays an important

role in order to build a great DSS.

The AHP method is one of the DSS method that

widely used. This method builds a comparison matrix

to define the weight of each criterion based on the

decision maker priority dan preferences. Demirtas et

Ciptayani, P., Saptarini, N. and Prihatini, P.

Decision Support System for Exported Grade Coffee Selection using AHP and TOPSIS.

DOI: 10.5220/0010939700003260

In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), pages 47-54

ISBN: 978-989-758-615-6; ISSN: 2975-8246

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

al. stated that comparing each criterion can guarantee

the result decision(Aktar Demirtas et al., 2015).

Recent study in AHP method conducted by Pujadi at

el. for teacher placement (Pujadi et al., 2017),

Hutasuhut et al. implemented AHP to find the best

restaurant (Hutasuhut et al., 2019), while Retrialisca

et al. using AHP on SBMPTN Try-Out (Retrialisca

et al., 2019). Considering that the criteria in coffee

quality assessment consist of benefit and cost criteria,

the method that deal with it was needed. TOPSIS

method calculated the closeness score of each

alternative and guaranteed that the best alternative has

the shortest distance to the positive ideal solution and

the farthest distance to the negative ideal solution

(Madi et al., 2016). The objective of this study is to

combine the AHP and TOPSIS method to build a DSS

in assessing quality of coffee to be exported. AHP

was used to comparing each criterion in order to get

the criteria weight, while TOPSIS was used to rank

each alternative based on the closeness score. The

combination of AHP and TOPSIS was study by

Iswari et al. (2019) to select the outstanding student

and Bagi et al. (2020) for high achieving student. Bagi

et al (2020) found that combining both methods can

speed up the selection process and making the results

more objective. Iswari et al. (2019) found that

combining AHP and TOPSIS was better than

TOPSIS.

2 METHODOLOGY

This study combining the AHP and TOPSIS to build

a DSS for coffee selection to be exported. The AHP

method was used to calculate the weight of criteria by

build the comparison matrix. Finally, TOPSIS was

implemented to rank the alternatives.

2.1 Analytic Hierarchy Process (AHP)

Every decision-making process has criteria and

alternatives. Although using the same criteria and

alternatives, the decision result may be different

between one decision maker and others. This can be

happened because each decision maker has their own

preference and priority. This study using AHP to

compare the priority of each criterion to other criteria

using comparison matrix. The AHP follows the steps

below (Qing, 2011):

Step 1: Build the comparison matrix A of each

criterion based on Saaty scale (Irvanizam, 2017)

Step 2: Build the the normalized comparison matrix

B using Equation 1

𝑏



=𝑎



𝑎











)

where n is the number of criteria, i,j = 1, 2, … n and

is the element of matrix A.

Step 3: Calculate the row-sum (v) of matrix B using

Equation 2

𝑣



= 𝑏









)

where n is the number of criteria, i = 1, 2, … n and b

is the element of matrix B.

Step 4: Normalize the v

to get the weight (W) of each

criterion using Equation 3

𝑤



=𝑣



𝑣











)

where n is the number of criteria, i = 1, 2, … n, and v

is the row-sum of i

criterion.

Step 5: Consistency check. This step is conducted to

guarantee that the matrix A inputted by user is

consistent. First of all, the eigen value (λ

max

) will be

calculated using Equation 4.

𝜆



=

∑

𝑎



𝑤







𝑛𝑤







)

where n is the number of criteria, a

is element of

matrix A, and w

is the weight of i

criterion.

The value of CI was calculated using Equation 5

𝐶𝐼=(𝜆



−𝑛)(𝑛−1

⁄

)

where n is the number of criteria and 𝜆



is the

eigen value.

The consistency ratio (CR) is calculated using the

Equation 6

𝐶𝑅=𝐶𝐼 𝑅𝐼

⁄

)

where RI is random index value. The RI value used in

this study was taken from(Franek & Kresta, 2014).

The matrix is considered to be consistent if the value

of CR was no more than 0.1.

2.2 Technique for Order of Preference

by Similarity to Ideal Solution

(TOPSIS)

TOPSIS method is one of the methods for DSS. The

coffee selection case in this study has two kinds of

criteria, named benefit and cost. The TOPSIS method

final result is the closeness score. The closeness score

indicates the distance of the alternative from the

positive and negative ideal solution. The positive

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

ideal solution maximizes the benefit criteria and

minimize the cost. On the other hand, the negative

ideal minimize the benefit criteria and maximize the

cost (Madi et al., 2016).

Consider there is matrix X

mxn

, where m is the

number of alternatives and n is the number of criteria.

The matrix element x

is the value of the i

alternative

in j

criterion. TOPSIS method follows the step

below (Pavić & Novoselac, 2013):

Step 1: Build normalized decision matrix R using

Equation 7.

𝑟



𝑥





∑

𝑥









(7)

Step 2: Build normalized weighted matrix (V) using

Equation 8

𝑣



=𝑤



𝑟



(8)

where w

(j= 1, 2, …n) is the weight of j

criterion.

Step 3: Determine the positive (A

) and negative (A

) ideal solution using Equation 9 and 10 respectively

𝑎





=

𝑚𝑎𝑥



𝑣



,𝑖𝑓 𝑐



𝑖𝑠 𝑏𝑒𝑛𝑒𝑓𝑖𝑡

𝑚𝑖𝑛



𝑣



,𝑖𝑓 𝑐



𝑖𝑠 𝑐𝑜𝑠𝑡

(9)

𝑎





=

𝑚𝑖𝑛



𝑣



,𝑖𝑓𝑐



𝑖𝑠 𝑏𝑒𝑛𝑒𝑓𝑖𝑡

𝑚𝑎𝑥



𝑣



,𝑖𝑓 𝑐



𝑖𝑠 𝑐𝑜𝑠𝑡

(10)

where c

is the j th criterion.

Step 4: Calculate the alternative distance (D) from A

and A

using Equation 11 and 12 respectively

𝐷







(𝑣



−𝑎





)







(11)

𝐷







(𝑣



−𝑎





)







(12)

Step 5: Calculate the closeness (C) using Equation 13

𝐶



=𝐷





(𝐷





+𝐷





)

⁄

(13)

the closeness score is the final score used to rank the

alternatives.

2.3 Combining AHP and TOPSIS

The combination of AHP and TOPSIS in this study is

expected to give the best result of DSS. The AHP

suits for determining the weight of criteria, while

TOPSIS will deal with the benefit and cost criteria to

rank the alternatives. Combination of these two

methods is shown in Figure 1. Before conducting the

TOPSIS, it is need to read all the alternatives and the

value/score of each alternative in each criterion. The

closeness score resulted by the TOPSIS method will

be sorted descending to rank the alternatives.

The flowchart of AHP step is shown in Figure 2.

The first step is to read all the priority of each

criterion compare to other criteria. The value of

Start

Calculate the criteria weight using AHP

Read alternative

More alternative?

Calculate the closeness score using TOPSIS

Sort the alternatives based on the closeness score

Finish

yes

Figure 1: The combination of AHP and TOPSIS.

Start

Finish

Build the comparison matrix

Build normalized comparison matrix based on Equation 1

Calculate the row-sum(v) using Equation 2

Calculate the criteria weight (W) using Equation 3

Calculate eigen value (lamda) using Equation 4

Calculate CI value using Equation 5

Calculate CR value using Equation 6

CR < 0.1?

yes

Read the priority comparison of criteria

AHP

Figure 2: The flowchart of AHP.

Decision Support System for Exported Grade Coffee Selection using AHP and TOPSIS

priority using Saaty scale (1-9). The decision maker

only needs to input the upper triangle of comparison

matrix, and the algorithm will automatically calculate

the rest. After the comparison matrix build, the next

step is followed all the step describe in the previous

section.

All of the steps in TOPSIS are shown in Figure 3.

Using criteria weight from AHP step, the normalized

weighted matrix was built. This matrix was used to

calculate the positive and negative ideal solution in

order to find the closeness score of each alternative.

Start

Finish

Build normalized decision matrix using Equation 7

Build normalized weighted matrix using Equation 8

Calculate positive and negative ideal solution using

Equation 9 and 10

Calculate the distance to ideal positive and negative

solution using Equation 11 and 12

Calculate closeness score using Equation 13

TOPSIS

Figure 3: The flowchart of TOPSIS.

3 RESULTS

3.1 Criteria and Data

All criteria used in this study was adapted from

Indonesia National Standard SNI 01-2907-2008

about coffee bean. The criteria consist of benefit

criteria: general criteria (C1), bean size (C2) and cost

criteria: grade (C3). The C1 has two sub criteria:

water content (G1) and dirt level/waste (G2). The

water content of coffee must be no more than 12.5%,

while the waste of coffee has to be less than 0.5%.

Water level was determined by calculating the

reduction in coffee weight before and after the drying

process in the oven. Waste was the percentage of

placenta, attached seeds (clusters), seed fragments,

skin fragments, flat seeds and twigs found in 1000

grams of coffee sample. The bean size was classified

in three category namely big (≥ 7.5 mm), medium (6.5

mm – 7.5 mm), small (5.5 mm – 6.5 mm). The grade

of coffee was determined by counting the imperfect

bean in 300 grams of coffee. This study used ten

alternatives. Table value of each alternative in every

criterion is shown in Table 1. Figure 4 shows the

multilevel tree of the coffee selection.

This study used ten alternatives for simulating the

algorithm performance. All of the alternatives was

wet processing Robusta from varied suppliers. Score

of alternatives in G1 and G2 will be normalized using

Equation 14 and 15. Table 2 shows the normalized

result and the final score of C1. Because the G1 and

G2 have the equal weight, so the C1 score is the

average of both G1 and G2. The value of each

criterion will be converted into scale of 1 to 5 and

shown in Table 3.

𝑥=



100 ,𝑖𝑓𝑤𝑎𝑡𝑒𝑟𝑐𝑜𝑛𝑡𝑒𝑛𝑡≤1%

𝑤𝑎𝑡𝑒

𝑟

𝑐𝑜𝑛𝑡𝑒𝑛𝑡

∗ 100,𝑖𝑓𝑤𝑎𝑡𝑒𝑟𝑐𝑜𝑛𝑡𝑒𝑛𝑡>1%

(14)

𝑥=



100 ,𝑖𝑓𝑑𝑖𝑟𝑡𝑙𝑒𝑣𝑒𝑙≤0.1%

𝑑𝑖

𝑟

𝑡

𝑙𝑒𝑣𝑒𝑙

∗ 100,𝑖𝑓 𝑑𝑖𝑟𝑡 𝑙𝑒𝑣𝑒𝑙>0.1%

(15)

Goal : Select coffee to be

exported

C1 : General

criteria

C2 : bean

size

C3 : grade

Alt 1 Alt 2 Alt 3 Alt n

Criteria

Alternatives

G1 : water

content

G2 : dirt

level/waste

Figure 4: The multilevel tree of coffee selection.

Table 1: Data of Alternatives.

Alternative

C2 C3

G1(%) G2(%)

Alt 1 10 0.32 Big 22

Alt 2 2 0.21 Bi

201

Alt 3 5 0.48 Medium 20

Alt 4 7 0.12 Bi

Alt 5 1 0.21 Big 8

Alt 6 1 0.25 Mediu

120

Alt 7 3 0.39 Mediu

Alt 8 4 0.10 Bi

Alt 9 8 0.10 Bi

Alt 10 11 0.18 Mediu

189

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

Table 2: The final score of C1.

Alternative G1 G2 C1

Alt 1 10.00 31.25 20.63

Alt 2 50.00 47.62 48.81

Alt 3 20.00 20.83 20.42

Alt 4 14.29 83.33 48.81

Alt 5 100.00 47.62 73.81

Alt 6 100.00 40.00 70.00

Alt 7 33.33 25.64 29.49

Alt 8 25.00 100.00 62.50

Alt 9 12.50 100.00 56.25

Alt 10 9.09 55.56 32.32

Table 3: The criteria conversion value.

Alternative C1 C2 C3

Alt 1 2 5 1

Alt 2 3 5 5

Alt 3 2 3 1

Alt 4 3 5 3

Alt 5 4 5 1

Alt 6 4 3 4

Alt 7 2 3 1

Alt 8 4 5 3

Alt 9 4 5 2

Alt 10 2 3 5

3.2 Criteria Weight using AHP

The AHP calculate the criteria weight by build the

comparison matrix A. First of all, user have to input

the priority of one criterion compare to others using

Saaty scale. Figure 5 shows the comparison matrix of

each criterion. Based on Saaty scale, the criteria C1 is

almost absolutely important than C2 as the value of

A(1,2) = 8. On the other hand, the value of element

A(2,1) will be 1/8.

The normalized comparison matrix B will be build

using Equation 1. The matrix B is shown in Figure 6.

The value of each element is equals to the value of the

corresponding element in matrix A divided by the

sum of corresponding column. For example:

B(1,1) = A(1,1)/ (A(1,1) + A(1,2) + A(1,3))

B(1,1) = 1/ (1 + 1/8 + 1/5) = 0.75

After the normalizing the comparison matrix, the

row-sum (V) will be calculated using Equation 2. The

matrix V is shown in Figure 7. The element of V(1,1)

equals to the sum of B(1,1), B(1,2) and B(1,3), so

B(1,1) = 0.75 + 0.67 + 0.79 = 2.21.

The weight of each criteria W can be calculated

from V using Equation 3. The weight of criteria is

calculated by dividing the corresponding in V by the

sum of all V element. The weight of each criteria is

shown in Figure 8.

One of the advantages of AHP is the guarantee of

consistency input from decision maker. To ensure

that the priority inputs is consistent, then the

consistency ratio (CR) will be calculated. The first

step to get CR is to calculate the λ

max

based on

Equation 4. The matrix X consist of element from

matrix V divided by the corresponding W multiply by

the number of alternatives. For example X(1,1) =

V(1,1)/(W(1,1)*n) = 2.21/(0.74*3) = 1.032. The

matrix X is shown in Figure 9. The value of λ

max

1.032 + 1.003 + 1.009 = 3.045

𝐴=

𝐶1

𝐶2 𝐶3

𝐶1

𝐶2

𝐶3







Figure 5: Comparison matrix of each criterion.

𝐵=

𝐶1

𝐶2 𝐶3

𝐶1

𝐶2

𝐶3



0.75 0.67

0.79

0.09 0.08

0.15 0.25

0.05

0.16



Figure 6: Normalized comparison matrix.

𝑉=

𝐶1

𝐶2

𝐶3



2.21

0.23

0.56



Figure 7: Normalized comparison matrix.

𝑊=

𝐶1

𝐶2

𝐶3



0.74

0.08

0.19



Figure 8: Weight matrix.

𝑋=

𝐶1

𝐶2

𝐶3



1.032

1.003

1.009



Figure 9: Matrix X.

The next step is to calculate the value of CI based on

Equation 5.

CI = (λ

max

-n)/(n-1)

CI = (3.045 -3)/(3-1)

CI = 0.02

The last step is to calculate the value of CR using

Equation 6. The value of RI for n = 3 is 0.58, so the

CR is:

CR = CI/RI

CR = 0.02/0.58 = 0.04

Because CR is below 0.1, then the input of

comparison matrix is considered to be consistent and

the weight W can be used for the next step.

Decision Support System for Exported Grade Coffee Selection using AHP and TOPSIS

3.3 Alternative Rank using TOPSIS

The first step in TOPSIS is to build the normalized

decision matrix R. To make it easy to read, the matrix

was described as a table. The normalized decision

matrix was build using Equation 7. The matrix R was

built from the Table 3. To build matrix R, there were

some steps as follow:

1. Square all the element in Table 3;

2. Summing all the element in column and store

the value as s

;

3. Calculate the square root of s

and store it as t

;

4. The value of R is equals to the corresponding

element in Table 3 divided by t

corresponding column (in the same criterion).

The next step is to build the weighted normalized

matrix (V) based on Equation 8. The value of elemen

V shown in Table 4 is calculated from the

multiplication of the corresponding element in matrix

R and the corresponding weight of criteria (w

) from

the Figure 8.

Positive (A

) and negative (A

) ideal solution is

calculated using Equation 9 and 10 respectively.

Because C1 and C2 are benefit criteria, then the

positive ideal solution will be the maximum value of

all alternative in the corresponding criterion from

matrix V (Table 4), while for C3 as the cost criteria,

the positive ideal solution is the minimum value. The

value of A

is the vice versa. Figure 10 show the value

of A

and A

Table 4: The weighted normalized matrix.

Alternative C1 C2 C3

Alt 1 0.298 0.141 0.019

Alt 2 0.670 0.141 0.486

Alt 3 0.298 0.051 0.019

Alt 4 0.670 0.141 0.175

Alt 5 1.191 0.141 0.019

Alt 6 1.191 0.051 0.311

Alt 7 0.298 0.051 0.019

Alt 8 1.191 0.141 0.175

Alt 9 1.191 0.141 0.078

Alt 10 0.298 0.051 0.486

Figure 10: Positive and negative ideal solution.

Table 5: The distance to positive and negative ideal

solution.

Alternative D

Alt 1 0.89332 0.89332

Alt 2 0.69914 0.69914

Alt 3 0.89785 0.89785

Alt 4 0.54377 0.54377

Alt 5 0.00000 0.00000

Alt 6 0.30492 0.30492

Alt 7 0.89785 0.89785

Alt 8 0.15537 0.15537

Alt 9 0.05826 0.05826

Alt 10 1.01163 1.01163

Table 6: The ranking and closeness score.

Rankin

Alternative Closeness

1 Alt 5 1.00

2 Alt 9 0.94

3 Alt 8 0.86

4 Alt 6 0.75

5 Alt 4 0.48

6 Alt 2 0.35

7 Alt 1 0.35

8 Alt 3 0.34

9 Alt 7 0.34

10 Alt 10 0.00

The distance of the alternative in to the A

) and

) is calculated using Equation 11 and 12

respectively and shown in Table 5. The step to

calculate the distance is as follow:

1. Substract the value of matrix v

i,j

in Table 4 by

the corresponding a

for positive distance a

for negative one, then store the value in e

i,j

;

2. Square the value of e

i,j

;

3. The distance of alternative Alt

from the A

the square root of the sum all from the e

i,j

the corresponding alternative.

The last step is to calculate the closeness score based

on Equation 13. The ranking of alternatives and

closeness score is shown in Table 6.

3.4 Discussion

The analysis is done by building a chart of the

closeness score and a chart of the value of each

alternative on the criteria. The chart of the closeness

score in Figure 11 shows that Alternative 5 be the 1

rank, followed by Alternatives 9 and 8 respectively.

The chart in Figure 12 show that the four alternatives

have the same score on criteria C1 and C2. For the

score on criteria C1, the three alternatives have the

highest score compared to other alternatives (except

for Alternative 6). Because the C1 criterion has a

much higher weight than the other criteria, it is make

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

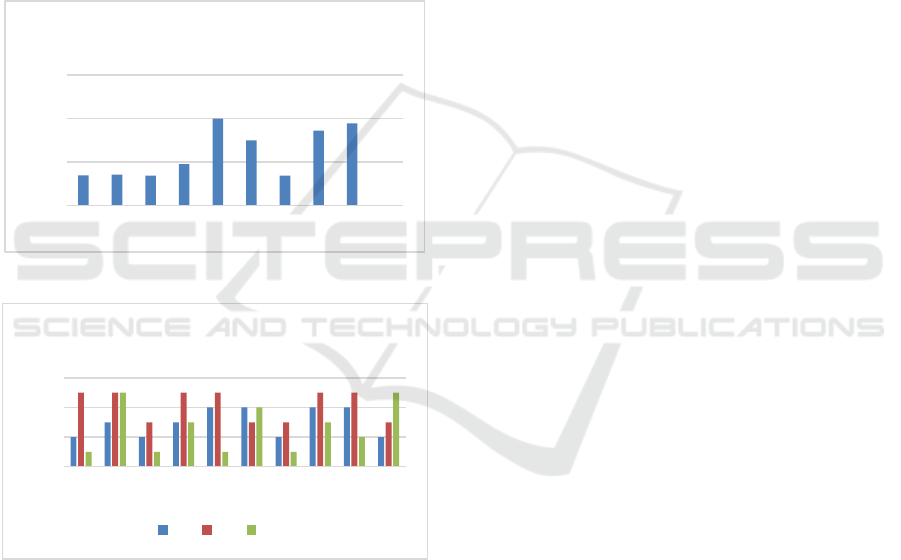
sense that alternatives with a high score in C1 will

have a greater chance of to be in the top rank. C3

weight is higher than C2, although not as high as C1,

but this will affect rankings. Because of the same

score in C1 and C2, then the score in C3 will affect

the ranking order of the three alternatives. In this case

Alternative 5 becomes the 1

rank because the value

of C3 is the lowest, then followed by Alternative 9

and finally Alternative 8. The value of C3 is cost, so

the bigger the value, the lower the ranking.

Alternative 6 becomes the 4

rank, although its C1

score is the same as the three other alternatives in the

top position, but the high C3 and lower C2 scores

make Alternative 6 rank below the other three

alternatives.

Figure 11: The closeness chart.

Figure 12: The score of all alternatives in each criterion.

Although C1 has a much higher weight than the

other two criteria, it is clear that ranking is not always

the same as the value of C1. For example, the score

of C1 for Alternative 2 is one level greater than

Alternative 1, but it turns out that Alternative 2 and

Alternative 1 have the same closeness value. This

shows that the other two criteria, C2 and C3 still play

a role in determining the ranking, although they are

not as strong as C1. Alternative 2 has a much higher

C3 value than Alternative 1.

From the chart that has been described, it can be

seen that the C1 criterion has a significant weight

compared to the other two criteria in determining the

ranking of an alternative. However, the other two

criteria still have a contribute in determining the

ranking, so that the ranking is not always in line with

the C1 criteria.

4 CONCLUSIONS

Decision support systems (DSS) can provide

recommendations for decision makers according to

their preferences against existing criteria. This study

aims to build a DSS for the selection of export coffee.

The method used in this research was AHP and

TOPSIS. AHP was used to determine the weight of

the criteria based on input in the form of priority by

users following the Saaty scale. The calculated

weights by AHP were used for rank all alternatives

using TOPSIS. TOPSIS resulted the closeness score

that guarantee the alternative have closest distance to

the positive ideal solution and the furthest from the

negative ideal solution. The combination of these two

methods has succeeded in building DSS and

providing recommendations in the form of ranking

alternatives according to the preferences of decision

makers and the value of each alternative. The best

closeness score was Alternative 5 with the final score

1. This final score is achieved because the value of C1

as the most significant benefit criteria was high and

the criteria C3 as the cost criteria was low. System

development still has to be done. System testing

needs to be done by making detailed and clear test

scenarios, so that the tester will be able to test the DSS

correctly and structured.

ACKNOWLEDGEMENTS

We sincerely thank to the Politeknik Negeri Bali for

the research fund through the agreement with.

REFERENCES

Aktar Demirtas, E., Buruk, Y., & Sağır, M. (2015). a Multi-

Criteria Job Evaluation Method for a State Bank.

International Journal of the Analytic Hierarchy

Process, 7(2). https://doi.org/10.13033/ijahp.v7i2.264

Bagi,Y. S., Suyono, S. & Tomatala, M. F. (2020). Decision

Support System for High Achieving Students Selection

Using AHP and TOPSIS. 2020 2nd International

Conference on Cybernetics and Intelligent System

0,00

0,50

1,00

1,50

A1 A2 A3 A4 A5 A6 A7 A8 A9 A10

Closeness

0,00

2,00

4,00

6,00

A1 A2 A3 A4 A5 A6 A7 A8 A9 A10

Alternative Score

C1 C2 C3

Decision Support System for Exported Grade Coffee Selection using AHP and TOPSIS

(ICORIS), 1-5, https://doi:10.1109/ICORIS50180

.2020.9320823

Belaid, A., & Razmak, J. (2013). Multi-Criteria Decision

Support Systems: A glorious history and a promising

future C3 - 2013 5th International Conference on

Modeling, Simulation and Applied Optimization,

ICMSAO 2013. https://www.scopus.com/inward/rec

ord.uri?eid=2-s2.0-84881409317&doi=10.1109%2FI

CMSAO.2013.6552678&partnerID=40&md5=651660

7cf04f36dce0d8f4efb62799cd

Ciptayani, P. I., Saptarini, N. G. A. P. H., Santiary, P. A.

W., & Astawa, I. N. G. A. (2018). Decision Support

System for Tourist Destination using the Combination

of AHP and SAW. Proceedings - 2nd East Indonesia

Conference on Computer and Information Technology:

Internet of Things for Industry, EIConCIT 2018, 271–

275. https://doi.org/10.1109/EIConCIT.2018.8878638

Franek, J., & Kresta, A. (2014). Judgment Scales and

Consistency Measure in AHP. Procedia Economics and

Finance, 12(March), 164–173. https://doi.org/10.101

6/s2212-5671(14)00332-3

Hutasuhut, D. I. G., Adhar, D., Alfma, O., Nasution, A. B.,

& Ginting, E. (2019). Decision Support System for

Finding the Best Restaurant Using AHP Method. 2018

6th International Conference on Cyber and IT Service

Management, CITSM 2018, Citsm, 6–10.

https://doi.org/10.1109/CITSM.2018.8674269

ICO, I. C. O. (2021). Coffee year production by country.

Data, May 2021(August), 7–9.

Irvanizam, I. (2017). Multiple attribute decision making

with simple additive weighting approach for selecting

the scholarship recipients at Syiah Kuala university.

Proceedings - 2017 International Con. on Electrical

Engineering and Informatics: Advancing Knowledge,

Research, and Technology for Humanity, ICELTICs

2017, 2018-January(October 2017), 245–250.

https://doi.org/10.1109/ICELTICS.2017.8253272

Iswari, V., Arini, F., & Muslim, M. (2019). Decision

Support System for the Selection of Outstanding

Students Using the AHP-TOPSIS Combination Method.

Lontar Komputer: Jurnal Ilmiah Teknologi Informasi,

40-48. https://doi:10.24843/LKJITI.2019.v10.i01.p05

Liu, H. & Qi,F. (2017). Analytic hierarchy process based

judgment model of highly cited papers in journal. IEEE

2nd International Conference on Big Data Analysis

(ICBDA) 2017, 649-652, https://doi.org/10.1109/ICB

DA.2017.8078716.

Madi, E. N., Garibaldi, J. M., & Wagner, C. (2016). An

exploration of issues and limitations in current methods

of topsis and fuzzy TOPSIS. 2016 IEEE International

Conference on Fuzzy Systems, FUZZ-IEEE 2016,

2098–2105. https://doi.org/10.1109/FUZZ-IEEE.2016.

7737950

Neves, M. F., Trombin, V. G., Lopes, F. F., Kalaki, R., &

Milan, P. (2011). World consumption of fruit juices,

nectars, and still drinks. The Orange Juice Business,

119–119.https://doi.org/10.3920/978-90-8686-739-4_32

Panda, M., & Jagadev, A. K. (2018). TOPSIS in Multi-

Criteria Decision Making: A Survey. Proceedings - 2nd

International Conference on Data Science and

Business Analytics, ICDSBA 2018, 51–54.

https://doi.org/10.1109/ICDSBA.2018.00017

Pavić, Z., & Novoselac, V. (2013). Notes on TOPSIS

Method. International Journal of Research in

Engineering and Science, 1(2), 5–12.

https://www.researchgate.net/publication/285886027_

Notes_on_TOPSIS_Method%0Awww.ijres.org

Pujadi, T., Fathurrozi, A., & Theresia, S. (2017). Using

Analytical Hierarchy Process for the decision support

system in teacher placement. Proceedings of 2016

International Conference on Information Management

and Technology, ICIMTech 2016, November, 182–187.

https://doi.org/10.1109/ICIMTech.2016.7930326

Qing, K. (2011). A Research on the Entrepreneurial

Opportunity Identification Based on the AHP-TOPSIS

Method. Proceedings of the 8Th International

Conference on Innovation and Management, 650–655.

Retrialisca, F., Effendi, Y. A., & Nuzulita, N. (2019).

Decision Support System and Recommendation on

SBMPTN Try-Out with Analytic Hierarchy Process

(AHP). Proceedings - 2019 International Conference

on Computer Science, Information Technology, and

Electrical Engineering, ICOMITEE 2019, 1, 169–174.

https://doi.org/10.1109/ICOMITEE.2019.8921040

Taillandier, P., Stinckwich, S., Taillandier, P., Stinckwich,

S., Taillandier, P., & Stinckwich, S. (2013). Using the

PROMETHEE multi-criteria decision making method

to define new exploration strategies for rescue robots

To cite this version : Using the PROMETHEE Multi-

Criteria Decision Making Method to Define New

Exploration Strategies for Rescue Robots. 321–326.

Tanjung, D. Y. H., & Adawiyah, R. (2019). Optimizing

Selection of Decision Support System with Fuzzy

Simple Additive Weighting. 2018 6th International

Conference on Cyber and IT Service Management,

CITSM 2018, Citsm, 1–4. https://doi.org/10.1109

/CITSM.2018.8674360

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science