Numerical Study the Effect of Undulation to Mitigate Erosion Elbow

Sultana Yafita Mawaddah, Lohdy Diana and Hendrik Elvian Gayuh Prasetya

Power Plant Engineering, Politeknik Elektronika Negeri Surabaya, Surabaya, Indonesia

Keywords: Erosion, Wear, Sand, Elbow, CFD, Computational Fluid Dynamics.

Abstract: Wear is a problem that is often encountered in the production process. It can cause erosion in the production

section of the pipe. Wear and tear can cause erosion resulting in leakage in the pipe, so it is necessary to

predict erosion on the elbow pipe. In this study, CFD modeling on ANSYS 19.1 application was used to

predict erosion in air flow with variations in undulation and combined with a twist configuration can reduce

erosion in the elbow pipe. This is to determine whether the modeling with a certain number of undulation and

combined with a twist configuration can reduce erosion in the elbow pipe. Changes in flow greatly affect the

rate of erosion because they can affect the interaction of particles with the wall and the speed of impact. The

final result of this research is that the pipe with the 3-undulation variation reduces erosion by 38%, while the

pipe with the 5-undulation variation reduces erosion by 22% compared to the planned pipe.

1 INTRODUCTION

Wear is a problem that is often encountered in the

production process. This is because it can cause

erosion in the production section of the pipe. The

process is repeated over and over again, resulting in

the pipe will often experience friction and pressure

with coal particles. Coal particles gain momentum

from the fluid passing through the flow path and

impacting the walls, resulting in erosion (Yudhatama,

Purbawanto, and Jatimurti 2018). Pneumatic particles

that move generally can trigger the erosion process

and impact the wall. The impact produces particle

interactions (Duarte and de Souza 2017). In addition,

the mixture of gases and sand particles passing

through the pipe combined with the velocity and

nature of the fluid creates a risk for different

equipment. Therefore, it is expected to be able to

predict erosion accurately (Strømme 2015).

A simulation was carried out in this study to

determine the erosion rate at the pulverizer outlet pipe

using 4-undulation and 8-undulation variations.

Undulation is a waveform in a pipe by combining

similar circles and varying in several angles. This

aims to determine the pipe location that may

experience the earliest leakage due to coal and the

best geometry to reduce erosion. Then the results of

this study can then be used as a reference to prevent

erosion on pipe elbows in various industries.

2 NUMERICAL METHOD

Computational Fluid Dynamics (CFD) is the art of

replacing integral and partial differential equations

into discrete algebraic equations, which can then be

solved to obtain solutions in the form of flow values

at discrete points of space and time (Anderson 1995).

In the case of air fluid flow using sand, the CFD

model equation is used. (Diana et al. 2020)

2.1 Flow Modelling

Flow modeling is the first step in the erosion

prediction stage using CFD to solve the Navier-

Stokes equation or adjust the fluid motion equation.

In most circumstances, the fluid flow through the pipe

is critically affected by the presence of the pipe wall.

The no-slip condition between the fluid and the wall

causes a change in the mean velocity field in the near

wall region, where viscous damping and kinematic

blocking reduce the velocity and normal fluctuations

near the wall. However, a large gradient in the mean

velocity causes the production of turbulent kinetic

energy which consequently builds up turbulent flow

towards the center of the pipe as the fluid flow

approaches the core region of the pipe (Wee and Yap

2019).

Mawaddah, S., Diana, L. and Prasetya, H.

Numerical Study the Effect of Undulation to Mitigate Erosion Elbow.

DOI: 10.5220/0010945400003260

In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), pages 339-347

ISBN: 978-989-758-615-6; ISSN: 2975-8246

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

339

2.2 Secondary Phase Modelling

Discrete phase modeling was chosen to model the

secondary phase because the volume fraction of sand

in the fluid flow is below 10% (Wee and Yap 2019).

The particle trajectory is calculated by integrating the

particle motion under the Lagrangian frame of

reference, where the drag force, pressure gradient

force, and buoyancy forces are considered as follows:





⃗





⃗





⃗





⃗





⃗

)

Drag force F





⃗

is the force resulting from the

interaction between solid particles and a continuously

moving fluid. Of all the resulting particle forces, the

hydrodynamic or drag force F





⃗

has the dominant

effect on determining the trajectory of the particle.

The equation F





⃗

is given as follows:





⃗

18μ









(u

⃗

−u





⃗

)

(2)

Where C



is the drag coefficient and Re



is the

Reynold number of the particle. The values of C



and



are obtained by the following equation:



= a













(3)



ρd



u



⃗

−u





⃗



(4)

Where a



, a



dan a



are constant smooth spherical

particles. F





⃗

is the pressure gradient force of the

particles with the exchange of pressure between

particles. The equation governing F





⃗

is:





⃗

= 



∇P

(5)

The Buoyancy Force is the force that holds the

particles from the fluid, the equation that governs the

Buoyancy Force is:





⃗

= 



− ρ





g

⃗

(6)

Particle dispersion due to turbulence in the fluid

phase can be corrected using the stochastic tracking

model (Wee and Yap 2019).

3 PARTICLE WALL

INTERACTION

For non-rotating particles, the interaction of the

particles with the wall causes a loss of energy due to

the inelastic impact with the wall. This causes the

particle to bounce off the boundary as its momentum

changes. The change in momentum is defined as the

coefficient of restitution. The normal coefficient of

restitution is the sum of the momentum in the

direction normal to the wall that holds the particle

after collision with the boundary. Similarly, the

tangential coefficient of restitution is the sum of the

momentum in the direction tangential to the wall

holding the particle. The effects of particle behavior

with walls were described in the application of the

Forder Rebound Model. The Ford Rebound Model

was chosen based on the type of collision used, which

is sand and iron particles (Wee and Yap 2019). It is

possible more stable to predict the interaction of the

particles with the walls in this final project.

4 EROSION MODELLING

The equation used is a variation of the speed and

impact angel performed by Oka and Yoshida. The

equation uses a model based on the same material at

varying speeds. In the Oka equation (Oka, Okamura,

and Yoshida 2005), the erosion damage is written as:

𝐸

(

𝑎

)

=𝑔(𝑎)𝐸



(7)

Where 𝑔(𝑎) is the impact angle using

trigonometric functions and initial Vickers hardness

(Hv). n1 and n2 are exponents obtained from eroded

material hardness and other impact conditions.

𝑔

(

𝑎

)

(

𝑠𝑖𝑛𝑎

)



1 + 𝐻𝑣

(

1−𝑠𝑖𝑛𝑎

)





(8)

is a representation of erosion at the normal

collision angle, it is related to the impact speed,

particle diameter, and the hardness of the eroded

material. Then the equation is:

𝐸



=81.714 𝐻𝑣

.

(

𝑈𝑝

𝑈𝑟𝑒𝑓

)



(

𝐷𝑝

𝐷𝑟𝑒𝑓

)



(9)

𝑈𝑝 and 𝐷𝑝 are the impact velocity and diameter,

while 𝑈𝑟𝑒𝑓 and 𝐷𝑟𝑒𝑓 are references to the impact

velocity and diameter as described by Oka (Oka,

Okamura, and Yoshida 2005). While k2 is the

exponent of eroded material hardness and property of

the particle. For k3 is a parameter taken from the

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

340

property of the particle. Thus, the erosion rate can be

calculated with the desired wall domain with the

equation:

𝐸𝑓=

𝐴

𝑓

𝑚



𝐸(𝑎)



()

(10)

Where 𝐴𝑓 is the wall surface area, 𝑚



is the

particle flow rate and 𝐸𝑓 is the erosion ratio.

5 CFD MODELLING

5.1 Geometry

Undulation is a waveform with settings on the

number of loops configured with angle settings. In

this final project, 3-undulation and 5-undulation

configurations are used and make a pipe that twists

along the inlet flow of the elbow pipe.

Figure 1: Pipe section scheme with 3 undulation.

Figure 2: Pipe section scheme with 5 undulation.

Table 1: Pipe Properties.

Properties Value unit

Elbow pipe diameter 76.2 mm

Elbow pipe inlet length 1000 mm

Elbow pipe outlet length 600 mm

Elbow pipe radius 90

114.3 mm

6 MESHING

Meshing is an important stage in CFD, this is because

meshing divides the components to be analyzed into

smaller elements. In general, the cell shape of

meshing is divided into 4 shapes for 3D geometry,

namely tetrahedron, pyramid, triangular prism, and

hexahedron.

Table 2: Comparison of the number of cells for each

variation.

Pipe Type

Number of

cell

Element

quality

Plan pipe 464662 0.45123

3-undulation pipe 540129 0.39183

5-undulation pipa 539532 0.52148

Meshing on the elbow will use a hexahedron cell

shape. This is because it shows that the use of the

hexahedron shape has a good mesh size value

(a)

(b)

Figure 3: Pipe section scheme mesh.

(a)

(c)

(

)

(c)

(b)

Numerical Study the Effect of Undulation to Mitigate Erosion Elbow

341

7 BOUNDARY CONDITION

The boundary condition is the boundary condition of

the mathematical equation and analysis is used.

Boundary conditions are used as parameters to be

executed by FLUENT.

Table 3: Boundary condition.

Boundar

condition Set up

Inlet

Velocity inlet

DPM, discreate phase

BC t

pe : escape

Wall

Solid material :

aluminiu

Outle

Pressure outle

8 MATERIAL PROPERTIES

There are two properties used, as shown in Table 4

and Table 5. The study used air-fluid and sand

injection.

Table 4: Air-Fluid Properties.

Material

Velocity

(m/s)

Viscosity

(Kg/ms)

Density

(Kg/m

)

Air 80

1.8 × 10



1.125

Table 5: Sand Properties.

Properties Value Unit

Shape Factor 0.53 -

min

65 µm

max

360 µm

mean

177 µm

Spread diameter (n) 4.10 -

Density 2650 Kg/m

9 SET UP

Initial setup is an important stage in the simulation.

This is because the setup is a process in choosing the

right model for the case. In this study, the commercial

program ANSYS Workbench 19.1 was used with the

Fluid Flow (Fluent) package. FLUENT settings as

follows:

Table 6: Set Up Fluent.

Solver

Pressure-Based Steady State

Solve

Solution

Scheme

SIMPLE algorithm (Segregated)

Spatial

Discretization

Gradient

Least Squares

Cell Based

Pressure Second Orde

Momentum

Second Order

Upwin

Specific

Dissipation

rate

Second Order

Upwind

Reynold

Stresses

Second Order

Upwin

Table 7: Set Up Fluid Properties.

Fluid air

Thermal -

Multiphase -

Model Turbulent

Realizable k-𝜀

Near-wall treatment Scalable wall function

Fluid viscosity 1.8 E-05 [kg/ms]

Velocity inlet 80 [m/s]

Wall condition No slip, smooth wall

Gravity 9.81 [m/s

]

Particle flow rate 0.78 [m/s]

Temperature 25

[C]

Pressure 101325 [Pa]

Density 1.18 [kgm

-3

]

Table 8: Set Up Sand Properties.

Injection type surface

Erosion model Oka

Drag law Spherical

Distribution Diameter Uniform

10 RESULT AND DISCUSSION

10.1 Mesh Independence

Mesh independence is based on the erosion ratio

value in ANSYS Workbench 19.1. From all the mesh

variations, the best variation will be chosen by

considering the situation in the simulation. Mesh

independence in this study project uses 4 variations

of mesh, namely:

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

342

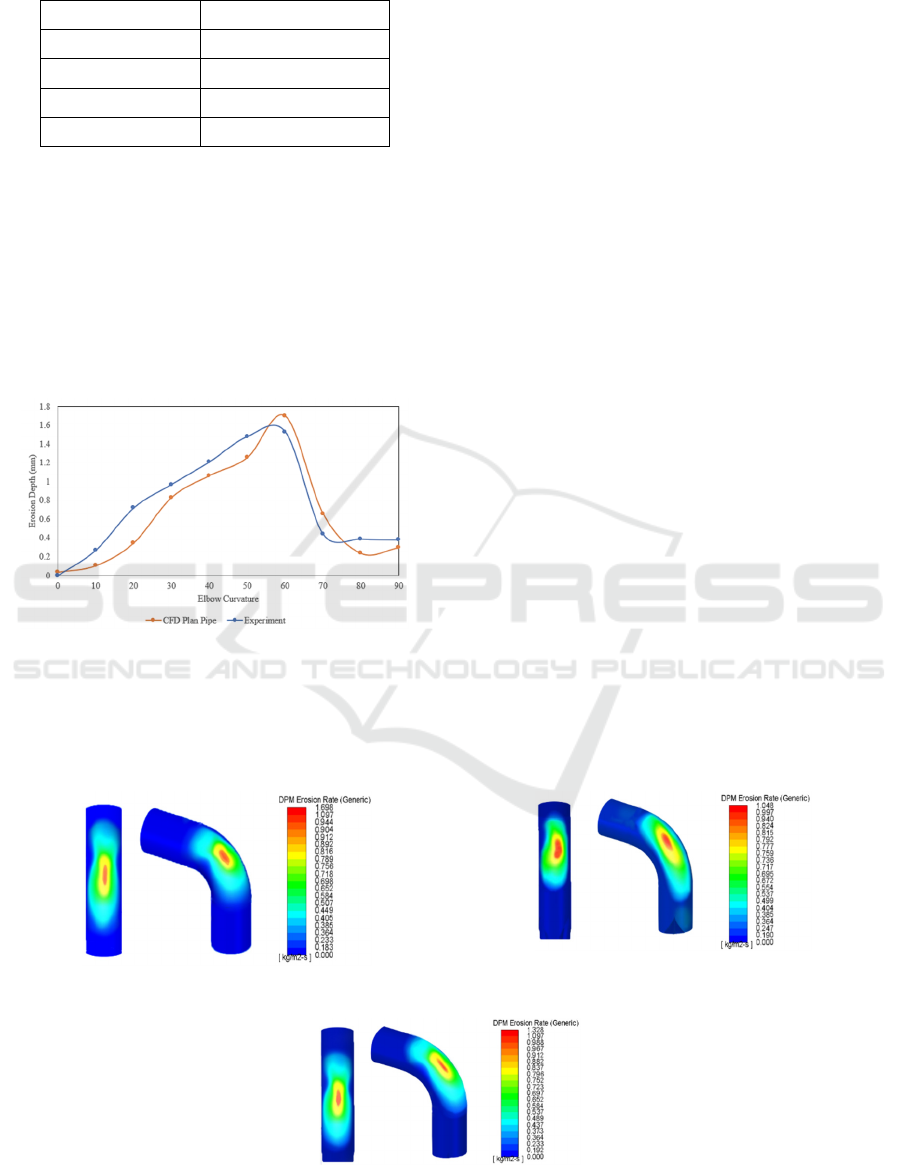
Table 9: Mesh independence.

Mesh Cell number

A 78459

B 464662

C 631611

D 785452

At a fluid velocity of 80 m/s, the highest erosion

rate results, namely meshing B, so that the next

approach will use meshing B, but by taking into

account geometric variations it is necessary to review

the quality of the meshing not only in terms of the

number of cells.

11 VALIDATION

Figure 4: Comparison graph of experimental data and CFD

data at a fluid velocity of 80 m/s.

Validation is an activity to prove the results obtained

through the same stages and processes as the

reference. Validation is done so that the results

obtained are close to the desired and research gets

maximum results in observation

In this study, validation was carried out by

comparing the graph of the erosion rate results

obtained with the erosion rate graph from the

reference journal (Wee and Yap 2019).

Because in the simulation there is no twisted pipe

configuration, the validation is done by comparing

the 90

elbow pipe with the reference. In this case, the

validation error reaches 7.36%, this is possible

because of the simulation situation that allows

loading too much data, as well as experimental data

that cannot be adjusted to conditions similar to ideal

conditions.

12 THE COMPARISON OF

VARIATION PIPE

In the observations, several things can affect the rate

of erosion. Among others:

• Particle impact velocity

• Particle impact angle

• Properties of particles

• The target material (in this final project,

stainless steel 316 is used)

Undulation is a circular shape on the elbow pipe

to get a very turbulent flow result. Naturally, the

particles will follow the results of the turbulent flow,

the particles will spread throughout the pipe wall.

With a pipe shape like this, the impact on the elbow

pipe will decrease in the same point concentration. In

the plan pipe the particles will focus more on the same

point because there are no obstacles before turning 90

(a) (b)

(

)

Figure 5: Contour DPM Erosion Rate (a) pipa plan, (b) 3-undulation pipe (c) 5-undulation pipe.

Numerical Study the Effect of Undulation to Mitigate Erosion Elbow

343

degrees. In this case, the things that affect the rate of

erosion are caused by the roughness of the walls and

the collisions between particles.

On the other hand, the variation pipe has a circular

shape and is designed to limit the movement of

particles. Compared to the plan pipe, the variation of

the pipe makes the elbows have a low risk of erosion.

This is because the wall is designed to have

undulation as a limited space for particle velocity.

particles with pipe walls. Experiments are the best

way to accurately determine the erosion rate problem

that occurs. However, to make it easier to do

numerical computational studies to understand the

erosion rate phenomenon that occurs in many

workpieces.

Figure 5 shows the erosion phenomenon and its

estimate in mm/year. Figure 5 (b) has the lowest

erosion value compared to other variations. This

result was obtained because the concentration of

particles that hit one point was reduced and scattered

at several other points. This is evidenced by the low

impact velocity value resulting in a low erosion rate.

Figure 6: Graph of Erosion Rate Against Elbow Curvative

at Centerline.

Figure 6 shows the graph of the erosion rate in

each variation having a graphic shape that is almost

the same as the planned pipe having the highest value.

In the plan pipe, all particles are focused on entering

the same tunnel so that they strike the same angle,

while for the 3-undulation pipe and 5-undulation pipe

variations, there is a special space to make the

particles turbulent and spread throughout the pipe.

This phenomenon causes the erosion rate value for 3-

undulation and 5-undulation pipes to be lower than

plan pipes. This result is almost similar to the study

conducted by Duarte (Duarte and de Souza 2017)

where the small amount of undulation results in a

lower erosion value.

There is a comparison of the experimental test

conducted by Christopher B. Solnordal (Solnordal,

Wong, and Boulanger 2015) with the CFD simulation

carried out. In Figure 4.3 it can be seen that the

experimental test value is higher than the CFD value

on the planned pipe. In this case, many things

happened in the experimental test which was not

ideal. When compared with computational

simulation, the experimental value can be influenced

by environmental conditions that can affect the

simulation value.

Figure 6 shows the results of erosion at the

centerline of the extrados pipe, in this case, it can be

seen that the 3-undulation pipe has the lowest erosion

peak value compared to the experimental, plan pipe,

and 5-undulation pipe. Extrados is the outer profile of

the pipe, while intrados is the inner profile of the pipe.

In Figure 5 both sides (extrados and intrados)

experience different erosion, on the intrados side the

pipe forms a region called separated region, where

separated region results in low velocity of the pipe.

This causes no erosion on the intrados side of the

pipe.

(a) (b)

Figure 7: (a) schematic of the x-y section of the pipe (b)

schematic of the profile of the x-z section of the pipe.

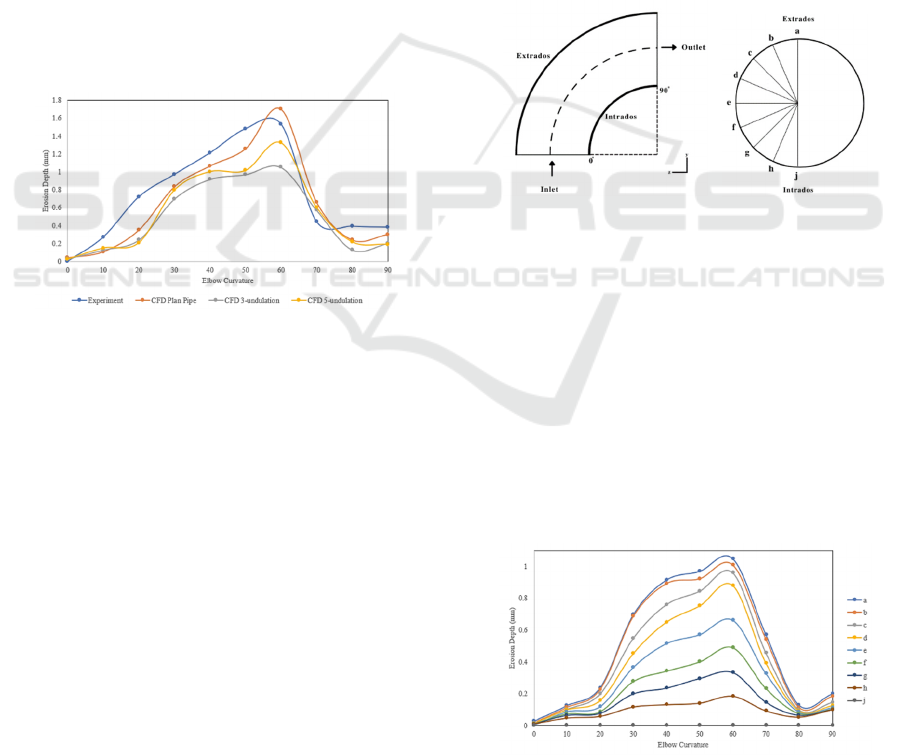
To get more accurate results, knowing the erosion

value on the pipe profile is carried out. It aims to

observe the distribution of erosion on 3-undulation

and 5-undulation pipes. The profile used is an x-y

cross-section with 9 points from extrados to intrados.

Figure 7 shows a schematic showing the inlet point at

and the outlet point at 90

, as well as the x-y and x-

z cross-sectional profiles on the pipe. This treatment

is to make it easier to analyze the erosion relationship

with the position on the pipe profile

Figure 8: Graph of representation of erosion rate on 3-

undulation profile.

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

344

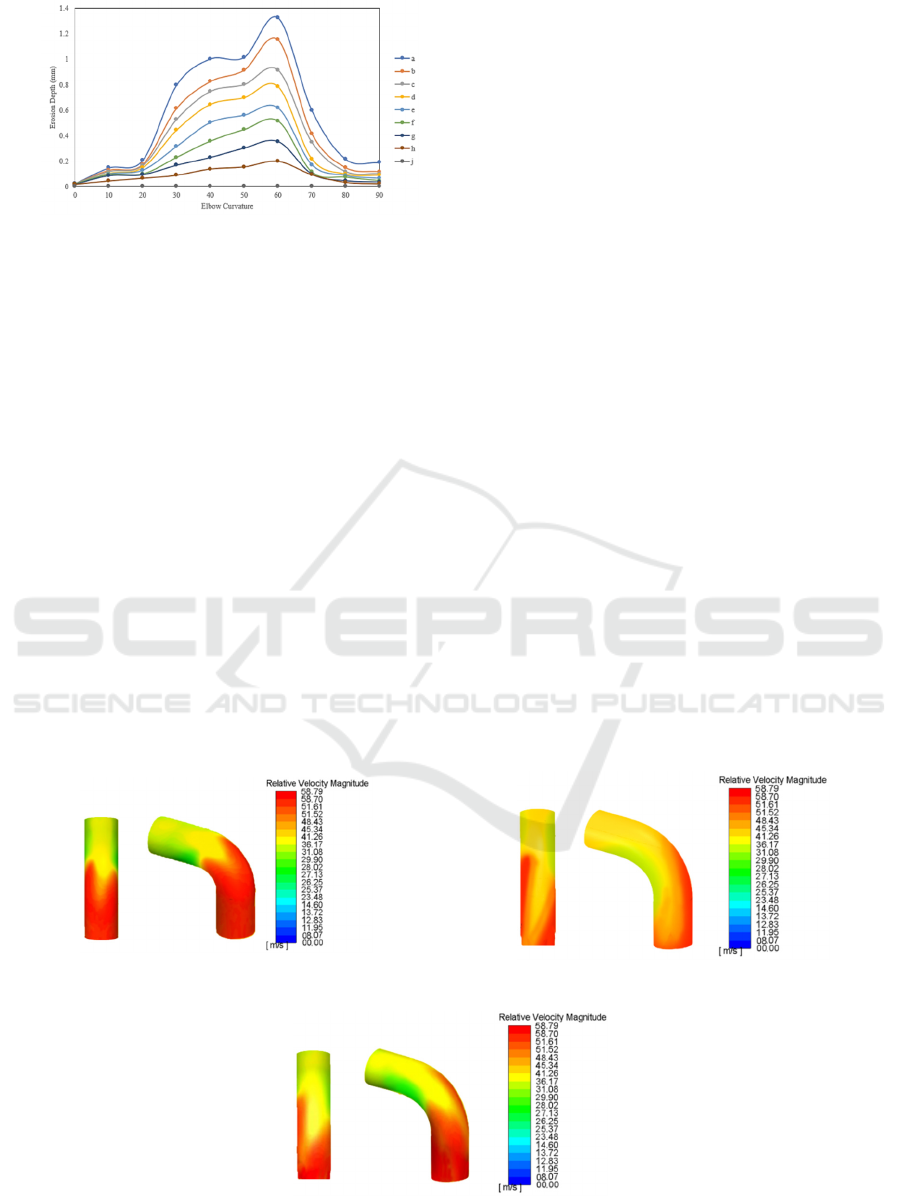
Figure 9: Graph of representation of erosion rate on 5-

undulation profile.

In Figures, 8 and 9 the highest erosion rate values

are at an angle of 60

. It was observed on the 3-

undulation pipe that the erosion difference in the a-b

profile was 0.038, the b-c profile was 0.051, the c-d

profile was 0.079. Meanwhile, in the 5-undulation

pipe, the erosion difference in the a-b profile is 0.169,

the b-c profile is 0.240, the c-d profile is 0.127.

From this case, it is explained that the decrease in

erosion value at the peak point of the 60

centerline

angle (profile A) of the pipe has an impact on

increasing erosion in the area around the centerline.

This proves that the decrease in erosion is caused by

the spread of sand particles, that the impact can be

evenly distributed on each pipe profile. This can be

observed directly by looking at the slope of Figures 8

and 9, wherein the 5-undulation pipe. The peak value

of erosion has a far difference compared to other

angles, and Figure 9 has a sharp indentation at an

angle of 60

. However, the impact produced by the

distributed particles does not make the erosion

profiles b, c and d in 3-undulation pipes have higher

yields than 5-undulation pipes. In terms of quantity,

the lowest erosion rate was experienced by the 3-

undulation pipe. Although the area around the center

line has almost the same erosion value, it does not

make the 3-undulation pipe value worse. It is proven

that table 4.1 on 3-pipe undulation pipe can reduce

erosion up to 38%.

The value of the erosion rate is not only caused by

different geometries, but the impact velocity also

affects. The provision of special space to make

changes to the flow in the pipe also has an impact on

the rate of erosion, with undulation, the flow in the

pipe will become very turbulent (turbulent) so that it

can slow down the velocity of particle impact on the

pipe elbow.

In Figure 6 it can be seen that the value of the

erosion rate has a significant difference at an angle of

– 60

. This is due to the fact that the impact

velocity value is also reduced at an angle of 30

– 60

High erosion values result in the possibility of pipe

leaks occurring.

The difference in the value of the erosion rate

caused by the impact velocity can also be seen from

the velocity contour in Figure 10. As previously

explained on the intrados side of the pipe, it forms a

region called a separated region. The separated region

has a low velocity so that the impact velocity becomes

weaker. At certain angles on the pipe extrados, the

erosion value becomes very high, such as an angle of

. This causes erosion, the injection of particles

hitting the extrados area having more energy than

increasing velocity.

(a) (b)

(c)

Figure 10: Contour velocity on (a) plan pipe, (b) 3-undulation pipe, (c) 5-undulation pipe.

Numerical Study the Effect of Undulation to Mitigate Erosion Elbow

345

Erosion is not only influenced by moving particles

or collisions between particles, but the fluid that flows

along with the particles is a determining factor for

erosion. Therefore, the velocity of the elbow pipe can

also be analyzed to determine the cause of erosion.

In the results of the velocity contour in Figure 10,

it can be seen that the velocity contour on the pipe

plan in Figure 5 (a), has the highest value.

Meanwhile, 3-undulation and 5-undulation pipes

have lower speeds. The impact of this phenomenon is

to reduce the rate of erosion (figure 5). The velocity

contour shows that the velocity value decreases from

the extrados to the intrados, this is caused by a

separate area on the pipe, this area is called a

separated region. A separated region is an area where

the lowest velocity value is on the inside of the pipe.

The 5-undulation form has a value that is almost

similar to the planned pipe, this can be due to the more

the number of undulations the pipe wall shape will be

closer to a circle or plan pipe compared to the 3-

undulation form.

Figure 11: Graph of representation of erosion rate on 5-

undulation profile.

The 5-undulation form has a value that is almost

similar to the plan pipe, this can be due to the more

the number of undulations the pipe wall shape will be

closer to a circle or plan pipe compared to the 3-

undulation form.

Table 10: Comparison of % erosion reduction in pipes with

variations.

Variation erosion value in 60

% erosion

reduction

pipa plan 1.69875 -

3-undulation 1.04865 38.26

5-undulation 1.32466 22.02

Table 10 shows the results that the % erosion

reduction value produced by 3-undulation pipes is

higher than 5-undulation pipes. In the 3-undulation

pipe, erosion can be reduced to reach 38.26%, while

in the 5-undulation pipe the erosion can be reduced to

22.02% of the planned pipe. This shows that the pipe

design with 3-undulation can be considered in the

future as a tool to reduce the rate of erosion.

13 CONCLUSION

This research is a study of sand erosion on the elbow

pipe. Gas flow is used to determine the rate of erosion

at 90

pipe bends. Making 3-undulation and 5-

undulation designs is an effort to reduce the erosion

phenomenon in pipe bends. In this study, the

following results were obtained:

• Changes in flow greatly affect the rate of

erosion because they can affect the interaction

of particles with the wall and the velocity of

impact. The highest erosion value remains on

the plan pipe and the lowest erosion value on

the 3-undulation pipe.

• 3-undulation pipe reduces erosion by 38.26%

while 5-undulation reduces erosion by 22.02%

ACKNOWLEDGEMENT

The authors acknowledge to PENS (Politeknik

Elektronika Negeri Surabaya) for support this

research.

REFERENCES

Anderson, Jd. 1995. “Computational Fluid Dynamics: The

Basics with Applications. 1995.” McGrawhill Inc.

https://doi.org/10.1017/CBO9780511780066.

Diana, L., A. G. Safitra, D. Ichsani, and S. Nugroho. 2020.

“CFD Analysis of Airflow Through Prism Obstacles

Inside Solar Air Heater Channel.” Journal of Physics:

Conference Series 1577 (1). https://doi.org/10.1088/

1742-6596/1577/1/012038.

Duarte, Carlos Antonio Ribeiro, and Francisco José de

Souza. 2017. “Innovative Pipe Wall Design to Mitigate

Elbow Erosion: A CFD Analysis.” Wear.

https://doi.org/10.1016/j.wear.2017.03.015.

Oka, Y. I., K. Okamura, and T. Yoshida. 2005. “Practical

Estimation of Erosion Damage Caused by Solid Particle

Impact: Part 1: Effects of Impact Parameters on a

Predictive Equation.” In Wear. https://doi.org/10.1016/

j.wear.2005.01.039.

Solnordal, Christopher B., Chong Y. Wong, and Joan

Boulanger. 2015. “An Experimental and Numerical

Analysis of Erosion Caused by Sand Pneumatically

Conveyed through a Standard Pipe Elbow.” Wear 336–

337: 43–57. https://doi.org/10.1016/j.wear.2015.04.017.

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

346

Strømme, Erik Grimm. 2015. “Simulation and Evaluation

of Slurry Erosion.” 83.

Wee, Siaw Khur, and Yung Jian Yap. 2019. “CFD Study of

Sand Erosion in Pipeline.” Journal of Petroleum

Science and Engineering. https://doi.org/10.1016/

j.petrol.2019.01.001.

Yudhatama, Ido Widya, Mas Irfan Purbawanto, and Wikan

Jatimurti. 2018. “Computational Fluid Dynamics

(CFD) Simulation of Sand Particle Erosion in Turbulent

Gas Fluid Flow in Vertical-Horizontal Elbow.” Jurnal

Teknik ITS. https://doi.org/10.12962/j23373539.v7i2.3

0445.

Numerical Study the Effect of Undulation to Mitigate Erosion Elbow

347