Effect of Material Type, Temperature, and Layer Thickness on PLA
and PETG from 3D Printer Products by Tensile Test
Etik Puspitasari, Syamsul Hadi and Moh. Hartono
State Polytechnic of Malang, Soekarno Hatta Street no 9, Malang City, Indonesia
Keywords: 3D Design, 3D Printer, Factorial Design, PETG, PLA, Plastic Specimen, Tensile Test.
Abstract: Many plastic products are produced from 3D printers. The problem to know the strength of the right materials,
researchers try to test the results of plastic specimens from 3D printers with the tensile test. Product size
according to ASTM D638 standard using PLA (Polylactic Acid), and Polyethylene terephthalate glycol
(PETG) filaments. The purpose is to determine the effect of material type, temperature, and thickness of PLA
and PETG filament layers from 3D printer results with tensile tests. The method used is factorial design. The
results of the maximum tensile strength on PLA material while the lowest on PETG. At the highest
temperature, the maximum tensile strength is reached at 260 °C, and the lowest is 220°C. That the higher the
temperature, the greater the effect on the tensile strength. And the highest layer thickness for maximum tensile
strength is 0.3 mm, the lowest layer is 0.1 mm and has a maximum tensile strength of 3.651 N/mm2. The
thicker the layers, the greater the effect on the tensile strength. There is an interaction effect between 3
variables. 3D designs and product prototypes for an additional hanger for a motorcycle by 3D printers have
been made.
1 INTRODUCTION
3D printers are one of the current and future
technologies that must be studied. Where the science
of reverse engineering is developing. Reverse
engineering is the process of analyzing an existing
product as a reference for designing similar products
by minimizing and increasing product advantages
(Daywin et al., 2019). Prototype product design with
the 3D printer is required. Rapid prototyping process
with emphasis on application(Davim, J. P., Kumar,
K., Zindani, 2020). Currently, many plastic products
are produced from 3D printers. 3D printers are very
practical in product development to print three-
dimensional objects such as parts for prototypes,
machine parts, robotics parts, electronic circuit parts,
and other plastic products, etc. Which are drawn from
3D software which is then transferred to 3D printer
software files and then printed on the machine 3D
printers. Preliminary design for 3D printing and
proper technique ensures the success of 3D printing
(Micallef J, 2015).
Digital manufacturing has become an intrinsic
part of the modeling profession, so the practitioner or
product designer must be skilled in traditional hand-
made techniques and digital technologies(Lansdown
H, 2019). Designer in designing a product, one of
which must take into account what material is right
for the product in terms of material strength or cost.
This has been done in previous studies related to the
strength of the PLA material on plastic specimens
produced by 3D printers with a layer thickness of 0.1-
0.5 mm. Indicating that the test results show are not
linear or the thicker the strength is not always Greater,
and the specimen increases. The strongest is in the
layer thickness of 0.35 mm.(Puspitasari et al., 2021).
The visual results of plastic test specimens with a 3D
printer are the smaller the layer used, the smoother
and more aesthetically pleasing(Puspitasari, 2020).
The types of materials or filaments in 3D printers
are Polylactic Acid (PLA), Acrylonitrile Butadiene
Styrene (ABS), Polyethylene terephthalate glycol
(PETG), Nylon (PA), Thermoplastic Elastomers
(TPE), and Polycarbonate (PC). Some filaments have
unique motifs such as wood, namely Wood filaments,
a combination of PLA and metal, and Polyvinyl
Alcohol (PVA).
PLA and PETG were chosen because researchers
wanted to prove which material had the best material
strength. Based on research that printing two types of
filaments, namely polylactic acid (PLA), and
polyethylene terephthalate glycol (PETG). the main
572
Puspitasari, E., Hadi, S. and Hartono, M.
Effect of Material Type, Temperature, and Layer Thickness on PLA and PETG from 3D Printer Products by Tensile Test.
DOI: 10.5220/0010949300003260
In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), pages 572-580
ISBN: 978-989-758-615-6; ISSN: 2975-8246
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

objective of the study was to find, through simulation
and mechanical compression tests, the maximum
prototype deformation of the adapter and to identify
the best material regarding mechanical resistance.
The result shows that the maximum deformation for
PETG is 0.5976 mm and PLA is 0.3103 mm. From
the research results, PLA has shown a lower
deformation value, but PETG was chosen as the
impression material because no cracks or fractures
were found during the research trials (Silva &
Guilhon, 2019).
A tensile test is carried out by gripping the test
object with a known cross-sectional area on the jaws
of the testing machine and so that the test object
experiences a gradually increasing tensile force
(Higgins, 2006).
With the above background, the researcher will
design and make a tensile test plastic specimen
pattern using a 3D printer which will later be tested
with a tensile test. The purpose of this research is to
analyze the effect of material type, temperature, and
layer thickness on the tensile strength of 3D printer
products with PLA and PETG materials. Analyzing
the effect of interaction between material type,
temperature, and layers thickness on the tensile
strength of 3D printer products with PLA and PETG
materials. And able to make 3D designs and
prototypes of 3D printer products from the research
results that have been obtained.
2 RESEARCH METHODOLOGY
This research was carried out at the Department of
Mechanical Engineering, State Polytechnic of
Malang which has tensile test equipment. The
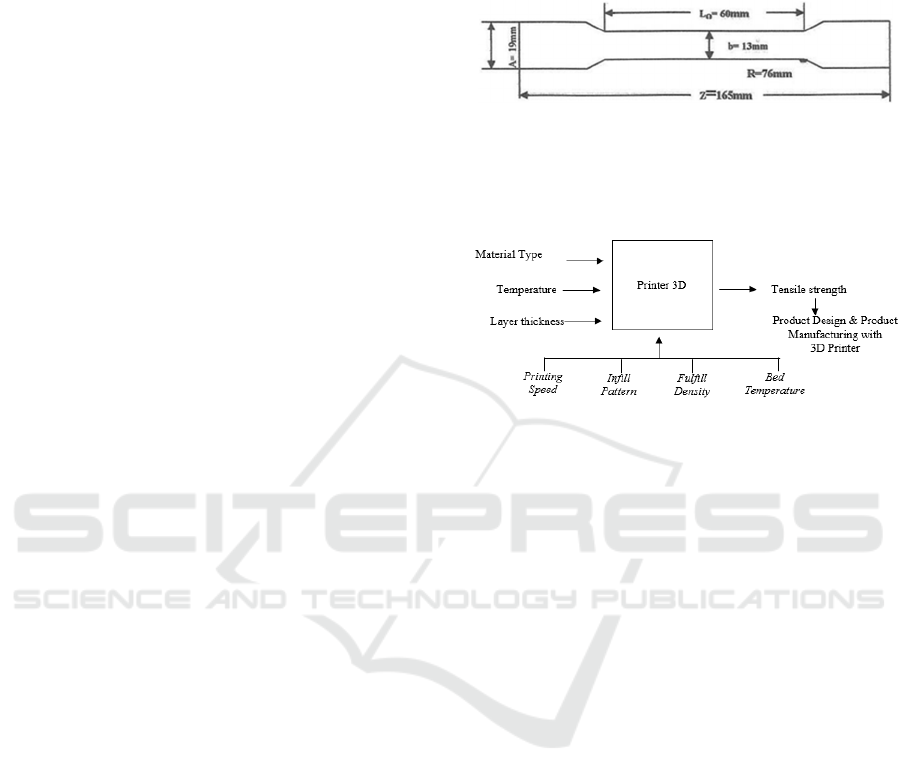
variable data that will be used are as follows :
1. Independent variables:
a. Layer thickness 0.1mm, 0.2mm, 0.3mm
b. Temperature 220°C, 240°C, 260C
c. Material Type PLA and PETG
2. Dependent Variable Tensile Test Results
3. Controlled Variables:
a. Printing speed: 70mm/s
b. Infill pattern: lines
c. Fulfill density: 100%
d. Bed Temperature: 60°C
Specimens made must be based on the ASTM
D638 Type 1 standard with the following dimensions:
165 mm long, 19 mm wide, and 5 mm thick. Based
on (Materials et al., 2006) on the ASTM D638 Type
1 standard for the standard test method for tensile
testing of plastic specimens, the thickness of the
specimen is up to 7 mm and can be less than 7 mm.
Plastic specimens to be made with a 3D printer can be
seen in Figure 1 below.
Figure 1: Product Design of 3D printed plastic specimens
for Tensile Test testing.
From the variable data above, it can be seen in
Figure 2 the following research block diagram:
Figure 2: Research block diagram.
The research hypothesis is an assumption that is
not necessarily true in research, so to find the truth of
this research, the research hypothesis can be seen as
follows:
1. Research hypothesis is "There is an effect
between material type, temperature, and layer
thickness on the tensile strength of 3D printer
products made of PLA and PETG materials"
2. Hypothesis Nul (H0) is as follows:
a. There is no effect of material type on the tensile
strength of 3D printer products made of PLA
and PETG materials.
b. There is no effect of temperature on the tensile
strength of 3D printer products made of PLA
and PETG materials.
c. There is no effect of layer thickness on the tensile
strength of 3D printer products made of PLA
and PETG materials.
d. There is no interaction effect between material
type, temperature, and layer thickness on the
tensile strength of PLA and PETG 3D printer
products
3. Alternative hypothesis (H1) is as follows:
a. There is an effect of material type on the tensile
strength of 3D printer products made of PLA
and PETG materials.
Effect of Material Type, Temperature, and Layer Thickness on PLA and PETG from 3D Printer Products by Tensile Test
573

b. There is an effect of temperature on the tensile
strength of 3D printer products made of PLA
and PETG materials.
c. There is an effect of layer thickness on the tensile
strength of 3D printer products made of PLA
and PETG materials.
d. There is an interaction effect between material
type, temperature, and layer thickness on the
tensile strength of 3D printer products made
from PLA and PETG materials.
Data Processing and Analysis method
After drawing the tensile test specimen design
according to the ASTM D638 standard with drawing
software and saved in STL format, the data is entered
into CURA for data processing according to variables
and then converted into a GCODE file. Then print it
using a 3D printer. The results of the tensile test
specimens were carried out by tensile testing on PLA
and PETG specimens where specimen there were 27
specimens multiplied by 3, so the total specimen
tested was 54 specimens, in this study, there were
only 45 data because PETG at 220 C temperature
could not be printed and temperature too low. After
that, the data obtained will be recorded. Then the data
from the tensile test results will be processed by
factorial design using Minitab software. Then make
product designs and manufacture products with a 3D
printer.
3 RESULT AND DISCUSSION
The following are the results of the 3D design of the
tensile test specimen according to the ASTM D638
standard. Save the drawing design with the STL file
format. can be seen in the following Figure 3
Figure 3: Specimen Design 3D Tensile test standard ASTM
D638.
Open the specimen drawing design file to the
CURA software for setting the independent variable
and dependent variable. can be seen in the following
Figure 4:
Figure 4: Setting specimen parameters with CURA.
After that the process of making tensile test
specimens with a 3D printer is carried out, it can be
seen in Figure 5:
Figure 5: 3D Printer Process.
The following are the results of tensile test specimens
from PLA and PETG from 3D printers, which can be
seen in the following Figures 6 and 7
Figure 6: Results of tensile test specimens from PLA from
3D printers.
iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science
574

Figure 7: Results of tensile test specimens PETG from 3D
printers.
The time needed to make one tensile test specimen is
as follows.
1. On a 0.1 mm thick layer with a temperature of 220
C, 240 C, 260 C, it takes an average of 3 hours 57
minutes 10 seconds per 1 specimen.
2. At 0.2 mm thick layer with a temperature of 220
C, 240 C, 260 C takes an average of 2 hours 4
minutes 40 seconds per 1 specimen.
3. Layer thickness of 0.3 mm with temperatures of
220 C, 240 C, 260 C takes an average of 1 hour 26
minutes 57 seconds per 1 specimen.
All of the results of the ASTM D638 standard tensile
test specimen can be seen in Figures 8 and 9 as
follows:
Figure 8: Tensile test specimen results with PLA filament
from a 3D printer.
Figure 9: Tensile test specimen results with PETG filament
from a 3D printer.
Before calculating the stress and strain, it is
necessary to calculate the cross-sectional area (A)
first because it greatly affects the tensile stress. The
cross-sectional area of each specimen is measured
and recorded to obtain the results of the tensile stress.
To find the cross-sectional area (A) that is Wc or the
width of the inside of the specimen multiplied by the
thickness (t).
The cross-sectional area of the design according
to the ASTM D638 standard is Wc = 13 mm and t =
5 mm, then A = 65 mm (drawing dimensions). can be
seen in the formula below:
A = Wc x t (1)
Where :
A = Specimen cross-sectional area
Wc = Width Gauge Area
t = Specimen thickness
The process of measuring tensile test objects from
PLA and PETG that have been printed with a 3D
printer using a caliper with an accuracy of 0.02 mm
to calculate the actual dimensions with the above
formula (1) so that it can calculate the actual cross-
sectional area. can be seen in Figure 10 below:
Figure 10: The process of measuring the PETG tensile test
specimen from a 3D printer.
Effect of Material Type, Temperature, and Layer Thickness on PLA and PETG from 3D Printer Products by Tensile Test
575

The following is the tensile test process which can
be seen in Figure 11 below:
Figure 11: Tensile test process of 3D printer specimen.
The results of the calculation of the cross-
sectional area (A) are used to calculate the tensile
stress (σ). So that the best tensile stress is obtained in
the material, temperature, and layer thickness which
will be tested by Factorial Design.
The tensile test is then carried out. The results of
the tensile test of 3D printer specimens from PLA in
Figure 12 are below:
Figure 12: Tensile test results of PLA specimens from 3D
printer.
The tensile test is carried out with a tensile testing
machine. The standard used in the tensile test is the
ASTM D638 standard. (Budiono, 2015).
To find the value of the tensile stress that occurs
is determined by the following formula (ASTM D
638 Standard). Based on (Hadi Syamsul, 2016) the
tensile stress formula can be seen from formula 2
below
σ = F/A (2)
Where :
σ: Tensile Stress (N/mm2)
F: Tensile Load (N)
A: Specimen cross-sectional (mm
2
)
The following are the results of the tensile stress
testing of the 3D printer tensile test specimen from
the PLA filament. The data will be processed by
factorial design. which can be seen in Table 1 below:
Table 1: Tensile Stress Test Results of PLA.
The tensile test is then carried out. The results of
the tensile test of the 3D printer specimen from PETG
in Figure 13 are below:
Figure 13: Tensile Test Results of PETG Specimens from
3D printers.
The following are the results of the tensile stress
testing of the 3D printer tensile test specimen from
the PETG filament. The data will be processed by
factorial design, which can be seen in Table 1 below:
iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science
576

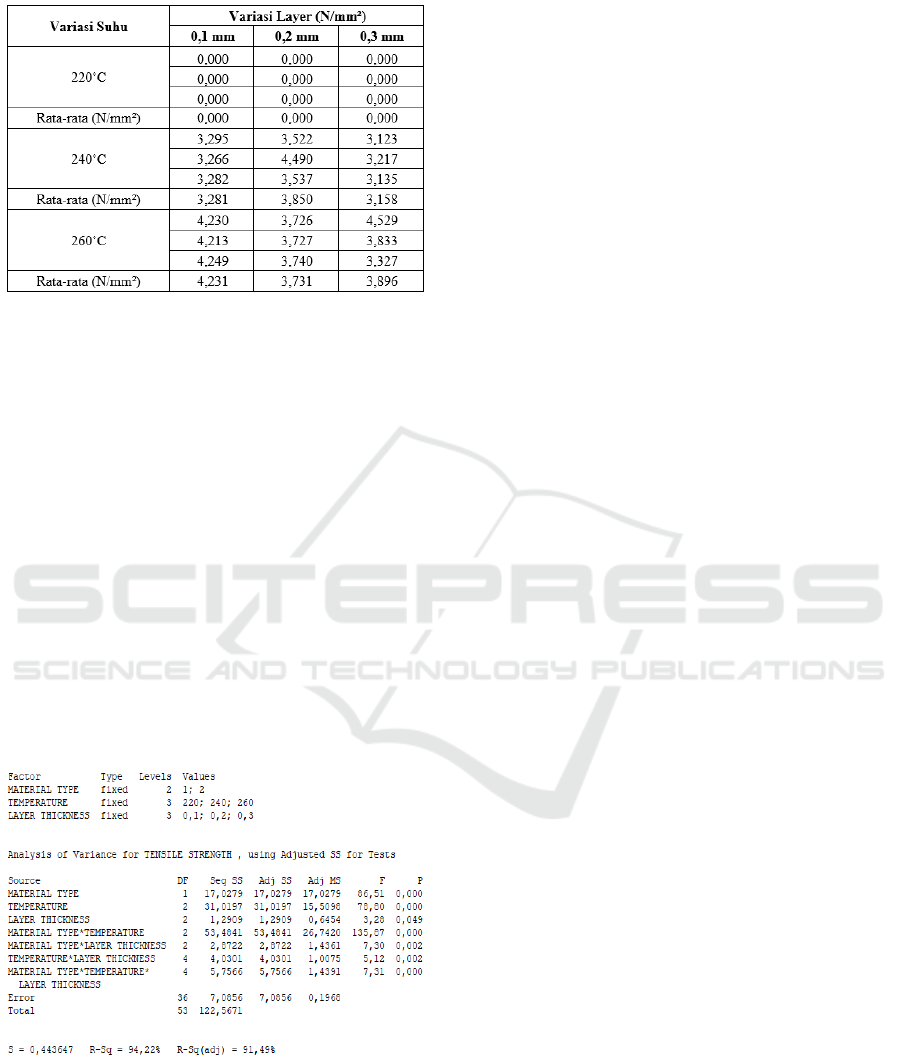
Table 2: Tensile Stress Test Results of PETG.
Table 2 shows that the temperature of 220 C is
zero because the temperature is too low for the PETG
filament so that a tensile test specimen cannot be
made.
Analysis of Tensile Test Results with Factorial
Design
After testing the tensile test on the PLA and PETG
specimens and getting the results of the tensile stress
and strain values as above. Then the data was
analyzed using Factorial Design with Minitab.
Because researchers wanted to see whether or not
there was an influence or not from 3 independent
variables, namely the type of material, namely PLA
and PETG, the temperature is 220 °C, 240 °C, 260 °C,
and the layer thickness is 0.1 mm; 0.2mm; 0.3mm.
The following results of the tensile stress analysis on
the tensile test specimen test with a 3D printer in
Figure 14 below:
Figure 14: Factorial Design Result of Tensile Strength .
From the results of the Factorial Design in Figure
4.15, the first variable, namely the type of PLA and
PETG material, has a p-value of 0.000, and the value
is less than = 0.05. can be concluded that the
hypothesis (H0a) is rejected, and the alternative
hypothesis (H1a) is accepted, namely "There is an
effect of material type on the tensile strength of 3D
printer products made of PLA and PETG materials".
For the second variable, temperature with a p-value
of 0.000, the value is less than = 0.05. can be
concluded that the hypothesis (H0b) is rejected, and
the alternative hypothesis (H1b) of the study is
accepted, namely "There is an effect of temperature
on the tensile strength of the 3D printer product, PLA
and PETG materials." The third variable is layer
thickness with a p-value of 0.049, the value is less
than = 0.05. It can be concluded that the hypothesis
(H0c) is rejected and the alternative hypothesis (H1c)
of the study is accepted, namely "There is an effect of
layer thickness on the tensile strength of 3D printer
products made of PLA and PETG materials"
In the summary model, the values are the
reference data and part of the Factorial Design
analysis. The standard deviation value (S) is the
average deviation of the data points with the average
data. can be seen in Figure 14 that the value of S in
the data processing results is 0.443647 which means
that the deviation value of the data point with the
average data is 0.443647. The coefficient of
determination (R-sq) is the percentage contribution of
the influence given by the independent variable to the
dependent variable. In Figure 14 the coefficient of
determination has a value of 94.22% which means
that the influence of the independent variables,
namely the type of material, temperature, and layer
thickness, affects 94.22% of the dependent variable,
namely tensile strength. makes the remaining 5.78%
an error in the form of other independent variables
outside the material type, temperature, and layer
thickness as well as errors in testing or other things
that affect tensile strength.
In Figure 14, it is found that the interaction
between the variables of material type and
temperature is mutually influential, this is evidenced
by the p-value of 0.000, the value is less than = 0.05.
The second interaction found that the interaction
between the material type variable and layer thickness
also had an effect, this was evidenced by the p-value
of 0.002, the value was less than = 0.05. In the third
interaction, temperature and layer thickness variables
have an effect, this is evidenced by the p-value of
0.002, the value is less than = 0.05. The fourth
interaction of the three variables. Namely, the type of
material, temperature, and layer thickness interact
and influence each other, this is evidenced by the p-
value of 0.000, the value is less than = 0.05.
Effect of Material Type, Temperature, and Layer Thickness on PLA and PETG from 3D Printer Products by Tensile Test
577

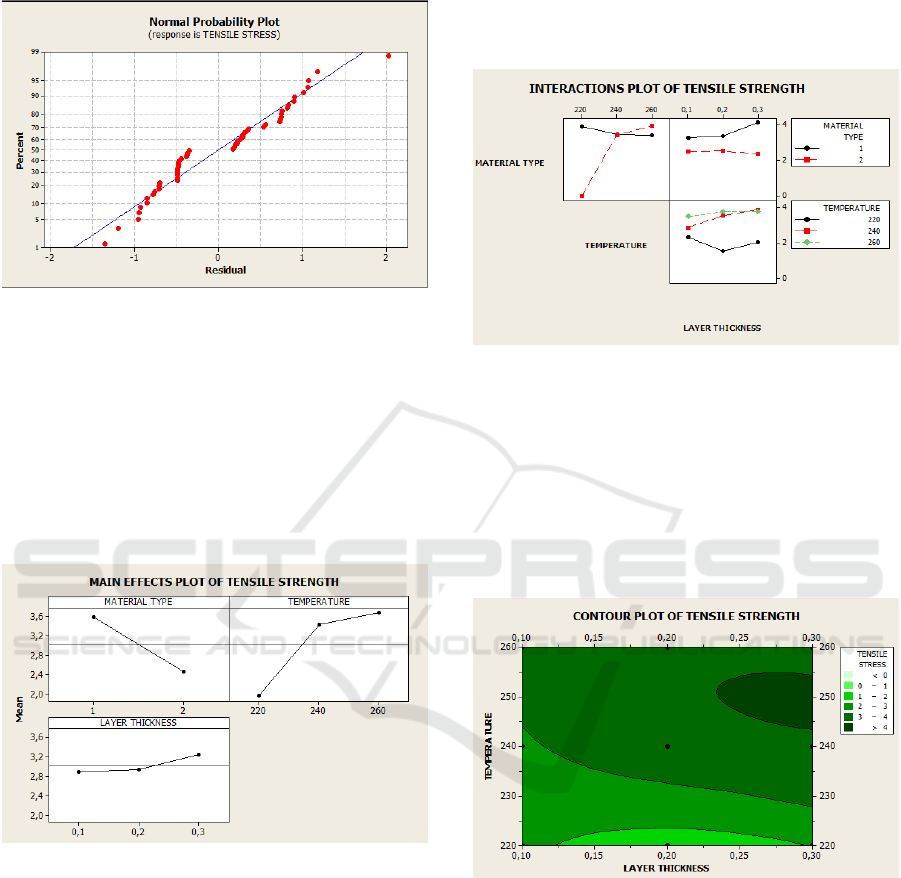
Next is the normality graph is shown in Figure 15
below:
Figure 15: Normality Probability Plot.
The normality probability plot in Figure 15 above
shows that the data is on the Normal line and
approaching the diagonal line, so it is stated that the
data is Normal.
Main effect plot for maximum tensile strength
where tensile strength is sometimes called ultimate
strength. which is the maximum stress that can be
received by a material before breaking. The results of
data processing can be seen in Figure 16 below:
Figure 16: Main Effect Plot of tensile strength for PLA and
PETG.
In Figure 16 above, the maximum tensile strength
for this type of material is at No. 1, namely PLA,
while the lowest is at No. 2, namely PETG. The
highest maximum tensile strength temperature is
achieved at a temperature of 260 °C, and the lowest is
at a temperature of 220 °C. It can be seen that the
higher the temperature, the greater the effect on
tensile strength. And the highest layer thickness for
maximum tensile strength is at layer 0.3 mm, and the
lowest is at layer 0.1 mm. It can be seen that the
thicker the layer, the greater the effect on tensile
strength.
The analysis of the interactions plot of the
tensile strength analyzes the effect of the
interaction between the type of material,
temperature, and layer thickness. And the results
are obtained as shown in Figure 17 below:
Figure 17: Interactions Plot of Tensile Strength.
From Figure 17 above, the interaction between
material type, temperature, and layer thickness shows
that the highest interaction between material type and
layer thickness is in type 1, namely PLA with a layer
thickness of 0.3 mm, the highest temperature
interaction is at a temperature of 260°C.
Furthermore, the contour plot for tensile strength
can be seen in Figure 18 below:
Figure 18: Contour Plot of tensile strength.
In Figure 18 above, it can be seen that the area
that has large tensile strength and > 4 N/mm2 is at a
layer thickness of 0.25-0.30 mm and a temperature
between 240-255 °C. Furthermore, the area that has
the smallest tensile stress of 1-2 N/mm2 is at a layer
thickness of 0.125-0.30 mm with a temperature
between 220 °C.
Designs and Prototypes of 3D Printers for an
additional hanger for a motorcycle
iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science
578

From the research obtained above, the best tensile
strength for PLA material with a layer thickness of
0.3 mm and a temperature of 260°C is 3.651 N/mm2,
from these results the researcher makes an additional
hanger for a motorcycle design and will then make a
prototype printed on a 3D printer. The background for
making this design is the application of the research
results obtained where the product to be made
contains elements of tensile strength because the
function of the product is as a hanger of goods where
it accepts loads and tensile forces. In addition, the
background of this design was made because the
researcher got the idea when buying a lot of items
with a lot of plastic bags that had to be hung on a
motorcycle hanger, it was not enough because there
was only one hanger so the researcher wanted to make
a hanger that had 3 branches so that when this product
placed on the original motorcycle hanger can load
more goods. This product can be used in all brands of
motorcycles because it has been pre-measured. The
following 2D and 3D designs for the additional
hanger for a motorcycle can be seen in Figures 19 and
20 below:
Figure 19: 3D design of additional hanger for a motorcycle..
Figure 20: Printer 3D result of additional hanger for a
motorcycle.
Figure 21: Application of additional hanger for a
motorcycle.
Based on Figure 21 the addition of these tools can
increase the capacity to carry goods on a motorcycle.
The time of making an additional hanger for a
motorcycle product takes 6 hours 28 minutes for 1
product. This proves that 3D printers are suitable for
making prototypes or making small quantities of
products. Not suitable for mass production. Based on
research Rapid Prototyping Techniques are for
custom-made products and not for mass manufacture
(Davim, J. P., Kumar, K., Zindani, 2020). For mass
production, it is recommended to use injection
molding but must make a mold. The advantage of 3D
printers is that there is no need to make molds or
prints and complex designs can be made on a 3D
printer. based on research (Davim, J. P., Kumar, K.,
Zindani, 2020), Rapid Prototyping Techniques are for
custom made products and not for mass manufacture.
4 CONCLUSION
1. There is an effect of material type, temperature,
and thickness on the tensile strength of 3D printer
products with PLA and PETG material. The
hypothesis (H1) is accepted. Supported by the
factorial design method where the P-value of the
three variables is less than the value of = 0.05. The
maximum stress is on the type of PLA material
while the lowest is on the PETG. The highest
maximum tensile stress temperature is achieved at
a temperature of 260 °C and the lowest is at a
temperature of 220 °C. It can be seen that the
higher the temperature, the greater the effect on
Effect of Material Type, Temperature, and Layer Thickness on PLA and PETG from 3D Printer Products by Tensile Test
579

tensile strength. And the highest layer thickness
for maximum tensile strength is at layer 0.3 mm
and the lowest layer is 0.1 mm and has a
maximum tensile strength of 3.651 N/mm2. It can
be seen that the thicker the layer, the greater the
effect on tensile strength.
2. There is an interaction effect between material
type, temperature, and layer thickness on the
tensile strength of 3D printer products with PLA
and PETG materials. Supported by the factorial
design method where the interaction value of the
three variables above the P-value is less than the
value of = 0.05.
3. 3D designs and product prototypes for an
additional hanger for a motorcycle by 3D printers
have been made according to the results of the
research.
ACKNOWLEDGMENT
The research team from Mechanical Engineering of
the State Polytechnic of Malang has carried out
research, to all parties who have helped this activity
and P2M of the State Polytechnic of Malang.
REFERENCES
Budiono. (2015). Pengujian kuat tarik terhadap produk
hasil 3d printing dengan variasi ketebalan layer 0,2 mm
dan 0,3 mm yang menggunakanan bahan abs
(acrylonitrile butadiene styrene).
Davim, J. P., Kumar, K., Zindani, D. (2020). (2020). Rapid
Prototyping, Rapid Tooling and Reverse Engineering:
From Biological Models to 3D Bioprinters. Germany:
De Gruyter.
Daywin, F. J., Utama, D. W., Kosasih, W., & Wiliam, K.
(2019). Perancangan Mesin 3d Printer Dengan Metode
Reverse Engineering (Studi Kasus di Laboratorium
Mekatronika dan Robotics Universitas Tarumanagara).
Jurnal Ilmiah Teknik Industri, 7(2), 79–89.
https://doi.org/10.24912/jitiuntar.v7i2.5929
Hadi Syamsul. (2016). Teknologi Bahan. Penerbit Andi,
Yogyakarta.
Higgins, R.. (2006). Materials for Engineers and
Technicians. 4th ed. UK: Newnes.
Lansdown H. (2019). Digital Modelmaking: Laser Cutting,
3D Printing and Reverse Engineering. The Crowood
Press.
Materials, P., Materials, E. I., Matrix, P., Materials, C., &
Specimens, P. (2006). Standard Test Method for
Tensile Properties of Plastics 1. January 2004, 1–15.
https://doi.org/10.1520/D0638-14
Micallef J. (2015). Beginning Design for 3D Printing.
Apress.
Puspitasari, E. (2020). Analisa Pola Spesimen Plastik Uji
Pukul Charpy Dengan Menggunakan Printer 3D. Jurnal
Teknik Ilmu Dan Aplikasi, 9. https://doi.org/10.33795/
jtia.v9i2.33
Puspitasari, E., Wirawan, W., & Hadi, S. (2021). Analisis
Lapisan Cetak Printer 3d Spesimen Plastik Pla
Kelipatan 0,05 mm TERHADAP ENERGI PUKUL.
Info-Teknik, 21(2), 139. https://doi.org/10.20527/
infotek.v21i2.10049
Silva, A., & Guilhon, D. (2019). Comparative analysis of
ankle prosthesis connector adapters in 3D printed using
PLA and PETG. IFMBE Proceedings, 70(1), 155–161.
https://doi.org/10.1007/978-981-13-2119-1_24
iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science
580