Natural Frequencies and Mode Shapes of Human Tympanic

Membrane in Myringoplasty

Hidayat

, Sudarsono

, Ruspita Sihombing

, Rozaini Othman

and Minir

Department of Mechanical Engineering, Politeknik Negeri Samarinda, Jl. Ciptomangunkusumo, Samarinda, Indonesia

Department of Mechanical Engineering, Universitas Halu Oleo, Kampus Hijau, Kendari, Indonesia

Faculty of Mechanical Engineering, Universiti Teknologi MARA, Pematang Sauh, Malaysia

minirpolnes@gmail.com

Keywords:

Tympanic Membrane, Natural Frequency, Finite Element Method, Eigenvalue Analysis.

Abstract:

The tympanic membrane of the human ear, sometimes called the eardrum, is a thin membrane that separates

the outer and middle ears. Perforation of the tympanic membrane might result in longer-lasting hearing loss.

This research aims to determine the natural frequencies and mode shape of the tympanic membrane by using

the finite element method. The geometric model of the human tympanic membrane was created using CAD

software (Solidworks) based on previously published physical parameters reported by other researchers. Then,

Hypermesh was used to carry out eigenvalue analysis by imported the geometrical model. Two analysis

models were used to compare the dynamic behavior, namely normal tympanic membrane and reconstruction

of the membrane, using sliced cartilage myringoplasty. The thickness of the sliced cartilage was varied from

0.05 to 0.5 mm. Finally, the natural frequency and mode shape of reconstruction of the tympanic membrane

is the same as normal tympanic membrane when cartilage thickness is 0.4 mm.

INTRODUCTION

Hearing loss is one of the most severe issues that

people face in their daily lives. Numerous examples

of conductive hearing loss have occurred due to

issues with the tympanic membrane or ossicles. A

perforated tympanic membrane or perforated

eardrum, such as a holed tympanic membrane, is

associated with liquid discharge from the middle ear

through the ear canal. Tympanic membrane

perforation refers to a hole in the thin membrane that

divides the outer and middle ears.

Many researchers studying the human middle ear

system used finite element analysis to replicate the

tympanic membrane's dynamic behavior. The human

hearing system's sensitivity to these qualities is

determined. The characteristics that dictate the

membrane's bending stiffness properties have been

investigated, mainly two critical parameters: the

tympanic membrane's Young's modulus and the

eardrum thickness (Caminos, Garcia-Manrique,

Lima-Rodriguez, & Gonzalez-Herrera, 2018).

Another study calculates the viscous damping within

the tympanic membrane, which may assist in

smoothing the wideband response of a possibly

highly resonant TM and Examine the role of an

unusual element of human middle-ear anatomy: the

narrow mucosal epithelial fold that connects the

manubrium's midsection to the TM (De Greef et al.,

2014). The next study calculates Young's modulus of

a thin-shell model of the eardrum with subject-

specific geometry that is numerically adjusted to

match measured pressured forms (Ghadarghadar,

Agrawal, Samani, & Ladak, 2013). Simulation of the

dynamic behavior of tympanic membrane perforation

had been done using the finite element method

(Hidayat, Sudarsono, & Othman, 2020). The

frequency responses of the human middle ear system

with eardrum perforation using the finite element

method were investigated by researchers (Hidayat,

Sudarsono, Aviva, & Othman, 2019). The best graft

thickness for cartilage myringoplasty was determined

using finite element analysis in patients with varying

diameters of tympanic membrane (TM) holes (Lee et

al., 2007). A study predicted the conductive hearing

loss would increase with increasing perforation size

(Mehta, Rosowski, Voss, O'Neil, & Merchant, 2006).

The simulation of the effect of perforation on the

pressure difference across the TM by including a

channel for sound coupling from the ear canal to the

Hidayat, ., Sudarsono, ., Sihombing, R., Othman, R. and Minir, .

Natural Frequencies and Mode Shapes of Human Tympanic Membrane in Myringoplasty.

DOI: 10.5220/0010961600003260

In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), pages 1169-1172

ISBN: 978-989-758-615-6; ISSN: 2975-8246

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

1169

middle-ear cavity through the perforation (Voss,

Rosowski, Merchant, & Peake, 2001). A study to

determine the acoustic transmission properties of

cartilage with various thicknesses and its mechanical

deformation in response to air pressure changes

(Zahnert, Hüttenbrink, Mürbe, & Bornitz, 2000).

However, there is no report on the tympanic

membrane reconstruction using sliced cartilage

performing eigenvalue analysis to determine the

dynamic behavior. In the present study, the natural

frequencies and mode shapes were determined to find

out the proper thickness of sliced cartilage used for

the reconstruction of tympanic membrane

perforation. The three-dimensional model of the

human tympanic membrane was created using CAD

software. The human tympanic

membrane was

considered a flat elliptical shape.

Then, the

Hypermesh was used to generate the finite

element

model of the tympanic membrane. Two types

finite element model, namely model I and model

II. Model I has the same material properties as the

material used to close the hole at the center of the

membrane then the model II used sliced cartilage

myringoplasty. Finally, eigenvalue analysis was

performed to determine the proper thickness of

cartilage myringoplasty by comparing the natural

frequencies and mode shapes of the model I and II.

MATERIALS AND METHOD

2.1 Finite Element Model of Human

Tympanic Membrane

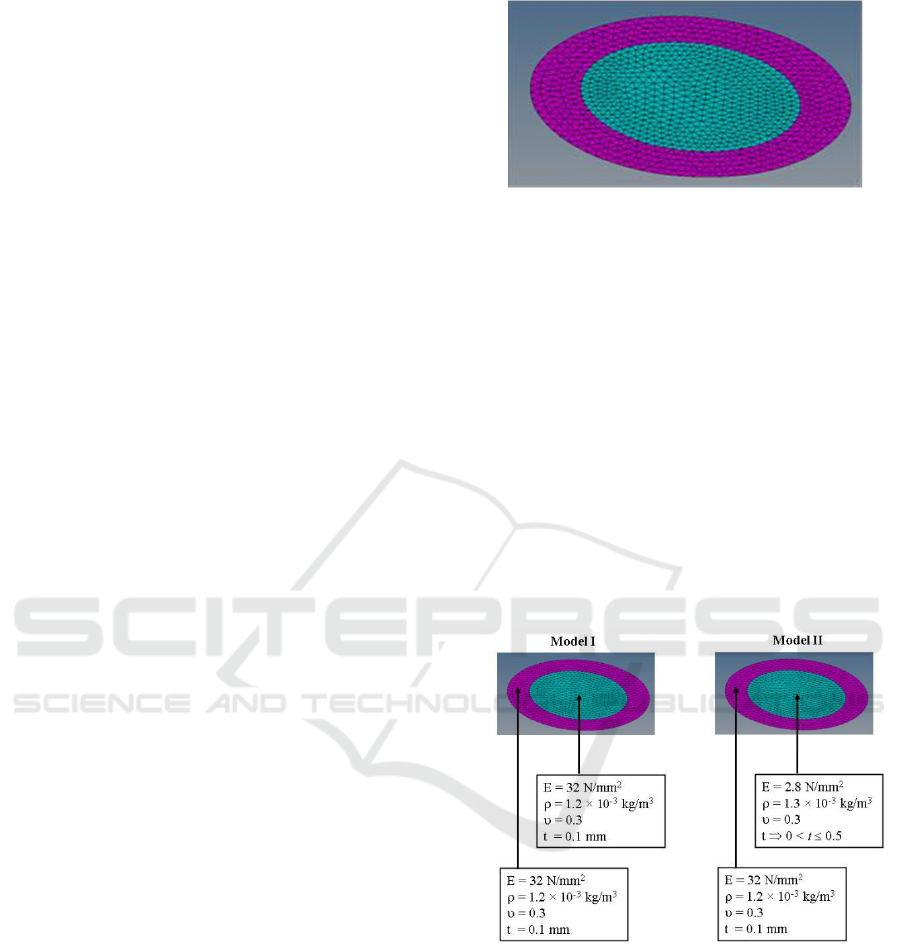
Figure 1 shows the finite element model of the

human tympanic membrane. The human tympanic

membrane shown in Fig. 1 was considered a flat

elliptic shape. The dimensions of flat elliptic shape

are 10 mm and 9 mm for major and minor axis,

respectively. This research used a tympanic

membrane repaired by sliced cartilage at the center of

the membrane. The value of 0.1 mm was used as the

thickness of the membrane. Then, the thickness of

cartilage was varied from 0.02 to 0.5 mm. In this

study, two types of material properties were used to

compare the natural frequencies and mode shapes of

the human tympanic membrane, considered as Model

I and Model II.

Figure 1: Finite Element Model of Human Tympanic

Membrane.

Then, the fixed boundary condition was used around

the shape of the tympanic membrane. The six-node

triangular element was used to divide the tympanic

membrane into 1155 pieces of finite elements.

2.2 Material Properties

Figure 2 shows the material properties of model I

and model II. Firstly, the cartilage used in

myringoplasty at the center of the tympanic

membrane in the model I was defined the same as the

material properties of the human tympanic

membrane. Secondly, the sliced cartilage with the

value of 2.8 N/mm

was used as Young's modulus at

the center of the human tympanic membrane.

Figure 2: Material Properties of Model I and Model II.

As for the mass density, the value of 1.2 × 10

-3

kg/mm

was used, which is the same value as the

human tympanic membrane. Then, the mass density of

sliced cartilage myringoplasty is 1.2 × 10

-3

kg/mm

Both models used the value of 0.3 for Poisson's ratio.

Finally, the Optistruct of Hypermesh was used to

carry out eigenvalue analysis of the model I and II.

Eigenvalue analysis was used to obtain the natural

frequencies and mode shapes of both models of the

human tympanic membrane. In this research, the 1

and 2

natural frequencies and mode shapes will be

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

1170

compared to each other in order to show the dynamic

behavior of models I and II.

RESULT AND DISCUSSION

3.1 Result

Figure 3 shows the mode shape of the 1

natural

frequency of the human tympanic membrane. The 1

natural frequency was obtained at 440 Hz. The model

I and II have similar mode shapes for all-natural

frequencies, which shows the fundamental shape for

a vibrating circular membrane. The mode number is

(0,1) due to the absence of nodal diameters but the

presence of a circular node (the outside edge).

Figure 3: The Mode Shape of the 1

Natural Frequency.

Figure 4 shows the 1

natural frequency of the

human tympanic membrane. In the eigenvalue

analysis, the thickness of sliced cartilage was varied

from 0.02 mm to 0.5 mm. Furthermore, the natural

frequencies of model II were increased due to the

effect of thickness of sliced cartilage. Thus, model I

and model II have the same natural frequency when

the thickness of sliced cartilage is 0.42 mm.

Figure 4: The 1

Natural Frequency of Tym

Membrane.

Figure 5 shows the mode shape of the 2nd natural

frequency.

The

mode

shape

model

and

are

similar

mode

for

the

natural

frequency

the

809

Hz.

this

case,

the

mode

shape

the

tympanic

membrane

(1,1),

which

has

single

nodal

diameter

and a single circular node (the outside edge).

Figure 5: The Mode Shape of the 2

Natural Frequency.

Figure 6 shows the 2

natural frequency of the

tympanic membrane. The 2

natural frequency of

model II was increased when the thickness of the

cartilage myringoplasty become larger. Finally, the

natural frequency for both models has the same

value when the thickness of cartilage myringoplasty

is 0.398 mm.

Figure 6: The 2

Natural Frequency of Tympanic

Membrane.

3.2 Discussion

The use of cartilage in TM restoration has been

established, most notably in situations of chronic

tubal dysfunction, adhesion processes, and complete

or recurrent TM abnormalities. This work uses

eigenvalue analysis to determine the natural

frequency of the human ear system with a healed

tympanic membrane following myringoplasty with

various cartilage thicknesses. The first and second

natural frequencies of the normal tympanic

membrane and different thicknesses of reconstruction

membrane with cartilage myringoplasty were

compared. The study estimated the optimum cartilage

Natural Frequencies and Mode Shapes of Human Tympanic Membrane in Myringoplasty

1171

thickness for myringoplasty using frequency

response analysis but did not include dynamic

behavior, such as natural frequency and mode shape.

In order to clarify this result, the natural frequency

and mode shape of the human tympanic membrane

using the actual shape to define the optimum

thickness of sliced cartilage myringoplasty.

CONCLUSIONS

The effect of various thicknesses on the natural

frequency of the human middle ear system during

myringoplasty was examined in this study.

Eigenvalue analysis of the tympanic membrane with

a flat elliptic shape had been carried out to obtain the

natural frequencies and mode shapes. The first and

second natural frequencies and modes shapes for each

model had been compared. The value of around 0.4

mm was defined as the thickness of sliced cartilage in

myringoplasty.

REFERENCES

Caminos, L., Garcia-Manrique, J., Lima-Rodriguez, A., &

Gonzalez-Herrera, A. (2018). Analysis of the

mechanical properties of the human tympanic

membrane and its influence on the dynamic

behaviour of the human hearing system. Applied

Bionics and Biomechanics

2018. https://doi.

org/10.1155/2018/1736957

De Greef, D., Aernouts, J., Aerts, J., Cheng, J. T., Horwitz,

R., Rosowski, J. J., & Dirckx, J. J. J. (2014).

Viscoelastic properties of the human tympanic

membrane studied with stroboscopic holography and

finite element modeling. Hearing Research,

312(2014), 69–80. https://doi.org/10.1016/j.heares.

2014.03.002

Ghadarghadar, N., Agrawal, S. K., Samani, A., & Ladak,

H. M. (2013). Estimation of the quasi-static Young’s

modulus of the eardrum using a pressurization

technique. Computer Methods and Programs in

Biomedicine

110(3), 231–239.

https://doi.org/10.1016/j.cmpb.2012.11.006 Hidayat, H.,

Sudarsono, S., Aviva, D., & Othman, R. (2019).

Frequency response of the human middle ear system

with eardrum perforation. IJSTR, 8(4).

Hidayat, Sudarsono, & Othman, R. (2020). Dynamic

Behavior of Human Tympanic Membrane

Perforation

Using Finite Element Method. IOP Conference

Series: Materials Science and

Engineering

797,

12025.https://doi.org/10.1088/1757-899x/797/1/012025

Lee, C. F., Chen, J. H., Chou, Y. F., Hsu, L. P., Chen, P. R.,

& Liu, T. C. (2007). Optimal graft thickness for

different sizes of tympanic membrane perforation in

cartilage myringoplasty: A finite element analysis.

Laryngoscope

117

(4),

725–730. https://doi.org/10.

1097/mlg.0b013e318031f0e7

Mehta, R. P., Rosowski, J. J., Voss, S. E., O’Neil, E., &

Merchant, S. N. (2006). Determinants of hearing loss in

perforations of the tympanic membrane. Otology

and

Neurotology

27(2), 136–143. https://doi.org/10.1097/

01.mao.0000176177.17636. 53

Voss, S. E., Rosowski, J. J., Merchant, S. N., & Peake, W.

T. (2001). Middle-ear function with tympanic-

membrane perforations. II. A simple model. The

Journal of the Acoustical Society of America, 110(3),

1445–1452. https://doi.org/10.1121/1.1394196

Zahnert, T., Hüttenbrink, K. B., Mürbe, D., & Bornitz, M.

(2000). Experimental investigations of the use of

cartilage in tympanic membrane reconstruction.

American Journal of Otology, 21(3), 322–328.

https://doi.org/10.1016/s0196-0709(00)80039-3

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

1172