Performance Evaluation using FLC to

Optimize the Output Power PV

Indhana Sudiharto, Farid Dwi Murdianto and Eni Wulandari

Department of Electrical Engineering, Electronic Engineering Polytechnic Institute of Surabaya, Surabaya, Indonesia

Keywords: Fuzzy Logic Controller, Solar Cell, Zeta Converter.

Abstract: The role of renewable energy is needed to support the necessity of electricity. One of the renewable energy is

solar power. Solar power is converted into electrical energy using a solar panel that produces DC electrical

energy. The unstable of the power is cause by the intensity of the sun and temperature on the surface that

fluctuate. The solution to the problem is needed a system to stabilize the power of the solar cell. A converter

with a controller in the circuit of a power stabilizer. In this paper, the selection of the converter is based on

the load requirements. The load requires a converter like a buck-boost converter. Zeta converter is the

converter that’s chosen in this paper. Zeta converter is a DC-DC converter that can produce increasing and

decreasing output voltage. But, the output voltage of zeta converter is unstable. Thus, the zeta converter

requires good control. In this paper is using Fuzzy Logic Controller. When the system is controlled by a fuzzy

logic controller the average error obtained from the system is 0.05% with the average efficiency is 99.44%

and the average time to achieve a steady state is 0.234 s. in addition to the test, this paper is comparing the

performance of the fuzzy controller with the PI controller. The error that’s obtained when the system is

controlled using a PI controller the average error of the system is 0.0026% with an average efficiency is

93.86% and the average time to achieve a steady state is 0.593s.

1 INTRODUCTION

Along with the times, electronic technology is

growing rapidly. But in reality, the more sophisticated

technology causes the consumption of electrical

energy that’s needed also increasingly large. The

increase in electricity consumption is not comparable

to the availability of fossil fuels. So, it needs

renewable energy to support the electrical energy.

Renewable energy has a lot of advantages. One of

them is friendly to the environment. Renewable

energy can also reduce waste. There are many types

of renewable energy. One of them is solar power

(Sudiharto I, 2018). A component that’s used to

convert solar power into electrical power is the solar

panel. Solar panel changes solar power into DC

electrical power. Factors that influence the power of

solar panels include the irradiation of the sun and the

temperature of the solar panel. Because the output

power is produced depends on the magnitude of the

sun’s intensity, so when the intensity of the sun

fluctuates the power that’s produced also fluctuates

(Farid Dwi Murdianto, 2018). So from the problem is

needed a system to stabilize the output power. The

converter with the controller is a circuit of a power

stabilizer. The converter is used based on the type of

load. The load requires a converter like a buck-boost

converter. Zeta converter is the converter that’s

chosen in this paper. A zeta converter is a converter

that converts electrical energy DC into electrical

energy DC with the value of the output voltage can be

higher or lower than the input voltage. This zeta

converter will transfer and stabilize the output power

of the PV (Soedibyo, 2015).

Figure 1: Block diagram system.

Figure 1 shows the overall system that is going to

be discussed in this paper. From the block diagram, it

can be seen that the zeta converter is controlled by the

Fuzzy Logic Controller. The fuzzy logic controller is

used to stabilize the output voltage of the zeta

Sudiharto, I., Murdianto, F. and Wulandari, E.

Performance Evaluation using FLC to Optimize the Output Power PV.

DOI: 10.5220/0010963500003260

In Proceedings of the 4th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2021), pages 1267-1275

ISBN: 978-989-758-615-6; ISSN: 2975-8246

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

1267

converter. This paper is comparing the performance

of the Fuzzy controller with the PI controller. When

the system is controlled by the fuzzy logic controller

the average error obtained from the system is 0.05%

with the average efficiency is 99.44%. then, when the

system is controlled using a PI controller of 0..26%

with an average efficiency is 93.68% (Indhana

Sudiharto, 2019).

2 SYSTEM MODELLING

2.1 Photovoltaic Module

The solar panel is a semiconductor component that

changes solar energy into DC electrical energy. The

solar panel has a working principle which is when the

sunlight hits the surface of the solar panel, electrons,

and holes will emerge (M. Z. Efendi, 2017). Electrons

and holes that arise around the p-n junction move

towards the n layer and towards the p layer. So that

the movement of electrons and holes arise potential

differences in the load and also arise an electric

current that flows through the load (S. Islam, 2014; S.

Siddiqua, 2016). When the solar panel gets the sun’s

light the electricity that’s generated from the ability

of the solar panel device to produce voltage when it

is given a load and current through the load. Factors

that influence the output voltage of the solar panels

other than sunlight are solar radiation and the angle of

incidence of sunlight (Sattianadan D., 2017).

In this paper is using solar panel 100 WP. So we

should know the specification solar panel 100 WP.

Here are the specifications of the solar panel 100 WP

that will be used

Voltage at Maximum Power : 17.8V

Open Circuit Voltage (V

) : 21.8V

Current at Maximum Power (I

) : 5.62A

Short Circuit Current (I

) : 6.05A

Maximum Power (P

max

) : 100WP

From the specification, it can be calculated the

component of the zeta converter.

2.2 Topology Zeta Converter

Zeta converter is one of the isolated DC to DC

converter that’s operated in CCM. Zeta converter has

a positive output voltage that operates like a buck-

boost converter (Falin, 2018). The following is a

picture of the working principle of zeta converter

when MOSFET is in “On” and “Off” conditions.

Figure 2: When MOSFET is “On State”.

Figure 2 shows that the MOSFET is in “On state”.

When the MOSFET “On state” diode is open, the

output voltage that’s connected in series with inductor

will charge the capacitor coupling. The value of

the voltage across the inductor is +V

, and the

voltage across the diode is V

+ V

OUT

(Ahana

Malhotra, 2016).

Figure 3: When MOSFET is “Off State”.

Figure 3 shows that the MOSFET is in “Off state”.

When the MOSFET is in “Off state”, the diode will

be closed, so the voltage that passes through the

inductor L

is the output voltage that’s connected in

parallel with the output capacitor. When the output

voltage fills the output capacitor, the voltage that will

pass through the MOSFET at “Off” condition is V

+ V

OUT

. The voltage that’s through in the inductor L

is the relative output voltage of the negative drain’s

MOSFET (Antonio M.S.S. Andrade, 2015).

From the circumstances which are when the

MOSFET “On state” and “Off state” can be obtained

equations that are used to determine the value of duty

and component values on the converter. Following is

the equation for calculating the duty value and

converter component value (Ashvini Admane, 2018;

U. Jayashree, 2017).

outin

out





(1)

inppL IKI







)(

(2)

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

1268

swppL







)(

(min)1(min)1

)

swinC

fVV







(min)

)

swoutC

fVV







)

swo

out





(min)

)

D : Duty cycle (%)

: Input voltage (v)

out

: Output voltage (v)

ΔI

: inductor current ripple (A)

: switching frequency (kHz)

: input current (A)

1a (min)

: inductor 1 (uH)

1b (min)

: inductor 2 (uH)

: input capacitor (uF)

ΔV

cin

: input capacitor voltage ripple (V)

: input capacitor (uF)

ΔV

: voltage ripple capacitor coupling (V)

: coupling capacitor (uF)

ΔV

: output voltage ripple (V)

OUT

: output capacitor (uF)

From equation 1 until 6 can be calculated the

value of the component zeta converter. Here’s the

calculation component of the zeta converter.

Input Voltage (V

) : 78 V

Switching Frequency (f

) : 100 kHz

Input Capacitor (C

) : 42.57 uF

Inductor Current Ripple (ΔIL

(PP)

) : 6 A

Inductor 1 (L

) : 47.97 uH

Coupling Capacitor (C

) : 22 uF

Inductor 2 (L

) : 47.97uH

Output Voltage Ripple (ΔV

OUT

) : 0.025 V

Output Capacitor (C

OUT

) : 36.9 uF

Output Voltage (V

OUT

) : 204.9

2.3 Modelling of Fuzzy Controller

There are several methods in the fuzzy logic

controller. In this paper is using Sugeno’s method.

The output of the fuzzy logic controller is a linear

equation (Indhana Sudiharto S. F., 2018).

Figure 4: Block diagram fuzzy logic controller.

Figure 4 shows a block diagram of the fuzzy logic

controller. There is a process tabulation of data in the

fuzzy logic controller. In the process of fuzzy, there

are stages in the planning consisting of fuzzification,

rule base, and defuzzification (Narendiran S., 2016).

The first stage determines the membership function

using 2 inputs, namely error, and delta error.

Figure 5: Design of membership function input “error”.

Figure 5 shows the design of membership

function input “error” using 7 membership functions.

Figure 6: Design of membership function input “delta

error”.

Figure 6 shows the design of membership

function input “delta error” using 7 membership

functions.

Figure 7: Design membership function output fuzzy

controller.

Figure 7 is the design of the membership function

output fuzzy controller which will be used to

determine the results of the IF-THEN rules structure.

After designing the membership function input

error, delta error, and output the next is designing a

Performance Evaluation using FLC to Optimize the Output Power PV

1269

rule base. This rule usually uses a statement if then

that describes as action in response to various fuzzy

inputs. The rules are written in the membership

function linguistic table pattern. The table consists of

two inputs is error and delta error as well as one

output (Epyk Sunarno, 2019). These rules can be

written in the form of a matrix as shown in Table 1.

Table 1: Design of rule base fuzzy.

Table 1 shows the design results of the rule base

Figure 8: The surface of the results rule base fuzzy.

Figure 8 shows the surface that gets f/rom the

design rule base fuzzy logic controller.

3 SIMULATION AND

DISCUSSION

The performance of the Fuzzy Logic Controller is

tested using simulation. The simulation of the zeta

converter with a fuzzy logic controller is shown in

Figure 9.

In this paper, the zeta converter is simulated using

Powersim Simulation (PSIM) software.

This simulation uses a solar cell as a source of

converter. Each solar cell has a power of 100WP. This

system requires 12 solar panels with 4 solar panels is

connected in series and 3 solar panels is connected in

parallel. So the amount of the input power is 1.2 kW

with the output voltage 78 V.

Figure 9: Simulation of zeta converter with Fuzzy Logic

Controller.

Figure 9 shows the zeta converter that has been

simulated with a fuzzy controller using 12 solar

panels. In the sub-circuit, there are 3 solar panels

which is 1 solar panel represents 4 solar panels that

are connected in series. The voltage at maximum

power (V

) is 17.8 V and the maximum power (P

max

)

is 100 Watts. After being simulated it can be seen the

response of the system when using controls without

disturbance or with disturbance. Besides that, it can

also be seen the comparison of responses to the

system when it is controlled using a fuzzy controller

and PI controller. In this paper, the load uses the

power setting. So, it uses the set point of power.

Figure 10: Response system when without control or using

duty manual 72.4%.

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

1270

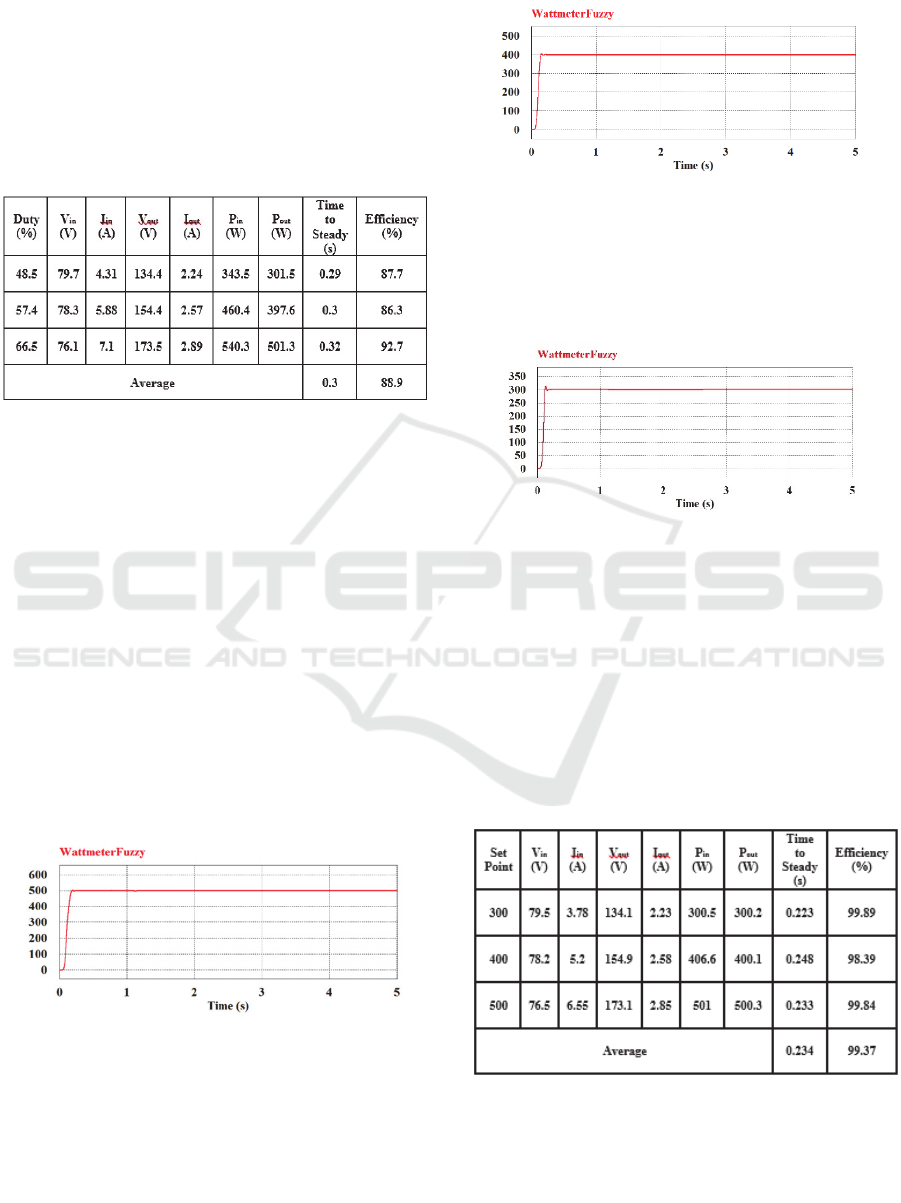
Figure 10 is the response when without control or

using duty according to the calculation that is 72.4%.

it can be seen that at 72.4% duty, the output power is

707.49 watts. So it must be set manually according to

the set point that’s used. Figure 10 has been simulated

with the output power is 301.5 watts, 397.6 watts, and

501.3 watts. The results of this simulation can be seen

in the Table 2.

Table 2: The results of the simulation open loop system.

Table 2 is the results of the simulation when the

system is in an open-loop or without control. This

open-loop condition was initially carried out by

calculating the amount of duty when the output power

was 300 watts, 400 watts, and 500 watts. After

knowing the value of duty through the design, then it

is simulated to validate whether the value of the duty

is according to the output power. If it is not

appropriate the value of duty is changed manually by

estimating the value.

Table 2 also presents efficiency without control.

The resulting average efficiency value is 88.97% and

the average time to achieve steady-state is 0.3 s. The

resulting efficient value is not optimal so that the

control is needed to be more optimal.

Because the output power in the simulation value

is greater than the desired design, control is needed.

This paper uses a fuzzy logic controller.

Figure 11: Response system is controlled by fuzzy at set

point 500 watts.

Figure 11 is the response when the system is

controlled by a fuzzy controller with the set point 500

watts. At the set point 500 watts, it turns out that the

value of duty obtained is smaller than the value of

design duty. So the output power on the system is

according to the set point that’s wanted.

Figure 12: Response system is controlled by fuzzy at set

point 400 watts.

Figure 12 is the response when the system is

controlled by a fuzzy controller with a set point of 400

watts. It can be seen that the wattmeter shows the

power is according to the set point that’s wanted.

Figure 13: Response system is controlled by fuzzy at set

point 300 watts.

Figure 13 is the response of the system when the

system is controlled by a fuzzy controller with a set

point of 300 watts. It can be seen the value of the

response is according to the set point value that’s

given.

The results of the simulation from figure 11,

figure 12, figure 13 can be seen in Table 3.

Table 3: Results of the simulation when closed-loop system

or using fuzzy logic controller.

Table 3 is the results of the simulation using a

fuzzy logic controller. The working principle of this

fuzzy controller is increasing duty if the power of the

converter is smaller than the set point. And will

reduce the duty cycle if the power of the converter is

Performance Evaluation using FLC to Optimize the Output Power PV

1271

greater than the set point. In this case, the fuzzy

controller is expected to optimize the output power so

that the resulting efficiency is better than the open-

loop system. It can be seen in the table the average

efficiency values when using this fuzzy controller are

99.37%.

In the table 3, shows the time that’s needed to

achieve a steady-state. The average time to achieve a

steady-state on this control is 0.234 seconds.

After the system is given control so that the value

of the output system is according to the set point.

Then the system is given a disturbance on the input

side. Disturbance in the form of changes in solar

irradiation. The purpose is to test the reliability of the

control that’s used. Reliability can be seen whether

when the disturbance complete, the system can return

to the initial set point.

Figure 14: Response system is controlled by fuzzy when

there’s disturbance with set point 500 watts.

Figure 14 shows the response of the system with

fuzzy control when there is disturbance. The set point

of the system is 500 watts. Disturbance is given in

seconds 2 to 2.5. So that after 2.5 seconds the system

will return to the initial set point.

Figure 15: Response system is controlled by fuzzy when

there’s disturbance with set point 400 watts.

Figure 15 shows the response when it is controlled

by a fuzzy controller when there is a disturbance. The

set point of the system is 400 watts. At the set point

400 watts, the disturbance is smaller than the

disturbance at the set point 500 watts.

Figure 16: Response system is controlled by fuzzy when

there’s disturbance with set point 300 watts.

Figure 16 is the response of the system that’s

controlled by a fuzzy controller when there is a

disturbance. The set point of the system is 300 watts.

The resulting response is not so visible because the

value of the input power system is greater than the

desired output power.

In addition to testing the reliability of control by

giving disturbance, the control that’s used in this

paper can also be tested by comparing when the

system uses the PI controller.

Figure 17: Response system when it’s controlled by PI

controller at set point 500 watts.

Figure 17 shows the response system when the

system is controlled by the PI controller. The set point

of the system is 500 watts. It can be seen in the

response that the output power is stable at a value of

500 watts. And even though it's already stable, there's

still an error.

Figure 18: Response system when it’s controlled by PI

controller at set point 400 watts.

Figure 18 shows the response of the system when

controlled by the PI controller. The second set point

of the system is 400 watts. The set point is used to

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

1272

control the power to be stable. It can be seen the

response system is stable at a value of 400 watts.

Nevertheless, there is still an error.

Figure 19: Response system when it’s controlled by PI

controller at set point 300 watts.

Figure 19 shows the response of the system when

the system is controlled by the PI controller. The last

set point of the system is 300 watts. From the set

point, it can be seen that the output power is more

stable at values close to 300 watts.

The results of the simulation from figure 17,

figure 18, figure 19 can be seen in Table 4.

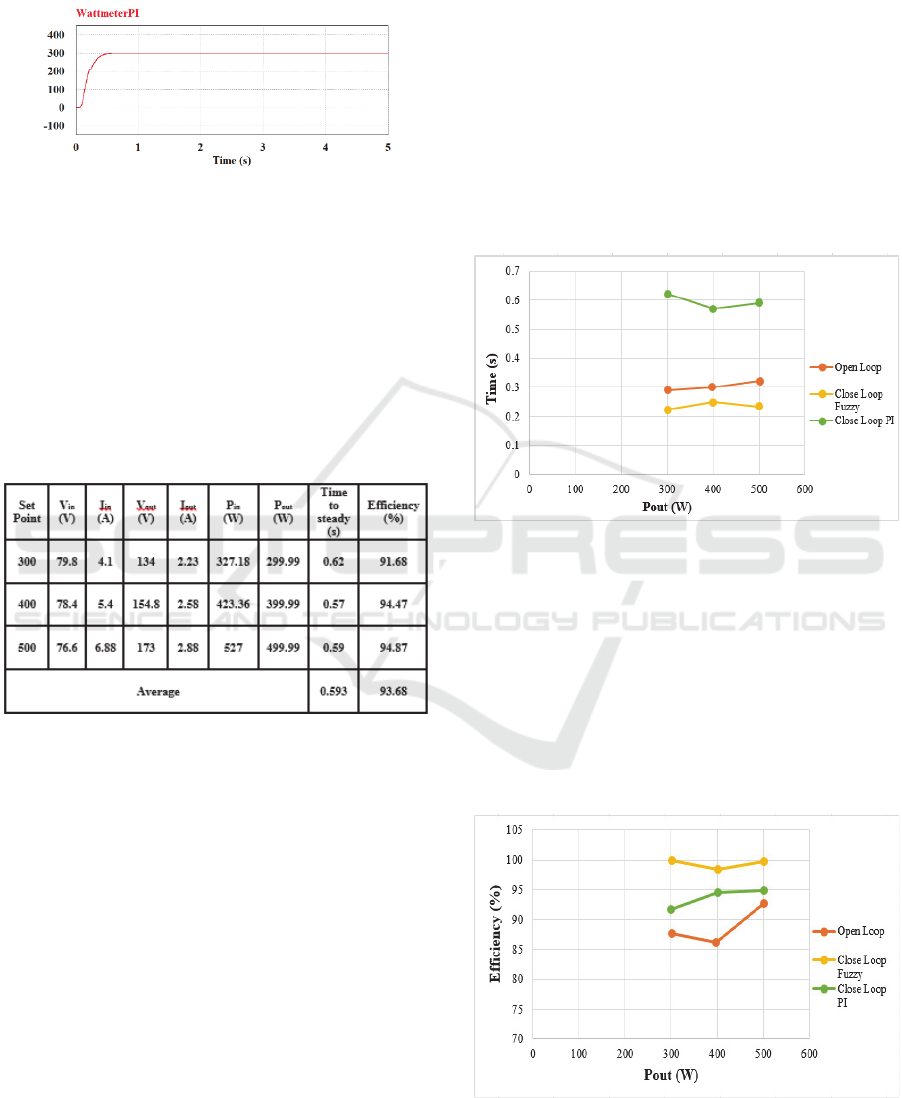
Table 4: Results of the simulation close loop system PI

controller.

Table 4 is the results of the simulation when the

close loop system. This close loop system is

controlled by the PI controller. From the table can be

seen the output power is according to the set point.

Where the working principle of the PI controller is the

same as the Fuzzy Logic Controller. When the output

power is smaller than the set point, the control will

automatically increase the duty cycle. And if the

output power is greater than the set point, the control

will automatically reduce the duty cycle. So that the

output power is according to the set point and it is

expected that the error value between the set point and

the reference is small. From this small error, the

average efficiency on the system is better than the

average efficiency of the system in the open-loop

condition but this efficiency of the system is smaller

than the average efficiency in the close loop system

using a fuzzy logic controller. The average efficiency

of the close loop system that is controlled by the PI

controller is 93.68%.

Table 4 can also be seen that the average time the

control to achieve a steady-state is 0.593 seconds. So

for optimizing efficiency and also speed up time to

achieve a steady-state, on the system need the control

to be improved by using a controller that can produce

smaller errors.

From table 2, table 3 and table 4 can be compared

that the fuzzy controller can optimize output power

and produce greater efficiency than the PI controller.

And the time to achieve a steady-state on the fuzzy

controller is faster than the PI controller. The

comparison can be seen in the graphic.

Figure 20: The graph of the comparison time to achieve

steady-state when open-loop system, close loop system

using FLC, and close loop system using the PI controller.

Figure 20 shows the comparison time to achieve

steady-state when the open-loop system, close loop

system using a PI controller, and close loop system

using FLC. That graphic. From that picture, it can be

seen that the fastest time to achieve a steady-state is a

close loop system using FLC. And the longest time to

achieve a steady-state is a close loop system using PI

Controller.

Figure 21: The graph of the comparison efficiency when

open-loop system, close loop system using FLC, and close

loop system using the PI controller.

Performance Evaluation using FLC to Optimize the Output Power PV

1273

Figure 21 shows the comparison efficiency when

the open-loop system, close loop system using a PI

controller, and close loop system using FLC. From

that picture, it can be seen that the value of the biggest

efficiency is a close loop system using FLC. And the

value of the smallest efficiency is an open-loop

system.

4 CONCLUSION

In this paper, the Fuzzy Logic Controller controls the

zeta converter with the set points of 300 watts, 400

watts, and 500 watts. The results of the simulation

indicate that the system is controlled by fuzzy works

well. This can be compared when the system is

without control. The value of the output power is not

according to the calculation of output power. So the

system is controlled to the output power is stable.

When the system is controlled, it is necessary to test

the reliability of the control. Control reliability testing

is done by giving disturbance in seconds 2 to 2.5 s.

After 2.5 s, the system will return to the initial set

point. From the results of the simulation, it is shown

that the fuzzy controller requires an average time to

achieve the set point of 0.234 s. While in the PI

controller, the time that’s needed to achieve the set

point was 0.593 s and the results of the simulation

when the system without control requires an average

time to achieve the set point of 0.3 s. The average

error of the system that is controlled by fuzzy is

0.05% with the efficiency obtained by 99.37%. While

the average error of PI is 0.002% with an efficiency

obtained of 93.68%. And the last, the average error

without control is 0.453% with an efficiency obtained

of 88.97%. So the time is needed for the fuzzy

controller to achieve a steady is faster than the time

needed for the PI controller to achieve steady-state

(Anjaly DAS, 2018)Also, it can be said that Fuzzy

control is suitable for increasing the efficiency of the

zeta converter.

REFERENCES

Sudiharto, Indhana; Sunarno, Epyk; Farid Dwi; Kurniasari,

Desy Nanda (2018). Robustness Analysis of PI

Controller to Constant Output Power with Dynamic

Load Condition in DC Nanogrid System. IEEE 2018

3rd International Conference on Information

Technology, 402-405.

Farid Dwi Murdianto; Moh. Zaenal Efendi; Kukuh

Widarsono; Miftahul Azizi (2018). Robustness

Analysis of PID Controller Bidirectional SEPIC/ZETA

for Energy Management in DC Nanogrid Isolated

System, IEEE 2018 3rd International Conference on

Information Technology, Information and Electrical

Engineering, 406-411.

Soedibyo; Budi Amri; Mochamad Ashari (2015). The

Comparative Study of Buck-Boost, CUK, Sepic, and

Zeta Converters for Maximum Power Point Tracking

Photovoltaic Using P&O Method, IEEE 2015 2nd

International Journal of Int. Conference on Information

Technology, Computer and Electrical Engineering,

327-332.

Indhana Sudiharto; Epyk Sunarno; Farid Dwi Murdianto;

Eni Wulandari (2019). Robustness Analysis of PI

Controller to Optimizing the Output Power for Energy

Management in DC Microgrid System, IEEE 2019 2nd

International Conference on Applied Information

Technology and Innovation, 105-110.

M. Z. Efendi, F. D. Murdianto, and R. E. Setiawan (2017).

Modelling and Simulation of MPPT Sepic Converter

using Modified PSO to Overcome Partial Shading

Impact on DC Microgrid System, IEEE 2017

International Electronics Symposium on Engineering

Technology and Application, 27-32.

S. Islam, S. B. Azad, H. Fakir and R. Rahman, A. Azad

(2014). Development of Electric Stove for the Smart

Use of Solar Photovoltaic Energy, IEEE 2014

International Journal of Region 10 Humanitarian

Technology Conference, 94-98.

S. Siddiqua, S. Firuz, B. M. Nur, R. J. Shaon, S. J.

Chowdhury, and A. Azad (2016). Development of

Double Burner Smart Electric Stove Powered by Solar

Photovoltaic Energy, IEEE 2016 International Journal

of Global Humanitarian Technology Conference, 451-

458.

Sattianadan D., Roopam Jha, Deepak Kumar Nayak (2017).

Maximum Power Point Tracking for a Grid Connected

Photovoltaic System using Sliding Mode Control, IAES

Core International Journal of Power Electronics and

Drive Systems, Vol. 8, 1785-1792.

Jeff Falin (2014). Designing DC/DC Converter based on

Zeta Topology, analog application Journal Texas, 121-

128.

Ahana Malhotra, Shitiz Vij, Dr. Prerna Gaur, Charvi

Malhotra (2016). Design, Analysis and Performance of

Zeta Converter in Renewable Energy Systems, IEEE

2016 International Conference on Computing for

Sustainable Global Development.

Antonio M.S.S. Andrade, Luciano Schuch, Mario L. da S.

Martins (2015). Photovoltaic Battery Charger based on

Zeta Converter : Analysis, Design and Experimental

Results, IEEE 2015 24th International Symposium on

Industrial Electronics, 379-384.

Ashvini Admane, Dr. Harikumar Naidu (2018). Analysis

and Design Of Zeta Converter, International Journal

for Innovative Research in Multidisciplinary Field,

Vol. 4, 161-167.

U. Jayashree, R. H. Pearl Nightingale, S. Divya (2017).

Implementation of basic MPPT techniques for zeta

converter, IEEE 2017 3rd International Conference on

iCAST-ES 2021 - International Conference on Applied Science and Technology on Engineering Science

1274

Science Technology Engineering & Management, 601-

604.

Indhana Sudiharto, Sutedjo, Farid Dwi Murdianto, Epyk

Sunarno, Syechu Dwitya Nugraha, Ony Asrarul Qudsi

(2018). Design and Implementation Unipolar SPWM

FullBridge Inverter Using Fuzzy Sugeno in DC

Microgrid Isolated System, IEEE 2018 3rd

International Conference on Information Technology,

Information Systems and Electrical Engineering, 368-

373.

Narendiran S., Sarat Kumar Sahoo, Raa Das, Ashwin

Kumar Sahoo (2016). Fuzzy Logic Controller based

Maximum Power Point Tracking for PV System, IEEE

2016 3rd International Conference on Electrical

Energy System, 29-34.

Epyk Sunarno, Indhana Sudiharto, Syechu Dwitya

Nugraha, Farid Dwi Murdianto, Suryono, Ony Asrarul

Qudsi (2019). Design and Implementation

Bidirectional SEPIC/ZETA Converter using Fuzzy

Logic Controller in DC Microgrid Application,

IOPscience 2019 International Converence on

Engineering, Technology and Innovative Researches,

1-7.

Anjaly DAS, Khrisnakumari T. (2018). Comparison of PI

Controller and Fuzzy Logic Controller for The

Improvement of Power Factor In Smps, IEEE 2018 2nd

International Conference on Inventive Communication

and Computational Technologies, 1597-1602.

Performance Evaluation using FLC to Optimize the Output Power PV

1275