The Scatter of Retinal Position Affects the Formation of Orientation

Map

Chong Jiao

, Ming Li

and Dewen Hu

College of Intelligence Science and Technology, National University of Defense Technology, Changsha, Hunan, China

Keywords: Visual Cortex, Orientation Map, MDS, Pinwheel, Salt-And-Pepper Map.

Abstract: The neurons in the primary visual cortex of mammals have been found to have significant orientation

selectivity. In the higher mammals, the neurons with similar preferred orientation clustered together to form

a pinwheel-like pattern, which is thought as a strategy to reduce wiring cost. In contrast, the preferred

orientation of neurons in rodents are randomly distributed, which is termed as salt-and-pepper map. Why the

mammals have such two distinct organizational pattern remains to be explored and this will be important for

understanding the principles of the visual information processing in cortex. In this paper, we used a

multidimensional scaling (MDS) model to study the spatial distribution of the preferred orientation and

retinotopic position with the objective of minimizing wiring cost. Our results suggested that the scatter of

retinotopic position in an orientation column was a critical factor on the formation of pinwheel map or salt-

and-pepper map; higher mammals with ordered retinotopic position tend to have continuous map while

rodents with relatively larger scatter of retinotopic position tend to have random map.

1 INTRODUCTION

Even though the deep learning (LeCun et al. 2015)

technology has achieved incredible performance on

many vision tasks, it still suffers from problems such

as overfitting and lack of explanation (Krizhevsky et

al. 2017). The study on the information processing in

the biological visual system will provide an

opportunity to solve these problems and will be an

important step towards general artificial intelligence

(Bashivan et al. 2019, George et al. 2017). This paper

focus on the organization of orientation map in the

primary visual cortex of mammals. Neurons in the

primary visual cortex of mammals have significant

orientation selectivity (Hubel and Wiesel 1962,

Hubel and Wiesel 1959); only the light stimuli at the

preferred orientation could evoke the response of

neurons most effectively. In the higher mammals

including carnivorous and primates, the neurons with

similar orientation will cluster together to form a

highly ordered pinwheel-like pattern (Bonhoeffer and

Grinvald 1991, Ohki et al. 2006). Specifically, the

orientation preference of neurons gradually changes

https://orcid.org/0000-0002-3504-9707

https://orcid.org/0000-0002-9471-9897

across the cortex to form pinwheel-like patters where

orientation changes from 0 degree to 180 degrees

around the pinwheel center, clockwise or

anticlockwise. In contrast, the neurons in the primary

visual cortex of rodents are randomly distributed

irrespective of the orientation preference (Ohki et al.

2005), which is termed as salt-and-pepper map. The

study on why this distinct orientation map exist in the

mammals will help us understand the principles of

visual information processing in the cortex.

There have been many models developed to study

the origin of pinwheel map, such as the simple spin

model (Cowan and Friedman 1990), dimension

reduction model (Durbin and Mitchison 1990) and

the coordinated map including multi-features(Yu et

al. 2005). These models achieved realistic map like

the experimental findings. However, they did not

explain why the rodents lacks orientation map.

Recently, Weigand proposed a multi-dimensional

(MDS) model to study the difference of orientation

map in rodents and higher mammals (Weigand et al.

2017), and suggested the number of cells could be an

important factor leading to the difference of

orientation map. However, their model did not agree

https://orcid.org/0000-0001-7357-0053

146

Jiao, C., Li, M. and Hu, D.

The Scatter of Retinal Position Affects the Formation of Orientation Map.

DOI: 10.5220/0011206800003444

In Proceedings of the 2nd Conference on Artiﬁcial Intelligence and Healthcare (CAIH 2021), pages 146-151

ISBN: 978-989-758-594-4

with the experimental observation very well

(Ibbotson and Jung 2020) because they overlooked

other features of neurons; for instance, retinotopic

position was also an prominent feature of neurons in

the primary visual cortex..

In this paper, we extend the MDS model to study

the map of retinotopic position and orientation

preference simultaneously. We optimized the spatial

distribution of these two tuning properties by

minimizing the wiring cost, equivalently speaking, by

putting neurons with similar tuning preference

together. Our results suggested that the competition

between retinotopic position and orientation could

explain the emergence of pinwheel map and salt-and-

pepper map. Specifically, the scatter of retinotopic

position in an orientation column was a critical factor

on the formation of pinwheel map or salt-and-pepper

map; higher mammals with ordered retinotopic

position tend to have continuous map of orientation

while rodents with relatively larger scatter of

retinotopic position tend to have random map.

2 METHODS

From the view of dimension reduction framework

(Durbin and Mitchison 1990), the visual map can be

thought as a projection from high dimensional feature

space onto the two dimensional cortex surface.

Similar features should be mapped in close vicinity to

reduce wiring cost (Weigand et al. 2017) and enhance

robust computation (Stringer et al. 2019). This

motivated us to compare the optimal placement of

orientation preference of neurons with the observed

orientation map in the experiments, which will help

us to understand the mechanisms behind the neuronal

map. Specifically, we tried to obtain the optimal

orientation map by placing neurons according to their

tuning similarity and studied which factor leads to the

emergence of pinwheel-like map like in higher

mammals or random map like in rodents. MDS is a

classical method to transform the inputs from the high

dimensional space to subspace while preserving the

distance in the original space (Borg and Groenen

2005), which has been successfully used to study the

spatial distribution of orientation preference

(Weigand et al. 2017). However, they only

considered the spatial distribution according to the

orientation similarity but ignoring the contribution of

other tuning properties to the final spatial

distribution. In fact, the feature maps, especially the

retinotopic position and orientation preferences, are

strongly dependent (Durbin and Mitchison 1990, Yu

et al. 2005).

In this paper, we extend the method to study the

spatial distribution of both the orientation preference

and retinotopic position simultaneously. The method

is illustrated in Figure 1. The receptive field

properties (including retinotopic position,

orientation, spatial frequency et al) are represented by

a vector 𝑣



. We defined the connection probability of

two neurons based on their tuning similarity as in

equation (1).

𝜌(𝑖, 𝑗) = 𝑎 + 𝑏 ∗ 𝑒



∥







∥







(1)

Where a is the constant connection probability

between two arbitrary neurons, b is the gain of the

selectivity. The feature selectivity is controlled by the

parameter 𝜎, which is illustrated in figure 2. With a

random process defined with the connection

probability, we could obtain the binary connection

matrix C.

Spatial distribution

of cells

High dimensional

feature space

Binary connection

matrix

MDS

Figure 1: Method to obtain the optimal spatial distribution with MDS model.

To get the dissimilarities of each paired neurons,

we used Jaccard distance in equation (2) as the feature

distance, which was the same as in previous study

(Weigand et al. 2017).

JD = 1 −

|𝑪



⋂𝑪



|𝑪



⋃𝑪



(2)

Where 𝑪



is the set of all other neurons which

has a connection with neuron i. With the

dissimilarities defined for each pair of neurons, we

could use the metric MDS to get the spatial

distribution of these neurons in a two-dimensional

space. the whole process was illustrated in Figure 1.

Our method is an modification to the method in

The Scatter of Retinal Position Affects the Formation of Orientation Map

147

(Weigand et al. 2017) to support the high dimensional

feature space rather than only orientation for the

original method.

In this paper, we studied the retinotopic position

and orientation preference simultaneously. The

feature vector can be defined as a 4-dimensional

vector as (𝑥, 𝑦, 𝑟 ∗ cos(2𝜃), 𝑟 ∗ sin(2𝜃)), where x

and y denote the cartesian coordinates of retinotopic

position, 𝜃 denotes the preferred orientation and r is

the orientation selectivity. The MDS operation was

implemented by the mdscale function in Matlab.

Figure 2: Connection probability function with different

feature selectivity.

3 EXPERIMENTAL RESULTS

3.1 Spatial Distribution of Orientation

Preference

We first studied the spatial distribution when only

considering the orientation preference. With the

method in section 2, we first defined the feature

vector as ( 𝑟 ∗ cos(2𝜃), 𝑟 ∗ sin(2𝜃)) , where 𝜃

denotes the preferred orientation. We studied the

impact of orientation selectivity 𝜎 and the number

of cells N on the final spatial distribution. All the

preferred orientation was uniformly distributed in

(0, 𝜋).

Figure 3: Pinwheel patterns emerges with increasing

number of cells or greater orientation selectivity.

With the MDS transformation (see Methods), the

results are illustrated in Figure 3. The color of each

cell is assigned according to their orientation

preference, which was illustrated in the bottom right

corner. It can be seen in Figure 3 that increasing the

selectivity (decreasing 𝜎, from left to right) will lead

to the emergence of pinwheel map. In addition,

increasing the number of cells (from top to bottom)

will also result in the appearance of pinwheel pattern.

Our results is similar to the report in(Weigand et al.

2017), which proved our adaptation to

multidimension model was valid. However, this

results was not fully consistent with the experimental

observation (Ibbotson and Jung 2020). Part of the

reason was that this modelling methods ignored the

interdependence of cortex maps, which had been

found in the experimental results. For instance, the

orientation, ocular dominance, and spatial frequency

domains has been demonstrated a clear influence of

each other (Yu et al. 2005). This motivated us to

model multi-features simultaneously.

3.2 The Spatial Distribution of

Retinotopic Position

Figure 4: The spatial distribution of retinotopic position

becomes ordered with increasing number of cells or feature

selectivity.

Besides the orientation, one of the most prominent

features is the retinotopic position. Thus, we further

studied the distribution of retinotopic position with

the same method. The feature space is a two-

dimensional vector defined as (x, y), which are the

cartesian coordinates of retinotopic position

respectively. In this model, both of x and y were

CAIH 2021 - Conference on Artiﬁcial Intelligence and Healthcare

148

uniformly distributed in the range of (0, 1). The

results are illustrated in figure 4. The colors from blue

to red corresponds to the value of 0 to 1. For each

parameter combination, top panel denotes the

distribution of x and the bottom panel denotes the

distribution of y. It can be seen in Figure 4 that the

ordered map appeared when increasing the number of

cells (from top to bottom) or increasing the feature

selectivity (from left to right), which was similar to

the results on the orientation distribution. An

interesting finding is that the gradient of x and y is

near orthogonal to each other in the ordered map

(bottom right) even though we did not constrain their

relation explicitly, which suggested our model could

capture the dependent relations of different features.

3.3 Mapping the Orientation and

Retinotopic Position

Simultaneously

We further studied the spatial distribution of

retinotopic position and preferred orientation

simultaneously to study the interdependence of both

cortex maps. The feature space is defined as

(𝑥,𝑦,𝑟∗𝑐𝑜𝑠(2𝜃),𝑟∗𝑠𝑖𝑛(2𝜃))(see Methods). The

range of the retinotopic position reflect the scatter of

retinotopic position in the orientation column. Thus,

we define the domain of x and y as (0, SZ), where SZ

defined the scatter of retinotopic position in the

orientation column. We set the number of cells

N=300 and feature selectivity 𝜎=1.2. With this

configuration, both distribution of retinotopic

position and orientation should appear as an ordered

map if we consider these features independently (see

Figure 3 and Figure 4). We want to know the impact

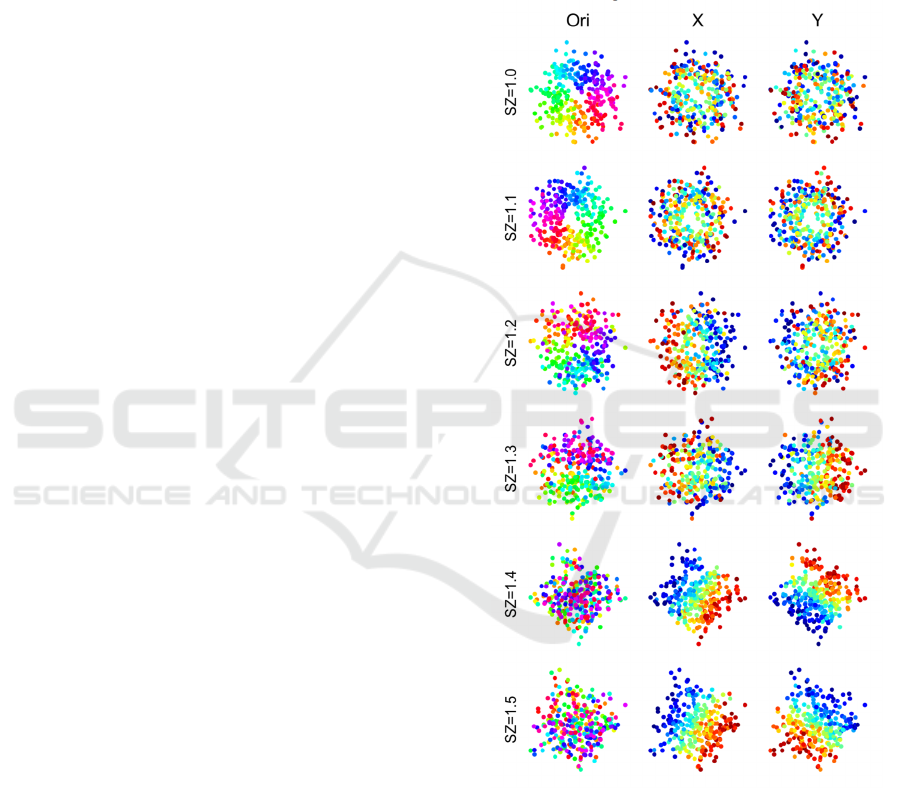
of SZ on the optimal spatial distribution. The results

can be seen in Figure 5 that, when increasing the SZ,

the retinotopic position gradually dominates the

spatial distribution of neurons and the pinwheel map

of orientation in the first row became randomly

distributed.

This situation was reminiscent of the

experimental results that rodents tend to have greater

scatter of retinotopic position compared to cat or

Macaque (Marshel et al. 2011, Schuett et al. 2002,

Van den Bergh et al. 2010), which suggested the

scatter of retinotopic position might be an important

factor to the emergence of orientation map.

To quantify the pinwheel pattern, we used the

correlation coefficients between preferred orientation

and azimuth in the spatial distribution. This index was

also used by the previous research (Ohki et al. 2006,

Weigand et al. 2017). To obtain the correlation

coefficients between orientation and azimuth, we

denoted the preferred orientation at the azimuth of 𝜋

as 𝜋/2, and the subtract this orientation to obtain the

preferred orientation relative to this angle. To reduce

the estimation error, we only consider the cells which

lie at the azimuth in the range of (𝜋/4, 7𝜋/4). The

results were shown in Figure 6 and it can be seen that

the linear correlation gradually disappeared when

increasing the SZ, which was in agreement with the

observation in Figure 5.

Figure 5. The spatial distribution of tuning preferences

including orientation (Ori) and retinotopical position (X

and Y) changes with the scatter size in an orientation

column.

The Scatter of Retinal Position Affects the Formation of Orientation Map

149

Figure 6. The scatter plot of preferred orientation (Ori)

versus azimuth for different scatter size.

We further explored the change of the squared of

correlation coefficients (𝑅



) with the scatter (SZ). We

computed the corresponding 𝑅



for SZ in the range

of (1.0, 1.5) and repeat 15 times for each parameter

configuration. Figure 7 gave the variation curve of

𝑅



with the change of SZ. It was clear that the 𝑅



had a sharp decrease when the SZ exceed some value,

which suggested a transition of orientation map from

pinwheel-like pattern to a totally random map.

Figure 7. The squared correlation coefficients ( 𝑹

𝟐

)

decreases with scatter size; the shadow area indicates

standard bias; the sharp decrease of 𝑹

𝟐

indicates a

transition from pinwheel-like map to a totally random map.

4 CONCLUSIONS

In this paper, we extend the MDS model (Weigand et

al. 2017) to study the optimal placement of

retinotopic position and orientation simultaneously

with the objective of minimizing wiring cost. Our

first result revealed that the feature selectivity and the

number of cells were both important factors for the

emergence of ordered map, which was consistent

with previous study (Weigand et al. 2017). Moreover,

we further extended this model and found that when

considered the orientation preference and retinotopic

position simultaneously, the scatter of retinotopic

position had great impact on the appearance of

pinwheel map. In particular, when the scatter of

retinotopic position exceed some threshold, the

pinwheel map sharply disappeared and deteriorated

into a random map. In fact, the study on mouse

retinotopic mapping indeed showed a larger scatter

compared with cat (Garrett et al. 2014). Our results

also were in consistent with the report that the central-

to-peripheral ratio (CP ratio) of retinal cell density

can be used to predict the pinwheel map (Ibbotson

and Jung 2020). The central vision tends to have

greater cortical magnification factor and less scatter.

This means that mammals with higher CP ratio will

have less scatter in the central vision thus having a

greater chance to form pinwheel map. Recent study

on mouse also found a cortex region with enhanced

spatial resolution like the fovea of higher mammals

(van Beest et al. 2021), which suggested that the

functional architecture of visual cortex of higher

mammals and rodents might not have huge difference

as previously thought. Our results implied that the

pinwheel map of higher mammals and random map

of rodents might emerge with the scatter of

retinotopic position even though they have no

difference in the organizational principles.

However, a through survey and quantitative

estimate of the degrees of scatter for mammals is

required to obtain a solid conclusion. Besides the

retinotopic position and orientation, the ocular

dominance and spatial frequency are also important

features for neurons in the primary visual cortex.

Experimental studies suggested that these functional

maps had subtle interdependent relations (Nauhaus et

al. 2016, Nauhaus et al. 2012). A comprehensive

model including all of these factors might provide

insights about the organization of cortex map of

mammals.

ACKNOWLEDGEMENTS

This research was funded by the National Natural

Science Foundation of China, grant number

6207022592.

REFERENCES

Bashivan, P., Kar, K., DiCarlo, J.J. (2019). Neural

population control via deep image synthesis. Science.

364, eaav9436.

CAIH 2021 - Conference on Artiﬁcial Intelligence and Healthcare

150

van Beest, E.H., Mukherjee, S., Kirchberger, L., Schnabel,

U.H., van der Togt, C., Teeuwen, R.R.M., Barsegyan,

A., Meyer, A.F., Poort, J., Roelfsema, P.R., et al.

(2021). Mouse visual cortex contains a region of

enhanced spatial resolution. Nat Commun. 12, 4029.

Bonhoeffer, T., Grinvald, A. (1991). Iso-orientation

domains in cat visual cortex are arranged in pinwheel-

like patterns. Nature. 353, 429–431.

Borg, I., Groenen, P.J.F. (2005). Modern multidimensional

scaling: theory and applications. 2nd ed. (New York:

Springer),.

Cowan, J.D., Friedman, A.E. (1990). Simple Spin Models

for the Development of Ocular Dominance Columns

and Iso-Orientation Patches. NIPS. In NIPS, .

Durbin, R., Mitchison, G. (1990). A dimension reduction

framework for understanding cortical maps. Nature.

343, 644–647.

Garrett, M.E., Nauhaus, I., Marshel, J.H., Callaway, E.M.

(2014). Topography and Areal Organization of Mouse

Visual Cortex. J Neurosci. 34, 12587–12600.

George, D., Lehrach, W., Kansky, K., Lázaro-Gredilla, M.,

Laan, C., Marthi, B., Lou, X., Meng, Z., Liu, Y., Wang,

H., et al. (2017). A generative vision model that trains

with high data efficiency and breaks text-based

CAPTCHAs. Science. 358, eaag2612.

Hubel, D.H., Wiesel, T.N. (1959). Receptive fields of

single neurones in the cat’s striate cortex. J Physiol.

148, 574–591.

Hubel, D.H., Wiesel, T.N. (1962). Receptive fields,

binocular interaction and functional architecture in the

cat’s visual cortex. J Physiol. 160, 106–154.

Ibbotson, M., Jung, Y.J. (2020). Origins of Functional

Organization in the Visual Cortex. Front Syst Neurosci.

14, 10.

Krizhevsky, A., Sutskever, I., Hinton, G.E. (2017).

ImageNet classification with deep convolutional neural

networks. Commun ACM. 60, 84–90.

LeCun, Y., Bengio, Y., Hinton, G. (2015). Deep learning.

Nature. 521, 436–444.

Marshel, J.H., Garrett, M.E., Nauhaus, I., Callaway, E.M.

(2011). Functional specialization of seven mouse visual

cortical areas. Neuron. 72, 1040–1054.

Nauhaus, I., Nielsen, K.J., Callaway, E.M. (2016). Efficient

Receptive Field Tiling in Primate V1. Neuron. 91, 893–

904.

Nauhaus, I., Nielsen, K.J., Disney, A.A., Callaway, E.M.

(2012). Orthogonal micro-organization of orientation

and spatial frequency in primate primary visual cortex.

Nat Neurosci. 15, 1683–1690.

Ohki, K., Chung, S., Ch’ng, Y.H., Kara, P., Reid, R.C.

(2005). Functional imaging with cellular resolution

reveals precise micro-architecture in visual cortex.

Nature. 433, 597–603.

Ohki, K., Chung, S., Kara, P., Hübener, M., Bonhoeffer, T.,

Reid, R.C. (2006). Highly ordered arrangement of

single neurons in orientation pinwheels. Nature. 442,

925–928.

Schuett, S., Bonhoeffer, T., Hübener, M. (2002). Mapping

retinotopic structure in mouse visual cortex with optical

imaging. J Neurosci Off J Soc Neurosci. 22, 6549–

6559.

Stringer, C., Pachitariu, M., Steinmetz, N., Carandini, M.,

Harris, K.D. (2019). High-dimensional geometry of

population responses in visual cortex. Nature. 571,

361–365.

Van den Bergh, G., Zhang, B., Arckens, L., Chino, Y.M.

(2010). Receptive-field Properties of V1 and V2

Neurons in Mice and Macaque monkeys. J Comp

Neurol. 518, 2051–2070.

Weigand, M., Sartori, F., Cuntz, H. (2017). Universal

transition from unstructured to structured neural maps.

Proc Natl Acad Sci. 114, E4057–E4064.

Yu, H., Farley, B.J., Jin, D.Z., Sur, M. (2005). The

Coordinated Mapping of Visual Space and Response

Features in Visual Cortex. Neuron. 47, 267–280.

The Scatter of Retinal Position Affects the Formation of Orientation Map

151