Research on the Effect of Psammotherapy on the Pulsating Flow of

Conical Curved Femoral Artery

Rongchang Fu

a

and Xiaoke Han

b

School of Mechanical Engineering, Xinjiang University, Huarui Street777, Urumqi, China

Keywords: Fluid-Solid Coupling, Wall Shear Stress, Tapered Blood Vessel, Psammotherapy, Von-Mises Equivalent

Stress.

Abstract: Objective This paper is to study the effect of psammotherapy on the hemodynamicsof the conical curved tube

of the femoral artery in humans, and further reveal the mechanism of psammotherapy from the perspective of

hemodynamics. Methods Based on CT images of the human aorta, a three-dimensional finite element model

of the conical curved tube of the femoral artery was established, and the heart rate, the peak velocity and the

inner diameter of the femoral artery measured in the experiment were used as initial conditions and boundary

conditions for finite element numerical simulation, then the blood flow velocity, wall shear stress and Von

Mises stress of curved blood vessels before and after psammotherapy were obtained and compared. Results

The blood flow velocities of the conical curved femoral artery increased by 18%, 29%, 19% and 45% at

t=0.15 min, 0.30 min, 0.45 min and 0.60 min after psammotherapy compared with before psammotherapy;

the flow velocity of secondary reflux was significantly weakened, and the wall shear stress increased by 18%,

5%, 13%, and 14%, respectively; Von-Mises stress increased by 189%, 115%, 84%, and 338%, respectively.

Conclusion Research shows that psammotherapy can improve the fluidity of the femoral artery blood and

increase the wall shear stress, which has a corresponding improvement effect on the prevention of the

deposition of substances in the arteries; the phenomenon of secondary reflux velocity after psammotherapy is

significantly reduced to avoid the deposition of substances in the blood, and it has a certain clinically positive

effect on preventing the formation of atherosclerosis, but after psammotherapy , the Von-Mises equivalent

stress increases and the increase is also relatively large, indicating that psammotherapy has a potential risk of

vascular rupture.

1 INTRODUCTION

With the acceleration of the pace of modern life,

people's pressure is increasing rapidly, and the body

and mind are exhausted. Therefore, physical therapy

has attracted more and more attention.

Psammotherapy derived from the unique warm

temperate arid desert climate in Turpan, Xinjiang,

China is a kind of physical therapy. As it has no side

effects, and can improve blood circulation, promote

metabolism, and strengthen the body, loses weight,

beauty, and health care, it is loved by lots of people.

According to statistics, there are about 50,000 people

who have psammotherapy in the psammotherapy

center of Turpan Uyghur Hospital every year.

Psammotherapy is a method of curing diseases by

a

https://orcid.org/0000-0002-7045-7597

b

https://orcid.org/0000-0001-6587-0574

burying sand. Its principle is to use the naturally

formed magnetic sand to comprehensively act on the

human body through heat transfer, magnetic field

action, and sand action force, so as to get rid of illness

and keep fit (Kurban 2011). The influencing factors

of psammotherapy are complex and involve many

disciplines, so it is difficult to explore the mechanism

of its curative effect. Scholars at home and abroad

have carried out research on the curative effect

mechanism of psammotherapy from the aspects of

heat transfer, bone mechanics, clinical medicine, etc.

Nyazi Aishan (Niaz

2002)

research has shown that

psammotherapy is effective for various types of

Osteoarthrltis (OA) and other types of rheumatic

diseases. In addition, changes in hemorheology

indicators are correlated with the occurrence,

Fu, R. and Han, X.

Research on the Effect of Psammotherapy on the Pulsating Flow of Conical Curved Femoral Artery.

DOI: 10.5220/0011316200003444

In Proceedings of the 2nd Conference on Artiﬁcial Intelligence and Healthcare (CAIH 2021), pages 261-268

ISBN: 978-989-758-594-4

Copyright

c

261

development, treatment and prevention of OA

(Chang, Chang, Xu

2009),

therefore, relevant

scholars are engaged in research to reveal the

therapeutic mechanism of psammotherapy from

hemorheology and hemodynamics. Wei Rong et al.

(Wei, Mahemuti, Yang

2009)

studied the

hemorheology and hemodynamics of rabbit knee

osteoarthritis through experiments in New Zealand

rabbit, their research has pointed out that

psammotherapy can improve the whole blood

viscosity index of model animals; in addition, it can

speed up the blood flow in the femoral artery of the

lower limbs at the sand-buried site and reduce

vascular resistance. Bureby Yiming et al. (Yiming, Fu

2016)

studied the effect of psammotherapy on the

hemodynamics of the human femoral artery

bifurcation under the condition of fluid-solid

coupling. However, in the current study to reveal the

mechanism of psammotherapy curative effect from

the perspective of hemodynamics, the three-

dimensional finite element model of blood vessels has

not been taken into account the taper of blood vessels,

and the blood was supposed as Newtonian fluid.

Moreover, arterial diseases mostly occur at the places

where the geometric shape of arteries changes,

namely, the stenosis, bifurcation and curvature of

vessels (Xu, Guo, Wang

2017)

. Therefore, exploring

the influence of psammotherapy on the

hemodynamics of conical curved tubes based on non-

Newtonian fluids is one of the focuses of this paper.

Based on the experimental research, this paper studies

the distribution of blood flow field, wall shear stress

and Von-Mises equivalent stress in the conical vessel

of the femoral artery before and after psammotherapy

based on non-Newtonian fluids, so as to provide a

theoretical basis for revealing the therapeutic

mechanism of psammotherapy on vascular diseases.

2 MATERIALS AND METHODS

2.1 Geometric Model

CT was used to collect real human lower limb images,

apply medical image processing software to extract

femoral artery blood vessels, and then reverse

engineering method (Schulze-Bauer, Morth,

Holzapfel 2003

)

was applied to segment and smooth

the femoral artery conical tube, and the three-

dimensional reconstruction model of the fluid domain

(blood flow) of the blood vessel was constructed

under the condition of maintaining the original

physiological and anatomical characteristics. The

reverse engineering method reference (Zhang, Zhang,

Gao 2002) was used to study the femoral artery. a

blood vessel wall with a thickness of 1 mm was

constructed, and a three-dimensional geometric

model of the blood vessel wall was obtained, as

shown in Figure 1. The place where the geometric

shape of the conical curved femoral artery changes is

prone to more complicated flow conditions (Yang,

Yu, Liu, Hong 2014), and many vascular and blood

diseases often occur in such places, so the inner and

outer sides of the conical curved femoral artery were

selected as monitoring points. The inner monitoring

points are A, B, C, D and the outer monitoring points

are a, b, c, d, and they are distributed along the taper,

mainly to monitor the time-varying fluid velocity of

these points.

Figure 1: Three-dimensional geometric model of blood vessel.

2.2 Finite Element Calculation

The finite element analysis software ICEM meshing

was used for meshing, and ANSYS 18.0 was used for

bidirectional fluid-solid coupling analysis. The fluid-

solid coupling calculation mainly used the fluid

solver and the solid structure solver to calculate the

fluid-solid interaction problem at the same time. The

fluid solver mainly calculated physical quantities

such as pressure, velocity, temperature, and

composition of the flow field, while the solid

structure solver calculated physical quantities such as

displacement, stress, and strain. Among these

solution variables, the physical quantities that exist in

CAIH 2021 - Conference on Artiﬁcial Intelligence and Healthcare

262

both fluid and solid solutions were pressure and

displacement. In the fluid solver, the pressure was the

direct solution, while in the solid solver, the pressure

can be used as a load. In the solid solver, the

displacement was the direct solution quantity, while

in the fluid solver, the displacement can be used as a

load, which is expressed as a calculation domain

motion or deformation.

2.3 Initial Conditions, Boundary

Conditions and Material Properties

The blood flow is a pulsating flow, which was

achieved by setting the initial speed of the pulsation

in this paper. According to the experimental results of

the research group, the subjects were selected from a

healthy group of 22~27 years old, a total of 59 people.

Among them, 26 males were 172~176 cm tall and

weighed 67~75 kg; 33 females were tall and weighed

46~60 kg. After signing the informed consent form

with the subject, the psammotherapy test was carried

out. Each psammotherapy time was 30 minutes, once

a day, and 15 days was a course of treatment. SPSS

software was used to process the peak blood flow

velocity, inner diameter and heart rate before and

after femoral artery psammotherapy (as shown in

Table 1). As

60

T

heart rate

=

,

=

2

T

π

ω

,the angular

velocity was determined. Since the pulsation velocity

can be considered to change according to a sine

function within a pulsation cycle, the initial condition

of the femoral artery was set as the pulsating blood

flow velocity (Yiming, Fu

2017)

, that is,

=

in

v 0.93 sin 7.99t()

,

out

v 1.23 sin 9.70t= ()

; the

outlet pressure was set to p=0. The boundary

conditions of the femoral artery wall were set to have

no penetration and no slip boundary.

The blood vessel wall was set an incompressible

isotropic material (Liu，Wu，Dhanjoo

2015)

, and

its density

3

soild

1150 kg m

ρ

=

, Elastic modulus,

E

5Mpa=

and Poisson's ratio

0.45

ν

=

The density

of blood

33

blood

1.05 10 kg m .

ρ

=×

Table 1: Femoral artery hemodynamic indexes before and after psammotherapy (n = 59).

parameter

Before psammotherapy After psammotherapy

speed /(cm·s-1) 92. 51 ± 8. 87 122. 51 ± 16. 98

Inner diameter /cm 0. 76 ± 0. 11 0. 78 ± 0. 11

Heart rate 76. 32 ± 11. 40 92. 69 ± 16. 09

Cardiac cycle /s 0. 789 0 0. 651 6

2.4 Governing Equation

A large number of studies have shown that animal

blood has the characteristics of non-Newtonian fluid,

and the shear force and shear strain rate of blood are

nonlinear. Here we set the blood as an incompressible

non-Newtonian fluid, select the non-Newtonian flow

model, and the flow control equation (Matos ，

Oliveira

2013)

is:

0u∇⋅ =

(1)

()

u u

u

p

t

ρρ

τ

+ ∇

∂

=−∇ +∇

∂

 

(2)

In the formula, the stress tensor τ̄ and the strain

rate tensor γ̄ are nonlinear relations:

()

τμ

γ

=

(3)

This paper selects the model of Carreau-Yasuda

(Morales, Larrabide, Geers, Aguilar, Frangi

2013)

:

()

1/

z

0

1

nz

μμ λ

μμ γ

−

∞



+− +



=

(4)

According to the literature, parameters are

respectively set as 𝜆 = 0.110𝑠 , 𝑛 = 0.392 ,

3

0

22 10 pa s

μ

−

×=⋅

,

3

2.2 10 pa s

μ

∞

−

=× ⋅

,

z 0.644=

, dynamic viscosity

μ

In addition, the control equation of the blood

vessel wall model (Chatziprodromou, Tricoli,

Poulikakos, Ventikos 2007) is expressed as follows:

ij s s

a

ρ

σ

=∇⋅

(5)

Here 𝜎



represents the stress tensor of the blood

vessel wall; 𝑎



represents the acceleration of the

blood vessel wall; 𝜌



represents the density of the

blood vessel wall.

When the coupling between the fluid and the solid

occurs, the contact surface between the fluid and the

solid needs to establish a corresponding relationship

to meet this condition. Fluid and solid will transmit

displacement and speed through the contact surface

Research on the Effect of Psammotherapy on the Pulsating Flow of Conical Curved Femoral Artery

263

between them. The following conditions should be

met on the contact surface between fluid and solid:

s

ij s

s

dd

nTn

UU

σ



=



⋅=⋅





=



(6)

In these equations, the subscript s represents the

physical quantity of the blood vessel wall; n

represents the boundary normal; d represents the

displacement.

3 RESULT

3.1 Distribution of Blood Flow Field

before and after Psammotherapy

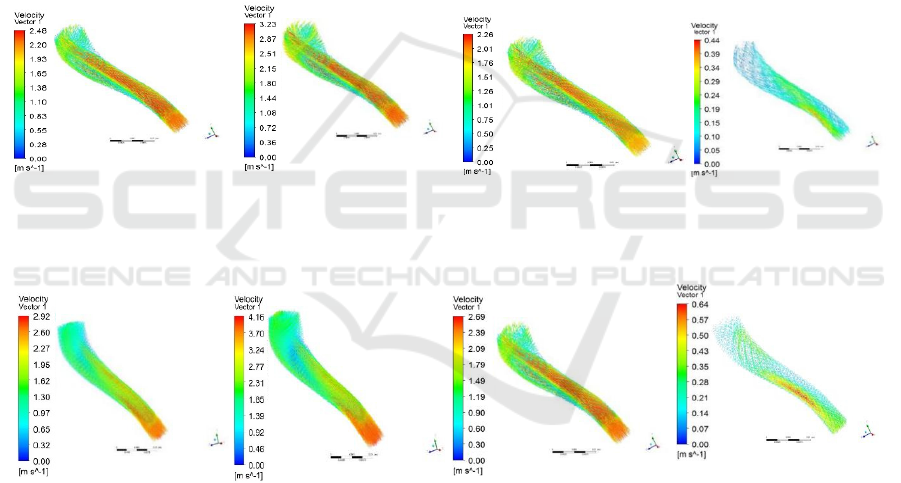
Figure 2 shows the velocity distribution cloud map of

the tapered femoral artery during a cardiac cycle.

Figure 2A is the cloud map of different instantaneous

velocity distributions before psammotherapy, and

Figure 2B is the cloud map of different instantaneous

velocity distributions after psammotherapy. Figure 2

shows that, before psammotherapy, the central area of

the front blood flow velocity moves to the inside to a

certain extent, resulting in a low velocity area on the

outside of the blood vessel, so vortexes are generated

in this area. Compared with before psammotherapy,

the gradient of blood flow velocity in the radial

direction of the conical femoral artery curve is less

drastic after sand therapy, and the possibility of

bidirectional eddy is reduced; the blood flow field is

more evenly distributed after psammotherapy than

before psammotherapy, and the resulting low-

velocity area is decreasin.

(1).t=0.15s (2).t=0.30s (3).t=0.45s (4).t=0.60s

A. Before psammotherapy

(1).t=0.15s (2).t=0.30s (3).t=0.45s (4).t=0.60s

B. After psammotherapy

Figure 2: Velocity distribution cloud diagram in the conical curved femoral artery.

Table 2 is a comparison table of the maximum

speed before and after psammotherapy. The relative

change of the maximum speed is the absolute change

of the same instantaneous maximum speed before and

after psammotherapy divided by the percentage of the

maximum speed before psammotherapy. Table 2

shows that the maximum speed after psammotherapy

is higher than that before psammotherapy. The

maximum speeds of before and after psammotherapy

are reached at 0.30s, and the absolute change of the

maximum speed is also the largest. The relative

change of the maximum speed is the largest at 0.60s.

Figure 3 shows the speed change with time curve

of the conical curved femoral artery of the inner

monitoring point A~D and the outer monitoring point

a~d. It is found that the speed of the inner side of the

bend changes significantly with time before

psammotherapy, while the inner speed change after

CAIH 2021 - Conference on Artiﬁcial Intelligence and Healthcare

264

psammotherapy is relatively gentle, the difference

between these points is not obvious, and the average

maximum value is also reduced; the blood flow

velocity at some points before the curved lateral

psammotherapy is lower, and the blood flow speed

increases after the psammotherapy, but the variation

range of blood flow velocity after sand therapy is

relatively small compared with that before

psammotherapy, and the flow is relatively smooth.

Table 2: Comparison of maximum speed before and after psammotherapy.

Time

(s)

Maximum

speed before

psammotherapy

(m/s)

Maximum speed

after psammotherapy

(m/s)

Absolute change

of maximum speed

(m/s)

Relative change of

maximum speed (%)

0.15 2.48 2.92 0.44 18

0.30 3.23 4.16 0.93 29

0.45 2.26 2.69 0.43 19

0.60 0.44 0.64 0.2 45

A. Before psammotherapy

B.

After psammotherapy

Figure 3.

3.2 Wall Shear Stress Distribution

before and after Psammotherapy

Figure 4A is the distribution diagram of wall shear

stress with time before psammotherapy, and Figure

4B is the distribution cloud diagram of wall shear

stress with time after psammotherapy. Figure 4 shows

that, at the curve of conical vessels, the blood first

decompresses and speed increases, then its speed

decelerates and pressurizes, and finally the boundary

layer falls off, so that the velocity changes greatly,

and the shear stress of the blood vessel wall is also

more obvious. As the taper of the blood vessel

increases, the wall shear stress caused by the

acceleration of the flow speed also gradually

increases. Compared with before psammotherapy ,

the blood vessel wall shear stress distribution after

psammotherapy is more uniform overall.

Research on the Effect of Psammotherapy on the Pulsating Flow of Conical Curved Femoral Artery

265

Table 3 is a comparison table of the maximum

wall shear stress before and after psammotherapy.

The relative change of the maximum wall shear stress

is the absolute change of the maximum wall shear

stress at the same instant before and after

psammotherapy divided by the percentage of the

maximum wall shear stress before psammotherapy.

Table 3 shows the maximum wall shear stress

after psammotherapy is higher than the maximum

wall shear stress before psammotherapy. When 0.30s,

the maximum wall shear stress before and after

psammotherapy is the largest, but the maximum

absolute change of the maximum wall shear stress

occurs at 0.15s, and the relative change of the

maximum wall shear stress is the largest at 0.15s.

(1).t=0.15s (2).t=0.30s (3).t=0.45s (4).t=0.60s

A. Before psammotherapy

(1).t=0.15s (2).t=0.30s (3).t=0.45s (4).t=0.60s

B. After psammotherapy

Figure 4: Cone-curved artery wall shear stress distribution cloud map.

Table 3: Comparison of maximum wall shear stress before and after psammotherapy.

Time (s)

Maximum wall

shear stress before

psammotherapy (Pa)

Maximum wall

shear stress after

psammotherapy (Pa)

Absolute change of

maximum wall shear

stress (Pa)

Relative change

of maximum wall

shear stress (%)

0.15 30.85 36.31 5.46 18

0.30 43.23 45.58 2.35 5

0.45 39.25 44.49 5.24 13

0.60 12.86 14.70 1.84 14

3.3 Vascular Von-Mises Equivalent

Stress Distribution before and after

Psammotherapy

The blood vessel is an elastic body. Under the

coupling action of the blood vessel and the blood, the

blood vessel will produce a certain deformation. The

Von-Mises equivalent stress distribution of blood

vessels before and after psammotherapy is shown in

Figure 5. The Von-Mises equivalent stress

is the stress for judging whether the material has

yielded, and its expression is 𝜎



=







[(𝜎



−𝜎



)



+(𝜎



−𝜎



)



+(𝜎



−𝜎



)



] , where

σ



， σ



，σ



are the three principal stresses of the

dangerous point.

When the Von-Mises stress is less than the yield

stress, the material is in elastic state, otherwise it is

plastic state. Figure 5 shows that the Von-Mises stress

on both sides of the vessel with the largest curvature

CAIH 2021 - Conference on Artiﬁcial Intelligence and Healthcare

266

(1).t=0.15s (2).t=0.30s (3).t=0.45s (4).t=0.60s

A. Before psammotherapy

(1).t=0.15s (2).t=0.30s (3).t=0.45s (4).t=0.60s

B. After psammotherapy

Figure 5: Von-Mises equivalent stress distribution cloud diagram of conical curved artery.

Table 4: Comparison of maximum Von-Mises equivalent stress before and after psammotherapy.

Time (s)

Maximum Von-

Mises equivalent stress

before psammotherapy

(kPa)

Maximum Von-

Mises equivalent stress

after psammotherapy

(kPa)

Maximum

absolute change of

Von-Mises

equivalent stress

(kPa)

Maximum

relative change of

Von-Mises

equivalent stress (%)

0.15 71.50 207.31 135.81 189

0.30 38.72 83.13 44.41 115

0.45 110.39 202.95 92.56 84

0.60 31.16 136.55 105.39 338

is the largest, and the distribution law before and after

psammotherapy is basically the same.

Table 4 is the comparison table of the maximum

Von-Mises equivalent stress before and after

psammotherapy. The maximum relative change of

Von-Mises equivalent stress is the absolute change of

the same instantaneous maximum Von-Mises

equivalent stress before and after psammotherapy

divided by the percentage of Von-Mises equivalent

stress of the maximum before psammotherapy.

Table 4 shows that the maximum Von-Mises

equivalent stress after psammotherapy is higher than

the maximum Von-Mises equivalent stress before

psammotherapy. The maximum Von-Mises

equivalent stress is at 0.45s before psammotherapy.

The effect force reaches the peak value of 110.39kPa,

the maximum Von-Mises equivalent stress reaches

the peak value of 207.31kPa at 0.15s after

psammotherapy, and the maximum absolute change

of the maximum Von-Mises equivalent stress occurs

at 0.15s, and its value is 135.81kPa. The maximum

relative change of the maximum Von-Mises

equivalent stress occurs at 0.6s, and its value is 338%.

4 CONCLUSIONS

After psammotherapy, the blood flow field changes,

the blood flow velocity increases, and the blood flow

field is improved. Compared with before

psammotherapy, the speed gradient of blood flow is

relatively weakened at the conical bend, and the blood

flow field distribution is relatively even compared

with before psammotherapy. After psammotherapy,

the blood flow velocity changes relatively smoothly

Research on the Effect of Psammotherapy on the Pulsating Flow of Conical Curved Femoral Artery

267

and the blood flow velocity increases in the conical

curve, which can effectively prevent the deposition of

large substances in the blood, so that the large

substances can be transported with the blood, and the

shear stress of blood vessel wall increases effectively

to prevent the thickening of blood vessel wall after

psammotherapy. Studies on blood flow velocity and

wall shear stress show that psammotherapy has a

positive effect on preventing the formation of

atherosclerosis. However, after psammotherapy, the

von-Mises equivalent stress increased, and this

increase is relatively large and has a potential risk of

vascular rupture.

This paper considers the non-Newtonian

characteristics of blood, and the reverse CT scan of

the human blood vessel model can effectively

approach the physiological conditions of the human

body. However, there are still shortcomings in the

calculation. As we all know, blood is not just plasma,

but also includes blood cells and other substances,

which makes it become a multiphase flow problem.

To be more similar to the real human body, these

problems will be all considered in future research.

ACKNOWLEDGEMENTS

This paper is supported by the National Natural

Science Foundation of China (31460245) and Natural

Science Foundation of Xinjiang Uygur Autonomous

Region of China (2014211A005).

REFERENCES

Abdul Saramu·Sidura·Usman·Yasheng Shatar·Kurban,

(2011) The characteristics and mechanism of sand

burial therapy, Chinese Journal of Ethnic Medicine, No.

9, P54-56

Bureby Yiming, Fu Rongchang. (2016) Hemodynamic

effects from sand therapy of Uyghur medicine on the

branch of femoral artery[J]. Journal of Medical

Biomechanics, 31(05): 431-436.

Bureby Yiming, Fu Rongchang. (2017) Numerical

simulation of two-way fluid-solid coupling

hemodynamics of femoral artery under Uyghur

medicine psammotherapy [J]. Chinese Journal of

Biomedical Engineering, 36(04): 507-511.

Chang Yongchao, Chang Yanqing, Xu Deying, (2009)

Changes of hemorheological indexes in patients with

osteoarthritis, Orthopedics of Traditional Chinese

Medicine, Volume 21, Issue 9, P35-36

Chatziprodromou I, Tricoli A, Poulikakos D, Ventikos Y.

(2007) Haemodynamics and wall remodelling of a

growing cerebral aneurysm: a computational model[J].

Journal of Biomechanics 40 (2): 412-426.

Liu Guiying, Wu Jianhuang, Dhanjoo N G, et al. (2015)

Hemodynamic characterization of transient blood flow

in right coronary arteries with varying curvature and

side - branch bifurcation angles [J]. Computers in

Biology and Medicine, 64: 117-126.

Matos H M, Oliveira P J. (2013) Steady and unsteady non-

Newtonian inelastic flows in a planar T-junction[J].

International Journal of Heat and Fluid Flow, 39: 102-

126.

Morales H G, Larrabide I, Geers A J, Aguilar M L, Frangi

A F. (2013) Newtonian and non Newtonian blood flow

in coiled cerebral aneurysms [J]. Journal of

Biomechanics, 46 (13): 2158-2164.

Niaz Aishan, (2002) Research on the treatment of

rheumatism with psammotherapy in Turpan, Xinjiang,

Chinese Journal of Ethnic Medicine, Issue 1, P21-22

Schulze-Bauer CA, Morth C, Holzapfel GA. (2003) Passive

biaxial me-chanical response of aged human iliac

arteries[J]. J Biomech En-g, 125(3): 395-406.

Wei Rong, Dilinal Mahemuti, Yang Shaoling, (2009)

Uyghur psammotherapy on blood rheology and

hemodynamics of rabbit knee osteoarthritis[J]. Science

& Technology Review, 27(3): P84-86.

Xu Xiangyu, Guo Pan, Wang Xiaofeng, et al. (2017) Using

dynamic grid technology to simulate the development

of atherosclerosis[J]. Journal of Medical

Biomechanics,4(36):336-341.

Yang Jinyou, Yu Hang, Liu Jing, Hong Yang. (2014) A

hierarchical model of abdominal aortic aneurysm based

on fluid-structure coupling analysis[J]. Biomedical

Engineering and Clinics, 4(18):310-314.

Zhang Mei, Zhang Yun, Gao Yuehua. (2002) Comparative

study on the normal value of carotid artery and femoral

artery intima-media layer thickness[J]. Chinese

Medical Imaging Technology, 18(1): 32-33.

CAIH 2021 - Conference on Artiﬁcial Intelligence and Healthcare

268