Density based Anomaly Detection for Wind Turbine Condition

Monitoring

Johannes Bernhard

1,4,*

, Jonas Schmidt

2,4

and Mark Schutera

3,4

Karlsruhe Institute of Technology, Institute for Information Processing Technologies, Germany

University of Osnabrück, Institute of Cognitive Science, Germany

Karlsruhe Institute of Technology, Institute for Automation and Applied Informatics, Germany

ZF Friedrichshafen AG, Research and Development, Germany

Keywords: Condition monitoring, Machine learning, Environmental engineering, Anomaly detection.

Abstract: Unsupervised and explainable approaches are critical in anomaly detection for mechanical systems. This work

proposes a density-based k-nearest neighbor method to combine an unsupervised learning setup with the

added value of explainability. The algorithm is applied to detect anomalies in vibration data from acceleration

sensors or microphones. In a training phase, we transform healthy vibration data into mel-spectrograms and

extract feature patches representing healthy turbines' vibration energy distribution. We determine anomaly

scores by calculating a k-nearest neighbor similarity between operational feature patches and healthy feature

patches. Hence, we use basic statistical methods with interpretable results, which contrasts with deep learning

techniques. The evaluation paradigm is data from damaged and healthy wind turbines and a secondary

machine audio data set. This work introduces and explores a novel sensor-level anomaly score. The model

identified all damaged sequences as anomalies on the wind turbine sequences. Furthermore, the method

achieved competitive results on the more complex DCASE sound anomaly dataset. Concluding, our anomaly

score lays the foundations for an interpretable condition monitoring system.

1 INTRODUCTION

Renewable energy sources drive the energy

transformation and are central for supply reliability.

Applied machine learning and data mining methods

carry the developments of the transitions in the

energy sector (Arnoldt, 2010). The utilization of

unsupervised methods has been a research area for

wind turbines (Sheng, 2014) and multiple

other application domains (Masino, 2017) (Bernhard,

2021/1) (Hofmockel, 2018). Anomaly detection with

structure-born sound data describes detecting

suspicious noises in a sound sequence that differs

from the sound source's common character.

Especially in machine condition monitoring, there is

great economic potential because the standstill of

complex production plants or wind turbines causes

serious economic damage. Data acquisition is a near-

impossible task, as the anomalous samples are sparse

and usually highly diversified. As such, it is difficult

to collect sufficient data samples from the anomaly

class to comprehensively represent the intra-class

variability and the unbalanced domains (Schutera,

2019). The notorious limitations of data acquisition

and sparse target domains in machine learning

(Bernhard, 2021/2) can be coped by unsupervised

learning and encoding approaches (Schutera, 2020).

In the field of acoustic anomaly detection, Gaussian

mixture models (Dufaux, 2000), hidden Markov

models (Chan, 2010), and support vector machines

(Aurino, 2014) are common approaches. In recent

years, neural networks have obtained superior results

by modeling the regular, normal data samples with an

encoder-decoder architecture (Koizumi, 2018)

(Kawaguchi, 2017), using the reconstruction loss as a

cue an anomaly measure. We show that with an

algorithmic simple, density-based k-nearest neighbor

method, we achieve high performance on two data

sets, including different machine types and wind

turbine data. Condition monitoring on wind turbine

gearbox data has been of interest due to the significant

downtime gearbox damages caused (Sheng, 2011/1).

There are different data modalities for condition

monitoring on wind turbine gearboxes, such as

lubricant pressure (Wang, 2016), temperature

monitoring (Feng, 2013), or performance monitoring

Bernhard, J., Schmidt, J. and Schutera, M.

Density based Anomaly Detection for Wind Turbine Condition Monitoring.

DOI: 10.5220/0011358600003355

In Proceedings of the 1st International Joint Conference on Energy and Environmental Engineering (CoEEE 2021), pages 87-93

ISBN: 978-989-758-599-9

(Sharma, 2013). However, particular interest has been

put into analyzing vibration signals (Zappala, 2014),

which allow for direct sampling of structure-borne

sound from gearbox components. For vibration data

condition monitoring, amplitude analysis on specific

frequency ranges can be used for automatic fault

detection (Antoniadou, 2015). For online fault

detection algorithms, in current work impulse

analysis in the frequency spectrum has been proposed

(Gong, 2014).

In detail, this work examines:

• A density-based k-nearest neighbor anomaly

detection method for wind turbines and

machine vibration data.

• The design and introduction of a sensor-level,

frequency-based explainable anomaly score.

Especially in condition monitoring and predictive

maintenance, the interpretability and explainability of

anomaly scores are important and add value. By

allowing insights into the nature and type of the

detected anomaly, the explainability of the approach

simplifies and supports the maintenance or other

interventions to the monitored machines.

2 DATA

In real-world machine deployment, anomalous

vibration signals are the exception and are of various

kinds; this impedes data acquisition of anomalous

samples. Therefore, the data sets for unsupervised

detection of anomalous vibration signals are

composed of a training set consisting of normal

vibration samples only, a validation and test set

consisting of normal and anomalous samples. In the

following, we outline two data sets with these

required characteristics.

2.1 NREL Wind Turbine

The wind turbine gearbox condition monitoring

vibration analysis benchmarking data sets (Sheng,

2014) consists of data from a stall-controlled, three-

bladed, upwind turbine with a rated power of 750kW

(Sheng, 2011/2). The vibration data of the wind

turbine is collected by three IMI 626B02 and five IMI

626B01 accelerometers, in







. Mounted on the

outside of the gearbox. The sample rate is 40 kHz per

sensor channel. The whole data set comprises ten

healthy H (normal) vibration sequences of one minute

each and ten damaged D (anomalous) vibration

sequences of one minute each. Training is based on

the sequences H1-H4. Validation is based on the

sequences H5-H6 and D1-D2. For testing, the

sequences H7-H10 and D3-D10 are deployed and

evaluated.

2.2 DCASE2020 Anomaly Challenge

Data Set

The unsupervised detection of anomalous sounds

for machine condition monitoring data set (Koizumi,

2019) (Purohit, 2019) consists of data from six

machine types (toy car, toy conveyor, valve, pump,

fan, and Slider) with three to four machine instances.

The whole data set comprises a training set of around

2000 (normal) sequences, a validation set of two

times 100-200 (normal and anomalous) sequences,

and a test set of around 400 (unlabeled) sequences for

each machine instance. Each sequence represents an

audio recording of around ten seconds.

3 ANOMALY DETECTION

ARCHITECTURE

Anomaly detection is a data science discipline that

focuses on finding outlier data points that indicate a

significant deviation towards an underlying

distribution. Hence, the model should learn features

that describe patterns in the training data. The

presence or absence of these patterns in the test data

points helps estimating whether the point is part of the

estimated distribution during training.

This paper uses a density-based anomaly

detection method that incorporates a k-nearest

neighbor search of frequency patterns. First, the data

must be transposed into a fitting feature

representation to create a metric space that is useful

to the model. Transforming the sensor signals into a

mel-spectrogram that comprises the vibration

behavior on different frequency ranges serves this

purpose. Afterward, forming a histogram with fixed

bins for each frequency range converts the

spectrogram data. The following subsections describe

the model's workflow to set up a training library,

depicted in figure 1.

CoEEE 2021 - International Joint Conference on Energy and Environmental Engineering

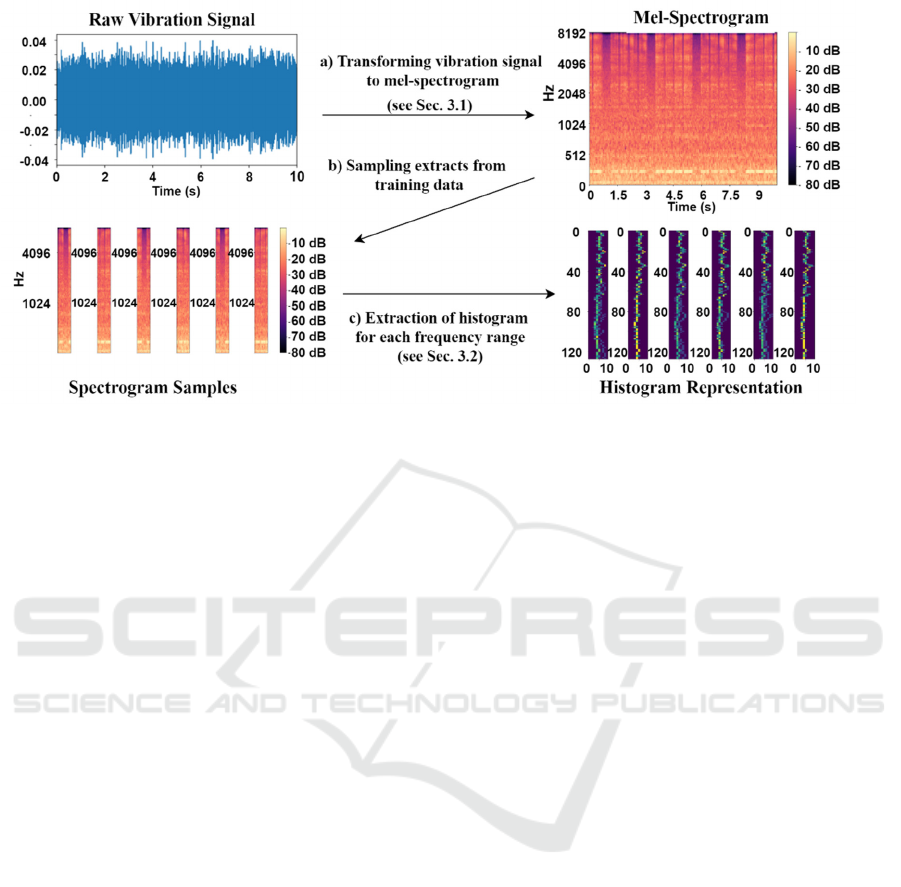
Figure 1. The feature extraction process for the training library. a) Vibration data files are transformed into spectrograms

(mel-spectrogram processing) to provide a detailed representation of the frequency spectrum. b) A library (spectrogram

sampling) that describes normal behavior, consisting of sampled short frames, is set up. c) Each frame translates into the

feature representation by generating a histogram for each frequency bin (frequency band histogram feature extraction).

3.1 Data Preparation

The general audio classification approach extracts

features from the temporal vibration signal specific to

each class. Current state-of-the-art algorithms often

use mel-spectrograms to transform the vibration

signal from time to frequency domain. This time-

frequency representation allows a good extraction of

the frequency patterns and, at the same time, a

dimensional reduction compared to a regular

spectrogram. Log-mel-energies were by far the most

popular feature in DCASE Task 4 (Serizel, 2019). For

a mel-spectrogram, a Discrete Fourier Transform of

the input signal is determined, and the power

spectrum is converted to log-scale. A vibration signal

of a previously defined window length is the input to

calculate the DFT. This window then runs over the

entire file to display the power spectrum change over

time. Based on a person's relative perceived pitch, the

frequencies are then converted into mel-scale,

creating a mel-spectrogram (see figure 1a and

figure 2). Since the frequency resolution is higher in

the lower range and decreases for higher frequencies,

this time-frequency representation is particularly

suitable for machine condition monitoring. Most of

the observed signal's energy is in the lower range.

Finally, the spectrograms for each type of machine

are normalized.

3.2 Feature Extraction

The underlying assumption for the anomaly detection

method in this paper is that the vibration data of

damaged wind turbines will have intensities in

different frequency ranges than the vibration data of

healthy wind turbines. Hence, if over a given time

frame, for normal and anomalous data, a histogram

for a given frequency range displays different value

distributions. Therefore, calculating the distance

between their histograms for each frequency range

yields the spectrograms' similarity. The model

focuses on small extracts with length 𝑙 along the

entire spectrogram's time axis, subsequently denoted

frames (see figure 1b). Hence, with frame length 𝑙, a

spectrogram 𝑺 of size 𝑓𝑛, where 𝑓 denotes the

number of frequency bins, and 𝑛 denotes the total

number of time steps, can be cut into a maximum

of 𝑛𝑙1 frames 𝑬 of size 𝑓𝑙. To create a

feature representation of the value distribution for a

given frame and frequency range 𝑖∈1,…,𝑓, a

histogram 𝒉

,

of row 𝑖 with 𝑏 bins is generated (see

figure 1c). The maximum and minimum intensity

observed on the frequency range of 𝑖 in the training

data equal each histogram's maximum and minimum

values. Therefore, a frame 𝑬 of size 𝑓𝑙 is used to

generate a histogram matrix 𝑯𝒉

,

,…,𝒉

,





size 𝑓𝑏.

Density based Anomaly Detection for Wind Turbine Condition Monitoring

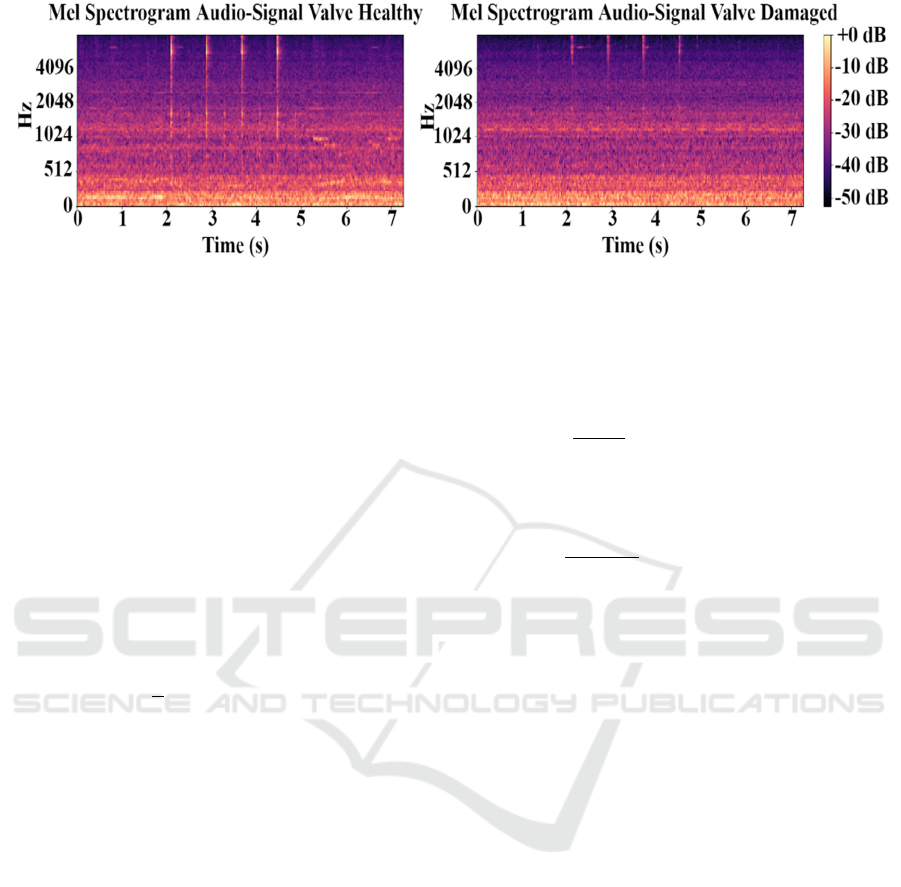
Figure 2. Mel-spectrogram of audio data depicted as frequency (Hz) over time (s). A comparison of healthy and damaged

valve audio data shows the signal’s energy distribution difference.

3.3 Anomaly Score Calculation

To apply a k-nearest neighbor search (see equation

(1)) for anomalies, a set of training features must be

generated describing normal vibration behavior. This

is done by uniformly sampling 𝑣 data points from the

set of all training data frames and converting the

sampled frames to histogram matrices that are added

to the training library ℒ 𝑯





∈,…,

. To get the

anomaly value of a test frame, the frame is

transformed into the histogram matrix 𝑯



. The

anomaly score is then calculated as the average

distance to the k-nearest neighbors:

𝐴 

𝑘

𝑂𝒅











with 𝑑



 ||𝑯



𝑯





being the distance vector from

𝑯



to ℒ and 𝑂𝒅 being a function that arranges the

distance vector 𝒅 in ascending order. For calculating

the anomaly score of a whole test-spectrogram, the

anomaly scores of each frame are evaluated and

averaged.

The whole process of calculating the anomaly score

for a test sequence 𝒙 of arbitrary length is expressed

by the function 𝑀



𝒙



3.4 Anomaly Detection Metrics

Metrics for benchmarking anomaly detection systems

are Area Under Curve (𝐴𝑈𝐶, see equation (2)) and

partial Area Under Curve (𝑝𝐴𝑈𝐶, see equation (3)),

which are independent of decision rules and thus

provide a reliable measure for anomaly detection. We

divide the set of test data in 𝒩



(normal) and

𝒩



(anomalous) test data. Let 𝒙













and

𝒙













be the normal and anomalous test sequences

in descending order of their average anomaly score.

By using the flooring function

⌊

∙

⌋

and the step

function 𝐺∙, which is 1 when the input is above 0,

and 0 otherwise, the metrics are defined as:

𝐴𝑈𝐶 

𝒩



𝒩



𝐺



𝑀𝑥





𝑀



𝑥









𝒩





𝒩





(2)

𝑝𝐴𝑈𝐶 

⌊

𝑝𝒩



⌋

𝒩



𝐺



𝑀



𝒙







𝑀



𝒙









𝒩





⌊

𝒩



⌋



(3)

We choose 𝑝0.1 and thus estimate how high

the probability is that our model, with a false positive

rate of a maximum of 10%, predicts for a random

normal test sample a lower anomaly score than for a

random anomalous test sample.

4 EXPERIMENTS

The NREL wind turbine data set is split into training

and validation data, as detailed in section 2. Each of

the nine sensor channels initiates the training of a

sensor channel-specific model. Hence, for each time

frame, there are nine individual anomaly scores.

Averaging the anomaly scores provides the

evaluation of the wind turbine's cumulative behavior.

4.1 Training Parameters

The model's performance relies on a set of

hyperparameters that can be adjusted: Number of mels

𝑓 specifies the number of mel-bins, indicating the

frequency resolution on the mel-scale. We use an fft-

length of 1024 with hop size 512 and a Hanning

window (Gautam, 1996). Extract length 𝑙 specifies the

number of time steps that are included in one frame.

CoEEE 2021 - International Joint Conference on Energy and Environmental Engineering

Figure 3. Anomaly scores across the sensors with different mounting positions [2] for damaged and healthy wind turbine data.

The sensors’ emerging anomaly pattern potentially supports during troubleshooting and hints at specific failure cases.

During extraction of the frames, we used a stride

parameter of 15 that defines the number of time steps

the window is shifted for the next frame. While a high

𝑙 allows to reduce noise and focus on periodic

patterns, it also bears the risk of significant

anomalous spikes being vanished by normal behavior

before and after. Number of histogram bins 𝑏

specifies the resolution of the intensity distribution.

Choosing 𝑏 allows adjusting the model's sensitivity

towards noise. Number of nearest neighbors 𝑘

specifies the number of training data points for the

anomaly score evaluation. The hardware setup for

training, inference, and evaluation consisted of an

NVIDIA Tesla P100 GPU (16GB GPU memory).

5 RESULTS

5.1 Anomaly Detection Performance

Deployed on the NREL wind turbine data, the model

distinguishes between healthy and damaged samples.

Figure 3 depicts the anomaly scores for damaged and

healthy wind turbine data across all sensor types.

Table 1 shows the averaged anomaly scores for each

sequence with the respective standard deviation. The

model achieves a clear delineation between the

anomalous (anomaly scores approx. 310, see table 1)

and healthy samples (anomaly score approx. 78, see

table 1) of the wind turbine.

Furthermore, the model achieves AUC scores

above 70% and pAUC scores above 65% across all

machine types and IDs on the DCASE2020 data set

(see table 2). Especially machine toy car experiences

robust results, while the machine valve poses a

challenge to the proposed model. The model

outperforms the deep-learning baseline model on

every machine other than slider.

5.2 Model Interpretability

Our model's implementation on the wind turbine data

allows evaluating the vibration behavior on sensor-

level (see figure 3). High anomaly scores on specific

sensors indicate damage location. Our model supports

interpretable anomaly scores in contrast to deep

learning-driven anomaly detection approaches, such

as auto-encoders. High scores can be tracked down to

and explained by the distribution of intensity values

on specific frequency ranges and individual sensors.

Tracking allows the analysis of anomalous patterns

and the comparison with previous occurrences.

Hence, the model detects general anomalies and lays

the foundation for anomaly classification and

prediction.

Table 1. Anomaly score estimation for wind turbine data. Scores are averaged across sensor types and time steps. There is a

clear delineation between the anomaly scores for healthy wind turbine recordings and the anomaly scores for damaged wind

turbine recordings. Training parameters: l = 128, f = 40, b = 8, k = 4.

H7 H8 H9 H10 D3 D4 D5 D6 D7 D8 D9 D10

mean 77.0 77.3 78.0 79.4 309.1 313.4 308.7 305.8 311.7 310.9 313.9 311.9

Std. ±1.01 ±0.96 ±1.26 ±0.88 ±1.03 ±1.01 ±0.92 ±1.05 ±1.05 ±1.10 ±1.05 ±0.92

Density based Anomaly Detection for Wind Turbine Condition Monitoring

Table 2. Performance comparison between the proposed model and the DCASE2020 Challenge 2 baseline model (Koizumi,

2020). They implemented a classical deep-learning auto-encoder approach to find anomalous behavior in the sound files. As

a result, the model manages to achieve a significant anomaly detection performance on each machine. Furthermore, the model

outperforms the baseline model on every machine type except slider.

Proposed Model

(ours)

Baseline Proposed Model

(ours)

Baseline

AUC

(%)

pAUC

(%)

AUC

(%)

pAUC

(%)

AUC

(%)

pAUC

(%)

AUC

(%)

pAU

(

)

Toy Car f = 128 l = 75 b = 10 k = 2 Toy

Conve

f = 128 l = 70 b = 5 k = 2

ID 1 95.6 80.6 81.4 68.4 ID 1 87.1 71.0 78.1 64.3

ID 2 98.9 94.5 86.0 77.7 ID 2 67.2 52.4 64.2 56.0

ID 3 92.5 78.1 63.3 55.2 ID 3 79.2 66.7 75.3 61.0

ID 4 98.9 96.6 84.5 69.0 Avera

e 77.8 63.4 72.5 60.4

Average 96.4 87.5 78.8 67.6

Fan

= 128 l= 75 b =

=4 Pum

= 128 l= 7

b =

ID 1 60.5 51.9 54.4 49.4 ID 1 76.2 55.4 67.2 56.7

ID 2 89.5 65.9 73.4 54.8 ID 2 83.6 75.8 61.5 58.1

ID 3 78.3 58.9 61.6 53.3 ID 3 94.1 77.1 88.3 67.1

ID 4 81.1 57.0 73.9 52.4 ID 4 78.7 57.5 74.6 58.0

Average 77.3 58.4 65.8 52.5 Average 83.2 66.4 72.9 56.0

lider

= 128 l= 75 b = 5

=5 Valve

= 128 l= 35 b = 1

ID 1 98.5 93.7 97.0 81.4 ID 1 74.1 55.3 68.8 51.7

ID 2 81.6 65.5 79.0 63.7 ID 2 68.7 51.8 68.2 51.8

ID 3 83.0 55.0 94.3 72.0 ID 3 75.2 51.4 74.3 52.0

ID 4 60.9 51.2 69.6 49.0 ID 4 62.8 48.6 53.9 48.4

Avera

e 81.0 66.3 84.8 66.5 Avera

e 70.2 51.8 66.3 51.0

6 DISCUSSION

We introduce a method for effective fault detection on

vibration data with this work. The proposed method

uses spectrogram transformations of the input signal

to automatically extract healthy signals'

characteristics over the whole frequency spectrum by

building histogram representations. The analysis

pipeline can identify the core frequency windows and

characteristics without prior knowledge of the

underlying mechanical system.

Using the k-nearest neighbor anomaly detection

method, the systems deployment signals are examined

for damages or malfunctions. This method was tested

on sound signals and vibration signals to prove its

viability.

There is a range of potential future work to

improve the presented approach: Starting with

deploying the approach to related areas, such as

premature fault prediction or supervised fault

classification by comparing the extracted features of

An interactive implementation of the model can

be found in: https://github.com/VanLock9988/

Vibration_Data_Anomaly_Detection

deployment data to previously observed features.

Another extension introduces the ability to recognize

long-term dependencies by estimating conditional

distributions. Not only recognizing anomalous

frequency patterns but also anomalous sequences of

frequency patterns.

We are confident that this work supports

practitioners when deploying condition monitoring or

predictive maintenance algorithms

. Further, we hope

to stimulate research on overcoming the restrictions

imposed by unbalanced domains in acoustic anomaly

data sets while ensuring interpretability.

REFERENCES

Antoniadou, I., Manson, G., Staszewski, W. J., Barszcz, T.,

& Worden, K. (2015). A time-frequency analysis

approach for condition monitoring of a wind turbine

gearbox under varying load conditions. (Elsevier, Ed.)

Mechanical Systems and Signal Processing, 64, 188-

216.

CoEEE 2021 - International Joint Conference on Energy and Environmental Engineering

Arnoldt, A., König, S., Mikut, R., & Bretschneider, P.

(2010). Application of Data Mining Methods for Power

Forecast of Wind Power Plants. Proc., 9th International

Workshop on Large-scale Integration of Wind Power

and Transmission Networks for Offshore Wind Farms,

Quebec.

Aurino, F., Folla, M., Gargiulo, F., Moscato, V., Picariello,

A., & Sansone, C. (2014). One-class SVM based

approach for detecting anomalous audio events.

International Conference on Intelligent Networking and

Collaborative Systems, (pp. 145-151). IEEE.

Bernhard, J., Schulik, T., Schutera, M., & Sax, E. (2021/2).

Adaptive test case selection for DNN-based perception

functions. IEEE International Symposium on Systems

Engineering (ISSE), (pp. 1-7). IEEE.

Bernhard, J., Schutera, M., & Sax, E. (2021/1). Optimizing

test-set diversity: Trajectory clustering for scenario-

based testing of automated driving systems. IEEE

International Intelligent Transportation Systems

Conference (ITSC), (pp. 1371-1378). IEEE.

Chan, C. F., & Eric, W. M. (2010). An abnormal sound

detection and classification system for surveillance

applications. 18th European Signal Processing

Conference, (pp. 1851-1855). IEEE,

Chang, F. K., Markmiller, J. F., Yang, J., & Kim, Y. (2011).

Structural health monitoring. System health

management: with aerospace applications. John Wiley

& Sons.

Dufaux, A., Besacier, L., Ansorge, M., & Pellandini, F.

(2000). Automatic sound detection and recognition for

noisy environment. 10th European Signal Processing

Conference. IEEE.

Feng, Y., Qiu, Y., Crabtree, C. J., Long, H., & Tavner, P. J.

(2013). Monitoring wind turbine gearboxes. (W. O.

Library, Ed.) Wind Energy, 16(5), 728-740.

Gautam, J. K., Kumar, A., & Saxena, R. (1996). On the

modified Bartlett-Hanning window (family). IEEE

Transactions on Signal Processing, 44(8), 2098-2102.

Gong, X., & Qiao, W. (2014). Current-based mechanical

fault detection for direct-drive wind turbines via

synchronous sampling and impulse detection. (IEEE,

Ed.) IEEE Transactions on Industrial Electronics, 62(3),

1693-1702.

Hofmockel, J., & Sax, E. (2018). Isolation Forest for

Anomaly Detection in Raw Vehicle Sensor Data.

International Conference on Vehicle Technology and

Intelligent Transport Systems (VEHITS).

Kawaguchi, Y., & Endo, T. (2017). How can we detect

anomalies from subsampled audio signals? 27th IEEE

International Workshop on Machine Learning for

Signal Processing (MLSP), (pp. 1-6). IEEE.

Koizumi, Y. a. (2018). Unsupervised detection of

anomalous sound based on deep learning and the

neyman- pearson lemma. IEEE/ACM Trans-actions on

Audio, Speech, and Language Processing. 27(1), 212-

224.

Koizumi, Y., Saito, S., Uematsu, H., Harada, N., & Imoto,

K. (2019). ToyADMOS: A dataset of miniature-

machine operating sounds for anomalous sound

detection. IEEE Workshop on Applications of Signal

Processing to Audio and Acoustics (WASPAA), (pp.

313-317). IEEE.

Koizumi, Y., Kawaguchi, Y., Imoto, K., Nakamura, T.,

Nikaido, Y., Tanabe, R., ... & Harada, N. (2020).

Description and discussion on DCASE2020 challenge

task2: Unsupervised anomalous sound detection for

machine condition monitoring. arXiv preprint

arXiv:2006.05822.

Masino, J., Pinay, J., Reischl, M., & Gauterin, F. (2017).

Road surface prediction from acoustical measurements

in the tire cavity using support vector machine. Applied

Acoustics, 125 41-48.

Purohit, H., Tanabe, R., Ichige, K., Endo, T., Nikaido, Y.,

Suefusa, K., & Kawaguchi, Y. (2019). MIMII Dataset:

Sound Dataset for Malfunctioning Industrial Machine

Investigation and Inspection. Proceedings of the

Detection and Classification of Acoustic Scenes and

Events 2019 Workshop (DCASE2019), (pp. 209-213).

Schutera, M., Hafner, F. M., Vogt, H., Abhau, J., & Reischl,

M. (2019). Domain is of the Essence: Data Deployment

for City-Scale Multi-Camera Vehicle Re-Identification.

16th IEEE Inter-national Conference on Advanced

Video and Signal Based Surveillance (AVSS). (pp 1-6).

IEEE.

Schutera, M., Hussein, M., Abhau, J., Mikut, R., & Reischl,

M. (2020). Night-to-Day: Online Image-to-Image

Translation for Object Detection Within Autonomous

Driving by Night. IEEE Trans-actions on Intelligent

Vehicles.

Serizel, R., & Turpault, N. (2019). Sound event detection

from partially annotated data: Trends and challenges.

IcETRAN conference.

Sharma, S., & Mahto, D. G. (2013). Condition monitoring

of wind turbines: a review. Global Journal of

Researches in Engineering, Mechanical and Mechanics

Engineering, 13(6).

Sheng, S. (2011/2). Investigation of various condition

monitoring techniques based on a damaged wind turbine

gearbox (No. NREL/CP-5000-51753). National

Renewable Energy Lab.(NREL), Golden, CO (United

States).

Sheng, S. (2014). Wind turbine gearbox condition moni-

toring vibration analysis benchmarking datasets.

National Renewable Energy Laboratory, Golden.

Sheng, S., Link, H., LaCava, W., van Dam, J., McNiff, B.,

Veers, P., ... & Oyague, F. (2011/1). Wind turbine

drivetrain condition monitoring during GRC phase 1

and phase 2 testing (No. NREL/TP-5000-52748).

National Renewable Energy Lab.(NREL), Golden, CO

(United States).

Wang, L., Zhang, Z., Long, H., Xu, J., & Liu, R. (2016).

Wind turbine gearbox failure identification with deep

neural networks. IEEE Transactions on Industrial

Informatics, 13(3), 1360-1368.

Zappalá, D., Tavner, P. J., Crabtree, C. J., & Sheng, S.

(2014). Side-band algorithm for automatic wind turbine

gearbox fault detection and diagnosis. (W. O. Library,

Ed.) IET Renewable Power Generation, 8(4), 380-389.

Density based Anomaly Detection for Wind Turbine Condition Monitoring