Improved Whale Optimization Algorithm and Support Vector
Machine for Remaining Useful Life Prediction of Lithium-ion
Batteries
Y. Z. Wang
1
, Y. L. Ni
1,*
, Y. Z. Zhang
2
, Z. L. Shen
3
, S. D. Zhang
1
and J. G. Wang
1
1
Jilin Province International Research Center of Precision Drive and Intelligent Control, Northeast Electric Power
University, Jilin 132012, China
2
Zhang Jiakou Wind, Photovoltaic and Energy Storage Demonstration Station Co., Ltd. State Grid Xinyuan Company,
Zhang Jiakou 075000, China
3
Dalian Power Plant, Huaneng Power International Inc., Dalian 116100, China
Keywords: Lithium-ion battery, Remaining useful life, Support vector machine, Whale optimization algorithm.
Abstract: Prediction of remaining useful life (RUL) of Lithium-ion batteries (LIBs) is a key component of the
prognostics and health management (PHM). A method based on improved whale optimization algorithm and
support vector machine (IWOA-SVM) is proposed, which can improve the prediction accuracy for RUL of
LIBs and timely maintain and replace the battery to ensure the safety and stability of the energy storage
system. With the number of iterations increase, the WOA algorithm inevitably falls into local optimal solution.
Therefore, the adaptive weights are introduced to improve the global search ability of the WOA algorithm.
To verify the performance of the proposed method, the five test functions are utilized to compare with WOA
algorithm. Experimental data simulations were performed using NASA Ames Prognostics Center of
Excellence (PCoE) datasets to verify the proposed method. Compared with the SVM and WOA-SVM
methods, the results show that the proposed method can accurately ensure RUL prediction accuracy.
1 INTRODUCTION
Lithium-ion batteries (LIBs) have been widely used
in electric vehicles (EVs) and energy storage systems
(ESS) due to their high energy densities, low self-
discharge rate, and long lifetime (Xiong R, Tian J, Mu
H and Wang C, 2017). With the service of LIBs, the
safety problems caused by the degradation of LIBs
have attracted much attention. Remaining useful life
(RUL) is the number of times from the current time
to the failure threshold under a certain condition, and
it is an indicator for evaluating the state of health for
LIBs (Wang Y, Ni Y, Lu S, Wang J and Zhang X,
2019). The battery performance is rapidly degraded
when the capacity of LIB is reduced by 70%-80% of
the rated capacity (Duong P L T and Raghavan N,
2018). Accurately predicting the remaining useful life
(RUL) of LIBs is of great significance to battery
maintenance and prevention of dangerous accidents.
There are mainly two methods in predicting the
RUL of LIBs, one is the model-based methods such
as the particle filter (PF) (Lyu C, Lai Q, Ge T, Yu H,
Wang L and Ma N, 2017), the other one is the data-
driven approaches such as the artificial neural
networks (ANN) (You G W, Park S and Oh D, 2017)
and support vector machine (SVM) (Patil M, Tagade
P, Hariharan K, Kolake S, Song T, Yeo T and Doo S,
2015). The model-based methods analyse the
operating mechanism of the battery from the
perspective of the electrochemical mechanism for
LIBs and are difficult to model due to the complexity
of capacity degradation trajectory for LIBs (Zhang Y,
Xiong R, He H and Pecht M G, 2019). Guha et al.
(Guha A and Patra A, 2018) proposes a fractional-
order equivalent circuit model (FOECM), which the
parameters are determined via recursive least-squares
method and a fractional-order state variable filter and
estimate the electrochemical impedance spectrum
(EIS), then combine with PF method to predict RUL
of LIBs. The data-driven approaches do not require
consideration of electrochemical mechanisms, which
mine the hidden information from the historical
degradation data. Qin et al. (Qin T, Zeng S and Guo
Wang, Y., Ni, Y., Zhang, Y., Shen, Z., Zhang, S. and Wang, J.
Improved Whale Optimization Algorithm and Support Vector Machine for Remaining Useful Life Prediction of Lithium-ion Batteries.
DOI: 10.5220/0011359300003355
In Proceedings of the 1st International Joint Conference on Energy and Environmental Engineering (CoEEE 2021), pages 115-121
ISBN: 978-989-758-599-9
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
115

J, 2015) utilized particle swarm optimization (PSO)
to optimize the support vector regression (SVR)
kernel parameter and can obtain accurate prediction
results. Li et al. (Li L, Liu Z, Tseng M and Chiu A,
2019) proposed the improved bird swarm algorithm
to optimize least squares SVM (IBSA-LSSVM) and
improve the prediction accuracy of battery RUL. Gao
et al. (Gao D and Huang M, J., 2017) employed the
PSO algorithm to search the kernel parameters of the
multi-kernel SVM (MSVM) model to improve the
RUL prediction accuracy. Li et al. (Li S and Fang H,
2017) proposed the WOA algorithm to select the
parameter of SVR. Although the SVM method can
predict RUL of LIBs, there is still problem in how to
select the optimal parameters and provide high
accuracy.
The main contribution of this work is to establish
the IWOA-SVM method to improve the prediction
accuracy of RUL for LIBs. The WOA-SVM method
cannot ensure the prediction accuracy due to the
WOA algorithm easily falls into the local optimal
solution, therefore, the adaptive weights are
introduced to solve this shortcoming. The
performance of the IWOA algorithm is verified via
five test functions. Besides, compared with the SVM
and WOA-SVM methods, the results show that the
IWOA-SVM method can provide higher prediction
accuracy of RUL for LIBs.
The remainder of this work is organized as
follows: Section 2 reviews the related method and the
detailed implementation of the proposed method is
presented. The experimental results by comparing
with SVM and WOA-SVM methods are presented in
Section 3. Section 4 presents the conclusions.
2 MODEL ESTABLISHMENT
2.1 SVM Method
When the support vector machine (SVM) (Wei J,
Dong G and Chen Z, 2018) is utilized for regression
prediction, according to given simple set
},...,2,1|),{( miyxD
ii
==
, (
m
i
Rx ∈
,
R
y
i
∈
), where
i
x
is the i-th input value,
R
y
i
∈
denotes the i-th output
value, and
m
represents the total number of samples.
Therefore, the regression of SVM can be denoted as:
bxwxf
T
+⋅= )()( φ
(1)
where
w
is a weight,
φ
represents a nonlinear
mapping, and
b
denotes the intercept. The dual
problem of SVM can be obtained by introducing the
Lagrangian multipliers:
))(
ˆ
)(),()
ˆ
)(
ˆ
(
2
1
(min
,
ˆ
,

−++−−−−
m
i
ii
m
i
ii
m
ji
jijjii
yayaxxKaaaa
ii
εε
αα
(2)





=≤≤
=−

miCaa
aa
ts
ii
m
i
ii
,...2,1,
ˆ
,0
,0)
ˆ
(
..
(3)
where
i
a
,
i
a
ˆ
,
j
a
, and
j
a
ˆ
are the Lagrangian
multipliers,
),(
ji
xxK
is the kernel function, and the
radial basis function
))2/(||||exp(),(
22
σ
jijiRBF
xxxxK −−=
is chose in the SVR. Where
σ
is the parameter of
kernel function. Therefore, the regression function of
the SVM can be presented:
bxxKaaxf
n
i
jiRBFii
+−=

),()
ˆ
()(
(4)
2.2 Whale Optimization Algorithm and
Improved Whale Optimization
Algorithm
2.2.1 Whale Optimization Algorithm
The WOA (Mirjalili S and Lewis A, 2016) is a meta-
heuristic optimization algorithm that mainly
simulates the humpback whale hunting behavior,
namely the bubble-net hunting method.
1) Encircling the prey: The humpback whales can
quickly encircle the prey after noticing the prey, and
constantly update its position, which can be denoted
as
|)()(| tXtXCD




−⋅=
∗
(5)
DAtXtX




⋅−=+
∗
)()1(
(6)
where
t
is the current iteration,
∗
X
denotes the
position of the current optimal solution, and
X
indicates the position of the whale.
A

and C

are the
coefficient vector.
2) Bubble net attacking: Two approaches of
shrinking encircling mechanism and the location is
updated by spiral are presented to model the whale
hunting behavior, which the mathematical model can
be expressed as follows:





≥+⋅⋅
′
<⋅
=+
∗
∗
5.0)()2cos(
5.0)(
)1(
piftXleD
pifDA-tX
tX
bl





π
(7)
where
D
′

represents the distance between the i-th
whale and the current optimal position,
b
is a the
constant coefficient utilized to define the logarithmic
spiral form,
l
denotes the random number between -
CoEEE 2021 - International Joint Conference on Energy and Environmental Engineering
116

1 and 1, and
p
denotes the random number between
0 and 1.
3) Search for prey: When
1|A| ≥
, the humpback
whales are randomly selected to force them away
from a reference whale to find a better prey in order
to enhance the global search ability of the algorithm.
The mathematical model is expressed as follows:
DAXtX
rand



⋅−=+ )1(
(8)
where
|| XXCD
rand




−⋅=
and
rand
X

denotes the position
vector of the whale randomly selected.
2.2.2 Improved Whale Optimization
Algorithm
The introduction of adaptive inertia weight in the
WOA algorithm (IWOA) makes the algorithm
adaptively update the position of the WOA algorithm
to improve the optimization accuracy. The model can
be expressed as follows:





≥⋅+⋅⋅
′
<⋅⋅⋅
=+
∗
∗
5.0)()2cos(
5.0)(
)1(
1
1
piftXwleD
pifDAw-tXw
tX
bl
2





π
(9)
where
]5.0))/(5.0[cos(5.0
1
−∗∗−= Ttw
π
is the
adaptive coefficient of the current optimal position
and
]5.0))/(5.0[cos(5.0
2
+∗∗= Ttw
π
represents the
adaptive coefficient of the encircling step.
To test the search ability of the IWOA algorithm,
compared with WOA algorithm through five test
functions. The five test functions are presented in
table 1. The number of population (
NP
) is 40 and the
number of maximum iteration (
iterMax_
) is 100 for
two algorithms. Each function calculates 10 times for
each algorithm in 2 dimensions (D) and 30 D, and the
test results are shown in table 2.
Table 1: The five test functions.
Test functions Range The optimal value

=
=
n
i
i
xf
1
2
1
[-100,100] 0

=
=
n
i
i
ixf
1
2
2
[-10,10] 0
∏

=
=
+=
n
i
i
n
i
i
xxf
1
1
3
[-10,10] 0

=
+−=
n
i
ii
xxf
1
2
4
]10)2cos(10[ π
[-5.12,5.12] 0

∏
=
=
+−=
n
i
n
i
i
i
i
x
xf
1
1
2
5
1)cos(
4000
1
[-600,600] 0
Table 2: The test results for the methods.
Function Algorithm
The best value
2 D/30 D
The worth value
2 D/30 D
Mean value
2 D/30 D
1
f
WOA 8.26e-40/3.42e-16 1.13e-28/3.25e-11 1.29e-29/3.39e-12
IWOA 5.21e-161/2.14e-156 4.67e-138/1.91e-116 4.74e-139/1.91e-117
2
f
WOA 1.18e-41/9.22e-16 3.14e-28/1.53e-12 3.40e-29/1.58e-13
IWOA 2.95e-180/3.09e-169 4.00e-139/3.83e-130 4.00e-140/3.83e-131
3
f
WOA 4.91e-21/1.41e-10 6.51e-18/1.20e-08 9.00e-19/2.12e-09
IWOA 4.01e-86/2.64e-80 8.23e-72/6.98e-69 8.87e-73/8.25e-70
4
f
WOA 0/2.27e-13 7.11e-15/11.49 1.78e-15/1.15
IWOA 0/0 0/0 0/0
5
f
WOA 0/6.66e-16 5.92e-02/3.05e-12 1.13e-02/7.69e-13
IWOA 0/0 0/0 0/0
Improved Whale Optimization Algorithm and Support Vector Machine for Remaining Useful Life Prediction of Lithium-ion Batteries
117

By the comparison results in table 2, the IWOA
algorithm obtain the optimal value of the five
functions better than the WOA algorithm. For
example, when the test function is
5
f
in 2 D, the
mean value of the WOA algorithm is 1.13e-02,
whereas the IWOA algorithm is 0, which indicates the
IWOA algorithm can obtain the optimal value. By the
comparison results in table 2, the IWOA algorithm
obtain the optimal value of the
4
f
and
5
f
two test
functions. Besides, with the dimensions increase, the
convergence accuracy of the WOA algorithm cannot
be provided, whereas the IWOA algorithm can be
guaranteed. It can be concluded that the search
stability of the proposed method better than the WOA
algorithm.
2.3 The Parameters of SVM Method
Optimized by the IWOA Algorithm
The problem of getting into the local optimal solution
can be solved via the IWOA algorithm and the better
parameters of SVM method can be obtained. The
framework of RUL prediction for LIBs by the IWOA-
SVM model is shown in figure 1.
Figure 1: The framework of RUL prediction for LIBs based
on IWOA-SVM method.
The special steps of IWOA-SVM can be
described as follows:
Step 1. Data processing: Divided the data into the
training samples and the testing samples.
Step 2. Set related parameters:
NP
is 20, the
lower boundary is
lb
=0.01, the upper boundary is
ub
=100, and
iterMax_
is 100.
Step 3. Calculate the fitness of the whales and
update the position.
Step 4. The parameters of SVM can be obtained
via IWOA algorithm.
Step 5. Predict the RUL of LIBs: Verify the
proposed method by the testing samples and predict
RUL of LIBs.
3 RUL PREDICTION OF LIBs
BASED ON IWOA-SVM
METHOD
3.1 Capacity Datasets for LIBs
The datasets of LIBs are obtained from the NASA
Prognostics Center of Excellence (PCoE) (Goebel K,
Saha B, Saxena A, Celaya J R and Christophersen J
P, 2008). The commercial available 18650 LIBs with
the nominal capacity of 2Ah are utilized to test at
room temperature of 25℃. Firstly, the LIBs were in
constant current (CC) charge model at 1.5 A until the
voltage achieved 4.2 V, then kept on a constant
voltage (CV) model until the charge current dropped
to 20 mA. The discharge process was in CC model at
2 A until the voltage fell to the cutoff voltage. The
LIBs B0005 (B5) and B0007 (B7) of NASA are
utilized to experiment and the failure threshold is
taken as 72% of the nominal capacity. The
degradation trend of two batteries are presented in
figure 2.
Figure 2: The capacity degradation trajectory of two
batteries.
3.2 Performance Evaluation Criterion
The mean absolute error (MAE) and the root mean
square error (RMSE) are utilized to measure the
accuracy of forecasting,

−=
n
i
yy
n
MAE |
ˆ
|
1
(10)
Start
Data processing
Training samples Testing samples
Set related
parameters
Calculate the fitness of
the whales and update
the position
Parameters of
SVM by IWOA
algorithm
Prediction
result
End
CoEEE 2021 - International Joint Conference on Energy and Environmental Engineering
118


−=
n
i
yy
n
RMSE
2
)
ˆ
(
1
(11)
where
y
ˆ
is the predicted capacity value, and
y
denotes the true capacity value.
3.2.1 RUL Estimation of LIBs
To verify the prediction performance of the proposed
method, the capacity datasets of batteries B5 and B7
are utilized to test and compared with SVM and
WOA-SVM methods. The detailed parameter settings
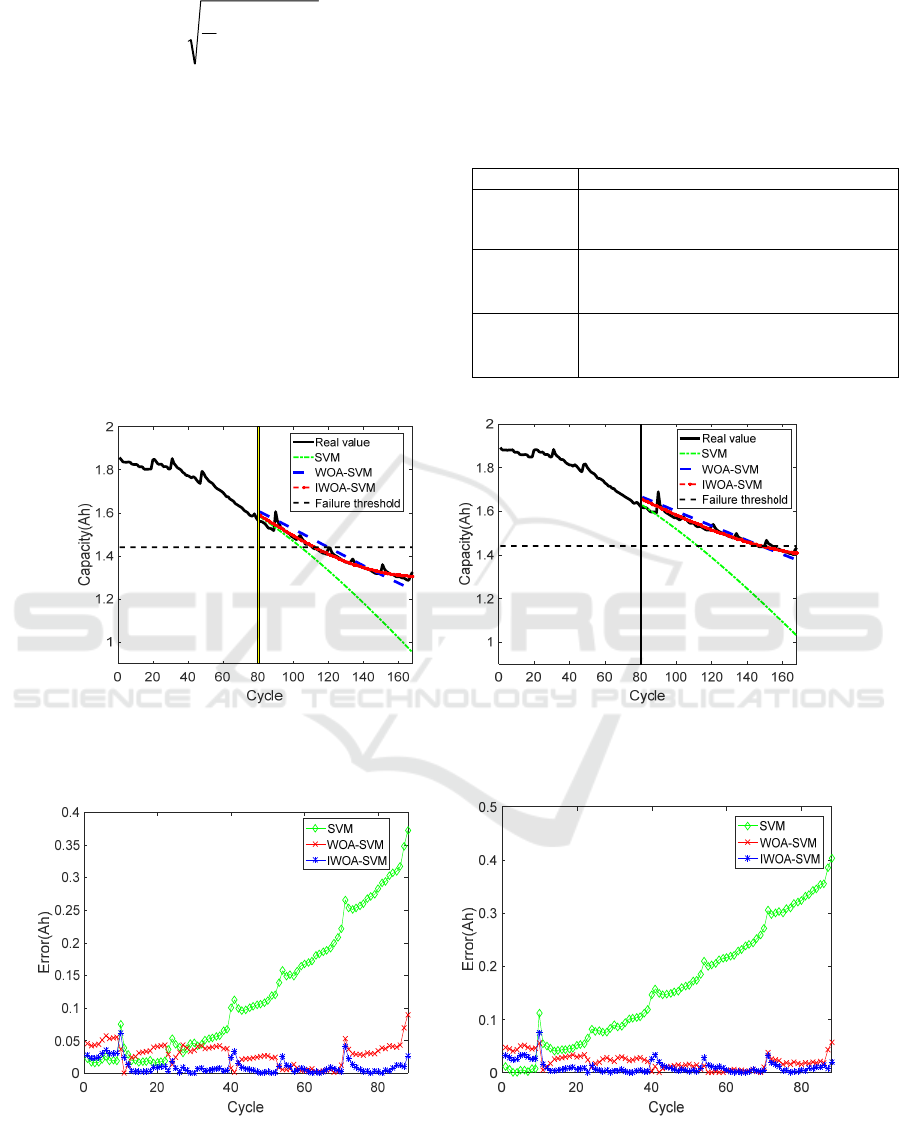
are shown in table 3. The RUL prediction of LIBs is
carried at the starting point (SP) is cycle 80 and the
prediction results of three methods are shown in
figure 3. The absolute values of the error are
presented between the real and predicted values of the
two batteries in figure 4. Besides, the results of the
RUL prediction are represented in table 4. In table 4,
the RUL value is the real RUL value and the PRUL
denotes the predicted RUL value.
Table 3: The parameter settings for three methods.
Algorith
m
Parameter settings
SVM
20=NP
,
100_ =iterMax
,
10=C
,
01.0=g
WOA-
SVM
20=NP
,
100_ =iterMax
,
]100,01.0[=C
,
]100,01.0[=g
IWOA-
SVM
20=NP
,
100_ =iterMax
,
]100,01.0[=C
,
]100,01.0[=g
(a) B5 (b)B7
Figure 3: The curves of RUL prediction for three methods:(a) B5; (b)B7.
(a) B5 (b) B7
Figure 4: The absolute values of the error for three methods: (a) B5; (b)B7.
Improved Whale Optimization Algorithm and Support Vector Machine for Remaining Useful Life Prediction of Lithium-ion Batteries
119

Table 4: The results of the RUL prediction based on three methods.
No. SP RUL
SVM WOA-SVM IWOA-SVM
PRUL AE MAE
RM
SE
PRUL AE MAE
RM
SE
PRUL AE MAE
RM
SE
B5
80
31 25 6 0.125 0.161 40 9 0.028 0.032 32 1 0.010 0.015
B7 66 33 33 0.162 0.196 68 2 0.021 0.025 67 1 0.011 0.016
From the table 4, the AE (It should be noted that
the AE is absolute error between the RUL value and
the PRUL value) values of SVM and WOA-SVM
methods are 6 and 9 based on the battery B5,
respectively. Whereas the IWOA-SVM is six times
smaller than that of the SVM method and nine times
smaller than that of the WOA-SVM method. For
battery B7, the MAE value of SVM is 0.162, whereas
the proposed method is fourteen times smaller than
that of the SVM method, besides, the RMSE value of
the proposed method is twelve times smaller than that
of the SVM method. It can be concluded that the
proposed method can provide higher accuracy than
other two methods.
To further verify the effectiveness of the proposed
method, compared with other up-to-date methods, the
results as shown in table 5. An integrated quantum
PSO and SVR (QPSO-SVR) method established in
Ref. (Wang Z, Zeng S, Guo J and Qin T, 2018) was
compared with PSO-SVR method. As shown in table
5, the AE values of PSO-SVR and QPSO-SVR
methods are 7 and 5, respectively, whereas the
proposed method is 1. Therefore, it can be concluded
that the proposed method can provide higher accuracy
for predicting the RUL of LIBs.
Table 5: The comparison results of the proposed method
with other methods.
N
o.
Meth
od
Thresh
old
(Ah)
S
P
RU
L
PR
UL
AE
(cyc
le)
RM
SE
B
5
PSO-
SVR[
16]
1.4
8
0
44 51 7 0.04
QPS
O-
SVR[
16]
1.4
8
0
44 49 5 0.02
IWO
A-
SVM
1.4
8
0
44 44 1 0.01
4 CONCLUSIONS
A method is proposed based on improved whale
optimization algorithm and SVM for predicting RUL
of LIBs. To avoid the WOA algorithm falls into the
local solution, the adaptive weights are introduced to
solve this shortcoming. Compared with the WOA
algorithm via the five test functions in 2 dimensions
and 30 dimensions, respectively, the optimal value of
the IWOA algorithm can be obtained better than that
of the WOA algorithm, which indicates that the
IWOA algorithm can obtain higher convergence
accuracy. Besides, the datasets of NASA are utilized
to validate the performance of the proposed method.
Compared with SVM and WOA-SVM methods, it
can be concluded that the RMSE value of the
proposed method is less than 0.02 for all test batteries.
Therefore, the proposed method can provide higher
prediction accuracy for the RUL of LIBs. In the
future, the further work is to utilize the IWOA
algorithm to optimize the parameters of multi-kernel
SVM (MSVM) model for providing more prediction
accuracy of battery RUL.
ACKNOWLEDGMENTS
This work is supported by the National Natural
Science Foundation of China under Grant 51176028
and 51376042, the Major Scientific and
Technological Project of Jilin Province of China
under Grant 20180201004SF, and the Scientific and
Technological Project of State Grid Corporation of
China under Grant 52010119002F.
REFERENCES
Xiong R, Tian J, Mu H and Wang C. (2017). Appl. Energy,
207.
Wang Y, Ni Y, Lu S, Wang J and Zhang X. (2019). IEEE T
Veh. Technol., 68.
Duong P L T and Raghavan N. (2018). Microelectron.
Reliab., 81.
Lyu C, Lai Q, Ge T, Yu H, Wang L and Ma N. (2017).
Energy, 120.
You G W, Park S and Oh D. (2017). IEEE Trans Ind.
Electro., 64, 6.
Patil M, Tagade P, Hariharan K, Kolake S, Song T, Yeo T
and Doo S. (2015). Appl. Energy, 159.
Zhang Y, Xiong R, He H and Pecht M G. (2019). IEEE
CoEEE 2021 - International Joint Conference on Energy and Environmental Engineering
120

Trans. Ind. Electron., 66, 2.
Guha A and Patra A. (2018). IEEE Trans. on Instru. Meas.,
67, 8.
Qin T, Zeng S and Guo J. (2015). Microelectron. Reliab.,
55, 9.
Li L, Liu Z, Tseng M and Chiu A. (2019). Appl. Soft
Comput., 74.
Gao D and Huang M, J. (2017). Power Electron., 17, 5.
Li S and Fang H. (2017). 36th Chinese Control Conference
(CCC), Dalian.
Wei J, Dong G and Chen Z. (2018). IEEE Trans. Ind.
Electron., 65, 7.
Mirjalili S and Lewis A. (2016). Adv. Eng. Softw., 95.
Goebel K, Saha B, Saxena A, Celaya J R and
Christophersen J P. (2008). IEEE Instru. Meas. Mag.,
11, 4.
Wang Z, Zeng S, Guo J and Qin T. (2018). PLoS One, 13,
7.
Improved Whale Optimization Algorithm and Support Vector Machine for Remaining Useful Life Prediction of Lithium-ion Batteries
121