Test Quality Assessment and Adaptive Algorithm Based on IRT Models
Alexander A. Kostikov
1 a
, Kateryna V. Vlasenko
2,3 b
, Iryna V. Lovianova
4 c
,
Vadim V. Khoroshailo
1 d
and Natalia S. Hrudkina
1 e
1
Donbass State Engineering Academy, 72 Academichna Str. , Kramatorsk, 84313, Ukraine
2
National University of “Kyiv Mohyla Academy”, 2 Skovorody Str., Kyiv, 04070, Ukraine
3
Limited Liability Company Technical University “Metinvest Polytechnic”, 80 Pivdenne Hwy, Zaporizhzhia, 69008,
Ukraine
4
Kryvyi Rih State Pedagogical Univeristy, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine
Keywords:
Adaptive Algorithm, Rasch Model, Item Response Theory (IRT), Information Function of Test, Latent
Variables, Birnbaum Model.
Abstract:
In this paper the algorithm for adaptive testing of students’ knowledge in distance learning and an assess-
ment of its effectiveness in the educational process has been proposed. The results of the study are based on
the achievements of modern testing theory IRT. The objective of the study was to build test items that allow
adequately assessing the student’s achievements and automating the assessment process using an adaptive al-
gorithm. To achieve this goal, mathematical models of modern testing theory IRT were used, namely, the
Rasch model, 2-PL and 3-PL Birnbaum models. The important outcomes of this work are a thorough analysis
of the developed test tasks, identification of their shortcomings and automation of the process of assessing stu-
dents’ knowledge using an adaptive algorithm based on the methods of modern testing theory IRT. The paper
provides an overview of the results of the application of modern test theory, a description and block diagram
of the proposed algorithm and the results of its application in the real educational process. The effectiveness
of using this algorithm for the objective assessment of students’ knowledge has been experimentally shown.
The test quality has been assessed using the IRT models.
1 INTRODUCTION
1.1 Motivation and Research
Challenges of the Study
Important components of the educational process are
the quality control of the assimilation of knowledge
in higher education and the assessment of the degree
to which students achieve their educational goals.
Recently, distance learning has become widespread,
which has become especially relevant in connection
with the COVID19 pandemic. In this regard, there is
a problem of the adequacy of knowledge assessment
with the help of computer testing. The solution to this
problem is of great importance, because it allows you
a
https://orcid.org/0000-0003-3503-4836
b
https://orcid.org/0000-0002-8920-5680
c
https://orcid.org/0000-0003-3186-2837
d
https://orcid.org/0000-0001-6539-8329
e
https://orcid.org/0000-0002-0914-8875
to reduce the time for knowledge control, facilitate
the work of teachers, and immediately get the result
of the assessment.
While solving this problem, we faced the follow-
ing challenges:
1. Choice of research methodology.
2. Experimental verification of the research results.
Our studies were evaluated on the results of mod-
ern testing theory, which allows us to adequately as-
sess the quality of test items and create effective adap-
tive knowledge assessment algorithms based on them.
To test knowledge, test items of varying complexity
were developed for the discipline “Higher Mathemat-
ics” to assess the level of students’ knowledge of with
different levels of training.
1.2 Problem Statement
Modern approaches to assessing students’ academic
achievements are based on the use of classical testing
Kostikov, A., Vlasenko, K., Lovianova, I., Khoroshailo, V. and Hrudkina, N.
Test Quality Assessment and Adaptive Algorithm Based on IRT Models.
DOI: 10.5220/0012061900003431
In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 103-117
ISBN: 978-989-758-662-0
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
103

theory and Item Response Theory (IRT). The mathe-
matical background of pedagogical measurement the-
ory was created in the works of (Andersen, 1973; An-
drich, 2021; Avanesov, 1980; Guttman, 1944; Lord
et al., 1968; Maslak et al., 2005; Rasch, 1960; Wright
and Linacre, 1987; Wright and Masters, 1982). In
IRT, the concept of a latent variable is used. The term
“latent variable (parameter)” is usually understood as
a theoretical concept that characterizes a certain hid-
den property or quality (for example, the level of stu-
dents’ ability, the difficulty of the test task), which
cannot be directly measured. The advantages of the
classical testing theory are the provision of informa-
tion about the indicators of the knowledge quality of
the subjects, the clarity of the performed calculations
and the simple interpretation of the processing data.
The main disadvantage is the dependence of the re-
sults of evaluating the participants’ parameters on the
difficulty of the proposed tasks. Application of IRT,
based on Rasch models, provides the possibility of the
evaluation independence of the latent parameter “abil-
ity level” calculated values of participants α
i
from the
values of the “item difficulty” β
i
. This helps to in-
crease the objectivity of the obtained assessments of
the students’ ability level and allows to build effective
algorithms for assessing knowledge.
The purpose of this paper is to develop an al-
gorithm of adaptive testing for objective assessment
of students’ knowledge in distance learning, which
becomes especially relevant in the quarantine of
COVID-19.
1.3 State of Arts and Review
The educational standards of the new generation are
based on a competency-based approach to assessing
the quality of a student’s training, when it is not his
knowledge that is tested, first of all, but his readiness
to apply it in practice and to act productively in a non-
standard situation, the ability to create the required
mode of action. Therefore, the quality of training is
understood as the degree of the student’s readiness to
demonstrate the relevant competencies. The general-
ization of the world experience in the implementation
of the competence-based approach to assessing learn-
ing outcomes allows us to make the following conclu-
sions that determine the main approaches to assessing
the level of competence mastery, the main of which
are the following:
1. competencies are dynamic, since they are not an
invariable quality in the structure of a pupil’s per-
sonality, but are able to develop, improve or com-
pletely disappear in the absence of an incentive to
manifest them. Therefore, we can talk about the
level of competence, assess it quantitatively, and
monitor it.
2. when assessing learning outcomes, it is necessary
to consider them in dynamics, which requires di-
agnostics of the educational process using moni-
toring procedures
3. the level of possession of a competence is a hidden
(latent) parameter of the pupil and direct measure-
ment is not amenable. It can be estimated with a
certain probability. Therefore, when evaluating it,
a probabilistic approach should be used.
It follows from this that in order to create tools for
the automated assessment of the learning outcomes, it
is necessary, first of all, to solve two problems:
1. develop theoretical and methodological founda-
tions for modeling and parameterization of the
learning process and the diagnostic tools used to
evaluate its results.
2. theoretically substantiate and implement
software-algorithmic means for processing
the results of participants’ diagnostics (testing,
questionnaires), as well as tools for assessing
learning outcomes and the quality of diagnostic
tools.
The theoretical and methodological basis for solv-
ing these problems was the study results, first of all,
by such Brown (Brown, 1910), Cronbach (Cronbach,
1951), Guilford (Guilford, 1942), Gulliksen (Gullik-
sen, 1986), Guttman (Guttman, 1944), Kuder and
Richardson (Kuder and Richardson, 1937), Luce and
Tukey (Luce and Tukey, 1964), Lord et al. (Lord
et al., 1968), Sax (Sax, 1989), Spearman (Spearman,
1910). They developed the theoretical foundations
for the creation of diagnostic materials and the clas-
sical approach to processing, analysis and interpreta-
tion of diagnostic results: the conceptual apparatus
of the classical test theory, criteria and indicators of
the quality of diagnostic tools, methodological basics
of their design and quality expertise. The issues of
scaling and comparison of processing data have been
deeply investigated.
The theoretical basis for the creation of tools for
automatic assessment of the results of the educational
process has received its further development due to
the creation of the IRT (Item Response Theory) the
foundations of which are set out in the works of (An-
drich, 2021, 2005; Andersen, 1973; Bezruczko, 2005;
Bond et al., 2020; Andrich et al., 2001; van der Linden
and Hambleton, 1997; Ingebo, 1997; Eckes, 2011;
Lord, 1980; Perline et al., 1979; Smith and Smith,
2004; Rasch, 1960; Fischer and Molenaar, 1995; Wil-
son, 2005; Wright and Masters, 1982; Wright, 1977;
Wright and Stone, 1979; Wright and Linacre, 1987).
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
104

Currently, IRT mathematical models are widely
used to assess the quality of test items. In (Tjabolo
and Otaya, 2019) the quality of the questions of
school exams was assessed using 1, 2,3-PL models.
As a result of the study, school exam questions were
classified into two categories(the good and the bad
categories) based on the value of the difficulty level
of the test items.
In (Amelia and Kriswantoro, 2017) the quality of
items in chemistry was also assessed using 1-PL, 2-
PL and 3-PL models. By these models, assessments
of the students’ ability level, the difficulty level of
test items were obtained, and the difference in the
obtained assessments was analyzed. Various adap-
tive algorithms based on the Rasch model have been
proposed in the works (Al-A’ali, 2006; Zaqoot et al.,
2021) Despite the large number of papers devoted
to the creation of adaptive algorithms based on IRT
models, we could hardly find any reference to works
that would consider an adaptive algorithm selecting
the model that best suits the test data. The adaptive
algorithm proposed by us can use any of three IRT
models: 1-PL, 2-PL and 3-PL.
2 ALGORITHM OF ADAPTIVE
TESTING BASED ON RASCH
MODEL
Adaptive testing is a type of testing in which the or-
der of presentation of test items and the difficulty of
the next task depends on the participant’s answers to
previous items. The basis of adaptive testing systems
are statistical models. Very easy and very difficult
tasks are automatically uninformative. Therefore, for
most tests, the optimal level of difficulty is the item,
to which the correct answer is given by about half of
the test participants.
The difficulties of the test items is determined ex-
perimentally, and the measurement process consists
of determining the percentage of participants who are
able to give the correct answer to the task in previ-
ous experiments. The problem of developing adap-
tive algorithms has been considered in (Weiss, 1982;
Al-A’ali, 2006; Weiss, 2004).
The Rasch model was used to construct the adap-
tive testing algorithm. This model is defined by for-
mulas:
P
ni
=
exp(θ
n
− β
i
)
1 + exp(θ
n
− β
i
)
(1)
where P
ni
is the probability that the participant n, n =
1, . . . , N with the ability θ
n
correctly performs the task
i, i = 1, . . . , I, with the difficulty β
i
.
To start the algorithm, it is necessary to determine
the initial levels of difficulties. To this end, at the
beginning of the testing session the accumulation of
primary information about the level of preparation of
the participant is carried out. To do this, participant
receive N
p
tasks with an average level of difficulty.
Tasks to determine the initial level of the participant
are chosen by the teacher. Then, using the received
answers, the initial estimation of the ability level of
the student is calculated, and also recalculation of the
difficulty level current values of test items is carried
out.
The initial assessment of the ability level of the
i-th student (in logs) is based on the formula:
θ
0
i
= ln

p
i
q
i

, i = 1, 2 · · · N, (2)
where N is the number of test participants, p
i
is the
proportion of correct answers of the i-th participant
to all tasks, q
i
is the proportion of incorrect answers
(q
i
= 1 − p
i
).
The difficulty level of test items in logs is deter-
mined by the formula:
β
0
j
= ln

q
j
p
j

, j = 1, 2 · · · M, (3)
where M is the number of test items, p
j
is the propor-
tion of correct answers of all participants to the j-th
test item, q
j
is the proportion of incorrect answers.
At the next stage, the initial values in the logs of
the ability level of participants θ
0
i
and the initial val-
ues in the logs of the difficulty level of the test item
β
0
j
are reduced to a same interval scale (Lord et al.,
1968). The formula for such transition is based on the
idea of reducing the impact of the items difficulty on
the assessments of test participants.
Pre-calculating the average value of the initial log-
its of the students’ ability level
θ =
N
∑
i=1
θ
0
i
N
and the standard deviation V of the initial values dis-
tribution of the parameter θ
V
2
=
N
∑
i=1

θ
0
i
− θ

2
N − 1
,
we obtain a formula for calculating the difficulty level
logit of the j-th item
β
j
= θ +Y · β
0
j
, j = 1, M, (4)
where
Y =

1 +
V
2
2.89

1
2
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
105

Similarly, calculating
β =
M
∑
j=1
β
0
j
M
, W =
v
u
u
u
t
M
∑
j

β
0
j
− β

2
M − 1
we get the formula for calculating the ability level
logit of the i-th student:
θ
i
= β + X · θ
0
i
, i = 1, N, (5)
where X =

1 +
W
2
2.89

1
2
.
The obtained values allow to compare the level of
students’ ability with the level of test item difficulty.
If θ
i
− β
j
is a negative quantity and is large in mod-
ulus, then the problem of difficulty β
j
is too difficult
for a student with the ability level θ
i
, and it will not
be useful for measuring the level of knowledge of the
i-th student. If this difference is positive and large in
modulus, then the task is too easy, it has long been
mastered by the student. If θ
i
− β
j
, then the proba-
bility that the student correctly completes the task is
equal to 0.5.
The information function of the i-th problem for
the Rasch model (1) I
i
(θ) is defined as the product
of the probability of the correct answer P
i
(θ) to this
problem on the probability of the incorrect answer
Q
i
(θ) (Lord et al., 1968)
I
i
(θ) = P
i
(θ) · Q
i
(θ) (6)
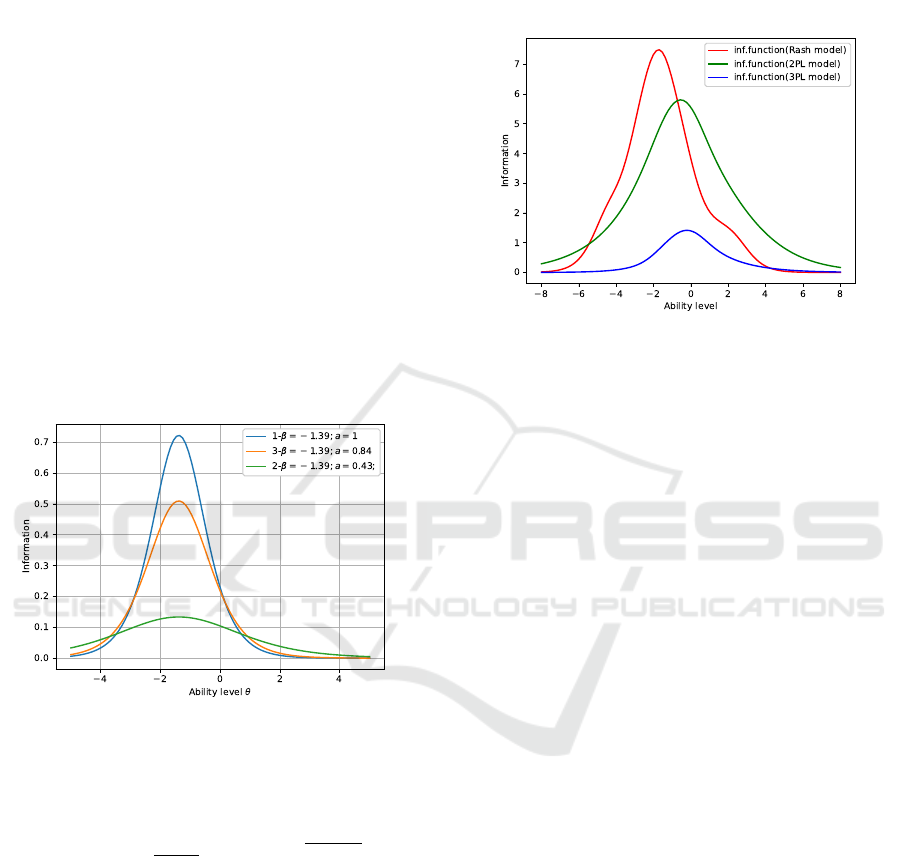
Figure 1 shows the information function of the i-
th item. Figure 1 shows that the test item, the answer
to which all students know, does not provide any in-
formation, as well as the item, the answer to which
no one knows. We get useful information when some
participants know the answer to the task and some do
not.
Figure 1: Information function of the test task.
The information function of the test is calculated
as the sum of the information functions of the test
items (Lord et al., 1968):
I(θ) = D
2
·
M
∑
j=1
I
j
(θ) (7)
where D is the correction factor (D = 1.7), necessary
to approximate the distribution of logistic probability
to the law of normal distribution.
After calculating the information function, the
measurement error SE is calculated, the value of
which is used to check the condition of the end of the
test procedure.
In the Rusch model, the measurement error de-
pends on the level of training θ and is calculated by
the formula (Lord et al., 1968):
SE(θ) =
1
p
I(θ)
. (8)
If the error takes a value less than the threshold
set by the teacher, the adaptive testing algorithm ends.
Otherwise, the following test task is selected. To se-
lect the next task, use the value of θ
i
, calculated by
formula (5). The next task is the one whose difficulty
level is closest to the current assessment of the ability
level of the participant. This task has the largest in-
formation contribution and its choice reduces the total
number of required test tasks.
Thus, the developed adaptive testing algorithm
consists of the following stages:
1. Selection of 5 tasks of average difficulty from the
bank of questions, which is determined by the
teacher.
2. Finding the initial level of student’s ability θ
0
i
and
the initial difficulty level of items β
0
j
by formulas
(2) and (3).
3. Summary of the obtained initial values θ
0
i
and β
0
j
to a single interval scale using formulas (5) and
(4).
4. Calculation of the information function of test
tasks to which the student answered by formulas
(6) and (7).
5. Finding the measurement error by the formula (8).
6. If the measurement error is less than the threshold,
the adaptive testing is completed.
7. If not, then the next task is selected from the con-
dition


θ
i
− β
j


= min.
8. Then the algorithm is repeated starting from point
3.
The block diagram of the algorithm is shown in
figure 2. The proposed algorithm can use any of three
models: 1-PL, 2-PL and 3-PL.
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
106

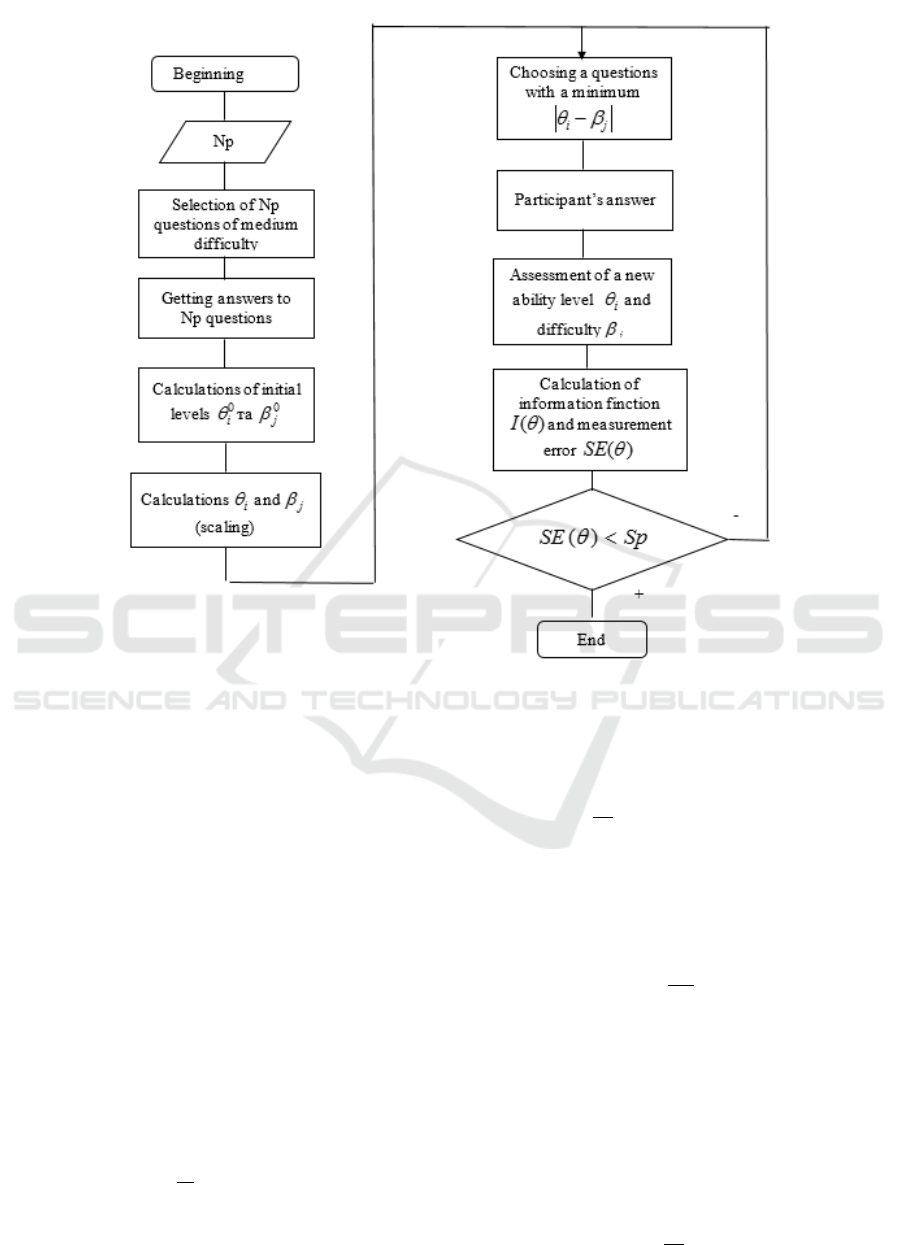
Figure 2: Block diagram of the adaptive testing algorithm.
3 RESULTS OF TEST ANALYSYS
BASED ON THE RASCH
MODEL
Let us consider the procedure for calculating the pa-
rameters of student ability level θ
i
and item difficulty
parameter β
i
from empirical data. As initial data we
will take results of testing of students in Moodle sys-
tem on discipline “Higher Mathematics” of the Math-
ematics and Modeling Departement of the Donbass
State Engineering Academy (table 1). Table 1 shows
the records of the first 10 test participants. A total of
50 participants took part in the testing.
The test in this discipline consisted of 20 ques-
tions. First, it is necessary to calculate the proportions
of correct p
i
and incorrect q
i
answers of participants.
These values are calculated by formulas
p
i
=
R
i
N
, q
i
= 1 − p
i
, (9)
where R
i
is the number of correct answers for the i-th
test item, = 1, 2, ..., n, and n is the number of items
in the test. For example, for the first participant of
testing we have
p
1
=
18
20
= 0.9, q
1
= 1 − 0.9 = 0.1
The values p
i
and q
i
are given in columns 3 and 4
of table 1.
Next, calculate the initial values θ
0
1
of the ability
level of participants by formula (2). For the first par-
ticipant we have
θ
0
1
= ln
0.9
0.1
= 2.197
Using the statistical module Moodle, the follow-
ing characteristics were obtained for test tasks: facil-
ity index (F), standard deviation (SD), random guess
score (RGS), intended weight, effective weight, dis-
tinction, distinction efficiency.
These data are shown in table 2.
Based on the data in table 2, we can estimate the
initial values of the item difficulty parameter. By for-
mula (3) for the first problem we obtain
β
0
1
= ln
2
98
= −3.891
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
107

Table 1: Test results in the Moodle system in the discipline “Higher Mathematics” of the Mathematics and Modeling Depart-
ment of the Donbass State Engineering Academy.
Participant’s number Score Number of correct answers p
i
q
i
θ
0
i
1 90 18 0.9 0.1 2.197225
2 75 15 0.75 0.25 1.098612
3 85 17 0.85 0.15 1.734601
4 100 20 1 0 ∞
5 75 15 0.75 0.25 1.098612
6 100 20 1 0 ∞
7 90 18 0.9 0.1 2.197225
8 90 18 0.9 0.1 2.197225
9 70 14 0.7 0.3 0.847298
10 85 17 0.85 0.15 1.734601
Table 2: Statistical characteristics obtained using the statistical module of the Moodle system based on the results of final
testing in the discipline “Higher Mathematics”.
Q# F SD RGS Intended weight Effective weight Distinction Distinguishing efficiency
1 98.00% 14.14% 33.33% 5.00% -11.54% -28.62%
2 94.00% 23.99% 33.33% 5.00% 3.41% 6.93% 11.28%
3 90.00% 30.30% 16.67% 5.00% 6.75% 44.07% 65.85%
4 94.00% 23.99% 20.00% 5.00% 4.66% 22.91% 39.11%
5 96.00% 19.79% 20.00% 5.00% 3.34% 11.72% 23.66%
6 90.00% 30.30% 14.29% 5.00% 3.18% -1.53% -2.22%
7 92.00% 27.40% 14.29% 5.00% 6.32% 43.38% 70.79%
8 84.00% 37.03% 20.00% 5.00% 6.48% 26.08% 35.44%
9 88.00% 32.83% 20.00% 5.00% 5.32% 17.26% 23.76%
10 74.00% 44.31% 20.00% 5.00% 9.75% 68.31% 84.84%
11 98.00% 14.14% 20.00% 5.00% 2.85% 14.64% 35.69%
12 100.00% 0.00% 16.67% 5.00% 0.00%
13 94.00% 23.99% 33.33% 5.00% 4.93% 27.00% 45.87%
14 90.00% 30.30% 33.33% 5.00% 5.51% 23.81% 34.88%
15 88.00% 32.83% 25.00% 5.00% 5.32% 17.26% 23.76%
16 90.00% 30.30% 33.33% 5.00% 5.51% 23.81% 33.33%
17 42.00% 49.86% 20.00% 5.00% 5.23% -2.60% -3.57%
18 80.00% 40.41% 33.33% 5.00% 8.11% 45.46% 56.25%
19 56.00% 50.14% 20.00% 5.00% 7.01% 13.80% 17.23%
20 82.00% 38.81% 20.00% 5.00% 6.32% 21.10% 27.68%
The results of calculations of the initial values of
the item difficulty parameter are given in table 3.
As can be seen from table 3, all participants in the
quiz answered the 12th item, so the score was equal to
infinity with a minus sign. But practically at β >-6 the
probability value P
i
(β) close to one. These items are
performed by all participants and they become redun-
dant. Items with β > 6 are also useless. Such items
will not be overcome by any participant and they do
not carry any information about differences in the stu-
dents’ ability levels.
In tables 1 and 3, the parameter values θ
0
i
and
β
0
i
are on different interval scales. In order to reduce
them to a single scale of standard estimates, it is nec-
essary to calculate the variances V
2
and W
2
using the
data from tables 1 and 3. Infinite data are excluded
from consideration.
Calculating the variance, we obtain
V
2
=
∑
N
i=1

θ
0
i
− θ

2
N − 1
= 0.634,
W
2
=
∑
M
j

β
0
j
− β

2
M − 1
= 4.873
Next, we calculate the angular coefficients (Lord
et al., 1968):
Y =

1 +
V
2
2.89

1
2
= 1.104
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
108

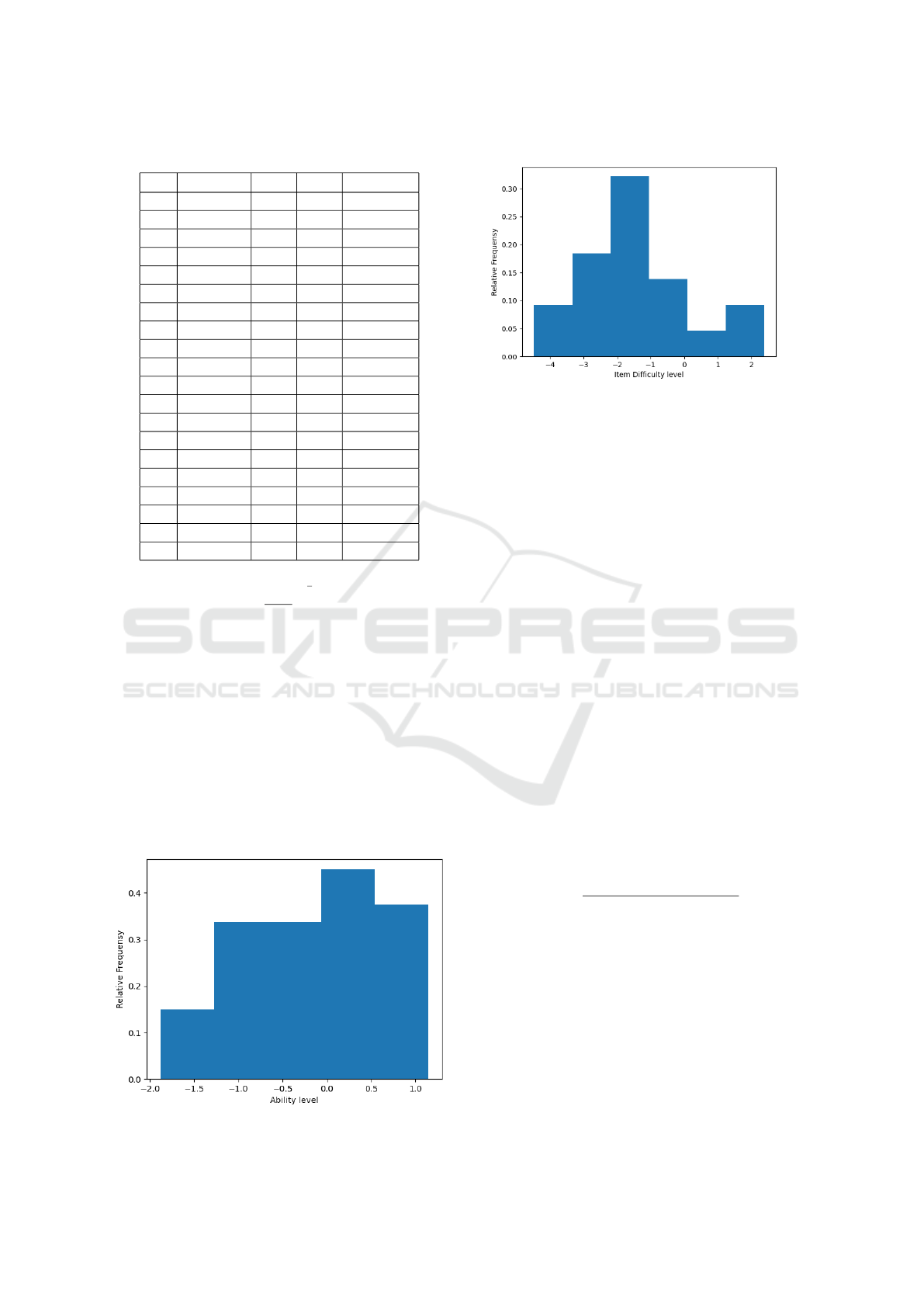
Table 3: Initial values β
0
i
of the item difficulty parameter.
Q# Progress p
i
q
i
β
0
i
1 98.00% 0.98 0.02 -3.89182
2 94.00% 0.94 0.06 -2.75154
3 90.00% 0.90 0.10 -2.19722
4 94.00% 0.94 0.06 -2.75154
5 96.00% 0.96 0.04 -3.17805
6 90.00% 0.90 0.10 -2.19722
7 92.00% 0.92 0.08 -2.44235
8 84.00% 0.84 0.16 -1.65823
9 88.00% 0.88 0.12 -1.99243
10 74,00% 0.74 0.26 -1.04597
11 98.00% 0.98 0.02 -3.89182
12 100.00% 1.00 0.00 -∞
13 94.00% 0.94 0.06 -2.75154
14 90.00% 0.90 0.10 -2.19722
15 88.00% 0.88 0.12 -1.99243
16 90.00% 0.90 0.10 -2.19722
17 42,00% 0.42 0.58 0.322773
18 80.00% 0.80 0.20 -1.38629
19 56,00% 0.56 0.44 -0.24116
20 82.00% 0.82 0.18 -1.51635
X =

1 +
W
2
2.89

1
2
= 1.63
Next on the formulas
θ
i
= −2.103 + 1.104θ
0
i
β
i
= 1.86 + 1.63β
0
i
calculate the scaled values β
i
and θ
i
of the parameters.
In tables 4 and 5 scaled parameter values are pro-
vided.
For the analysis of test items quality we will cre-
ate histograms of students’ ability levels and levels
of items difficulties on the basis of the received data.
These histograms are shown in figure 3 and figure 4.
Figure 3: Ability levels histogram.
Figure 4: Items difficulty levels histogram
The histograms of the distributions of ability lev-
els and difficulty levels of test items are visually sim-
ilar to a normal distribution, which is typical for a
good test. However, the distribution of difficulty lev-
els of test items has a negative maximum, which in-
dicates that there are more simple than difficult tasks
in the test. The presence of a large number of easy
tasks leads to the fact that assessments of the level of
preparation of students will be inflated. This is clearly
seen from the histogram of the training levels of the
test participants, which clearly shows that the range of
ability levels is from -1.8 to 2.3 logs, while the range
of items difficulties levels is from -1.8 to 1.2 logs.
The sum of the scaled difficulty levels of test items
is -27.93.
This means that the test items are very easy. This
test is not balanced, it contains a lot of easy items. It is
necessary to strive to ensure that this amount is close
to zero. Thus, the assessment of latent parameters al-
lows to determine noninformative items that should
be excluded from the quiz. The use of the developed
adaptive algorithm will allow to objectively assess the
level of students’ knowledge.
Now for all test tasks we construct characteristic
curves using the relation (10)
P
j
=
1
1 + exp(−1.702(θ− β
j
))
(10)
where P
j
is the probability that the participant with the
ability θ correctly performs the task j, j = 1, . . . , M,
with the difficulty β
j
.
The graph of these characteristic curves is shown
in figure 5.
Figure 5 shows that the characteristic curves for
the items 1-2, 4-6, 8-11, 12-13 coincide, and the
curves for tasks 17-18, 18-19 are more than 0.5
log apart. Thus, the characteristic curves are un-
even. Since tasks with the same level of difficulty do
not provide additional information when measuring a
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
109

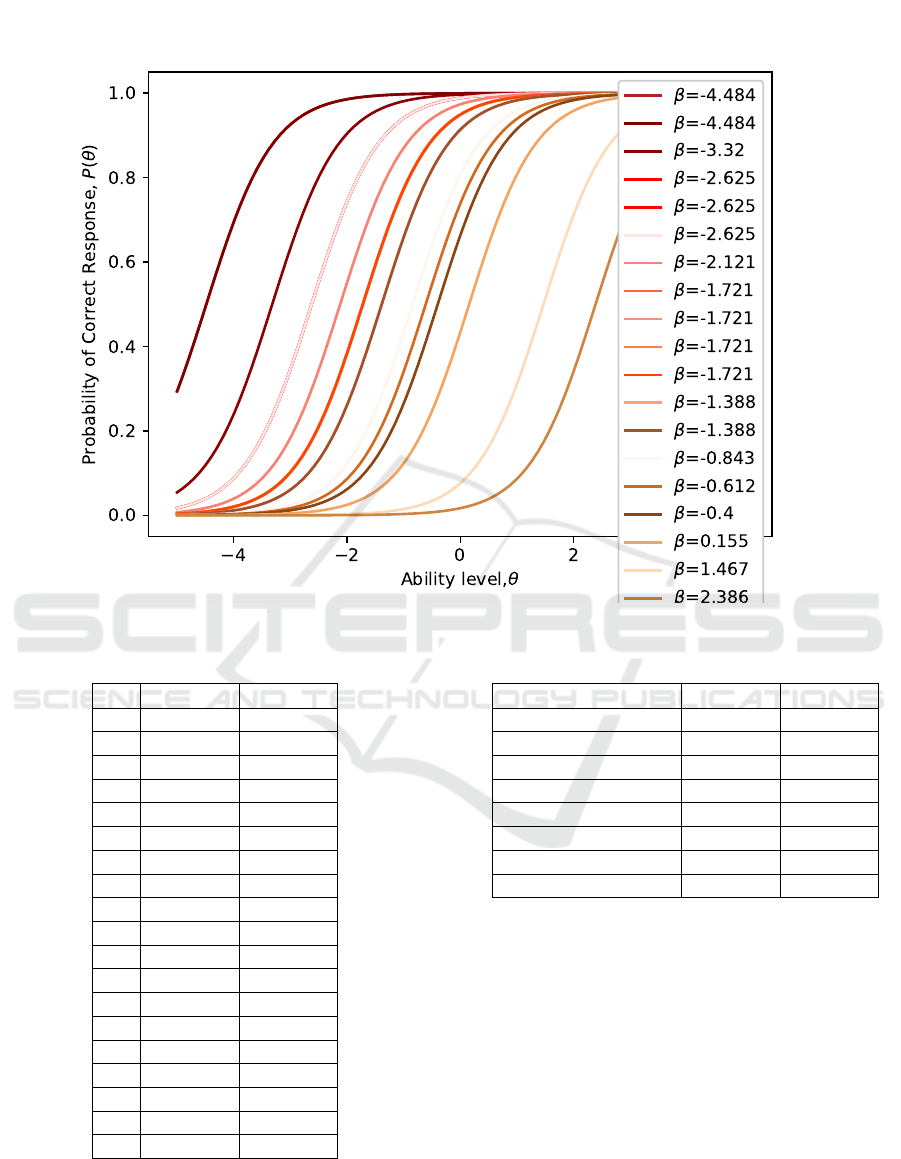
Figure 5: Characteristic curves of test items.
Table 4: Scaled values of item difficulty parameter β
i
.
Q# β
0
i
β
i
1 -3.89182 -4.48367
2 -2.75154 -2,625
3 -2.19722 -1.72148
4 -2.75154 -2.625
5 -3.17805 -3.32023
6 -2.19722 -1.72148
7 -2.44235 -2.12103
8 -1.65823 -0.84291
9 -1.99243 -1.38766
10 -1.04597 0.155071
11 -3.89182 -4.48367
13 -2.75154 -2,625
14 -2.19722 -1.72148
15 -1.99243 -1.38766
16 -2.19722 -1.72148
17 0.322773 2.386121
18 -1.38629 -0.39966
19 -0.24116 1.466906
20 -1.51635 -0.61165
given level of knowledge, one should be left out of
the tasks that match in terms of difficulty, and the rest
should be deleted. It is necessary to keep the item that
Table 5: Scaled values of the ability level θ
i
.
Participant’s number θ
0
i
θ
i
1 2.197225 0.322736
2 1.098612 -0.89013
3 1.734601 -0.188
5 1.098612 -0.89013
7 2.197225 0.322736
8 2.197225 0.322736
9 0.847298 -1.16758
10 1.734601 -0.188
is most different from the remaining items in the test.
To create a quality test, it is necessary to remove tasks
1, 5, 6, 10, 11, 12 from the test and add to the test
items with difficulty that is in the interval between the
complexity of 17-18 and 18-19 items.
The graph of the information function of test items
and the test as a whole, defined by formulas (6) and
(7), is shown in figure 6. Figure 6 shows that the infor-
mation function has one clearly expressed maximum.
This is a sign of a “good” test. However, it can be
seen that the test contains a lot of easy test items with
difficulties in the interval (-3; -2), which can be ex-
cluded from the test. Also in the test there are many
easy tasks with the same difficulties, which can also
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
110

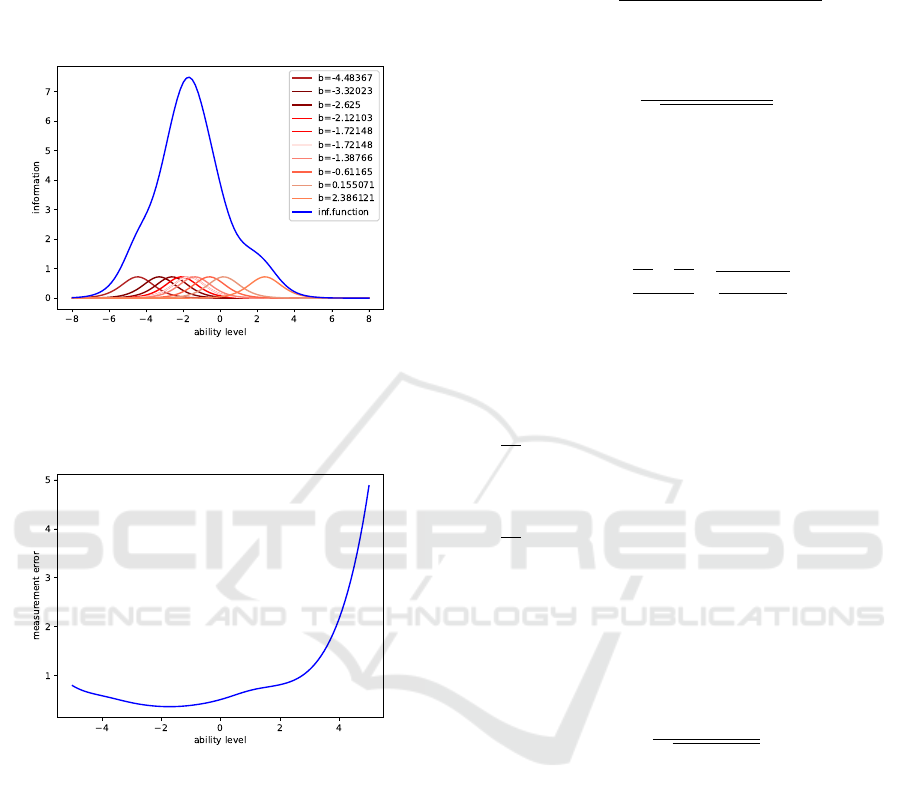
be excluded from the test without violation of its in-
formation content. However, the more difficult tasks
(with difficulties of 1-2 logits) are clearly not enough
in the test, so it is necessary to add more complex
tasks.
Figure 6: Information functions of the test and test items.
The graph of the measurement error, depending on
the level of training, is shown in figure 7.
Figure 7: Measurement error graph.
It can be seen from the graph that the measure-
ment error is large for the values of the ability in the
interval (2, 4), which is associated with the lack of test
items of increased difficulty.
4 RESULTS OF TEST ANALYSIS
BY 2PL AND 3PL BIRNBAUM
MODEL
The two-parameter (2PL) Birnbaum model differs
from the Rasch model by the presence of the a
j
pa-
rameter, which characterizes the differentiating abil-
ity of the j-th task. According to this model, the prob-
ability of a correct answer by an examinee with θ abil-
ity level to a test item with β
j
difficulty is determined
by the formula:
P
j
(θ) =
1
1 + exp(−1.7a
j
(θ − β
j
))
The a
j
parameter is defined by the relation
a
j
=
(r
bis
)
j
r
1 −

(r
bis
)
j

2
where (r
bis
)
j
is the biserial correlation coefficient of
the j-th task. Often, instead of this coefficient, a point
biserial coefficient r
j
ab
is used – correlation coefficient
of each task with student individual score
r
j
pb
=
X
1
− X
0
s
x
r
n
1
n
0
n(n − 1)
(11)
Here n
1
is the number of students who completed
this item;
n
0
– the number of students who did not complete
it;
n = n
0
+ n
1
– total number of students;
X
1
– average individual score of students who
coped with the given item (the ratio of the sum of in-
dividual scores of students who completed this item
to n
1
);
X
0
– the average individual score of students who
did not cope with this iten (the ratio of the sum of
individual scores of students who did not completed
this item, to n
0
);
s
x
is the standard deviation for the individual
scores of all students.
So, we will assume that
a
j
≈
r
j
pb
r
1 −

r
j
pb

2
(12)
The parameter a
j
is directly proportional to the
slope of the characteristic curve at the inflection point.
The greater the value of this parameter, the greater
the steepness of the characteristic curve and, there-
fore, the greater the differentiating ability of the item.
Therefore, to compare the levels of student’s knowl-
edge among themselves, it is important to select items
depending on the values of the parameter a
j
.
The table 6 shows the values of the point biserial
coefficient r
j
pb
, the parameter a
j
and the difficulty of
the items β
j
. These parameters are calculated by for-
mulas (4), (11), (12) respectively.
To obtain a test with a good distinguishing abil-
ity, we will use the following recommendations for
selecting items. First of all, it is necessary to exclude
tasks 7 and 3 from the test, which have a negative
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
111

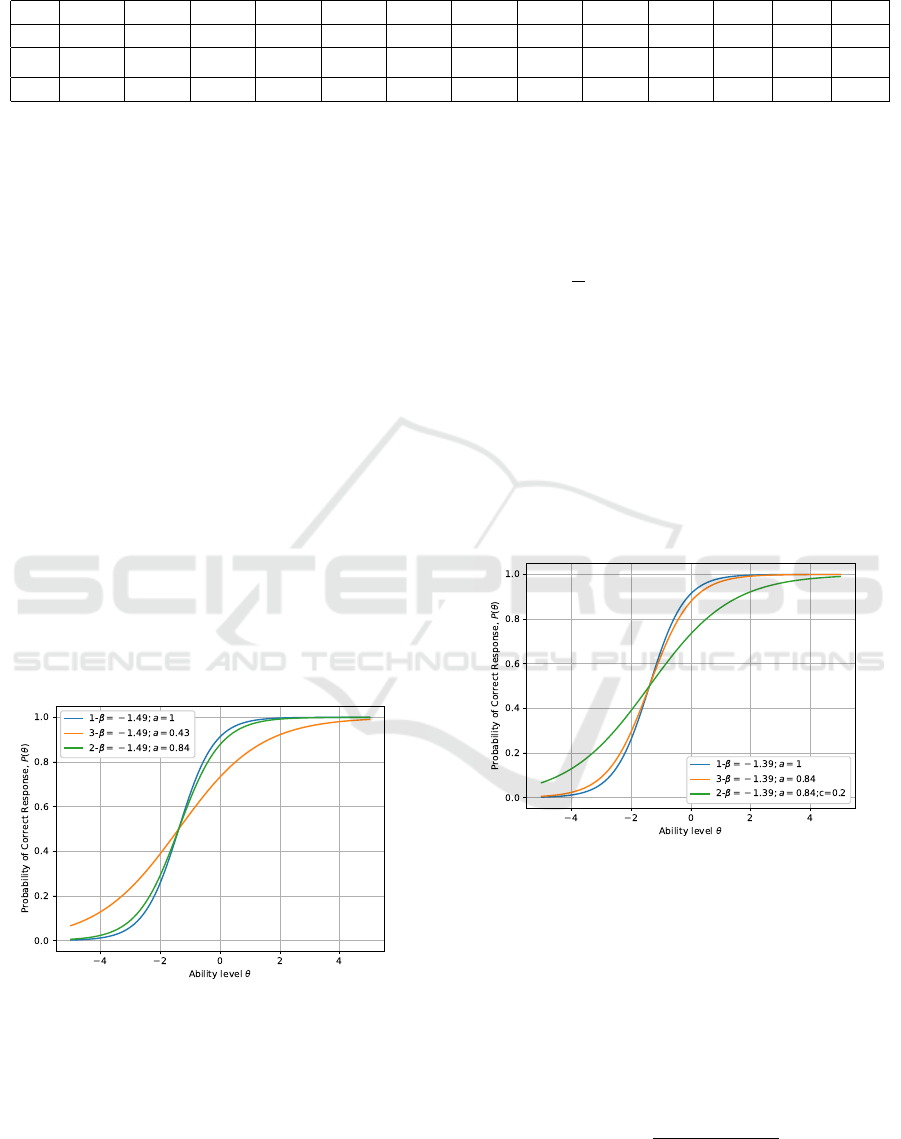
Table 6: The values of the parameters r
j
pb
,a
j
and β
j
.
Q# 7 3 6 14 16 9 15 8 20 18 10 19 17
β
j
-2.12 -1.72 -1.72 -1.72 -1.72 -1.39 -1.39 -0.84 -0.61 -0.40 0.16 1.47 2.39
r
j
pb
-0.01 -0.14 0.00 0.26 0.43 0.40 0.64 0.26 0.59 0.65 0.65 0.49 0.35
a
j
-0.01 -0.15 0.00 0.27 0.47 0.43 0.84 0.27 0.73 0.84 0.85 0.56 0.37
value of the discrimination parameter. This is due to
the fact that examinee with a low level of knowledge
respond well to them and poorly – with a high level
of knowledge, which is contrary to common sense.
This is due to guessing, when a student with a low
level of knowledge randomly selects the correct an-
swer. In addition, it is necessary to select tasks with
sufficiently large values – from the interval (0.5; 2.5).
In the test, from this point of view, tasks 6, 14, 8 will
be the worst. Further analysis involves the selection
of tasks with the greatest differentiating ability with
equal difficulty.
Consider tasks 9 and 15, which have the same
difficulty and differ in the parameter a
j
:a
9
= 0.43,
a
15
= 0.84. According to the one-parameter Rasch
model, both tasks have the same probability curve for
the correct answer of the subjects (curve 1, figure 8),
that is, from the point of view of the differentiating
ability of the tasks, they are indistinguishable. In the
case of a two-parameter model, we obtain two differ-
ent characteristic curves: steeper (2) for task 15 and
less steep (3) for task 9. Thus, when minimizing the
length of the test, task 15 is preferable.
Figure 8: Comparison of the Rasch model and the two-
parameter Birnbaum model for items 9 and 15.
The test in question is a closed-type test with
the choice of a single correct answer out of five of-
fered for each task. In such cases, in order to reduce
the guessing effect, it is proposed to use the three-
parameter Birnbaum model.
This Birnbaum model contains one more parame-
ter c
j
, which characterizes the probability of a correct
answer to the task j if this answer is guessed and not
based on knowledge. In this case, the probability of
the correct answer of the subjects to the task of the j
test is expressed by the formula
P
j
(θ) = c
j
+ (1 − c
j
)(1 + exp (−1, 7a
j
(θ − β
j
)))
−1
,
where c
j
=
1
k
j
, k
j
is the number of responses to task
j. In the test under consideration k
j
= 5, c
j
= 0.2.
The characteristic curves of these tasks cross the
line P
j
(θ) = c
j
, so the characteristic curves them-
selves become flatter, which leads to a decrease in the
differentiating ability of the test.
The figure 9 shows the probability curves for the
correct answer of the subjects to item 5, depending
on the ability level θ, corresponding to the Rasch
model(curve 1),the two-parameter model (curve 3)
and the three-parameter model (curve 2).
Figure 9: Characteristic curves for item 15 according to
Rasch and Birnbaum models.
Let us compare the information functions for the
Rasch and Birnbaum models. For the Rasch model,
the information function is determined by relation (6).
For the two-parameter Birnbaum model, the informa-
tion function is given by the expression
I
j
(θ) = 2.89a
j
2
P
j
(θ)Q
j
(θ).
For the three-parameter Birnbaum model, the in-
formation function has the form
I
j
(θ) =
2.89a
j
2
(1 − c
j
)
R
i
(θ)Q
i
(θ)
,
where R
i
(θ) = (c
j
+ exp(1.7a
j
(θ − β
j
))) and
Q
i
(θ) = (1 + exp (−1.7a
j
(θ − β
j
)))
2
.
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
112

The maximum value of the information function
for the Rasch model and the two-parameter Birnbaum
model is reached at the inflection point of the charac-
teristic curve, that is, when the difficulty (in logits)
is equal to the ability level. The maximum value of
the information function for the Rasch model and the
two-parameter Birnbaum model is reached at the in-
flection point of the characteristic curve, that is, when
the difficulty (in logits) is equal to the level of knowl-
edge (in logits). Thus, for θ
i
, tasks with difficulty val-
ues β from the neighborhood of the point θ
i
are the
most informative (in logits). Thus, for θ
i
, tasks with
difficulty values β from the neighborhood of the point
θ
i
are the most informative.
In the figure 10, for items 9 and 15 of the test,
information functions are shown: according to the
Rasch model (curve 1 – common for two items), ac-
cording to the two-parameter model for item 9 (curve
2) and for item 15 (curve 3). The difficulty of tasks
is equal to -1.39, therefore these items are the most
informative for values close to -1.39.
Figure 10: Information functions for items 9 and 15.
In the case of the three-parameter Birnbaum
model, the maximum information function is reached
at the point
θ
max
= β
j
+
1
1, 7a
j

0.5 + 0.5
p
1 + 8c
j

.
For items 9, with difficulty β = −1.39, the max-
imum of the information function is reached at the
point θ
max
= 2, and for task 15, with the same diffi-
culty, at the point θ
max
= 2. The information function
of the entire test is determined by the formula 7. The
information function of the entire test must have one
clearly defined maximum, otherwise the test needs to
be improved, items with difficulties corresponding to
the failure areas of the information function should be
added to it.
The figure 11 shows the information functions
of the entire test, based on the Rasch model, two-
parameter (2PL) model, three-parameter (3PL) Birn-
baum model. In the test under consideration, this con-
dition is satisfied because each curve has one maxi-
mum point.
Figure 11: Information functions of test.
So, for the test in the discipline “Higher Mathe-
matics”, two Birnbaum models were built: two- and
three-parameter. If we consider that the test should
correspond to these models, it is necessary to get
rid of some tasks, and change others. In particular,
from the point of view of a normatively oriented
test, it should have a sufficiently high differentiating
ability. Therefore, tasks 9 and 14 should be removed,
which are identical in difficulty with tasks 15 and
16, respectively, and differ in lower differentiating
ability. In addition, it is necessary to replace or
change tasks 6, 8, 17 so that their differentiating
ability increases. Tasks 7 and 3 with a negative value
of the discrimination parameter should be removed.
As regards the information functions, the graphs built
according to the three models, including the Rasch
model, did not reveal any contradictions between
theory and experiment.
To use the IRT model for assessing the quality
of test items, it is necessary that the test results
are adequate to this model. To check this fact, the
adequacy is assessed based on Pearson’s chi-squared
test. To calculate the value χ
2
β
j
for the j-th task,
all test participants are divided according to the
ability level into Q intervals, and for each interval
the average value of their ability level
¯
θ
q
is found.
The algorithm for dividing the range of change in the
value of θ into intervals is constructed in such a way
that if the level of ability of any participant coincides
with the interval border, it shifts to the right so much
that the value of this ability falls into the previous
interval.
χ
2
β
j
is calculated based on the expression (Baker
and Kim, 2017)
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
113

χ
2
β
j
=
Q
∑
q=1
(x
q j
− T
q
P
q j
)
2
δ
2
β
j
, (13)
where x
q j
is the number of test participants with
ability level
¯
θ
q
, who correctly answered the j-th test
item; T
q
is the total number of test participants with
ability level
¯
θ
q
; value δ
β
j
is calculated by the formula:
δ
β
j
=
q
T
q
P
q j
(1 − P
q j
). (14)
P
q j
is the probability expression of successful
completion of j-th item with difficulty β
j
by a par-
ticipant with the ability level
¯
θ
q
and is defined by IRT
models. To assess the adequasy of test results with
IRT models, we will use the R language tools. To do
this, we will load the test results saved in the input.csv
file with the CSV extension using the call
data<-read.csv("input.csv")
For data analysis, we use the ltm library of the R
language. To use this library, it must be installed and
loaded using the commands
install.package("ltm")
library("ltm")
After that, the following commaands can be used
to estimate Rasch model for test data.
f1<-rasch(data,constraint =
cbind(length(data)+1,1)))
To view the results of estimation, we use the fol-
lowing command
summary(data.rasch)
As a result, we obtain the following output:
Call:
rasch(data = data,
constraint = cbind(ncol(data) + 1, 1))
Model Summary:
log.Lik AIC BIC
-321.6515 681.3031 717.6315
Coefficients:
value std.err z.vals
Dffclt.v1 -4.3305 1.0338 -4.1888
Dffclt.v11 -4.3305 1.0338 -4.1888
Dffclt.v5 -3.5941 0.7533 -4.7712
Dffclt.v2 -3.1457 0.6323 -4.9751
Dffclt.v4 -3.1458 0.6323 -4.9751
Dffclt.v13 -3.1458 0.6323 -4.9751
Dffclt.v7 -2.8155 0.5619 -5.0104
Dffclt.v3 -2.5500 0.5151 -4.9510
Dffclt.v6 -2.5498 0.5150 -4.9509
Dffclt.v14 -2.5504 0.5151 -4.9511
Dffclt.v16 -2.5503 0.5151 -4.9511
Dffclt.v9 -2.3256 0.4813 -4.8319
Dffclt.v15 -2.3254 0.4813 -4.8318
Dffclt.v8 -1.9529 0.4355 -4.4842
Dffclt.v20 -1.7924 0.4193 -4.2750
Dffclt.v18 -1.6442 0.4060 -4.0502
Dffclt.v10 -1.2505 0.3775 -3.3122
Dffclt.v19 -0.2938 0.3435 -0.8552
Dffclt.v17 0.3859 0.3450 1.1184
Dscrmn 1.0000 NA NA
Integration:
method: Gauss-Hermite
quadrature points: 21
Optimization:
Convergence: 0
max(|grad|): 0.0014
quasi-Newton: BFGS
The output contains the following information:
log-likelyhood value (LogLik),the Akaike informa-
tion criterion (AIC),Bayesian information criteria
(BIC). AIC and BIC can be used to compare the rel-
ative fit of the models for the same data. The lower
AIC and BIC value, the better the model fits the data.
The output also include item difficulty estimates (Df-
fclt) with their standard error and z statistic. Us-
ing the functions ltm library, we can assess absolute
model fit. This assessment can be conducted using
chi-square test of the null hypothesis. The null hy-
pothesis is that our model fits the data. To determine
whether the model fit the individual items, we use the
following command
item.fit(data.rasch,simulate.p.value=FALSE)
After using these command we obtain the following
output:
Item-Fit Statistics and P-values
Call:
rasch(data = data,
constraint = cbind(ncol(data) + 1, 1))
Alternative: Items do not fit the model
Ability Categories: 10
Xˆ2 Pr(>Xˆ2)
v1 12.4481 0.0527
v11 12.4481 0.0527
v5 24.2183 0.0005
v2 35.3998 <0.0001
v4 18.3807 0.0053
v13 18.3807 0.0053
v7 12.7657 0.0469
v3 19.6667 0.0032
v6 17.7808 0.0068
v14 8.0073 0.2376
v16 9.8845 0.1296
v9 15.6480 0.0158
v15 15.6579 0.0157
v8 19.6375 0.0032
v20 9.4753 0.1486
v18 15.7466 0.0152
v10 24.7008 0.0004
v19 29.4453 0.0001
v17 19.5219 0.0034
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
114

Analysing this result, we can conclude that the
model does not accurately fit responses for the indi-
vidual tasks. Item 2 turned out to be the worst. Items
19,10 and 5 are also poorly consistent with the Rasch
model. Similar results can be obtained for the 2PL
Birnbaum model.
To obtain estimates of latent trait,we use the fol-
lowing commands:
data.2pl<-ltm(data˜z1)
summary(data.2pl)
As a result, we obtain
Call:
ltm(formula = data ˜ z1)
Model Summary:
log.Lik AIC BIC
-251.8978 579.7955 652.4524
Coefficients:
value std.err z.vals
Dffclt.v1 -3.6349 6.5440 -0.5555
Dffclt.v11 -3.6349 6.5440 -0.5555
Dffclt.v5 -2.8923 4.1718 -0.6933
Dffclt.v2 -2.3626 3.3693 -0.7012
Dffclt.v4 -2.5588 3.4556 -0.7405
Dffclt.v13 -4.1300 5.4315 -0.7604
Dffclt.v7 12.4254 34.7564 0.3575
Dffclt.v3 -9.4923 24.8491 -0.3820
Dffclt.v6 10.1668 23.5444 0.4318
Dffclt.v14 2.9872 2.4793 1.2049
Dffclt.v16 1.7069 1.2336 1.3837
Dffclt.v9 1.6604 1.0279 1.6154
Dffclt.v15 0.7883 151.3151 0.0052
Dffclt.v8 13.1975 51.8541 0.2545
Dffclt.v20 0.9232 0.5943 1.5533
Dffclt.v18 0.6679 2601.7180 0.0003
Dffclt.v10 0.4715 439.4082 0.0011
Dffclt.v19 -0.0204 65.1284 -0.0003
Dffclt.v17 -0.6392 797.0869 -0.0008
Dscrmn.v1 1.3535 1.8244 0.7419
Dscrmn.v11 1.3535 1.8244 0.7419
Dscrmn.v5 1.5005 1.5262 0.9832
Dscrmn.v2 1.7745 1.6673 1.0643
Dscrmn.v4 1.5215 1.4152 1.0751
Dscrmn.v13 0.7628 0.8333 0.9153
Dscrmn.v7 -0.1942 0.5450 -0.3563
Dscrmn.v3 0.2395 0.5988 0.4000
Dscrmn.v6 -0.2130 0.4947 -0.4305
Dscrmn.v14 -0.7469 0.5524 -1.3522
Dscrmn.v16 -1.5396 0.8178 -1.8827
Dscrmn.v9 -1.3673 0.6043 -2.2627
Dscrmn.v15 -27.8310 2871.9894 -0.0097
Dscrmn.v8 -0.1238 0.4912 -0.2521
Dscrmn.v20 -2.2078 0.9535 -2.3155
Dscrmn.v18 -36.3006 70169.1000 -0.0005
Dscrmn.v10 -44.8844 17157.7715 -0.0026
Dscrmn.v19 -38.3693 122239.5199 -0.0003
Dscrmn.v17 -33.1395 20052.6276 -0.0017
Integration:
method: Gauss-Hermite
quadrature points: 21
Optimization:
Convergence: 0
max(|grad|): 0.012
quasi-Newton: BFGS
Comparing AIC and BIC for the Rasch model
(AIC=681.3031, BIC=717.613) and for the 2PL Birn-
baum model (AIC=579.7955,BIC=652.4524) we can
conclude that 2PL model better fits the test data.
However, the function did not correctly calculate
the difficulty level for some items, as evidenced by
the std.err value. The presence of negative values
of the discrimination coefficient indicates that these
items does not fits the model. To assess the fit of each
items, we use χ
2
test.
item.fit(data.2pl,simulate.p.value=FALSE)
The output of this command is shown below:
Item-Fit Statistics and P-values
Call:
ltm(formula = data ˜ z1)
Alternative: Items do not fit the model
Ability Categories: 10
Xˆ2 Pr(>Xˆ2)
v1 17.2949 0.0272
v11 17.2949 0.0272
v5 5.7470 0.6756
v2 8.6983 0.3684
v4 8.6199 0.3754
v13 18.0006 0.0212
v7 27.8472 0.0005
v3 32.8960 0.0001
v6 15.0469 0.0582
v14 19.2362 0.0136
v16 15.7731 0.0457
v9 19.5417 0.0122
v15 0.2435 1
v8 22.2559 0.0045
v20 11.2384 0.1886
v18 0.7094 0.9995
v10 23.5588 0.0027
v19 18.7206 0.0164
v17 2.4617 0.9635
From this output we see that the 2PL Birnbaum
model did not fit items 3, 7, 10, 8, 19. Thus, by the
R language tools, it was established which items cor-
respond to the Rasch model and the two-parameter
Birnbaum model.
5 DISCUSSION
The purpose of this paper was to automate the pro-
cess of testing students’ knowledge, which is espe-
cially relevant for distance learning. To achieve this
goal an adaptive testing algorithm based on the Rasch
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
115

model was proposed and the modeling of the students’
knowledge assessment process using this algorithm
was carried out. The results of testing their knowl-
edge in the course “Higher Mathematics” obtained in
the Moodle system were taken as the initial values of
the tasks complexity and the levels of the students’
ability.
As a result of modeling, the levels of students’
abilities were recalculated. the information functions
of the test tasks and the entire test as a whole were
built. the standard measurement error was calculated.
depending on the student’s ability level. The analy-
sis of the obtained results allows us to conclude that
the test is not balanced and contains too many easy
tasks. They are tasks with numbers 1, 3, 11. Remov-
ing them from the test will reduce the number of test
items and speed up the process of determining the stu-
dent’s level of training.
A change in the assessment of the student’s ability
level as a result of testing indicates the need to intro-
duce an adaptive testing system into the educational
process which will improve the quality of assessment
of students’ knowledge.
These conclusions are confirmed by the works of
other authors. So in this paper (Al-A’ali, 2006) it was
shown that the use of adaptive testing based on IRT
made it possible to reduce the number of test tasks
and increase the reliability of determining the level
of student readiness. The effectiveness of the use of
adaptive testing to improve the quality of pedagogi-
cal measurements is evidenced by the works (Weiss,
1982, 2004).
6 CONCLUSIONS
In connection with the development of distance learn-
ing, the problem of automating the process of evalu-
ating students’ knowledge is becoming important. To
solve this problem, the achievements of modern test-
ing theory IRT were used. Mathematical models of
IRT provide the basis for building an adaptive testing
algorithm that allows you to automate the process of
knowledge assessment.
As a result of this work, the following results were
obtained:
1. An algorithm of adaptive knowledge assessment
based on the IRT approaches was proposed. This
algorithm consists of an initial assessment of the
difficulty level of test items and students’ abilities,
scaling of these parameters, selection of the next
question based on minimizing the module of their
difference and estimation of the measuring error
of the knowledge level by the information func-
tion of the proposed question.
2. The test parameters were evaluated on the basis of
IRT theory, which identified non-informative test
questions that should be excluded from the set of
test items.
3. The correspondence of the experimental data to
the Rasch and 2PL Birnbaum model was assessed
based on the Pearson’s chi-squared test by using
the language R, which made it possible to identify
tasks that require replacement or processing.
4. The quality of the test was examined using three
IRT models (Rasch model, 2PL and 3PL Birn-
baum model), which allowed for a more careful
selection of test items.
The results of the study showed the effectiveness
of using IRT to assess knowledge. An analysis of
these results allows us to conclude that the use of the
IRT methods to build an adaptive algorithm will au-
tomate the process of knowledge assessment and in-
crease the objectivity of assessment in distance learn-
ing. The use of several mathematical models in the
adaptive algorithm makes it possible to choose among
them the one that best fits the experimental data,
which will improve the accuracy of assessing the stu-
dent’s knowledge.
In the future, we plan to improve the adap-
tive algorithm for assessing educational achievements
by combining the Knowledge Space (KS) and IRT
(Mu
˜
noz-Merino et al., 2018).
REFERENCES
Al-A’ali, M. (2006). IRT-Item Response Theory As-
sessment for an Adaptive Teaching Assessment Sys-
tem. In Proceedings of the 10th WSEAS Inter-
national Conference on APPLIED MATHEMATICS,
MATH’06, page 518–522, Stevens Point, Wisconsin,
USA. World Scientific and Engineering Academy and
Society (WSEAS).
Amelia, R. N. and Kriswantoro, K. (2017). Implementa-
tion of Item Response Theory for Analysis of Test
Items Quality and Students’ Ability in Chemistry.
JKPK (Jurnal Kimia dan Pendidikan Kimia), 2(1):1–
12. https://doi.org/10.20961/jkpk.v2i1.8512.
Andersen, E. B. (1973). A goodness of fit test for the Rasch
model. Psychometrika, 38(1):123–140. https://doi.
org/10.1007/BF02291180.
Andrich, D. (2005). The Rasch model explained. In Applied
Rasch measurement: A book of exemplars, pages 27–
59. Springer.
Andrich, D. (2021). Rasch Models for Measurement.
Thousand Oaks. https://methods.sagepub.com/book/
rasch-models-for-measurement.
AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology
116

Andrich, D., Sheridan, B., and Luo, G. (2001).
RUMM2010: Rasch Unidimensional Measurement
Models. http://www.rummlab.com.au/.
Avanesov, V. S. (1980). The problem of psychological
tests. Soviet Education, 22(6):6–23. https://doi.org/
10.2753/RES1060-939322066.
Baker, F. B. and Kim, S.-H. (2017). The basics of item
response theory using R. Statistics for Social and Be-
havioral Sciences. Springer Cham. https://doi.org/10.
1007/978-3-319-54205-8.
Bezruczko, N., editor (2005). Rasch measurement in health
sciences. Jam Press Maple Grove, MN.
Bond, T., Yan, Z., and Heene, M. (2020). Applying the
Rasch model: Fundamental measurement in the hu-
man sciences. Routledge, fourth edition.
Brown, W. (1910). Some experimental results in the cor-
relation of mental abilities. British Journal of Psy-
chology, 1904-1920, 3(3):296–322. https://doi.org/10.
1111/j.2044-8295.1910.tb00207.x.
Cronbach, L. J. (1951). Coefficient alpha and the inter-
nal structure of tests. Psychometrika, 16(3):297–334.
https://doi.org/10.1007/BF02310555.
Eckes, T. (2011). Introduction to Many-Facet Rasch
Measurement. Peter Lang, Bern, Switzerland. url
”https://www.peterlang.com/view/title/13347”.
Fischer, G. H. and Molenaar, I. W., editors (1995). Rasch
models: Foundations, recent developments, and appli-
cations. Springer Science & Business Media. https:
//doi.org/10.1007/978-1-4612-4230-7.
Guilford, J. P. (1942). Fundamental Statistics in Psychology
and Education. McGraw-Hill Book Company, Inc.,
New York, US. https://archive.org/details/in.ernet.dli.
2015.228996.
Gulliksen, H. (1986). Perspective on Educa-
tional Measurement. Applied Psycholog-
ical Measurement, 10(2):109–132. https:
//doi.org/10.1177/014662168601000201.
Guttman, L. (1944). A Basis for Scaling Qualitative Data.
American Sociological Review, 9(2):139–150. https:
//doi.org/10.2307/2086306.
Ingebo, G. S. (1997). Probability in the Measure of Achieve-
ment. Mesa Press.
Kuder, G. F. and Richardson, M. W. (1937). The theory
of the estimation of test reliability. Psychometrika,
2(3):151–160. https://doi.org/10.1007/BF02288391.
Lord, F. M. (1980). Applications of Item Response Theory
To Practical Testing Problems. Routledge. https://doi.
org/10.4324/9780203056615.
Lord, F. M., Novick, M. R., and Birnbaum, A. (1968).
Statistical theories of mental test scores. Addison-
Wesley, Oxford.
Luce, R. D. and Tukey, J. W. (1964). Simultaneous conjoint
measurement: A new type of fundamental measure-
ment. Journal of Mathematical Psychology, 1(1):1–
27. https://doi.org/10.1016/0022-2496(64)90015-X.
Maslak, A. A., Karabatsos, G., Anisimova, T. S., and Os-
ipov, S. A. (2005). Measuring and comparing higher
education quality between countries worldwide. Jour-
nal of Applied Measurement, 6(4):432–442.
Mu
˜
noz-Merino, P. J., Novillo, R. G., and Kloos, C. D.
(2018). Assessment of skills and adaptive learning
for parametric exercises combining knowledge spaces
and item response theory. Applied Soft Computing,
68:110–124. https://doi.org/10.1016/j.asoc.2018.03.
045.
Perline, R., Wright, B. D., and Wainer, H. (1979).
The Rasch model as additive conjoint measurement.
Applied Psychological Measurement, 3(2):237–255.
https://doi.org/10.1177/014662167900300213.
Rasch, G. (1960). Studies in mathematical psychology: I.
Probabilistic models for some intelligence and attain-
ment tests. Nielsen & Lydiche.
Sax, G. (1989). Principles of educational and psychological
measurement and evaluation. Wadsworth Pub. Co.,
Belmont, 3rd edition.
Smith, E. V. and Smith, R. M., editors (2004). Introduction
to Rasch measurement: Theory, models and applica-
tions. JAM Press.
Spearman, C. (1910). Correlation calculated from faulty
data. British Journal of Psychology, 1904-1920,
3(3):271–295. https://doi.org/10.1111/j.2044-8295.
1910.tb00206.x.
Tjabolo, S. A. and Otaya, L. G. (2019). Quality of School
Exam Tests Based on Item Response Theory. Uni-
versal Journal of Educational Research, 7(10):2156–
2164. https://doi.org/10.13189/ujer.2019.071013.
van der Linden, W. J. and Hambleton, R. K., editors (1997).
Handbook of Modern Item Response Theory. Springer
Science & Business Media. https://doi.org/10.1007/
978-1-4757-2691-6.
Weiss, D. J. (1982). Improving measurement quality and ef-
ficiency with adaptive testing. Applied Psychological
Measurement, 6(4):473–492. https://doi.org/10.1177/
014662168200600408.
Weiss, D. J. (2004). Computerized adaptive testing for ef-
fective and efficient measurement in counseling and
education. Measurement and Evaluation in Counsel-
ing and Development, 37(2):70–84. https://doi.org/10.
1080/07481756.2004.11909751.
Wilson, M. (2005). Constructing Measures: An Item Re-
sponse Modeling Approach. Routledge.
Wright, B. D. (1977). Solving Measurement Problems
with the Rasch Model. Journal of Educational Mea-
surement, 14(2):97–116. http://www.jstor.org/stable/
1434010.
Wright, B. D. and Linacre, J. M. (1987). Dichotomous rasch
model derived from specific objectivity. Rasch mea-
surement transactions, 1(1):5–6. https://www.rasch.
org/rmt/rmt11a.htm.
Wright, B. D. and Masters, G. N. (1982). Rating scale anal-
ysis. Mesa Press, Chicago.
Wright, B. D. and Stone, M. H. (1979).
Best test design. Mesa Press, Chicago.
https://www.rasch.org/BTD RSA/pdf%20[reduced%
20size]/Best%20Test%20Design.pdf.
Zaqoot, W., Oh, L.-B., Koh, E., Seah, L. H., and Teo, H.-H.
(2021). The Use of Rasch Model to Create Adaptive
Practices in e-Learning Systems. In ACIS 2021 Pro-
ceedings, page 69. https://aisel.aisnet.org/acis2021/
69.
Test Quality Assessment and Adaptive Algorithm Based on IRT Models
117