Methodology for Assessing the Quality of an Educational Program and

Educational Activities of a Higher Education Institution Using a Neural

Network

Andriy V. Ryabko

1 a

, Tetiana A. Vakaliuk

2,3,4 b

, Oksana V. Zaika

1 c

, Roman P. Kukharchuk

1 d

Viacheslav V. Osadchyi

5 e

and Inesa V. Novitska

6 f

Olexander Dovzhenko Glukhiv National Pedagogical University, 24 Kyievo-Moskovska Str., Glukhiv, 41400, Ukraine

Zhytomyr Polytechnic State University, 103 Chudnivska Str., Zhytomyr, 10005, Ukraine

Institute for Digitalisation of Education of the NAES of Ukraine, 9 M. Berlynskoho Str., Kyiv, 04060, Ukraine

Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine

Borys Grinchenko Kyiv University, 18/2 Bulvarno-Kudriavska Str., Kyiv, 04053, Ukraine

Zhytomyr Ivan Franko State University, 30 Velyka Berdychivska Str., Zhytomyr, 10002, Ukraine

Keywords:

Evaluation Criteria, Educational Program, Educational Activities, Prognostication, Rating, ANFIS, Artiﬁcial

Neural Networks.

Abstract:

The article discusses a methodology for assessing the quality of educational programs and activities in higher

education institutions using artiﬁcial intelligence tools such as the adaptive system of neuro-fuzzy inference

(ANFIS) and an L-layer neural network. The purpose of the study was to address the problem of objectivity

in self-assessment and identify potential problems and shortcomings in educational activities before the start

of an accreditation examination. The study used student ratings on a four-level assessment scale as input

data for the L-layer neural network, and the criteria for assessing the quality of the educational program as

input variables for the ANFIS system. The hypothesis was that students with higher ratings of educational

achievement would provide more objective assessments of the quality criteria of the educational program

and activities. The results showed that the L-layer neural network made more accurate predictions than the

ANFIS model. The article suggests that this approach can provide higher education managers with qualitative

forecasts to determine the quality of educational services and identify potential problems before the start of

an accreditation examination. However, the study acknowledges the need for further research on larger data

volumes to improve the predictive capabilities of the models.

1 INTRODUCTION

In assessing the quality of education, as well as in

conducting pedagogical research, we are faced with

information that has non-numerical characteristics

that are difﬁcult to formalize. For example, the num-

ber of computers, the number of students, the area

of educational premises in a higher education insti-

tution are measurable, but the evaluation of the edu-

https://orcid.org/0000-0001-7728-6498

https://orcid.org/0000-0001-6825-4697

https://orcid.org/0000-0002-8479-9408

https://orcid.org/0000-0002-7588-7406

https://orcid.org/0000-0001-5659-4774

https://orcid.org/0000-0003-0780-0580

cational program and educational activities according

to the educational program is carried out according

to non-numerical criteria. The institution in the pro-

cess of self-assessment, and subsequently the experts

in the process of accreditation examination, must as-

sess according to the assessment scale, which covers

four levels of compliance with the criteria: A, B, E, F.

As a result, there is a need to build methods for

quantitative description of processes and subjects re-

lated to assessing the quality of the educational pro-

gram and educational activities. Of particular im-

portance is the quality of education, which means

some total indicator that reﬂects the results of the

educational institution, as well as compliance with

the needs and expectations of society (different so-

cial groups) in the formation of individual competen-

Ryabko, A., Vakaliuk, T., Zaika, O., Kukharchuk, R., Osadchyi, V. and Novitska, I.

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a Neural Network.

DOI: 10.5220/0012062800003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 179-198

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

179

cies. The methods of quantitative evaluation of the

educational program and educational activities under

this program will allow the higher education institu-

tion to identify existing shortcomings and potential

problems, as well as provide an opportunity to address

them before the accreditation examination.

Assessing the quality of educational programs and

educational activities is complicated by the fact that

the value of this indicator depends on many factors,

possibly with an unknown nature of inﬂuence. Also

in this case there is a speciﬁcity of the “product” of

education – a graduate of an educational institution,

which should be considered as a complex system.

There are various methods and algorithms for assess-

ing the quality of educational activities. In this study,

we propose a method of assessing the quality of edu-

cational programs and educational activities based on

the neuro-fuzzy approach, due to the active develop-

ment of analytical systems, based on the technology

of artiﬁcial intelligence. The most popular and proven

of these technologies are neural networks, which suc-

cessfully solve a variety of “fuzzy” tasks – predic-

tion, classiﬁcation, recognition of handwritten text,

language, images (Markova et al., 2018; Tarasenko

et al., 2019; Kirichek et al., 2019; Porokhnya and

Ostapenko, 2019; Horal et al., 2020; Valko and Os-

adchyi, 2020). In such problems, where traditional

technologies are powerless, neural networks often act

as the only effective solution. In this work, artiﬁcial

neural networks are used to solve the problem of as-

sessing the quality of educational programs and edu-

cational activities.

Mandatory conditions for accreditation are com-

pliance with the educational program and educational

activities of the higher education institution under this

educational program with the criteria established by

law. In particular, the forms and methods of teach-

ing should contribute to the achievement of the stated

goals of the educational program and program learn-

ing outcomes.

Since the educational program and educational

activities must meet the requirements of a student-

centered approach and the principles of academic

freedom, the hypothesis of the study is that based on a

sample of students and graduates of higher education,

the quality of educational programs and educational

activities, which will be able to adequately perform a

comprehensive assessment of the quality of the edu-

cational program and educational activities.

Intelligent data processing using a neural network

allows forming forecast probabilities of values of fu-

ture results of accreditation examination in a higher

education institution, which can contribute to the im-

provement of measures to improve the educational

program. The results of forecasting can be used by

the management of faculties and graduating depart-

ments as informative and recommendatory. In ad-

dition, guarantors of educational programs based on

forecasts can plan activities and individual work with

teachers to positively change the forecast. Thanks to

the analysis of the received data it is possible to reveal

weak points of the educational process that will give

the chance to modernize it.

With this in mind, the article aims to substanti-

ate, develop and implement a mathematical model of

a comprehensive assessment of the quality of educa-

tional programs and educational activities based on

the methods of the neuro-fuzzy approach.

1.1 Theoretical Background

Assessing the quality of educational activities accord-

ing to clearly deﬁned criteria and methodologies is

an important task in the process of accreditation of

educational programs, which are used to train appli-

cants for higher education in Ukraine. In the pro-

cess of preparing for accreditation and preparation of

materials for self-assessment of the educational pro-

gram, there are problems in determining the objec-

tivity of self-assessment and ﬁnding potential prob-

lems and shortcomings of educational activities. Due

to this problem, the urgent task is to ﬁnd mathematical

tools that could be used by managers of higher edu-

cation institutions in their approaches to determining

the quality of educational services offered.

The paradigm shift in educational philosophy and

practice has led to focusing primarily on student

learning outcomes. The educational process should

be results-oriented – what exactly students know and

can actually do. Accordingly, student-centered learn-

ing is an approach in which students inﬂuence the

content, activities, materials, and pace of their learn-

ing. This model of learning puts the student at the

center of the learning process (Black et al., 2015).

EU initiatives call for increased efﬁciency, inter-

national attractiveness, and competitiveness of higher

education institutions. W

achter et al. (W

achter et al.,

2015) considers different approaches to quality, qual-

ity assurance, and ratings, analyzes recent research,

critically analyzes these approaches in a compara-

tive perspective, provides recommendations and pol-

icy options for parliament.

The problem of determining a set of effective indi-

cators that are easy to determine and can be applied to

both large public universities and small regional pri-

vate colleges, from university programs to alternative

programs is also relevant for the United States (Ham-

merness and Klette, 2015).

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

180

Cherniak et al. (Cherniak et al., 2020) investigated

the possibility of assessing the quality of qualime-

try objects by graph analytical method, ie to apply

the principle of determining the area and volume un-

der curved surfaces both in the plane and in space,

which are created by combining estimates of individ-

ual quality indicators on a dimensionless scale. It is

shown that, as a rule, mathematical dependences are

nonlinear and their research is reduced to the devel-

opment of universal methods that could be applied to

objects of qualimetry, regardless of their nature, com-

plexity, importance, and more. Having unit quality in-

dicators in a single (dimensionless) rating scale, it is

proposed to determine a single comprehensive quality

indicator of the object of qualimetry using the method

of integration, which takes into account the evaluation

of unit quality indicators.

Parvu and Ipate (Parvu and Ipate, 2007) propose a

mathematical model based on a set of indicators that

are adapted to the classiﬁcation structure of intellec-

tual capital, which is unanimously recognized world-

wide, namely to the external and internal structure and

competence of employees. The Rompedet method, an

original product of the Romanian school of manage-

ment (Isac et al., 2010), was used as a mathematical

calculation tool.

When assessing the quality of education, we are

faced with a huge number of different criteria, each

of which may consist of many sub-criteria, therefore,

the task of assessing the quality of education in its

mathematical formulation is multi-criteria. Problem

situations that are modeled and described by linear

models and depend on many factors play an impor-

tant role, so solving a multicriteria decision-making

problem is often accompanied by solving multicrite-

ria linear programming problems, or in other words,

vector optimization problems.

Given these problems, mathematical models of in-

tegrated quality assessment using methods that are

based on the convolution of criteria were also of in-

terest for our study. Models and methods of multi-

criteria optimization are considered in (Kondruk and

Maliar, 2019), in particular, the method of additive

convolution of criteria and the method of multiplica-

tive and minimax convolution of criteria. The method

of multiplicative convolution of partial criteria to a

single generalized indicator, which provides as a nor-

malized divisor to use the maximum (minimum) val-

ues of partial criteria, obtaining which does not cause

signiﬁcant difﬁculties, ie is carried out on many avail-

able design solutions is considered in (Grytsyuk and

Grytsiuk, 2014). Chervak (Chervak, 2010) uses one

of the methods of solving the Paretian multicriteria

optimization problem as a mathematical tool of the

decision-making process. To organize the selection

problems on the same admissible set of alternatives,

the concept of the super criterion of any criterion is

introduced; if the criterion is a super criterion of this

criterion on this set, then the last criterion is a sub-

criteria of the ﬁrst. It is shown that the solution of

the problem of multicriteria selection by the Paretian

convolution is reduced to the solution of the problems

of scalar or lexicographic optimization.

The theory of artiﬁcial neural networks and mod-

els of deep learning is considered in the fundamental

works (Goodfellow et al., 2016; M

uller et al., 1995;

Sivanandam et al., 2006), system design based on a

neuro-fuzzy approach (Shtovba, 2007; Shtovba and

Pankevych, 2018).

The use of neural networks to classify the status

of a graduate of a higher education institution based

on selected academic, demographic, and other indica-

tors is considered by Lesinski et al. (Lesinski et al.,

2016). A multilayer neural network with feedback

is used as a model. The model was taught based

on more than 5,000 records of entrance exams and

university databases. Nine input variables consisted

of categorical and numerical data that contained in-

formation about high school education, test results,

assessment of high school teachers, parental assess-

ment, and others. Based on these inputs, the multi-

layer neural network predicted the success of univer-

sity entrants. With the help of the neural network,

it was possible to predict the success of graduates

and achieve the best performance with an accuracy

of classiﬁcation exceeding 95%. Black et al. (Black

et al., 2015) examining the relationship between qual-

ity and success of high school students in college

found no convincing evidence that exposure charac-

teristics of high school diminish over time teaching

students.

To address the issue of determining the quality

of educational training, Mahapatra and Khan (Ma-

hapatra and Khan, 2007) developed the EduQUAL

methodology and proposed an integrative approach

using neural networks to assess the quality of educa-

tion. Four neural network models based on a feedback

algorithm are used to predict the quality of education

for different stakeholders. This study showed that the

P-E Gap model is the best model for all stakeholders.

The need to introduce neural network technology

in educational courses of educational institutions in-

dicates by Semerikov et al. (Semerikov et al., 2022).

Educational neural networks are often used for fore-

casting. For example, students must choose courses

that interest them for the next semester. Due to lim-

itations, including lack of sufﬁcient resources and

the overhead of several courses, some universities

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

181

may not be able to teach all courses of the student’s

choice. Universities need to know each student’s re-

quirements for each course each semester for optimal

course planning. Kardan et al. (Kardan et al., 2013)

used a neural network to model student choice behav-

ior and apply the resulting function to predict the ﬁ-

nal enrollment of students for each course. The re-

sults showed high prediction accuracy based on ex-

perimental data. Arsad et al. (Arsad et al., 2013),

Osadchyi et al. (Osadchyi et al., 2018), Okubo et al.

(Okubo et al., 2017b) prove that the use of neural net-

works in predicting educational processes will allow

obtaining results with a much higher level of accu-

racy and less time. According to Abu Naser et al.

(Abu Naser et al., 2015), an artiﬁcial neural network

can correctly predict the success of more than 80% of

future students.

Chaban and Kukhtiak (Chaban and Kukhtiak,

2020) analyze the problem of the social system, which

consists of many students and teachers of higher ed-

ucation to create effective learning pairs “teacher-

student”. Elements of the theory of artiﬁcial intelli-

gence based on artiﬁcial neural networks were used

to form the mentioned learning pairs. Okubo et al.

(Okubo et al., 2017a) propose to use a recurrent neu-

ral network (RNN) to predict students’ ﬁnal grades

using journal data stored in educational systems.

Liu et al. (Liu et al., 2022) propose a method

for assessing the quality of preparation for graduate

school, which is based on the algorithm of neural net-

work backpropagation and stress testing. This method

creates a publicly available list of indicators consist-

ing of 19 criteria in 4 groups of criteria, such as at-

titudes towards teaching, teaching content, approach

to teaching, and the main characteristics of teachers.

After the neural network algorithm is used to deter-

mine the optimal parameters of the evaluation model,

a sensitivity test is used to identify indicators that have

a signiﬁcant impact on the quality of education. Also,

scenario analysis is used to study the impact of the

quality of education in pre-deﬁned situations, provid-

ing theoretical and empirical support for assessing the

quality of postgraduate teaching, improving the qual-

ity of education, and professional growth of teachers.

Educational institutions are constantly striving to

improve the services they offer, their goal is to have

the best teaching staff, improve the quality of teach-

ing and academic success of students. Knowledge of

the factors inﬂuencing student learning can help uni-

versities and learning centers adapt their curricula and

teaching methods to students’ needs. One of the ﬁrst

measures taken by educational institutions in the con-

text of the COVID-19 pandemic was the creation of

virtual learning environments (Pererva et al., 2020).

To understand the factors inﬂuencing the university

learning process in virtual learning environments, Ri-

vas et al. (Rivas et al., 2021) applied several automatic

learning methods to publicly available data sets, in-

cluding tree-like models and various types of artiﬁcial

neural networks.

The availability of educational data supported by

learning platforms provides opportunities to study

student behavior and solve problems in higher edu-

cation, optimize the educational environment and en-

sure decision-making using an artiﬁcial neural net-

work (Waheed et al., 2020).

Cader (Cader, 2020) uses a deep neural network to

assess students’ acquisition of knowledge and skills.

It is noted that the obstacle to the application of the

method in teaching is the relatively small amount of

data in the form of available estimates required for

neural network training. A new method of data aug-

mentation is proposed – asynchronous data augmen-

tation through pre-categorization, which solves this

problem. Using the proposed method, it is possible

to carry out neural network training even for small

amounts of data.

Do and Chen (Do and Chen, 2013) present a

neuro-fuzzy classiﬁer that used the results of previ-

ous exams and other related factors as input variables

and classiﬁed students based on their expected learn-

ing outcomes. The results showed that the proposed

approach achieved high accuracy compared to the re-

sults obtained based on other known approaches to

classiﬁcation, in particular, Naive Bayes, neural net-

works, and others.

Fazlollahtabar and Mahdavi (Fazlollahtabar and

Mahdavi, 2009) proposed a neuro-fuzzy approach

based on evolutionary techniques to obtain the opti-

mal learning pathway for both teacher and student.

The neuro-fuzzy approach allows providing recom-

mendations to the teacher for making pedagogical de-

cisions based on the student’s learning style. On the

other hand, the neural network approach is used for

the student to create a personalized curriculum proﬁle

based on the individual needs of the student in a fuzzy

environment.

Taylan and Karag

ozo

glu (Taylan and

Karag

ozo

glu, 2009) use a systematic approach

to designing a fuzzy inference system based on a

class of neural networks to assess student achieve-

ment. The developed method uses a fuzzy system,

supplemented by neural networks, to enhance some

of its characteristics, such as ﬂexibility, speed,

and adaptability, called the adaptive neuro-fuzzy

inference system (ANFIS). The results of the ANFIS

model are as reliable as statistical methods, but they

encourage a more natural way of interpreting student

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

182

learning outcomes.

In comparison with these works, this study ﬁlls a

gap in the methods of a comprehensive assessment of

the quality of educational programs and educational

activities based on a neuro-fuzzy approach.

1.2 Methods

In this study, methods of mathematical modeling and

computational experiment based on statistical pro-

cessing of data assessments of the quality of ed-

ucational programs and educational activities were

used. The essence of the methodology of mathemat-

ical modeling is to replace the original object with

its mathematical model and study it with the help of

computer technology. Processing, analysis, and in-

terpretation of calculation results were carried out by

constant comparison with the results of statistical pro-

cessing of expert estimates. In the course of the re-

search, reﬁnements were made and the mathematical

model was revised and the cycle of the computational

experiment was repeated.

The methodology for assessing the quality of the

curriculum and educational activities is built using

methods and tools of artiﬁcial intelligence, imple-

mented in the package Fuzzy Logic Toolbox system

MATLAB in the form of adaptive neuro-fuzzy output

ANFIS.

A fuzzy inference system can be represented as a

neuro-fuzzy network – a neural network of direct sig-

nal propagation of a special type, or ANFIS-model.

The architecture of a neuro-fuzzy network is isomor-

phic to a fuzzy knowledge base. Neuro-fuzzy net-

works use differentiated implementations of triangu-

lar norms (multiplication and probabilistic OR), as

well as smooth membership functions. This makes it

possible to use fast algorithms for training neural net-

works based on the backpropagation method to tune

neuro-fuzzy networks.

ANFIS implements the Sugeno fuzzy inference

system through a ﬁve-layer feed-forward neural net-

work. Purpose of network layers:

• ﬁrst layer – terms of input variables;

• the second layer – antecedents (parcels) of fuzzy

rules;

• the third layer is the normalization of the degree

of implementation of the rules;

• the fourth layer is the conclusion of the rules;

• ﬁfth layer – aggregation of the result obtained ac-

cording to different rules.

The network inputs are not allocated to a separate

layer. Figure 1 shows an ANFIS network with two

input variables (x

and x

) and four fuzzy rules. Three

terms are used for the linguistic evaluation of the input

variable, and two terms for the variable.

Figure 1: An example of an ANFIS network.

We will use the following notation:

• x

, x

, ..., x

– network inputs;

• y – network output;

• R

: if x

= a

1,r

, ..., x

= a

n,r

it y = b

0,r

+ b

1,r

... + b

n,r

is a fuzzy rule with a serial number r;

• m – number of rules r = 1, m,

• a

i,r

– fuzzy term with a membership function

) used for linguistic evaluation of a variable

in the r-th rule (r = 1, m, i = 1, n);

• b

q,r

are the conclusion coefﬁcients of the r-th rule

(r = 1, m, q = 0, n).

ANFIS-network works as follows.

Layer 1. Each node of the ﬁrst layer represents

one term with a bell membership function. The in-

puts of the network are connected only to their terms.

The number of nodes in the ﬁrst layer is equal to the

sum of the cardinalities of the term set of input vari-

ables. The degree of belonging of the value of the

input variable to the corresponding fuzzy term is fed

to the output of the node:

) =

1 +



−c



, (1)

where a, b and c are membership function parameters

that can be tuned.

Layer 2. The number of nodes in the second layer

is m. Each node of this layer corresponds to one fuzzy

rule. The node of the second layer is connected to the

nodes of the ﬁrst layer, which form the antecedents

of the corresponding rule. Therefore, each node of

the second layer can receive from 1 to n signals. The

output of the node is the degree of execution of the

rule, calculated as the product of the input signals.

Let us denote the outputs of the nodes of this layer as

, r = 1, m.

Layer 3. The number of nodes in the third layer is

also m. Each node of this layer calculates the relative

level of execution of the fuzzy rule according to the

formula:

∗

∑

j=1

. (2)

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

183

Layer 4. The number of nodes in the fourth layer

is also m. Each node is connected to one node of the

third layer, as well as to all inputs of the network (ﬁg-

ure 1 connections to the inputs are not shown). The

node of the fourth layer calculates the contribution of

one fuzzy rule to the network output by the formula:

= τ

∗

0,r

+ b

1,r

+ ... + b

n,r

). (3)

Layer 5. A single node of this layer sums up the

contributions of all rules:

y = y

+ ... + y

. (4)

Typical neural network training procedures can be

applied to tune an ANFIS network, as it uses only

differentiated features. It is common to use a com-

bination of gradient descent as a backpropagation

algorithm and the least-squares method. The error

backpropagation algorithm regulates the parameters

of rule antecedents, that is, membership functions.

The least-squares method evaluates the rule inference

coefﬁcients since they are linearly related to the net-

work output.

Each iteration of the tuning procedure is per-

formed in two steps.

In the ﬁrst stage, a training sample is fed to the

inputs, and, based on the discrepancy between the de-

sired and actual behavior of the network, the optimal

parameters of the nodes of the fourth layer are deter-

mined using the least-squares method.

In the second stage, the residual mismatch is trans-

mitted from the network output to the inputs, and the

parameters of the nodes of the ﬁrst layer are modiﬁed

by the backpropagation of the error. At the same time,

the rule inference coefﬁcients found at the previous

stage do not change. The iterative tuning procedure

continues as long as the mismatch exceeds a prede-

termined value. To tune the membership functions, in

addition to the error backpropagation method, other

optimization algorithms can be used, for example, the

Levenberg-Marquardt method.

The ANFIS editor in Matlab allows you to auto-

matically synthesize a neuro-fuzzy network from ex-

perimental data. In this case, the accessories of the

synthesized systems are tuned (trained) in such a way

as to minimize the deviations between the results of

fuzzy modeling and experimental data. The ANFIS

editor is loaded using the anﬁsedit command.

The ANFIS editor contains 3 top menus – File,

Edit and View, visualization area, ANFIS properties

area, data loading area, source fuzzy inference system

generation area, training area, testing area, current in-

formation output area, as well as Help and Close but-

tons, which allows you to call the help window and

close the ANFIS editor, respectively.

Participants in the experiment – full-time master’s

students (22 people) and graduates of higher educa-

tion institutions of the previous term of study are the

same specialties (32 people) – a total of 54 people.

This number of respondents is due to the number of

indicators of quality criteria because the data format

of the artiﬁcial network in MATLAB supports square

matrices, in this case, 54x54. Before the accredi-

tation examination, students were offered question-

naires with a proposal to assess the quality of the edu-

cational program and educational activities of the spe-

cialty on an assessment scale covering four levels: F,

E, B, A. Student assessments were used to form the

vector of artiﬁcial neural network inputs. After the ac-

creditation examination, the expert assessments were

used to check the quality of the prediction of the arti-

ﬁcial neural network.

The experience of European countries demon-

strates the expediency of involving students in accred-

itation examination. For example, the Polish Accred-

itation Commission consists of 80 – 90 members ap-

pointed by the Minister of Science and Higher Educa-

tion among the candidates nominated by the Senates

of higher education institutions, the conferences of

rectors of scientiﬁc schools and universities in Poland,

the Parliament of Students of Poland (the President

of the Student Parliament is a member of the Polish

Accreditation Commission). In Slovakia, Academic

Ranking and Rating Agency is a civic association

founded in 2004 on the initiative of former student

leaders and academics. The Slovenian Quality Assur-

ance Agency for Higher Education SQAA-NAKVIS

(Slovenian Quality Assurance Agency for Higher Ed-

ucation) appoints at least three members of each ex-

pert group, of which at least one foreign expert, an

expert in the ﬁeld of quality assessment of higher ed-

ucation and one representative from among students)

and others (Tryhub, 2016).

To ensure the representativeness of the sample, the

study of its design was carried out based on random-

ization. The decision on the statistical deviation of the

null hypothesis regarding the differences between the

averages, thus, was also associated with the procedure

of random sampling.

The rating scale covers four levels of compliance

by the requirements of the legislation (F, E, B, A)

(Verkhovna Rada of Ukraine, 2019). Also, the leg-

islation establishes 10 criteria for assessing the qual-

ity of the educational program (Verkhovna Rada of

Ukraine, 2019):

1) design and objectives of the educational program

(4);

2) structure and content of the educational program

(9);

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

184

3) access to the educational program and recognition

of learning outcomes (4);

4) teaching and learning according to the educational

program (5);

5) control measures, evaluation of applicants for

higher education and academic integrity (4);

6) human resources (6);

7) educational environment and material resources

(6);

8) internal quality assurance of the educational pro-

gram (7);

9) transparency and publicity (3);

10) learning through research (6).

In turn, each of these criteria has from 3 to 9 in-

dicators (the number is indicated in parentheses). To-

gether, all 10 criteria contain 54 indicators.

2 RESULTS

At the ﬁrst stage of the study, the collection and sta-

tistical processing of data on the results of the as-

sessment of students and graduates of higher educa-

tion educational programs and educational activities

on the educational program for each criterion.

In the second stage, a computational experiment

was performed. The cycle of the computational ex-

periment was carried out in several stages:

1) the choice of approximation and mathematical

formulation of the problem (construction of a

mathematical model of the phenomenon under

study);

2) development of a computational algorithm for

solving the problem;

3) implementation of the algorithm in the form of a

program for the PC;

4) settlements on the PC;

5) processing, analysis and interpretation of calcula-

tion results, comparison with the results of statis-

tical processing of expert estimates and, if neces-

sary, reﬁnement or revision of the mathematical

model, i.e. return to the ﬁrst stage and repeat the

cycle of the computational experiment.

Assessing the quality of the curriculum and learn-

ing activities is complicated by the fact that each of

the 10 criteria, in turn, consists of several indica-

tors (3-9) and is due to many factors, possibly with

an unknown nature of inﬂuence, which is also non-

numerical. To assess the quality of the curriculum and

training activities, it is proposed to use a two-tier sys-

tem based on the ANFIS package and artiﬁcial neural

networks to predict assessment scores.

The ANFIS hybrid system is a combination of the

Sugeno neuro-fuzzy inference method with the ability

to train a ﬁve-layer artiﬁcial neural network (ANN) of

direct propagation with a single output and multiple

inputs, which are fuzzy linguistic variables. As input

variables of the ANFIS system, we use the criteria for

evaluating the quality of the educational program of

10 groups of factors V

(i = 1, ..., 10).

The output variable of the ANFIS system is a nu-

merical assessment of the quality of the curriculum

and training activities and is deﬁned as a function

y = f (V

0).

Layer 1 of the ANFIS system for the linguistic

evaluation of input parameters uses the term set of

all possible values of the linguistic variable. A

V i

{“F”, “E”, “B”, “A”}. In symbolic form we write:

V i

= {F < i >, E < i >, B < i >, A < i >}. The term

set of the original linguistic variable y is the set of

values of quality assessments of the curriculum and

educational activities: T

= {F, E, B, A}. The outputs

of the nodes of layer 1 are the values of the member-

ship functions at speciﬁc values of the input variables.

Layer 2 is non-adaptive and deﬁnes the precondi-

tions of fuzzy production rules. Production rules –

a form of representation of human knowledge in the

form of a sentence type – if (condition), then (action).

The rules provide a formal way to present recommen-

dations, guidance, or strategies. They are ideal in

cases where the knowledge of the subject area arises

from the empirical associations accumulated during

the work on solving problems in a particular ﬁeld.

Each node of this layer is connected to those nodes

of layer 1, which form the prerequisites of the cor-

responding rule. To solve this problem, four fuzzy

production rules are formulated: P = {p

, p

because according to the features of the ANFIS net-

work, the number of network rules must correspond

to the dimension of the term set of the source variable

Nodes perform a fuzzy logical operation “I”

(min). The outputs of the nodes of this layer are the

degree of truth (fulﬁllment) of the preconditions of

each of the four fuzzy production rules, which are cal-

culated by the formulas:











= min(µ

), µ

))

= min(µ

), µ

))

= min(µ

), µ

))

= min(µ

), µ

))

(5)

Layer 3 normalizes the degree of implementation

of each of the fuzzy production rules (calculation of

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

185

the relative degree of implementation of the rules) as

follows:

∑

i=1

, (6)

where h = 1, ..., 4 is production rule number. Layer 4

calculates the contribution of each fuzzy production

rule to the output of the network according to the for-

mula.

(v,V) = w

(0)

+ v

(1)

+ v

(2)

+ v

(3)

+ v

(4)

+ v

(5)

(7)

where v

(0)

– coefﬁcients of the initial function (i =

0, ..., 5).

Layer 5 summarizes the contributions of all the

rules:

y =

∑

i=1

. (8)

Training of the ANFIS network was carried out

for 24 epochs by a hybrid method. During training,

the type of membership functions, the type of initial

function, and their coefﬁcients are selected. As a re-

sult of training a fuzzy network for four rules, Gaus-

sian functions were adopted as membership functions,

and a linear function was adopted as the initial func-

tion. As a result of training, membership functions

and their coefﬁcients were also obtained.

To assess each of the 10 groups of factors that

affect the quality of the curriculum and educational

activities by the evaluation criteria, 10 modules are

used, which are implemented using artiﬁcial neural

networks. Thus, it is necessary to design neural net-

works, a mathematical model of a comprehensive as-

sessment of the quality of the educational program

and educational activities based on the methods of the

neuro-fuzzy approach. For this purpose, the Neural

Network Toolbox was used. To form neural networks,

it is necessary to determine their topology, learning

mechanism, and testing procedure. Also, the training

of an artiﬁcial neural network requires input data –

a sample of answers of students and graduates with

reliable quality indicators, determined based on these

criteria.

A standard L-layer feedforward neural network

consists of a layer of input nodes (we will stick to

the position that it is not contained in the network as

an independent layer), (L − 1) hidden layers, and an

output layer that is connected in series in the forward

direction and does not contain a connection between

elements within a layer and feedback between layers.

The most popular class of multilayer feed-forward

networks is formed by multilayer perceptrons, where

each computational element uses a limit or sigmoidal

activation function. A multilayer perceptron can form

arbitrarily complex decision limits and implement ar-

bitrary Boolean functions. The development of a

backpropagation algorithm for determining weights

in a multilayer perceptron has made these networks

the most popular among researchers and users of neu-

ral networks. The vast majority of programs involve

the use of such multilayer perceptrons. Networks con-

sisting of successive layers of neurons are more com-

monly used. Although any network without feedback

can be represented as successive layers, the presence

of many neurons in each layer can signiﬁcantly speed

up calculations using matrix accelerators.

The popularity of perceptrons is due to a wide

range of available tasks that can be solved with their

help. In the general case, they solve the problem

of approximating multidimensional functions, that is,

constructing a multidimensional mapping F : x ⇒ y

that generalizes a given set of parameters {x

⇒ y

Depending on the type of output variables (the

type of input variables is not critical), the approxima-

tion of functions can take the form of classiﬁcation

(discrete set of initial values), or regression (continu-

ous initial values).

Many practical problems of pattern recognition,

noise ﬁltering, time series prediction, etc. come down

to basic settings. The reason for the popularity of

perceptrons is that, for their range of tasks, they are,

ﬁrstly, universal, and secondly, they are efﬁcient in

terms of the computational complexity of devices.

As a result of the development of neurocomput-

ing, a large number of efﬁcient models of neural net-

works have been created, focused on solving various

problems. Due to this, artiﬁcial neural networks are

successfully used to solve a wide class of practical

problems. Therefore, when solving a speciﬁc prob-

lem, it is necessary to solve the issue of choosing the

most appropriate neural network model, its parame-

ters, and the training method.

Typically, a network consists of many sensor ele-

ments (input nodes or source nodes) that form an in-

put layer; one or more hidden layers of computational

neurons, and one output layer of neurons. The input

signal propagates through the network in a forward di-

rection from layer to layer. Such networks are usually

called multilayer perceptrons. They are a generaliza-

tion of a single layer perceptron.

Multilayer perceptrons are successfully used to

solve various problems. At the same time, supervised

learning is performed using such a popular algorithm

as the error back-propagation algorithm. This method

consists of error correction (error-correction learning

rule). It can be thought of as a generalization of the

equally popular adaptive ﬁltering algorithm, the mean

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

186

squared error minimization (LMS) algorithm.

Multilayer perceptrons have three characteristic

features.

1. Each neuron of the network has a non-linear ac-

tivation function. It should be noted that this

non-linear function is smooth (that is, differenti-

ated everywhere), in contrast to the hard threshold

function used in the Rosenblatt perceptron. The

most popular form of a function that satisﬁes this

requirement is the sigmoidal nonlinearity, deﬁned

by the logistic function

1 + exp(−v

)

, (9)

where v

is the induced local ﬁeld (i.e., the

weighted sum of all synaptic inputs plus the limit

value) of neuron j; y

is the output of the neuron.

The presence of non-linearity plays a very impor-

tant role, since otherwise the “input-output” map-

ping of the network can be reduced to a conven-

tional single-layer perceptron. Moreover, the use

of the logistic function is biologically motivated,

since it takes into account the recovery phase of a

real neuron.

2. The network contains one or more layers of hid-

den neurons that are not part of the input or output

of the network. These neurons allow the network

to learn how to solve complex problems by se-

quentially extracting the most important features

of the input image (vector).

The network has a high degree of connectivity

(connectivity), implemented using synaptic connec-

tions. Changing the level of network connectivity re-

quires changing the plurality of synaptic connections

or their weights.

The combination of all these properties, along

with learning-by-doing, provides the computational

power of a multilayer perceptron. However, these

same qualities are the reason for the incompleteness

of modern knowledge about the behavior of such

networks. First, the distributed form of nonlinear-

ity and the high connectivity of the network signif-

icantly complicate the theoretical analysis of a mul-

tilayer perceptron. Second, the presence of hidden

neurons makes the learning process more difﬁcult to

visualize. It is in the learning process that it is nec-

essary to determine which signs of the input signal

should be given by hidden neurons. Then the learning

process becomes even more difﬁcult, since the search

must be performed in a wide range of possible func-

tions, and the choice must be made among alternative

representations of the input images.

The emergence of the backpropagation algorithm

was a landmark event in the development of neural

networks, since it implements a computationally efﬁ-

cient method for training a multilayer perceptron. The

backpropagation algorithm does not offer a truly op-

timal solution to all potential problems, but it is most

effective in learning multilayer machines.

An artiﬁcial neural network for the analysis of in-

dicators of the quality of the educational program and

educational activities will have the number of input

neurons (according to the number of indicators for all

criteria) 54; output neurons – 54. Input signals were

determined based on students’ assessments of each in-

dicator of this quality criterion, while the scale F, E,

B, A were translated into numerical 1; 2; 3; 4 respec-

tively. Part of the data is given in table 1.

Table 1: Input signals (T) based on students’ assessments of

quality criteria.

Indicators of Student grades

quality criteria 1 2 3 4 5 6 7 ... 54

1 3 4 3 3 4 3 4 . . . 4

2 4 3 3 3 4 3 3 . . . 4

3 3 3 4 3 4 4 3 . . . 4

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

54 4 3 3 3 4 3 3 . . . 4

It is important that the neural network can pre-

dict expert assessments if student and graduate assess-

ments are to be ranked in ascending order based on the

determination of the grade point average. According

to the hypothesis, we assume that students with higher

academic performance are better acquainted with the

goals, structure, and content of the educational pro-

gram, the process and characteristics of teaching and

learning according to the educational program, con-

trol measures, assessment system, and all other as-

pects of educational activities. assessments of the

quality of the educational program and educational

activities will be more objective.

The Neural Network Toolbox application package

Matlab Mathematical Modeling Environment (ver-

sion R2014a) was used in the work. After starting

the Matlab system, enter the nntool command on the

command line, which opens the window for entering

data and creating a neural network (Neural Network /

Data Manager) (ﬁgure 2).

After starting the MATLAB system, you need to

enter the tool command on the command line, which

will open the window for entering data and creating

a neural network (Neural Network / Data Manager).

Clicking the New button opens the Create Network

or Data window. After selecting the Data tab in the

Name ﬁeld you must enter a new name of the input

data “P”, and in the Value ﬁeld the values of the in-

put data, in which the numbers 1-54 are indicators of

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

187

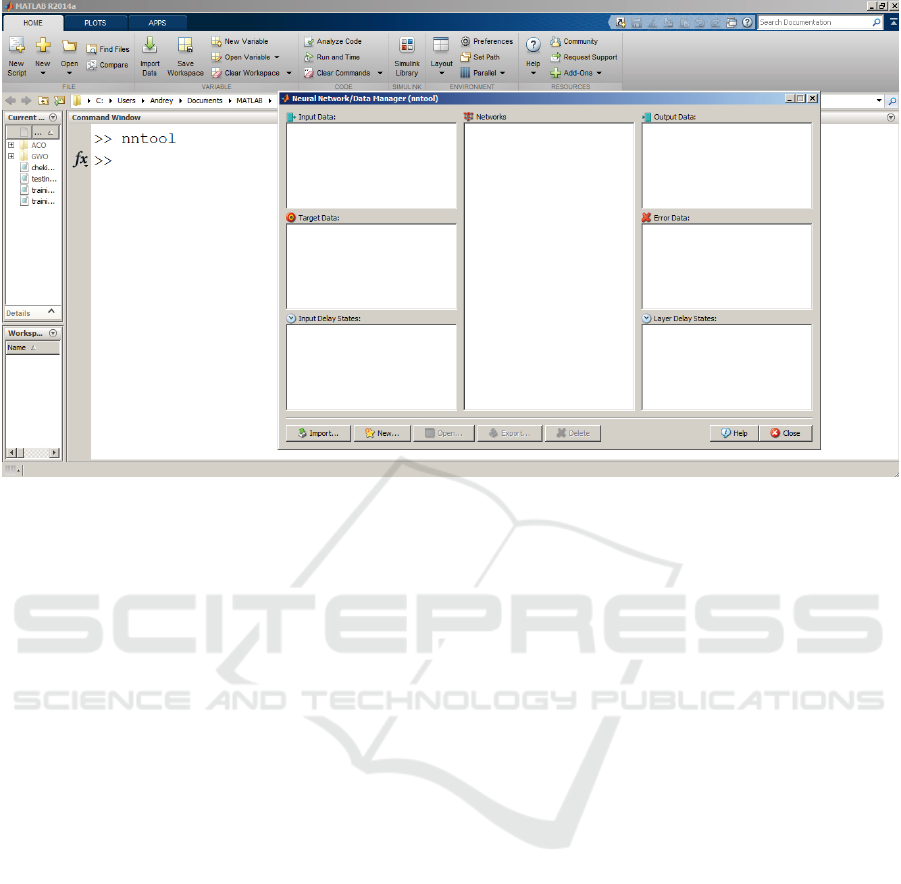
Figure 2: Data entry and neural network creation windows.

quality criteria, and 55-108 – students’ and graduates’

indicators quality criteria.

To create a new network, we chose New, to view

the data you need to select Import. The data is con-

tained in the P.mat ﬁle. This ﬁle is a matrix of two

lines, in which the numbers 1-54 are indicators of

quality criteria, and 55-108 – are the evaluation of stu-

dents and graduates on the indicators of quality crite-

ria. Its contents are stored in the P.txt ﬁle.

The next step is to import the data (ﬁgure 3).

The next step was to create data (“T”) – goals,

which are an array of size 54x54, which contains in-

formation about the grades given by the participants

of the experiment – full-time master’s students (22

people) and graduates of higher education institutions

there are specialties (32 people) – a total of 54 peo-

ple. This number of respondents is due to the number

of indicators of quality criteria because the data for-

mat of the artiﬁcial network in Matlab supports square

matrices, in this case, 54x54. The data is stored in a

T.mat ﬁle. Its contents can be viewed using a text ed-

itor.

We import data in the same way as for the array P.

In the next step, a neural network was created (ﬁg-

ure 4). An artiﬁcial neural network for the analysis of

indicators of the quality of the educational program

and educational activities will have the number of in-

put neurons (according to the number of indicators

for all criteria) 54; output neurons – 54. Input sig-

nals were determined based on students’ assessments

for each indicator of this quality criterion, while the

scales F, E, B, A were converted to numerical 1; 2; 3;

4 respectively.

The conﬁguration of the neural network of direct

propagation is chosen based on a heuristic rule: the

number of neurons of the hidden layer is equal to half

of the total number of input and output neurons. The

artiﬁcial neural network for the analysis of quality in-

dicators of the educational program and educational

activity will have the number of input neurons 2 (ac-

cording to the dimensionality of the data – indicators

of quality criteria and student evaluation); source neu-

rons 54, therefore, the number of hidden neurons is

28. The View button allows you to view the network

structure (ﬁgure 5).

In our case, 2 is the number of input neurons,

which is known to be selected based on the dimension

of the input data (1 – indicators of quality criteria; 2

– student assessments). Output neurons – 54. The

conﬁguration of the neural network of direct propaga-

tion (feed-forward backdrop) is chosen based on the

heuristic rule: the number of neurons in the hidden

layer is equal to half the total number of input and

output neurons, so the hidden layer has 28 neurons.

The next stage is network training and coaching.

Double-clicking with the left mouse button on the cre-

ated neural network network1 in the window of the

Neural Network / Data Manager opens a window with

the network.

The View tab presents the neural network itself.

Go to the Reinitialize Weights tab, where the Input

Ranges column selects the P input from the Get from

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

188

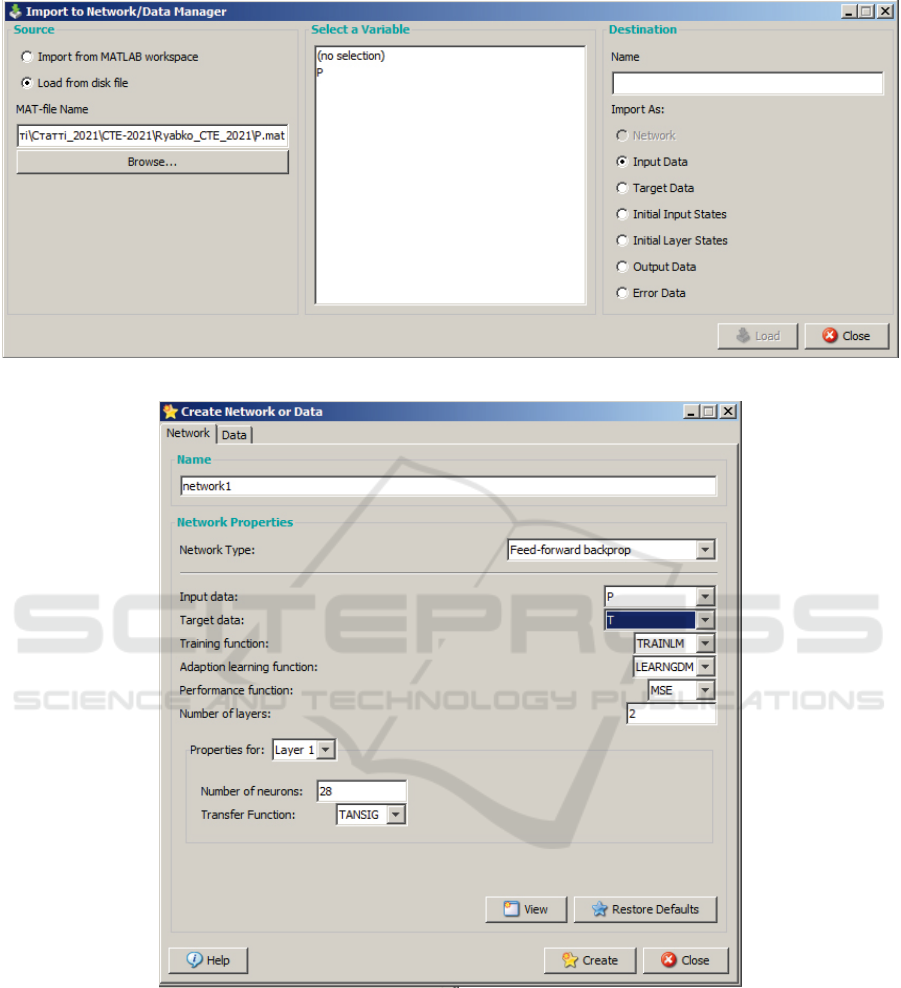
Figure 3: Importing data.

Figure 4: Creating a neural network.

the input list. Then press the Set Input Ranges and

Initialize Weights buttons in succession allowing us

to initialize the scales needed to initialize the entire

network.

The next step is network learning.

Learning the backpropagation method involves

two passes through all layers of the network: forward

and backward. In a forward pass, the image (incom-

ing vector) is fed to the sensor nodes of the network,

after which it propagates through the network from

layer to layer. As a result, a set of output signals is

generated, which is the actual response of the net-

work to a given input image. In forward traversal, all

synaptic weights of the network are ﬁxed. In a back-

ward pass, all synaptic weights are adjusted accord-

ing to the error correction rule, namely: the actual

output of the network is subtracted from the desired

(target) response, resulting in an error signal. This

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

189

Figure 5: The structure of the neural network.

signal subsequently propagates through the network

in the opposite direction of the synaptic connections.

Hence the name – backpropagation algorithm. The

synaptic weights are tuned to bring the network out-

put as close as possible to the desired statistical mean-

ing. The back-propagation algorithm is sometimes

referred to as the simpliﬁed back-propagation algo-

rithm. The learning process using this algorithm is

called back-propagation learning.

Going to the Train tab opens a learning window

in which P and T are selected instead of input data

and targets, respectively (ﬁgure 6). On the right of

the Training Results column, you need to change the

name of the Outputs and Errors to O and E, respec-

tively. Then pressing the Train Network button will

start network training, the process of which can be ob-

served in the Neural Network Training window. You

can close the window after graduation.

After the training was completed, two types of

data appeared in the Neural Network / Data Man-

ager window: Output Data (O) and Error Data (E).

Double-clicking on data O opens a window with data

output. By clicking the Export button in the man-

ager window, and then clicking Export again in the

window that opens, you can transfer the data to the

Matlab workspace, where it will be presented in the

most presentable form. You can view the results in

the O.mat and E.mat ﬁles.

You can calculate that the average network error is

0.0321, which indicates the efﬁciency of the system.

After learning the network, you can proceed to

data forecasting. Returning to the Neural Network /

Data Manager window, you need to create additional

input by clicking the New button. Going to the Data

tab, the name of the data changes, for example, to P1,

and the values are set as follows: values 1-54 still in-

dicate the numbers of indicators of quality criteria of

educational programs and educational activities, and

56-109 assessments of students and graduates quality,

and the last column – projected expert assessments.

Next, you need to return to the Network window.

In the Simulate tab of the input values house, the P1

Figure 6: Neural network learning.

array is selected, and the Outputs output value is re-

named to forecast (ﬁgure 7).

After clicking the Simulate Network button, you

can return to the Neural Network / Data Manager

window and, by clicking the Export button, copy the

source forecast array to the Matlab workspace. After

receiving the table in the workspace, pay attention to

the last column, which is responsible for forecasting

(ﬁgure 8).

The data obtained in the study can be viewed in

the forecast.mat ﬁle.

Comparing the data issued by the system and the

real data, we can see that the neural network does

make predictions that are quite close to reality. Com-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

190

Table 2: Output signals (O).

Indicators of Student grades

quality criteria 1 2 3 4 5 6 7 ... 54

1 3.1985 3.252 3.3058 3.3541 3.3933 3.4235 3.4475 . . . 3.9704

2 3.4521 3.3478 3.2644 3.2035 3.1633 3.1404 3.1319 . . . 3.9997

3 3.1516 3.1812 3.219 3.2627 3.3062 3.3417 3.3638 . . . 3.9992

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

54 4 3.4192 3.3522 3.3128 3.291 3.2798 3.2756 . . . 3.9716

Figure 7: Simulate.

pared with expert estimates, the average absolute er-

ror is 0.0321, the relative error is 7.08%.

In the second part of the experiment, forecasting

was carried out using a different type of neural net-

work – a neuro-fuzzy network, or ANFIS-model.

Expert estimates are used as validation data. Cre-

ate data ﬁles: training.dat, testing.dat, checking.dat.

It should be noted that attempts to consider large data

volumes lead to a reduction in the number of ob-

servations in the training sample and its simultane-

ous unjustiﬁed growth, which can negatively affect

the network’s ability to learn. So, ﬁrst you need to

turn the available information into a form that is un-

derstandable and meaningful for the neuro-fuzzy net-

work. Consider the average value of the assessment

of each of the 10 criteria for assessing the quality of

the educational program. For training, we use the av-

erage scores of all students for each of the 10 criteria.

For testing, the marks of students numbered from 12

to 30 are used, for veriﬁcation – the marks that were

put by 31 students.

We preliminarily transpose the data, so the num-

bers of students will be in the rows, and the grades ac-

cording to the quality criteria will be in the columns.

The data in the ﬁles contains 10 columns – 9 grades

(incoming) and 1 grade (source). The ﬁrst ﬁle con-

tains 54 lines and 10 columns. The second has 18

rows and 10 columns. The third has one row and 10

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

191

Figure 8: Getting a table with forecasting in the work area.

Table 3: Errors (E).

Indicators of Student grades

quality criteria 1 2 3 4 5 6 7 ... 54

1 -0.199 0.748 -0.306 -0.354 0.607 -0.424 0.552 . . . 0.0000237

2 0.548 -0.348 -0.264 -0.203 0.837 -0.140 -0.132 . . . 0.029607

3 -0.152 -0.181 0.781 -0.263 0.694 0.658 -0.364 . . . 0.00027

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

54 0.58076 -0.3522 -0.3128 -0.2909 0.7202 -0.2755 -0.2769 . . . 0.028442

Table 4: Neural network forecast and expert evaluation.

Indicators of Forecast Estimates

quality criteria

1 3.999977 4

2 3.974844 4

3 3.999750 4

4 3.999379 3

5 3.956661 4

6 3.991731 4

7 3.985698 4

. . . . . . . . .

54 3.970182 4

columns.

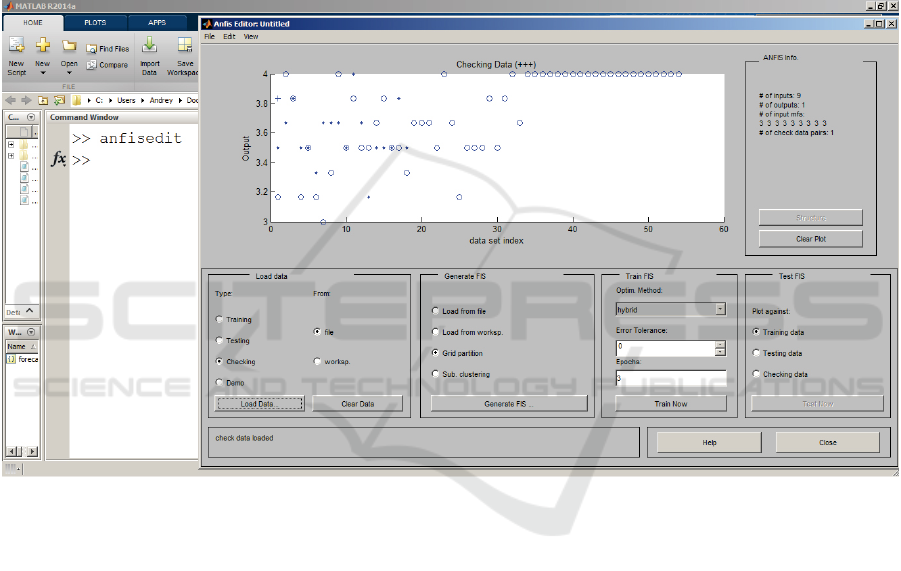
Anﬁs Editor is used to building MATLAB fuzzy

neural networks. Run the editor with the anﬁsedit

command. In the Load data menu, select Training,

and From disk, click the load data button. In the win-

dow that opens, select the previously created train-

ing.dat ﬁle. In the Load data menu, select Testing and

From disk, click the load data button. In the window

that opens, select the previously created testing.dat.

In the Load data menu, select Checking and From

disk, and click the load data button. In the window

that opens, select the previously created checking.dat.

The visualization area contains two types of informa-

tion: when training the system, the learning curve in

the form of a graph of the dependence of the learning

error on the iteration ordinal number; when loading

data and testing the system – experimental data and

simulation results.

Experimental data and simulation results are dis-

played as a set of points in two-dimensional space. In

this case, the serial number of the data line in the sam-

ple (training, test, or control) is plotted along the ab-

scissa axis, and the value of the initial variable of this

sample line is plotted along the ordinate axis. The fol-

lowing markers are used: blue dot (.) – test set; blue

circle (o) – training sample; blue plus (+) – control

sample; a red asterisk (*) – simulation results.

Then, having set the Generate FIS menu switch

to the Grid partition position, you should press the

Generate FIS button. In this case, the model has 10

input variables, each of which corresponds to 9 terms

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

192

Training.dat ﬁle (ﬁrst three lines):

3.5000 3.3333 3.5000 3.4000 3.5000 3.3333 3.3333 3.5714 3.3333 3.1667

4.0000 3.4444 3.2500 3.8000 3.7500 3.5000 3.6667 3.4286 3.6667 4.0000

3.2500 3.6667 3.2500 3.4000 3.5000 3.6667 3.0000 3.5714 4.0000 3.8333

Testing.dat ﬁle (ﬁrst four lines):

3.2500 3.4444 3.7500 3.6000 3.2500 3.8333 3.5000 3.4286 3.6667 3.5000

3.7500 3.6667 4.0000 3.2000 3.5000 3.3333 3.1667 3.8571 3.6667 3.6667

4.0000 3.5556 3.5000 3.6000 3.5000 3.8333 3.5000 3.2857 3.3333 3.8333

3.5000 3.5556 3.2500 3.4000 3.5000 3.6667 3.6667 3.5714 4.0000 3.5000

Checking.dat ﬁle:

3.5000 3.3333 3.2500 3.4000 4.0000 3.3333 3.8333 3.2857 3.0000 3.8333

Figure 9: Data for network training and validation.

of the gaussmf type. The original variable is deter-

mined by a linear function. Let’s generate a Sugeno-

type fuzzy inference system by pressing the Generate

FIS button. In the window that opens, set 3 mem-

bership functions of the gaussmf type for each input

variable. The choice of the property function here is

because we assume a normal distribution for a random

variable, deﬁned by a Gaussian function according to

probability theory. For the output variable, we set the

membership function const.

To train the hybrid network, we will choose the

backdrop method (error backpropagation) with an er-

ror level of 0 and a number of cycles of 10. Let’s start

training the hybrid network (ﬁgure 10).

As can be seen from ﬁgure 10, according to the

training results, the average error is approximately

0.007.

We test the fuzzy inference system ﬁrst on the

training set.

Now let’s test the resulting fuzzy inference sys-

tem on the known values of expert estimates. Now

we download this sample in testing mode in the Anﬁs

editor. The results are shown in Figure 12. The mean

score of the experts is 3.99; network prediction of the

neural fuzzy network is 3.51. The relative forecast

error is 12.57%.

Comparing the prediction errors of the neuro-

fuzzy network (12.57%) and the L-layer feed-forward

neural network (7.08%), we can see that the lat-

ter makes a more accurate prediction. It should be

noted that the ANFIS model requires signiﬁcantly

more computing resources from the computer, which

forced us to reduce the number of input variables to

10, which corresponded to the number of program

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

193

Figure 10: Network training error.

Figure 11: Network training results.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

194

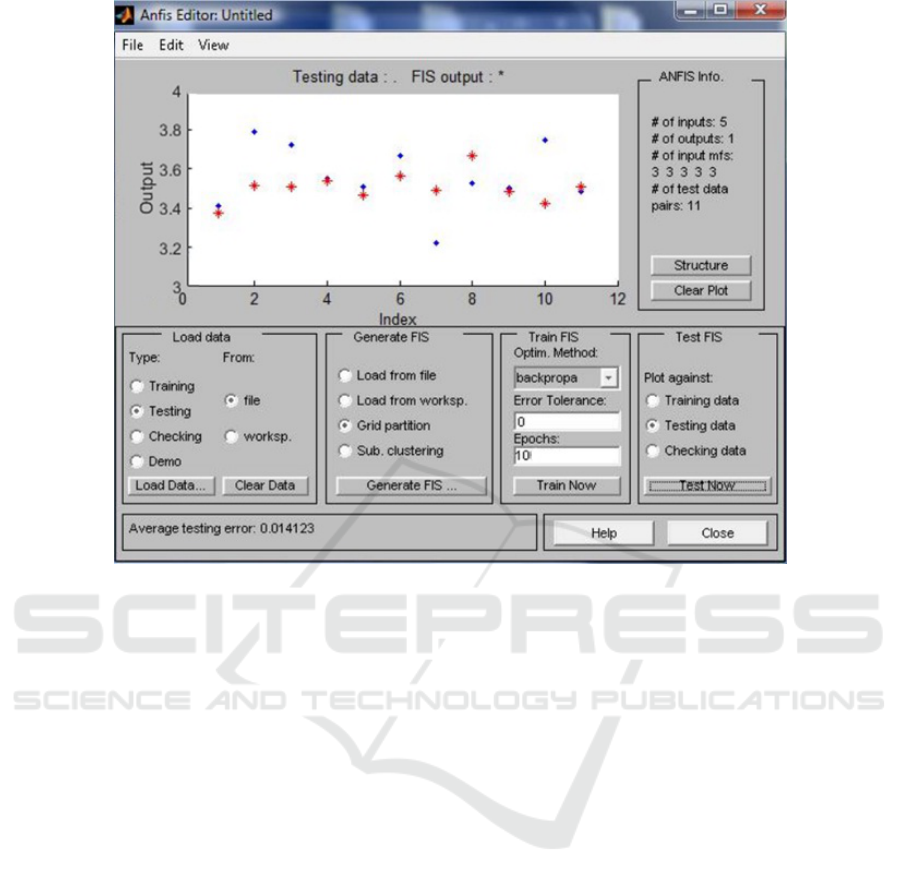
Figure 12: The results of network testing on known values of expert estimates.

evaluation criteria, and use the average values of qual-

ity indicators for each of the criteria. Of course, the

problem requires further study of large data volumes

of other accreditation examinations, but in general,

this approach has demonstrated very good predictive

capabilities.

Table 4 also shows that the quality of the pro-

gram and educational activities is at a fairly high level,

which reﬂects the average score of the peer review.

3 DISCUSSION

The study aimed to demonstrate the possibility of pre-

dicting the assessment of the quality of educational

programs and educational activities can be adequately

addressed through an artiﬁcial neural network and ob-

tain a comprehensive assessment of the quality of ed-

ucational programs and educational activities based

on a possible neuro-fuzzy approach. The mathemat-

ical model involves the use of neural networks and

is based on the technology of analytical processing

of statistical data. Standard methods of mathematical

statistics are used to analyze the estimates received

from respondents.

Debatable are proposals for using students as ex-

perts in the educational program and educational ac-

tivities; it is more appropriate to use teachers from

other educational institutions, but in the process of

preparing for introspection, this approach can be con-

sidered quite appropriate.

The results of the neural network should be con-

sidered not as ﬁnal, but as a test. As noted, for more

detailed conclusions, it is necessary to train the net-

work on a larger amount of experimental data.

The network structure has room for further im-

provement and customization in future studies.

The assumption that based on a sample of stu-

dents and graduates of higher education the quality

of the educational program and educational activities

can prepare a sample for setting up and teaching ar-

tiﬁcial neural networks is conﬁrmed by ordering the

quality of the curriculum of students and graduates.

teaching. In practice, this allows you to predict the re-

sults and identify existing shortcomings and eliminate

them before the accreditation examination. However,

the difﬁculty of this method is to choose the architec-

ture of the neural network and prepare a training sam-

ple to conﬁgure the neural network. In particular, in

the future, it is planned to increase the volume of the

input vector of the artiﬁcial neural network, and the

form is based on estimates of teachers, stakeholders,

and experts.

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

195

4 CONCLUSIONS

As a result of a mathematical model of a compre-

hensive evaluation of the quality of educational pro-

grams and educational activities based on the methods

of neuro-fuzzy approach, ﬁrst managed to work out

a mechanism for obtaining a quantitative evaluation

of educational programs and educational activities in

this program that will allow the institution of higher

education detect shortcomings and potential problems

and solve them before the accreditation examination.

Secondly, based on a sample of students and grad-

uates of higher education to evaluate the quality of

educational programs and educational activities, you

can prepare a training sample for setting up and learn-

ing an artiﬁcial neural network that can adequately

perform a comprehensive assessment of educational

programs and educational activities. This can be done

by arranging the assessments of the quality of the cur-

riculum and the educational activities of students and

graduates in ascending order based on the determina-

tion of the average grade point average. It is empha-

sized that these methods are effective provided they

meet the requirements of a student-centered approach

and the principles of academic freedom.

Based on a sample of students and graduates of

higher education, the quality of the educational pro-

gram and educational activities was prepared to pre-

pare a training sample for setting up and teaching ar-

tiﬁcial neural network, which was able to adequately

perform a comprehensive assessment of the quality

of educational programs and educational activities. A

comparison of the results of the operation of an ar-

tiﬁcial neural network of direct propagation with one

output and several inputs with real data shows that the

neural network does make predictions close to reality.

Compared with expert estimates, the average absolute

error was 0.0321; the relative error was 7.08%.

The results of the study can be used in the prac-

tice of higher education institutions to predict the re-

sults and identify existing shortcomings and eliminate

them before the accreditation examination.

We see prospects for further research in the ap-

plication of software products based on the theory of

neural networks to automate the processes of the or-

ganization, control, and analysis of the educational

process; introduction of neural network software for

direct training of students in certain disciplines.

REFERENCES

Abu Naser, S., Zaqout, I., Abu Ghosh, M., Atallah, R., and

Alajrami, E. (2015). Predicting student performance

using artiﬁcial neural network: In the faculty of en-

gineering and information technology. International

Journal of Hybrid Information Technology, 8(2):221–

228. https://doi.org/10.14257/ijhit.2015.8.2.20.

Arsad, P. M., Buniyamin, N., and Manan, J.-l. A. (2013).

A neural network students’ performance prediction

model (NNSPPM). In 2013 IEEE International Con-

ference on Smart Instrumentation, Measurement and

Applications (ICSIMA), pages 1–5. https://doi.org/10.

1109/ICSIMA.2013.6717966.

Black, S. E., Lincove, J., Cullinane, J., and Veron, R.

(2015). Can you leave high school behind? Eco-

nomics of Education Review, 46:52–63. https://doi.

org/10.1016/j.econedurev.2015.02.003.

Cader, A. (2020). The Potential for the Use of Deep Neu-

ral Networks in e-Learning Student Evaluation with

New Data Augmentation Method. In Bittencourt,

I. I., Cukurova, M., Muldner, K., Luckin, R., and

Mill

an, E., editors, Artiﬁcial Intelligence in Educa-

tion, pages 37–42, Cham. Springer International Pub-

lishing. https://doi.org/10.1007/978-3-030-52240-7

Chaban, H. and Kukhtiak, O. (2020). Application of the ar-

tiﬁcial neural networks theory in problems of applied

pedagogy of higher education institutions. Ukrainian

Educational Journal, (1):51–56. https://doi.org/10.

32405/2411-1317-2020-1-51-56.

Cherniak, O., Sorocolat, N., and Kanytska, I. (2020).

Graph analytical method for determining the complex

quality indicator of qualimetry objects. Innovative

Technologies and Scientiﬁc Solutions for Industries,

4(14):169–175. https://doi.org/10.30837/ITSSI.2020.

14.169.

Chervak, O. Y. (2010). Teoriya optymalnogo vyboru.

Pidkryteriyi paretivskoyi zgortky kryteriyiv [The the-

ory of optimal choice. Sub-criteria for convolution

of Pareto criteria]. Naukovyj visnyk Uzhgorodskogo

universytetu, 30:28–30. https://dspace.uzhnu.edu.ua/

jspui/handle/lib/7372.

Do, Q. H. and Chen, J.-F. (2013). A neuro-fuzzy approach

in the classiﬁcation of students’ academic perfor-

mance. Computational intelligence and neuroscience,

2013:179097. https://doi.org/10.1155/2013/179097.

Fazlollahtabar, H. and Mahdavi, I. (2009). User/tutor opti-

mal learning path in e-learning using comprehensive

neuro-fuzzy approach. Educational Research Review,

4(2):142–155. https://doi.org/10.1016/j.edurev.2009.

02.001.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. Adaptive Computation and Machine Learn-

ing series. MIT Press. http://www.deeplearningbook.

org.

Grytsyuk, Y. I. and Grytsiuk, M. Y. (2014). The Pecu-

liarities of Multiplicative Coagulation a Partial Cri-

teria Into One Generalized Index. Scientiﬁc Bul-

letin of UNFU, 24(11):341–352. https://nv.nltu.edu.

ua/Archive/2014/24 11/57.pdf.

Hammerness, K. and Klette, K. (2015). Indicators of

quality in teacher education: Looking at features

of teacher education from an international perspec-

tive. In Promoting and sustaining a quality teacher

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

196

workforce, volume 27 of International Perspectives

on Education and Society, pages 239–277. Emerald

Group Publishing Limited. https://doi.org/10.1108/

S1479-367920140000027013.

Horal, L., Khvostina, I., Reznik, N., Shyiko, V., Yashcher-

itsyna, N., Korol, S., and Zaselskiy, V. (2020).

Predicting the economic efﬁciency of the business

model of an industrial enterprise using machine learn-

ing methods. In Kiv, A., editor, Proceedings of

the Selected Papers of the Special Edition of In-

ternational Conference on Monitoring, Modeling &

Management of Emergent Economy (M3E2-MLPEED

2020), Odessa, Ukraine, July 13-18, 2020, volume

2713 of CEUR Workshop Proceedings, pages 334–

351. CEUR-WS.org. https://ceur-ws.org/Vol-2713/

paper37.pdf.

Isac, C., Nita, D., and Dura, C. (2010). Optimizing

Franchising Investment Decision Using Elec-

tre and Rompedet Methods. The IUP Jour-

nal of Managerial Economics, 8(1/2):7–32.

https://www.iupindia.in/510/IJME

Optimizing

Franchising Investment Decision 7.html.

Kardan, A. A., Sadeghi, H., Ghidary, S. S., and Sani,

M. R. F. (2013). Prediction of student course selec-

tion in online higher education institutes using neural

network. Computers & Education, 65:1–11. https:

//doi.org/10.1016/j.compedu.2013.01.015.

Kirichek, G., Harkusha, V., Timenko, A., and Kulykovska,

N. (2019). System for detecting network anoma-

lies using a hybrid of an uncontrolled and con-

trolled neural network. CEUR Workshop Proceed-

ings, 2546:138–148. https://ceur-ws.org/Vol-2546/

paper09.pdf.

Kondruk, N. E. and Maliar, M. M. (2019). Bagatokry-

terialna optymizatsiia liniinykh system [Multicriteria

optimization of linear systems]. Autdor-Shark, Uzh-

gorod, Ukraine. https://dspace.uzhnu.edu.ua/jspui/

handle/lib/24042.

Lesinski, G., Corns, S., and Dagli, C. (2016). Application

of an Artiﬁcial Neural Network to Predict Graduation

Success at the United States Military Academy. Pro-

cedia Computer Science, 95:375–382. https://doi.org/

10.1016/j.procs.2016.09.348.

Liu, C., Feng, Y., and Yuling, W. (2022). An innova-

tive evaluation method for undergraduate education:

an approach based on bp neural network and stress

testing. Studies in Higher Education, 47(1):212–228.

https://doi.org/10.1080/03075079.2020.1739013.

Mahapatra, S. S. and Khan, M. S. (2007). A neural net-

work approach for assessing quality in technical edu-

cation: an empirical study. International Journal of

Productivity and Quality Management, 2(3):287–306.

https://doi.org/10.1504/IJPQM.2007.012451.

Markova, O. M., Semerikov, S., and Popel, M. (2018).

Cocalc as a learning tool for neural network simula-

tion in the special course ”foundations of mathematic

informatics”. In Ermolayev, V., Su

arez-Figueroa,

M. C., Yakovyna, V., Kharchenko, V. S., Kobets,

V., Kravtsov, H., Peschanenko, V. S., Prytula, Y.,

Nikitchenko, M. S., and Spivakovsky, A., editors, Pro-

ceedings of the 14th International Conference on ICT

in Education, Research and Industrial Applications.

Integration, Harmonization and Knowledge Transfer.

Volume II: Workshops, Kyiv, Ukraine, May 14-17,

2018, volume 2104 of CEUR Workshop Proceedings,

pages 388–403. CEUR-WS.org. https://ceur-ws.org/

Vol-2104/paper 204.pdf.

uller, B., Reinhardt, J., and Strickland, M. T. (1995). Neu-

ral Networks: An Introduction. Physics of Neural Net-

works. Springer-Verlag Berlin Heidelberg, 2 edition.

https://doi.org/10.1007/978-3-642-57760-4.

Okubo, F., Yamashita, T., Shimada, A., and Konomi, S.

(2017a). Students’ performance prediction using data

of multiple courses by recurrent neural network. In

Mohd Ayub, A. F., Mitrovic, A., Yang, J.-C., Wong,

S. L., and Chen, W., editors, Proceedings of the 25th

International Conference on Computers in Education,

ICCE 2017 - Main Conference Proceedings, page 439

– 444. Asia-Paciﬁc Society for Computers in Educa-

tion. https://www.apsce.net/icce/icce2017/140.115.

135.84/icce/icce2017/sites/default/ﬁles/proceedings/

main/C3/Students%20Performance%20Prediction%

20Using%20Data%20of%20Multiple%20Courses%

20by%20Recurrent%20Neural%20Network.pdf.

Okubo, F., Yamashita, T., Shimada, A., and Ogata, H.

(2017b). A neural network approach for students’

performance prediction. In Proceedings of the Sev-

enth International Learning Analytics & Knowledge

Conference, LAK ’17, page 598–599, New York, NY,

USA. Association for Computing Machinery. https:

//doi.org/10.1145/3027385.3029479.

Osadchyi, V., Kruglyk, V., and Bukreyev, D. (2018). De-

velopment of a software product for forecasting the

entrance of applicants to higher educational institu-

tions. Ukrainian Journal of Educational Studies and

Information Technology, 6(3):55–69. https://doi.org/

10.32919/uesit.2018.03.06.

Parvu, I. and Ipate, D. M. (2007). Mathematical model of

measuring the quality of services of the higher ed-

ucation institutions. Journal of Applied Economic

Sciences, 2(1(2)

Fall2007). https://EconPapers.repec.

org/RePEc:ush:jaessh:v:2:y:2007:i:1(2) fall2007:5.

Pererva, V. V., Lavrentieva, O. O., Lakomova, O. I., Zaval-

niuk, O. S., and Tolmachev, S. T. (2020). The tech-

nique of the use of virtual learning environment in the

process of organizing the future teachers’ terminolog-

ical work by specialty. CTE Workshop Proceedings,

7:321–346. https://doi.org/10.55056/cte.363.

Porokhnya, V. and Ostapenko, O. (2019). Neural network

and index forecasting of the strategies of development

of the armed forces of ukraine depending on their own

economic opportunities and encroachments of the ag-

gressor states. In Kiv, A., Semerikov, S., Soloviev,

V. N., Kibalnyk, L., Danylchuk, H., and Matviy-

chuk, A., editors, Proceedings of the Selected Pa-

pers of the 8th International Conference on Monitor-

ing, Modeling & Management of Emergent Economy,

M3E2-EEMLPEED 2019, Odessa, Ukraine, May 22-

24, 2019, volume 2422 of CEUR Workshop Proceed-

ings, pages 111–120. CEUR-WS.org. https://ceur-ws.

org/Vol-2422/paper09.pdf.

Rivas, A., Gonz

alez-Briones, A., Hern

andez, G., Prieto,

Methodology for Assessing the Quality of an Educational Program and Educational Activities of a Higher Education Institution Using a

Neural Network

197

J., and Chamoso, P. (2021). Artiﬁcial neural net-

work analysis of the academic performance of stu-

dents in virtual learning environments. Neurocomput-

ing, 423:713–720. https://doi.org/10.1016/j.neucom.

2020.02.125.

Semerikov, S., Teplytskyi, I., Yechkalo, Y., Markova, O.,

Soloviev, V., and Kiv, A. (2022). Using spread-

sheets as learning tools for neural network simulation.

Ukrainian Journal of Educational Studies and Infor-

mation Technology, 10(3):42–68. https://doi.org/10.

32919/uesit.2022.03.04.

Shtovba, S. and Pankevych, O. (2018). Fuzzy technology-

based cause detection of structural cracks of stone

buildings. In Ermolayev, V., Su

arez-Figueroa, M. C.,

Lawrynowicz, A., Palma, R., Yakovyna, V., Mayr,

H. C., Nikitchenko, M. S., and Spivakovsky, A., edi-

tors, Proceedings of the 14th International Conference

on ICT in Education, Research and Industrial Appli-

cations. Integration, Harmonization and Knowledge

Transfer. Volume I: Main Conference, Kyiv, Ukraine,

May 14-17, 2018, volume 2105 of CEUR Workshop

Proceedings, pages 209–218. CEUR-WS.org. https:

//ceur-ws.org/Vol-2105/10000209.pdf.

Shtovba, S. D. (2007). Proektirovanie nechetkikh

sistem sredstvami MatLab [Fuzzy systems de-

sign of by means of MatLab]. Goryachaya

Liniya–Telekom, Moscow. http://pistunovi.inf.ua/

shtovba proek nechet sistem matlab.pdf.

Sivanandam, S. N., Sumathi, S., and Deepa, S. N. (2006).

Introduction to neural networks using Matlab 6.0.

Tata McGraw-Hill Education, New Delhi.

Tarasenko, A. O., Yakimov, Y. V., and Soloviev, V. N.

(2019). Convolutional neural networks for image clas-

siﬁcation. CEUR Workshop Proceedings, 2546:101–

114. https://ceur-ws.org/Vol-2546/paper06.pdf.

Taylan, O. and Karag

ozo

glu, B. (2009). An adaptive

neuro-fuzzy model for prediction of student’s aca-

demic performance. Computers & Industrial Engi-

neering, 57(3):732–741. https://doi.org/10.1016/j.cie.

2009.01.019.

Tryhub, I. (2016). Professional training of experts in the

ﬁeld of education in Slavic Eastern European coun-

tries. Pedagogical process: theory and practice, 4:78–

78. https://tinyurl.com/4vb4ysub.

Valko, N. and Osadchyi, V. (2020). Education individual-

ization by means of artiﬁcial neural networks. E3S

Web of Conferences, 166:10021. https://doi.org/110.

1051/e3sconf/202016610021.

Verkhovna Rada of Ukraine (2019). Regulations on the

accreditation of educational programs, which provide

training for higher education. https://zakon.rada.gov.

ua/laws/show/z0880-19\#Text.

Waheed, H., Hassan, S.-U., Aljohani, N. R., Hardman, J.,

Alelyani, S., and Nawaz, R. (2020). Predicting aca-

demic performance of students from VLE big data

using deep learning models. Computers in Human

Behavior, 104:106189. https://doi.org/10.1016/j.chb.

2019.106189.

achter, B., Kelo, M., Lam, Q., Effertz, P., Jost, C., and

Kottowski, S. (2015). University quality indicators: a

critical assessment. Technical report, Directorate Gen-

eral for Internal Policies, Policy Department B: Struc-

tural and Cohesion Policies. https://doi.org/10.2861/

426164.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

198