Complex Systems and Complex Thinking Within the Framework of

Education 4.0

Andrii O. Bielinskyi

1,2 a

, Arnold E. Kiv

3,4 b

and Vladimir N. Soloviev

1,5 c

Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine

State University of Economics and Technology, 16 Medychna Str., Kryvyi Rih, 50005, Ukraine

Ben-Gurion University of the Negev, P.O.B. 653, Beer Sheva, 8410501, Israel

South Ukrainian National Pedagogical University named after K. D. Ushynsky,

26 Staroportofrankivska Str., Odesa, 65020, Ukraine

Kyiv National Economic University named after Vadym Hetman, 54/1 Peremogy Avenue, Kyiv, 03680, Ukraine

Keywords:

Education 4.0, Synergetics, Complex systems, Complex thinking, Chaos, Self-organization,

Interdisciplinarity.

Abstract:

The presented paper raises the question of how the principles of Education 4.0 and the theory of self-

organization (synergetics) can help in the reformation of the higher education system, and how interdisci-

plinary research can be useful for both teachers and students. In this paper, we give a brief review of different

studies devoted to Education 4.0 and synergetics concepts. Next, we demonstrate the most important char-

acteristics of complex systems and conceptually simplest methods for complex systems modelling. As part

of the complex systems modeling course, which will ﬁrst be presented to students of physics and mathemat-

ics, and then, possibly, to students of other specialties, we present signals of seismic activity, gravitational

waves, magnetic activity, and stress-strain signal for a typical metal in the process of destruction. Our study

demonstrates that complex systems theory and its toolkit can help to study phenomena of various nature and

indentify (forecast) their catastrophic states. This kind of analysis can serve as a good basis for the formation

of professional skills and universal competencies.

1 INTRODUCTION

In 2021, Syukuro Manabe, Klaus Hasselmann, and

Giorgio Parisi were awarded the Nobel Prize in

Physics “for groundbreaking contributions to our

understanding of complex physical systems” (Nobel

Foundation, 2021). That is a sign that the study of

complex systems is of paramount importance. Nev-

ertheless, we need to deal with the problems of their

implementation in the educational process.

The education system in the world today is in a

state of crisis. This is evidenced by the following

trends: a further increase in the number of illiterate

people in the world; the widespread decline in the

quality of education; the growing gap between edu-

cation and culture, education and science; alienation

of the student from the educational process.

https://orcid.org/0000-0002-2821-2895

https://orcid.org/0000-0002-0991-2343

https://orcid.org/0000-0002-4945-202X

This situation in the world at the present stage

makes the problem of ﬁnding a new paradigm of ed-

ucation urgent, since the possibility of sustainable

development of society, successful overcoming of

global problems, regional and national conﬂicts char-

acteristic of the present time of the development of

civilization is closely related to the achieved level of

education of all members of society (Karlov, 1998).

But the education system is always based on a certain

scientiﬁc understanding of the world and man, which

determines the goals and objectives of education, its

content, principles and methods.

Education 4.0 is such paradigm of education in

which complex thinking, reasoning, teaching meth-

ods, and techniques become central to support educa-

tional processes for the formation of citizens commit-

ted to society and its complexity (Ram

ırez-Montoya

et al., 2022). Modern generation of students meet

business tasks which nowadays demand a wide range

of knowledge, skills, and abilities: integrative, criti-

cal, systemic, scientiﬁc, innovative thinking; enabling

Bielinskyi, A., Kiv, A. and Soloviev, V.

Complex Systems and Complex Thinking Within the Framework of Education 4.0.

DOI: 10.5220/0012062900003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 199-219

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

199

analysis, synthesis, continues learning, problem solv-

ing. Without an extensive range of different ﬁelds of

science, it is problematic to be an active transformer

of the society. The complexity paradigm proposes

new point of view in which contradictory parts of a

system compose into interrelated. For soling com-

plex task, the encounter and the exchange between all

researchers and academicians in disjunctive domains

are necessary.

Figure 1 represents core components that enable

to design innovative pedagogical environments in

terms of Education 4.0 with correct technologies and

infrastructures which will carry out best practices.

Modern technological environment embraces ad-

vances of humanity that provide high capacities and

performance capabilities in many systems and plat-

forms. Such technologies provide high level of dig-

italization, virtualization, and dataﬁcation. Due to

corresponding spectrum of possibilities and student-

central environment, we are able to seek, prepare, and

graduate new highly competitive professionals capa-

ble to propose innovative solutions for current world.

Searching for real-world challenges and combining

educational experience with ICTs, students are able

to transfer from theory to practice very quickly.

Open education, innovations, science, and tech-

nologies are the cornerstones of Education 4.0. It

relies on personalized learning pathways, innovative

digital and management tools complemented with

such trending computer science topics as artiﬁcial

intelligence (AI), blockchain, robotics, virtual real-

ity, etc. Especially should be emphasized AI which

provides a framework for understanding complex

systems behavior: how multi-agent, interconnected,

and intelligent environments interact with each other,

mostly producing non-linear and non-predictable dy-

namics.

The heyday of education in the XVII-XVIII cen-

turies, which happened through the development and

spread of classical mechanics of the New Time, led to

the determination of the picture of the world, where

the studied elements are unchangeable, and the laws

of classical mechanics are universal and apply to all

types of motion of matter.

Such real-world systems as a pandemic, storm,

transport systems, the world-wide web, stock and

crypto indices are presented to be complex, irre-

versible, and sensitive to initial perturbations (Hip-

kins, 2021). Following deterministic paradigm, where

each phenomenon has a cause and at the same time

there is a cause of other phenomena, i.e., all the pro-

cesses taking place in the world are predetermined

and predictable, we would encounter that real-world

systems neither precisely random nor deterministic.

Complex systems tend to display ordered features and

unpredictable dynamics simultaneously (Ovens et al.,

2013).

Therefore, such ideological and methodological

principles as rationalism, determinism, mechanis-

mism and reductionism began to dominate in scien-

tiﬁc knowledge, which also had a decisive inﬂuence

on the education system: on the forms of knowledge

acquisition, presentation of material, organizational

principles of education.

The discovery by synergetics of the processes of

self-organization in inanimate nature clearly shows

that the transition from disorder to order, accompa-

nied by the emergence of self-organization and sta-

ble structures, the replacement of old structures with

new ones occurs according to speciﬁc internal laws

inherent in certain forms of the movement of matter.

Ultimately, it is the qualitative and quantitative cri-

teria of self-organization that characterize the level of

complexity and perfection of the corresponding forms

of movement (Haken, 1977, 1982). Based on these

ideas, it is possible to develop a classiﬁcation of types,

forms, properties of matter according to their degree

of complexity, perfection of organization, and thereby

the degree of development. In this regard, develop-

ment itself appears as a very complex, self-organizing

process of movement from simple to complex, from

less organized and perfect to more organized and per-

fect. In other words, development, in contrast to the

movement that characterizes any changes in general,

acts as a directed change associated with the emer-

gence of a new one.

The post-non-classical stage of the development

of science shows that rigid determinism and reduc-

tionism, which serve as the basis of the mechanistic

view of the world, cannot be considered as univer-

sal principles of scientiﬁc knowledge, since an ex-

tensive class of phenomena and processes does not

ﬁt into the framework of linear, equilibrium and re-

versible schemes. In the world around us, a very

real irreversibility plays an essential role, which is the

basis of the majority of self-organization processes.

Reversibility and rigid determinism in the world are

applicable only in simple limiting cases, and irre-

versibility and randomness should be considered not

as an exception, but as a general rule.

To integrate the synergetics approach into the ed-

ucational process, it is important to instill in students

ways of setting and solving problems of being and

developing complex systems in various spheres: eco-

nomic, social, natural, etc. It is equally important,

at the beginning of studying the methods of study-

ing complex systems, to instill in students at ﬁrst or

repeat with them the concepts of self-organization,

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

200

Figure 1: Core components for effective learning in Education 4.0 (Ram

ırez-Montoya et al., 2022).

chaos, destructive phenomena, to voice the difference

between complex and complicated systems, etc.

Complex systems are a ﬁeld of research that is

now acquiring the characteristic features of a well-

formed area of science with its own object, conceptual

apparatus, and methods of analysis (Thurner, 2017).

The concept of a complex system is gradually becom-

ing one of the fundamental concepts of modern sci-

ence, or, more broadly, it is increasingly appearing in

a general cultural context. The expansion of the scope

of application of this concept, as well as the iden-

tiﬁcation and awareness of an increasing number of

phenomena where it is applicable, causes difﬁculties

in its exact deﬁnition. Although the science of com-

plex systems covers a broad interdisciplinary ﬁeld of

research, the methods and concepts of physics (dy-

namical systems theory, quantum mechanics, statisti-

cal physics) are central to it.

So, the processes of self-organization in non-

equilibrium conditions correspond to the dialectical

interaction between chance and necessity, ﬂuctua-

tions and deterministic laws. Near bifurcations, the

main role is played by chaos, randomness, while de-

terministic connections dominate in the intervals be-

tween bifurcations. The ways of development of self-

organizing systems are not predetermined. Probabil-

ity appears not as a product of our ignorance, but as an

inevitable expression of chaos at the points of bifur-

cations. This means the end of the classical ideal of

omniscience and creates the need to revise the princi-

ple of mechanical rationalism as the dominant scien-

tiﬁc explanation of reality. The traditional education

system, based on the principles of classical science,

cannot effectively fulﬁll the role of a means of mas-

tering the world by a person.

Hence, there is a need to provide new principles

and ideas of the complex systems paradigm in the

sphere of Education 4.0.

2 ANALYSIS OF PREVIOUS

STUDIES

For building a new way of learning and education,

we must be aware that linear thinking and methods

are very dangerous in non-linear world (J

org et al.,

2007). Consequently, we should tend to a new way of

thinking beyond dualism, reductionism, and the idea

Complex Systems and Complex Thinking Within the Framework of Education 4.0

201

of controllable and perfectly predictable events.

Analysis of scientiﬁc sources and publications

shows that today there is an opinion that synerget-

ics could provide signiﬁcant assistance in the search

for a new paradigm of education. A synergistic

approach to understanding patterns operating in na-

ture is associated with the names of Haken (Haken,

1977, 1982, 1984, 2004; Haken and Schiepek, 2006),

Prigogine (Prigogine, 1989, 1980; Prigogine and

Stengers, 1984, 1997; Nicolis and Prigogine, 1989).

Some scientists believe that synergetics, as a theory of

self-organization of complex systems, describes the

general (common) that is in their development, edu-

cation is a complex system, and therefore synergetics,

which today is developed by various branches of sci-

entiﬁc knowledge, necessarily becomes its new phi-

losophy. However, despite the existence of a sufﬁ-

cient number of works devoted to the application of

synergetics in various spheres of human activity, the

methodological and practical context of synergetics in

the philosophy of education remains insufﬁciently de-

veloped. This is especially true for applying a syner-

gistic approach to understanding the higher education

system.

In contrast to the traditional interdisciplinary ap-

proach in education, the goal is not only to pro-

vide knowledge, but also to teach to hear and un-

derstand colleagues working in different specialties,

to develop skills of dialogue between specialists in

different branches of scientiﬁc knowledge. Thus,

complexity theory is transdisciplinary rather than in-

terdisciplinary: members of research team from dif-

ferent ﬁelds of science such as physics and economics

are able to work together if they are sufﬁciently in-

formed about one anothers’s perspectives and motives

(Benthem, 2002). The need for such a dialogue is be-

coming more and more palpable. Since the theoretical

physicist Haken (Haken, 2004) introduced this con-

cept into scientiﬁc use, the world has been accumu-

lating some experience in the use of synergetics and

in the study of social and educational systems.

Research conducted in schools and universities

shows that interactive chaotic environments are very

productive for developing creative thinking. The re-

sults of work in this area were presented by Davis-

Seaver et al. (Davis-Seaver et al., 2000), who an-

alyzed the learning process at three levels – from a

single point of balance, statement of fact, statement

of a single point of view to learning on the verge of

chaos, when there are many points of view, when rea-

soning develops in different directions, when students

listen to the opinions of others and on this basis de-

velop their own judgments. The role of the teacher is

not to spread knowledge and evaluate the correctness

of judgments, but to monitor the progress of reason-

ing and transfer the learning process from one level

to another. As a result, the understanding becomes

deeper, more versatile, and the incentives for learn-

ing are largely created by the energy of the group,

and not by the diligence of the teacher. In the con-

text of revealing a person’s creative abilities, a syn-

ergistic approach to education seeks not to eradicate

chaos, but to ﬁnd the relationship between order and

disorder that would be most fruitful (Kremen, 2013).

The above-mentioned concept of chaos from the

point of view of synergetics loses its negative con-

notation. As Prigogine and Stengers (Prigogine and

Stengers, 1997) notes, instability can be a condition

for stable and dynamic development. Only systems

that are far from equilibrium are able to organize and

evolve spontaneously. Thus, there is no development

without instability. And if the system is strict against

the implementation of new units, new units (‘innova-

tors’) die”. In higher education, self-organizing sys-

tems are the Student, Teacher, their interrelation, etc.

(Taranenko, 2014).

Jacobson and Wilensky (Jacobson and Wilensky,

2006; Wilensky and Jacobson, 2014) emphasize dif-

ferent research issues that need to be explored. They

present such principles in studying complex phenom-

ena as

• experiencing complex systems phenomena;

• making the complex systems conceptual frame-

work explicit (Council, 2000);

• encouraging collaboration, discussion, and reﬂec-

tion; the design of environments for learning

about complex systems needs to take advantage

of lessons learned from the extensive research

on pedagogy that foster collaboration, discussion,

and reﬂection (National Research Council, 2000);

• constructing theories, models, and experiments;

• learning trajectories for deep understandings and

explorations.

With a given appropriate conceptual and represen-

tational scaffolding in the learning environment, stu-

dents should be able to tap into their everyday expe-

riences and channel and enhance these experiences to

construct understandings of complex systems that are

cognitively robust. Nowadays, students should have

more possibilities to explore world through computa-

tional modeling which progressive scientists use al-

most everyday.

Jackson (Jackson, 1995) and other, such as Pagels

(Pagels, 1988), have observed how the use of com-

putational tools in science allows dramatically en-

hanced capabilities to investigate complex and dy-

namical systems that otherwise could not be systemat-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

202

ically investigated by scientists. These computational

modeling approaches include cellular automata, net-

work and agent-based modeling, neural networks, ge-

netic algorithms, Monte Carlo simulations, and so

on that are generally used in conjunction with scien-

tiﬁc visualization techniques. Examples of complex

systems that have been investigated with advanced

computational modeling techniques include climate

change (West and Dowlatabadi, 1998), urban trans-

portation models (Balmer et al., 2004; Helbing and

Nagel, 2004; Noth et al., 2003), and economics (An-

derson et al., 1988; Arthur et al., 1997; Axelrod, 1997;

Epstein and Axtell, 1996b). New communities of sci-

entiﬁc practice have also emerged in which computa-

tional modeling techniques, in particular agent-based

models and genetic algorithms, are being used to cre-

ate synthetic worlds such as artiﬁcial life (Langton,

1989, 1995) and societies (Epstein and Axtell, 1996a)

that allow tremendous ﬂexibility to explore theoreti-

cal and research questions in the physical, biological,

and social sciences that would be difﬁcult or impossi-

ble in “real” or nonsynthetic settings.

org et al. (J

org et al., 2007) addressed their study

to the theory of complexity, arguing that the present

paradigms in the ﬁeld of education neglect the inher-

ent complexity of educational reality and therefore are

not able to give an adequate understanding of real-

ity. They discussed the importance of studying com-

plex systems paradigm and its integration into educa-

tional process. In their opinion, complexity paradigm

should help to uncover some of the myths we live by,

but it is not necessary an unlimited source of truth. It

is rather a better alternative for our rapidly evolving

world in which we already encounter ‘deprivation of

our culture’ (Midgley, 2001) and ‘perversion in sys-

tem of education’ (Baistrocchi, 2018)

Costan et al. (Costan et al., 2021) investigated

the existing barriers to Education 4.0 implementation.

They collected a systematic review of the 30 jour-

nal articles on Engineering, Social Sciences, Com-

puter Science, Business, Management, and Account-

ing generated from the initial search on Scopus, which

were in turn related to Education 4.0. Their analysis

provided 12 existing barriers for Education 4.0 im-

plementation: cybersecurity threat, costly, skills gap

of human capital, apprehensive stakeholders, lack of

training resources, lack of collaboration, knowledge

gap for the customization of curriculum design, insuf-

ﬁcient available technologies, health issues, time con-

straint for material preparation, complexity of learn-

ing platforms, and insufﬁcient foundation of basic ed-

ucation. Furthermore, a theoretical predictive model

was constructed to present the causal relationships in

modeling the problems associated with implementing

Education 4.0.

Sigahi and Sznelwar (Sigahi and Sznelwar, 2022)

studied following questions: (1) how complexity

thinking could be applied to engineering education;

(2) how that could contribute to current engineer-

ing challenges; (3) what were different complex-

ity approaches in engineering and how to integrate

them. They conducted a review from ﬁfty eight jour-

nal articles and ﬁve book chapters. They discussed:

engineering axiology; epistemological and ontologi-

cal perspectives; complex thinking and competences;

systematic transformations of engineering education,

etc. Were identiﬁed main gaps of such education and

discussed different thoughts on topic complexity.

Complexity captures even physical education

(Bielinskyi et al., 2022). Swedish National Agency

for Education presented new curriculum which in-

cluded such term as complex movement. Researchers

(Janemalm et al., 2019) provided insights into the

meanings of complex movements in the context of

physical education in Sweden. Using a discourse an-

alytic methodology, six policy texts were examined.

The study suggests that there is needed greater con-

sensus as complex movement can have a wide range

of meaning, have a context-depended meaning, and

for different audiences will be understood in individ-

ual ways.

New paradigm of thinking and teaching concerns

even sustainable development. It aims to equip learn-

ers with necessary knowledge about complex sus-

tainability problems and develop in students creative

thinking to acquire innovative sustainable solutions.

Green et al. (Green et al., 2022) formed a random-

ized controlled trial to understand whether an inno-

vative sustainability learning tools help to increase

the understanding of a speciﬁc sustainability prob-

lem. Their learning toolkit incorporates two fac-

tors – system thinking and system dynamic simula-

tion. They also tested whether those factors help to

transfer knowledge to a second problem with a sim-

ilar system structure. They used different statistical

techniques to analyse the effect of the factors on sus-

tainability understanding. Their research presented

that the effectiveness of education for sustainable de-

velopment increased signiﬁcantly. Participants gave

qualitative feedback on usefulness of systems think-

ing and simulation.

Network science (graph theory) is the key data

analysis instrument for solving problems through

their graph representations. For Education 4.0 it is

one of the main ﬁelds of science which must be in-

cluded into learning process. Many real-world com-

plex systems exhibit common organizing principles,

non-trivial patterns that were derived with graph the-

Complex Systems and Complex Thinking Within the Framework of Education 4.0

203

ory. Therefore, network science can be considered as

highly interdisciplinary research ﬁeld (B

orner et al.,

2008). Weber et al. (Weber et al., 2021) addressed

their study to sustainability problems through the tool

of network science and presented schematically how

complex, real-world sustainability problems can be

considered through the prism of graph theory (ﬁg-

ure 2).

As the environmental, economic, and political

problems of humanity have become global, complex

and nonlinear, traditional ideas about individual re-

sponsibility are becoming questionable. We need to

study and teach new models of collective behavior

that take into account the different degrees of our in-

dividual abilities and understanding of what is hap-

pening.

We believe that the study of the apparatus of

physics, graph theory, and computer science is now

of paramount importance for the further development

of both our society and the entire universe.

In further we need to understand how to grow

an interest of students in constructing and revising

computational models with multi-agent or qualitative

modeling software, and how model building activities

may enhance student conduct of real world experi-

ments related to the phenomena under consideration

(Abrahamson and Wilensky, 2005a,b; Jackson et al.,

2000).

3 THE MOST IMPORTANT

PROPERTIES OF COMPLEX

SYSTEMS TO BE STUDIED

Based on the previously described characteristics and

the direction in which we should move, it becomes

clear that synergetics (the theory of complex systems)

is the foundation of almost any system. Including

pedagogical. Although the initial direction of re-

search within this paradigm was physical systems, the

latest objects of research on various manifestations of

complexity also appear in the context of business or-

ganization and economics. For example, Wheatley

(Wheatley, 2006) suggests that we view organizations

as being more like living organisms than machines.

As such, we need to modify traditional views on con-

trolling organizations. Wheatley (Wheatley, 2006) ar-

gues that organizations are dynamic, nonlinear net-

works of relationships and cannot be separated into

parts while maintaining their essential identity.

Complexity thinkers have been seeking for com-

mon characteristics in a tremendous range of sim-

ple and complex systems: dependence on initial per-

turbations, long-term correlations, multi-layered and

multi-scale, mutual and reciprocal, etc.

In general, they are

• dynamic;

• non-equilibrium and have the potential to change

suddenly and may take one path out of an inﬁnite

number of others (bifurcate);

• open systems, that is interchange energy (and in-

formation) with their surroundings;

• depended. What happens next depends on what

happened previously;

• systems where the whole is more than the sum of

its parts;

• causal and yet indeterminate;

• irreversible, since the interaction of parts together

is transforming;

• multi-agent. They composed of a diversity of

agents that interact with each other, mutually af-

fect each other, and in so doing generate novel,

emergent behavior for the system as a whole. The

system is constantly adapting to the conditions

around it and over time it evolves;

• co-evolving and move spontaneously towards the

edge of chaos.

3.1 Time Series Data

In order to maintain students’ interest in studying

complex systems and their corresponding data anal-

ysis tools, programming languages, etc. (Shumway

and Stoffer, 2016; Fulcher et al., 2013), it is impor-

tant to select truly interesting and complex systems

(series). It is equally important that the studied sys-

tems are within the framework of the specialty that

students are guided by. However, since we strive for

an interdisciplinary approach, the study, for example,

by biologists of the corresponding nonlinear methods

on the example of the same socio-economic series or

physical ones can also be beneﬁcial for general devel-

opment.

Complexity theory is subdivided into hard and soft

complexity. Hard complexity theory stands for ana-

lytical analysis that concern with the nature of reality,

while soft complexity aims to describe social and liv-

ing systems. Davis and Sumara (Davis and Sumara,

2006) proposes such term as “complexity thinking”

which lies somewhere in between hard and soft skills.

We support such idea and would like to promote it

among ordinary citizens who are not specialists and,

particularly, among universities and their student. Fo-

cusing on interdisciplinarity, both hard and soft skills,

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

204

Figure 2: Sustainability problems that are solved through network science.

teachers and students will be more creative and pro-

ductive in their further research. Knowing about in-

terconnections across different disciplines, there are

much more possibilities for collaborative research be-

tween different faculties and there is larger probabil-

ity that people will be able to ﬁnd common topics for

communication and will be engaged to cooperate.

The goal of this work is to present the basic char-

acteristics of complex systems, which should be intro-

duced to students during the course of studying com-

plex systems, and the basic sets of methods that allow

analyzing the varying randomness (complexity) of the

system during the development of the studied signals.

In this paper, we present some of the most fun-

damental, applied, robust, and powerful methods on

the example of four physical signals: seismic (SEI),

gravitational wave (GW), the distribution storm time

(Dst) index, and stress-strain (σ(ε)) signal for a typi-

cal metal in the process of destruction.

SEI dataset constructed by Bladford (Bladford,

1993). Each event has 2048 points ﬁxed at a seismic

recording station in Scandinavia.

We used GW data GW150914 from Events of

LIGO Open Science Center and select strain data (H1

and L1) after noise subtraction (The LIGO Scien-

tiﬁc Collaboration and the Virgo Collaboration, 2016)

(https://www.ligo.org/detections/GW150914.php).

The Dst index is an index of magnetic activity

derived from a network of nearequatorial geomag-

netic observatories that measures the intensity of the

globally symmetrical equatorial electrojet (“ring cur-

rent”). Dst is maintained at National Centers for Envi-

ronmental Information (National Centers for environ-

mental information, 2021) from 1957 to the present.

Dst equivalent equatorial magnetic disturbance in-

dices are derived from hourly scalings of low-latitude

horizontal magnetic variation. They show the effect

of the globally symmetrical westward ﬂowing high al-

titude equatorial ring current, which causes the “main

phase” depression worldwide in the H-component

ﬁeld during large magnetic storms. In this paper, the

time series of hourly values of the storm on March

13, 1989 is investigated. It is the strongest storm in

the space age in several ways; the power system of

the province of Quebec was out of order. The peak of

the storm falls in the middle of the time series (point

1000).

The stress-strain signal σ(ε) contains integrated

information about the structural transformations of

the spectrum of defects in the material under study

(point, dislocations, pores, cracks) depending on the

applied stress.

In order to study changes of complexity dynam-

ically, i.e., to get not only one value that will char-

acterize the whole system, but an array of values,

where each value will reﬂect the complexity of a

signal in a speciﬁc period, we use sliding window

approach (Soloviev and Belinskyi, 2018a; Bielinskyi

et al., 2021b,c).

In ﬁgures 3a and 3b is presented the dynamics

of all physical signals that could be studied during

physics classes. However, students of other faculties

Complex Systems and Complex Thinking Within the Framework of Education 4.0

205

(a) (b)

Figure 3: The signals of SEI, GW, and Dst in normalized scale (a). Stress-strain curve in absolute scale (b).

can also be interested.

Figure 3b shows a typical dependence σ(ε) with 4

highlighted characteristic areas. In the ﬁrst of them,

elastic (reversible), point defects dominate. In the

second region of plastic ﬂow and hardening, disloca-

tions multiply and move. It is the most informative.

The third region is characterized by a quasi-stationary

process of accumulation of pores and microcracks, as

well as the nucleation of a neck. Finally, the last re-

gion is the phase of the formation of a global crack,

ending with the destruction (rupture) of the material.

3.2 Fat-Tailed Distribution

When studying complex systems, we inevitably en-

counter power distributions characterized by thick

tails. A classic example is the power-law of divid-

ing words by their frequency of use in a text, known

as Zipf’s law (Zipf, 1950).

In economics, this is the law of wealth distribu-

tion among individuals (Pareto, 1896); in demogra-

phy, the distribution of cities by their size (Auer-

bach, 1913); in biology, the distribution of the size

of forest patches (Saravia et al., 2018); in scientom-

etry, the distribution of citations (Brzezi

nski, 2014).

In general, a wide class of phenomena is described

in the framework of distributions with a degree de-

pendence, but the researcher (student) will have to

ﬁnd out the nature of such a dependence, which

can be caused by many factors: critical phenom-

ena, processes with preference, self-organized criti-

cality, multiplicative processes with connections, op-

timization and path-dependent nonergodic processes,

the phase space of which decreases with evolution

(Domp, 1996; Sornette, 2006; Bak et al., 1987; Man-

delbrot, 1953; Corominas-Murtra et al., 2015).

First of all, it will be important to build an em-

pirical distribution for our data (ﬁgure 4). Having vi-

sualized the series we study in this paper, we can al-

ready be convinced of the non-Gaussian dynamics of

the presented systems.

In the course of our research, we have determined

that the L

evy α-stable distribution most successfully

covers the key statistical characteristics of both the

economic (Bielinskyi et al., 2019, 2021a,c) and those

systems that are presented in this paper. Figures 5a

to 5d show the window dynamics of the α index de-

rived from the L

evy distribution that characterizes the

“heaviness” of tails.

From the ﬁgures above we can observe that the

dynamics of all signals is beyond normal. Index of

stability α decreases during regions of instability, in-

dicating an increase in the tails of the distribution.

3.3 Multifractality

When studying various types of systems, we often en-

counter both fractal (self-similar) structures and sets

of different fractal dimensions (Stanley and Meakin,

1988). In such problems, it is necessary to take into

account the entire range of critical indicators that

characterize different moments in the distribution of

observed quantities. Such properties usually relate

to the term “multifractality” (Sreenivasan and Men-

eveau, 1986).

There are several different algorithms that allow

the obtention of multifractal spectra from time series.

The most famous is the MF-DFA (Kantelhardt et al.,

2002; de Freitas et al., 2019; Eghdami et al., 2018).

Based on the MF-DFA procedure, we select the

maximum value of such a quantitative characteristic

of multifractality as the singularity strength (Ashke-

nazy et al., 2003), although in the corresponding sec-

tion of fractal (multifractal) analysis, it would be nec-

essary to characterize and demonstrate the dynamics

of all multifractality indicators. The following ﬁgure

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

206

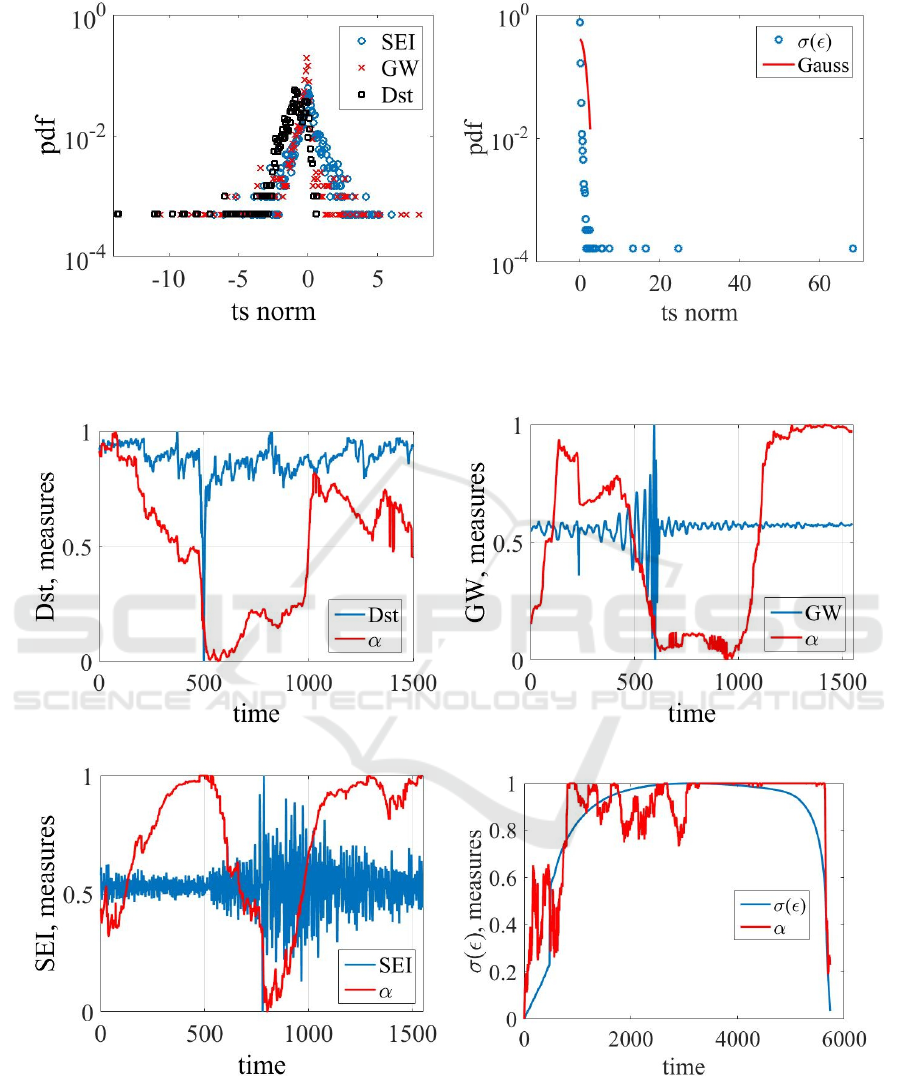
(a) (b)

Figure 4: Probability density functions (PDF’s) of Dst, Sei, and GW (normalized time series – ts norm) (a). PDF of σ(ε)

signal comparing to along with the Gaussian curve (b).

(a) (b)

Figure 5: The dynamics of four signals and their α index of stability.

shows the window dynamics of the maximum value

of the singularity strength.

Figure 6 demonstrates the increase of multifractal-

ity during period of collapse. For Dst, SEI, and σ(ε)

critical periods become more multifractal, whereas

for GW we have the opposite relation.

Complex Systems and Complex Thinking Within the Framework of Education 4.0

207

(a)

(b)

(c)

(d)

Figure 6: The dynamics of four signals and their α

max

index of multifractality.

3.4 Network Analysis

Equally important is the network analysis of complex

systems. Today, networks play a central role in mod-

eling complex systems, as they offer a way to describe

different types of relationships between agents that

act as endpoints in the network. Complex networks

can characterize information, social, economic, bio-

logical, neural, and other systems (Newman, 2003;

Boccaletti et al., 2014, 2006; Baiesi and Paczuski,

2004). For example, a society can be represented as

a network, where each individual (university, wealth,

city) can be represented as nodes of a graph, and the

connection between them through edges. For cities,

edges can represent a road, where the possibilities of

movement can vary, and therefore a different weight

can be determined for each edge.

In general, the computer network model is a ran-

dom graph, the law of mutual arrangement of edges

and vertices for which is deﬁned by the probability

distribution.

The simplest of networked objects, so-called

Erd

os-R

enyi, or random graphs (Erd

os and R

enyi,

1959). Such graphs can be characterized within

the framework of the Poisson distribution, but most

complex systems, as already noted, are characterized

within the framework of distributions with heavy tails.

One of the most interesting characteristics of net-

works is the vertex degree. The vertex degree distri-

bution for many real-world networks shows a power-

law dependence. Such networks are called scale-

independent. Scale-free networks are often charac-

terized by very short average distances between ran-

domly chosen pairs of nodes that may have a strong

impact on the whole dynamics.

In addition to the topology of graphs, you can also

study their quantitative characteristics. In our case,

using the window procedure, we get a variable graph

representation of our signal over time. For the pre-

sented work, we calculated the maximum vertex de-

gree of the graph (D

max

), since this measure is one of

the conceptually simplest measures, although many

other measures can be represented. It is worth not-

ing that there are also various algorithms for con-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

208

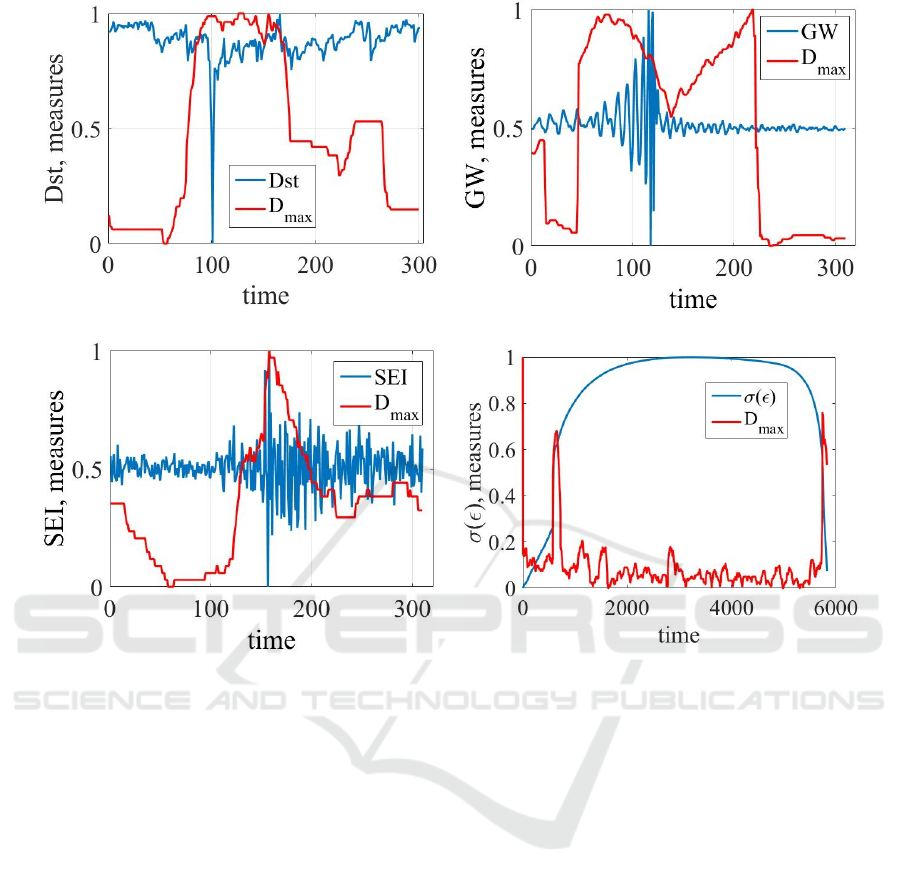
(a)

(b)

(c)

(d)

Figure 7: The dynamics of four signals and their D

max

in accordance with the visibility graph.

verting a time series to a graph. We would like

to emphasize the visibility graph algorithms (Bielin-

skyi et al., 2021c,b; Juan and Guzm

an-Vargas, 2013;

Kundu et al., 2021; Soloviev and Belinskiy, 2018;

Bielinskyi and Soloviev, 2018) (ﬁgure 7) and one

based on recurrence analysis (Donner et al., 2011)

(ﬁgure 8).

The index of maximum degree D

max

start to in-

crease during abnormal phenomena. We can make a

conclusion that crisis period is presented to be more

concentrated in terms of graph comparing to normal

dynamics.

3.5 Recurrence Analysis

Processes in nature are characterized by pronounced

recurrent behavior, such as periodicity or irregular

cyclicity.

Moreover, the recurrence (repeatability) of states

in the sense of passing a further trajectory quite close

to the previous one is a fundamental property of dissi-

pative dynamical systems. This property was noted in

the 1880s by the French mathematician Poincar

e and

subsequently formulated in the form of the “recur-

rence theorem”, published in 1890 (Poincar

e, 1890).

The essence of this fundamental property is that,

despite the fact that even the smallest perturbation in

a complex dynamical system can lead the system to

an exponential deviation from its state, after a while

the system tends to return to a state that is somewhat

close to the previous one, and goes through similar

stages of evolution.

In 1987, Eckmann et al. (Eckmann et al., 1987)

proposed a method for mapping the recurrence of

phase space trajectories to N ×N matrix. The appear-

ance of a recurrence diagram allows us to judge the

nature of processes occurring in the system, the pres-

ence and inﬂuence of noise, states of repetition and

fading (laminarity), and the implementation of sud-

den changes (extreme events) during the evolution of

the system. If you look at recurrent diagrams in more

detail, you can ﬁnd small-scale structures (textures)

consisting of simple points, diagonal, horizontal, and

vertical lines, which in turn correspond to chaotic,

repetitive, or laminar states.

Using combinations of these states, Zbilut and

Complex Systems and Complex Thinking Within the Framework of Education 4.0

209

(a) (b)

(c)

(d)

Figure 8: The dynamics of four signals and their D

max

in accordance with the algorithm based on recurrence analysis.

Webber (Zbilut and Webber, 1992; Webber and Zbi-

lut, 1994) developed a tool for calculating a series of

measures based on the distribution of recurrent points

on a recurrence matrix. Later, the toolkit for quantita-

tive recurrent analysis was supplemented by Marwan

and Kurths (Marwan and Kurths, 2002). The tools of

quantitative recurrent analysis include the recurrence

rate, determined by the ratio of recurrent points to the

total number of points on the recurrence matrix un-

der study. In addition to the recurrence measure, in

the course of analyzing complex systems, it would

be possible to present such measures as determinism,

divergence, entropy, trend, and so on (Soloviev and

Belinskiy, 2018; Soloviev and Belinskyi, 2018a; Der-

bentsev et al., 2020; Fan et al., 2018; Lin et al., 2015;

Banerjee et al., 2021).

In this paper, we will focus on the recurrence rate

and present it for the already speciﬁed series (ﬁg-

ure 9).

Figure 9 demonstrates RR measure that indicates

the probability of ﬁnding recurrent (close to each

other) points. Our empirical results show that due

to abrupt changes that correspond to crisis state, the

probability of ﬁnding recurrent points become lower.

This indicator starts to decrease even before crash,

which makes it as indicator-precursor of such events.

3.6 Entropy and Non-Extensive

Statistics

The Boltzmann-Gibbs statistical entropy and the clas-

sical statistical mechanics associated with it are ex-

tremely useful tools for studying a wide range of sim-

ple systems that are characterized by a small range of

space-time correlations (short memory), the additiv-

ity of noise, the presence of intense chaos, the ergod-

icity of dynamic processes, the Euclidean geometry

of phase space, the locality of interaction between el-

ements, the Gaussian probability distributions, etc.

The Boltzmann-Gibbs statistical entropy is a fun-

damental concept of the school section and the univer-

sity course of thermodynamics and statistical physics.

In statistical mechanics, entropy denotes the num-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

210

(a)

(b)

(c)

(d)

(e)

(f)

Figure 9: Phase space portrait and recurrence plot of GW (a-b). The dynamics of RR for GW (b), Dst (c), SEI (d), and σ(ε)

(f).

Complex Systems and Complex Thinking Within the Framework of Education 4.0

211

(a)

(b)

Figure 10: Autocorrelation of SEI, GW and Dst (a), and sliding window autocorrelation for σ(ε) (b).

(a)

(b)

(c)

(d)

Figure 11: The pdf’s of the four signals, Gaussian, and q-Gaussian functions (a-d).

ber of possible conﬁgurations of a thermodynamic

system. The notion of entropy can be associated with

the uncertainty in the system (Clausius, 1870; Boltz-

mann, 1970). In 1948, Shannon transformed classi-

cal statistical entropy to information entropy (Shan-

non, 1948). Since then, a number of other types of

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

212

information entropy have been developed (Karakatsa-

nis et al., 2013; Javaherian and Mollaei, 2021; Litvi-

nenko, 2019; Posadas et al., 2021).

In order to study many real-world systems, it is

necessary to go beyond the standard course of ther-

modynamics, statistical physics, and classical Shan-

non entropy. A whole range of natural, artiﬁcial and

social systems, which, unlike those mentioned above,

are characterized by a long range of spatio-temporal

correlations and non-Gaussian processes.

Since the non-Gaussian and multifractal behav-

ior of the studied systems was presented previously,

we will depict the autocorrelation function in the ﬁg-

ure 10a, as it should demonstrate an indicator decline.

This fact will indicate the dependence of the follow-

ing values on the previous ones.

It is also worth mentioning that such systems are

characterized by multiplicative noise, the presence

of weak chaos (vanishing maximum Lyapunov expo-

nent), non-ergodicity of dynamic processes, hierarchy

(usually multifractality) of the geometry of the phase

space, the presence of asymptotically power-law sta-

tistical distributions. A fairly wide class of these com-

plex systems (although not all) it is adequately de-

scribed by non-additive statistics based on the Tsallis

parametric entropy.

Figures 11a to 11c show the q-Gaussian distribu-

tion from the Tsallis statistics for the considered se-

ries in comparison with the classical Gaussian one.

Autocorrelation plot (ﬁgure 10a) represents that

the highest long-range dependence has the signal of

magnetic activity, and autocorrelation with the slid-

ing window approach for σ(ε) signal represents how

increases dependence between defects during transi-

tion from elastic region to the region of plastic ﬂow

and hardening.

Figures 11a to 11d present that signals which dy-

namics exceeds ±10σ are described more appropri-

ately in terms of q-Gaussian distribution. Parameter q

represented the degree of non-extensivity in each sys-

tem. With the higher q, we expect more multifractal,

chaotic, and dependent dynamics.

3.7 Reversibility and Irreversibility

The last characteristic that we would like to mention

is time-reversibility. Temporary irreversibility is a key

property of non-equilibrium systems.

Again, such systems are characterized by the pres-

ence of memory, while reversibility increases with

more noisy and unpredictable signals. Thus, by cal-

culating the irreversibility, we determine the degree of

nonlinearity and predictability. It is important to note

that the signiﬁcant time reversibility excludes linear

Gaussian processes as a model of generating dynam-

ics. Within the framework of the systems we are con-

sidering, we need to think about methods of nonlinear

dynamics and non-Gaussian ones (Lawrance, 1991;

Stone et al., 1996).

Over the past decade, various methods have been

proposed for calculating the degree of irreversibility

in systems (Daw et al., 2000; Kennel, 2004; Lacasa

et al., 2012; Donges et al., 2013; Flanagan and La-

casa, 2016; Costa et al., 2005; Zanin et al., 2018; Jiang

et al., 2016) and we have presented how to use some

of them for crises identiﬁcation (Bielinskyi et al.,

2021b). For pedagogical purposes, along with the

mentioned concept of multifractality and entropy, we

would like to present irreversibility based on the mul-

tifractal approach (Jiang et al., 2016) and permutation

patterns (Zanin et al., 2018). The last mentioned ap-

proach could be taught within the section of entropy

approaches if we were teaching students. However,

the calculation of irreversibility based on graph the-

ory is also possible (Lacasa et al., 2012; Donges et al.,

2013; Flanagan and Lacasa, 2016).

Figures 12a to 12d show the mentioned measures

of irreversibility for the studied signals.

In ﬁgure 12 we can see that abnormal periods are

followed with the increase of irreversibility in sig-

nal. In our opinion, permutation-based irreversibil-

ity is most stable comparing to the second one. Nev-

ertheless, additional improvements of algorithm for

their calculations can be made, and indicators of irre-

versibility based on graph theory can be studied.

4 CONCLUSION

Nowadays real-world challenges and mass integration

of information and communication technologies in

every sphere of our life demand an evolution of a ped-

agogical sector. Consequently, increasing complex-

ity of all social structures require multidisciplinary

projects, which can provide valuable experience and

competencies not only for colleagues from seemingly

independent disciplines, but also for students from the

same ﬁelds.

The analysis of the adaptive nature of many com-

plex systems led to the creation of methods and

the development of concepts that were successfully

applied to describe formally similar phenomena in

chemical, biological, social and other systems of

agents of non-physical nature. It is sometimes argued

that if physics is the science of the four fundamental

forces that matter interacts with.

It is still relevant to create appropriate open inno-

vation laboratories (Cortes et al., 2020) in which will

Complex Systems and Complex Thinking Within the Framework of Education 4.0

213

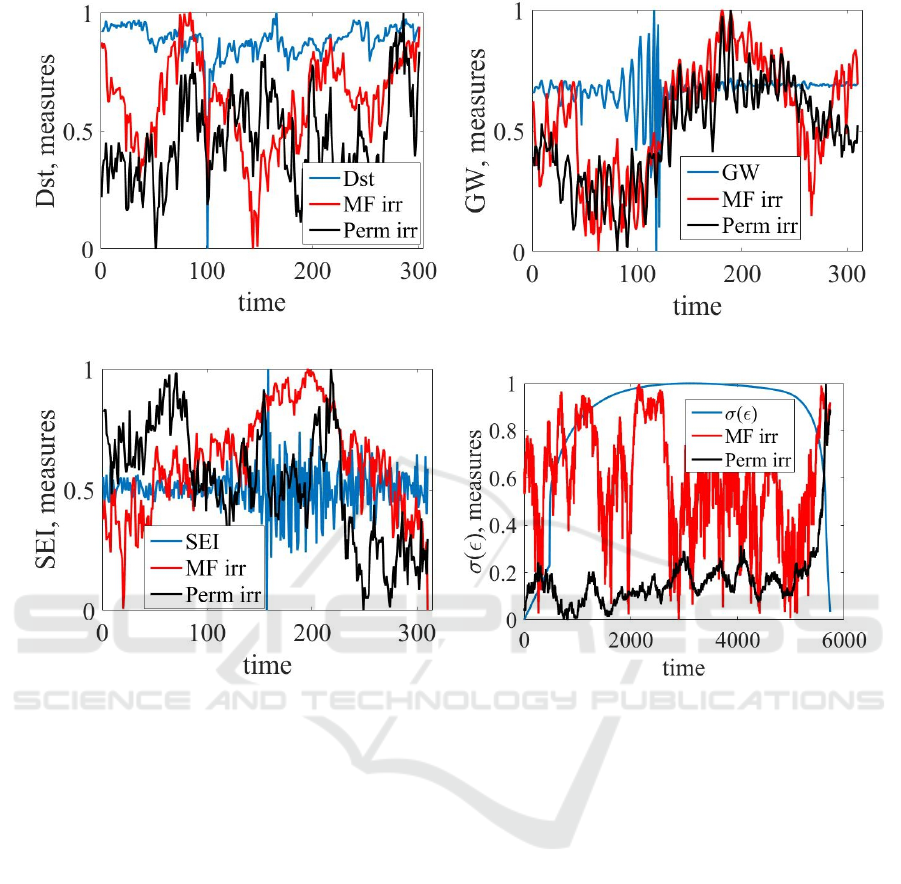
(a)

(b)

(c)

(d)

Figure 12: The dynamics of irreversibility measures along with the studied signals.

be possible adaptation of various solutions from the

ﬁelds of physics, higher mathematics, and computer

science to social sciences.

In this paper, we have presented some of the

most signiﬁcant approaches on the example of SEI,

GW, Dst, and σ(ε). Empirical results emphasize that

we can not only study critical processes (as in the

ﬁrst three cases), but also physical objects in which

these (critical) processes alternate with (quasi)-linear

and even catastrophic (destruction). Obviously, to-

day’s transformations towards Industry 4.0 gave us a

wide range of different indicators and signals to study

(Chen et al., 2019; Liu et al., 2019), and the task is

to get students interested in learning the appropriate

complexity theory tools and developing their com-

plexity thinking.

The theory of complex systems is obviously not

limited to the methods presented in this paper. Fur-

ther, we would like to supplement the presented ma-

terial with entropy (Soloviev and Belinskyi, 2018b;

Soloviev et al., 2019, 2020b), chaotic algorithms

(Soloviev et al., 2020a), and, for example, the tools of

random matrix theory (Soloviev and Belinskiy, 2019;

Bielinskyi et al., 2021c).

REFERENCES

Abrahamson, D. and Wilensky, U. (2005a). Collabora-

tion and equity in classroom activities using Statistics

As Multi-Participant Learning-Environment Resource

(S.A.M.P.L.E.R.). In Stroup, W., Wilensky, U., and

Lee, C. D., editors, Patterns in group learning with

next-generation network technology.

Abrahamson, D. and Wilensky, U. (2005b). The stratiﬁed

learning zone: Examining collaborative-learning de-

rooms. In White, D. Y. and Gutstein, E. H., editors,

Equity and diversity studies in mathematics learn-

ing and instruction. Conference: annual meeting of

the American Educational Research Associationan-

nual meeting of the American Educational Research

Association.

Anderson, P. W., Arrow, K. J., and Pines, D., editors

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

214

(1988). The Economy As An Evolving Complex Sys-

tem. Addison-Wesley, 1 edition.

Arthur, W. B., Durlauf, S. N., and Lane, D. A., editors

(1997). The Economy As An Evolving Complex Sys-

tem II. Addison-Wesley, 1 edition.

Ashkenazy, Y., Baker, D. R., Gildor, H., and Havlin,

S. (2003). Nonlinearity and multifractality of cli-

mate change in the past 420,000 years. Geophysical

Research Letters, 30(22):4. https://doi.org/10.1029/

2003GL018099.

Auerbach, F. (1913). Das gesetz der

bev

olkerungskonzentration, Petermanns. Ge-

ographische Mitteilungen, 59:74–76.

Axelrod, R. (1997). The Complexity of Cooperation:

Agent-Based Models of Competition and Collabora-

tion. Princeton Studies in Complexity. Princeton Uni-

versity Press.

Baiesi, M. and Paczuski, M. (2004). Scale-free networks

of earthquakes and aftershocks. Physical Review E,

69(6). https://doi.org/10.1103/physreve.69.066106.

Baistrocchi, S. (2018). Edgar Morin: Seven complex

lessons in education for the future. Early Years Educa-

tor, 20(6):38–44. https://doi.org/10.12968/eyed.2018.

20.6.38.

Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-

organized criticality: An explanation of the 1/f noise.

Phys. Rev. Lett., 59:381–384. https://doi.org/10.1103/

PhysRevLett.59.381.

Balmer, M., Nagel, K., and Raney, B. (2004). Large-

Scale Multi-Agent Simulations for Transportation

Applications. Journal of Intelligent Transporta-

tion Systems, 8(4):205–221. https://doi.org/10.1080/

15472450490523892.

Banerjee, A., Goswami, B., Hirata, Y., Eroglu, D., Merz, B.,

Kurths, J., and Marwan, N. (2021). Recurrence analy-

sis of extreme event-like data. Nonlinear Processes in

Geophysics, 28(2):213–229. https://npg.copernicus.

org/articles/28/213/2021/.

Benthem, J. (2002). Science and Society in Flux. In Tin-

demans, P. A. J., Verrijn-Stuart, A. A., and Visser, R.

P. W., editors, The Future of the Sciences and Human-

ities: Four Analytical Essays and a Critical Debate

on the Future of Scholastic Endeavor, pages 63–90.

Amsterdam University Press. https://doi.org/10.1515/

9789048503667-005.

Bielinskyi, A., Khvostina, I., Mamanazarov, A., Matviy-

chuk, A., Semerikov, S., Serdyuk, O., Solovieva,

V., and Soloviev, V. N. (2021a). Predictors of oil

shocks. Econophysical approach in environmental sci-

ence. IOP Conference Series: Earth and Environ-

mental Science, 628:012019. https://doi.org/10.1088/

1755-1315/628/1/012019.

Bielinskyi, A., Soloviev, V. N., Semerikov, S., and

Solovieva, V. (2019). Detecting Stock Crashes Using

Levy Distribution. In Kiv, A., Semerikov, S., Soloviev,

V. N., Kibalnyk, L., Danylchuk, H., and Matviy-

chuk, A., editors, Proceedings of the Selected Pa-

pers of the 8th International Conference on Monitor-

ing, Modeling & Management of Emergent Economy,

M3E2-EEMLPEED 2019, Odessa, Ukraine, May 22-

24, 2019, volume 2422 of CEUR Workshop Proceed-

ings, pages 420–433. CEUR-WS.org. https://ceur-ws.

org/Vol-2422/paper34.pdf.

Bielinskyi, A. O., Hushko, S. V., Matviychuk, A. V.,

Serdyuk, O. A., Semerikov, S. O., and Soloviev, V. N.

(2021b). Irreversibility of ﬁnancial time series: a case

of crisis. In Kiv, A. E., Soloviev, V. N., and Se-

merikov, S. O., editors, Proceedings of the Selected

and Revised Papers of 9th International Conference

on Monitoring, Modeling & Management of Emergent

Economy (M3E2-MLPEED 2021), Odessa, Ukraine,

May 26-28, 2021, volume 3048 of CEUR Workshop

Proceedings, pages 134–150. CEUR-WS.org. http:

//ceur-ws.org/Vol-3048/paper04.pdf.

Bielinskyi, A. O., Kiv, A. E., Prikhozha, Y. O., Slusarenko,

M. A., and Soloviev, V. N. (2022). Complex systems

and physics education. CTE Workshop Proceedings,

9:56–80.

Bielinskyi, A. O., Serdyuk, O. A., Semerikov, S. O., and

Soloviev, V. N. (2021c). Econophysics of cryptocur-

rency crashes: a systematic review. In Kiv, A. E.,

Soloviev, V. N., and Semerikov, S. O., editors, Pro-

ceedings of the Selected and Revised Papers of 9th

International Conference on Monitoring, Modeling &

Management of Emergent Economy (M3E2-MLPEED

2021), Odessa, Ukraine, May 26-28, 2021, volume

3048 of CEUR Workshop Proceedings, pages 31–133.

CEUR-WS.org. http://ceur-ws.org/Vol-3048/paper03.

pdf.

Bielinskyi, A. O. and Soloviev, V. N. (2018). Complex

network precursors of crashes and critical events in

the cryptocurrency market. CEUR Workshop Pro-

ceedings, 2292:37–45. http://ceur-ws.org/Vol-2292/

paper02.pdf.

Bladford, R. R. (1993). Discrimination of earthquakes

and explosions. Report AFTAC-TR-93-044 HQ,

Air Force Technical Applications Center, Patrick Air

Force Base FL 32925-6001. https://apps.dtic.mil/sti/

pdfs/ADA267638.pdf.

Boccaletti, S., Bianconi, G., Criado, R., del Genio, C. I.,

omez-Garde

nes, J., Romance, M., Sendi

na-Nadal,

I., Wang, Z., and Zanin, M. (2014). The struc-

ture and dynamics of multilayer networks. Physics

Reports, 544(1):1–122. https://doi.org/10.1016/j.

physrep.2014.07.001.

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and

Hwang, D.-U. (2006). Complex networks: Struc-

ture and dynamics. Physics Reports, 424(4):175–308.

https://doi.org/10.1016/j.physrep.2005.10.009.

Boltzmann, L. (1970). Weitere Studien

uber das

armegleichgewicht unter Gasmolek

ulen, volume 67,

pages 115–225. Vieweg+Teubner Verlag. https://doi.

org/10.1007/978-3-322-84986-1 3.

orner, K., Sanyal, S., and Vespignani, A. (2008). Net-

work Science. Annual Rev. Info. Sci & Technol.,

41(1):537–607. https://doi.org/10.5555/1658843.

1658862.

Brzezi

nski, M. (2014). Power laws in citation distributions:

Evidence from Scopus. Working Papers 2014-05,

Faculty of Economic Sciences, University of Warsaw.

https://ideas.repec.org/p/war/wpaper/2014-05.html.

Complex Systems and Complex Thinking Within the Framework of Education 4.0

215

Chen, Y., Manchester, W. B., Hero, A. O., Toth, G.,

DuFumier, B., Zhou, T., Wang, X., Zhu, H.,

Sun, Z., and Gombosi, T. I. (2019). Identify-

ing Solar Flare Precursors Using Time Series of

SDO/HMI Images and SHARP Parameters. Space

Weather, 17(10):1404–1426. https://doi.org/10.1029/

2019sw002214.

Clausius, R. (1870). XVI. On a mechanical theo-

rem applicable to heat. The London, Edinburgh,

and Dublin Philosophical Magazine and Journal of

Science, 40(265):122–127. https://doi.org/10.1080/

14786447008640370.

Corominas-Murtra, B., Hanel, R., and Thurner, S. (2015).

Understanding scaling through history-dependent pro-

cesses with collapsing sample space. Proceedings

of the National Academy of Sciences, 112(17):5348–

5353. https://doi,org/10.1073/pnas.1420946112.

Cortes, D., Ramirez, J., and Molina, A. (2020). Open in-

novation laboratory: Education 4.0 environments to

improve competencies in scholars. In Proceedings of

18th LACCEI International Multi-Conference for En-

gineering, Education Caribbean Conference for En-

gineering and Technology: Engineering, Integration,

and Alliances for a Sustainable Development. Hemi-

spheric Cooperation for Competitiveness and Pros-

perity on a Knowledge-Based Economy, pages 1–8.

Lawrence Erlbaum Associates, Inc. https://doi.org/

https://doi.org/10.18687/laccei2020.1.1.422.

Costa, M., Goldberger, A. L., and Peng, C.-K. (2005).

Broken Asymmetry of the Human Heartbeat: Loss

of Time Irreversibility in Aging and Disease. Phys.

Rev. Lett., 95:198102. https://doi.org/10.1103/

PhysRevLett.95.198102.

Costan, E., Gonzales, G., Gonzales, R., Enriquez, L.,

Costan, F., Suladay, D., Atibing, N. M., Aro, J. L.,

Evangelista, S. S., Maturan, F., Selerio, E., and

Ocampo, L. (2021). Education 4.0 in Developing

Economies: A Systematic Literature Review of Im-

plementation Barriers and Future Research Agenda.

Sustainability, 13(22):12763. https://doi.org/10.3390/

su132212763.

Council, N. R. (2000). How People Learn: Brain, Mind,

Experience, and School: Expanded Edition. The

National Academies Press, Washington, DC. https:

//10.17226/9853.

Davis, B. and Sumara, D. (2006). Complexity and Edu-

cation: Inquiries Into Learning, Teaching, and Re-

search. Routledge.

Davis-Seaver, J., Leﬂore, D., and Smith, T. (2000).

Promoting critical thinking at the university level.

National forum of teacher educational journal,

10E(3):1–11. http://www.nationalforum.com/

Electronic%20Journal%20Volumes/Davis-Seaver%

20Jane%20Promoting%20Critical%20Thinking%

20at%20the%20University%20Level.pdf.

Daw, C. S., Finney, C. E. A., and Kennel, M. B. (2000).

Symbolic approach for measuring temporal “irre-

versibility”. Phys. Rev. E, 62:1912–1921. https:

//doi.org/10.1103/PhysRevE.62.1912.

de Freitas, D. B., Nepomuceno, M. M. F., and De Medeiros,

J. R. (2019). Multifractal signatures of gravitational

waves detected by LIGO. https://arxiv.org/abs/1912.

12967.

Derbentsev, V., Semerikov, S., Serdyuk, O., Solovieva, V.,

and Soloviev, V. (2020). Recurrence based entropies

for sustainability indices. E3S Web Conf., 166:13031.

https://doi.org/10.1051/e3sconf/202016613031.

Domp, C. (1996). The Critical Point: A Historical Intro-

duction To The Modern Theory Of Critical Phenom-

ena. CRC Press, 1 edition. https://doi.org/10.1201/

9781482295269.

Donges, J. F., Donner, R. V., and Kurths, J. (2013). Test-

ing time series irreversibility using complex network

methods. EPL (Europhysics Letters), 102(1):10004.

https://doi.org/10.1209/0295-5075/102/10004.

Donner, R. V., Small, M., Donges, J. F., Marwan, N., Zou,

Y., Xiang, R., and Kurths, J. (2011). Recurrence-

Based Time Series Analysis by Means of Complex

Network Methods. International Journal of Bifurca-

tion and Chaos, 21(04):1019–1046.

Eckmann, J.-P., Kamphorst, S. O., and Ruelle, D. (1987).

Recurrence Plots of Dynamical Systems. Europhysics

Letters (EPL), 4(9):973–977. https://doi.org/10.1209/

0295-5075/4/9/004.

Eghdami, I., Panahi, H., and Movahed, S. M. S. (2018).

Multifractal Analysis of Pulsar Timing Residuals: As-

sessment of Gravitational Wave Detection. The Astro-

physical Journal, 864(2):162. https://doi.org/10.3847/

1538-4357/aad7b9.

Epstein, J. and Axtell, R. (1996a). Growing artiﬁcial soci-

eties: Social science from the bottom up. MIT.

Epstein, J. M. and Axtell, R. (1996b). Growing Artiﬁcial

Societies: Social Science from the Bottom Up, vol-

ume 1. The MIT Press, 1 edition. https://EconPapers.

repec.org/RePEc:mtp:titles:0262550253.

Erd

os, P. and R

enyi, A. (1959). On Random Graphs

I. Publicationes Mathematicae Debrecen, 6:290–

297. https://snap.stanford.edu/class/cs224w-readings/

erdos59random.pdf.

Fan, Z., Chen, Q., Sun, G., Mastorakis, N., and Zhuang,

X. (2018). Nonlinear analysis of gravitational wave

signals based on recurrence quantiﬁcation analysis.

MATEC Web Conf., 210:05011. https://doi.org/10.

1051/matecconf/201821005011.

Flanagan, R. and Lacasa, L. (2016). Irreversibility of ﬁ-

nancial time series: A graph-theoretical approach.

Physics Letters A, 380(20):1689–1697. https://doi.

org/10.1016/j.physleta.2016.03.011.

Fulcher, B. D., Little, M. A., and Jones, N. S. (2013).

Highly comparative time-series analysis: the empir-

ical structure of time series and their methods. Jour-

nal of The Royal Society Interface, 10(83):20130048.

https://doi.org/10.1098/rsif.2013.0048.

Green, C., Molloy, O., and Duggan, J. (2022). An Em-

pirical Study of the Impact of Systems Thinking and

Simulation on Sustainability Education. Sustainabil-

ity, 14(1):394. https://doi.org/10.3390/su14010394.

Haken, H. (1977). Synergetics. Physics Bulletin, 28(9):412.

Haken, H. (1982). Synergetics: Formation of Ordered

Structures out of Chaos. Leonardo, 15(1):66–67. http:

//www.jstor.org/stable/1574350.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

216

Haken, H. (1984). Can synergetics be of use to manage-

ment theory? In Self-organization and management

of social systems, pages 33–41. Springer.

Haken, H. (2004). Synergetics: Introduction and Advanced

Topics. Springer, Berlin, Heidelberg, 1 edition. https:

//10.1007/978-3-662-10184-1.

Haken, H. and Schiepek, G. (2006). Synergetik in der Psy-

chologie: Selbstorganisation verstehen und gestalten.

Hogrefe G

ottingen.

Helbing, D. and Nagel, K. (2004). The physics of

trafﬁc and regional development. Contemporary

Physics, 45(5):405–426. https://doi.org/10.1080/

00107510410001715944.

Hipkins, R. (2021). Teaching for Complex Systems Think-

ing. NZCER Press.

Jackson, E. A. (1995). The second metamorphosis of sci-

ence: A second view. SFI Working Papers 96-05-

059, Santa Fe Institute. https://EconPapers.repec.org/

RePEc:wop:saﬁwp:95-01-001.

Jackson, S., Krajcik, J., and Soloway, E. (2000). Model-

It: A design retrospective. In Jacobson, M. J. and

Kozma, R. B., editors, Innovations in science and

mathematics education: Advanced designs for tech-

nologies of learning, pages 77–115. Lawrence Erl-

baum Associates, Inc.

Jacobson, M. J. and Wilensky, U. (2006). Complex Systems

in Education: Scientiﬁc and Educational Importance

and Implications for the Learning Sciences. Journal

of the Learning Sciences, 15(1):11–34. https://doi.org/

10.1207/s15327809jls1501 4.

Janemalm, L., Quennerstedt, M., and Barker, D. (2019).

What is complex in complex movement? A dis-

course analysis of conceptualizations of movement in

the Swedish physical education curriculum. Euro-

pean Physical Education Review, 25(4):1146–1160.

https://doi.org/10.1177/1356336X18803977.

Javaherian, M. and Mollaei, S. (2021). Multiscale entropy

analysis of gravitational waves. Adv. High Energy

Phys., 2021:6643546. https://doi.org/10.1155/2021/

6643546.

Jiang, C., Shang, P., and Shi, W. (2016). Multiscale mul-

tifractal time irreversibility analysis of stock markets.

Physica A: Statistical Mechanics and its Applications,

462:492–507. https://doi.org/10.1016/j.physa.2016.

06.092.

Juan, B. A.-S. and Guzm

an-Vargas, L. (2013). Earthquake

magnitude time series: scaling behavior of visibility

networks. The European Physical Journal B: Con-

densed Matter and Complex Systems, 86(11):1–10.

https://doi.org/10.1140/epjb/e2013-40762-2.

org, T., Davis, B., and Nickmans, G. (2007). Towards a

new, complexity science of learning and education.

Educational Research Review, 2(2):145–156. https:

//doi.org/10.1016/j.edurev.2007.09.002.

Kantelhardt, J. W., Zschiegner, S. A., Koscielny-Bunde, E.,

Havlin, S., Bunde, A., and Stanley, H. (2002). Multi-

fractal detrended ﬂuctuation analysis of nonstationary

time series. Physica A: Statistical Mechanics and its

Applications, 316(1):87–114. https://doi.org/10.1016/

S0378-4371(02)01383-3.

Karakatsanis, L. P., Pavlos, G. P., and Xenakis, M. N.

(2013). Tsallis non-extensive statistics, intermittent

turbulence, SOC and chaos in the solar plasma. Part

two: Solar ﬂares dynamics. Physica A: Statistical

Mechanics and its Applications, 392(18):3920–3944.

https://doi.org/10.1016/j.physa.2013.05.010.

Karlov, N. V. (1998). Preobrazovaniye obrazovaniya. Vo-

prosy ﬁlosoﬁi, 11:3–20.

Kennel, M. B. (2004). Testing time symmetry in time se-

ries using data compression dictionaries. Phys. Rev.

E, 69:056208. https://10.1103/PhysRevE.69.056208.

Kremen, V. (2013). Pedahohichna synerhetyka: poniatiino-

katehorialnyi syntez. Teoriia i praktyka upravlinnia

sotsialnymy systemamy, 3:3–19.

Kundu, S., Opris, A., Yukutake, Y., and Hatano, T. (2021).

Extracting Correlations in Earthquake Time Series

Using Visibility Graph Analysis. Frontiers in Physics,

9:179.

Lacasa, L., Nu

nez, A., Rold

an, E., Parrondo, J. M. R., and

Luque, B. (2012). Time series irreversibility: a vis-

ibility graph approach. Eur. Phys. J. B, 85(6):217.

https://doi.org/10.1140/epjb/e2012-20809-8.

Langton, C., editor (1989). Artiﬁcial life. Addison-Wesley.

Langton, C., editor (1995). Artiﬁcial life: Overview. MIT.

Lawrance, A. J. (1991). Directionality and Reversibility in

Time Series. International Statistical Review / Re-

vue Internationale de Statistique, 59(1):67–79. http:

//www.jstor.org/stable/1403575.

Lin, M., Zhao, G., and Wang, G. (2015). Recurrence quan-

tiﬁcation analysis for detecting dynamical changes in

earthquake magnitude time series. International Jour-

nal of Modern Physics C, 26(07):1550077. https:

//doi.org/10.1142/S0129183115500771.

Litvinenko, Y. E. (2019). A Maximum Entropy Argument

for the Slopes of Power-law Particle Spectra in Solar

Flares. The Astrophysical Journal, 880(1):20. https:

//doi.org/10.3847/1538-4357/ab2760.

Liu, H., Liu, C., Wang, J. T. L., and Wang, H. (2019). Pre-

dicting Solar Flares Using a Long Short-term Mem-

ory Network. The Astrophysical Journal, 877(2):121.

https://doi.org/10.3847/1538-4357/ab1b3c.

Mandelbrot, B. B. (1953). An Informational Theory of the

Statistical Structure of Languages. Communication

Theory, pages 486–502.

Marwan, N. and Kurths, J. (2002). Nonlinear analysis of

bivariate data with cross recurrence plots. Physics

Letters A, 302(5-6):299–307. https://doi.org/10.1016/

s0375-9601(02)01170-2.

Midgley, M. (2001). Science and poetry. Routledge, Lon-

don.

National Centers for environmental information (2021).

The Disturbance Storm Time Index. https://www.

ngdc.noaa.gov/geomag/indices/dst.html.

National Research Council (2000). Inquiry and the Na-

tional Science Education Standards: A Guide for

Teaching and Learning. The National Academies

Press, Washington, DC. https://10.17226/9596.

Newman, M. E. J. (2003). The Structure and Function of

Complex Networks. SIAM Review, 45(2):167–256.

https://doi.org/10.1137/s003614450342480.

Complex Systems and Complex Thinking Within the Framework of Education 4.0

217

Nicolis, G. and Prigogine, I. (1989). Exploring complexity:

An Introduction. W.H. Freeman New York.

Nobel Foundation (2021). Press release: The nobel prize

in physics 2021. https://www.nobelprize.org/prizes/

physics/2021/press-release/.

Noth, M., Borning, A., and Waddell, P. (2003). An

extensible, modular architecture for simulating ur-

ban development, transportation, and environmental

impacts. Computers, Environment and Urban Sys-

tems, 27(2):181–203. https://www.sciencedirect.com/

science/article/pii/S0198971501000308.

Ovens, A., Hopper, T., and Butler, J. (2013). Complexity

Thinking in Physical Education: Reframing Curricu-

lum, Pedagogy and Research. Routledge, 1 edition.

https://doi.org/10.4324/9780203126455.

Pagels, H. (1988). The Dreams of Reason: The Computer

and the Rise of the Sciences of Complexity. Simon &

Schuster.

Pareto, V. (1896). Cours d’

Economie Politique, volume 1.

Poincar

e, H. (1890). Sur le probl

eme des trois corps et les

equations de la dynamique. Acta Math, 13:1–270.

Posadas, A., Morales, J., and Posadas-Garzon, A. (2021).

Earthquakes and entropy: Characterization of occur-

rence of earthquakes in Southern Spain and Alboran

Sea. Chaos: An Interdisciplinary Journal of Nonlin-

ear Science, 31(4):043124. https://doi.org/10.1063/5.

0031844.

Prigogine, I. (1980). From Being to Becoming Time and

Complexity in the Physical Sciences. W.H. Freeman.

Prigogine, I. (1989). The philosophy of instability.

Futures, 21(4):396–400. https://doi.org/10.1016/

S0016-3287(89)80009-6.

Prigogine, I. and Stengers, I. (1984). Order Out of Chaos

Man’s New Dialogue with Nature. Bantam Books.

Prigogine, I. and Stengers, I. (1997). The End of Certainty.

Free Press.

Ram

ırez-Montoya, M. S., Castillo-Mart

ınez, I. M.,

Sanabria-Z, J., and Miranda, J. (2022). Com-

plex Thinking in the Framework of Education 4.0

and Open Innovation – A Systematic Literature Re-

view. Journal of Open Innovation: Technology, Mar-

ket, and Complexity, 8(1):4. https://doi.org/10.3390/

joitmc8010004.

Saravia, L. A., Doyle, S. R., and Bond-Lamberty, B.

(2018). Power laws and critical fragmentation in

global forests. Scientiﬁc Reports, 8(1):17766. https:

//doi.org/10.1038/s41598-018-36120-w.

Shannon, C. E. (1948). A Mathematical Theory of

Communication. Bell System Technical Journal,

27(3):379–423. https://doi.org/10.1002/j.1538-7305.

1948.tb01338.x.

Shumway, R. H. and Stoffer, D. S. (2016). Time Se-

ries Analysis and Its Applications. With R Examples.

Springer Texts in Statistics. Springer, 4 edition.

Sigahi, T. F. A. C. and Sznelwar, L. I. (2022). Explor-

ing applications of complexity theory in engineering

education research: A systematic literature review.

Journal of Engineering Education, 111(1):232–260.

https://doi.org/10.1002/jee.20438.

Soloviev, V. N. and Belinskiy, A. (2018). Complex Systems

Theory and Crashes of Cryptocurrency Market. In Er-

molayev, V., Su

arez-Figueroa, M. C., Yakovyna, V.,

Mayr, H. C., Nikitchenko, M. S., and Spivakovsky, A.,

editors, Information and Communication Technolo-

gies in Education, Research, and Industrial Applica-

tions - 14th International Conference, ICTERI 2018,

Kyiv, Ukraine, May 14-17, 2018, Revised Selected Pa-

pers, volume 1007 of Communications in Computer

and Information Science, pages 276–297. Springer.

https://doi.org/10.1007/978-3-030-13929-2 14.

Soloviev, V. N. and Belinskiy, A. (2019). Complex Sys-

tems Theory and Crashes of Cryptocurrency Mar-

ket. Communications in Computer and Information

Science, 1007:276 – 297. https://doi.org/10.1007/

978-3-030-13929-2 14.

Soloviev, V. N. and Belinskyi, A. (2018a). Methods of Non-

linear Dynamics and the Construction of Cryptocur-

rency Crisis Phenomena Precursors. In Ermolayev, V.,

arez-Figueroa, M. C., Yakovyna, V., Kharchenko,

V. S., Kobets, V., Kravtsov, H., Peschanenko, V. S.,

Prytula, Y., Nikitchenko, M. S., and Spivakovsky, A.,

editors, Proceedings of the 14th International Confer-

ence on ICT in Education, Research and Industrial

Applications. Integration, Harmonization and Knowl-

edge Transfer. Volume II: Workshops, Kyiv, Ukraine,

May 14-17, 2018, volume 2104 of CEUR Workshop

Proceedings, pages 116–127. CEUR-WS.org. https:

//ceur-ws.org/Vol-2104/paper 175.pdf.

Soloviev, V. N. and Belinskyi, A. (2018b). Methods of Non-

linear Dynamics and the Construction of Cryptocur-

rency Crisis Phenomena Precursors. In Ermolayev, V.,

arez-Figueroa, M. C., Yakovyna, V., Kharchenko,

V. S., Kobets, V., Kravtsov, H., Peschanenko, V. S.,

Prytula, Y., Nikitchenko, M. S., and Spivakovsky, A.,

editors, Proceedings of the 14th International Confer-

ence on ICT in Education, Research and Industrial

Applications. Integration, Harmonization and Knowl-

edge Transfer. Volume II: Workshops, Kyiv, Ukraine,

May 14-17, 2018, volume 2104 of CEUR Workshop

Proceedings, pages 116–127. CEUR-WS.org. http:

//ceur-ws.org/Vol-2104/paper 175.pdf.

Soloviev, V. N., Bielinskyi, A., Serdyuk, O., Solovieva,

V., and Semerikov, S. (2020a). Lyapunov Expo-

nents as Indicators of the Stock Market Crashes. In

Sokolov, O., Zholtkevych, G., Yakovyna, V., Tara-

sich, Y., Kharchenko, V., Kobets, V., Burov, O., Se-

merikov, S., and Kravtsov, H., editors, Proceedings

of the 16th International Conference on ICT in Ed-

ucation, Research and Industrial Applications. Inte-

gration, Harmonization and Knowledge Transfer. Vol-

ume II: Workshops, Kharkiv, Ukraine, October 06-10,

2020, volume 2732 of CEUR Workshop Proceedings,

pages 455–470. CEUR-WS.org. http://ceur-ws.org/

Vol-2732/20200455.pdf.

Soloviev, V. N., Bielinskyi, A., and Solovieva, V. (2019).

Entropy Analysis of Crisis Phenomena for DJIA In-

dex. In Ermolayev, V., Mallet, F., Yakovyna, V.,

Kharchenko, V. S., Kobets, V., Kornilowicz, A.,

Kravtsov, H., Nikitchenko, M. S., Semerikov, S., and

Spivakovsky, A., editors, Proceedings of the 15th

International Conference on ICT in Education, Re-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

218

search and Industrial Applications. Integration, Har-

monization and Knowledge Transfer. Volume II: Work-

shops, Kherson, Ukraine, June 12-15, 2019, volume

2393 of CEUR Workshop Proceedings, pages 434–

449. CEUR-WS.org. http://ceur-ws.org/Vol-2393/

paper 375.pdf.

Soloviev, V. N., Bielinskyi, A. O., and Kharadzjan, N. A.

(2020b). Coverage of the coronavirus pandemic

through entropy measures. CEUR Workshop Pro-

ceedings, 2832:24–42. http://ceur-ws.org/Vol-2832/

paper02.pdf.

Sornette, D. (2006). Critical Phenomena in Natural Sci-

ences. Chaos, Fractals, Selforganization and Disor-

der: Concepts and Tools. Springer Series in Syner-

getics. Springer-Verlag, 2 edition. https://doi.org/10.

1007/3-540-33182-4.

Sreenivasan, K. R. and Meneveau, C. (1986). The

fractal facets of turbulence. Journal of Fluid

Mechanics, 173:357–386. https://doi.org/10.1017/

S0022112086001209.

Stanley, H. E. and Meakin, P. (1988). Multifrac-

tal phenomena in physics and chemistry. Na-

ture, 335:405–409. https://ui.adsabs.harvard.edu/abs/

1988Natur.335..405S.

Stone, L., Landan, G., and May, R. M. (1996). Detect-

ing TimeArrow: a method for identifying nonlinearity

and deterministic chaos in time-series data. Proceed-

ings of the Royal Society of London. Series B: Biolog-

ical Sciences, 263(1376):1509–1513. https://doi.org/

10.1098/rspb.1996.0220.

Taranenko, T. M. (2014). Synerhetychnyi pidkhid v orha-

nizatsii navchalno-vykhovnoho protsessu. Tavriiskyi

visnyk osvity, 1(45):10–15.

The LIGO Scientiﬁc Collaboration and the Virgo Collab-

oration (2016). Observation of Gravitational Waves

from a Binary Black Hole Merger. Physical Review

Letters, 116(6):061102. https://doi.org/10.1103%

2Fphysrevlett.116.061102.

Thurner, S., editor (2017). 43 Visions for Complexity, vol-

ume 3 of Exploring Complexity. World Scientiﬁc, Sin-

gapore. http://pure.iiasa.ac.at/id/eprint/14000/.

Webber, C. L. and Zbilut, J. P. (1994). Dynamical assess-

ment of physiological systems and states using re-

currence plot strategies. Journal of Applied Physi-

ology, 76(2):965–973. https://doi.org/10.1152/jappl.

1994.76.2.965.

Weber, J., Lindenmeyer, C., Lio, P., and Lapkin, A.

(2021). Teaching sustainability as complex systems

approach: a sustainable development goals work-

shop. International Journal of Sustainability in

Higher Education, 22(8):25–41. https://doi.org/10.

1108/IJSHE-06-2020-0209.

West, J. J. and Dowlatabadi, H. (1998). On assessing

the economic impacts of sea-level rise on developed

coasts. In Downing, T. E., Olsthoorn, A. A., and Tol,

R. S. J., editors, Climate, Change and Risk, page 16.

1 edition.

Wheatley, M. J. (2006). Leadership and the New Science:

Discovering order in a chaotic world. Berrett-Koehler

Publishers, 3 edition.

Wilensky, U. and Jacobson, M. (2014). Complex sys-

tems and the learning sciences. In The Cambridge

Handbook of the Learning Sciences, Second Edition,

pages 319–338. Cambridge University Press. https:

//doi.org/10.1017/CBO9781139519526.020.

Zanin, M., Rodr

ıguez-Gonz

alez, A., Menasalvas Ruiz, E.,

and Papo, D. (2018). Assessing Time Series Re-

versibility through Permutation Patterns. Entropy,

20(9):665. https://doi.org/10.3390/e20090665.

Zbilut, J. P. and Webber, C. L. (1992). Embeddings and

delays as derived from quantiﬁcation of recurrence

plots. Physics Letters A, 171(3):199–203. https:

//doi.org/10.1016/0375-9601(92)90426-M.

Zipf, G. K. (1950). Human Behavior and the Principle of

Least Effort. The Economic Journal, 60(240):808–

810. http://www.jstor.org/stable/2226729.

Complex Systems and Complex Thinking Within the Framework of Education 4.0

219