Using the Gran1 Program in Mathematics Lessons

Myroslav I. Zhaldak

1 a

, Yurii V. Horoshko

2 b

, Nataliia P. Franchuk

1,3 c

, Vasyl M. Franchuk

1 d

Oksana Z. Garpul

4 e

and Hanna Y. Tsybko

2 f

National Pedagogical Dragomanov University, 9 Pyrohova Str., Kyiv, 01601, Ukraine

Taras Shevchenko National University “Chernihiv Colehium”, 53 Hetman Polubotko Str., Chernihiv, 14013, Ukraine

Institute for Digitalisation of Education of the NAES of Ukraine, 9 M. Berlynskoho Str., Kyiv, 04060, Ukraine

Vasyl Stefanyk Precarpathian National University, 57 Shevchenko Str., Ivano-Frankivsk, 76025, Ukraine

Keywords:

A Software Package Gran, Mathematics, Gran1, Mathematical Problems, Cloud Technology.

Abstract:

The article considers the mathematical software package Gran. There are described examples of solving

problems by the graphical method using the Gran1 program, which can be used in the process of teaching

mathematics at school. The issues under consideration are quite complex, and their solving without software

such as Gran1 for graphical analysis of various issues is quite time-consuming. The range of tasks that can be

solved using the Gran software package, in particular, the Gran1 program, is quite wide and needs a creative

approach. Their analysis and solution can have a positive effect not only on the mental but also on the general

cultural development of students. The purpose of the study is to consider examples of the effective use of the

GRAN complex in mathematics lessons for solving issues of different levels of complexity.

1 INTRODUCTION

On February 26, 2021, Ukrainian science suffered a

heavy loss. A well-known scientist in Ukraine and

the world, the founder of a powerful scientiﬁc school,

Myroslav Ivanovych Zhaldak, Doctor of Pedagogi-

cal Sciences, professor, academician of the National

Academy of Pedagogical Sciences of Ukraine, passed

away. One of the most signiﬁcant contributions of

Myroslav Ivanovich to science and education is the

Gran software complex conceived by him and devel-

oped under his leadership. The Gran program com-

plex has received an author’s certiﬁcate, it is recom-

mended by the Ministry of Education and Science of

Ukraine for use in secondary and higher education in-

stitutions of Ukraine, and is also known abroad, for

example in Poland.

Myroslav Ivanovych Zhaldak began active scien-

tiﬁc and pedagogical activities at a time when com-

puterized means of searching, collecting, storing, pro-

https://orcid.org/0000-0001-5570-2235

https://orcid.org/0000-0001-9290-7563

https://orcid.org/0000-0002-0213-143X

https://orcid.org/0000-0002-9443-6520

https://orcid.org/0000-0002-1181-8524

https://orcid.org/0000-0002-1861-3003

cessing, presenting, and transmitting various data be-

gan to be introduced into the educational process.

He emphasized that this opens broad perspectives

for humanitarian education and human learning, con-

tributes to the deepening and expansion of the theo-

retical foundations of knowledge, gives practical sig-

niﬁcance to learning results, creates conditions for re-

vealing the creative potential of children, taking into

account their age characteristics and experience, indi-

vidual requests, and abilities. At the same time, the

teacher is not forced to use any speciﬁc method of

presentation, consolidation of knowledge and control,

any speciﬁc content, methods, forms of organization

and teaching tools, to maintain a certain balance be-

tween independent preparation of students and group

work, etc. (Zhaldak, 1989).

Teacher should determine all these aspects accord-

ing to his own preferences, with speciﬁc conditions of

work, with individual features of pupils and of whole

class. It’s clear that it’s impossible and unnecessary

to teach all the children equally, to form equal knowl-

edge in various subjects for all the children, to claim

reaching equal level of logical and creative thinking

development, equal perception of reality. It also re-

lates to teaching mathematics, methods of problems

solving, plotting and analysis of mathematical mod-

els for various processes and phenomena, results in-

Zhaldak, M., Horoshko, Y., Franchuk, N., Franchuk, V., Garpul, O. and Tsybko, H.

Using the Gran1 Program in Mathematics Lessons.

DOI: 10.5220/0012063800003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 293-302

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

293

terpretation, and generalization of results of this anal-

ysis. At the same time there arise a lot of difﬁcul-

ties dealing with the content, methods, organization

forms and means of study, necessary knowledge lev-

els in various subjects for every pupil (Bobyliev and

Vihrova, 2021).

Of particular importance is the teaching of natu-

ral sciences and mathematics, during which students

must consider and build models of various processes

and phenomena, and then explore them, analyzing

their various features and characteristics, possibly us-

ing different information and communication mod-

els to perform calculations or experiments, and based

on the results of such analysis, synthesizing the rel-

evant conclusions. This approach to learning allows

students to effectively develop logical, critical, cre-

ative thinking, scientiﬁc worldview, creative approach

to solving various problems, their correct vision and

ability to explain their nature and essence (Zhaldak

et al., 2021).

The speciﬁed educational aspects can be effec-

tively implemented using the pedagogical software

complex GRAN, created under the creative leadership

of Myroslav Ivanovich Zhaldak.

We consider the advantages of the speciﬁed soft-

ware complex to be:

• convenient user interface, in particular, the possi-

bility of using most services without a keyboard;

• availability of English and Polish localizations;

• methodical support developed over several

decades, including teaching aids recommended

by the Ministry of Education and school text-

books;

• conﬁrmation of the effectiveness of the program

by the results of numerous candidate and doc-

toral dissertations on the methodology of teaching

mathematics and computer science.

2 THEORETICAL BACKGROUND

For the study, scientiﬁc publications and supporting

sources in the following areas were analyzed: theory

and practice in mathematics teaching development

(Jaworski, 2006), development of mathematical and

logical thinking (Astaﬁeva et al., 2019), mathemati-

cal speech of students (Semenikhina and Drushlyak,

2015), using the Gran software package in mathemat-

ics lessons (Zhaldak et al., 2012, 2020) and other.

Since 2003, the Gran software complex has

been used in some educational institutions in Poland

(Smirnova-Trybulska, 2003; Smyrnova-Trybulska,

2004).

The widespread introduction of modern ICT tools

in the educational process makes it possible to sig-

niﬁcantly strengthen the links between the content of

education and everyday life, to give the results of

training practical signiﬁcance, applicability to solv-

ing everyday life problems, satisfying practical needs,

which is one of the aspects of the humanization of ed-

ucation.

At the same time, the informatization of the ed-

ucational process should be based on the creation

and widespread introduction into everyday pedagog-

ical practice of new computer-oriented methodolog-

ical teaching systems for all academic disciplines

without exception on the principles of gradual and

non-antagonistic, without destructive restructurings

and reforms, embedding information and communi-

cation technologies into existing didactic systems, a

harmonious combination of traditional and computer-

oriented learning technologies, not denying and dis-

carding the achievements of pedagogical science of

the past, but, on the contrary, their improvement and

strengthening, including through the pedagogically

balanced and expedient use of achievements in the

development of computer technology and communi-

cations.

However, it is important to understand that not all

tasks require the use of a computer. Scientiﬁc analysis

of creative, productive thinking shows that the main

thing in the process of thinking is not so much op-

erational and technical procedures and programs for

solving already set tasks, but rather building a model

of a problem situation, putting forward a hypothe-

sis, guessing, formulating a problem, setting a task.

The modern development of computer software has

reached a level where in many cases the algorithm

for achieving the goal can be built automatically. In

this case, instructions to the computer can be given in

terms of the desired results, and not in descriptions of

the processes leading to such results. The main difﬁ-

culty is to characterize the desired results in a quali-

ﬁed and accurate manner, which puts forward appro-

priate requirements for the overall rigor and logic of

the user’s thinking.

3 RESULTS

The latest version of the software Gran1, Gran2D,

Gran3D, as well as some training manuals can be ob-

tained on the website: https://ktoi.npu.edu.ua. All

materials posted on this site are distributed free of

charge (Gran, 2021).

Let’s consider some examples of solving some

math problems using the cloud version of Gran1.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

294

Note that the names of services, help, tips, mes-

sages, etc., depending on the settings provided in the

program, can be provided in one of four languages:

Ukrainian, Russian, English, Polish.

Suppose it is necessary to solve an equation

f (x) = 0, i.e., in domain of dependence y = f (x) ﬁnd

all the values of the argument x that their correspond-

ing values f (x) are equal to zero.

When the dependence y = f (x) is represented

graphically, to ﬁnd a solution of the equation f (x) = 0

means to ﬁnd all the points on the graph of depen-

dence y = f (x) that have zero ordinates. In other

words, it is necessary to ﬁnd points that lie both on the

graph of dependence y = f (x) and on the axis Ox that

is described by the equation y = 0. That is, one should

ﬁnd points that lie on the line (straight or curve) that

has equation y = f (x) as well as on the line, that has

equation y = 0.

Plotting graph of the dependence y = f (x) with

the help of the command “Graph /Plot” and setting

cursor in corresponding points for getting their ordi-

nates makes it easy to determine abscises of all the

points on the graph of dependence y = f (x) that also

lie on the axis Ox.

Examples

1. Find solutions of the equation x

−2 = 0.

Plot a graph of the dependence y = x

−2 and set

cursor so that the cursor’s abscissa coincides with the

intersection point of the graph and the axis Ox. The

result is as follows x

≈ −1.4, x

≈ 1.4 (ﬁgure 1).

If it is necessary to precise the roots one can en-

large a part of the graph or change the segment of

function determination and plot the graph in quite

small areas of the points deﬁned before, with the help

of enlarged zoom.

2. Find solutions of the equation

x −1

x + 1

−3 = 0.

Plot a graph of the dependence

y = abs (x −1) +abs(x + 1) −3

and make sure that any point on the axis Ox of the

segment [−1, 1] lies on the graph of a considered de-

pendence (ﬁgure 2). Thus, for the equation exists un-

limited set of solutions and any value x ∈ [−1, 1] is a

solution of the equation.

3. Find solutions of the equation

sinx + 2 −ln x = 0.

Plot a graph of the dependence

y = sin (x) + 2 −ln(x)

on the segment [−1, 40] (ﬁgure 3) and make sure

(considering properties of functions sinx and ln x),

that out of the segment [−1, 40] there aren’t roots of

the equation.

While considering the graph of dependence

y = sin (x) + 2 −ln(x),

represented in the ﬁgure 3, one can suppose that the

equation sin(x) +2 −ln (x) = 0 has 6 solutions:

≈ 3.9; x

≈ 6.1; x

≈ 9.2;

≈ 13.2; x

≈ 14.9; x

≈ 20.25.

If high accuracy of calculation is not necessary,

such conclusion can be accepted.

However, if higher accuracy of results is required

one should enlarge the zoom of plotting in quite small

areas of the points x

, x

(ﬁgure 4,

ﬁgure 5) to sure that the equation has 5 solutions:

= 3.851, x

= 6.088, x

= 9.203,

= 13.184, x

= 14.928

It should be noted that precise analytical solution

of the equation cannot be found, while the search of

its approximate solutions without graphical plotting

requires laborious calculations and careful analysis of

the results.

The calculus mathematics investigates special

methods of search approximate solutions of equations

of the form f (x) = 0 on given segment [a, b] (bisec-

tion method, chord method, tangent method, iteration

method etc.).

Sometimes it is convenient to represent the equa-

tion f (x) = 0 in the following form:

(x) − f

(x) = 0

where f

(x) − f

(x) = f (x), or a problem leads to

searching solutions of the equation of the form

(x) = f

(x).

In this case it is convenient to plot graphs of the de-

pendencies y = f

(x) and y = f

(x), then set cursor

in intersection points of the graphs and determine co-

ordinates of the points lying on both graphs simulta-

neously. Abscissas x of the points are solutions of the

equation f

(x) = f

(x). If the values x are found in a

such way, the values f

(x) and f

(x) are equal.

4. Find solutions of the equation:

√

x +

sin(10x) = log

(x + 3.5).

Plot graphs of the dependencies

y =

√

x +

sin(10x)

and y = log

0.5

(x + 3.5) and make sure that the equa-

tion has unique solution. Set cursor in the intersection

point of the graphs to get x ≈−1.3 (ﬁgure 6).

Using the Gran1 Program in Mathematics Lessons

295

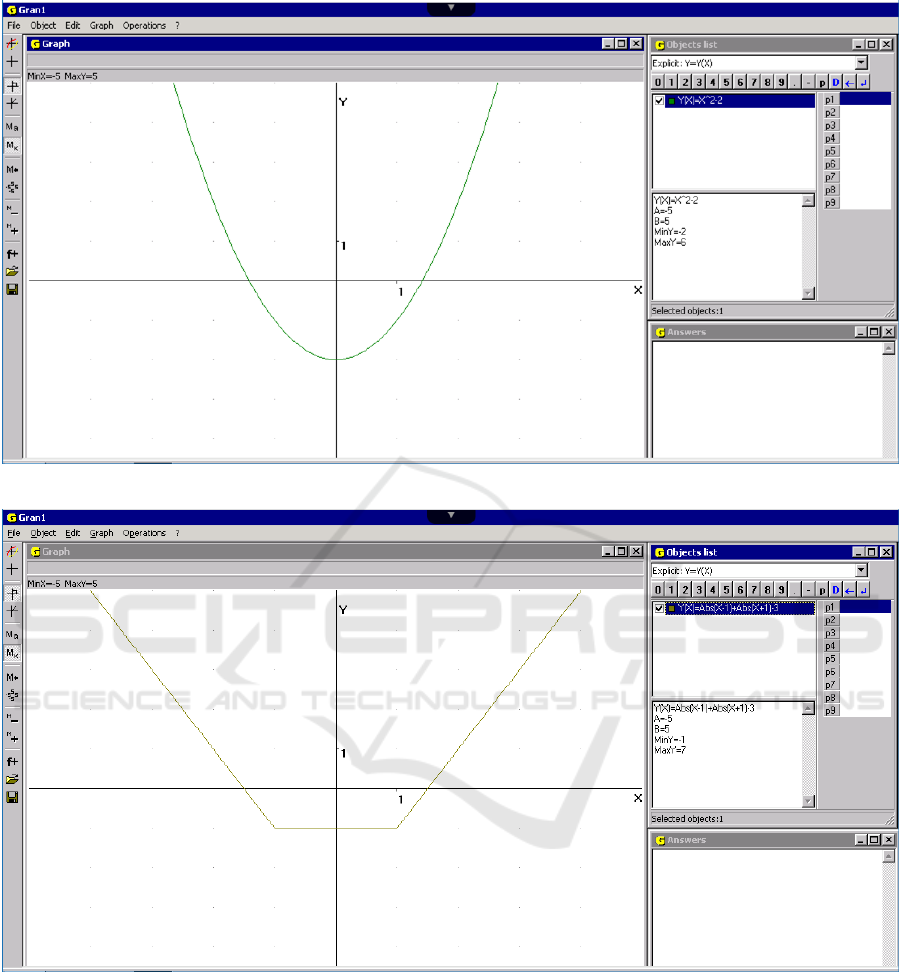
Figure 1: Graph of a given function y = x

−2.

Figure 2: Graph of a given function

x −1

x + 1

−3 = 0.

Now solve the system of equations of the form



(x, y) = 0,

where G

(x, y) and G

(x, y) are some expressions of

two variables x and y.

Set the type of dependence G

(x, y) = 0 and

plot graphs of the dependencies G

(x, y) = 0 and

(x, y) = 0, then set cursor in intersection points

of the graphs and determine coordinates of the points

that meet both equations

(x, y) = 0 and G

(x, y) = 0

i.e. coordinates of intersection points of the lines de-

scribed by the equations

(x, y) = 0 and G

(x, y) = 0.

5. Solve the system of equations



+ y

= 16,

lg(xy) = 0.1

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

296

Figure 3: Graph of the dependence y = sin (x) + 2 −ln(x).

Figure 4: Increasing the scale of graphic constructions in rather small points.

Represent the equations in the following form:

0 = x

+ y

−16, 0 = lg(xy) −0.1 and plot graphs

of the dependencies (ﬁgure 7).

Set cursor in each of intersection points of the

graphs and obtain:

1. x ≈−3.99, y ≈ −0.31;

2. x ≈−0.31, y ≈ 3.99;

3. x ≈0.31, y ≈ 3.99;

4. x ≈3.99, y ≈ 0.31.

For more precise determination of coordinates

of the intersection points of graphs one should en-

large the zoom of plotting, i.e., use the command

Using the Gran1 Program in Mathematics Lessons

297

Figure 5: Enlarged scale of graphic construction y = sin(x) + 2 −ln (x).

Figure 6: The point of intersection of graphs of functions.

,,Zoom in” or change bounds for the variables x and

y. For example, if we change the zoom by setting the

bounds MinX = −4.5, MaxX = −3.5, MinY = −0.5,

MaxY = 0.1 and plot the corresponding graphs, we

obtain the image represented in the ﬁgure 8. Use

the coordinate cursor to get x ≈ −3.988, y ≈−0.316,

and while cursor is moving, the third digit after the

comma is changing (is deﬁned more exactly).

One can put MinX = −4.0, MaxX = −3.98,

MinY = −0.32, MaxY = −0.3 (using the command

“Graph / Zoom / User zoom”) to obtain x ≈−3.9875,

y ≈ −0.3157, and while the cursor is moving, the

fourth digit after comma is changing (is deﬁned more

exactly).

It should be noted that the problem of ﬁnding solu-

tions of the equation f (x) = 0 can be also considered

as the problem of solving the system of equations



0 = y − f (x) ,

0 = y,

and the problem of ﬁnding solutions of the equation

(x) = f

(x) as the problem of solving the system of

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

298

Figure 7: Two equations are graphically represented.

Figure 8: Graphically, two equations are presented on a modiﬁed scale.

equations



0 = y − f

(x),

0 = −f

(x).

In many cases ﬁnding solutions of the system of

equations

{

(x, y) = 0, G

(x, y) = 0

}

with the help

of plotting is unique suitable method for practical use

since the method of variable exclusion or other meth-

ods are very difﬁcult or lead to wrong results.

6. Solve the system of equations (ﬁgure 9)



0 = sin (xy) + cos (x −y),

0 =

−lg (x + y).

In this case it is impossible to exclude one of the

variables x or y and it is difﬁcult to offer any prac-

tically suitable way of solution besides the graphical

method.

It is obvious that plotting can be used for deter-

mination of intersection points of lines independently

of types of the dependencies. For example, if it is

Using the Gran1 Program in Mathematics Lessons

299

Figure 9: The system of equations



0 = sin (xy) + cos(x −y),

0 =

−lg(x + y).

is presented graphically.

required to determine coordinates of points of the cir-

cle x

+ y

= 9, that lie on the parabola y =

−2

or on the ﬁve-petalled (pentapetalous) rose (5ϕ) (ﬁg-

ure 10), one should plot the graphs and obtain coordi-

nates of the required points (with accuracy up to hun-

dredths) with the help of the coordinate cursor:

1. x = −2.89, y = −0.81; x = −2.89, y = 0.39;

2. x = 2.89, y = −0.81; x = 2.89, y = 0.39;

3. x = −2.18, y = −2.06; x = 2.18, y = −2.06;

4. x = −2.63, y = 1.44; x = 2.63, y = 1.44;

5. x = −1.29, y = −2.71; x = 1.29, y = −2.71;

6. x = −0.55, y = 2.95; x = 0.55, y = 2.95.

In this case it is impossible to exclude one of the

variables x or y and it is difﬁcult to offer any prac-

tically suitable way of solution besides the graphical

method.

4 CONCLUSIONS

The research examines the GRAN software complex,

known in Ukraine and abroad.

Its expediency and effectiveness of use in the ed-

ucational process of secondary and higher schools is

conﬁrmed by many years of practice, numerous re-

search results for obtaining scientiﬁc degrees of doc-

tors and candidates of sciences in the ﬁeld of teaching

mathematics and informatics (Vlasenko et al., 2020).

The approach to the study of mathematics, pro-

posed by Myroslav Ivanovych Zhaldak, gives a clear

Figure 10: Dependence graphs.

idea of the concepts being studied, develops ﬁgura-

tive thinking, spatial imagination, allows one to pen-

etrate deeply enough into the essence of the studied

phenomenon, to solve the problem informally. At

the same time, clariﬁcation of the problem, formu-

lation of the problem, development of the appropri-

ate mathematical model, and material interpretation

of the results obtained with the help of a computer

come to the fore. All technical operations related to

processing the built mathematical model, implemen-

tation of the solution search method, design, and pre-

sentation of the results of input data processing rely

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

300

on the computer. It was to implement this approach

that the GRAN software complex was developed.

Some selected problems proposed in the study

demonstrate the expediency of using the GRAN com-

plex for in-depth study of mathematics. Namely:

the ability to conduct the necessary numerical exper-

iment; quickly perform the necessary calculations or

graphic constructions; to test the hypothesis; check

the problem-solving method; to be able to analyze and

explain the results obtained with the help of a com-

puter; ﬁnd out the limits of use. When learning math-

ematical methods, the use of a computer or the chosen

method of solving a problem is extremely important.

The problems presented in the work were success-

fully used by the authors of the study during classes

in various informatics disciplines, including computer

modeling and computer mathematics.

A signiﬁcant improvement of the GRAN complex

has recently been its transfer to the cloud, which pro-

vides access to its services from any platform through

a browser (Zhaldak and Franchuk, 2020). To get to

the virtual desktop on a remote server, you must ac-

cess the browser services and in the input line above

the desktop enter the address https://gran.npu.edu.ua,

then press the Enter key on the keyboard (or in the list

of appropriate symbols on the screen “press” the label

with the word “Go” in the case when using a smart-

phone or other laptop computer where there is no key-

board). As a result, a virtual desktop will open on

which in the line “Username” you should select from

the proposed list one of the available names, such as

“gran”, and then in the line “Password” enter pass-

word “gran” (Zhaldak et al., 2021).

Currently, the expediency and possibility of trans-

ferring the entire GRAN complex of individual ser-

vices into a mobile application is being investigated.

REFERENCES

Astaﬁeva, M., Bodnenko, D., and Proshkin, V. (2019).

Cloud-oriented training technologies as a means of

forming the XXI century skills of future mathemat-

ics teachers. In Ermolayev, V., Mallet, F., Yakovyna,

V., Mayr, H. C., and Spivakovsky, A., editors, Pro-

ceedings of the 15th International Conference on ICT

in Education, Research and Industrial Applications.

Integration, Harmonization and Knowledge Trans-

fer. Volume I: Main Conference, Kherson, Ukraine,

June 12-15, 2019, volume 2387 of CEUR Workshop

Proceedings, pages 507–512. CEUR-WS.org. http:

//ceur-ws.org/Vol-2387/20190507.pdf.

Bobyliev, D. Y. and Vihrova, E. V. (2021). Problems and

prospects of distance learning in teaching fundamental

subjects to future Mathematics teachers. Journal of

Physics: Conference Series, 1840. https://iopscience.

iop.org/article/10.1088/1742-6596/1840/1/012002.

Gran (2021). Download – software. https://ktoi.ﬁ.npu.edu.

ua/zavantazhyty/category/4-prohramni-zasoby.

Jaworski, B. (2006). Theory and Practice in Mathematics

Teaching Development: Critical Inquiry as a Mode

of Learning in Teaching. Journal of Mathematics

Teacher Education, 9(2):187–211. https://doi.org/10.

1007/s10857-005-1223-z.

Semenikhina, O. and Drushlyak, M. (2015). On the Results

of a Study of the Willingness and the Readiness to

Use Dynamic Mathematics Software by Future Math

Teachers. In Batsakis, S., Mayr, H. C., Yakovyna,

V., Nikitchenko, M. S., Zholtkevych, G., Kharchenko,

V. S., Kravtsov, H., Kobets, V., Peschanenko, V. S.,

Ermolayev, V., Bobalo, Y., and Spivakovsky, A., edi-

tors, Proceedings of the 11th International Conference

on ICT in Education, Research and Industrial Appli-

cations: Integration, Harmonization and Knowledge

Transfer, Lviv, Ukraine, May 14-16, 2015, volume

1356 of CEUR Workshop Proceedings, pages 21–34.

CEUR-WS.org. http://ceur-ws.org/Vol-1356/paper

pdf.

Smirnova-Trybulska, E. M. (2003). GRAN1, GRAN-2D,

GRAN-3D programs for teaching mathematics. Com-

puter at school and family, (8):10–17.

Smyrnova-Trybulska, E. M. (2004). The basics of using

a computer: guide for students of higher educational

institutions. Sosnowiec.

Vlasenko, K., Volkov, S., Sitak, I., Lovianova, I., and

Bobyliev, D. (2020). Usability analysis of on-

line educational courses on the platform “Higher

school mathematics teacher”. E3S Web of Confer-

ences, 166:10012. https://doi.org/10.1051/e3sconf/

202016610012.

Zhaldak, M. I. (1989). Sistema podgotovki uchitelya k

ispol’zovaniyu informatsionnoy tekhnologii v ucheb-

nom protsesse [The system of preparing a teacher for

the use of information technology in the educational

process]. A dissertation in the form of a scientiﬁc

report for the degree of Doctor of Pedagogical Sci-

ences on specialty 13.00.02 – theory and methods of

teaching informatics, Kyiv State Pedagogical Institute

named after A. M. Gorky. http://elibrary.kdpu.edu.ua/

handle/0564/1365.

Zhaldak, M. I. and Franchuk, V. M. (2020). Some ap-

plications of cloud technology in mathematical cal-

culations. Scientiﬁc journal of National Pedagogi-

cal Dragomanov University. Series 2 Computer-based

learning systems, (22(29)):3–17. https://doi.org/10.

31392/NPU-nc.series2.2020.22(29).01.

Zhaldak, M. I., Franchuk, V. M., and Franchuk, N. P.

(2021). Some applications of cloud technologies in

mathematical calculations. Journal of Physics: Con-

ference Series, 1840:012001. https://iopscience.iop.

org/article/10.1088/1742-6596/1840/1/012001.

Zhaldak, M. I., Goroshko, Y. V., Vinnychenko, E. F., and

Tsybko, G. Y. (2012). Mathematics with a computer:

The teacher’s guide. National Dragomanov Pedagog-

ical University, Kyiv, 3 edition. http://erpub.chnpu.

edu.ua:8080/jspui/handle/123456789/1523.

Using the Gran1 Program in Mathematics Lessons

301

Zhaldak, M. I., Kuzmina, N. M., and Mykhalin,

H. O. (2020). Teoriia ymovirnostei i matematy-

chna statystyka : Pidruchnyk dlia studentiv ﬁzyko-

matematychnykh ta informatychnykh spetsialnostei

pedahohichnykh universytetiv [Probability Theory

and Mathematical Statistics. Textbook for students of

physics, mathematics, and computer science special-

ties of pedagogical universities]. National Drago-

manov Pedagogical University, Kyiv, 4 edition. http:

//enpuir.npu.edu.ua/handle/123456789/35207.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

302