Pre-Service Teachers’ Preparation for Students’ Computer Modeling

Skills Formation (on the Example of GeoGebra)

Olena V. Semenikhina

1 a

, Marina G. Drushlyak

1 b

, Volodymyr V. Proshkin

2 c

and

Pavlo P. Mulesa

3 d

Makarenko Sumy State Pedagogical University, 87 Romenska Str., Sumy, 40002, Ukraine

Borys Grinchenko Kyiv University, 18/2 Bulvarno-Kudriavska, Str., Kyiv, 04053, Ukraine

Uzhhorod National University, 3 Narodna Sq., Uzhgorod, 88000, Ukraine

ﬁ

Keywords:

Modeling Skills, Skills Development Methodology, Cloud Service, GeoGebra Cloud Service, Constructive

Approach, Modeling, Interesting Curves, Math Problems, Professional Training.

Abstract:

Modeling as a leading method of scientiﬁc knowledge and a means of developing intellectual skills of young

people. The students’ modeling skills can be successfully formed under the condition of appropriate advanced

teacher training, and therefore models and methods of pre-service teachers’ preparation for students’ mod-

eling skills formation are in demand in modern society. The model of pre-service teachers’ preparation for

the formation of students’ computer modeling skills is based on the consistent achievement of three goals:

1) mastering GeoGebra computer tools; 2) formation of pre-service teachers’ skills to model (on the material

of interesting curves in Analytical Geometry or word problems in secondary school); 3) formation of students’

skills to select and/or formulate author’s problems that can be solved by the modeling method in GeoGebra.

The content on which the model is implemented was a special course on mastering GeoGebra and two ex-

perimental modules “Modeling interesting curves” and “Word problems modelling”. According to the sign

test the developed model allows successful pre-service teachers’ preparation to develop students’ computer

modeling skills.

1 INTRODUCTION

Modern science operates with various methods,

among which modeling is one of the most popular.

This method allows you to move away from the ob-

ject’s ideal representation and use its analogue, which

retains the most important characteristics that allow

you to talk about the object properties after certain

changes or inﬂuences on it.

The development of computer technologies has

contributed not only to the revival of the modeling

method, but also led to the emergence of specialized

environments, where it became possible to model var-

ious objects (processes) based on a constructive ap-

proach. At the same time, the widespread use of

smartphones and tablets that have access to the Inter-

net has led to the emergence of cloud services, which

https://orcid.org/0000-0002-3896-8151

https://orcid.org/0000-0002-9648-2248

https://orcid.org/0000-0002-9785-0612

https://orcid.org/0000-0002-3437-8082

also allow you to model objects of different nature.

However, methods of using cloud services to develop

modeling skills are just beginning to be developed and

implemented, and therefore are not well established

and need experimental conﬁrmation.

2 LITERATURE REVIEW

The authors believe that the pre-service teachers’

preparation for the formation of students’ computer

modeling skills is based on the perception of a con-

structive approach as the leading one in the formation

of modeling skills.

The importance of developing constructive skills

of youth is emphasized in the ﬁndings of Lak-

sha (Laksha, 2011), Kononenko (Kononenko, 2010),

Ivanina (Ivanina, 2010), and the formation of model-

ing skills by individual scientists is associated with

the formation of research skills (Bilousova et al.,

2022). Ziatdinov and Valles (Ziatdinov and Valles,

338

Semenikhina, O., Drushlyak, M., Proshkin, V. and Mulesa, P.

Pre-Service Teachersâ

Z Preparation for Studentsâ

Z Computer Modeling Skills Formation (on the Example of GeoGebra).

DOI: 10.5220/0012064200003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 338-348

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2022) think that “while the model is being con-

structed, the student can stumble upon a pathway that

results in a better understanding of the connection

present amidst the model world and reality”. Flehan-

tov et al. (Flehantov et al., 2022) performed a study

to investigate the effectiveness of GeoGebra in gain-

ing and cultivating knowledge on mathematical mod-

eling. Marciuc et al. (Marciuc et al., 2016) empha-

size, that use of GeoGebra offers a speciﬁc, construc-

tivist, teaching approach that allows students to inde-

pendently build their own models while offering guid-

ance.

Analysis of the problem shows that with the ad-

vent of specialized mathematics software its solution

has focused not so much on understanding the algo-

rithms of elementary constructions, but on the ability

to use computer tools and the ability to visualize the

result. The latter, in particular, is emphasized in the

ﬁndings of Bilousova and Zhytyenyova (Bilousova

and Zhytyenyova, 2017). For example, Lenchuk and

Franovskyi (Lenchuk and Franovskyi, 2016) consider

it possible to expand the visual presentation of infor-

mation in the ﬁeld of planimetry by reproducing the

real state of operation of its objects, resorting, as a

priority, to visual methods of activity based on con-

structive modeling. Regarding the ability to use tools,

it should be noted the emergence of cloud services,

including specialized services.

Different aspects of educational using of cloud

technologies and services are examined in the studies

of (Shakeabubakor et al., 2015; Smith et al., 2014).

For example, Shakeabubakor et al. (Shakeabubakor

et al., 2015) explore advantages of using cloud tech-

nologies in research, such as availability of vari-

ous tools and applications for analyses and collect-

ing data, for managing and organizing references, for

communication with peers and experts, the absence of

constraints, the access to cloud resources from any-

where any time that has an active Internet connection,

etc. (Smith et al., 2014). They offer the approach

to applying of cloud services for enhancing the pro-

ductivity of university research activities, increasing

competitiveness and ﬂexibility of educational institu-

tions.

Shyshkina and Popel (Shyshkina and Popel, 2013)

consider the problems of implementation of cloud

technology services in the educational process, de-

scribe the current state of development and use of

cloud technology services in educational institutions

and analyze the content of educational and scientiﬁc

components of cloud-based educational environment.

The use of specialized software for modeling

mathematical objects is mentioned in (Sheng, 2014).

Rubio et al. (Rubio et al., 2015) emphasize that

by fusing modeling and digital technologies through

simulation, there are obtained learning environments

that promote the development of knowledge and skills

of scientiﬁc thinking in students. The teaching of stu-

dents to model is discussed in (C¸ ekmez, 2020). Au-

thor discuss the pedagogical value of a real-world

phenomenon selected for a modelling activity, fol-

lowed by the implementation sequence of the activity

in the classroom. C¸ ekmez (C¸ ekmez, 2023) believes

that pre-service mathematics teachers should be fa-

miliar with the potential use of computers in mathe-

matical modelling.

Currently, cloud versions of well-known environ-

ments with mathematical modeling capabilities are

available, including SageMath. We can also add Ge-

oGebra cloud service to this list, because it “can be

considered a very creative tool for mathematical mod-

eling” (Ziatdinov and Valles, 2022).

Experience in using GeoGebra cloud service (vi-

sualization of mathematical objects; organization of

not only analytical but also empirical search for an-

swers in determining individual characteristics of

mathematical objects; organization of home computer

experiment) (Drushlyak et al., 2021a; Hrybiuk, 2020;

Semenikhina et al., 2019b,a) allowed us to consider

GeoGebra as means for formation of students’ mod-

eling skills.

However, the analysis of scientiﬁc ﬁndings con-

ﬁrmed the lack of established models of pre-service

teachers’ preparation for the formation of students’

modeling skills based on GeoGebra, which deter-

mined the purpose of our study: to develop and ex-

perimentally test the model of pre-service teachers’

preparation for the formation of students’ computer

modeling skills (based on GeoGebra).

3 MATERIAL AND METHODS

Experimental base was Makarenko Sumy State Peda-

gogical University. The total number of respondents

is 51 people (students, pre-service mathematics and

computer science teachers).

The model of pre-service teachers’ preparation for

the formation of students’ computer modeling skills

is based on the consistent achievement of three goals:

1) mastering GeoGebra computer tools; 2) formation

of pre-service teachers’ skills to model (on the mate-

rial of interesting curves in Analytical Geometry or

word problems in secondary school); 3) formation

of students’ skills to select and/or formulate author’s

problems that can be solved by the modeling method

in GeoGebra.

To test the effectiveness of the developed model, a

Pre-Service Teachersâ

Z Preparation for Studentsâ

Z Computer Modeling Skills Formation (on the Example of GeoGebra)

339

pedagogical experiment was organized, which lasted

3 years (2019-2021) and was conducted among pre-

service mathematics and computer science teachers.

The model was implemented using the free Ge-

oGebra software (https://www.geogebra.org) in the

study of the disciplines “Dynamic Mathematics

Software” for pre-service mathematics teachers and

“Computer Mathematics Systems” for pre-service

computer science teachers (2nd year). Within the

discipline “Methods of teaching mathematics” and

“Methods of teaching computer science” (3rd year)

were introduced experimental modules “Modeling of

interesting curves” (10 hours – 2 lecture hours and 8

laboratory hours) to achieve the second goal; “Model-

ing of word problems” (6 laboratory hours) to achieve

the third goal.

Testing the effectiveness of the methodology in-

volved two tests: after mastering GeoGebra and after

studying the second module.

Students were offered two typical problems for

modeling the Conic sections by its geometric deﬁni-

tion (the problems differed from each other in the ini-

tial conditions, for example, the distance between the

foci was different or one of the foci was at a speciﬁc

point in a given coordinate system, etc.) and motion

word problem.

The solution of the problems was evaluated by the

following indicators (table 1, 2).

Since the results of the tests were dependent and

each time provided for the accumulation of marks, the

Table 1: Indicators of the formation of modeling skills

(Module “Interesting Curves”).

No Indicators Marks

1 Ability to take into account the analyti-

cal relationship between the elements

2 Ability to take into account the geomet-

ric relationship between the elements

3 Ability to use Locus 1

4 Ability to use Trace 1

5 Ability to demonstrate the change of the

curve shape when changing the input

data

6 Ability to construct a model visually

correct (location, color, size and style of

geometric objects)

7 Ability to add dynamic text to study nu-

merical characteristics

8 Ability to write an algorithm for con-

structing a model

9 Ability to reproduce the steps of the al-

gorithm to construct the model

10 Ability to interpret the result of a com-

puter experiment

Table 2: Indicators of the formation of modeling skills

(Module “Word Problems”).

No Indicators Marks

1 Ability to analyze the problem 1

2 Ability to establish a relations between

data and questions

3 Ability to use Slider 1

4 Ability to use Dynamic Text 1

5 Ability to use Button 1

6 Ability to use Check Box 1

7 Ability to use Image 1

8 Ability to construct a model visually

correct (location, color, size, etc.)

9 Ability to write an algorithm and repro-

duce the steps of the algorithm to con-

struct the model

10 Ability to interpret the result of a com-

puter solution

sign test was used. The number of respondents, whose

total score decreased (“–”), did not change (“0”) and

increased (“+”), was ﬁxed.

In accordance with the experiment purpose and

the sign test, the null hypothesis was formulated: the

developed model does not provide successful pre-

service teachers preparation for the formation of stu-

dents’ computer modeling skills. Then the alterna-

tive hypothesis was “the author’s methodology con-

tributes to the formation of such skills”.

The constructed hypotheses deﬁne the one-sided

sign test for checking the dependent samples. Ac-

cording to the decision-making rule (Grabar and

Krasnjanskaja, 1977) the null hypothesis of inefﬁ-

ciency / effectiveness of the author’s methodology

was accepted or rejected.

4 CONSTRUCTIVE APPROACH

The constructive approach is characterized by the fact

that acquaintance with the properties of concepts be-

gins with constructive activities for their “discovery”

and assimilation with a gradual transition to deﬁni-

tions and logical proofs. This, in particular, simpliﬁes

the perception of the Geometry course, makes it more

accessible, while raising the scientiﬁc level through

the intensiﬁcation of educatees’ research activities.

The use of the constructive approach contributes

to the fact that the activity is manifested in the grad-

ual transition of actions for the construction of ob-

jects from the executive level (is characterized by ex-

ternal regulation), then to reproductive (is marked by

internal regulation of actions in the construction of

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

340

known structures), then to the applied level (using

the method of construction), and, ﬁnally, the creative

level (involves the construction of new objects) (ﬁg-

ure 1) (Tukholko, 2018).

Figure 1: Constructive approach activity levels.

We consider constructive tasks to be one of

the means of implementing a constructive approach.

Many authors use the term “constructive tasks” in a

sense identical to construction problems. However,

the peculiarities of the constructive approach require

the use for its implementation and other tasks, the

solution of which requires the implementation of a

particular constructive activity. Therefore, for exam-

ple, Lisimova (Lisimova, 1997) considers construc-

tive tasks as tasks for construction, imaging, mea-

surement, geometric design and structural-geometric

modeling. Dalinger (Dalinger, 2012) considers con-

structive tasks as “problems in the process of solving

which reveal the material conditions of geometric ﬁg-

ures. Their purpose is to identify the essential features

of ideas that are formed through the material condi-

tions of their origin”.

Constructive tasks can be a base for establishing

new properties of ﬁgures (concepts formation), for

the consolidation of knowledge, for repetition, con-

trol, intensiﬁcation of research activities. “The pecu-

liarity of constructive tasks is that they can be solved

both logically and ﬁguratively or visually effective”

(Dalinger, 2012).

When solving constructive tasks, there is a pro-

ductive activity that motivates to think independently

(methods of constructing have to be developed inde-

pendently), and not reproductive activity, which is of-

ten not an independent mental process, but is a repe-

tition of known steps (Dalinger, 2012).

Mastering the system of knowledge and skills can

take place on two levels: constructive and analytical.

The main feature of the constructive level of mastery

of the material is its visual and constructive aware-

ness. This is manifested:

• in the ability to recognize objects that belong and

do not belong to the content of this concept, give

examples, demonstrate the existence of the stud-

ied ﬁgures by construction;

• in the knowledge of their most essential proper-

ties and the ability to apply known properties in

solving problems.

The constructive approach provides “points of

support” for Geometry study at a higher abstract level,

which is characterized by the ability to formulate def-

initions of concepts, statements and prove already in

formal language, rather than the language of geomet-

ric images.

5 MODEL OF PRE-SERVICE

TEACHERS’ PREPARATION

FOR STUDENTS’ COMPUTER

MODELING SKILLS

FORMATION (BASED ON

GEOGEBRA)

The model of pre-service teachers’ preparation for

the formation of students’ computer modeling skills

(based on GeoGebra) is based on the perception of a

constructive approach as leading in the formation of

modeling skills and requires the use of certain forms,

methods and teaching purpose (ﬁgure 2). Let’s dwell

on them in more detail.

The purpose of implementing the developed

model is pre-service teachers’ preparation for stu-

dents’ computer modeling skills formation.

The content on which the model is implemented

was a special course on mastering GeoGebra and two

experimental modules.

Module “Modeling interesting curves”

Nowadays, their study in the classical course of

Analytical Geometry is possible in three ways:

• analytical description and further study of curves

– at ﬁrst analytical (parametric, implicit, explicit)

equations, usually of conics, are given and then

they are investigated;

• study of curves as locus with a given property – at

ﬁrst the geometric deﬁnitions of curves are given,

on the basis of which their analytical equations are

written (as a rule, these are conics, conchoid of

Nicomedes, limac¸on of Pascal, strophoid, cissoid

of Diocles, lemniscate of Bernoulli, Cassini oval);

• study of curves generated in the kinematic way (as

the trajectory of a point), usually cycloidal curves

(ﬁgure 3), folium of Descartes, witch of Agnesi,

logarithmic spiral.

Module “Word problems modelling”

Among other things, the general method of solv-

ing word problems includes knowledge of the solving

steps. The solving steps include: analysis of the prob-

lem text; translation of the text into the mathematics

Pre-Service Teachersâ

Z Preparation for Studentsâ

Z Computer Modeling Skills Formation (on the Example of GeoGebra)

341

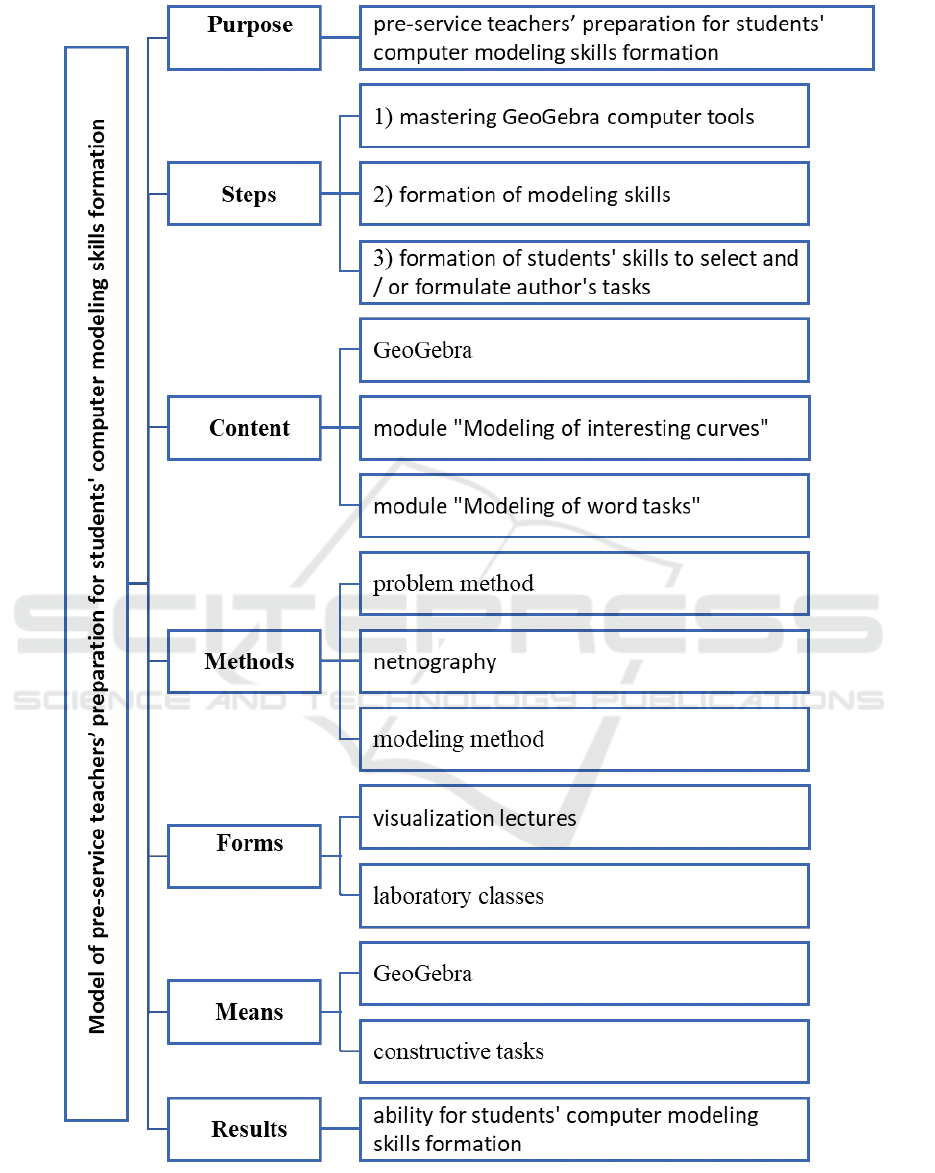
Figure 2: Model of pre-service teachers’ preparation for students’ computer modeling skills formation.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

342

Figure 3: Construction of a hypocycloid using the Locus tool.

Figure 4: Word problem modelling based on GeoGebra (https://www.geogebra.org/m/fmupxx5a).

Pre-Service Teachersâ

Z Preparation for Studentsâ

Z Computer Modeling Skills Formation (on the Example of GeoGebra)

343

language (modeling); establishing the relationship be-

tween the input data and the problem question; draw-

ing up a problem solution plan; implementation of the

solution plan; checking and evaluating the problem

solution.

The essence of the method of modeling in solving

word problems is to translate the text of the problem

into the language of visual models of various kinds:

drawings, diagrams, graphs, tables, symbols, formu-

las, equations, etc. The translation of the text into the

form of a visual model allows you to identify proper-

ties and relationships that are often difﬁcult to detect

when reading the text (ﬁgure 4).

Learning forms of the model are visualization lec-

tures and laboratory classes.

Among the teaching methods used problem

method, modeling method and netnography.

GeoGebra, constructive tasks and instructional

materials are learning means.

The model of pre-service teachers’ preparation for

students’ computer modeling skills formation is im-

plemented in three stages:

1) mastering GeoGebra computer tools;

2) pre-service teachers’ preparation to modele (on

the material of interesting curves in Analytical

Geometry or word Math problems in secondary

school);

3) formation of students’ skills to select and/or for-

mulate author’s problems that can be solved by

the modeling method in GeoGebra.

In the ﬁrst stage, GeoGebra computer tools are

mastered: students get acquainted with the possi-

bilities of using GeoGebra to solve different classes

of math problems. Particular emphasis should be

placed on tools of geometric constructions and slid-

ers, thanks to which it is possible to change the con-

structed structure in an interactive mode.

The methodology of forming the skills to model

interesting curves is as follows: the teacher on a

common online platform informs about constructive

approaches to the construction of various curves,

which were studied in ancient times (the netnography

method). He brieﬂy tells about how such construc-

tions were done (compass and ruler, one compass, two

compasses, one or two rulers, etc.), or gives an exam-

ple of practically oriented problems that are solved us-

ing interesting curves. After that, the teacher demon-

strates one of the described constructions in GeoGe-

bra cloud service, and then asks students to write

an algorithm for the above construction (the problem

method).

Then the teacher asks students according to the al-

gorithm (provided to each student) to reproduce the

construction and demonstrate the result, to analyze

errors, and if not, to analyze possible limit cases. Af-

ter that, students are offered the deﬁnition of curves

generated in mechanical way together with the al-

gorithms of their construction in the cloud service;

students must model this type of curve according to

the existing algorithm. Then together with students,

the task of the following type is carried out: algo-

rithms of curves construction are offered and after

their construction, students need to characterize prop-

erties of the modeled curves, to give them deﬁnitions

or kinematic characteristics. After completing this

type of task, students are offered only the deﬁnition

of the curves or their kinematic characteristics, and

they must model the curve themselves.

The methodology should be brieﬂy described as

follows. Step 1 – the teacher offers an example of a

curve model through the deﬁnition (the teacher step

by step models the curve), and students must inde-

pendently compile an algorithm for constructing the

model. Step 2 – the teacher offers a description-

deﬁnition of the curve and provides a ready-made al-

gorithm according to which students model the curve

independently. Step 3 – the teacher offers an algo-

rithm for constructing a curve model, and students

need to characterize the properties of the curve or

give its deﬁnition based on the results. Step 4 – stu-

dents are offered deﬁnitions of curves that they have

to model them.

More details about the methodology in (Drushlyak

et al., 2021b).

The method of the second stage described by us

differs from the traditional one, as the latter usually

involves only step 2 and step 4, which does not al-

low students to understand the algorithms involved in

building a model, to develop the ability to compare

step-by-step ideas and steps. There is also no practice

of qualitative analysis of the algorithm (which is pro-

vided by step 3 and which is supported by the “step-

by-step playback service” in GeoGebra). This is what

we consider to be fundamentally important for the ef-

fective learning of modeling skills and what makes

the GeoGebra service possible.

Mastering the module “Modeling of word prob-

lems” involves providing students with instructional

materials with examples of solving word problems in

GeoGebra. At the ﬁrst lesson, students must complete

tasks on modeling word problems of the school math-

ematics course on the model and independently. For

the second lesson, students have to prepare 10 word

problems, up to 5 of which provide instructional ma-

terials for solving in GeoGebra. Students must ex-

change developed didactic materials, solve problems

and return them for testing. For the third lesson, stu-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

344

Figure 5: The problem of proportional division (author Nataliia Kishchuk, https://www.geogebra.org/m/bhw6xbcp).

(a) Construction of a parabola, Locus tool.

(b) Visual model of the motion problem.

Figure 6: Visual models.

dents should check the tasks performed by another

student and analyze the errors, which should be pre-

sented to the general public for discussion.

We will describe in more detail the method of

teaching this module.

The method of forming the skills to model word

problems is as follows: the teacher on the cloud ser-

vice https://www.geogebra.org/ introduces students

with examples of visual models for word problems

(the method of netnography, ﬁgure 5). This brieﬂy

dwells on how such constructions were carried out

(using Slider, Text, Button, Check Box). After that

he demonstrates one of the described constructions in

GeoGebra cloud service (ﬁgure 4), and then asks stu-

dents to prescribe the algorithm of the given construc-

tion (the problem method).

Then the teacher asks students according to the al-

gorithm (provided to each student) to reproduce the

construction and demonstrate the result, to analyze

possible errors.

Brieﬂy, the technique should be described as fol-

lows:

Step 1 – the teacher offers an example of a visual

model of a word problem, and students must indepen-

dently create an algorithm for a model constructing;

Step 2 – the teacher offers a ready-made algorithm

by which students independently reproduce the visual

model;

Step 3 – students are offered a type of word prob-

lems (motion problems, work problems, alloy mix-

tures problems, etc.), they select the appropriate prob-

lem and independently construct a visual model.

It should also be noted that in the conditions

of distance learning, GeoGebra service allows the

demonstration of shared constructions and the ability

to work with models at any time from anywhere.

Pre-Service Teachersâ

Z Preparation for Studentsâ

Z Computer Modeling Skills Formation (on the Example of GeoGebra)

345

Table 3: The results of students’ tests.

Student Mark 1 Mark 2 Student Mark 1 Mark 2 Student Mark 1 Mark 2

1 10 10 18 13 12 35 17 17

2 13 11 19 11 16 36 12 13

3 12 12 20 9 10 37 11 13

4 5 9 21 8 8 38 11 13

5 14 14 22 9 11 39 9 12

6 6 7 23 9 11 40 9 13

7 9 10 24 9 9 41 9 11

8 10 12 25 9 9 42 9 11

9 12 12 26 7 16 43 7 10

10 12 11 27 15 15 44 9 12

11 11 12 28 13 14 45 7 10

12 11 15 29 14 15 46 8 9

13 6 6 30 11 11 47 13 11

14 5 9 31 11 12 48 15 14

15 7 12 32 11 12 49 16 16

16 9 9 33 12 12 50 12 13

17 9 11 34 7 9 51 12 11

6 STATISTICAL ANALYSIS OF

RESULTS

The effectiveness of the developed model was tested

on the basis of two tests. Students had to solve prob-

lem 1 (for example, to build a curve for which “A

point and a line, the distance between which is equal

to a are given. A line is drawn through an arbitrary

point X of the line and the point. The points at a dis-

tance b from point X are marked. Find the locus of

such points”, ﬁgure 6 (a)) and problem 2 (for exam-

ple, to build a visual model for the problem “From

points A and B, the distance between which is 210 km,

car and truck moved to meet each other. The speed of

a car is 80 km/h, and a truck – 60 km/h. What will be

the distance between the machines in half an hour?”,

ﬁgure 6 (b)) before the experiment and after the ex-

periment.

Assessment of the solutions of problem 1 was car-

ried out through the assessment of skills: take into

account the analytical and geometric relationship be-

tween the elements; use the Locus and Trace tools;

successfully visualize the model; add dynamic text to

demonstrate numerical characteristics; develop an al-

gorithm for model constructing; reproduce the steps

of the algorithm for the model constructing; interpret

the result of a computer experiment (in more detail in

table 1). Assessment of the solutions of problem 2

was carried out through the assessment of skills: the

ability to analyze the text of the problem; establish

a relationship between the input data and the ques-

tion; use Slider, Text, Button, Check Box, Image; suc-

cessfully visualize the model; to develop an algorithm

for a model constructing; reproduce commands of the

model construction algorithm; check and evaluate the

computer solution of the problem (more details in ta-

ble 2).

The results of the tests are presented in table 3.

These marks were used to determine the number

of respondents whose total score decreased (“–”), did

not change (“0”) and increased (“+”) (table 4).

Table 4: Dynamics of scores based on the results of stu-

dents’ tests

Dynamics of scores

Number of

respondents

Negative, ”–” 6

Without changes, “0” 13

Positive, ”+” 32

Number of changes, n = “–”+“ + ” 38

7 CONCLUSIONS

1. The development of information technology has

actualized the perception of modeling as a lead-

ing method of scientiﬁc knowledge and a means

of developing intellectual skills of young people.

Thus for the decision of many mathematical prob-

lems the method of modeling which is realized on

the basis of the constructive approach is used.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

346

2. The students’ ability to model can be success-

fully formed under the condition of appropriate

advanced teacher training, and therefore models

and methods of pre-service teachers’ preparation

for students’ modeling skills formation are in de-

mand in modern society.

3. The developed model of pre-service teachers’

preparation for students’ modeling skills forma-

tion (based on GeoGebra) is based on the per-

ception of a constructive approach as a leader in

the development of intellectual skills of young

people. Its implementation is based on a special

course on mastering GeoGebra and two experi-

mental modules “Modeling curves” and “Model-

ing word problems”, mastering which involves the

use of appropriate forms (visualization lectures

and laboratory classes), methods (problem, mod-

eling and netnography) and training means (Ge-

oGebra, constructive tasks and instructional ma-

terials).

4. The model of pre-service teachers’ preparation

for students’ modeling skills formation is imple-

mented in three stages: 1) mastering the GeoGe-

bra computer tools; 2) formation of pre-service

teachers’ skills to model; 3) formation of stu-

dents’ skills to select and/or formulate author’s

problems that can be solved by the method of

modeling in GeoGebra.

5. The developed model is focused not only on

the pre-service teachers’ preparation for students’

modeling skills formation with GeoGebra, but

also thanks to the role-playing game in the third

stage of its implementation allows awareness of

their own mistakes in future professional activi-

ties and typical mistakes of students.

Further scientiﬁc research is needed to implement

the methodology: in the training of teachers of natu-

ral specialties (biology, chemistry, geography); in the

conditions of mobile training; based on other special-

ized software.

REFERENCES

Bilousova, L. I., Gryzun, L. E., Lytvynova, S. H., and

Pikalova, V. V. (2022). Modelling in GeoGebra in

the Context of Holistic Approach Realization in Math-

ematical Training of Pre-service Specialists. In Se-

merikov, S., Osadchyi, V., and Kuzminska, O., edi-

tors, Proceedings of the 1st Symposium on Advances

in Educational Technology - Volume 1: AET, pages

499–510. INSTICC, SciTePress. https://doi.org/10.

5220/0010925700003364.

Bilousova, L. I. and Zhytyenyova, N. V. (2017). Func-

tional approach to the use of technology of visualiza-

tion for intensiﬁcation of learning process. Informa-

tion Technologies and Learning Tools, 57(1):38–49.

https://doi.org/10.33407/itlt.v57i1.1525.

Dalinger, V. A. (2012). Metodicheskie osobennosti

obucheniia uchashchikhsia planimetrii v stereomet-

richeskoi srede [Methodological features of teaching

students planimetry in a stereometric environment].

Sovremennye naukoemkie tekhnologii, (7):59–61.

https://top-technologies.ru/ru/article/view?id=30743.

Drushlyak, M. G., Semenikhina, O. V., Proshkin, V. V.,

Kharchenko, S. Y., and Lukashova, T. D. (2021a).

Methodology of formation of modeling skills based

on a constructive approach (on the example of ge-

ogebra). CTE Workshop Proceedings, 8:458–472.

https://doi.org/10.55056/cte.300.

Drushlyak, M. G., Semenikhina, O. V., Proshkin, V. V.,

Kharchenko, S. Y., and Lukashova, T. D. (2021b).

Methodology of formation of modeling skills based

on a constructive approach (on the example of ge-

ogebra). CTE Workshop Proceedings, 8:458–472.

https://doi.org/10.55056/cte.300.

Flehantov, L. O., Ovsiienko, Y. I., Antonets, A. V., and

Soloviev, V. N. (2022). Using Dynamic Vector Dia-

grams to Study Mechanical Motion Models at Agrar-

ian University with GeoGebra. In Semerikov, S.,

Osadchyi, V., and Kuzminska, O., editors, Proceed-

ings of the 1st Symposium on Advances in Educa-

tional Technology - Volume 1: AET, pages 336–

353. INSTICC, SciTePress. https://doi.org/10.5220/

0010924200003364.

Grabar, M. I. and Krasnjanskaja, K. A. (1977). Application

of mathematical statistics in pedagogical researches.

Nonparametric methods. Pedagogika, Moscow.

Hrybiuk, O. (2020). System of dynamic mathematics of Ge-

oGebra as a means of supporting general and special

abilities of students in the process of research learn-

ing: practical work experience. Physical and Mathe-

matical Education, (2(24)):37–51. https://doi.org/10.

31110/2413-1571-2020-024-2-006.

Ivanina, T. A. (2010). Rol konstruktivnoi deiatelnosti

v razvitii rebenka [The role of constructive ac-

tivity in the development of the child]. Bul-

letin of the Krasnoyarsk State Pedagogical Univer-

sity, (2):124–128. https://cyberleninka.ru/article/n/

rol-konstruktivnoy-deyatelnosti-v-razvitii-rebyonka.

Kononenko, N. V. (2010). Peculiarities of development

of pupils’ mental process structural component in the

ﬁeld of geometry. Scientiﬁc notes of the Trans-Baikal

State University. Series: Physics, mathematics, engi-

neering, technology, 94:128–131. https://tinyurl.com/

2r33up2n.

Laksha, H. I. (2011). The formation of constructive

mathematics skills of pupils in teaching alge-

bra in 7 – 9 grades. PhD thesis, Minsk. https:

//elib.bspu.by/bitstream/doc/505/1/%D0%90%D0%

B2%D1%82%D0%BE%D1%80%D0%B5%D1%

84%D0%B5%D1%80%D0%B0%D1%82%20%

D0%9B%D0%B0%D0%BA%D1%88%D0%B0.pdf.

Pre-Service Teachersâ

Z Preparation for Studentsâ

Z Computer Modeling Skills Formation (on the Example of GeoGebra)

347

Lenchuk, I. G. and Franovskyi, A. T. (2016). Computer

modeling of problems of plane geometry: the inver-

sion method. Information Technologies and Learning

Tools, 56:88–106. https://doi.org/10.33407/itlt.v56i6.

1485.

Lisimova, O. A. (1997). Sistema konstruktivnykh zadach

kak metod izucheniia planimetrii v 7 klasse [The sys-

tem of design tasks as a method for studying planime-

try in grade 7]. PhD thesis, Herzen State Pedagogical

University of Russia, Saint Petersburg.

Marciuc, D., Miron, C., and Barna, E. S. (2016). Us-

ing GeoGebra software in the teaching of oscillatory

motions. Romanian Reports in Physics, 68(3):1296–

1311. https://rrp.nipne.ro/2016

68 3/A35.pdf.

Rubio, L., Prieto, J., and Ortiz B, J. (2015). La matem

atica

en la simulaci

on con geogebra. Una experiencia con

el movimiento en ca

ıda libre. IJERI: International

Journal of Educational Research and Innovation,

(5):90–111. https://www.upo.es/revistas/index.php/

IJERI/article/view/1586.

Semenikhina, E., Drushlyak, M., Bondarenko, Y., Kon-

dratiuk, S., and Dehtiarova, N. (2019a). Cloud-based

Service GeoGebra and Its Use in the Educational Pro-

cess: the BYOD-approach. TEM Journal, 8(1):65–72.

https://doi.org/10.18421/TEM81-08.

Semenikhina, O. V., Drushliak, M. G., and Khvorostina,

Y. V. (2019b). Use of GeoGebra cloud service in fu-

ture math teachers’ teaching. Information Technolo-

gies and Learning Tools, 73(5):48–66. https://doi.org/

10.33407/itlt.v73i5.2500.

Shakeabubakor, A. A., Sundararajan, E., and Hamdan,

A. R. (2015). Cloud Computing Services and Ap-

plications to Improve Productivity of University Re-

searchers. International Journal of Information and

Electronics Engineering, 5(2):153–157. https://doi.

org/10.7763/IJIEE.2015.V5.521.

Sheng, J. (2014). Study on Mathematical Model-

ing Software MATLAB Teaching in Higher

Vocational Colleges. International Jour-

nal of Technology Management, (6):127–130.

https://qikan.cqvip.com/Qikan/Article/Detail?id=

49483643&from=Qikan Article Detail.

Shyshkina, M. P. and Popel, M. V. (2013). Cloud based

learning environment of educational institutions: The

current state and research prospects. Information

Technologies and Learning Tools, 37(5):66–80. https:

//doi.org/10.33407/itlt.v37i5.903.

Smith, A., Bhogal, J., and Sharma, M. (2014). Cloud Com-

puting: Adoption Considerations for Business and Ed-

ucation. In 2014 International Conference on Fu-

ture Internet of Things and Cloud, pages 302–307.

https://doi.org/10.1109/FiCloud.2014.54.

Tukholko, L. L. (2018). Development of Constructive

Activity of X–XI-Grades Pupils When Teaching

Geometry. PhD thesis, Belarusian State University,

Minsk. https://elib.bsu.by/bitstream/123456789/

194893/1/%D0%90%D0%B2%D1%82%D0%BE%

D1%80%D0%B5%D1%84%D0%B5%D1%80%

D0%B0%D1%82%20%D0%A2%D1%83%D1%

85%D0%BE%D0%BB%D0%BA%D0%BE.pdf.

Ziatdinov, R. and Valles, J. R. (2022). Synthesis of Mod-

eling, Visualization, and Programming in GeoGebra

as an Effective Approach for Teaching and Learn-

ing STEM Topics. Mathematics, 10(3):398. https:

//doi.org/10.3390/math10030398.

C¸ ekmez, E. (2020). Using dynamic mathematics software

to model a real-world phenomenon in the classroom.

Interactive Learning Environments, 28(4):526–538.

https://doi.org/10.1080/10494820.2019.1674882.

C¸ ekmez, E. (2023). An example of the use of GeoGebra for

simulation: Buffon’s needle problem. International

Journal of Mathematical Education in Science and

Technology, 54(1):132–140. https://doi.org/10.1080/

0020739X.2022.2034063.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

348