System-Forming Aspects of the Computer Science and Mathematics

Teachers’ Readiness to Develop and Use Computer Didactic Games in

Educational Process

Oksana V. Klochko

1 a

, Roman S. Gurevych

1 b

, Vasyl M. Fedorets

2 c

, Vitalii I. Klochko

3 d

Oleh L. Konoshevskyi

1 e

and Mariana M. Kovtoniuk

1 f

Vinnytsia Mykhailo Kotsiubynskyi State Pedagogical University, 32 Ostrozhskogo Str., Vinnytsia, 21100, Ukraine

Vinnytsia Academy of Continuing Education, 13 Hrushevskoho Str., Vinnytsia, 21050, Ukraine

Vinnytsia National Technical University, 95 Khmelnytsky Hwy., Vinnytsia, 21021, Ukraine

Keywords:

Readiness, Visual-Spatial Aspects, Computer Science Teacher, Mathematics Teacher, Computer Didactic

Games, Educational Process, Professional Activity, Life-Long Learning.

Abstract:

The research, based on the actualization of the innovative paradigm, the ideas of child-centrism, and the analy-

sis of system-formal aspects, presents the conceptualization of readiness of computer science and mathematics

teachers to develop and use CDGs in the educational process. The results of a practically oriented research

state of this readiness are presented, which is considered as an integrated professional and personal ability

of the teacher, consisting of motivational-value, cognitive-active and personal-reﬂective components and is

aimed at using CDGs in the educational process as a relevant innovative technology. In the system of the

cognitive-activity component, the spatial aspect is analyzed. Actualization of the spatial aspect is considered

as a way of revealing the phenomenology of real and virtual spaces, presented as signiﬁcant pedagogical en-

vironments of cognitive-semantic and spatial-value contexts. Based on the generalization of the results of the

study of motivational-value, cognitive-active and personal-reﬂective criteria of the readiness of computer sci-

ence and mathematics teachers to develop and use CDGs, the average level of its formation was determined.

The main educational strategies aimed at improving this readiness are determined, among which the addition

of educational programs with topics that reﬂect the ways and practices of applying CDGs in the preparation

of future computer science and mathematics teachers, their retraining and advanced training are relevant; the

use of innovative pedagogical technologies for the formation of computer science and mathematics teachers

to develop and use CDGs in the educational process, etc.

1 INTRODUCTION

The current direction of today’s education is creat-

ing conditions for shaping an individual who is at

the same time professionally competent, socially en-

gaged and creative. The content of the knowledge to

be acquired by modern specialists, its volume, the set

of skills necessary for professional activities are con-

stantly changing and increasing. All spheres of edu-

cation are searching for ways to intensify and quickly

modernize the training system, improve education

quality by using digital technologies as an instrument

https://orcid.org/0000-0002-6505-9455

https://orcid.org/0000-0003-1304-3870

https://orcid.org/0000-0001-9936-3458

https://orcid.org/0000-0002-9415-4451

https://orcid.org/0000-0001-8408-1829

https://orcid.org/0000-0002-7444-1234

for human activities and a new and fundamentally dif-

ferent way of education. This led to the development

of new methods and forms for the provision of educa-

tion (Yevtuch et al., 2021; Semerikov et al., 2021a,b;

Klochko et al., 2020; Mayer, 2019; Bollin et al., 2021;

Rocha and Barroso, 2021; Picka et al., 2022; Vakaliuk

et al., 2023).

One of the most important tasks of the educational

system today is to introduce educational technologies

that could facilitate the formation of a creative and

active personality, able to meet the challenges and to

achieve the desired goals. The above highlights the

importance of the development and implementation

of different approaches to the realization of educa-

tional tasks, aimed at the development of students’

creative activities.

A computer science and mathematics teacher to-

day has to understand the efﬁcient pedagogical tech-

488

Klochko, O., Gurevych, R., Fedorets, V., Klochko, V., Konoshevskyi, O. and Kovtoniuk, M.

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games in Educational Process.

DOI: 10.5220/0012065600003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 488-514

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

nologies and effectively use digital technologies in

teaching informatics. The use of gaming technologies

and computer didactic games (CDGs), in particular, is

one of such approaches.

The games accompany people throughout life and

this phenomenon greatly attracts the interest of re-

searchers. In the current situation, they may be a great

motivation for students to learn speciﬁc subjects on

the one hand and a way to facilitate teachers’ work on

the other.

Let’s consider the pedagogical and value under-

standing of the phenomenon of computer games. Ac-

cordingly, we will reveal the debatable understanding

of computer games as an innovative educational di-

rection and a system of modern digital technologies

that can bring qualitative changes to the educational

process.

Today’s teachers’ succeed in mastering educa-

tional electronic resources that they use in the class

(Klochko et al., 2020, 2022b; Rybka, 2018; Picka

et al., 2022). CDGs as a system of education may

be an integral part of electronic educational resources.

Computer didactic games present a type of electronic

educational resource that targets students and func-

tions on the basis of digital technologies, presenting

a chain of tasks built on the basis of the development

education. CDGs do not change but complement tra-

ditional game forms and classes, and present a natural

way to attract students to the latest information tech-

nologies (Bollin et al., 2021; Klochko et al., 2020,

2022b). The practical application of such games

demonstrates that they remain valuable educational

tools as they have the following advantages (Mayer,

2019): a new way of working provokes students’ in-

terest in education; practical manipulation assists the

processes of learning,memorization, increases cog-

nitive abilities, enables the realization of individual

learning strategies and stimulates students’ capacity

for research and talent; attractive sounds, actions and

colors make games interesting and help students to

obtain information in a user-friendly form.

CDGs may be divided into three groups (Tobias

and Fletcher, 2012):

1. Educational. They contribute to students’ educa-

tion: develop basic mathematical and computer

science skills, familiarize the child with the alpha-

bet, to obtain and improve knowledge of chem-

istry, physics, geography etc. (ﬁgure 1).

2. Developing. They contribute to students’ cogni-

tive development, encourage activities and inde-

pendent creative work, develop memory, logical

thinking, develop reading skills, etc. (ﬁgure 2).

Figure 1: Bristar: Heroes of Math and Magic (Bristar,

2021).

Figure 2: Scratch: About Scratch (Scratch, 2022).

2. Diagnostic. They determine the level of develop-

ment of students’ skills (ﬁgure 1).

The studies carried out up to now demonstrate

that important skills may be acquired, developed or

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

489

supported by CDGs. The spatial visualization (ro-

tation and mental manipulation by two- and three-

dimension objects), for example, improves during the

reproduction of the video game (Subrahmanyam and

Greenﬁeld, 1994; Klochko et al., 2020). CDGs are

a perfect environment for promoting authentic educa-

tional processes: advancing a process of learning-by-

doing and thus enabling a student to control his/her

own training experience; provide an experience in

simulating interactive scenarios that students deal

with in the real world; the use as an environment for

active learning and improving task solving skills.

Conducting an overview of this problematic, we

will present current directions and important results

and ideas of introducing computer didactic games into

the educational process.

Oliveira et al. (Oliveira et al., 2023) analyzed

a large volume of literature (2108 studies) and pre-

sented a panoramic view of the problem, – they identi-

ﬁed a spectrum of rather contradictory trends and ed-

ucational phenomena of the use of computer games.

According to the results indicated by the authors,

gamiﬁcation in education is studied in the following

areas (Oliveira et al., 2023): deﬁnition of the phe-

nomenon of different perception of gamiﬁcation de-

sign by people; increasing the involvement in activi-

ties and the effectiveness of students’ activities; actu-

alization of the variability and diversity of the imple-

mentation of educational activities; increasing inter-

est and motivation to study; promoting the considera-

tion of the individuality of students and their personal

preferences in the learning process; actualization of

the use of different learning styles; taking into ac-

count the perception and effectiveness of various ped-

agogical methods, orientation towards the transforma-

tion and variability of the structure of knowledge. At

the same time, the authors note that gamiﬁcation can

produce contradictory educational results, which re-

late to both increasing the effectiveness of learning

and motivation for it and interest in it. Important is

their observation that in studies (Oliveira et al., 2023):

for the adaptation of educational systems, students

are mainly involved only as users; there is no sufﬁ-

cient comparison of adapted gamiﬁcation with non-

personalized gamiﬁcation in the works; there is insuf-

ﬁcient evidence of the impact of adapted gamiﬁcation

on student experiences; cultural and gender aspects

of gamiﬁcation are not studied; research does not re-

veal the role of an adapted gamiﬁed educational en-

vironment in relation to its design. The researchers’

ideas that the actualization of cultural, gender, de-

mographic, characterological, and design aspects can

affect the effectiveness of gamiﬁcation are relevant.

Signiﬁcant in this context is the problem of personal-

ization and design.

The effectiveness of education with electronic ed-

ucational game resources in mathematics, conducted

during the study “Rozumnyky” (Smart kids) is de-

scribed in (Bykov et al., 2017). Researches argue that

using electronic educational game resources in the ed-

ucational process contributes to the improvement of

students’ motivation, thinking, and memory and actu-

alizes integrative learning and the development of key

and subject competencies (Bykov et al., 2017).

The research publications gave consideration to

the question of development and efﬁcient implemen-

tation of CDGs or their elements into the educational

process on different levels of education. Relevant in

this aspect is the research of Zhaldak (Zhaldak, 2012)

devoted to the problem of providing educational in-

stitutions with educational software. This problem is

revealed by the authors in the context of humane ideas

of a harmonious combination of computer-oriented

learning technologies and information culture with

existing pedagogical traditions. Information tech-

nologies are also represented as one of the effective

ways of humanizing the educational process and ex-

panding the communication of its participants. Ped-

agogical, health-preserving and spatial aspects of the

use of digital technologies, in particular, work with an

interactive whiteboard, are revealed in the mentioned

research.

System-organizing methodological aspects of the

formation of educational technologies were consid-

ered in the research of Semerikov et al. (Semerikov

et al., 2021b) by rethinking the concepts of “methodi-

cal” and “methodologic/methodical system” and de-

termining ways to develop a “new class of teach-

ing methods – computer-based training systems”. In

particular, they built a model of a computer-oriented

method of teaching informatics for future mathemat-

ics teachers, aimed at forming their informatics com-

petence, a component of which is a method of training

competences in programming and computer games

development (Semerikov et al., 2021b).

Hakak et al. (Hakak et al., 2019) explore the issue

of gamiﬁcation based on cloud technologies. They

point to the need to create a gamiﬁed learning en-

vironment and present an option for a gamiﬁed cur-

riculum, within which different educational subjects

can be integrated. From a spatial point of view, this

study demonstrates an attempt to create a digital edu-

cational quasi-space as “smart”, interactive and inte-

grating different subject areas.

Based on the application of the Preferred Report-

ing Items for Systematic Review and Meta-Analyses

(PRISMA) methodology in three multidisciplinary

databases of educational centers. Manzano-Le

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

490

et al. (Manzano-Le

on et al., 2021) conducted research

on gamiﬁcation. The authors indicate that gamiﬁca-

tion is an effective means of inﬂuencing the academic

performance and motivation of students.

The majority of the studies in this sphere concern

primary education. To a lesser extent, attention is

paid to secondary and higher education. The studies

have mostly been carried out based on the examples

of using CDGs to learn mathematics and languages.

Game is a priority activity for pre-school children and

remains an active way of discovering the world for

primary school children (Varina et al., 2022). Using

games in the educational process for young pupils and

seniors remains less researched, since children of this

age group are educated on the basis of the activities-

oriented approach with the use of more formal ways

of learning.

Michala et al. (Michala et al., 2018) present the

beneﬁts of using CDGs in secondary school for the

development of cognitive and emotion management

skills. The authors’ use of Greek art and culture when

using CDGs is interesting. The use of CDGs and

Greek art actualizes the expressive visual-spatial as-

pect of learning. This reveals the signiﬁcance and

educational effectiveness of interconnected spatial,

visual-spatial and visual-cognitive aspects.

Rybka (Rybka, 2018) undertook a study in which

she examined the phenomenon of gamiﬁcation based

on the example of using computer games for teach-

ing philosophy in engineering higher educational in-

stitutions. The author identiﬁed destructive and neg-

ative phenomena in the process of using game forms,

suggested ways to overcome them. She emphasizes

that game practices, as those that activate and nurture

emotional intelligence, are especially necessary and

valuable for students studying at engineering higher

educational institutions.

Research by Rocha and Barroso (Rocha and Bar-

roso, 2021) is inclusively focused on the design and

implementation of a game application for cognitive

rehabilitation of children with special educational

needs and the elderly. Preliminary results showed that

their computer didactic game can be used as an auxil-

iary tool in special education and in rehabilitation.

Determining the innovative trend and the

practical-technological signiﬁcance of the implemen-

tation of computer didactic games in the educational

process, we actualize the problem of forming a

model of the computer science and mathematics

teachers’ readiness to develop and use CDGs on the

selection of system-forming aspects. The speciﬁed

system-forming aspects are understood as method-

ological and conceptual prerequisites that constitute

the speciﬁed readiness not only axiomatically, but

through the disclosure of the multidimensional

nature of the problem. We highlight the following

system-forming aspects of the computer science

and mathematics teachers’ readiness to develop and

use CDGs: innovative, cognitive-activity, personal-

reﬂective, motivational-valuable, valuable, spatial

which is considered as spatial-cognitive and visual-

spatial, temporal, cultural and educational, creative,

communicative. In this study, we consider the ﬁrst

six system-forming aspects.

The innovative aspect was considered above in

the pedagogical and value understanding of the im-

plementation of gamiﬁcation in the educational pro-

cess. Accordingly, this aspect represents the signif-

icance, features and direction of the introduction of

CDGs into the educational process as an innovative

trend. The innovative orientation of computer didac-

tic games is realized in relation to the concept of the

triangle of knowledge (Unger et al., 2020), which in-

cludes a close interaction of education, science and

innovation.

The following four aspects cognitive-active,

personal-reﬂective, motivational-valuable, valuable

are relatively traditional. They are used integratively

or individually when forming models of readiness,

skills, and competencies. Therefore, three of the spec-

iﬁed aspects – cognitive-active, personal-reﬂective,

motivational-valued – are considered as its compo-

nents in our model. All other aspects to one degree

or another take part in the constitution of readiness.

Special attention in the development of readiness

is given to the spatial aspect, which we consider prac-

tically oriented as spatial-cognitive and visual-spatial.

The use of the spatial aspect in the formation of readi-

ness is determined by the understanding of the com-

puter science and mathematics teachers’ readiness to

develop and use CDGs as a complex anthropological

and cultural-educational phenomenon in which spa-

tiality and visuality are expressive and signiﬁcant.

As an example, we will present a study that is

close in its orientation to our readiness development.

Chen et al. (Chen et al., 2020) analyze ﬁve key

components of game literacy – (1) basic game lit-

eracy, (2) high-level game literacy, (3) instructional

design for game learning, (4) organization and man-

agement of game-based learning, and (5) evaluation

of game-based learning needed by teachers to im-

plement game-based learning. The authors empha-

size the importance of educational design when im-

plementing game-based learning. The result of the

research by Mathe et al. (Mathe et al., 2018) is the

conclusion that the effectiveness of the use of digi-

tal games by Swedish teachers depends on the com-

petence and motivation of teachers for professional

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

491

development, on the availability of appropriate game

resources. Nousiainen et al. (Nousiainen et al., 2018)

present four basic competencies – pedagogical, tech-

nological, collaborative and creative, which are nec-

essary for teachers to effectively implement game

pedagogy.

The use of didactic games, as well as game meth-

ods and technologies in general, contributes to a

deeper methodological and value understanding of the

environment in which they are implemented. First

of all, it concerns virtual and real space. Tradition-

ally, space is understood as a background where the

educational process is implemented. In the system

of modern postmodern scientiﬁc and methodological

ideas, space is like time and the processes that are in

them, or rather, with their help, are implemented in-

tegratively and holistically. Currently, visual-spatial

approaches that have demonstrated their effectiveness

in various ﬁelds of knowledge and life practices are

relevant. One of such signiﬁcant practices and tech-

nologies, which for their effective implementation re-

quire the active inclusion (or at least consideration)

of the “visual-spatial” factor, are games. In addition

to the indicated scientiﬁc and methodological trends

and practical requests, we consider the issue of the

development of the computer science and mathemat-

ics teachers’ readiness to develop and use CDGs in

the context of actualizing the spatial factor.

Accordingly, in this methodology, from a cogni-

tive and axiological point of view, spatial phenom-

ena, as well as real and virtual spaces, are consid-

ered signiﬁcant for the technologicalization of edu-

cation and for the professionalization of mathematics

and computer science teachers. In the scientiﬁc ped-

agogical literature, the visual-spatial aspect of the de-

velopment of the computer science and mathematics

teachers’ readiness to develop and use CDGs is not

sufﬁciently disclosed. This, taking into account the

above-mentioned trends of modern science and the

socio-cultural sphere and requests for the effective-

ness of the practical implementation of game-based

learning methods, deﬁnes the researched problem as

urgent.

For the methodological understanding of space,

including virtual and spatial phenomena, the work of

Avetysian (Avetysian, 2020), which reveals the mean-

ing and nature of visuality, is relevant. In this study,

the authors turn to the classical ideas of visuality by

Merleau-Ponty (Merleau-Ponty, 2005) and Deleuze

(Deleuze, 1989). At the same time, they emphasize

ideas about: the semantic independence of the visual

dimension of culture from language, the principle of

the activity of a visual object, the peculiarities of the

viewer’s interaction with visual phenomena. Thanks

to these ideas of visuality, we understand space not as

a background against which certain events take place,

but as a special spatial world with active spatial phe-

nomena. From the cultural and educational point of

view, the application of the presented ideas of visual

theory for the development of the teacher’s readiness

to use didactic games is relevant. This is due to the

fact that the visual-spatial aspect in the speciﬁed com-

puter technology is one of the system-organizing fac-

tors.

In the theoretical and technological aspects of the

application of the spatial approach and the idea of vi-

suality, research by various authors is relevant.

Briantseva (Briantseva, 2016) reveals the pecu-

liarities of designing digital didactic visual tools.

ackman and Pilebro (B

ackman and Pilebro, 1999)

present a study conducted within the framework of vi-

sual pedagogy, the results of which indicate improved

cooperation during dental treatment in preschool chil-

dren with autism. Du et al. (Du et al., 2022) present

ways of helping children with autism spectrum dis-

order in teaching dental care based on the use of vi-

sual pedagogy tools. Drushliak (Drushliak, 2021) re-

veals the signiﬁcance and features of visual informa-

tion culture of future mathematics and computer sci-

ence teachers and presents its model. Aiello and Parry

(Aiello and Parry, 2019) reveal the features of visual

communication. They emphasize the idea close to us,

that visuality and visual means are a signiﬁcant aspect

of many disciplinary scientiﬁc and practical spheres.

At the same time, the importance of visuality is not

sufﬁciently realized. Goldfarb (Goldfarb, 2002) con-

siders visual pedagogy, visual technology as relevant

directly in the education and life of people, as it needs

further purposeful development.

In scientiﬁc literature, the issue of developing the

computer science and mathematics teachers’ readi-

ness to develop and use CDGs is insufﬁciently dis-

closed. Issues of actualization of spatial aspects in

the system of the speciﬁed readiness, both during its

development and during implementation, are not suf-

ﬁciently disclosed. Taking into account the impor-

tance and innovativeness of the use of computer di-

dactic games for the implementation of the processes

of technologization, virtualization, digitalization, ax-

iologisation, humanization of education, as well as

for the development of the professionalization of the

teacher and the formation of his innovative culture,

the speciﬁed problem is presented as an actual.

The purpose purpose of the research is to study

the value, cognitive-activity, personal-reﬂective and

visual-spatial aspects of the computer science and

mathematics teachers’ readiness to develop and use

computer didactic games.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

492

2 SELECTION OF METHODS

AND DIAGNOSTICS

Information on how CDGs are being developed and

used in the educational process was generated follow-

ing the results of the analysis of public educational

standards (Cabinet of Ministers of Ukraine, 2011),

typical educational programs, curricula, other nor-

mative documents, methodological works of teach-

ers and literature sources. Analysis as for the com-

puter science and mathematics teachers’ readiness to

develop and use CDGs in the educational process

was carried out by using empirical research methods

(observation of teaching activities, questionnaires, in-

terviews), as well as verbal-communicative and psy-

chodiagnostic research methods.

The research used a system of methods and ap-

proaches. Axiological, systemic, spatial, visual-

spatial, cognitive-spatial, psychological, anthropolog-

ical, and teleological (Milat, 2017) approaches were

used. The methods of mathematical statistics, in par-

ticular, descriptive statistics, cluster analysis, were

used to process the research results. To develop

a model of the computer science and mathematics

teachers’ readiness to develop and use CDGs, the

method of pedagogical modeling was used.

The readiness of computer science and mathemat-

ics teachers to develop and use computer didactic

games was determined on the basis of three gener-

alizing criteria. The names of the three criteria corre-

spond to the three components of this readiness. Thus,

we distinguish the following criteria: motivational-

valuable, cognitive-active, personal-reﬂective. Ac-

cordingly, these criteria reﬂect the contents and mean-

ings on the basis of which the components of readi-

ness are formed. The criteria were determined as a

result of the use of various diagnostic methods, in-

cluding the author’s, as well as by analyzing the ed-

ucational achievements of teachers. Each criterion is

characterized by three levels (low, medium, high) of

the formation of a certain component of readiness.

The results were summarized and interpreted based

on the criteria. According to each criterion, we char-

acterized the level of formation of its indicators. Ac-

cording to each criterion for evaluating the computer

science and mathematics teachers’ readiness to de-

velop and use CDGs in the educational process, we

characterized the level of formation of its indicators.

Motivational-value criterion:

• Low: there is no interest in the development of

CDGs; there is a fragmented and limited interest

in certain topics; lack of motivation and interest

in using CDGs; the selection of CDGs is random;

there is no interest in training in the use and de-

velopment of CDGs.

• Medium: existing interest in the development of

CDGs, related to the results; there is a responsi-

ble attitude to learning in the absence of creative

activity; formal interest; motivation is due to the

need to implement CDGs; existing interest in the

application of CDGs in professional activity, re-

lated to its results; there is a responsible attitude to

training in the development and use of CDGs; lack

of understanding of the beneﬁts of using CDGs in

professional activities; episodic manifestation of

creative activity.

• High: Internalization and awareness of the val-

ues of this activity, purposefulness in the imple-

mented CDGs, formation of educational and cog-

nitive motives, existing motivated and responsi-

ble attitude to the use of CDGs in the educational

process, awareness of the educational and innova-

tive signiﬁcance of cognitive motives, systematic

manifestation of creative activity, orientation to-

wards achieving success, professional orientation

for self-improvement; conscious choice of this di-

dactic tool; training in the development and use

of CDGs for the purpose of professional growth;

motivated professional focus on the development

and application of modern CDGs.

Cognitive-active criterion:

• Low: low level of knowledge on the development

and use of CDGs, their low reproducibility, lack

of systematicity; solving simple typical tasks with

the help of others; the ability to use modern CDGs

in professional activities is partially fragmentary

in nature; fragmentary cognitive needs, interests,

motives for developing and using CDGs.

• Medium: the average level of knowledge on the

development and use of CDGs (partial system

knowledge) and their fragmentary reproducibil-

ity; solving standard tasks on the development and

use of CDGs with the help of others; the ability to

independently solve the issue of choosing a CDGs

is not inherent; the presence of cognitive needs,

interests, motives for the development and use of

CDGs.

• High: high level of knowledge (systemic, cre-

ative nature), knowledge of development and use

of CDGs; the ability to independently solve typi-

cal problems, solving non-standard problems, full

reproducibility, independent search for solution

methods, the ability to generate new approaches

in the development and application of CDGs; the

ability to master modern knowledge, generating

ideas, creativity in solving tasks, the ability to in-

dependently master the means of modern CDGs,

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

493

the search for and use of innovations, independent

assessment of the appropriateness of the selec-

tion of modern CDGs; available cognitive activity,

the desire to master modern knowledge, the avail-

ability of methods of scientiﬁc research activity,

the professional orientation of cognitive activity

in theoretical and practical activities; independent

solving of problems of professional orientation of

medium and high levels of complexity of devel-

opment and use of modern CDGs tools; the pres-

ence of elements of creativity in solving problems,

the ability to analyze, synthesize and establish re-

lationships between socio-economic phenomena

and processes; solving non-standard professional

tasks, tasks of a high level of complexity; creative

approach to solving; critical, contextual thinking;

independence in assessing compliance and choos-

ing tools of modern CDGs in solving professional

problems; independent mastery of modern CDGs

in order to solve professional problems, ability to

work in a team.

personal-reﬂectiv criterion:

• Low: there is a fragmented ability to introspect;

inability to plan activities in the process of de-

veloping and using CDGs; low capacity for self-

control and self-regulation; there are inefﬁcient

methods and methods of organizing this activ-

ity, which are not purposefully formed; awareness

of the content of the activity has a fragmentary

spontaneous manifestation; in the vast majority

of cases, the quality of performed tasks is inad-

equately assessed; fragmentary, random manifes-

tation of the ability to self-educate; inability to in-

dependently master material on CDGs.

• Medium: the presence of self-analysis skills,

which is mainly manifested under the inﬂuence

of external factors; existing activity planning for

the development and use of CDGs and the abil-

ity to self-monitor and self-regulate in individual

cases, mainly under the inﬂuence of external fac-

tors; there is a fragmentary manifestation of one’s

own style of activity in the development and use

of CDGs; separate manifestations of a conscious

and purposeful own style of activity; awareness

of the content of the activity and possessing the

ability to evaluate and ensure the quality of the

work performed on the development and use of

CDGs; there is a non-systematic manifestation of

the ability to independently master the material of

individual topics on the development and use of

CDGs.

• High: implementation of a conscious and ade-

quate self-analysis, awareness and prediction of

the results and consequences of the development

and use of CDGs; existing planning of activi-

ties for the development and use of CDGs and

the ability to self-monitor and self-regulate; cog-

nitive abilities aimed at self-development; self-

organizations that are managed and initiated by

the individual himself; available skills to inde-

pendently overcome obstacles; the characteristic

deepness of the self-organization process in the

system of activities for the development and use

of CDGs; there are effective techniques and ways

of organizing one’s own style of activity for the

development and use of CDGs, its conscious and

purposeful formation with elements of creativity

and innovation; awareness of the content of the

development and use of CDGs and the ability to

evaluate and ensure the quality of the work per-

formed; the ability to determine promising direc-

tions for the development and use of the latest

CDGs in professional activities, possessing the

skills to choose and use modern CDGs tools; ca-

pable of self-education in this direction; the abil-

ity to implement knowledge, skills and abilities

to achieve the goal of professional activity in the

development and use of CDGs; the ability to self-

realize, systematic, persistent manifestation, the

ability to achieve success in this activity.

The following techniques were used in the re-

search: “Diagnostics of motivation for success

and fear of failures” (Rean et al., 2000); tests

and questionnaires on determining levels of for-

mation of motivational-value, cognitive-activity and

personality-reﬂexive components; “Self-controlling

Abilities” (Peisakhov, 1984); “Self-Efﬁcacy Test”

(Sherer et al., 1982); “Research of Strong-willed Self-

regulation” (Zverkov and Eidman, 1990).

Questionnaires were used in the research: Ques-

tionnaire for determining the computer science and

mathematics teachers’ value orientations as for the

development and implementation of CDGs in edu-

cational process (developed by Klochko (Klochko,

2018) on the basis of Rean et al. (Rean et al., 2000)

method); Questionnaire for diagnostics of motivation

for success and fear of failures (Rean et al., 2000);

Questionnaire for determining the signiﬁcance of

readiness for the development and implementation of

CDGs for successful professional activities (Greene

et al., 1997; Volochkov, 2007); Questionnaire to de-

termine the percentage distribution of computer sci-

ence and mathematics teachers by levels of the abil-

ity to self-governance (Peisakhov, 1984; Sherer et al.,

1982; Zverkov and Eidman, 1990); Questionnaire for

determining the indicators of cognitive-activity cri-

terion of evaluation of computer science and mathe-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

494

matics teachers’ readiness to develop CDGs and im-

plement them into the educational process (devel-

oped by Klochko (Klochko, 2018) based on Raven

(Raven, 1989) methods); Questionnaire to deter-

mine the percentage distribution of computer sci-

ence and mathematics teachers by levels of the abil-

ity to self-control (Peisakhov, 1984; Zverkov and Ei-

dman, 1990); Questionnaire for determining the Indi-

cators of personality-reﬂexive criterion for evaluation

of computer science and mathematics teachers’ readi-

ness for CDGs development and implementation (de-

veloped by Klochko (Klochko, 2018) based on Rean

et al. (Rean et al., 2000) methods); Fedorets-Klochko

questionnaire for determining the value interpretation

of space by computer science and mathematics teach-

ers.

The ”Questionnaire for determining the com-

puter science and mathematics teachers’ value ori-

entations as for the development and implementa-

tion of CDGs in educational process” contained the

following questions (developed by Gurevych et al.

(Gurevych et al., 2020) on the basis of Rean et al.

(Rean et al., 2000) method):

1. Achieving professional success.

2. Developing personal strengths and abilities.

3. Acquiring professional and information compe-

tencies.

4. Providing material comfort.

5. Achieving recognition and respect in professional

sphere.

6. Improvement of social status.

7. Striving to new achievements.

8. Self development and self improvement.

9. Recognition and respect of managers.

10. Achieving students’ respect.

11. Developing students’ interest to computer sci-

ences.

12. Possibilities to show one’s potential.

13. Possibility to improve pedagogical skills.

14. Possibilities to introduce new methods and forms

of activities.

Respondents answered the questions of the ques-

tionnaire in accordance with two areas – development

of CDGs and introduction of CDGs into the educa-

tional process.

The ”Questionnaire for determining the indica-

tors of cognitive-activity criterion of evaluation of

computer science and mathematics teachers’ readi-

ness to develop CDGs and implement them into the

educational process” contained the following ques-

tions (developed by Gurevych et al. (Gurevych et al.,

2020) based on Raven (Raven, 1989) methods):

I. According to the development of CDGs:

1. I am aware.

2. I have knowledge.

3. I have skills.

4. Able to develop.

5. Realize didactic peculiarities.

6. Realize basic functional possibilities.

7. Realize basic requirements to development.

8. I know how to select topics.

9. I can develop design.

10. I know peculiarities of psychological inﬂuence

on age groups of children.

11. I know how to classify games.

12. I know the basic classes of software.

II. According to the implementation CDGs into the

educational process:

1. I am aware.

2. I have knowledge.

3. I have skills.

4. Able to use.

5. Realize psychological peculiarities.

6. Realize basic functional possibilities.

7. Realize basic requirements to implementation.

8. I know how to select games aimed at attaining

lesson’s goal.

9. I know how to select games aimed at realization

of person-centered approach.

10. Implement with the aim to ensure cross curricu-

lum connections.

11. I know how to classify games.

12. I know which software to use in this sphere.

The ”Questionnaire for determining the Indi-

cators of personality-reﬂexive criterion for evalua-

tion of computer science and mathematics teachers’

readiness for CDGs development and implementa-

tion” contained the following questions (developed

by Klochko (Klochko, 2018) based on Rean et al.

(Rean et al., 2000) methods (Gurevych et al., 2020)):

I. According to the development of CDGs:

1. I am a qualiﬁed developer.

2. I strictly determine a purpose of the develop-

ment.

3. I work much to improve competencies.

4. I want to achieve high results.

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

495

5. I know my weaknesses and strive to improve

them.

6. I constantly search for new methods, forms and

ways for realization.

7. I know what to work with and what to learn in

the nearest future.

II. According to the implementation CDGs into the

educational process:

1. I am a qualiﬁed user.

2. I strictly determine a purpose of implementa-

tion.

3. I work much to improve competencies.

4. I want to achieve high results.

5. I know my weaknesses and strive to improve

them.

6. I constantly search for new methods, forms and

ways for realization.

7. I know how to use and look for necessary

means.

The methodology is aimed at actualizing and re-

vealing the spatial aspect of computer science and

mathematics teachers’ readiness for the development

and use of computer didactic games. In this work,

to reveal the phenomenology of CDGs, we turn to

their understanding and application not only in the

mental-semiotic and cognitive-operational planes, but

as a spatial or, more precisely, “cognitive-spatial”

phenomenon. The speciﬁed methodological insights

correspond to the ideology of the “visual turn” and

“spatial turn” in the methodology of science. A sig-

niﬁcant aspect of considering the indicated method-

ological trends, as signiﬁcant, is that we can purpose-

fully represent virtual reality, ﬁrst of all, as a special

informational and meaning-making space. It is im-

portant to understand the real physical space also as a

special content-semantic or “cognitive-spatial” ﬁeld,

as a meaningful background or context actively in-

cluded in the educational process. Accordingly, the

use of digital technologies of virtual reality with the

active participation of the teacher contributes to the

“transformation” of physical space into the content-

semantic or “cognitive-spatial” ﬁeld of the educa-

tional process. In our opinion, the decisive factor

in the speciﬁed “cognitive transformations” of virtual

reality and real space is the use of game methods.

In our opinion, this is due to the fact that in the se-

mantics of the game in its semantic contexts, the spa-

tial component is relevant but at the same time “hid-

den”. The game, which ﬁrst appears in childhood, is

primarily aimed at the child’s understanding of him-

self as a spatial phenomenon, as well as at revealing

his ability to navigate in space, which, accordingly,

are cognitive processes. Such a cognitive manifes-

tation of life corresponds to the idea of autopoiesis

of Maturana Romes

ın and Varela (Maturana Romes

ın

and Varela, 2009). These authors interpret life as a

cognitive autopoietic process. Accordingly, we ex-

pand and reﬁne the speciﬁed understanding of Mat-

urana Romes

ın and Varela (Maturana Romes

ın and

Varela, 2009) to this educational context. We can note

that for a person it is also a spatial and visual process.

In this work, a “Fedorets-Klochko questionnaire for

determining the value interpretation of space by com-

puter science and mathematics teachers” was devel-

oped to analyze the understanding of computer sci-

ence and mathematics teachers about space as a spe-

cial educational value, space as a possible tool for the

intellectual development of a child, space as a back-

ground and a component of didactic games. An im-

portant methodological prerequisite for the develop-

ment of this questionnaire was the idea of contex-

tual learning, which can be interpreted as follows:

a teacher who understands the surrounding environ-

ment, including space, as a way, as a condition or even

as a “soft” teaching tool, will be more effective, com-

petent and according to the nature of the child, use

CDGs and other methods, in the implementation of

which the spatial aspect is relevant.

The ”Fedorets-Klochko questionnaires for deter-

mining the value interpretation of space by a teacher

of mathematics and computer science” contained the

following questions:

1. The purposeful use of space and spatial phenom-

ena is an important pedagogical condition for ef-

fective disclosure of the content of educational

material in mathematics and computer science.

2. The use of virtual space, augmented reality and

digital technologies is a important pedagogical

condition for the effective disclosure of the con-

tent of educational material in mathematics and

computer science.

3. An integrative consideration of spatial phenomena

and virtual space as meaning-forming and system-

forming factors of the educational process is rele-

vant for effective learning.

4. Virtual space, as well as real space, can be con-

sidered as a meaning-making matrix when imple-

menting game-based learning methods.

5. The game-learning methods and actualization of

phenomena of real space and virtual reality are

presented as conceptualization tools that form a

metaspace of meanings in the study of mathemat-

ics and computer science.

6. In order to improve the efﬁciency of professional

activity, the teacher should apply the phenom-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

496

ena of real space and virtual reality in order to

present the educational material logically in an

“expanded” and illustrative format.

7. Both real and virtual space have their own meta-

logic, which is revealed when using game meth-

ods.

8. Game learning methods and animation reveal the

meaning-making aspect of real and virtual space,

which can be purposefully applied in the study of

mathematics and computer science.

9. The possibility of actualizing the phenomena of

real space and virtual reality is considered as an

instrumental value in the professional activity of a

teacher of mathematics and computer science.

10. The actualization of the phenomena of real space

and virtual and augmented reality corresponds to

the spatial essence of human nature.

We will present the ideas and content-semantic

aspects underlying the “Fedorets-Klochko question-

naire for determining the value interpretation of space

by computer science and mathematics teachers”. This

questionnaire is aimed not only at diagnosing the

teacher’s value interpretation of real and virtual space,

but also at actualizing spatial issues as signiﬁcant in

the study of mathematics and computer science. The

reﬂective aspect of this questionnaire is also impor-

tant, which reveals to the teacher ways of understand-

ing spatial phenomena as educational and life values

(in particular, the value of harmonization).

Question № 1 – “The purposeful use of space and

spatial phenomena is an important pedagogical con-

dition for effective disclosure of the content of edu-

cational material in mathematics and computer sci-

ence” – deﬁnes and actualizes the problems of real

physical space represented as a “pedagogical tool”

and a pedagogical condition for studying mathemat-

ics and computer science. It is clear that the real

space becomes such a “pedagogical tool” by trans-

forming into an educational semantic and meaning-

forming context (space) by integrating the semiotic

ﬁeld of the lesson. This happens with the purposeful

application of various educational methods (in partic-

ular, game ones) during the implementation of which

spatial phenomena are actualized.

Question № 2 – “The use of virtual space, aug-

mented reality and digital technologies is a impor-

tant pedagogical condition for the effective disclosure

of the content of educational material in mathemat-

ics and computer science” – purposefully deﬁnes and

actualizes the problems of virtual space, represented

as an established pedagogical environment and at the

same time digital technology, which is used for learn-

ing mathematics and computer science. Virtual space

by its very nature is an intellectual product and, ac-

cordingly, can be considered as an operational and

educational environment and, accordingly, a ﬁeld of

knowledge and meanings. An important ant aspect of

this virtual space is that it can largely model the real

space one as it corresponds to human nature, includ-

ing spatial thinking, the prerequisite for the formation

of which is a developed human visual analyzer.

Question № 3 – “An integrative consideration

of spatial phenomena and virtual space as meaning-

forming and system-forming factors of the educa-

tional process is relevant for effective learning” – de-

ﬁnes and actualizes the issue of the integrative appli-

cation of virtual space and real space phenomena as

a pedagogical condition and a “spatial” component of

mathematics and computer science learning technolo-

gies. The methodological meaning of this question is

the idea that the purposeful integrative application of

technologies of both virtual space and phenomena of

real space should give a synergistic and harmonizing

educational effect. In children it is necessary to ac-

tualize mathematical thinking through visual percep-

tion and mathematical interpretations of the “world of

things”, “the world of geometric ﬁgures”, “the world

as a three-dimensional space” through the applica-

tion of landscape pedagogy and through the visual

disclosure of the phenomenology of the real world.

As additional effects, it can be noted that this will

also contribute to the preservation of physical and

psychological health and aestheticization of the ed-

ucational process. The speciﬁed “work” with real

space in combination with the use of virtual space

should form the student’s understanding of virtual re-

ality as a special tool and the world included in the

real world. If the speciﬁed harmonization is not car-

ried out, then the opposite effect is possible – the real

three-dimensional space, as well as the world as a

whole, will be considered by the student as a com-

ponent of the virtual. This, in addition to the nega-

tive impact on the psyche, will not give the opportu-

nity to fully reveal the student’s cognitive potential.

Therefore, in the educational process, according to

the ancient Greek idea about the harmonious nature

of man, between virtual reality and real space and the

world, not competitive interactions should be formed,

but synergistic, complementary and harmonious inter-

actions.

Question № 4 – “Virtual space, as well as real

space, can be considered as a meaning-making ma-

trix when implementing game-based learning meth-

ods” – reveals the anthropobiological dimension of

the teacher’s understanding of spatial phenomena.

Accordingly, within the semantic framework of this

question, the space is simultaneously considered: in-

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

497

actively as a neutral background or condition where

the game is implemented, and also as an active learn-

ing tool – as a speciﬁc context ﬁlled with contents and

meanings.

Question № 5 – “The game-learning methods and

actualization of phenomena of real space and virtual

reality are presented as conceptualization tools that

form a metaspace of meanings in the study of mathe-

matics and computer science” – presents game learn-

ing methods not only as activity-cognitive, but also

as cognitive-spatial learning phenomena, which can

form “quasi-spaces” (spaces of meanings) that partic-

ipate in the development of informatic and mathemat-

ical meanings and concepts.

In question № 6 – “In order to increase the ef-

ﬁciency of professional activity, the teacher should

apply the phenomena of real space and virtual real-

ity in order to present the educational material log-

ically in an “expanded” and illustrative format” –

the physical characteristics of spatial reality (ﬁrst of

all, length) are reﬂected. Virtual reality is developed

based on the transformation of the characteristics of

real space. This can be represented as the “logic of

space” and, accordingly, consider spatial phenomena

in the format of “didactics of space”, which real space

determines due to its length (according to Descartes

(Descartes, 2018)). From the standpoint of pedagog-

ical psychophysiology, we interpret the concept of an

expanded representation of educational material, ﬁrst

of all, as a demonstration of certain features, regu-

larities, phenomena, both spatial structures and rela-

tionships between them. For example, the process of

multiplication or addition can be depicted as subject

operations in the spatial and subject ﬁelds. This will

be an expanded format that clearly illustrates a cer-

tain arithmetic operation through “spatial logic”. In

this case, we demonstrate the indicated operations in

detail. As the indicated operation is understood, it

is “transferred” into the symbolic space. The speci-

ﬁed aspect of “transfer” to the middle (interiorization

into mental reality) leads to the phenomenon of “col-

lapse” whose essence is that operations that were rep-

resented through the “logic of space” and the “logic of

object actions” (for example, the close location of two

groups of objects in “spatial semantics” of which was

interpreted as addition) are transformed into a certain

generalizing symbol in which the cognitive operation

itself (for example, revealed during the demonstra-

tion of the operation with the help of objects) may

no longer be displayed as spatial interactions (loca-

tion). The speciﬁed features of the actualization of

the subject ﬁeld and the understanding of space as a

meaning-making context are presented in the classi-

cal concept of the step-by-step formation of mental

actions by Gal’perin (Gal’perin, 2012).

In question № 7 – “Both real and virtual space

have their own metalogic, which is revealed when us-

ing game methods”, game methods are represented

as actualizing and revealing the “multidimensional” –

semiotics, axiology and contextuality of space (real

and virtual). These game methods essentially trans-

form the real space into the quasi-space of the game

by “ﬁlling” it with speciﬁc meanings. Real or virtual

space becomes a semiotic-symbolic ﬁeld in which

and thanks to which the speciﬁed game is imple-

mented, forming conceptualization skills in the child,

which are transformed into components of mathemat-

ical thinking.

Question № 8 – “Game learning methods and ani-

mation reveal the meaning-making aspect of real and

virtual space, which can be purposefully applied in

the study of mathematics and computer science” –

points out the importance of the purposeful use of real

and virtual space for the representation of mathemat-

ical and informational phenomena. That is, consid-

eration of the structure of space and the objects that

ﬁll it as environmental prerequisites for the develop-

ment of mathematical thinking of rational-logical and

multidimensional and systemic external and internal

realities is actualized.

In question № 9 – “The possibility of actualizing

the phenomena of real space and virtual reality is con-

sidered as an instrumental value in the professional

activity of a teacher of mathematics and computer

science” – space is revealed as a special instrumen-

tal value that can underlie the formation of meanings

and goals of educational activities. In the speciﬁed

question, ideas about space are presented as a valu-

able context of educational practices.

Question № 10 – “The actualization of the phe-

nomena of real space and virtual and augmented re-

ality corresponds to the spatial essence of human na-

ture” – reﬂects the phenomenology of man as a spatial

being. In this issue, human nature is considered mul-

tidimensionally and, accordingly, space is presented

as a prerequisite and component of human physical-

ity and its intelligence. This cognitive understanding

of space and the corporeality associated with it cor-

responds to the ideas of Lakoff and Johnson (Lakoff

and Johnson, 1980) on corporeal mind and corporeal

cognitivism. This question is aimed at understand-

ing a person in whom his integrity and physical and

intellectual-spiritual essence has a signiﬁcant and sys-

temic spatial aspect, which accordingly forms an an-

thropic image of a person who is harmonized with

the world. That is, human nature is related to nature

as such. The idea of “anthropo-spatial” and “spatial-

cognitive” intentionalities of a person, which must be

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

498

revealed in the conditions of the educational process,

is embedded in this general question.

The processing of the survey results was carried

out using cluster analysis in order to identify groups

of respondents and to determine ways of forming

and improving the computer science and mathemat-

ics teachers’ readiness to develop and use CDGs in

the educational process. Cluster analysis was per-

formed using the SimpleKMeans method and the

Weka framework for data analysis and machine learn-

ing (WEKA, 2021). We described the SimpleKMeans

algorithm in the research (Klochko et al., 2022a;

Berry and Linoff, 2011). Dunn, DB, SD, CDbw and

S Dbw algorithms were used in the process of data

preprocessing in order to determine the recommended

number of clusters (Brito Da Silva et al., 2020; Mosh-

taghi et al., 2018) (table 1). The structure with the

number of clusters 4 was chosen as the best in terms

of compactness and resolution.

Table 1: Optimal number of clusters, calculated with the

help of quality indices.

Index Algorithms SimpleKMeans

Dunn 4

DB 4

SD 3

CDbw 3

S Dbw 5

The study was conducted in two stages: Stage

I – 2017-2020, 183 computer science and mathemat-

ics teachers from different regions of Ukraine partici-

pated in the study (Gurevych et al., 2020); Stage II –

2022, 123 computer science and mathematics teach-

ers from different regions of Ukraine and Republic of

Moldova participated in the study.

3 RESULTS AND DISCUSSION

The central theoretical result of this research is the

formation of a model of the computer science and

mathematics teachers’ readiness to develop and use

CDGs in educational process. In addition to the ax-

iomatic and systematic approach, which includes the

development of the ﬁeld of problematization with the

selection of the main aspects of the problem, the spec-

iﬁed issue is solved by conducting research (presented

below) (ﬁgure 3).

The development of this readiness model is based

on teleological (target), anthropological and systemic

approaches. Within the framework of the teleological

approach, the harmonious, innovative development of

the personality, which includes the formation of key

and digital competencies, is considered as a prerequi-

site for the realization of the sustainable development

goals and the innovative trend.

This model of readiness of the computer sci-

ence and mathematics teachers’ readiness to de-

velop and use CDGs is based on the pedagog-

ical value and teleological understanding of the

main aspects. The speciﬁed aspects are con-

sidered as system-forming in the development of

this readiness. We distinguish the following

system-forming aspects – innovative, cognitive-

active, personal-reﬂective, motivational-value, valu-

able, spatial, which is considered as spatial-cognitive

and visual-spatial, temporal, cultural-educational,

communicative aspects (ﬁgure 3). Let’s consider

these aspects in more detail.

Among the speciﬁed aspects, we consider

cognitive-active, personal-reﬂective, motivational-

value aspects as “internal” or anthropological, as

such, which can be present in the mental reality of

a professional personality. Based on the actualization

and selection of the speciﬁed aspects as profession-

ally signiﬁcant, a structure of readiness is developed.

The speciﬁed aspects correspond to the name of readi-

ness components and reﬂect the corresponding pro-

fessionally signiﬁcant meanings and directions. The

speciﬁed “internal” aspects are formed on the basis

of activity-semantic and teleological integration of in-

dividual aspects: cognitive, activity, personal, reﬂec-

tive, motivational, value. Such integration of the spec-

iﬁed aspects reﬂects deep professionally signiﬁcant

features, which we present below.

The integrated cognitive-activity aspect in the

readiness model is transformed into its component of

the same name. It reﬂects the cognitive and func-

tional speciﬁcs of the professional activity of a teacher

of mathematics and informatics and the peculiarities

of the intellectualized process of studying these disci-

plines.

The personal-reﬂective aspect, which in the readi-

ness model is transformed into the component of the

same name. He characterizes reﬂection as a deﬁning

professional ability of a computer science and mathe-

matics teachers, which is necessary when studying the

speciﬁed educational disciplines. Reﬂexivity in this

aspect is a professional ability that determines the per-

sonal and professional potential, in particular, for the

implementation of control and veriﬁcation of logical

operations. Therefore, reﬂexivity, both as a cognitive

and as a personal quality, is quite developed among

specialists in mathematics and computer science. For

its realization, reﬂexivity must be deeply included in

the being of a professional, in his personality. Accord-

ingly, the speciﬁed specialists should be capable of

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

499

Figure 3: System-forming aspects of the model of the computer science and mathematics teachers’ readiness to develop and

use CDGs.

long-term, psychologically exhausting work on ﬁnd-

ing optimal solutions, which includes purposeful ac-

tivities to correct possible errors.

The motivational-value aspect, which in the readi-

ness model is transformed into the component of

the same name, reﬂects the humanistic and human-

oriented idea of professionalization of a specialist

based on meaningful and internalized (that is, trans-

ferred to the inner mental reality) values, meanings,

images, intentions, etc. That is, the actualization

of the speciﬁed aspect and the component of readi-

ness corresponding to it is a way of axiologising and

a manifestation of humanistic, by its essence, peda-

gogy, which is based on values. In this aspect, the

idea of “internal motivation” is implemented in ac-

cordance with the self-determination theory (Deci and

Ryan, 2015).

In addition to those presented above, let’s con-

sider other relevant aspects, on the basis of which the

readiness of the computer science and mathematics

teacher to develop and use computer didactic games

is formed – innovative, valuable, spatial (considered

as spatial-cognitive and visual-spatial), temporal, cul-

tural, educational, communicative.

Due to the actualization of the innovative aspect,

the technological-innovative and socio-cultural sig-

niﬁcance of CDGs for the education of the future,

which is the education of sustainable development,

is problematized and revealed. CDGs are an inno-

vative technology, the implementation of which in

the educational process aims to move to a qualita-

tively new level of education. The innovative aspect

is also a determining goal (telosom) in developing the

computer science and mathematics teachers’ readi-

ness to develop and use CDGs. The innovative aspect,

which is primarily explicit (“external”) in relation to

the personality-professional during its internalization

(transfer into mental reality), is considered as part of

the cognitive-activity component of readiness. Pos-

session of the educational theory and practice of the

application of CDGs largely reﬂects the innovative-

ness of the teacher as a professional quality and as his

focus on self-development and creativity. It is signif-

icant that innovativeness is also considered as a value

reference point in the process of implementing CDGs.

The value aspect is primarily an external factor of

the cultural and educational space. When internaliz-

ing the value aspect, it is considered as part of the

motivational-value component of readiness, and in the

system of the cognitive-activity component in the for-

mat of value-oriented knowledge. The value aspect

determines the meanings and orientations that are sig-

niﬁcant in the readiness system.

The cultural and educational aspect reﬂects the

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

500

importance of professional and cultural contexts and

professionally signiﬁcant potentials of the educational

environment in which readiness is developed and im-

plemented. Guided by the anthropological ideas of

Hall (Hall, 1959, p. 10-11) about the contextuality of

cultures, we believe that the cultural and educational

aspect is a deﬁning professional context. The cultural

and educational environment contains values, mean-

ings, stereotypes of interaction, communication and

behavior, ideas, directions, etc. in a contextual for-

mat. The development of readiness includes cultural-

educational, value-semantic contexts and signiﬁcant

ideas that are present in them. Currently, there are

ideas of direction of innovation, child-centeredness,

humanization, technologization, non-violent commu-

nication, tolerance, freedom, democracy, profession-

alization, etc.

The communicative aspect contributes to the con-

sideration of CDGs during their development and im-

plementation as a special professional and commu-

nicative phenomenon, as a way of transferring knowl-

edge, ideas and technologies. This is due to the fact

that the game includes an expressive communicative

aspect and can be interpreted as a way of communi-

cation. Therefore, communicability is primarily em-

bedded in the structure of CDGs and the system of

readiness itself and in all three of its components.

The creative aspect contributes to the considera-

tion of CDGs and their implementation in the edu-

cational process as a creative phenomenon, which at

the same time also contributes to the disclosure of the

creative potential of an individual. Creativity, in turn,

is impossible without spontaneity, a certain creative

freedom, interpretability, social activity and, thus, it

is a guide to the ideas of democracy and freedom as

existential and educational values. Accordingly, the

development of the implementation of CDGs in the

educational process is a way of revealing creativity.

We consider the creative aspect of readiness as part of

the cognitive-activity component.

The temporal aspect actualizes the idea that CDG

is a temporal phenomenon, which is important to take

into consideration during their development and im-

plementation. In turn, CDG, due to its temporal speci-

ﬁcity, can contribute to the development of temporal

competence, provided that the temporal aspect is pur-

posefully actualized.

The spatial aspect is signiﬁcant due to the fact that

CDGs have a distinct spatial dimension, which must

be taken into consideration during their development

and implementation. We consider the spatial aspect

as spatial-cognitive and visual-spatial. The spatial-

cognitive aspect is aimed at developing the teachers’

ability to use spatial phenomena in the educational

process for the representation and illustration of ed-

ucational material. The visual-spatial aspect is aimed

at forming the ability to work with spatial phenomena,

which includes their comprehension and interpreta-

tion. This aspect is also aimed at the development

of visual-spatial intelligence. We consider the visual-

spatial aspect of internalization into the mental reality

of a professional personality within the framework of

the cognitive-activity component of readiness.

Concluding the theoretical consideration of this

problem, we will present the determination of the

computer science and mathematics teachers’ readi-

ness to develop and use CDGs in educational process.

By the computer science and mathematics teach-

ers’ readiness to develop and use CDGs, we under-

stand the integrated cognitive-activity professional-

personal ability of the teacher, which contains expres-

sive value-motivational and reﬂective components

and is aimed at implementation CDGs into the educa-

tional process, and is also implemented on the basis

modern directions – innovative development, human-

ism, child-centrism, creativity, communicativeness,

and taking into account spatial-temporal and cultural-

educational speciﬁcs.

Let’s proceed to consider the results of the study

aimed at determining the state of the computer sci-

ence and mathematics teachers’ readiness to develop

and use CDGs. The study was conducted to establish

the presented readiness structure.

The authors analyzed the results of the evalua-

tion of the components that constitute the readiness

of computer science and mathematics teachers to de-

velop and use CDGs into the educational process.

To evaluate and analyze the levels of components

of the computer science and mathematics teachers’

readiness to develop and use CDGs into the edu-

cational process, the following criteria were used:

the motivational-value criterion, the cognitive-activity

criterion, the personality-reﬂexive criterion.

The speciﬁed criteria integratively characterize

the same name corresponding readiness components.

Motivational-value component of readiness. Ac-

cordingly, the motivational-value criterion character-

izes a set of values, meanings, intentions, motives.

The awareness of these motives, values and meanings

is also important.

Interviewing, questioning and testing were used

in the evaluation of the motivational-value criterion

of computer science and mathematics teachers’ readi-

ness to develop and use CDGs in the educational pro-

cess (Gurevych et al., 2020). During questioning,

we were trying to realize to what extent the activi-

ties related to the development and implementation

of CDGs are understandable, relevant, necessary and

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

501

desirable (among the survey questions diagnostically

signiﬁcant were the following: “Do you agree that

readiness for the development and implementation of

CDGs is an important component of professional and

information competencies of today’s computer sci-

ence teachers?”, “Is it interesting for you to learn the

way of developing and implementing CDGs in the ed-

ucational process more deeply?”).

We also used the “Questionnaire for determining

the signiﬁcance of readiness for the development and

implementation of CDGs for successful professional

activities” (Greene et al., 1997; Volochkov, 2007).

Teachers’ responses showed that teachers are aware

of the importance of readiness for the development

and implementation of CDGs for the successful pro-

fessional activities (high level – 30,4 %, average –

50,1%, low – 19,5% of teachers) (Gurevych et al.,

2020) (see ﬁgure 4).

Figure 4: Signiﬁcance of readiness for the development and

implementation of CDGs for successful professional activ-

ities (high level – 30,4%, average – 50,1%, low – 19,5% of

teachers) (Gurevych et al., 2020).

Value orientations, which had become a subject

of study, also contribute to the achievement of pro-

fessional success in teaching computer science and

mathematics. For their diagnostics, the “Question-

naire for determining the computer science and math-

ematics teachers’ value orientations as for the devel-

opment and implementation of CDGs in educational

process was used” (developed by Klochko (Klochko,

2018) on the basis of Rean et al. (Rean et al., 2000)

method) (table 2, ﬁgure 5).

Thus, understanding the importance of the devel-

opment and implementation of CDGs into the ed-

ucational process, the dominating values of teach-

ers are the following: possibilities to introduce new

methods and forms of works with students, develop

students’interest to computer sciences, possibility to

improve pedagogical skills in using CDGs, self-

development, self-improvement as well as achiev-

ing professional success, development of personal

strengths, talents, acquiring professional and informa-

Table 2: Hierarchy of computer science and mathematics

teachers’ value orientations as for the development and im-

plementation of CDGs in educational process. (The ques-

tion number column is labeled “№”.)

Rating indicators Rating indicators

№ of the development of the using

of CDGs of CDGs

1 4 6

2 4 5

3 4 9

4 13 13

5 10 11

6 14 14

7 9 7

8 2 4

9 12 12

10 11 10

11 2 1

12 7 7

13 8 3

14 1 1

tion competencies in developing CDGs. The analy-

sis of discrepancies showed that teachers give more

priorities to using CDGs in the educational process

ratherthan developing them. In addition, the sphere

of CDGs development is of higher priority than their

implementation for acquiring professional and infor-

mation competencies.

Such results may mean that teachers do not fully

realize the possibilities of professional growth in

develop and using CDGs and do not comprehend

all possibilities and ways for improving their teach-

ing skills. It may be assumed that computer sci-

ence and mathematics teachers are sufﬁciently ori-

ented in the process of implementing new methods

and forms of works in the classroom. They know

how to develop students’ interest in computer sci-

ence, to improve teaching skills and strive to self-

development and self-improvement aimed at achiev-

ing professional success in the acquisition and devel-

opment corresponding knowledge, abilities and skills

in the sphere of CDGs. Additionally, there is a lack

of care for material comfort, improvement in social

status, recognition in the professional sphere, and

achievement of respect. However, computer science

and mathematics teachers were also observed to be

more oriented towards professional realization and

improvement, which dominated their requirement for

recognition and respect, improve social status, ensur-

ing material comfort.

The motivation for achievement favours an in-

crease in persistence, self-esteem, regulation of activi-

ties, the formation of readiness for the development of

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

502

Figure 5: Hierarchy of computer science and mathematics teachers’ value orientations as for the development and implemen-

tation of CDGs in educational process.

CDGs and their implementation into the educational

process. The results of the survey of computer sci-

ence and mathematics teachers show that following

the methodology “Diagnostics of motivation for suc-

cess and fear of failures” (Rean et al., 2000), 59,2%

of teachers have motivation on the average level (the

motivational pole is not clearly deﬁned), 21,4% of

teachers have a high level of motivation (motivation

for success is diagnosed), and 19,4% of teachers have

a low one (the motivation of fear of failure is diag-

nosed) (ﬁgure 6). The motivation for achievement

activates subjective efforts of computer science and

mathematics teachers, directed to the desired outcome

in personal and professional development.

According to the results of the study of the

motivational-value component of computer science

and mathematics teachers’ readiness to develop and

use CDGs in educational process, in particular, its

motivational-value component, we can conclude that

21,4% of teachers are diagnosed with motivation for

success and 30,4% of teachers are diagnosed with

high level of signiﬁcance of readiness for the devel-

opment and implementation of CDGs for successful

professional activities.

Personality-reﬂexive component of readiness.

This component was considered with the applica-

tion of research methods of the ability to self-control

Figure 6: Results of the diagnosis of motivation for success

and fear of failure (high level (motivation for success is di-

agnosed) – 21,4%, average – 59,2% (the motivational pole

is not clearly deﬁned), low – 19,4% of teachers (the moti-

vation of fear of failure is diagnosed).) (Gurevych et al.,

2020).

and reﬂective potential of the individual. “Question-

naire to determine the percentage distribution of com-

puter science and mathematics teachers by levels of

the ability to self-control” (Peisakhov, 1984; Zverkov

and Eidman, 1990) and “Questionnaire for determin-

ing the Indicators of personality-reﬂexive criterion

for evaluation of computer science and mathemat-

ics teachers’ readiness for CDGs development and

implementation” (developed by Klochko (Klochko,

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

503

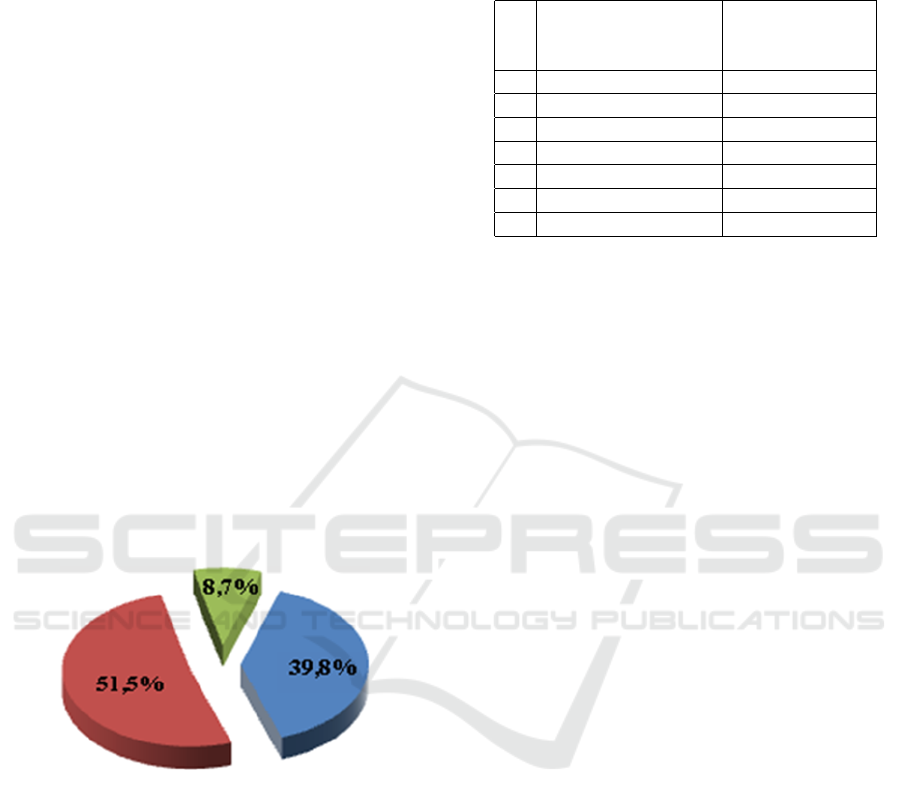
2018) based on Rean et al. (Rean et al., 2000) meth-

ods) were used for this purpose. Accordingly, the

personality-reﬂexive component was used, which is

characterized by the determination of the teacher’s

personal style of activities, the awareness of the con-

tent of activities, the abilities to evaluate outcomes

and consequences, the skills of self-education, self-

realization in the professional activities, and life-long

learning. The indicators of this criterion are: the abil-

ity for self-analysis, self-control, self-organization;

the availability of the personal style of activities; un-

derstanding the scope of the activities on CDGs de-

veloping and implementing; the self-education skills.

The study enabled us to set up the following

system-creative factors that determine the ability of

computer science and mathematics teachers for self-

control: restraint, sense of duty, will power, disci-

plined manner, and responsibility.

The research results, using the ability to self-

control and reﬂective potential of the individual meth-

ods, show that the average values of self-control qual-

ity levels of computer science and mathematics teach-

ers were distributed as follows: high level – 39,8%,

average level – 51,5%, low level – 8,7% (ﬁgure 7)

(Gurevych et al., 2020). In our opinion, such results

may be explained by job requirements and social con-

text.

Figure 7: Percentage distribution of computer science and

mathematics teachers by levels of the ability to self-control

(high level – 39,8%, average – 51,5%, low – 8,7% of teach-

ers).

Hence, as average indicators of the personality-

reﬂexive criterion of computer science and mathe-

matics teachers’ readiness to develop and implement

CDGs show that the highest rank belongs to teachers’

striving for strong performance in this area, for aware-

ness of shortcomings and sincere endeavor to im-

prove performance (diagnosed using the “Question-

naire for determining the Indicators of personality-

reﬂexive criterion for evaluation of computer science

and mathematics teachers’ readiness for CDGs de-

velopment and implementation”) (table 3, ﬁgure 8)

(Gurevych et al., 2020).

Summarizing the results of the research through

Table 3: Indicators of personality-reﬂexive criterion for

evaluation of computer science and mathematics teachers’

readiness for CDGs development and implementation. (The

question number column is labeled “№”.)

In the sphere of In the sphere of

№ CDGs development, implementation,

ranking ranking

1 7 4

2 5 2

3 6 6

4 1 1

5 2 3

6 4 5

7 3 7

their integrative consideration and interpretation

within the semantic framework of the personality-

reﬂexive criterion, we note that according to the self-

control indicator, most computer science and mathe-

matics teachers are diagnosed with medium and high

levels of the ability to self-control. According to the

results of diagnosing the indicators of the personal-

reﬂective criterion for assessing the computer science

and mathematics teachers’ readiness to develop and

use CDGs, it can be concluded that teachers mostly

want to achieve high results in the areas of developing

and using CDGs, know their shortcomings and strive

to correct them, try to work in the direction of ﬁnd-

ing new methods of techniques, forms, ways of im-

plementing CDGs, but to a lesser extent they work on

improving acquired competencies in this area.

Cognitive-activity component of readiness. For-

mation of computer science and mathematics teach-

ers’ readiness for the development and implementa-

tion of CDGs into the educational process has to be

based on practically oriented knowledge and intellec-

tual skills. The indicators of the cognitive-activity cri-

terion, which reﬂects the content and the technology

of development and implementation of CDGs, as well

as individual and psychological peculiarities of teach-

ers’ readiness, in particular cognitive, are: the ﬁeld

knowledge, the abilities to use the ﬁeld knowledge for

professional purposes and the cognitive activities.

Research according to the cognitive-activity cri-

terion was carried out using the “Questionnaire for

determining the indicators of cognitive-activity cri-

terion of evaluation of computer science and mathe-

matics teachers’ readiness to develop CDGs and im-

plement them into the educational process” (devel-

oped by Klochko (Klochko, 2018) based on Raven

(Raven, 1989) methods), “Questionnaire to deter-

mine the percentage distribution of computer sci-

ence and mathematics teachers by levels of the

ability to self-governance” (Peisakhov, 1984; Sherer

et al., 1982; Zverkov and Eidman, 1990), “Fedorets-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

504

Figure 8: Indicators of personality-reﬂexive criterion for evaluation of computer science and mathematics teachers’ readiness

for CDGs development and implementation.

Klochko questionnaire for determining the value in-

terpretation of space by computer science and mathe-

matics teachers”, as well by the analysis of results of

computer science and mathematics teachers’ knowl-

edge in CDGs development and implementation the-

ory (the method of monitoring quiz (oral and writ-

ten) were used). This criterion also reﬂects the im-

portance of metacognitive strategies, which include

the formed abilities for goal setting, self-evaluation,

self-management, planning, control, and intellectual

reﬂection. It is signiﬁcant that the mentioned intel-

lectual qualities should be essentially activity and,

accordingly, aimed at the professional sphere of the

teacher and, above all, at the development and use of

CDGs. Within the framework of this criterion, spa-

tiality is deﬁned as an actual direction of the teacher’s

intellectual development. The spatial aspect is pre-

sented as spatio-cognitive and visual-spatial. Accord-

ingly, within the semantic framework of spatiality, the

problematic of the teacher’s availability of valuable

knowledge, understanding, intellectual intentions and

reﬂections of both real and virtual spaces is actualized

(Yevtuch et al., 2021). The cognitive-activity crite-

rion for the evaluation of computer science and math-

ematics teachers’ readiness for development and im-

plementation of CDGs characterizes the level of the-

oretical knowledge, ability to use and create activities

that are of signiﬁcant importance in the professional

practice of computer science and mathematics teach-

ers.

The estimation of professional achievements,

however, does not fully reﬂect the level of com-

puter science and mathematics teachers’ knowledge

in this sphere, as it is a pretty formal indicator of their

readiness for the development and implementation of

CDGs. The average results of the quiz show that

computer science and mathematics teachers’ knowl-

edge in theory of CDGs development and implemen-

tation is as follows: high – 4,2% and 24,8%; average –

11,2% and 46,5%; low – 84,6% and 28,7% (ﬁgure 9,

ﬁgure 10) (Gurevych et al., 2020).

Figure 9: Average results of computer science and math-

ematics teachers’ knowledge in CDGs developing theory

(high level – 4,2%, average – 11,2%, low – 86,4% of teach-

ers) (Gurevych et al., 2020).

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

505

Figure 10: Average results of computer science and math-

ematics teachers’ knowledge in CDGs implementation the-

ory (high level – 24,8%, average – 46,5%, low – 28,7% of

teachers) (Gurevych et al., 2020).

Identifying the indicators of the cognitive-activity

criterion, we proceeded from the importance of

metacognitive strategies. Accordingly, with formed

meta-cognitive strategies the computer science and

mathematics teachers understand the process of de-

velopment and implementation of CDGs as a focused

and result-based management of the professional ac-

tivities and life-long learning that simulates abilities

to predict outcomes, plan, control, evaluate, monitor

and manage this process, overcome difﬁculties at the

time of achieving tactical and operational purposes as

well as strategic goals. we assumed that computer

science teachers understand the process of develop-

ment and implementation of CDGs as a focused and

result-based management of the professional activi-

ties and life-long learning that simulates abilities to

predict outcomes, plan, control, evaluate, monitor and

manage this process, overcome difﬁculties at the time

of achieving tactical and operational purposes as well

as strategic goals.

So, the results of the tests using the “Question-

naire to determine the percentage distribution of com-

puter science and mathematics teachers by levels of

the ability to self-governance” reveal that the com-

puter science and mathematics teachers’ ability to

self-governance, mainly, is on the average level. The

percentage distribution by ability levels is as follows:

35,7% – high, 53,0% – average, 11,3% – low level

(ﬁgure 11) (Gurevych et al., 2020). These data show

that computer science and mathematics teachers ac-

cording to the self-governance indicator, which to

a large extent integratively reﬂects the formation of

metacognitive strategies, are ready to develop and use

CDGs in educational process.

The study shows that the formation of the readi-

ness of computer science and mathematics teach-

ers to develop and implement CDGs into the educa-

tional process is impossible without the correspond-

ing knowledge and intellectual skills in these spheres,

such as: knowledge of CDGs’ tools of develop-

Figure 11: Percentage distribution of computer science

and mathematics teachers by levels of the ability to self-

governance (high level – 35,7%, average – 53,0%, low –

11,3% of teachers) (Gurevych et al., 2020).

ment and implementation (classiﬁcation, functional

possibilities, didactic peculiarities, development re-

quirements), skills in selection of topics, design de-

velopment, knowledge of psychological peculiarities

of students’ age groups, etc. (table 4, ﬁgure 12)

(Gurevych et al., 2020). The efﬁcient management

of this process demands knowledge of problem anal-

ysis, a clear vision of the situation, and the ability to

forecast and plan future actions.

Table 4: Indicators of cognitive-activity criterion of evalu-

ation of computer science and mathematics teachers’ readi-

ness to develop and implement CDGs into the educational

process. (The question number column is labeled “№”).

In the sphere of In the sphere of

№ CDGs development, implementation,

ranking ranking

1 1 1

2 7 3

3 8 4

4 10 5

5 8 12

6 6 10

7 11 8

8 2 2

9 12 11

10 4 8

11 3 5

12 5 7

Summarizing the results of the research through

their integrative consideration and interpretation

within the semantic framework of the cognitive-

activity criterion, we note that according to the in-

vestigated indicators of the cognitive-activity crite-

rion, the majority of respondents are diagnosed with

an average and high level of formation indicators of

cognitive-activity and self-governance. The average

level of theoretical knowledge of computer science

and mathematics teachers on the development and use

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

506

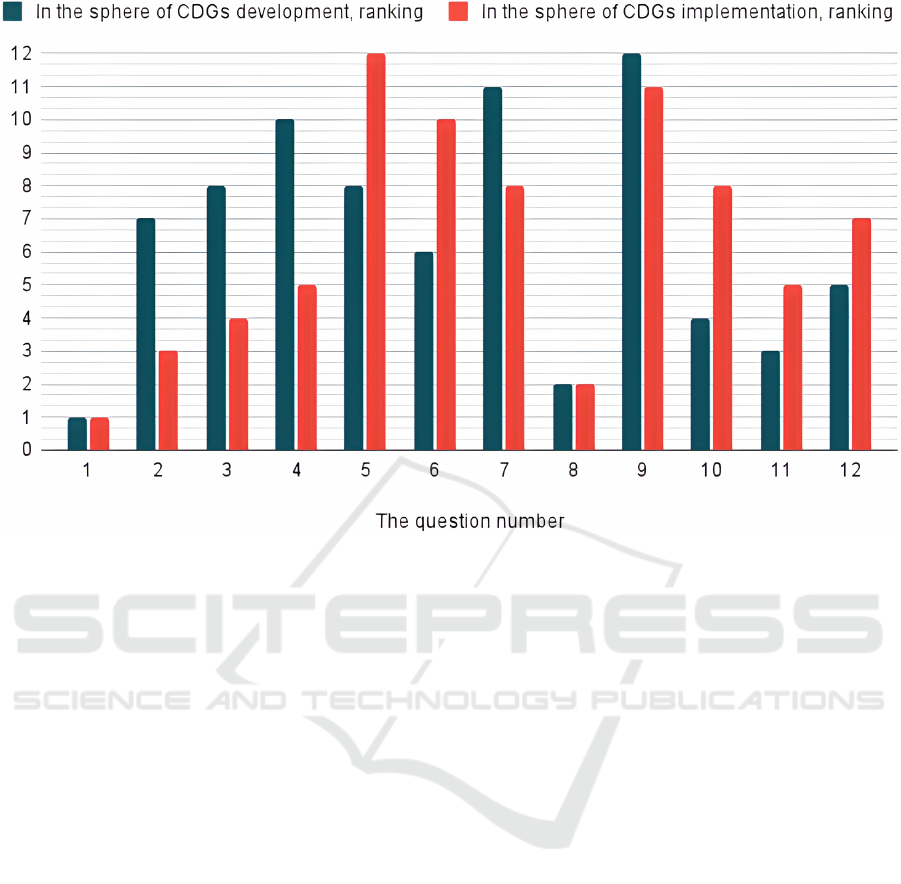
Figure 12: Indicators of cognitive-activity criterion of evaluation of computer science and mathematics teachers’ readiness to

develop and implement CDGs into the educational process.

of CDGs in the educational process was also diag-

nosed, respectively 11,2% and 46,5%, and the high

level of theoretical knowledge of computer science

and mathematics teachers on the use of CDGs, re-

spectively 4,2% and 24,8%. It should be empha-

sized that 86,4% of respondents are diagnosed with

a low level of theoretical knowledge on the devel-

opment of CDGs. This may be due to the fact that

in the process of training and retraining, professional

development of informatics and mathematics teach-

ers, less attention is given to the topic of developing

computer games for use in the educational process.

The study shows that computer science and mathe-

matics teachers fully understand the process of devel-

opment and implementation of CDGs, know how to

choose games aimed at achieving lesson objectives.

They have knowledge, skills and are able to use CDGs

in the educational process but have little experience

in their development. In their professional activities,

computer science and mathematics teachers also face

difﬁculties in understanding the psychological pecu-

liarities of using CDGs by students. Teachers also

have to deal with the issue of the deﬁnition of the main

functionalities of CDGs, since their selection directly

inﬂuences the realization of the student-centered ap-

proach.

During the II stage of the research, which took

place in 2022, the value interpretations of space by a

mathematics and computer science teacher were stud-

ied. This study is considered in the content-semantic

framework of the formation of the cognitive-activity

component of readiness that was studied. The spatial

direction of the research is determined by the fact that

the speciﬁcity of the development of the cognitive-

activity component of readiness is the actualization

of the spatial aspect. The spatial aspect is presented

in two formats: visual-spatial, which helps to re-

veal visual-spatial intelligence, and spatial-cognitive,

which is aimed at the teacher’s use of spatial phenom-

ena (both real and virtual spaces) for purposeful rep-

resentation and illustration of relevant topics in math-

ematics and computer science.

Let’s consider the results of the questionnaire us-

ing the “Fedorets-Klochko questionnaire for deter-

mining the value interpretation of space by computer

science and mathematics teachers” using the method-

ological and interpretive potential of cluster analysis.

In the process of applying the SimpleKMeans algo-

rithm to the clustering model, built on the basis of a

set of data obtained during the questionnaire survey, 4

clusters (number 0, 1, 2, 3) were formed, the centroids

of which are shown in the table 5 (ﬁgure 13).

Cluster № 0 is the largest in terms of volume and,

accordingly, formed 53% of the responses. The spec-

iﬁed cluster unites answers that deﬁne space (real and

virtual) as a “pedagogical-technological” value that

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

507

Table 5: Model and evaluation of clustering data using the SimpleKMeans algorithm. (The question number column is labeled

“№”.)

№ Cluster № 0, 53% Cluster № 1, 23% Cluster № 2, 13% Cluster № 3, 13%

1 2 1 1 3

2 3 1 1 3

3 2 2 0 3

4 2 1 0 3

5 2 1 0 3

6 2 0 1 3

7 2 1 2 3

8 2 2 2 3

9 2 1 0 3

10 1 0 3 3

is signiﬁcant in the process of teaching mathemat-

ics and computer science when using didactic com-

puter games (ﬁgure 14). This cluster deﬁnes the pos-

itive interpretation of space in quantitative represen-

tation as the middle between negative and highest.

Accordingly, a positive understanding of space as an

“pedagogical-instrumental” value can be purposefully

applied in the educational process. Cluster 0 dom-

inates in the speciﬁed sample is half. This domi-

nance indicates that the studied teachers, who make

up half of the sample, have a generally positive at-

titude towards this problem. At the same time, the

indicated “middle position” in the sample indicates a

not maximum readiness to actualize the spatial com-

ponent when using didactic computer games. The

not-total “fascination” with visual-spatial issues also

indicates the critical thinking and personal and intel-

lectual maturity of teachers, because the representa-

tion of space as an instrumental value is relatively

new and for many teachers it was revealed through

their questionnaires. As mentioned above, the pur-

pose of the survey was not only diagnosis, but also

actualization of the phenomenology of space as value-

oriented and technologically oriented. The trends of

Europeanization, democratization and humanization

of Ukrainian education deﬁned in the Concept of the

New Ukrainian School (Zhorova et al., 2022) play a

certain role in such a dominant, but at the same time,

“moderate” or “medium” distribution. The speciﬁed

educational trends contribute to the professional de-

velopment of the teacher. Accordingly, the teacher

develops as a competent, critical-thinking and inde-

pendent person who ﬁnds and forms “his” teaching

methodology and methods.

Clusters № 1 (23%) and Clusters № 2 (13%) (total

36%) include answers that represent space (real and

virtual) as a “pedagogical-technological” value that is

considered signiﬁcant, neutral or negative in the con-

text of teaching mathematics and computer science

when using didactic computers computer games. Ac-

cordingly, the answers can be presented as a contin-

uum from negative to positive – 0, 1, 2 and 3 (one

answer). The presence of cluster № 1 and cluster №

2 (total 36%), which are quite signiﬁcant in terms of

volume, which makes up more than a third, speaks of

a certain novelty and possible certain incomprehensi-

bility of the actualized issues, which are represented

in general terms, and not as a speciﬁc technology. It is

clear that at this stage the speciﬁed “visual-spatial ap-

proach” is ﬁrst of all revealed at the level of method-

ology in the form of general ideas and interpretations.

Cluster № 3, which is represented by 13% of re-

spondents’ answers, represents the highest level of

teachers’ interpretation of space (real and virtual) as

a technological value that is signiﬁcant in the process

of teaching mathematics and computer science when

using didactic computer games. We explain the rel-

atively small percentage of people who, at the high-

est level, interpret space (real and virtual) in a value-

oriented way, considering it as a probable component

of the implementation of computer didactic games,

by the relative novelty of such a spatial approach, the

complexity and non-traditionality of its implementa-

tion (ﬁgure 14). In this aspect, it can be noted that

the emergence of virtual space as a digital technology,

as a speciﬁc “anthropo-techno-cultural” phenomenon

and the actualization of game-based learning meth-

ods provides an opportunity to better understand the

educational signiﬁcance of the cognitive-valuable po-

tential of real space. In general, we observe a “shift”

in pedagogy towards the active use of environmen-

tal, contextual, “background” approaches to learning.

Accordingly, the environment, including space and

time, is understood not only as a background for the

educational process, but also as a special meaning-

ful and value-semantic aspect of learning or, even, a

“visual-spatial educational tool”.

Having analyzed the structure of the distribution

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

508

Figure 13: The centroid values of the clusters according to the question number of the “Fedorets-Klochko questionnaire for

determining the value interpretation of space by computer science and mathematics teachers” are presented in a bar and linear

charts.

of answers by clusters, it can be noted that it re-

ﬂects the indicated trends of the emergence and ac-

tive development of contextual approaches (including

visual-spatial) in education and the active use of digi-

tal technologies.

Summarizing and interpreting the results of the

research of the spatial aspect in the system of the

cognitive-activity component of the studied readiness,

we can note that they reveal the relevance and signif-

icance of this “visual-spatial-cognitive” direction of

the development of the speciﬁed readiness, ﬁrst of all

from a practical and pedagogical point of view. It

is important that many teachers understand the phe-

nomenology of real and virtual space as a signiﬁcant

pedagogical tool that corresponds to the current mod-

ern ideas of spatial pedagogy, existential pedagogy,

child-centeredness, and contextual learning.

We can say that we are witnessing the beginning

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

509

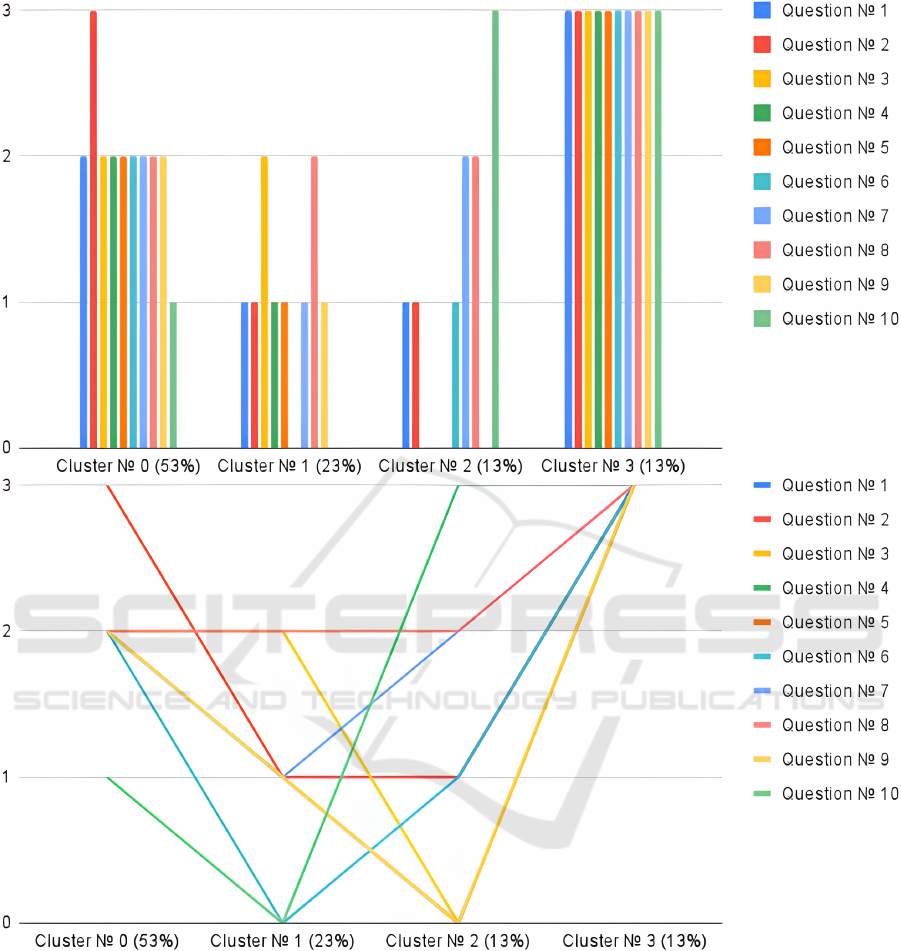
Figure 14: The centroid values of the clusters according to the cluster number of the “Fedorets-Klochko questionnaire for

determining the value interpretation of space by computer science and mathematics teachers” are presented in a bar and linear

chart.

of an active integrative application of digital, spatial,

game, axiological methods and technologies, which

corresponds to the paradigmatic attitudes of postmod-

ernism, including the ofﬁcially deﬁned direction of

sustainable development, which pays special attention

to the “terrestrial space” and the person in it.

4 CONCLUSIONS

The readiness of computer science and mathemat-

ics teachers to develop and use CDGs in the educa-

tional process is a complex integrative personality-

professional formation, consisting of motivational-

value, cognitive-activity and personality-reﬂexive

components, which speciﬁed in their corresponding

criteria.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

510

By the computer science and mathematics teach-

ers’ readiness to develop and use CDGs, we un-

derstand the integrated cognitive-activity profession-

alpersonal ability of the teacher, which contains

expressive value-motivational and reﬂective compo-

nents and is aimed at implementing CDGs into the

educational process, and is also implemented on the

basis of modern directions – innovative develop-

ment, humanism, child-centrism, creativity, commu-

nicativeness, and taking into account spatial-temporal

and cultural-educational speciﬁcs.

Determining the state of formation of the

motivational-value component of readiness, we can

indicate that according to the indicator of motivation

for success in professional activity, 59,2% of teachers

have an average level of motivation (the motivational

pole is not clearly deﬁned), 21,4% of teachers have a

high level of motivation (success motivation is diag-

nosed), and 19,4% of teachers have a low level (diag-

nosed lack of success motivation). According to the

indicator of the value of readiness for the development

and implementation of CDGs for successful profes-

sional activity, the following levels were determined:

30,4% – high, 50,1% – medium, 19,5% – low. There

is a certain correlation between the above indicators,

which indicates both the formation of the motivational

and value sphere and its professional orientation, as

well as its focus on the application of CDGs. The fol-

lowing value orientations in the ﬁeld of development

and use of CDGs in the educational process were also

determined to be signiﬁcant for teachers: “Possibili-

ties of introducing new methods and forms of working

with students”, which indicates developed innovative-

ness; “Development of students’ interest in studying

informatics”, which indicates the child-centered ori-

entation of teachers. Thus, analyzing and interpret-

ing the values of the above indicators, we can note

that according to the motivational-value criterion, an

average level of formation of the motivational-value

component of readiness is observed in most teachers.

According to the cognitive-activity component of

readiness according to the indicator of the ability

to self-governance, which reﬂects the formation of

metacognitive abilities, which includes goal setting,

self-esteem, self-management, planning, control, in-

tellectual reﬂection, the obtained percentage distri-

bution of its formation is 35,7% – high, 53,0% –

medium, 11,3% – low in terms of levels. The pres-

ence of the prevailing high and medium levels indi-

cates a sufﬁciently high initial level of formation of

metacognitive abilities, which are included both in the

composition of the studied readiness and in the pro-

fessional and pedagogical competences of a computer

science and mathematics teacher. The average level

of theoretical knowledge of informatics and mathe-

matics teachers regarding the development and use of

CDGs in the educational process was diagnosed: av-

erage – 11,2% and 46,5%; high – 4,2% and 24,8%;

low – 86,4% and 28,7%. Having analyzed the rel-

evant training programs, we believe that the reason

for such a state of the level of theoretical knowledge

is insufﬁcient training in the indicated direction, both

during university studies and during advanced train-

ing in the conditions of postgraduate education. The

state of formation of the cognitive-activity component

of the readiness of computer science and mathemat-

ics teachers for the development and implementation

of CDGs according to the spatial indicator, according

to the results of the cluster analysis, professional in-

terest was determined in 53% of teachers, in 13% –

a formed positive attitude is present, in 36% – in-

signiﬁcant interest or negative attitude. We explain

the small percentage of respondents who, at the high-

est level, interpret space (real and virtual) in a value-

oriented way, considering it as a probable spatial-

cognitive component of the implementation of CDGs,

by the relative novelty of such a spatial approach, the

complexity and unconventionality of its implementa-

tion. During the integrative examination of indicators

of the formation of the motivational-value component

in the semantic framework of its (motivational-value)

criterion, its average level of formation is determined.

The state of formation of the personal-reﬂective

component of computer science and mathematics

teachers’ readiness to develop and use CDGs accord-

ing to the indicator of the ability to self-control is

characterized by the following percentage distribu-

tion – high level – 39.8%, medium level – 51,5%, low

level – 8,7%. Predominance of medium and high lev-

els of self-control formation as a quality signiﬁcant

for the teacher’s professional activity, including the

implementation of developed professional mathemat-

ical and informational competencies. According to

the personal-reﬂexive indicator, the vast majority of

teachers are diagnosed with the desire to achieve high

results, knowledge of their shortcomings and the de-

sire to correct them, which indicates purposefulness,

the presence of professionally directed reﬂection and

innovative orientation. During the integrative exami-

nation of indicators of the formation of the personal-

reﬂexive component in the semantic framework of its

(personal-reﬂexive) criterion, the average level of its

formation is determined.

Summarizing the results of the research based on

consideration of motivational-value, cognitive-active

and personal-reﬂective criteria, we can say about the

diagnosis of the average level of computer science and

mathematics teachers’ readiness to develop and use

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

511

CDGs. Based on this, we deﬁne the following main

strategies for its improvement: supplementing educa-

tional programs with topics that represent the ways

and practices of applying CDGs in the preparation

of future computer science and mathematics teachers,

their retraining and advanced training; application of

competency-based, activity-based approaches in or-

der to develop teachers’ professional orientation to the

application of CDGs; to activate the use of innovative

pedagogical technologies for the formation of com-

puter science and mathematics teachers’ readiness to

develop and use CDGs; to carry out an analysis of the

application of CDGs in other countries and the recep-

tion of positive pedagogical experience in this direc-

tion.

REFERENCES

Aiello, G. and Parry, K. (2019). Visual Communication:

Understanding Images in Media Culture. Sage.

Avetysian, A. (2020). Methodological fundamentals of

visual theory in the philosophical projects of Mau-

rice Merleau-Ponty and Gilles Deleuze. Filosofska

Dumka, (5):81–92.

ackman, B. and Pilebro, C. (1999). Visual pedagogy in

dentistry for children with autism. ASDC journal of

dentistry for children, 66(5):325–31.

Berry, M. J. A. and Linoff, G. S. (2011). Data mining

techniques: for marketing, sales, and customer

relationship management. John Wiley & Sons, 2

edition. http://pzs.dstu.dp.ua/DataMining/bibl/Data%

20Mining%20Techniques%20For%20Marketing%

20Sales%20And%20Customer%20Relationship%

20Management%202Ed.pdf.

Bollin, A., Pasterk, S., Kesselbacher, M., Reci, E., Wieser,

M., and Lobnig, N. (2021). HCI in K12 Computer

Science Education – Using HCI as a Topic and a Di-

dactic Tool. In CHItaly 2021: 14th Biannual Con-

ference of the Italian SIGCHI Chapter, CHItaly ’21,

New York, NY, USA. Association for Computing Ma-

chinery. https://doi.org/10.1145/3464385.3464717.

Briantseva, H. (2016). Vizualnyy pidkhid do pedahohich-

noyi komunikatsiyi [A visual approach to pedagog-

ical communication]. Ukrainian Journal of Educa-

tional Studies and Information Technology, 4(2):1–9.

https://doi.org/10.32919/10.32919/uesit.2016.02.1-9.

Bristar (2021). Heroes of Math and

Magic. https://bristarstudio.com/en/games/

heroes-of-math-and-magic.

Brito Da Silva, L. E., Melton, N. M., and Wunsch, D. C.

(2020). Incremental Cluster Validity Indices for On-

line Learning of Hard Partitions: Extensions and

Comparative Study. IEEE Access, 8:22025–22047.

https://doi.org/10.1109/ACCESS.2020.2969849.

Bykov, V. Y., Lytvynova, S. H., and Melnyk, O. M. (2017).

Effectiveness of education with electronic educational

game resources in primary school. Information tech-

nologies and learning tools, 62(6):34–46. https://doi.

org/10.33407/itlt.v62i6.1937.

Cabinet of Ministers of Ukraine (2011). On approval

of the State standard of basic and complete general

secondary education. https://zakon.rada.gov.ua/laws/

show/1392-2011-%D0%BF?lang=en#Text.

Chen, S., Zhang, S., Qi, G. Y., and Yang, J. (2020).

Games literacy for teacher education: Towards the im-

plementation of game-based learning. Educational

Technology & Society, 23(2):77–92. https://www.

researchgate.net/publication/343228250.

Deci, E. L. and Ryan, R. M. (2015). Self-Determination

Theory. In Wright, J. D., editor, International Ency-

clopedia of the Social & Behavioral Sciences, pages

486–491. Elsevier, Oxford, 2 edition. https://doi.org/

10.1016/B978-0-08-097086-8.26036-4.

Deleuze, G. (1989). Cinema 1: The Movement Image. The

Athlone Press, London & New York.

Descartes, R. (2018). Finding a foundation for knowledge.

In Philosophy: An Innovative Introduction: Fictive

Narrative, Primary Texts, and Responsive Writing,

pages 126–137. Routledge. https://doi.org/10.4324/

9780429498336.

Drushliak, M. H. (2021). Sutnist ta struktura

vizualno-informatsiynoyi kultury maybutnikh

uchyteliv matematyky ta informatyky [The

essence and structure of the visual and infor-

mational culture of would-be mathematics and

computer science teachers]. Visnyk univer-

sytetu imeni Alfreda Nobelya, (1(21)):141–147.

https://doi.org/10.32342/2522-4115-2021-1-21-16.

Du, R. Y., Yang, W., Lam, P. P. Y., Yiu, C. K. Y., and

McGrath, C. P. (2022). Developing a Toothbrush-

ing Visual Pedagogy (TBVP) for Preschool Children

with Autism Spectrum Disorder. Journal of Autism

and Developmental Disorders, 52(1):327–338. https:

//doi.org/10.1007/s10803-021-04946-5.

Gal’perin, P. I. (2012). An experimental study in the

formation of mental actions. In Readings in Edu-

cational Psychology: Learning and Teaching, vol-

ume 66, pages 142–154. Routledge.

Goldfarb, B. (2002). Visual Pedagogy: Media Cultures in

and beyond the Classroom. Duke University Press.

https://doi.org/10.1215/9780822384052.

Greene, R. W., Abidin, R. R., and Kmetz, C. (1997).

The index of teaching stress: A measure of student-

teacher compatibility. Journal of School Psy-

chology, 35(3):239–259. https://doi.org/10.1016/

S0022-4405(97)00006-X.

Gurevych, R. S., Klochko, O. V., Klochko, V. I., Kovto-

niuk, M. M., and Opushko, N. R. (2020). Computer

science teachers’ readiness to develop and use com-

puter didactic games in educational process. Informa-

tion technologies and learning tools, 75(1):122–137.

https://doi.org/10.33407/itlt.v75i1.3394.

Hakak, S., Noor, N. F. M., Ayub, M. N., Affal, H.,

Hussin, N., ahmed, E., and Imran, M. (2019). Cloud-

assisted gamiﬁcation for education and learning – Re-

cent advances and challenges. Computers & Electri-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

512

cal Engineering, 74:22–34. https://doi.org/10.1016/j.

compeleceng.2019.01.002.

Hall, E. T. (1959). The Silent Language. Dou-

bleday & Company, Inc.,, Garden City, New

York. https://monoskop.org/images/5/57/

Hall Edward T The Silent Language.pdf.

Klochko, O., Fedorets, V., Tkachenko, S., and Maliar,

O. (2020). The Use of Digital Technologies for

Flipped Learning Implementation. In Sokolov,

O., Zholtkevych, G., Yakovyna, V., Tarasich, Y.,

Kharchenko, V., Kobets, V., Burov, O., Semerikov,

S., and Kravtsov, H., editors, Proceedings of the

16th International Conference on ICT in Educa-

tion, Research and Industrial Applications. Integra-

tion, Harmonization and Knowledge Transfer. Vol-

ume II: Workshops, Kharkiv, Ukraine, October 06-10,

2020, volume 2732 of CEUR Workshop Proceedings,

pages 1233–1248. CEUR-WS.org. https://ceur-ws.

org/Vol-2732/20201233.pdf.

Klochko, O. V. (2018). Teoretychni i metodychni zasady

profesiynoyi pidhotovky maybutnikh menedzheriv

ahrarnoho vyrobnytstva zasobamy suchasnykh

informatsiyno-komunikatsiynykh tekhnolohiy (Theo-

retical and methodical principles for future managers

professional training in agricultural production

using the latest information and communication

technologies). D.Sc. thesis, Vinnytsia Mykhailo

Kotsiubynskyi State Pedagogical University.

Klochko, O. V., Fedorets, V. M., Klochko, V. I., and Ko-

rmer, M. V. (2022a). The Use of Ensemble Classiﬁ-

cation and Clustering Methods of Machine Learning

in the Study of Internet Addiction of Students. In Se-

merikov, S., Osadchyi, V., and Kuzminska, O., edi-

tors, Proceedings of the 1st Symposium on Advances

in Educational Technology - Volume 1: AET, pages

241–260. INSTICC, SciTePress. https://doi.org/10.

5220/0010923500003364.

Klochko, O. V., Tkachenko, S. V., Babiichuk, I. M., Fe-

dorets, V. M., and Galych, T. V. (2022b). Using

Virtual Reality Technologies for Teaching Computer

Science at Secondary School. In Ignatenko, O.,

Kharchenko, V., Kobets, V., Kravtsov, H., Tarasich,

Y., Ermolayev, V., Esteban, D., Yakovyna, V., and Spi-

vakovsky, A., editors, ICTERI 2021 Workshops, pages

231–246, Cham. Springer International Publishing.

https://doi.org/10.1007/978-3-031-14841-5

15.

Lakoff, G. and Johnson, M. (1980). Metaphors

We Live By. The University of Chicago Press,

Chicago and London. https://archive.org/details/

metaphorsweliveb00lako.

Manzano-Le

on, A., Camacho-Lazarraga, P., Guerrero,

M. A., Guerrero-Puerta, L., Aguilar-Parra, J. M.,

Trigueros, R., and Alias, A. (2021). Between Level

Up and Game Over: A Systematic Literature Re-

view of Gamiﬁcation in Education. Sustainability,

13(4):2247. https://doi.org/10.3390/su13042247.

Mathe, M., Verhagen, H., and Wiklund, M. (2018). Dig-

ital Games in Education: Exploring Teachers’ Prac-

tices and Challenges From Play to Co-Design. In Pro-

ceedings of the 12th European Conference on Games

Based Learning, pages 388–395.

Maturana Romes

ın, H. and Varela, F. (2009). El

arbol del

conocimiento: las bases biol

ogicas del entendimiento

humano. Editorial Universitaria, Santiago de Chile.

https://repositorio.uchile.cl/handle/2250/119932.

Mayer, R. E. (2019). Computer Games in Education. An-

nual Review of Psychology, 70:531–549. https://doi.

org/10.1146/annurev-psych-010418-102744.

Merleau-Ponty, M. (2005). Phenomenology of Perception.

Routledge, London and New York. https://tinyurl.

com/59unk4e2.

Michala, M., Alexakos, C., and Tsolis, D. (2018). Mo-

bile Applications and Games for a Digital Educational

Program on Art and Culture in Secondary School. In

2018 9th International Conference on Information, In-

telligence, Systems and Applications (IISA), pages 1–

6. https://doi.org/10.1109/IISA.2018.8633697.

Milat, J. (2017). Teacher teleological competen-

cies. International Journal for Education,

Research and Trainning (IJERT), 3(1):34–42.

http://periodica.fzf.ukim.edu.mk/ijert/IJERT%

2003.1%20(2016-2017)/IJERT%202016-2017%

201.08%20Josip%20Milat%20-%20TEACHER%

20TELEOLOGICAL%20COMPETENCIES.pdf.

Moshtaghi, M., Bezdek, J. C., Erfani, S. M., Leckie, C.,

and Bailey, J. (2018). Online Cluster Validity Indices

for Streaming Data. https://doi.org/10.48550/ARXIV.

1801.02937.

Nousiainen, T., Kangas, M., Rikala, J., and Vesisenaho, M.

(2018). Teacher competencies in game-based peda-

gogy. Teaching and Teacher Education, 74:85–97.

https://doi.org/10.1016/j.tate.2018.04.012.

Oliveira, W., Hamari, J., Shi, L., Toda, A. M., Ro-

drigues, L., Palomino, P. T., and Isotani, S. (2023).

Tailored gamiﬁcation in education: A literature re-

view and future agenda. Education and Informa-

tion Technologies, 28(1):373–406. https://doi.org/10.

1007/s10639-022-11122-4.

Peisakhov, N. M. (1984). Regularities of the dynamics of

mental phenomena. KSU, Kazan.

Picka, K., Dosedla, M., Hrb

cek, J., and Hodis, Z. (2022).

Teachers’ experience with digital games in Czech pri-

mary schools. Entertainment Computing, 42:100483.

https://doi.org/10.1016/j.entcom.2022.100483.

Raven, J. (1989). The Raven Progressive Matrices: A Re-

view of National Norming Studies and Ethnic and So-

cioeconomic Variation Within the United States. Jour-

nal of Educational Measurement, 26(1):1–16. https:

//doi.org/10.1111/j.1745-3984.1989.tb00314.x.

Rean, A. A., Bordovskaya, N. V., and Rozum, S. I. (2000).

Psychology and Pedagogy. Peter, SPb.

Rocha, T. and Barroso, J. (2021). PLAY for LEARNING:

Serious Games to Assist Learning of Basic Didac-

tic Concepts: A Pilot Study. In Fang, X., editor,

HCI in Games: Serious and Immersive Games, vol-

ume 12790 of Lecture Notes in Computer Science,

pages 62–71, Cham. Springer International Publish-

ing. https://doi.org/10.1007/978-3-030-77414-1

Rybka, N. M. (2018). Gamiﬁcation and experience of using

computer games in teaching philosophy in technical

System-Forming Aspects of the Computer Science and Mathematics Teachersâ

Z Readiness to Develop and Use Computer Didactic Games

in Educational Process

513

institutions of higher education. Information Tech-

nologies and Learning Tools, 67(5):213–225. https:

//doi.org/10.33407/itlt.v67i5.2108.

Scratch (2022). Scratch: About Scratch. https://scratch.mit.

edu/about.

Semerikov, S. O., Mintii, M. M., and Mintii, I. S. (2021a).

Review of the course “Development of Virtual and

Augmented Reality Software” for STEM teachers:

implementation results and improvement potentials.

In Lytvynova, S. H. and Semerikov, S. O., ed-

itors, Proceedings of the 4th International Work-

shop on Augmented Reality in Education (AREdu

2021), Kryvyi Rih, Ukraine, May 11, 2021, volume

2898 of CEUR Workshop Proceedings, pages 159–

177. CEUR-WS.org. https://ceur-ws.org/Vol-2898/

paper09.pdf.

Semerikov, S. O., Teplytskyi, I. O., Soloviev, V. N., Hama-

niuk, V. A., Ponomareva, N. S., Kolgatin, O. H., Kol-

gatina, L. S., Byelyavtseva, T. V., Amelina, S. M., and

Tarasenko, R. O. (2021b). Methodic quest: Rein-

venting the system. Journal of Physics: Confer-

ence Series, 1840(1):012036. https://doi.org/10.1088/

1742-6596/1840/1/012036.

Sherer, M., Maddux, J. E., Mercandante, B., Prentice-Dunn,

S., Jacobs, B., and Rogers, R. W. (1982). The Self-

Efﬁcacy Scale: Construction and Validation. Psy-

chological Reports, 51(2):663–671. https://doi.org/

10.2466/pr0.1982.51.2.663.

Subrahmanyam, K. and Greenﬁeld, P. M. (1994). Effect

of video game practice on spatial skills in girls and

boys. Journal of Applied Developmental Psychology,

15(1):13–32. https://doi.org/10.1016/0193-3973(94)

90004-3.

Tobias, S. and Fletcher, D. (2012). Learning from Computer

Games: A Research Review. In De Wannemacker, S.,

Vandercruysse, S., and Clarebout, G., editors, Seri-

ous Games: The Challenge, volume 280 of Commu-

nications in Computer and Information Science, pages

6–17, Berlin, Heidelberg. Springer Berlin Heidelberg.

https://doi.org/10.1007/978-3-642-33814-4

Unger, M., Marsan, G. A., Meissner, D., Polt, W., and Cer-

vantes, M. (2020). New challenges for universities

in the knowledge triangle. The Journal of Technol-

ogy Transfer, 45(3):806–819. https://doi.org/10.1007/

s10961-018-9699-8.

Vakaliuk, T., Chyzhmotria, O., Chyzhmotria, O., Did-

kivska, S., and Kontsedailo, V. (2023). The use of

massive open online courses in teaching the funda-

mentals of programming to software engineers. Ed-

ucational Technology Quarterly. https://doi.org/10.

55056/etq.37.

Varina, H. B., Osadchyi, V. V., Goncharova, O. A., and

Sankov, S. M. (2022). Features of gamiﬁcation com-

ponent introduction during the development of con-

structive strategies for overcoming youth life crises.

Educational Dimension, 6:84–107. https://doi.org/10.

31812/educdim.4454.

Volochkov, A. A. (2007). Aktivnost subekta bytiia: integra-

tivnyi podkhod [Activity of the subject of being: inte-

grative approach]. Permskiy gosudarstvennyy peda-

gogicheskiy universitet, Perm.

WEKA (2021). Weka 3: Machine Learning Software in

Java. http://old-www.cms.waikato.ac.nz/

∼

ml/weka/.

Yevtuch, M. B., Fedorets, V. M., Klochko, O. V., Shyshk-

ina, M. P., and Dobryden, A. V. (2021). Develop-

ment of the health-preserving competence of a phys-

ical education teacher on the basis of N. Bernstein’s

theory of movements construction using virtual real-

ity technologies. In Lytvynova, S. H. and Semerikov,

S. O., editors, Proceedings of the 4th International

Workshop on Augmented Reality in Education (AREdu

2021), Kryvyi Rih, Ukraine, May 11, 2021, volume

2898 of CEUR Workshop Proceedings, pages 294–

314. CEUR-WS.org. https://ceur-ws.org/Vol-2898/

paper16.pdf.

Zhaldak, M. I., editor (2012). Otsinyuvannya yakosti

prohramnykh zasobiv navchalnoho pryznachennya

dlya zahalnoosvitnikh navchalnykh zakladiv [Evalua-

tion of the quality of educational software for general

educational institutions]. Pedahohichna dumka, Kyiv.

https://lib.iitta.gov.ua/619/.

Zhorova, I., Kokhanovska, O., Khudenko, O., Osypova,

N., and Kuzminska, O. (2022). Teachers’ training

for the use of digital tools of the formative assess-

ment in the implementation of the concept of the new

ukrainian school. Educational Technology Quarterly,

2022(1):56–72. https://doi.org/10.55056/etq.11.

Zverkov, A. and Eidman, Y. (1990). Diagnostika

volevogo samokontrolja (oprosnik VSK) [Diagnos-

tics of Strong-willed Self-regulation (VSK) question-

naire]. In Praktikum po psihodiagnostike. Psihodiag-

nostika motivacii i samoreguljacii [Workshop on psy-

chological diagnostics. Psychodiagnostics of motiva-

tion and self-regulation], pages 116–126. MGU.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

514