The ICT Usage in Teaching Maths to Children with Hearing Impairment

Kateryna Bondar

1,2 a

, Olena Shestopalova

2 b

and Tetiana Kramarenko

2 c

Freie Universit

at Berlin, 16-18 Kaiserswerther Str., Berlin, 14195, Germany

Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine

Keywords:

ICT, Mathematics Performance, Teaching Maths, Mathematical Skills of Students with Hearing Impairment,

GeoGebra.

Abstract:

The purpose of our research was the modiﬁcation of teaching strategies of maths for deaf and hard-of-hearing

learners. More speciﬁcally, we aimed to study the possibilities of optimal use of interactive exercises such

as LearningApps and GeoGebra Dynamic Mathematics system in order to provide methodical and didactic

support for training sessions, but also to assure independent study and implementation of monitoring activi-

ties. The developed visual materials for teaching children with hearing impairments were partially introduced

into the educational process in a pilot project for the retraining of 12 school teams working with children

with hearing impairments in Kryvyi Rih in educational strategies, for learning mathematics in grades 8-9 of

an inclusive type for instructors teaching in a mainstreamed classroom with a mix of hearing, deaf and hard-

of-hearing students (students 12-14 years old: N = 80 children with hearing impairments; data collected in

2019-2021). In the context of research goals the academic success (algebra, geometry), and mathematical

skills of students were analysed. According to the study results, there was a signiﬁcant increase in the mean

score of performance after the intervention than before the intervention. In other words, this increase rep-

resents the effectiveness of ICT educational methods. Furthermore, we highlighted some recommendations

for using online service LearningApps, GeoGebra Dynamic Mathematics system, and project-based learning

technologies in Mathematics, in particular.

1 BACKGROUND CONTEXT

On review of the literature, researchers have stated

that deaf and hard-of-hearing learners may lack gen-

eral vocabulary and the fundamental mathematical

vocabulary needed to be able to understand maths

concepts/processes such as seriation and classiﬁcation

(Ariapooran, 2017; Barrett, 2005; Nunes and Moreno,

1999; Ray, 2001). It is more difﬁcult for children who

are deaf or hard of hearing to acquire the connection

between language and maths concepts from their en-

vironment incidentally (e.g., from conversations with

parents and games with friends about the counting

of subjects). Without this type of natural learning,

a child with hearing impairment cannot boost begin-

ning maths concepts such as “more/less” or “one/a

lot” etc. without educational support (Barrett, 2005).

That is why most children with hearing impair-

ment (HI) have a gap of approximately three years

https://orcid.org/0000-0002-2441-4203

https://orcid.org/0000-0002-3401-1790

https://orcid.org/0000-0003-2125-2242

behind their hearing peers in mathematics (Nunes and

Moreno, 1999).

Despite the importance of communication with

other people as the basis of maths skills, communi-

cation with children with hearing impairments may

be problematic and poor. That is why these chil-

dren cannot take part in studying mathematical pro-

cesses such as problem-solving, developing logic and

reasoning, and effectively communicating mathemat-

ical ideas without communication skills and maths

vocabulary (Le Brun, 2022). Perhaps we can boost

maths Ukrainian vocabulary for deaf and hard-of-

hearing learners if we use Information and Commu-

nication technologies (ICT) for visualisation maths.

This is a relatively new area of enquiry, with little re-

search existing in the literature. The current research,

therefore, aims to investigate if using ICT for study

of maths becomes a booster and helps to improve

children’s performance on problem-solving tasks in

maths, to predict and make observations based on

the given information, which requires strong language

skills and the ability to critically think.

Bondar, K., Shestopalova, O. and Kramarenko, T.

The ICT Usage in Teaching Maths to Children with Hearing Impairment.

DOI: 10.5220/0012067300003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 721-732

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

721

2 ANALYSIS OF PUBLICATIONS

The world standard of inclusive education strategy is

based on the idea that students with special educa-

tional needs require support in getting key life com-

petencies such as cognitive, non-cognitive skills, and

“functional literacy” for independent life and social-

isation (UNICEF, 2020). Particularly, the success

of the students with hearing impairments in the tar-

geted acquisition of these key maths competencies

depends on class management, teaching approaches,

and methods such as the universal design of learning

or differential instruction with ICT (Global Education

Monitoring Report Team, 2020). ICT is also a school

subject in which students learn to use computers and

other electronic equipment to store and send informa-

tion (UNICEF, 2020).

According to a newsletter prepared by NORAD –

Norwegian Agency for Development Cooperation

and by AFD – Agence Franc¸aise de D

eveloppement

“Information and Communication A technology that

supports the inclusion of children with disabilities in

education” (National Deaf Center on Postsecondary

Outcomes, 2020b). ICTs can support the inclusion of

children with disabilities in education, allowing them

to overcome some of the barriers that cause their ex-

clusion. ICTs complement other face-to-face commu-

nication methods and tools such as teacher training

and inclusive pedagogy (de Dinechin and Boutard,

2021). ICT is a tool for both an inclusive and gender-

sensitive approach to education, which was intro-

duced over the two years 2020-2022 during the tran-

sition to distance education due to COVID-19 pan-

demics (UNICEF, 2020).

In general, when teaching mathematics, ICT for

deaf and hard-of-hearing learners can be divided into

three main categories:

• educational content and digital media, the purpose

of which is to convey lessons/skills to the stu-

dent (for example, a learning video on stochastics

with translation into sign language). An exam-

ple would be the development of Best Practices at

the Secondary Level of DeafTEC: Technological

Education Centre for Deaf and Hard-of-Hearing

Students (National Deaf Center on Postsecondary

Outcomes, 2020b).

• Software that serves as an intermediary to make

certain educational content/activities available

(e.g., GeoGebra for geometry or LearningApps)

(Rochester Institute of Technology, 2022a).

• Accessibility features that make the hardware ac-

cessible to everyone (e.g., software to convert

maths problem text into sign language) (National

Deaf Center on Postsecondary Outcomes, 2020a).

The main goal of the strategies of using ICT in

inclusive education is designed to promote access to

mathematics content based on the Standards of in-

structional strategies and should be based upon cur-

rent and accurate information about the child’s sen-

sory functioning. Most researchers agree that access

to appropriate ICTs can reduce differences in inclu-

sive education, and deaf and hard-of-hearing learn-

ers must have access to ICT-based programs being a

part of the schedule of school (Rochester Institute of

Technology, 2022b). That is why digital inclusion in

maths education as a process is a system of a student’s

empowerment through participation in education pro-

cesses with ICT-programs (de Dinechin and Boutard,

2021); individual curricula of studying maths (Ray,

2001); providing reasonable accommodation of ma-

terials (Ray, 2001). However, despite the huge po-

tential beneﬁts of ICT usage in inclusive education, it

only rarely worked in Ukrainian schools.

2.1 The Principles and Methods of

Mathematics with the Instruction of

Deaf and Hearing Students in

Mainstream Classes

We need to highlight that for teaching deaf and hard-

of-hearing learners, the same methods as for other

children are used. However, the peculiarities of the

psychophysical development of the students lead to

other ways of applying these methods. In particular,

the methods of teaching are remedial and develop-

mental, and they stimulate deaf and hard-of-hearing

learners to work independently and to take initiatives

(Fritz et al., 2019).

The principles and methods of maths education

in an inclusive class of the middle school are based

on the determination of needs of deaf and hard-of-

hearing learners:

Step one – to determine the current level of maths

knowledge, communicative skills, and maths vocabu-

lary of the children who are deaf or hard of hearing.

Step two – to determine the effective teach-

ing style (visual, kinesthetic, poly-sensory and an-

other one, especially if one of the styles dominates).

For mainstream classes it is important to use mul-

timedia approaches for a visual representation of

maths course content (e.g., GeoGebra for geometry or

LearningApps for particular stochastics is to achieve

strong mastering of knowledge, the formation of prac-

tical skills to solve problems on the basics of combi-

natorics, probability theory, and mathematical statis-

tics) (Kidd, 2018). Using LearningApps is especially

important for students who are relying on speechread-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

722

ing for receptive communication as it reduces eye-

strain. Also, there is an appropriate language model

that can effectively provide not only the vocabulary to

label objects but also a language model for expressing

concepts and ideas, using the child’s mode of commu-

nication in maths.

Step three – to identify speciﬁc aspects of the

child’s learning activities; where he or she needs out-

side help during the educational process. For ex-

ample, use more than one mode of presentation for

maths concepts. These may include manipulatives,

verbal, gestural, pictorial, and symbolic modes. En-

courage students to translate between modalities, par-

ticularly the language of mathematics, to make con-

nections (Kollosche et al., 2019). For example, in-

structional strategies of using GeoGebra visualisation

to provide an enriched learning environment that pro-

motes a wide range of real world, meaningful math-

ematical experiences with opportunities for explo-

ration and problem-solving in geometry. Initially in-

troduce word problems as informal stories with maths

facts through dramatization, using pictures, drawings,

and manipulatives, and then translating the action into

a maths sentence. Students can use images, objects,

and visualise or pantomime the action in a problem to

move from the concrete to more abstract representa-

tions of the problem.

2.2 Methods of Maths Teaching to

Children with Hearing Impairments

There are speciﬁc methods of class management and

teaching where children with hearing impairment

(Kidd, 2018; National Deaf Center on Postsecondary

Outcomes, 2020b; Nunes and Moreno, 1999; Ray,

2001; Singh, 2019). Firstly, teachers need to use al-

ternative forms of communication and the strategy

of studying maths based on non-verbal intelligence

and competences (seriation, analogy, systematisation)

(Fritz et al., 2019). The adaptation of the education

maths content to the cognitive abilities of the students

for children with HI, this is the removal of complex

verbal material.

Secondly, it is visual learning. Taking into account

the speciﬁcity of the HI, the types of showing objects

are additionally selected. For example, for children

with hearing impairment, the visual manuals should

be speciﬁc, with details that concentrate on the per-

ception of main things. The teacher needs some tips

for classroom management: slowing down the educa-

tional process. Communication of the information for

deaf and hard-of-hearing learners is carried out with

consideration of the slower perception of the verbal

information. For deaf and hard-of-hearing learners,

more time is given to think about the answer (Kidd,

2018).

Thirdly, repeatability in teaching. The repetition

variability should be used to ﬁll the gaps in the per-

ception of children with hearing impairment espe-

cially if we use ICT (Kidd, 2018). The optimization

of the work pace and fatigue dynamics of deaf and

hard-of-hearing learners. This tool is aimed at ac-

tivation of the students’ cognitive activities, support

of their ability to work and includes, in particular:

switching the students to different types of activities

to prevent fatigue (gamiﬁcation, visualisation, mod-

elling, extrapolation examples in classroom space);

using interesting facts, examples, and details in the

process of presentation of the material; emotional

presentation; organising the minutes of rest at the

lessons; creating success situations for the deaf and

hard-of-hearing learners (Shestopalova et al., 2019).

Conceptually, difﬁculties of deaf and hard-of-hearing

learners in middle school in maths class depend on the

expression of disorders and manifest themselves in

the following areas: fundamentally, it’s understanding

of spoken language and formation of active speech

(Barrett, 2005).

Generally, the main purpose of studying maths is

the formation of verbal-logical thinking children with

HI and well as the formation of the auditory-visual-

tactile perception of mathematical concepts (child

with HI asks questions to clarify details; makes deci-

sions on the use of approaches and materials learned

earlier; can explain decisions and establish logical

connections; knows how to systemize features; plans

activities) (Rochester Institute of Technology, 2022a;

Kidd, 2018).

3 CURRENT RESEARCH AND

HYPOTHESIS

We have a goal of comprehensive estimation of if

using ICT for the study of maths became a booster

and helps to improve HI children’s performance on

problem-solving tasks in maths and their ability to

predict and make observations based on the given in-

formation, which requires strong language skills and

the ability to critically think.

Learning difﬁculties in this category of children

are related to speech delay and speciﬁc problems in

conceptual and ﬁgurative thinking (Barrett, 2005). In

particular, the peculiarity of the formation of visual-

action thinking is that it occurs almost without speech,

which makes it imperfect and does not contribute to

the transition to the visual image level. In turn, the

formation of formal-logical thinking is also difﬁcult

The ICT Usage in Teaching Maths to Children with Hearing Impairment

723

(Le Brun, 2022).

That is why the purpose of our research is the

modiﬁcation of teaching strategies for deaf and hard-

of-hearing learners. More speciﬁcally, we aim to

study the possibilities of optimal use of interactive

exercises such as LearningApps and GeoGebra Dy-

namic Mathematics system in order to provide me-

thodical and didactic support for training sessions, but

also to assure independent study and implementation

of monitoring activities. Consequently, some aspects

of the problem of teaching maths to students with

hearing impairment can be eliminated through the use

of ICT as a provider of training materials through

adapted, assistive devices, information and commu-

nication technologies, and support. However, there

are some problems with ICT for children with hear-

ing impairment. ICT as a provider of training mate-

rials adapted for maths teaching to deaf and hard-of-

hearing learners is not ﬁrmly established and needs

further research and testing.

The research question that guided the present

study was: does ICT boost the maths skills of hearing

impaired teenagers? The current research hopes to ex-

tend on the work of previous research by investigating

that all three methods LearningApps, Geogebra, and

STEM boost maths skills.

4 METHOD

4.1 Design

The design of the study includes a model of ICT ap-

plication and the impact of effective inclusive educa-

tion strategies and methods on the process of learning

mathematics for children with hearing impairment.

The study utilised a within subject design with one

IV (intervention: pre vs post) and the DV being the

maths performance (as outlined in the Materials sec-

tion).

4.2 Procedure

The study consists of three stages:

The ﬁrst stage was to collect data for diagnos-

ing the level of mathematical abilities by analysing

the level of spatial thinking of the Raven’s Progres-

sive Matrices (Raven, 2020), Rey-Osterriet Compos-

ite Figures Test (ROCF), Gottschaldt’s Hidden Figure

Test (GHFT) and the educational achievements in al-

gebra and geometry of potential ICT users (students

with hearing impairments). Purpose: at this stage, in-

formation was collected on the level of performance

of a sample of students with hearing impairments, and

their spatial skills were analysed using diagnostics.

The second stage consisted of an analysis of exist-

ing ICTs for teaching mathematics (algebra and ge-

ometry) classes, their usefulness, limitations, require-

ments, etc., which served as the basis for reﬂection in

the analysis stage. Purpose: to study the possibilities

of optimal use of interactive exercises LearningApps

and the GeoGebra dynamic mathematics system for

methodological and didactic support of training ses-

sions, independent study, and control activities.

The third stage is the processing and analysis of

data in order to make recommendations on the ap-

propriateness of using ICT technologies in schools

in Kryvyi Rih (taking into account the usefulness of

ICTs, their cost, ease of use, impact on school in-

clusiveness, etc.). In addition, the main problems in

the implementation of ICT and inclusive education

programs were identiﬁed and recommendations were

given.

4.3 Participants

Implementation of ICT programs in educational

strategies signed in USL and voiced for learning

mathematics in grades 8-9 of an inclusive type for in-

structors teaching in a mainstreamed classroom with

a mix of hearing, deaf and hard-of-hearing students.

Table 1: Demographics of the sample (N = 80, mean age =

12.5; SD = 1.06).

Total of the Year deaf students

hard-of-hearing

students

2019 (N = 30) 8 22

2020 (N = 21) 6 15

2021 (N = 29) 10 19

Total 24 56

Overall, 80 participants took part in the study (40

females, 40 males; mean age = 12.5; SD = 1.06).

Thirty participants were deaf from birth and 70 with

hearing loss in early childhood (on average diagnosed

at the age of 3; SD = 1.5). Tables 1, 2 present the

detailed demographics of the sample.

Table 2: Demographics of the sample (N = 80, mean age =

12.5; SD = 1.06).

Mainstream class (N) Special class (N)

24 56

There was no signiﬁcant difference in intelli-

gence score between different educational levels,

F(5.49) = 2.46; p = .05. Participants were recruited

through the Department of Education and Science of

the Executive Committee of the Kryvyi Rih City and

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

724

advertising in Non-Governmental organisations.

The work of the research team was aimed at devel-

oping a concept for supporting inclusive mathemat-

ics education in Kryvyi Rih in cooperation with the

Department of Education and Science of the Execu-

tive Committee of the Kryvyi Rih City Council and

Kryvyi Rih State Pedagogical University. The devel-

oped visual materials for teaching children with hear-

ing impairments were partially introduced into the ed-

ucational process in a pilot project for the retraining

of 12 school teams working with children with hear-

ing impairments in Kryvyi Rih using STEM methods

and in the course of the Suziriya Mathematical Mul-

tidisciplinary Educational and Rehabilitation Centre

for children with hearing impairments in 2019-2021.

4.4 Materials

4.4.1 Academic Success

In the system of Ukrainian education, educational

success is assessed by summing up current grades in

the classroom, and test works on the topic on the basis

of a 12-point scale (max 12). The rating of grades is

available to all students in the class. In the context of

conducting mathematics lessons (algebra, geometry),

the mathematical skills of students were analysed.

4.4.2 Stereotype Threat

For our study, situational factors that increase stereo-

type threat may include expectations of difﬁculty

in maths, and the expectation of discrimination due

to one’s identiﬁcation with a negatively stereotyped

group of children with special educational needs. To

reduce the repetitive experience of stereotype threat

in teaching mathematics using ICT, we used a prelim-

inary diagnosis of the Rey-Osterriet Composite Fig-

ures Test, the Raven’s Progressive Matrices and the

Gottschaldt’s Hidden Figure Test, followed by the

identiﬁcation of the level of mathematical spatial abil-

ities, the level of intelligence. To anticipate a decline

in maths learning conﬁdence, poor performance, and

loss of interest in the relevant area of achievement, we

pre-reported individual scores to students, emphasis-

ing that they did well on tests and that their spatial

ability was sufﬁcient for maths learning.

4.4.3 Raven’s Progressive Matrices

Standard Progressive Matrices (RSPM) a classic

study using this test contains numerous motors used

for various purposes. RPM is a non-verbal test typi-

cally used to measure general human intelligence and

abstract reasoning and is regarded as a non-verbal es-

timate (Raven, 2020). The Raven Progressive Ma-

trices test is one of the non-verbal intelligence tests

and is based on two theories developed by Gestalt

psychology: the theory of form perception and the

so-called “neogenesis theory” by Charles Spearman

(Lovie, 1983). Raven’s matrices can be applied to

subjects with any linguistic composition and socio-

cultural background, with any level of speech devel-

opment. We used several algorithms for the psy-

chological interpretation of the results obtained: the

deﬁnition of intelligence according to the percentage

scale; the translation of the obtained results into an

IQ-indicator (Raven, 2020).

4.4.4 Gottschaldt’s Hidden Figure Test (GHFT)

This test measures ﬁgure-ground discrimination abil-

ities. A participant is asked to look at 30 masked ﬁg-

ures to ﬁnd one of the 5 reference ﬁgures. Masked

ﬁgures are presented in turn, it is necessary to record

the total time of the task by the subjects. An exam-

ple was given before starting the technique perform-

ing the exercise with the correct answer for children

with hearing impairments to be sure that they under-

stand the text of instruction. Calculation of results ob-

tained by respondents according to the method “Fig-

ures of Gottschaldt” was carried out according to the

formula:

I =

where I – index of ﬁeld dependence or ﬁeld indepen-

dence; N – the total number of points (correctly com-

pleted tasks); T – time to complete all tasks in min-

utes.

4.4.5 Rey-Osterriet Composite Figures Test

(ROCF)

Rey-Osterriet Composite Figures Test (ROCF) is a

neuropsychological technique, in which a participant

is asked to paint an image (subtest 1), and then paint it

from memory (subtest 2). The test ﬁgure itself (shown

in the ﬁgure) is made up of 18 elements, which can be

divided into three groups: the head form, the outer

elements, and the internal elements in the head form.

The technique allows for the development of memory,

deep-space functions, and deep-constructive habits. It

is signiﬁcant that this test is included in the interna-

tional list of tools for assessing cognitive dysfunctions

in neurology.

All tests have traditionally been used as psycho-

metric methods to assess factors of intelligence and/or

disturbances in spatial perception. Through their

The ICT Usage in Teaching Maths to Children with Hearing Impairment

725

combined use, researchers were able to obtain an in-

tegrative assessment of using ICT for the study of

maths that became a booster and helps for problem-

solving tasks in maths for a child to predict and make

observations based on the given information, which

requires strong language skills and the ability to crit-

ically think. Thus, it becomes possible to effectively

identify the problems and opportunities for using ICT.

4.4.6 Criteria for Assessing the Academic

Performance

The results of the e-learning course were examined to

make judgments on students’ academic performance.

In such a manner, in case of the absence of mistakes

in Gottschaldt’s Hidden Figure test, the child’s perfor-

mance was rated as high. If one or two mistakes were

made, the performance was deemed moderate. More

than two mistakes corresponded to low academic at-

tainment. The analysis of Raven’s test results used

several algorithms for the psychological interpreta-

tion of the results obtained: the deﬁnition of intelli-

gence according to the percentage scale; translation

of the obtained results into an IQ. When conducting

Rey-Osterriet Composite Figures Test (ROCF), the

level of student’s visual and spatial thinking was de-

termined high if the head form, the outer elements,

and the internal elements in the head form without

errors; average if the child was unable to copy form

and details without mistakes; and low if no tasks were

completed successfully.

4.5 Intervention Methods

The intervention lasted for each grade selected by the

researchers (8th and 9th grade of high school) for two

academic years (October to May) of online learning

under quarantine restrictions during the COVID-19

pandemic. The intervention was carried out by inte-

grating the ICT programs described in the article into

the methodology of teaching mathematics by teachers

and modifying the curriculum by the general school

support team (teacher’s assistants, psychologists, and

parents).

An example of adapted and modiﬁed planimetry

curricula for students with hearing impairments (Ge-

ometry, grade 8-9):

• Topic 1 (28 hours). Quadrilaterals. Quadrilateral,

its elements. The sum of the angles of a quadri-

lateral. Parallelogram, its properties and signs.

Rectangle, rhombus, square and their properties.

Trapeze. Inscribed and circumscribed quadrilat-

erals. Inscribed and central corners. Thales’ the-

orem. The middle line of a triangle, its properties

The middle line of a trapezoid, its properties.

• Topic 2 (14 hours). Similarity of triangles. Gener-

alized theorem of Thales. Similar triangles. Signs

of similarity of triangles.

• Topic 3 (22 hours). Polygons. Areas of poly-

gons. Polygon and its elements. Convex and non-

convex polygons. The sum of the angles of a con-

vex polygon. Inscribed and circumscribed poly-

gons. The concept of the area of a polygon. Main

properties of areas. Area of a rectangle, parallelo-

gram, triangle. The area of the trapezium.

• Topic 4 (20 hours). Solving right triangles. Sine,

cosine, tangent of an acute angle of a right trian-

gle. Theorem of Pythagoras. Perpendicular and

inclined, their properties. The ratio between the

sides and angles of a right triangle. The value of

sine, cosine, tangent of some angles. Solving right

triangles.

• Topic 5 (4 hours). Solving triangles. Sine, cosine,

tangent of angles from 0° to 180°. Basic trigono-

metric identity, reduction formulas.

• Topic 6 (16 hours). Cartesian coordinates on the

plane. Coordinates of the middle of the segment.

Distance between two points with given coordi-

nates. The equation of a circle and a straight line.

• Topic 7 (20 hours). Vectors on the plane. Vector.

Modulus and direction of the vector. Equality of

vectors. Coordinates of the vector. Adding and

subtracting vectors. Multiplication of a vector by

a number. Collinear vectors. Scalar product of

vectors.

4.5.1 Online Service LearningApps Usage for

Teaching the Students with HI

Based on the conducted research the authors devel-

oped the teaching aid (Kramarenko, 2019). The ﬁrst

part covers general guidelines for teaching pupils with

special educational needs using ICT and means of re-

mote technologies. The second section focuses on the

usage of LearningApps online training. The teach-

ing aid provides both references on worked out ex-

ercises and QR codes which are generated through

the service. The use of a variety of online re-

sources, including online services and learning en-

vironments, is becoming increasingly popular. One

of the prime examples of such environments is the

LearningApps multimedia didactic exercising service

(https://learningapps.org/). It is intended for the de-

velopment, storage, and usage of interactive exercises

in the educational process. Such exercises can be ap-

plied not only on a lesson with an interactive white-

board but also as individual tasks for students with

special needs (ﬁgure 1). A signiﬁcant advantage of

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

726

this service is the ability of task integration into Moo-

dle LMS.

The educational aim of using interactive exercises

of the LearningApps service in the study of Math-

ematics and in particular stochastics is to achieve

strong mastering of knowledge, the formation of prac-

tical skills to solve problems on the basics of combi-

natorics, probability theory, and mathematical statis-

tics, to show the connection between stochastics and

real life and to teach students to carry out non-typical

tasks.

4.5.2 Using GeoGebra in Mathematics Teaching

For the use of GeoGebra Maths Apps (Kramarenko,

2019) mathematics teachers are offered several visu-

als for visualisation of geometric constructions, the

hypothesis concerning the properties of geometric ﬁg-

ures, and the proof of theorems. GeoGebra Dynamic

Mathematics (https://www.geogebra.org/) visuals in-

clude the usage of mobile phone applications such as

Geometry, 3D-Calculator, Graphing Calculator, and

the visuals demonstrating stochastic experiments in

the teaching of probability theory and mathematical

statistics.

It is extremely positive that using both of the

above-mentioned services allows students to collabo-

rate in the offered virtual classes (Google Classroom).

These features have recently appeared. And they can

play a signiﬁcant role in socialisation, especially for

deaf and hard-of-hearing learners. As our research

has shown, Mathematics teachers practically do not

use them in their work. Partly because of a lack of

competence in this matter.

GeoGebra has become the leading provider of

dynamic mathematics software, supporting science,

technology, engineering, and mathematics (STEM)

education and innovations in teaching and learning

worldwide. We consider it reasonable to use the Ge-

oGebra Maths Apps in teaching deaf and hard-of-

hearing learners. The authors offered a mathematics

teacher a teaching guide and tasks for students to use

GeoGebra in teaching Planimetry and Stochastics. In

particular, the use of built-in functions for calculating

the values of combinatorial compounds, testing using

GeoGebra and examining electronic visuals that sim-

ulate accidental events by Sada (Sada, 2021).

To present an experiment demonstration, a teacher

can use the GeoGebra dynamic Maths program. In an

exercise developed by a teacher in advance, a student

will be able to simulate a large number of bone tosses

and monitor their results. In developing visuals that

model accidental events, we used the ideas of Sada

(Sada, 2021).

5 RESULTS

Data obtained before and after the intervention from

groups were analysed using descriptive and inferen-

tial statistics (t test, and repeated measures ANOVA),

by SPSS software version 17 at p < 0.05 signiﬁcance

level. Kolmogorov-Smirnov test determined whether

the data were normally distributed (p = 0.9) and also

homogeneity of variances with p = 0.21 was deter-

mined. Nonparametric statistics were used to describe

qualitative sociodemographic characteristics of par-

ticipants. T-tests were used to compute the mean

scores and compare the maths performance before

and after the intervention. This quasi-experimental

intervention study aimed to evaluate the effect of us-

ing ICT in maths courses.

The results of this study are based on the data of

80 students with hearing impairments participating in

the research. The mean and standard deviation of their

age was 12.5± 1.06. In this study, deaf students’ per-

formance in relation to the subjects (geometry, alge-

bra) was examined before and after the training using

ICT in the maths course.

To reduce the repetitive experience of stereotype

threat in teaching mathematics using ICT, we used a

preliminary diagnosis of the Rey-Osterriet Compos-

ite Figures Test, the Raven’s Progressive Matrices and

the Gottschaldt’s Hidden Figure Test, followed by the

identiﬁcation of the level of mathematical spatial abil-

ities, the level of intelligence (table 3). In addition,

children with hearing impairments are more (63) re-

lated to the ﬁeld-dependent style (1.9 ± 0.13) accord-

ing to the results of the Gottschild Figures and trust

visual impressions more and hardly overcome the vis-

ible ﬁeld when it is necessary to detail and structure

the situation (table 3).

A pretest of students’ maths performance indi-

cated that all children had a poor performance in

advanced geometry such that the mean total perfor-

mance score of students in the intervention group be-

fore the training was 6.3± 1.08; algebra (6.23± 1.04)

(table 4). Therefore, based on the independent t-test

results, there was no signiﬁcant difference between

the mean pretest scores in groups 2019-2021. The as-

sumption of equality of variances was also met (Lev-

ene’s test p = .920). Descriptive statistics are pre-

sented in table 4. The highest and the lowest mean

scores, obtained in various dimensions of the per-

formance checklist after the intervention, were on

the topics how the position of the center of a cir-

cle (9.2 ± 1.01) and learning about the concept of an

event, an impossible, accidental, and probable event

(8.6 ± 1.04), respectively.

The ICT Usage in Teaching Maths to Children with Hearing Impairment

727

Figure 1: Geometry exercise for the topic “Triangles” (LearningApps software).

Table 3: Descriptive stats table of mean performance scores of students (N = 80).

Raven’s Progr. Matr.

Rey-Osterriet Comp. Figures Test

Figures of Gottschaldt

101.8 ± 6.43 8.1 ± 2.36 1.9 ± 0.13

Note.

Data are presented as mean ± SD

IQ-index

Summary score of Copy Presence and Accuracy,

Organization (According to BQSS (Le Brun, 2022)).

I index.

6 DISCUSSION

The research question investigated in this study was:

does ICT boost the maths skills of hearing-impaired

teenagers? The current research extended the work of

previous research by investigating whether ICTs such

as LearningApps, Geogebra can boost maths skills.

Previous research showed that most children with

hearing impairment have a gap of approximately

three years behind their hearing peers in mathemat-

ics (Rochester Institute of Technology, 2022b). Our

participants before were known for their individual

scores on Rey-Osterriet Composite Figures Test, the

Raven’s Progressive Matrices, and the Gottschaldt’s

Hidden Figure Test, emphasising that they did well

on tests and that their spatial ability was sufﬁcient for

maths learning. This diagnostic was for the predic-

tion of reducing the repetitive experience of stereo-

type threat in teaching mathematics using ICT.

According to the study results, there was a signif-

icant increase in the mean score of performance af-

ter the intervention than before the intervention. In

other words, this increase represents the effectiveness

of ICT educational methods. Furthermore, we high-

lighted some recommendations for using online ser-

vice LearningApps, GeoGebra Dynamic Mathemat-

ics system.

6.1 Case Study – Example 1: Using

Online Service LearningApps for

Teaching the Children with HI

Let us demonstrate how LearningApps service inter-

active exercises can be applied at different stages of

learning maths. For example, at the stage of learning

about the concept of an event, an impossible, acci-

dental, and probable event, it is reasonable to offer

students an exercise to determine the type of event.

The following events appear alternately in the ex-

ercise window. A student should determine which

events are probable, which are impossible, and which

are accidental.

Task 1. Determine “which” type is the event.

In this task, each word is stressed. It is reason-

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

728

Table 4: Comparison of mean performance score of students before and after intervention (N = 80).

Performance Geometry Algebra

Before intervention 6.3 ± 1.08 6.23 ± 1.04

After intervention 8.1 ± 1.9 8.2 ± 1.6

Paired t-test results (P, t) 0.001, 0.61 0.002, 0.21

able to introduce exercises to children with hearing

impairment in such a way. In the following lessons,

this exercise can be also used at the stage of refreshing

students’ basic knowledge on the topic.

Students with SEN may ﬁnd it difﬁcult to under-

stand and memorise theoretical material, so it is best

ﬁrst to demonstrate examples of learned concepts and

then return to the theory when necessary. For this pur-

pose, it is reasonable to offer the students with special

educational needs the opportunity to ﬁnd a pair in the

LearningApps online service during the initial consol-

idation stage. In the process of studying events oper-

ations, one should use as many examples as possible,

reﬂecting not only the essence of these operations but

also the differences between them.

Children with hearing impairment can easily ﬁnd

both the sum and value of events using deﬁnitions.

So solving applied problems is important in this pro-

cess. After students have mastered the theorems of

adding incompatible events and multiplying indepen-

dent events, they use them to calculate the probability

of events, solving the corresponding problems.

Here are some other examples of tasks that can be

conveniently created in LearningApps templates and

used in Stochastics teaching.

Task 2. “Classiﬁcation” exercise. The essence of

this exercise is that the screen on the student’s com-

puter or mobile phone is divided into two ﬁelds: a

right triangle and an isosceles triangle. Next, students

are given deﬁnitions, properties, constituents, or ex-

amples of triangles to be referred to as a right triangle

or an isosceles one. After completing the exercise,

the student can “push” the button to the right from the

bottom to check if the tasks are done correctly.

Task 3. “Classiﬁcation” exercise. In ﬁgure 1 a

screenshot of the 7th grade geometry exercise on the

topic “Triangles” is presented (https://learningapps.

org/display?v=p1gk6f39a22). The exercise is in-

tended for students to repeat the types of triangles

and consolidate knowledge on the signs of equality

of triangles. A small number of words are used in

the exercise. Stress is placed before the correspond-

ing stressed syllables. Students must match concepts,

names of theorems with corresponding pictures.

Task 4. “Match” Exercise. The essence of this ex-

ercise is that a student should connect the notion with

its deﬁnition or example. For instance, the term “bi-

sector” refers to the deﬁnition of a bisector of a trian-

gle, to a certain notion corresponding to a picture that

illustrates it, to calculate the perimeter of a triangle, if

the lengths of its sides are given, etc.

The use of similar tests allows a teacher to deter-

mine the level of success of a child with hearing im-

pairment and to identify gaps in his/her knowledge.

It will help to correct his learning and to plan further

work. For example, the possibility of repeated repeti-

tion of the exercises created with LearningApps will

give students conﬁdence. It will also contribute to bet-

ter learning.

6.2 Case Study – Example 2: GeoGebra

Dynamic Mathematics System

We have upgraded the set of visuals offered by Sada

(Sada, 2021) to adapt it to students’ learning in

Ukrainian. For example, one of the exercises allows

us to see changes and patterns in the process of any

number of the tests carried out. The student can ob-

serve whether there is any tendency as the number of

falls in a single number increases, and compare it with

the number of falls in another number. Such activ-

ity in the lesson should be structured for a student

with special needs in the form of clearly formulated

actions, and algorithms for completing the task. In-

structions should be brief and clear, repeated several

times. It may be difﬁcult for a student with disabilities

to concentrate, so he or she has to be repeatedly urged

to carry out, to control this process until its comple-

tion. The task should be adapted so the student has

time to work at the pace of the whole class.

The task is complicated when the student is of-

fered the following exercise: modelling and counting

the results when throwing two, three or more dice and

calculating the sum of the falling numbers, etc. By

practising research on the tossing of two and three

coins, it may be easier for the student to imagine the

situation of tossing 4 coins and others. It gives a good

result and use of the lessons of planimetry, the library

of electronic visibility (Sada, 2021).

Task 5: How the position of the centre of a circle

described around a triangle is related to the view of a

triangle (ﬁgure 2).

It should be taken into consideration that the

GeoGebra Dynamic Mathematics system can be in-

stalled on smartphones. So the children with hearing

The ICT Usage in Teaching Maths to Children with Hearing Impairment

729

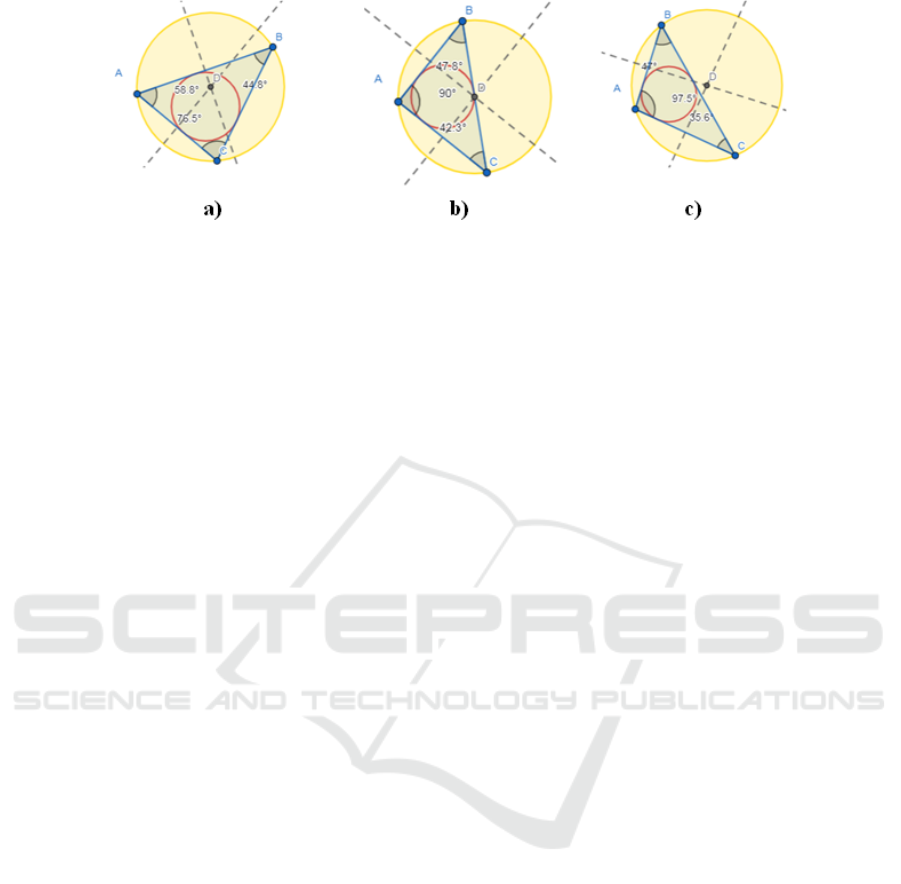
Figure 2: Investigation of the position of the centre described around a triangle of a circle (GeoGebra Geometry): a) an acute-

angled triangle, b) rectangular, c) obtuse.

impairment will be able to check the correctness of

their tasks during the lesson, especially when work-

ing independently or in groups. One can also start

the exercise by using the link or QR code for the ex-

ercise. It is enough for the student to install a code

scanner on his/her smartphone. One of these is the

free Qrafter application, which allows you instantly

to read QR codes using only your smartphone’s cam-

era and Internet access.

The use of GeoGebra in preparation for admission

to higher education institutions provides ample oppor-

tunities for students with special educational needs.

Using GeoGebra 3D Calculator, they will be able to

develop spatial imagination, master the techniques of

constructing spatial ﬁgures. A number of illustrations

for solving problems of open type of external inde-

pendent evaluation (EIE) are given by us in the man-

ual (Kramarenko, 2019). Here are some of them in

this article. These are two open-ended tasks with a

detailed answer, which are evaluated by examiners ac-

cording to special rules (EIE-2018).

Task 6. In a regular quadrangular pyramid

SABCD, the side of the base ABCD is equal to c,

and the side edge SA forms an angle a with the plane

of the base. A plane c is drawn through the base of

the height of the pyramid parallel to the plane ASD.

Construct a section of the pyramid SABCD plane in,

justify the type of section and determine its perimeter

(ﬁgure 3).

By studying the function line, students will be able

to use the GeoGebra Graphing Calculator to deter-

mine all possible solutions to an equation or inequal-

ity. This will provide visualization, help students bet-

ter understand the process of solving such complex

problems.

Task 7 (GeoGebra Geometry, grade 8-9). Con-

struct an arbitrary convex quadrilateral. Investigate:

a) the quadrilateral formed by the successive connec-

tion of the midpoints of this quadrilateral is a paral-

lelogram; b) the area of the resulting parallelogram is

half the area of the original quadrilateral (ﬁgure 4).

Using the same visualization, it would be possible to

investigate that the quadrilateral formed as a result of

mapping an arbitrary point relative to the midpoints

of the sides of the original quadrilateral is also a par-

allelogram. And therefore its area does not depend on

the choice of a point inside. However, the substantia-

tion of such a hypothesis goes beyond the mathemat-

ics curriculum for deaf children.

7 CONCLUSION

1. The conducted research proved the relevance of

the problem of modifying the strategy of teaching

mathematics to deaf and hard-of-hearing students

based on the implementation of distance learning

technologies. Studying the problems of teaching

mathematics to deaf and hard-of-hearing students

made it possible to draw the following conclu-

sions: the most important task of a teacher and

teacher’s assistant is to encourage deaf and hard-

of-hearing students to study; one of the effective

ways of teaching mathematics to students of the

speciﬁed categories is the use of remote technolo-

gies; in the text messages of visual aids offered to

students with hearing impairments, it is advisable

to emphasize each word so that they know how to

read the words correctly.

2. We found that the LearningApps educational en-

vironment can be used at different stages of the

lesson: during the organization of independent,

individual activities, in joint research activities.

Thanks to interactive exercises, deaf and hard

of hearing students should become active partic-

ipants in the educational process. The toolkit of

the service allows you to create training classes,

inviting them to your students by hyperlink. Since

deaf and hard-of-hearing students put much more

effort into the task, the system for evaluating the

educational achievements of such students can be

stimulating. After each student has completed

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

730

Figure 3: Examples of open-ended tasks (task 32 from EIE-2018 (https://zno.osvita.ua/mathematics/298/), GeoGebra 3D

Calculator).

Figure 4: Studying the shape of a quadrilateral using Ge-

oGebra.

each exercise, the teacher should analyze and

compare the expected results with the actual per-

formance of the students. A mandatory condi-

tion for teaching students with special educational

needs in mathematics is feedback: to ﬁnd out

whether students are satisﬁed with their work and

the knowledge they have acquired, whether they

understand the importance of this knowledge for

further study of the subject.

3. Using the proposed clariﬁcations will help a stu-

dent with hearing impairments to better under-

stand mathematical material. Therefore, the stu-

dent receives complete information if it is sup-

ported by visual perception of the text, tables, di-

agrams.

4. In order to investigate progressive shifts in the

learning of mathematics by deaf and hard of hear-

ing students using ICT, it is appropriate to com-

pare the shifts in the scores of the diagnostic test

and the test. Statistical groups can be analyzed by

two G-tests and Wilcoxon tests. These algorithms

involve the use of small sample sizes. So we used

it and tested it for individual academic groups. We

observed a trend of increasing values of the char-

acteristic (scored points) from the initial training

exercises to the control of the achieved level of

knowledge and skills.

The prospects of the research are related to the ex-

pediency of using the GeoGebra dynamic mathemat-

ics system for the development of spatial imagination

and spatial thinking, etc., in children with hearing im-

pairments.

REFERENCES

Ariapooran, S. (2017). Mathematics Motivation, Anxiety,

and Performance in Female Deaf/Hard-of-Hearing

and Hearing Students. Communication Disorders

Quarterly, 38(3):172–178. https://doi.org/10.1177/

1525740116681271.

Barrett, E. (2005). Mathematics: it’s all about language.

Master of Science of Secondary Education of Students

Who are Deaf or Hard of Hearing (NTID), Rochester

Institute of Technology. https://scholarworks.rit.edu/

theses/3996/.

de Dinechin, E. and Boutard, A. (2021). Infor-

mation and Communication Technologies (ICTs)

and Inclusive Education. Humanity & Inclu-

sion, Lyon. https://www.hi.org/sn uploads/document/

Inclusive-ICT-report 1.pdf.

Fritz, A., Haase, V. G., and R

anen, P., editors (2019).

International Handbook of Mathematical Learning

The ICT Usage in Teaching Maths to Children with Hearing Impairment

731

Difﬁculties: From the Laboratory to the Class-

room. Springer, Cham. https://doi.org/10.1007/

978-3-319-97148-3.

Global Education Monitoring Report Team (2020). 2020

Global Education Monitoring Report: Inclusion and

Education: All means all. https://gem-report-2020.

unesco.org/.

Kidd, D. H. (2018). Mathematics Learning: Keeping Deaf

Students Engaged. https://cutt.ly/J8dTD0Z.

Kollosche, D., Marcone, R., Knigge, M., Penteado, M. G.,

and Skovsmose, O., editors (2019). Inclusive Math-

ematics Education: State-of-the-Art Research from

Brazil and Germany. Springer, Cham. https://doi.org/

10.1007/978-3-030-11518-0.

Kramarenko, T. H. (2019). Vybrani pytannia elementarnoi

matematyky z GeoGebra [Selected questions of ele-

mentary mathematics with GeoGebra]. https://www.

geogebra.org/m/gqpk8yfu.

Le Brun, D. (2022). 7 tips for teaching the lan-

guage of maths to deaf learners. https:

//mathsnoproblem.com/blog/learner-focus/

tips-for-teaching-maths-to-deaf-learners/.

Lovie, A. D. (1983). Aspects of neogenesis: Spearman’s

system of cognition and applied psychology. In Bern,

S., Rappard, H., and van Hoorm, W., editors, Stud-

ies in the History of Psychology and the Social Sci-

ences: Proceedings of the First European Meeting of

Cheiron, International Society for the History of the

Behavioral and Social Sciences, pages 120–136. Psy-

chologisch Instituut van de Rijksuniversiteit Leiden,

Leiden, The Netherlands.

National Deaf Center on Postsecondary Outcomes (2020a).

Take Control of Your Online Learning: Tips for Deaf

College Students. https://cutt.ly/u8dTUMO.

National Deaf Center on Postsecondary Outcomes (2020b).

Tips for Instructors: Teaching Deaf Students Online.

https://cutt.ly/L8dTx5m.

Nunes, T. and Moreno, C. (1999). Is hearing impairment

a cause of difﬁculties in learning mathematics? In

Donlan, C., editor, The Development of Mathemati-

cal Skills, pages 227–254. Psychology Press. https:

//tinyurl.com/4yrv8z7b.

Raven, J. (2020). The Outstanding Properties

of the Standard Progressive Matrices Plus

test. http://eyeonsociety.co.uk/resources/

Outstanding-properties-of-SPM-PLUS.pdf.

Ray, E. (2001). Discovering mathematics: The chal-

lenges that deaf/hearing-impaired children en-

counter. ACE Papers: Student Edition, (11):62–

78. https://cdn.auckland.ac.nz/assets/education/

about/research/docs/FOED%20Papers/Issue%2011/

ACE Paper 6 Issue 11.doc.

Rochester Institute of Technology (2022a). STEM

Sign Video Dictionary. https://deaftec.org/

stem-dictionary/.

Rochester Institute of Technology (2022b). Teach-

ing Math to Deaf Students. https://deaftec.org/

teaching-learning/strategies-for-teaching-math/

teaching-math-to-deaf-students/.

Sada, M. (2021). Probabilidad: simulaciones y problemas.

https://www.geogebra.org/m/qjWuUAgs.

Shestopalova, O. P., Bondar, K. M., Sklianska, O. V.,

Doroshenko, L. V., Trushyk, O. V., Zhukova, L. V.,

and Smekhnova, T. V. (2019). Teoriia i praktyka inkli-

uzyvnoi osvity [Theory and Practice of Inclusive Ed-

ucation]. Proekt “Pidtrymka inkliuzyvnoi osvity u

m. Kryvyi Rih”, 2 edition. https://doi.org/10.31812/

123456789/3544.

Singh, S. (2019). Revisiting Inclusion of Children with

Hearing Impairment: Issues and Possibilities. In

Chennat, S., editor, Disability Inclusion and Inclu-

sive Education, pages 157–174. Springer, Singapore.

https://doi.org/10.1007/978-981-15-0524-9 8.

UNICEF (2020). COVID-19: Are children able to con-

tinue learning during school closures? A global anal-

ysis of the potential reach of remote learning policies.

UN, New York. https://digitallibrary.un.org/record/

3886022.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

732