Digital Learning Space to Improve the Conceptual Understanding of

Mathematics of non-Mathematical Specialties Students

Mariia M. Astaﬁeva

1 a

, Oksana M. Hlushak

1 b

, Oksana S. Lytvyn

1 c

and Volodymyr V. Proshkin

1 d

Borys Grinchenko Kyiv University, 18/2 Bulvarno-Kudriavska Str., Kyiv, 04053, Ukraine

ﬁ

Keywords:

Conceptual Knowledge, Conceptual Understanding of Mathematics, Mathematical Training of Students,

Digital Learning Space, Go-Lab, Derivative Functions.

Abstract:

The article considers the problem of improving the conceptual understanding of mathematics of non-

mathematical specialties students by means of digital learning space. The results of a survey of students

on the effectiveness of their mathematical training are presented. It is established that most often students

use procedural rather than conceptual knowledge, which complicates the application of mathematical meth-

ods on practice. As a result of the analysis of the most common strategies for teaching mathematics, the

author’s vision of teaching mathematics using digital tools is presented. Such teaching is aimed at forming

students’ conceptual mathematical knowledge, which is harmoniously combined with procedural knowledge.

A learning space has been developed to study the topic “Derivative”, where you can explore mathematical

concepts and relationships between them, formulate hypotheses, experiment, ask questions, draw conclusions

and discuss the results. One of the developed educational spaces is described, namely for studying the topic

“Derivative”. In it, you can explore mathematical concepts and relationships between them, formulate hy-

potheses, experiment, ask questions, draw conclusions, and discuss the results obtained. Digital tools are built

into the space, which allow to implement different types of educational activities of students (individual, group

and frontal) and thus ensure the effectiveness of the formation of conceptual knowledge about the derivative.

On the example of studying Lagrange’s theorem on ﬁnite increments and solving various applied mathemati-

cal problems, methods of forming a conceptual understanding of students’ mathematics are given.

1 INTRODUCTION

In modern high-tech and digitalized society, the main

trend in the development of mathematics is the pro-

cess of its penetration into various sciences – the

mathematization of science, which, in turn, leads to

mathematization and computerization of human prac-

tice. In these conditions, a competent specialist must

know the mathematical methods and models used in

his profession, be able to use them, be able to use ap-

propriate computer programs to develop new models

for his/her professional needs. That is, mathematical

training is a necessary and integral part of the training

of highly qualiﬁed specialists at all levels of higher

education.

Mathematical knowledge is dual: it is knowledge

https://orcid.org/0000-0002-2198-4614

https://orcid.org/0000-0001-9849-1140

https://orcid.org/0000-0002-5118-1003

https://orcid.org/0000-0002-9785-0612

of “what” and “why” (conceptual knowledge) and

knowledge of “how” (procedural knowledge). There-

fore, learning mathematics will be successful if this

process is aimed at understanding concepts and mas-

tering procedures.

Many works are devoted to the deﬁnition of the

content of the concepts “conceptual knowledge” and

“procedural knowledge”, their relationships, theo-

retical and methodological principles of formation

(Hiebert and Lefevre, 1986; Cobb, 1988; Byrnes and

Wasik, 1991). Based on them, it can be argued that

conceptual knowledge involves, in addition to knowl-

edge of concepts, facts, methods, understanding of the

relationships and interdependencies between them;

the ability to see the key idea of a method, to assess in

what contexts it may be useful; ﬁnd different solutions

to one problem; analyze and evaluate the obtained re-

sult.

Procedural knowledge involves a number of steps

that must be performed to solve the problem. Proce-

850

Astaﬁeva, M., Hlushak, O., Lytvyn, O. and Proshkin, V.

Digital Learning Space to Improve the Conceptual Understanding of Mathematics of non-Mathematical Specialties Students.

DOI: 10.5220/0012068400003431

In Proceedings of the 2nd Myroslav I. Zhaldak Symposium on Advances in Educational Technology (AET 2021), pages 850-859

ISBN: 978-989-758-662-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

dural knowledge includes knowledge of algorithms,

techniques and methods.

There are different views on the causal relation-

ship between conceptual and procedural knowledge

(Byrnes and Wasik, 1991; Rittle-Johnson et al., 2001;

Forrester and Chinnappan, 2010). Most researchers

believe that the effectiveness of learning is higher

if conceptual knowledge precedes procedural and its

knowledge is based on conceptual (Balka et al., 2012;

Nahdi and Jatisunda, 2020; Forrester and Chinnap-

pan, 2010). For example, Forrester and Chinnap-

pan (Forrester and Chinnappan, 2010) found in test-

ing students the dominance of their procedural skills

over conceptual knowledge. All common errors were

related to incorrect application of procedures due to

misunderstanding of their conceptual basis.

It should be noted that the purpose of mathemati-

cal training of students of non-mathematical special-

ties is not to master the knowledge of higher math-

ematics as a value that is important in itself. The

goal (and at the same time the motivation to study

mathematical disciplines) is the opportunity and abil-

ity to apply mathematics in his/her ﬁeld. Therefore,

questions arise: 1) how do different types of knowl-

edge (conceptual and procedural) affect this ability?

2) what should be the educational strategy aimed at

forming in students of non-mathematical specialties

conceptual mathematical knowledge that is harmo-

niously combined with procedural knowledge?

There are many methodological techniques that

allow you to implement this pedagogical task. But

the most effective, in our opinion, is research-oriented

teaching of mathematics using digital technologies

(Leung, 2006; Smetana and Bell, 2012; Astaﬁeva

et al., 2020). It involves active interaction between

teacher and student, which includes identifying prob-

lems, joint search for solutions, research, discussion,

consideration of alternatives, rethinking and evaluat-

ing the result. On the other hand, the use of ICT

provides active communication between teachers and

students, their independent research work (both indi-

vidual and group), competent and effective organiza-

tion of educational space and its management.

The aim of research – development and theoretical

substantiation of some methodical methods of using

digital learning space to improve the conceptual un-

derstanding of mathematics of non-mathematical spe-

cialties students.

Research methods:

• theoretical – analysis, synthesis, systematization

and generalization of scientiﬁc, methodological

literature, to determine the impact of conceptual

and procedural mathematical knowledge on the

ability to apply mathematics and study educa-

tional strategies of mathematical training of non-

mathematical specialties, deﬁnition of concep-

tual and categorical research apparatus (“concep-

tual knowledge”, “procedural knowledge”, “edu-

cational and research spaces”); generalization of

progressive ideas and existing shortcomings in

modern higher education to justify ways to im-

prove the mathematical training of students by

means of digital technologies that allow active

learning, in particular, to conduct experiments, re-

search and modeling;

• empirical: surveys to determine the effectiveness

of mathematical training of non-mathematical

specialties students.

2 RESULTS AND DISCUSSION

Borys Grinchenko Kyiv University trains, among oth-

ers, specialists in “Computer Science”, “Manage-

ment”, “Economics”, “Finance, Banking and Insur-

ance”. These educational programs include the study

of higher mathematics. In June 2022, we conducted a

survey of students of these specialties on the effec-

tiveness of their mathematical training. A total of

63 ﬁrst-fourth year students took part in the survey.

All students took a course in higher mathematics and

had the opportunity to use the acquired mathematical

knowledge in practice in the process of studying pro-

fessional disciplines.

Firstly, we asked students to assess the general

level of their mathematical training after studying the

discipline “Higher Mathematics” (on a 4-point scale:

1 – low, 2 – medium, 3 – sufﬁcient, 4 – high). It

turned out that the vast majority of students (74.6%

of respondents) believe that they have a sufﬁcient and

high level of mathematical training, 22.2% – medium,

3.2% – low. Interestingly, the answers of junior stu-

dents (I – II courses) were not fundamentally different

from the answers of senior students (III – IV courses).

Next, we found out if they feel the need to apply math-

ematical knowledge in the study of professional dis-

ciplines. The majority of students, 68.3%, answered

in the afﬁrmative – “yes” and “rather yes”, 22.2% of

respondents – “rather not”, 9.5% of students do not

feel the need to apply mathematical knowledge in the

study of professional disciplines.

We also tried to determine whether students had

to apply mathematical knowledge in the study of

professional disciplines (on a 4-point scale). 68.3%

of respondents answered that they use mathematical

knowledge in the study of professional disciplines,

23.8% – rather no, 7.9% – no. Figure 1 shows the

results of students’ survey.

Digital Learning Space to Improve the Conceptual Understanding of Mathematics of non-Mathematical Specialties Students

851

(a)

(b)

(c)

Figure 1: The results of students’ survey.

We compared the available empirical distribu-

tions using Pearson’s test χ

. It turned out that

emp

= 1.631 at χ

= 12.562 (at p = 0.05). Thus, we

can say that there is a certain relationship between the

level of mathematical training of students (ﬁgure 1a),

a sense of their need (ﬁgure 1b) and the real oppor-

tunity to apply mathematical knowledge on practice

(ﬁgure 1c). For example, 25.4% of students do not

appreciate the level of their own mathematical train-

ing, while 31.7% of respondents do not see a special

need and opportunity to apply mathematical knowl-

edge.

One of the key mathematical concepts is the con-

cept of “derivative of a function”. We asked students

to comment on the essence of this concept. As a re-

sult of self-assessment it was found that only 12.7%

of students believe that they remember the deﬁnition

well, understand the essence of this concept and use

it in the study of professional disciplines, 34.9% – re-

member the deﬁnition well, understand the essence

of the concept, but do not use it. study of professional

disciplines. The majority of students (52.4%) stated

that they had some information about the derivative

function or did not remember anything about it.

We decided to check the obtained results and

asked students to choose the correct deﬁnition of the

derivative function from the proposed options. The

majority of students (34 people or 54.0%) chose the

wrong answers. It should be noted that among them

14 people (22.2%), answering the previous question,

thought that they well understood the essence of the

concept of “derivative function”.

To test the conceptual understanding of the con-

cept of a derivative, we also asked students to ex-

plain in one word what a derivative is. Options were

proposed: speed, productivity, tangent, consequence,

area, work, mass. The correct options were cho-

sen: “speed” – 46%; “productivity” – 17.5% of stu-

dents. The majority of respondents (57.1%) chose the

“tangent” option, which indicates a lack of concep-

tual knowledge, ﬁrst of all, an understanding of the

essence of the concept of a derivative (a derivative

is not a tangent, but an angular coefﬁcient of a tan-

gent). Another number of students chose other wrong

options: consequence (28.6% of respondents), area

(11.1%), work (4.8%), mass (1.6%). It can be as-

sumed that the reason for the incorrect answer was

mainly the formal following of a certain algorithm for

using the derivative in solving applied problems. In

our opinion, students generally remember the rules of

differentiation, can use the table of derivatives, but do

not feel the main thing – the essence of the concept

of “derivative function”. Thus, most of them are not

able to use this concept in non-mathematical contexts.

Interestingly, among the 29 students who recognized

the correct deﬁnition of the derivative function from

the proposed ones, there were only two in which the

derivative was associated with both speed and produc-

tivity, and they did not choose the wrong options. And

this indicates the formality of knowledge and lack of

conceptual understanding of the concept of derivative

in the remaining 27 students.

The results of the survey, as well as the real expe-

rience of teaching mathematical disciplines to the au-

thors of the study showed that students of all special-

ties to some extent feel the need to apply mathemati-

cal knowledge in the study of professional disciplines,

as well as use this knowledge in practice. At the same

time, most students are more likely to use procedu-

ral rather than conceptual knowledge. In particular,

students work mechanically according to known algo-

rithms, schemes or rules, but have a poor understand-

ing of the essence of mathematical concepts, facts,

methods and tools.

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

852

The results of our survey are close to the results of

the study of Aydın and

Ozgeldi (Aydın and

Ozgeldi,

2019). The authors of this study, analyzing the suc-

cess of prospective elementary mathematics teachers

in solving PISA-2012 problems, found that few stu-

dents were able to give “mathematical explanations

for conceptual knowledge items, and that their con-

textual knowledge was fragmented” (in this article the

authors understand contextual knowledge those that

allow you to connect the real world – the context in

which the problem arises, with mathematics (S

aenz,

2009)). In addition, students had particular difﬁculty

with tasks that required a combination of conceptual

and procedural knowledge.

Thus, we approached the main question: what

teaching of mathematics to non-mathematical special-

ties students will be effective, how to teach that the

acquired mathematical knowledge became useful in

the future professional activity?

There are two extremes in teaching mathematics

to non-mathematical specialties students. The ﬁrst

is the desire for formal rigor of proofs of theoreti-

cal facts, formulations of deﬁnitions. Teachers are

supporters of this point of view, pay too much at-

tention to strict deductive reasoning. They, striving

for formal rigor (which is still not achieved due to

the limited time allocated in the educational programs

of non-mathematicians to study mathematical disci-

plines), often have little concern about how this ma-

terial will “work” in the future to solve problems that

lie outside mathematics.

The second extreme is a minimum of attention to

theoretical justiﬁcation, learning algorithms, solving

typical problems according to the instructions, the use

of certain formulas, and etc. Teachers are apologists

for this point of view, believing that they teach applied

mathematics, do not attach due importance to the jus-

tiﬁcation of certain actions, clarifying the limits of the

method, and etc. Such training critically limits the

ability of the future specialist to use mathematics as a

tool, because the mechanical implementation of cer-

tain procedures can lead to unreasonable and incorrect

decisions.

In both cases, students do not develop the abil-

ity to use mathematics to solve applied problems,

which is the purpose of teaching mathematics to non-

mathematical specialties students.

In our opinion, the course of higher mathemat-

ics (or a block of mathematical disciplines) for non-

mathematical specialties students should have an ap-

plied orientation. But it should not be narrowly util-

itarian and prescription, because applied mathemat-

ics is not a simpliﬁed version of “pure” mathematics.

Courses of mathematical disciplines should be based

on the necessary theoretical concepts: key mathemat-

ical concepts, facts, a set of ideas and methods that

have a wide range of applications. For mathematics to

be applied, deep knowledge of the essence of mathe-

matical concepts, facts, methods is required, i.e. con-

ceptual knowledge is required. It is also necessary to

have not only (and not so much!) deductive, but also

empirical thinking, which would be convincing, al-

though not necessarily strict from the standpoint of

“pure” mathematics. Rigor should be in the exact

(correct) presentation of the idea, not in the fetishiza-

tion of the form of presentation.

Teaching mathematics to “applicators” should, in

our opinion, pursue the following goals:

1) formation of conceptual understanding of key

mathematical concepts, facts, methods with illus-

tration of their applied application, study of the

corresponding mathematical apparatus;

2) developing basic skills of mathematical research

and mathematical modeling.

In view of this, we consider it effective to use

(as tools) digital technologies for the formation of

conceptual and procedural knowledge, which make it

possible to implement active learning, in particular, to

conduct experiments, research and modeling.

One of the platforms that has these tools is Go-

Lab. The Go-Lab project (Global Online Science

Labs) is a research innovation project co-ﬁnanced by

the European Commission. Its goal is to bring science

closer to pupils and students by providing open access

to online science laboratories created by scientists and

teachers from different countries (Next-Lab, 2022).

On the portal (https://www.golabz.eu) for the

teacher there is an opportunity to work with the base

of ready laboratories and training spaces (ILS). And

also create your own learning spaces in the Graasp

environment (https://graasp.eu/), using Go-Lab tools

and resources.

Go-Lab Inquiry Learning Spaces (ILSs or In-

quiry Spaces) are research-oriented activities struc-

tured through Go-Lab Inquiry Cycles, which can in-

clude laboratories, training resources, programs, on-

line services and other digital tools to provide and

support research learning (de Jong, 2015).

The functionality of such a space allows you to

organize a special environment. Here, under the guid-

ance of the teacher, students explore mathematical

concepts and the relationships between them, formu-

late hypotheses, experiment, ask questions, draw con-

clusions and discuss the results.

In fact, with the help of ILS, the teacher can en-

courage students to actively learn, using methods and

techniques that require students to conscious learning

Digital Learning Space to Improve the Conceptual Understanding of Mathematics of non-Mathematical Specialties Students

853

activities, to involve them in the process of construct-

ing new knowledge, research skills. The active partic-

ipation of the student in the educational process is the

key to the formation of conceptual understanding and

achievement of high results during training, as well as

his ability to apply the acquired knowledge and skills

in further professional activities.

An example of such a space can be created by edu-

cational and research space to study the topic “Deriva-

tive”.

The learning space contains tasks that involve

working with a variety of digital tools (ﬁgure 2 –

6). These tools are selected so that you can imple-

ment different types of student learning activities (in-

dividual, group and frontal) and ensure maximum ef-

ﬁciency in the formation of conceptual knowledge in

solving the problem.

There are things that integrated into the space:

• a ready – made Go-Lab laboratory (Labs), which

allows students to conduct research using com-

puter simulations;

• built – in GeoGebra environment for research and

geometric modeling;

• built – in online spreadsheets with the ability to

co-edit;

• TEXT Input forms for answers (the teacher has

the opportunity to see the answers of all students

from his proﬁle, and students see only their an-

swers);

• Apps Sticky Notes, in which participants in the

process can write down their ideas on stickers;

• Apps Concept Mapper for compiling problem-

solving algorithms;

• Padlet board for joint work of students and

teacher;

• Apps Quest 2.0 – tests to check the mastery of the

topic.

Let’s illustrate the use of these tools on some tasks

of our educational space “Derivative”.

Task 2. The motorcyclist moves in a straight

line according to the law x(t). When changing some

parameters of the motorcyclist’s movement, observe

how others change. Record the results of your ob-

servations in the form below. Can you independently

build graphs of speed and acceleration according to a

known graph of the law of motion? And the schedule

of the passed way according to the schedule of speed?

The task is performed in Go-Lab. When perform-

ing this task, students have the opportunity to conduct

an experiment by changing certain parameters of the

motorcyclist’s movement (ﬁgure 2).

One of the most important theorems of differential

calculus is Lagrange’s theorem on ﬁnite increments.

Theorem. If the function f (x) is continuous on

the interval [a; b] and differentiable on the interval

(a;b), then on this interval there exists a point c such

that the equality (Lagrange formula):

f (b) − f (a)

b − a

= f

′

(c).

The theorem has a simple (even obvious!) geo-

metric meaning: on a solid smooth curve connecting

two points, there is a point where the tangent is par-

allel to the chord. Students are given the task to ex-

perimentally “prove” the validity of the theorem. To

do this, they should draw a line parallel to the chord

AB, and then move this line parallel to itself and make

sure, thus, the validity of the theorem formulated in

geometric terms. The task is performed using the

built – in environment GeoGebra (ﬁgure 3).

Such a geometric illustration (and argumenta-

tion!) is quite convincing, it is intuitively clear.

Therefore, it is not necessary to “frighten” students,

for whom mathematics will not be the sphere of their

professional activity in the future, with a strict math-

ematical formulation of the theorem, especially – by

proving it. Students will easily come to the analyti-

cal formulation when they have before their eyes the

appropriate graphic image. The teacher can (if nec-

essary) provide assistance in the form of a question:

“What is the condition of parallel lines?”

With the pedagogical mediation of the teacher (or

without him), students, changing the curve, just as

easily establish graphically that the point c, which is

discussed in the theorem, may not be one (ﬁgure 4).

To improve the conceptual understanding of math-

ematics and the formation of conceptual knowledge,

it is important to clarify the implication links between

statements. Therefore, the chance will be lost if, when

studying Lagrange’s theorem, we do not stimulate

students to answer the question: “Are the conditions

of the theorem necessary, essential, is each of them

individually, sufﬁcient?” (Task 5). In this particular

situation, we organize the collective work of students

using the built – in online Google Sheet. Students ﬁll

in the so-called. conceptual table on the topic “La-

grange’s theorem” (ﬁgure 5).

What is a “conceptual spreadsheet”? A conceptual

table is a summary, organized, and structured infor-

mation about the content of a particular topic, ways

to solve a particular problem, the results of a study,

and etc. Students ﬁll in the spreadsheet collectively,

most often – working in small groups. At the same

time, they must demonstrate an understanding of the

essence of concepts, facts of this topic, their con-

nection with previously studied, physical, economic,

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

854

Figure 2: Computer simulation of the mechanical content of the derivative.

Figure 3: Graphic illustration of Lagrange’s theorem (point c is one).

etc. content, the ability to correlate different forms of

presentation of a mathematical content (verbal, sym-

bolic, graphic).

The work with the conceptual spreadsheet, which

summarizes the results of the study of the conditions

of Lagrange’s theorem (whether each of them is nec-

essary, essential, sufﬁcient) can be organized in differ-

ent ways. For example, one group of students formu-

lates conclusions, and another one provides a graph-

ical argumentation of the correctness (or incorrect-

ness) of the verbal conclusion. Or vice versa – one

group gives a graphic image, and the other one makes

a verbal conclusion that can be made on the basis of

this image.

It will be useful to ﬁnd out the mechanical mean-

ing of Lagrange’s formula (it indicates that when a

body moves according to the law s(t), then at some

point in time the velocity of the body will be equal to

its average velocity over a period of time).

Instead of a rigorous analytical proof of the theo-

rem, which will not add any more convincing (for ge-

ometric simulation) arguments to students, it is worth

considering various applications of the theorem in

physics, economics, computational mathematics, and

so on. It will be appropriate to draw students’ atten-

tion to the fact that the number c in the Lagrange for-

Digital Learning Space to Improve the Conceptual Understanding of Mathematics of non-Mathematical Specialties Students

855

Figure 4: Graphic illustration of Lagrange’s theorem (points c are two).

Figure 5: Conceptual spreadsheet on the topic “Lagrange’s theorem”.

mula is unknown, but the formula is useful in prob-

lems to estimate the difference between the values of

the function, and hence – proﬁt, work, distance trav-

eled and other quantities.

In the context of what has been said, it will be use-

ful, for example, to estimate the difference (Task 6):

arctan0.55 − arctan0.45

Solution. The function arctanx is continuous and

differentiable for all real x, so Lagrange’s theorem can

be applied. According to this theorem, we can say that

between the numbers 0.45 and 0.55 there is a number

c that the equality

arctan0.55 − arctan0.45

0.55 − 0.45

= (arctanx)

′

x=c

that is

arctan0.55 − arctan0.45 =

0.1

1 + c

Hence, given that function

1+x

decreases for pos-

itive x, we have

0.1

1 + 0.55

0.1

1 + c

0.1

1 + 0.45

or:

0.0767 < arctan0.55 − arctan0.45 < 0.0832

Students were asked (Task 8) to formulate ques-

tions on the topic “Derivative” to this ﬁgure, which

shows a graph of the function f (x) (ﬁgure 6).

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

856

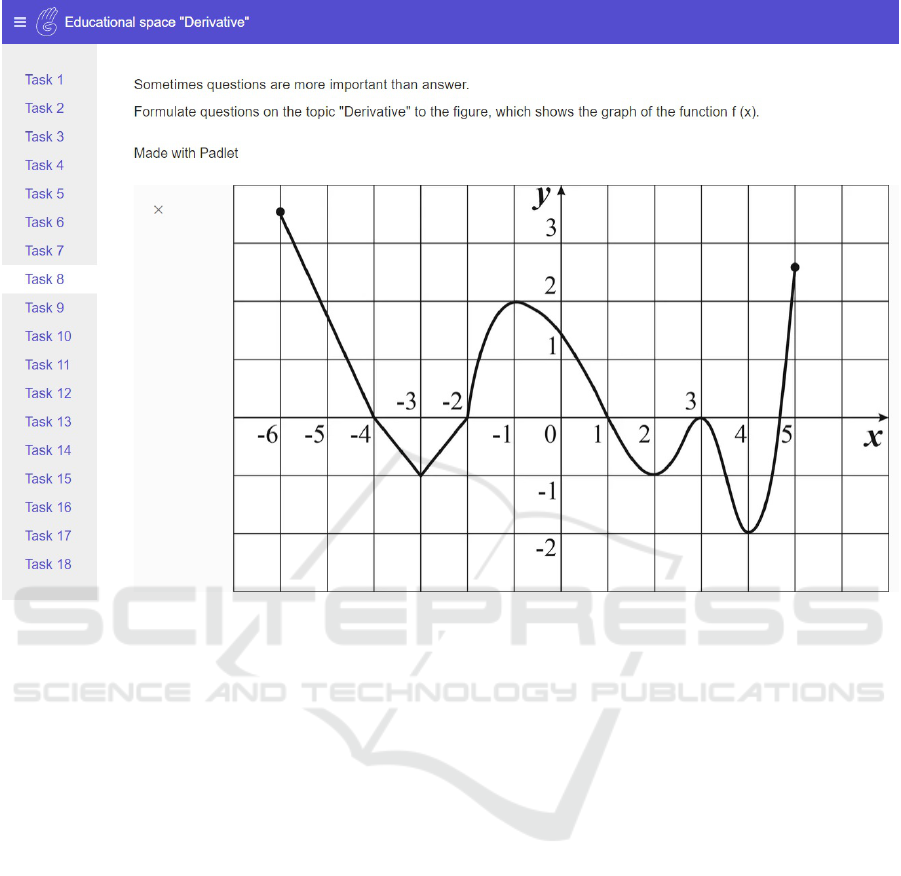
Figure 6: Task 8.

The ability to ask questions (form tasks) is one

of the signs of conceptual knowledge. Therefore, the

purpose of such tasks is to form a conceptual un-

derstanding of the concept of a derivative function,

in particular, its geometric content, and the ability to

graphically illustrate this understanding.

Students are divided into two subgroups. One for-

mulates questions or tasks, and the other provides an-

swers. In our space for this purpose the use of the

Padlet board where each student attaches the ques-

tions – answers is provided. At the same time, an

“editor” is appointed, who groups the same type of

questions, “forbids” questions that are not related to

the topic, and etc. Students attach the answers to the

questions next to the questions themselves. Then, un-

der the guidance of the teacher, questions and answers

are discussed with a vote for the best question.

Here are the most interesting, in our opinion,

questions (tasks) of freshmen:

1. Does it have the roots of an equation f

′

(x) = 0.

If so, is it possible to ﬁnd out: a) how much?

b) which ones?

2. Solve the inequality: f

′

(x) > 0 ( f

′

(x) < 0)..

3. Does the equation f

′′

(x) = 0 have roots? If so,

how much?

4. Does the inequality f

′′

(x) < 0 have integer solu-

tions? If so, how much? What are these solutions?

5. Does the function f

′

(x) have a breakpoint? If so,

what is the nature of these gaps?

6. Is it possible to determine the approximate value

of its derivative at the point: a) -1; b) 1. If possi-

ble, explain how to ﬁnd this value and ﬁnd it. If

not, then argue.

Task 10. Write an algorithm for approximating

the value of the function f (x) at the point x

+ ∆x us-

ing a differential. Such tasks form a conscious un-

derstanding of the algorithm, i.e. the construction of

procedural knowledge on the basis of conceptual.

It is suggested to perform this task in the Concept

Mapper application, which contains tools for plotting.

Task 11. The plant received an order from the

cannery to produce a batch of cylindrical cans of a

certain volume for canned olives. Design the shape of

the tin cans so that as little material as possible is used

to make them. Check out the various canned cylindri-

cal cans at your nearest supermarket. Is their packag-

ing economical in terms of the cost of materials for

their manufacture?

This is an optimization problem “from life”,

which requires the use of a differential calculus to

Digital Learning Space to Improve the Conceptual Understanding of Mathematics of non-Mathematical Specialties Students

857

solve it. We plan to use the Sticky Notes application

to solve this problem. Students describe their research

on stickers, which are placed in a common ﬁeld. In

this way, each student sees the results of others. Then

you can have a general discussion.

Conceptual understanding of mathematics in-

volves the ability to translate a real problem into the

language of mathematics and vice versa, to inter-

pret a mathematical result in the language of a real

non-mathematical context, in particular, to predict the

course of the process or the end result. To develop

such an ability (and, at the same time, to check its

formation) we offer the following task.

Task 17. The volume of products manufactured at

the enterprise is determined by the function

f (t) = −2t

+ 6t

+ 9,

where t is the time (in years). Give reasonable an-

swers to questions (1 – 6), without using the graph of

the function f (t):

1. During what period will production increase (de-

crease)?

2. Indicate the periods when the growth rate of pro-

duction accelerates (slows down), if any?

3. Is there a time when the nature of the rate of

growth (decline) of production changes to the op-

posite? If so, indicate this point.

4. When will the volume of production be the

largest?

5. Predict whether the volume of output may fall to

zero? If so, when will this happen. If not, why

not?

6. Imagine that you became the head (manager) of

this company after a year of its work. Would

you consider it necessary to change the produc-

tion strategy (function f (t))? If not, justify (for

example, all is well, because production is grow-

ing, i.e. the company operates efﬁciently). If your

answer is yes, then explaining what exactly would

alarm you?

7. On the basis of conducted in pp. 1 – 6 research

and analysis provide a graphic illustration of the

results.

Since all questions are formulated by the teacher

in advance, and the answers to them must be individ-

ual and explained, we consider it convenient to per-

form this task form TEXT Input. For graphic illustra-

tion (p. 7 of the task), we suggest using the GeoGebra

tools.

At the end of the study of the topic it is necessary

to assess the level and quality of knowledge. In the

digital space, these can be tests. To test the conceptual

understanding of mathematical concepts, facts, meth-

ods, the most appropriate are open tests. Because in

test tasks with the choice of the correct answer among

the proposed ones there is a temptation to just guess

it. And, even if we exclude guessing, there is a big

difference between choosing the right answer among

the several given (i.e. recognizing) and formulating it

yourself. Therefore, we believe that closed-type tests

should be avoided or minimized.

An example of an open – ended test task with Task

18 is: “A body moves rectilinearly according to the

law s(t) = −4 + 2t +t

(s is measured in meters, t is

measured in seconds). Find the speed of this body at

time (t = 3s). In response, write a number, for exam-

ple, 7”.

3 CONCLUSIONS AND

PROSPECTS FOR FURTHER

RESEARCH

1. As a result of a survey of non-mathematical spe-

cialties students, it was found that students to

some extent feel the need to apply mathemati-

cal knowledge in the study of professional disci-

plines, as well as to use this knowledge in prac-

tice. However, students do not sufﬁciently under-

stand the essence of mathematical concepts and

facts, the relationships and interdependencies be-

tween them. Therefore, they cannot always recog-

nize mathematical structures in non-mathematical

contexts and, therefore, apply mathematics effec-

tively.

2. The purpose of studying mathematics by non-

mathematical specialties students is to provide

them with the ability to apply mathematics to

solve professional problems. An analysis of the

various practices of teaching mathematics has re-

vealed that in many cases this goal is not achieved

due to the lack of a reasonable balance between

the formal rigor of the presentation of theoretical

principles and the teaching of procedures. There-

fore, the teaching of mathematics should pursue

the following goals: the formation of a concep-

tual understanding of key mathematical concepts,

facts, methods with an illustration of their appli-

cation, the study of the relevant mathematical ap-

paratus; developing basic skills of mathematical

research and mathematical modeling.

3. The described methods of using the digital edu-

cational space are designed to improve the con-

ceptual understanding of mathematics among stu-

dents of non-mathematical specialties through the

AET 2021 - Myroslav I. Zhaldak Symposium on Advances in Educational Technology

858

study of mathematical concepts and their connec-

tions, experimentation, formulation of questions,

hypotheses, conclusions, and discussion of the ob-

tained results.

4. Prospects for further research are to develop crite-

ria and indicators of conceptual understanding of

mathematics by non-mathematical specialties stu-

dents, as well as quantitative analysis of the effec-

tiveness of the use of digital learning space for the

formation of conceptual mathematical knowledge

of students.

ACKNOWLEDGEMENTS

The research was performed within the scientiﬁc

topic “Mathematical methods and digital technologies

in education, science, technology” (state registration

number: 0121U111924) of the Department of Com-

puter Science and Mathematics of Borys Grinchenko

Kyiv University.

REFERENCES

Astaﬁeva, M. M., Zhyltsov, O. B., Proshkin, V. V., and

Lytvyn, O. S. (2020). E-learning as a mean of form-

ing students’ mathematical competence in a research-

oriented educational process. CTE Workshop Pro-

ceedings, 7:674–689. https://doi.org/10.55056/cte.

421.

Aydın, U. and

Ozgeldi, M. (2019). The PISA Tasks: Unveil-

ing Prospective Elementary Mathematics Teachers’

Difﬁculties with Contextual, Conceptual, and Proce-

dural Knowledge. Scandinavian Journal of Educa-

tional Research, 63(1):105–123. https://doi.org/10.

1080/00313831.2017.1324906.

Balka, D., Hull, T., and Harbin Miles, R.

(2012). What is conceptual understanding?

https://nild.org/wp-content/uploads/2015/02/

What-is-Conceptual-Understanding.pdf.

Byrnes, J. P. and Wasik, B. A. (1991). Role of concep-

tual knowledge in mathematical procedural learning.

Developmental Psychology, 27(5):777–786. https:

//doi.org/10.1037/0012-1649.27.5.777.

Cobb, P. (1988). The Tension Between Theories of Learn-

ing and Instruction in Mathematics Education. Edu-

cational Psychologist, 23(2):87–103. https://doi.org/

10.1207/s15326985ep2302 2.

de Jong, T. (2015). Go-Lab Deliverable D1.4 Go-Lab

classroom scenarios handbook. Technical report, Go-

Lab consortium. https://telearn.archives-ouvertes.fr/

hal-01274922v1/preview/Go-Lab D1.4.pdf.

Forrester, P. A. and Chinnappan, M. (2010). The predomi-

nance of procedural knowledge in fractions. In Spar-

row, L., Kissane, B., and Hurst, C., editors, Shaping

the future of mathematics education: Proceedings of

the 33rd annual conference of the Mathematics Ed-

ucation Research Group of Australasia, pages 185–

192. MERGA Inc., Fremantle, WA. https://ro.uow.

edu.au/edupapers/770/.

Hiebert, J. and Lefevre, P. (1986). Conceptual and Pro-

cedural Knowledge in Mathematics: An Introductory

Analysis . In Hiebert, J., editor, Conceptual and Pro-

cedural Knowledge The Case of Mathematics, vol-

ume 2. Routledge, New York.

Leung, F. K. S. (2006). The Impact of Information and

Communication Technology on Our Understanding

of the Nature of Mathematics. For the Learning

of Mathematics, 26(1):29–35. http://www.jstor.org/

stable/40248521.

Nahdi, D. S. and Jatisunda, M. G. (2020). Conceptual

Understanding And Procedural Knowledge: A Case

Study on Learning Mathematics of Fractional Mate-

rial in Elementary School. Journal of Physics: Con-

ference Series, 1477(4):042037. https://doi.org/10.

1088/1742-6596/1477/4/042037.

Next-Lab (2022). About | NextLab Support. https://support.

golabz.eu/about.

Rittle-Johnson, B., Siegler, R. S., and Alibali, M. W. (2001).

Developing conceptual understanding and procedural

skill in mathematics: An iterative process. Journal of

Educational Psychology, 93(2):346–362. https://doi.

org/10.1037/0022-0663.93.2.346.

aenz, C. (2009). The role of contextual, conceptual

and procedural knowledge in activating mathemat-

ical competencies (PISA). Educational Studies in

Mathematics, 71(2):123–143. https://doi.org/10.1007/

s10649-008-9167-8.

Smetana, L. K. and Bell, R. L. (2012). Computer Simula-

tions to Support Science Instruction and Learning: A

critical review of the literature. International Jour-

nal of Science Education, 34(9):1337–1370. https:

//doi.org/10.1080/09500693.2011.605182.

Digital Learning Space to Improve the Conceptual Understanding of Mathematics of non-Mathematical Specialties Students

859