
NeuralQAAD: An Efficient Differentiable Framework for Compressing
High Resolution Consistent Point Clouds Datasets
Nicolas Wagner and Ulrich Schwanecke
RheinMain University of Applied Sciences, Wiesbaden, Germany
Keywords:
Point Clouds, Compression, Deep Learning.
Abstract:
In this paper, we propose NeuralQAAD, a differentiable point cloud compression framework that is fast,
robust to sampling, and applicable to consistent shapes with high detail resolution. Previous work that is able
to handle complex and non-smooth topologies is hardly scaleable to more than just a few thousand points. We
tackle the task with a novel neural network architecture characterized by weight sharing and autodecoding.
Our architecture uses parameters far more efficiently than previous work, allowing it to be deeper and more
scalable. We also show that the currently only tractable training criterion for point cloud compression, the
Chamfer distance, performances poorly for high resolutions. To overcome this issue, we pair our architecture
with a new training procedure based on a quadratic assignment problem. This procedure acts as a surrogate loss
and allows to implicitly minimize the more expressive Earth Movers Distance (EMD) even for point clouds
with way more than 10
6
points. As directly evaluating the EMD on high resolution point clouds is intractable,
we propose a new divide-and-conquer approach based on k-d trees, which we call EM-kD. The EM-kD is
shown to be a scaleable and fast but still reliable upper bound for the EMD. NeuralQAAD demonstrates on
three datasets (COMA, D-FAUST and Skulls) that it significantly outperforms the current state-of-the-art both
visually and qualitatively in terms of EM-kD.
1 INTRODUCTION
In recent years, deep learning has been successfully
applied to numerous computer vision and graphics
tasks, such as classification, segmentation, or com-
pression. However, most progress has been achieved
in the 2D domain based on the regular data struc-
ture of images. Unfortunately, the same methods
cannot easily be generalized to unstructured three-di-
mensional data. Memory consumption and computa-
tional cost usually increase rapidly in 3D, which lim-
its the applicability of GPU-accelerated algorithms.
In particular, gradient descent algorithms suffer from
this phenomenon. Especially irregular representa-
tions such as point clouds or meshes are only sparely
covered so far. However, as the typical output of 3D
scanners, high resolution point clouds are widely used
in autonomous driving, robotics, and other domains
to represent surfaces or volumes. A tool capable of
reducing the memory requirements of point clouds
that can be added to a differential pipeline is therefore
highly desirable. Unfortunately, point clouds pose a
particular challenge since points may not only be ir-
regularly but also sparsely scattered in space and, in
contrast to meshes, do not provide explicit neighbor-
hood information. Furthermore, the habit of neural
networks to generate smooth signals seems to hin-
der the reconstruction of high frequencies, complex
topologies, and discontinuities.
The current state-of-the-art in differentiable point
cloud compression mainly focuses on the idea of
folding one or multiple fixed input manifolds into a
target manifold (Chen et al., 2020; Groueix et al.,
2018; Deprelle et al., 2019). Regardless of the re-
spective concept, the size of the point clouds that
can be processed by current hardware is very limited,
since mainly pointwise neural networks are used. Re-
cently, sampling techniques have been used to over-
come this problem (see e.g. (Mescheder et al., 2019;
Groueix et al., 2018; Deprelle et al., 2019)). Thereby,
the difference between two point clouds is usually
measured using the Chamfer distance (see e.g. (Chen
et al., 2020; Groueix et al., 2018; Zhao et al., 2019)).
The popularity of the Chamfer distance stems from
its ability to measure the distance from a point in
one point cloud to its nearest neighbor in the other
and vice versa. However, using the Chamfer metric
on point cloud samples badly misguides gradient de-
Wagner, N. and Schwanecke, U.
NeuralQAAD: An Efficient Differentiable Framework for Compressing High Resolution Consistent Point Clouds Datasets.
DOI: 10.5220/0010772500003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
811-822
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
811

scent optimization algorithms. This is due to the fact
that not all points are considered when determining
the nearest neighbors of point cloud samples. There-
fore, with high probability, distances between false
matches are minimized. However, although a local
optimum can be achieved, high frequencies are usu-
ally lost as a result. This problem is particularly se-
vere when a point cloud is densely sampled and con-
tains detailed, fine structures. The most commonly
used PointNet encoders (Chen et al., 2020; Groueix
et al., 2018; Zhao et al., 2019) suffer from exactly this
problem as they rely on lossy global pooling layers
that can only be generalized to a limited extent. Even
worse, the Chamfer distance is generally known as an
unsuitable criterion for the similarity of point clouds
(Liu et al., 2020; Achlioptas et al., 2018). The earth
movers distance (EMD), that solves a linear assign-
ment problem (LAP) between compared point clouds,
is considered to be more appropriate (Liu et al., 2020;
Achlioptas et al., 2018). However, solving a linear as-
signment problem has a cubic running time for an ex-
act solution and even approximations are not efficient
enough for training neural networks on point clouds
with more than a few thousand points.
In this paper we present NeuralQAAD, a deep au-
todecoder for compact representation of high resolu-
tion point cloud datasets. NeuralQAAD is based on
a specific neural network architecture that overlays
multiple foldings defined on learned and shared fea-
tures to reconstruct point clouds. Our main contribu-
tions are
1. a new scaleable point cloud autodecoder architec-
ture that is able to efficiently recover high resolu-
tion consistent shapes,
2. training algorithms that are motivated by a newly
defined quadratic assignment problem (QAP),
3. a validation that our approach outperforms the
current state-of-the-art on high resolution point
clouds, and finally
4. a novel dataset of detailed skull CT-scans.
2 RELATED WORK
In the following, we give a brief overview of the three
main areas of related work: 1. algorithms and data
structures to process point clouds using deep learning,
2. neural network architectures for compressing point
clouds, and 3. assignment problems.
2.1 Deep Learning for 3D Point Clouds
Various data structures for representing 3D data in the
context of deep learning have been examined, includ-
ing meshes (Bruna et al., 2014), voxels (Wang et al.,
2018; Maturana and Scherer, 2015), multi-view (Su
et al., 2015), classifier space (Mescheder et al., 2019)
and point clouds (Qi et al., 2017a). Point clouds are
often the raw output of 3D scanners and are char-
acterized by irregularity, sparsity, missing neighbor-
hood information, and permutation invariance. To
cope with these challenges, many approaches convert
point clouds into other representations such as dis-
crete grids or polygonal meshes.
Nonetheless, each data structure comes with its
downsides. Voxelization of point clouds (Girdhar
et al., 2016; Sharma et al., 2016; Wu et al., 2016;
Roveri et al., 2018) enables the use of convolutional
neural networks but sacrifices sparsity. This leads
to significantly increased memory consumption and
decreased resolution. Utilizing meshes requires to
reconstruct neighborhood information. This can ei-
ther be done handcrafted, with the risk of wrongly
introducing a bias, or learned for a particular task
(Chen et al., 2020). In both cases, again, memory
consumption increases significantly due to the stor-
age of graph structures. Related to the transforma-
tion into meshes are approaches that define convo-
lution directly on point clouds (Tatarchenko et al.,
2018; Xu et al., 2018). Another approach is to em-
bed point clouds into a classifier space via fully con-
nected neural networks (Mescheder et al., 2019; Park
et al., 2019). However, this approach does not take
into account the advantages of point clouds, as neu-
ral networks tend to smooth the irregularity of point
clouds and thus may miss detailed structures. Also,
these methods are not trainable out of the box, as a
countable finite (point) set must be defined on an un-
countable space.
PointNet (Qi et al., 2017a) was the first neural net-
work to directly work on point clouds. It applies a
pointwise fully connected neural network to extract
pointwise features that are combined by max-pooling
to create global features. Thus, all the previously
mentioned disadvantages apply to PointNet. There is
numerous work on extending PointNet to be sensitive
to local structures (see e.g. (Qi et al., 2017b; Zhou
and Tuzel, 2018)). In this paper, we focus on unsuper-
vised learning. Most of the aforementioned methods
are only applicable in a supervised setting. We de-
ploy PointNet to produce intermediate encodings but
discard it for the final compression.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
812

2.2 Deep Point Cloud Compression
An autoencoder is the standard technique when it
comes to compressing data using deep learning. How-
ever, recent work (Park et al., 2019) demonstrates
that solely utilizing a decoder can be sufficient, at
least in the 3D domain. Here, the encoder is re-
placed by a trainable latent tensor. Deep generative
models like generative adversarial networks (GANs)
(Goodfellow et al., 2014) or variational autoencoders
(VAEs) (Kingma and Welling, 2014) can also be ap-
plied to reduce dimensionality. But they add over-
head complexity and are rarely used for this purpose,
although for VAEs (Zadeh et al., 2019) it may be suf-
ficient to train only one decoding part, just like for
standard autoencoders.
Most commonly, deep learning based compres-
sion methods for 3D point clouds either rely on vox-
elization (Girdhar et al., 2016; Sharma et al., 2016;
Wu et al., 2016) or have one neuron per point in a fully
connected output layer (Fan et al., 2017; Achlioptas
et al., 2018). The latter approaches are hardly train-
able for large-scale point clouds and require a huge
number of parameters even for small point clouds. In
contrast, FoldingNet (Yang et al., 2018) and Fold-
ingNet++ (Chen et al., 2020) rely on PointNet for
encoding and use pointwise decoders that are based
on the folding concept. Thereby folding describes
the process of transforming a fixed input point cloud
to a target point cloud by a pointwise neural net-
work. FoldingNet++ additionally learns graph struc-
tures for localized transformations partly avoiding
the problem of the smooth signal bias. Another ap-
proach based on the concept of folding is AtlasNet
(Groueix et al., 2018), which folds and translates mul-
tiple 2D patches to cover a target surface. The exten-
sion AtlasNetV2 (Deprelle et al., 2019) makes these
patches trainable. AtlasNet and AtlasNetV2 suffer
from the problem that they are hardly scalable and
sometimes fail to glue all patches together without
artifacts. Other pointwise autoencoders include 3D
Point Capsule Networks (Zhao et al., 2019), which
use multiple latent vectors per instance to capture dif-
ferent basis functions while using a dynamic routing
scheme (Sabour et al., 2017).
All of the state-of-the-art point cloud autoen-
coders (Chen et al., 2020; Groueix et al., 2018; Zhao
et al., 2019) are trained by optimizing the Chamfer
distance. Older approaches such as (Fan et al., 2017;
Achlioptas et al., 2018) trained on the earth mover
distance, as well, but are restricted in point cloud size.
In this work, we provide a surrogate loss for minimiz-
ing the EMD even for high resolution point clouds.
2.3 Assignment Problems
In its most general form, an assignment problem con-
sists of several agents and several tasks. The goal is
to find an assignment from the agents to the tasks that
minimizes some cost function. The term assignment
problem is often used as a synonym for the linear as-
signment problem (LAP). LAPs have the same num-
ber of agents and tasks. The cost function is defined
on all assignment pairs. Kuhn proposed a polynomial
time algorithm, known as the Hungarian algorithm
(Kuhn, 1955), that can solve a LAP in quartic runtime.
Later algorithms such as (Edmonds and Karp, 1972)
or (Jonker and Volgenant, 1986) improved to cubic
runtime. A fast and parallelizable ε-approximation
algorithm (the auction algorithm) to determine an al-
most optimal assignment was introduced in (Bert-
sekas, 1988) and used in (Fan et al., 2017) to cal-
culate the EMD. For NeuralQAAD, we use a GPU-
accelerated implementation of the Auction algorithm
(Liu et al., 2020). Although being fast in comparison
to previous algorithms, it is by no means fast enough
to act as a gradient descent criterion. Other assign-
ment approximations exist such as the Sinkhorn di-
vergence (Feydy et al., 2019), but to the best of our
knowledge none of them can be implemented effi-
ciently enough on GPUs for gradient-based optimiza-
tion.
Besides the LAPs, there are nonlinear assignment
problems which differ in the construction of the un-
derlying cost function. For nonlinear assignment
problems, the cost function can have more than two
dimensions. In this work, we utilize a four dimen-
sional quadratic assignment problem (QAP) to model
registration tasks. More precisely, we use the formu-
lation of (Beckman and Koopmans, 1957), in which
the general objective is to distribute a set of facilities
to an equally large set of locations. In contrast to the
LAP, there is no cost directly defined on pairs between
facilities and locations. Instead, costs are modeled by
a flow function between facilities and a distance func-
tion between locations. Given two facilities, the cost
of their assignment is calculated by multiplying the
flow between them with the distance between the lo-
cations to which they are assigned. This definition en-
sures that facilities that are linked by a high flow are
placed close together. However, finding an exact solu-
tion or even an ε−approximative solution for a QAP
is NP-hard (Burkard, 1984). Hence, even for small
instances, it is almost impossible to solve a QAP in a
reasonable time. In this paper, we propose algorithms
that can be efficiently executed on GPUs and allow
our architecture to follow quadratic assignments.
NeuralQAAD: An Efficient Differentiable Framework for Compressing High Resolution Consistent Point Clouds Datasets
813
Q
l
j
q
i
x
q
i
y
q
i
z
P
p
ix
p
iy
p
iz
l
2
l
1
l
N
l+3
MLP-Decoder
QAAD_Reassignment
QAAD_Greedy
Optimizer(q
i
, l
j
, MLP)
L
...
...
...
p
ix
p
iy
p
iz
...
...
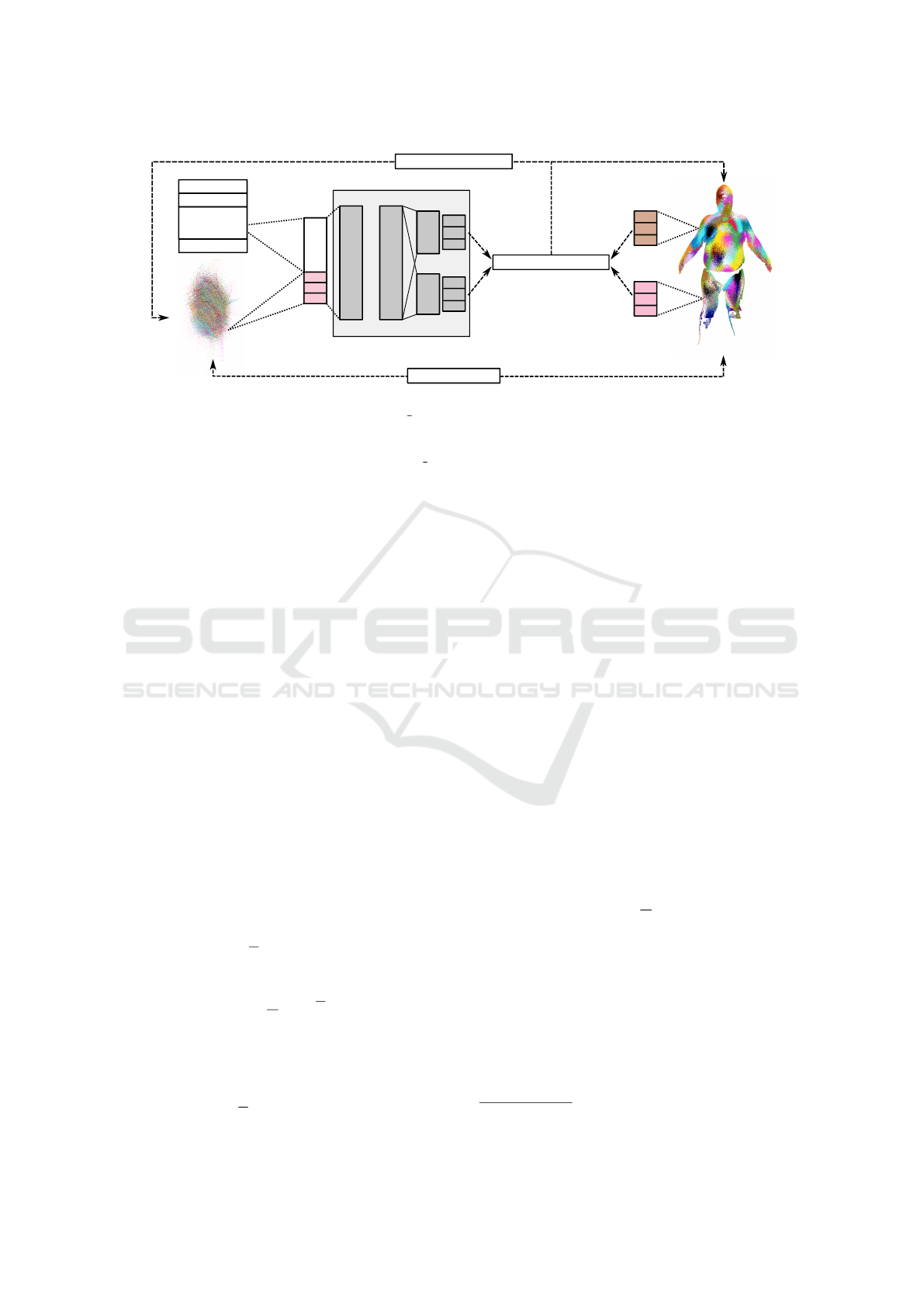
Figure 1: The topology and algorithms dedicated to NeuralQAAD. The initial assignment between the input point cloud Q
and a target point cloud P is determined by QAAD GREEDY. P is described by a latent vector l
j
and stored in the lookup
table L. A point q
i
is processed along with l
j
by a shared MLP to create common features. Subsequently, the common features
and q
i
are folded by a patch-specific MLP. The optimizer updates the input point q
i
, the latent code l
i
, and all MLP parameters
while improving the initial assignment through QAAD REASSIGNMENT.
3 METHOD
In the following, we give a formal description of the
addressed problem and derive constraints for a corre-
sponding deep learning solution. We then construct a
neural network architecture based on the concept of
folding (Yang et al., 2018) that satisfies these con-
straints. Finally, we demonstrate how to train this
architecture by designing and efficiently solving a
quadratic assignment problem. Figure 1 shows an
overview of the proposed NeuralQAAD architecture.
3.1 Problem Formulation
Given a set S = {P
i
| 1 ≤ i ≤ N} of 3D point clouds
P
i
=
p
i j
∈ R
3
| 1 ≤ j ≤ M
(1)
all having the same number of points, we seek for a
pair of functions f ,g where f : R
3·M
7→ R
l
,l M en-
codes a point cloud into a lower dimensional feature
vector
l
i
= f (P
i
) ∈ R
l
, (2)
and g : R
l
7→ R
3·M
decodes the feature vector l
i
back
into a point cloud
P
i
= g(l
i
) (3)
such that the error
E( f ,g) =
1
N
N
∑
i=1
d(P
i
,P
i
), (4)
is minimal with respect to some function d which
measures the similarity of two point clouds. As dis-
cussed in Section 2.2, folding transforms equation (3)
into
P
i
= g(l
i
,Q), (5)
where Q =
q
j
| 1 ≤ j ≤ M
is a single fixed input
point cloud.
As point clouds possess no explicit neighborhood
information and are invariant to permutations, the en-
coder function f should also have these properties.
Therefore, we further divide f into a pointwise local
feature descriptor
ˆ
f transforming the pointset P
i
into
a feature set
ˆ
F
i
=
ˆ
f (p
i j
) | 1 ≤ j ≤ M
(6)
and a permutation-invariant global feature descriptor
˜
f which converts the feature set into a lower dimen-
sional feature vector
˜
l
i
=
˜
f (
ˆ
F
i
) ∈ R
l
. (7)
Likewise, substituting the decoder function g with a
pointwise reconstruction function ˆg changes (5) into
ˆ
P
i
=
ˆ
p
i j
| 1 ≤ j ≤ M
with
ˆ
p
i j
= ˆg(
˜
l
i
,q
j
). (8)
Thus, instead of finding two functions f ,g that mini-
mizes (4), our objective is now to find three functions
ˆ
f , ˆg and
˜
f that minimize
E(
ˆ
f , ˆg,
˜
f ) =
1
N
N
∑
i=1
d(
ˆ
P
i
,P
i
). (9)
Minimizing (9) using deep learning algorithms, in
general, is very memory and computational intensive.
For example, a comparably small batch of 32 point
clouds each consisting of M = 65000 points is equal
to processing a rather large batch of around 2653
MNIST
1
images. Therefore the realization of
ˆ
f , ˆg
and
˜
f through deep neural networks requires compu-
tationally efficient and memory-optimized methods as
presented in the following.
1
http://yann.lecun.com/exdb/mnist/
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
814

3.2 EM-kD
The measure d for the similarity of point clouds is
typically chosen to be either the Chamfer distance
(Groueix et al., 2018; Zhao et al., 2019)
d
C
(
ˆ
P,P) =
∑
p∈P
min
ˆ
p∈
ˆ
P
k
p −
ˆ
p
k
2
+
∑
ˆ
p∈
ˆ
P
min
p∈P
k
p −
ˆ
p
k
2
(10)
or the augmented Chamfer distance (Chen et al.,
2020)
d
A
(
ˆ
P,P) = max
∑
p∈P
min
ˆ
p∈
ˆ
P
k
p −
ˆ
p
k
2
,
∑
ˆ
p∈
ˆ
P
min
p∈P
k
p −
ˆ
p
k
2
.
(11)
with previously detected weaknesses (Liu et al., 2020;
Achlioptas et al., 2018).
Compared to the Chamfer distance, the Earth
Mover Distance (EMD)
d
EMD
(
ˆ
P,P) = min
φ:P→
ˆ
P
∑
p∈P
k
p − φ(p)
k
2
(12)
is considered to be more representative for visual vari-
eties (Liu et al., 2020; Achlioptas et al., 2018) in case
that φ is (almost) a bijection. We define
argd
EMD
(
ˆ
P,P) = {(p,
ˆ
p = φ(p))}
p∈P
(13)
as the linear assignment problem (LAP) imposed by
the EMD.
Since the use of the EMD even for moderately
large point clouds leads to impracticable runtimes, we
introduce a divide-and-conquer approximation of the
real EMD, which we call EM-kD. The EM-kD is de-
fined as
d
EM−kD
(
ˆ
P,P) =
∑
(
ˆ
P ,P )∈k
d
(
ˆ
P)∇k
d
(P)
d
EMD
(
ˆ
P , P ), (14)
where the k
d
function constructs k-d tree subspaces
and ∇ defines the diagonal product that enumerates
the canonical subspace pairs. Afterwards, the (ap-
proximated) EMD between each subspace pair is
measured. In all our experiments we use the auction
algorithm as an EMD approximation.
The EM-kD closely approximates the EMD as can
be seen by considering the following two cases. First,
we assume that the low frequencies of both point
clouds are similar, i.e., the k-d subspaces will also
be similar. Here, the EM-kD may slightly overesti-
mate the EMD at most at the subspace boundaries.
The second case considers the situation where the low
frequencies of both point clouds are different and the
k-d subspaces are different as well. In this situation,
the EM-kD may significantly overestimate the EMD.
Overall, EM-kD judges similar to the EMD, but pe-
nalizes very dissimilar point clouds even more.
As a side benefit, the EM-kD may also be well
suited for other tasks where the EMD is typically
used, such as point cloud completion. While being
a reasonable upper bound of the true EMD, the EM-
kD is greatly scaleable as the subtask size of the auc-
tion algorithm can be controlled through the depth of
the k-d trees. In our experiments, using the EM-kD
reduces the runtime by more than an order of magni-
tude, more precisely by a factor of 36.
In all our experiments, we used the EM-kD to
evaluate NeuralQAAD. In Section 3.4 we present a
training procedure to implicitly optimizing the EM-
kD and hence the EMD.
3.3 Network Architecture
In the following, we discuss the three key compo-
nents that we have identified for a successful imple-
mentation of a scalable autodecoder for point clouds
based on a deep neural network. Since our approach
is mainly motivated by a Quadratic Assignment Prob-
lem and realizes an Auto Decoder, we call it Neu-
ralQAAD.
First, NeuralQAAD follows the idea of folding.
In contrast to previous work that folds a fixed (Yang
et al., 2018) or trainable (Deprelle et al., 2019) point
cloud by uniformly sampling a specific manifold such
as a square, we choose to deform a random sample of
the target data set as this is very likely to be closer to
any other sample than an arbitrary primitive geome-
try and thus is better suited for initialization. For a
dataset with strong low frequency changes, clustering
of multiple random examples may be even more ad-
vantageous, but we leave this for future research as it
turned out to be not beneficial in our experiments.
Second, we found that splitting the input point
cloud into K many patches that are independently
folded (Deprelle et al., 2019), i.e. K independent mul-
tilayer perceptrons (MLPs), is essential but also uses
resources highly inefficiently. Each patch has its own
set of parameters and thus its own set of extracted fea-
tures. Increasing the number of patches and thus the
number of MLPs, quickly limits their potential depth.
We observe that weight sharing across the first layers
of each MLP does not decrease the performance, but
enables the realization of deeper and/or wider archi-
tectures with the same number of parameters. Sim-
ilarly, low-level feature sharing can be used to scale
the number of patches.
Third, as discussed in Section 3.1, a batch of large
point clouds may not be processed at once. To cope
with this problem, NeuralQAAD only folds a sam-
NeuralQAAD: An Efficient Differentiable Framework for Compressing High Resolution Consistent Point Clouds Datasets
815

ple from each point cloud of a batch during a single
forward pass. Since the latent code
˜
l
i
of an instance
depends on all its related points, the encoding func-
tion
˜
f needs to be adapted. We realize
˜
f as a trainable
lookup table and thus renounce the explicit calcula-
tion of the pointwise function
ˆ
f . In addition to our
motivation for autodecoders to minimize memory us-
age, (Park et al., 2019) claims that this topology uti-
lizes computational resources more effectively.
Considering the three constituents just discussed,
the problem of finding functions
ˆ
f , ˆg and
˜
f that min-
imize (9) can now be rephrased into the problem of
training several multilayer perceptrons MLP
k
, one for
each input patch Q
k
, and a lookup table L ∈ R
N×l
such
that
E(MLP,L,Q) =
1
N
N
∑
i=1
d(P
i
,
ˆ
P
i
), (15)
is minimized, where the elements of
ˆ
P
i
are given as
ˆ
p
i, j
= MLP
k
(l
i
,q
k, j
),k ∈ K. (16)
Without loss of generality, we do not explicitly state
the split into various patches to simplify notation in
the following. The inverse assignment from each pre-
dicted point to its source point is given by q
k, j
=
MLP
+
k
(l
i
,
ˆ
p
i, j
),k ∈ K.
3.4 Training
Optimizing NeuralQAAD only on subsets of the in-
put point cloud Q directly affects the construction of
the loss function. The common pattern for calculat-
ing a distance between points clouds is similar to a
registration task that can be split into the two steps
1. Identifying a suitable matching between both
point clouds.
2. Determine the actual deformation of one point
cloud to the other.
Gradient descent is only done for the second step
whereas the first step characterizes how appropriate a
metric is. Apart from the fact that the Chamfer dis-
tance is not reliable and the EMD is not tractable,
another general consideration comes into play: The
matching that steers the folding process has to comply
with the predominant bias of neural networks, which
is smoothing. Therefore, we choose a matching that
allows the optimizer to follow the quadratic assign-
ment problem described next.
Given an input point cloud Q, a target point cloud
P, a weight function w(p,
ˆ
p) =
k
p −
ˆ
p
k
2
, and a flow
function f (q,
ˆ
q) =
1
/w(q,
ˆ
q) we want to find a bijective
mapping A : Q 7→ P such that
E(A) =
∑
q,
ˆ
q∈Q
f (q,
ˆ
q) · w(A(q), A(
ˆ
q)) (17)
is minimized. Intuitively speaking, this means that by
solving this quadratic assignment problem, we assure
that points close to each other in Q are matched with
points close to each other in P. Note that LAPs do not
exhibit this property and, hence, might inhibit gra-
dient descent. By construction, minimizing the dis-
tances between all QAP matches optimizes any cri-
terion like the EMD, EM-kD or Chamfer distances,
too.
Algorithm 1: Calculate an initial QAP solution A between a
target point cloud P and the image
ˆ
P of an input point cloud
Q. The image
ˆ
P is calculated by the NeuralQAAD MLP
given a latent vector l.
procedure QAAD GREEDY(l,Q,P)
// Predict input point cloud
ˆ
P = MLP(l,Q)
// Set of initial QAP solution
A =
/
0
// Assignment for each canonical k-d tree subspace pair
for (
ˆ
P ,P ) ∈ k
d
(
ˆ
P)∇k
d
(P) do
// Matching of EMD
A = arg d
EMD
(
ˆ
P ,P )
// If duplicates exist, use the smallest distance only
for (
ˆ
p,p) ∈ A do
if @(
¯
p,p) ∈ A : k(
¯
p − p)k < k(
ˆ
p − p)k then
A = A ∪ {(MLP
+
(l,
ˆ
p),p)}
// Randomly assign the remaining points
for (
ˆ
p,p) ∈ A do
if @(MLP
+
(l,
ˆ
p),
¯
p) ∈ A then
¯
p ∼ uni f orm({
¯
p ∈ P |@(q,
¯
p) ∈ A})
A = A ∪ {(MLP
+
(l,
ˆ
p),
¯
p))}
// Return the initial assignment
return A
On first sight, QAPs seem to be harder to solve
than LAPs. However, we do not need to solve them
explicitly, but remove the limitation of the optimizer
of following a linear assignment. The first step is a
greedy algorithm called QAAD GREEDY that gen-
erates an initial matching before gradient-descent.
The second step is a dynamic reassignment algorithm
called QAAD REASSIGNMENT, that monotonically
improves equation (15). During our experiments it
became evident that neither of the two steps alone
lead to a superior solution. The novel shared Neu-
ralQAAD architecture can also be trained on the aug-
mented Chamfer Distance training procedure which
already results in a significant performance improve-
ment and does not produce any additional assignment
overhead at all, but still is not as good as our QAAD
training scheme (see Section 4).
QAAD
GREEDY (see Algorithm 1) is conceptu-
ally similar to calculating the EM-kD. Instead of us-
ing the calculated distance between the input and the
target point cloud the determined LAP matches are
used as the initial assignment solution. To establish a
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
816

Algorithm 2: Refining the initial QAP solution A for a
query of points Q ⊂ Q of the input point cloud Q. At
this, the image
ˆ
P of the query given a latent code l is con-
structed by the current state of the NeuralQAAD MLP
and evaluated against the target point cloud P. However,
for efficiency only a subset P ⊂ P of the target is consid-
ered for reassignment.
procedure QAAD REASSIGNMENT(l,Q , P , A)
for q ∈ Q do
// Predict input subset and assign their nearest
// neighbors in target subset
A(q) = argmin
p∈P
k
MLP(l,q) − p
k
// Check current loss
L
B
= kMLP(l,q) − A(q)k
+kMLP(l,A
−1
(A(q))) − A(q)k
// Check loss after hypothetical reassignment
L
A
= kMLP(l,q) − A(q)k
+kMLP(l,A
−1
(A(q))) − A(q))k
// Decide where reassignment is beneficial
if L
A
≤ L
B
then
// Delete old assignment
A = A \ {(q,A(q))}
A = A \ {(A
−1
(A(q)), A(q))}
// Add new assignment
A = A ∪ {(q,A(q))}
A = A ∪ {(A
−1
(A(q)), A(q))}
// Return the refined assignment
return A
perfect matching, which is not guaranteed by the auc-
tion algorithm, the input point closest to a repeat-
edly chosen target point is matched. Any remain-
ing points are randomly matched. Like for the EM-
kD, QAAD GREEDY can be efficiently parallelized
on a GPU. Even for the largest tested dataset D-Faust
(Bogo et al., 2017) QAAD GREEDY runs only min-
utes. Additionally, since it only runs once, the runtime
is negligible considering the common training time of
neural networks.
Since the input point cloud is trainable,
QAAD GREEDY may make assignment errors
at subspace borders and the initial matching is
still an approximation of a linear assignment.
QAAD REASSIGNMENT (see Algorithm 2) con-
ducts reassignments during gradient descent that ease
the training of NeuralQAAD. At this, given a latent
code, a sample of the input point cloud is predicted
and the nearest neighbor from a sample of the target
point cloud is found for each prediction. This can
be efficiently done in parallel on a CPU using k-d
trees or other suitable data structures. Newer GPU
architectures that refrain from warp-based computa-
tion also allow for efficient GPU implementations.
The k-d trees are build and queried with only a
few samples per training step and, hence, add little
overhead. Subsequently, the input points that are
actually assigned to the nearest neighbors are also
predicted. Reassignment is based on comparing the
summed loss of both predictions under the actual
matching with the summed loss of both predictions
after a hypothetical pointwise swap. In case the latter
loss is smaller, a reassignment is conducted. Hence,
each reassignment is guaranteed to reduce the error
defined by equation (15). More importantly, the
optimizer is no longer biased towards minimizing the
distance of an optimal linear assignment.
The distance measure in this algorithm can be ar-
bitrarily chosen, but due to the targeted EM-kD, we
rely on the mean squared error. As we only process
point cloud subsets, we enforce a sampling proce-
dure that outputs the same number of points for each
patch. This allows us to efficiently implement Neu-
ralQAAD as a grouped convolution. In contrast to
previous implementations that sequentially run each
MLP per patch, we can make use of all GPU resources
and achieve a significant speedup that makes using
hundreds of patches practical for the first time.
4 EXPERIMENTS
In this section, we validate NeuralQAAD and its un-
derlying assumptions. We start with an overview of
the datasets used and some implementation details.
Subsequently, we show that NeuralQAAD performs
significantly better on high resolution points clouds
than existing approaches. Specifically, we compare
against the AtlasNetV2 deformation architecture (De-
prelle et al., 2019), the only other state-of-the-art dif-
ferentiable approach that is out-of-the-box applica-
ble to point clouds with more than a few thousand
points. Finally, we demonstrate the benefit of each
NeuralQAAD design choice in an ablation study and
the robustness of our approach in the number of sam-
pled training points.
4.1 Datasets
Our experiments are based on the three different
datasets COMA (Ranjan et al., 2018), D-Faust (Bogo
et al., 2017) and Skulls. COMA, captures 20466
scans of extreme expressions from 12 different indi-
viduals captured by a multi-camera stereo setup. D-
Faust, is a 4D full body dataset that includes 40 000
multi-camera scans of humans in motion. We use
about 6576 scans that contain more than 110000
points and about 13 744 scans that contain more than
130000 points from COMA and D-Faust respectively.
Skulls is a new artificially generated point cloud
dataset constructed using a multilinear model (Achen-
bach et al., 2018) that is based on a skull template fit-
NeuralQAAD: An Efficient Differentiable Framework for Compressing High Resolution Consistent Point Clouds Datasets
817

ted to 42 CT scans of human skulls (Gietzen et al.,
2019). The dataset consists of 4096 point clouds.
Each point cloud is composed of 65 536 points and
includes fine-grained parts such as the nasal bones or
teeth. In contrast to the other datasets, it consists not
only of surfaces but also of volumetric structures. We
will make this dataset public as a new high resolution
point cloud test dataset.
4.2 Implementation Details
For all our experiments we implemented the Neu-
ralQAAD folding operation with six fully connected
layers with output dimensions 256-128-128-128-64-
3 using PyTorch. In this implementation, the first
four layers are shared across all patches (see Fig-
ure 1 for an architecture overview). To guarantee the
same number of parameters for the AtlasNetV2 de-
coder while allowing it to be sufficiently deep, wide,
and computationally tractable we construct the fold-
ing operation of AtlasNetV2 with four layers of size
128 (no sharing) and adapt the number of patches if
needed. SELU (Klambauer et al., 2017) is applied as
a nonlinearity to every but the output layer for both
NeuralQAAD and AtlasNetV2. Adam (Kingma and
Ba, 2015) is used as the optimizer and initialized with
a learning rate of 0.001. We sample 4096 points for
COMA as well as D-Faust and 2048 points for Skulls
per instance and training step, resulting in low GPU
memory consumption.
AtlasNetV2 is trained until we can no longer ob-
serve any significant improvement, which was the
case for all data sets after 150 epochs at the latest.
To show that our architecture is also superior with-
out our novel QAAD training scheme we also train
NeuralQAAD for 150 epochs with the AtlasNetV2
training scheme. Essentially, this means minimiz-
ing the augmented Chamfer loss on point cloud sam-
ples. For this purpose, we deploy a PointNet encoder,
too, which we discard as soon as our QAAD training
scheme is utilized. Nevertheless, the PointNet em-
beddings are reused to initialize the lookup table. For
all experiments except the convergence NeuralQAAD
experiment, we train for 450 additional epochs. All
experiments are conducted on TITAN RTX GPUs
and a AMD Ryzen™ Threadripper™ 3970X CPU.
In comparison, the experiments of AtlasNetV2 have a
noticeably longer runtime than those of NeuralQAAD
since we use the released sequential implementation
of AtlasNetV2. For instance, training AtlasNetV2 on
D-Faust takes over a day whereas NeuralQAAD only
requires two hours. For all experiments, we use the
same hyperparameters for the auction algorithm i.e.
100 iterations with an epsilon of 1. The EM-kD is
calculated with a subspace size of 1024.
4.3 Reconstruction of High Resolution
Point Clouds
Skulls: The Skulls dataset contains point clouds that
can be linearly reduced to 42 latent variables using
principal component analysis. Additionally, in our
experiments, we nonlinearly compress each skull to a
latent vector of size 10. Although this seems to be an
easy task at first sight, results of AtlasNetV2 demon-
strate the contrary.
We process Skulls in a batch size of 16 instances
and use 16 patches for both NeuralQAAD and At-
lasNetV2. The visual results can be seen in Figure
2. NeuralQAAD is able to recover almost all low
as well as high frequencies. In contrast, AtlasNetV2
fails in both. From the side view, it can be clearly
recognized that detailed and non-manifold structures
as teeth and the nasal area are lost by AtlasNetV2
to a huge extent but can be fully reconstructed by
NeuralQAAD. In addition, rather coarse structures
like the eye socket (front view) or the skullcap (front
and side view) are badly recovered by AtlasNetV2,
whereas NeuralQAAD does not suffer. We mainly
attribute the better volumetric reconstruction capabil-
ities to the improved training procedure. However,
also the effects of weight sharing can be observed
visually. AtlasNetV2 clearly struggles in gluing to-
gether individual patches. This does not seem to be
an issue for NeuralQAAD that works on shared low
level features. The visual impressions are strongly
supported by the measured EM-kD losses stated in
Table 1. Training on the augmented Chamfer loss
alone leads to an improvement of 21% in terms of
EM-kD. After training our approach to convergence,
we even get an improvement of 78% and achieve a
compression ratio of 3311:1 (# of dataset floats : # of
network parameter and embedding floats).
D-Faust: The D-Faust dataset predominantly con-
tains low-frequency structures. We compress each
instance to a latent code of size 256. Training is
conducted with batches of size 16 while using 128
patches for NeuralQAAD. To ensure comparability in
the number of parameters AtlasNetV2 can only uti-
lize 28 patches. Visual results are depicted in Figure
3a. Unlike the volumetric Skulls dataset, here we can
recover a surface for each point cloud to facilitate vi-
sual comparison of reconstruction results. For surface
reconstruction, we used the simple ball-pivoting algo-
rithm (Bernardini et al., 1999) with identical hyperpa-
rameters for all experiments. From all perspectives, it
becomes evident that AtlasNetV2 merges even coarse
structured extremities and, as with Skulls, struggles to
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
818

Table 1: Reconstruction EM-kD for the datasets Skull, D-Faust and COMA. Convergence is indicated with ∞. On all datasets
NeuralQAAD performances significantly better than the previous state-of-the-art AtlasNetV2 even if trained only with the
augmented Chamfer loss. For the D-Faust dataset, NeuralQAAD achieves significant improvements with and without QAP
training, indicating that the scalability of NeuralQAAD in the number of patches is the main performance factor. However,
for the COMA dataset both the scalability in the number of patches as well as the QAP training procedure lead to huge
performance jumps. For Skulls, mainly the novel QAP training procedure improves on the current state of the art.
Data
Architecture
Trained with
Epochs
AtlasNetV2 NeuralQAAD & Encoder NeuralQAAD
Aug. Chamfer Aug. Chamfer MSE + QAAD GREEDY + QAAD REASSIGN.
∞ (=150) 150 600 600 600 ∞
Skulls 30.681 24.004 419.230 18.312 10.481 6.708
D-Faust 0.076 0.023 0.187 0.015 0.011 0.010
COMA 200.083 139.230 2448.076 74.893 47.593 18.554
NeuralQAAD Original AtlasNetV2
Figure 2: Front and side views on NeuralQAAD reconstructions of Skulls (Achenbach et al., 2018). Each skull is compressed
to a latent vector of size 10. Low as well as high frequencies can be mostly recovered by NeuralQAAD in contrast to
AtlasNetV2 that fails on low frequencies like the skullcap or on high frequencies like the teeth.
stitch together individual patches. NeuralQAAD, by
contrast, is able to almost fully recover all prevalent
structures and forming a smooth surface across patch
borders.
The EM-kD reconstruction losses for D-Faust
stated in Tab. 1 show a significant improvement
through NeuralQAAD. However, they tell a differ-
ent story as for Skulls. Already after training Neu-
ralQAAD with the augmented Chamfer distance, the
EM-kD decreases by about 69%. Further, our train-
ing scheme leads to a total drop in EM-kD of 86%
after convergence and achieves a compression ratio
of 1144:1. Combined, both numbers indicate that the
scalability of NeuralQAAD in the number of patches
is the dominant factor of performance for D-Faust
whereas the training scheme plays a minor role.
The D-Faust experiments reveal another interest-
ing observation. In Figure 4 the trainable input point
clouds are shown. Although initialized with a random
example of the respective dataset, only for D-Faust a
full deformation can be noticed. The egg-like struc-
ture seems to be favorable if strong low frequency
changes occur which is not the case for Skulls and
COMA (see next Section).
COMA: COMA is the most challenging dataset as
each point cloud contains almost as many points as
those of D-Faust but is restricted to the facial area and,
hence, captures an enormous amount of details. As
for D-Faust, we compress each instance into a latent
code of size 256, conduct training with a batch size
of 16, and make use of 128 patches for NeuralQAAD
as well as 28 patches for AtlasNetV2. Surface recon-
structions are shown in Figure 3b. For both instances
shown, NeuralQAAD is found to capture way more
fine-grained structures than AtlasNetV2 while being
less noisy. Even coarse structures like the ear in the
first instance can not be recovered by AtlasNetV2.
The EM-kD outcomes stated in Table 1 suggest
that for COMA the number of patches as well as the
QAP training scheme are essential and neither alone
suffices. Training NeuralQAAD on the augmented
Chamfer distance achieves a 30% better performance
than AtlasNetV2. Applying the QAP training proce-
dure further improves NeuralQAAD by 90% overall
after convergence and results in a compression ratio
of 748:1.
NeuralQAAD: An Efficient Differentiable Framework for Compressing High Resolution Consistent Point Clouds Datasets
819
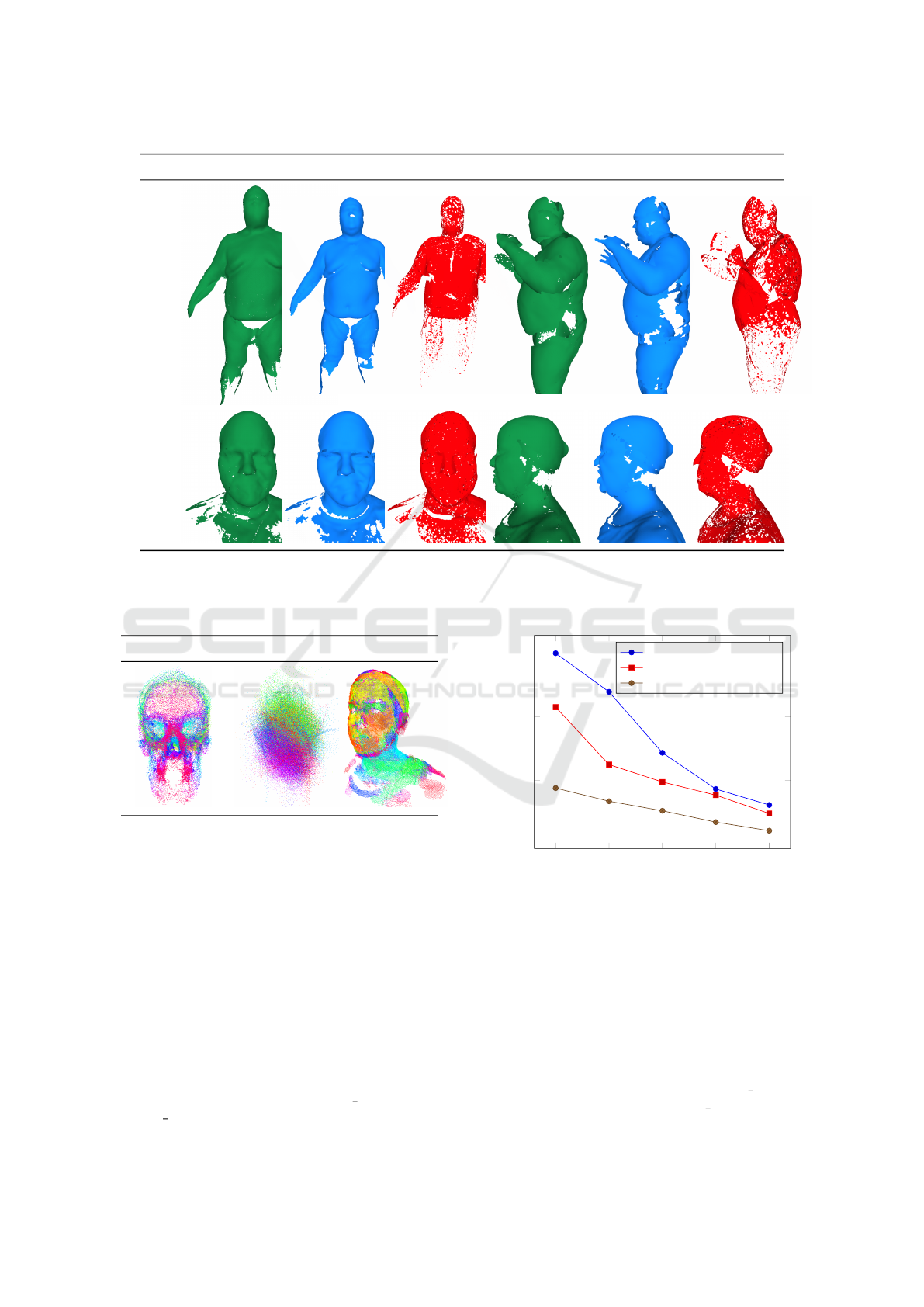
NeuralQAAD Original AtlasNetV2 NeuralQAAD Original AtlasNetV2
a)
b)
Figure 3: a) Front and side views on NeuralQAAD reconstructions of D-Faust (Bogo et al., 2017). The differences between
NeuralQAAD and AtlasNetV2 are clearly visible as AtlasNetV2 is not able to recover even coarse structures like extremities.
b) Front and side views on NeuralQAAD reconstructions of COMA (Ranjan et al., 2018). As for D-Faust, most detailed
structures are reconstructed by NeuralQAAD whereas AtlasNetV2 even looses coarse structures.
Skulls D-Faust COMA
Figure 4: Combined trainable input patches after QAP
training for the evaluated dataset. Colors reflect assignment
to patches. For Skulls and COMA, datasets mostly defined
by changes in high frequencies, the input point clouds looks
like noisy instances. D-Faust, mostly defined by changes
in low frequencies, exhibits a fully deformed input point
cloud.
4.4 Ablation Study & Scalability
In this section we ground the major and novel de-
sign choices made for NeuralQAAD. In the preceding
section, we already discussed the number of patches
as well as shared low-level features as the key suc-
cess factors for D-Faust and COMA proving the con-
cept of weight sharing. However, we did not dis-
cuss the isolated impact of QAAD GREEDY and
QAAD REASSIGNMENT, yet.
2
7
2
8
2
9
2
10
2
11
0
50
100
150
# Sampled Points
EM-kD
AtlasNetV2
NeuralQAAD (Only Arch.)
NeuralQAAD
Figure 5: EM-kD for AtlasNetV2, NeuralQAAD architec-
ture trained on the augmented Chamfer distance, and Neu-
ralQAAD trained with our training scheme related to the
number of sampled points per training step. The Skulls
dataset is used.
In a baseline experiment (see MSE & Decoder in
Table 1) we trained NeuralQAAD to minimize the
MSE of a random assignment. As expected, this
culminates in extraordinary bad results as the crite-
rion does not even follow the properties of a LAP.
In the subsequent experiment (see QAAD GREEDY
in Table 1), we observe that QAAD GREEDY solves
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
820

this issues but can clearly not be made responsi-
ble for the overall performance of NeuralQAAD.
Additionally applying QAAD REASSIGNMENT (see
QAAD REASSIGNMENT in Table 1) and, hence, fol-
lowing the smoothing bias of neural networks, boosts
the results again. In summary, the conducted experi-
ments strongly support the capabilities and the neces-
sity of the proposed contributions.
The behavior of NeuralQAAD, in the case where
the number of sampled points is reduced, is very ro-
bust. Figure 5 shows that NeuralQAAD, with and
without our training scheme, is always superior to
AtlasNetV2, regardless of the number of sampled
points. More importantly, when the number of sam-
pled points is reduced, the performance loss is signifi-
cantly lower than with AtlasNetV2. The observed ro-
bustness to sampling demonstrates the efficiency and
scalability of NeuralQAAD with respect to the size
of the point clouds to be processed. This also equips
NeuralQAAD for the future, in which the resolution
of point clouds will most probably continue to in-
crease in most areas.
5 CONCLUSION
We introduced a new scaleable and robust point
cloud autodecoder architecture called NeuralQAAD
together with a novel training scheme. Its scalability
comes from low level feature sharing across multiple
foldable patches. In addition, refraining from classi-
cal encoders makes NeuralQAAD robust to sampling.
Our novel training scheme is based on two newly
developed algorithms to efficiently determine an ap-
proximate solution that follows the smoothing bias of
neural networks. We showed that NeuralQAAD pro-
vides better results than the previous state-of-the-art
applicable to high resolution point clouds. Our com-
parisons are based on the EM-kD, a novel scalable
and fast upper bound for the EMD. In our experi-
ments, the EM-kD has proven to reasonably reflect
visual differences between point clouds.
The next steps will be to make our approach ap-
plicable to generative models and to bridge the gap
to correspondence problems. Although at first glance
generative tasks seem to be a straightforward ex-
tension, preliminary results have shown an unstable
training process. Recent advancements in continuous
learning might be adaptable to diminish the effects of
sampling.
REFERENCES
Achenbach, J., Brylka, R., Gietzen, T., zum Hebel, K.,
Sch
¨
omer, E., Schulze, R., Botsch, M., and Schwa-
necke, U. (2018). A multilinear model for bidirec-
tional craniofacial reconstruction. In VCBM 2018,
pages 67–76.
Achlioptas, P., Diamanti, O., Mitliagkas, I., and Guibas,
L. J. (2018). Learning representations and generative
models for 3d point clouds. In ICML 2018, pages 40–
49.
Beckman, M. and Koopmans, T. (1957). Assignment prob-
lems and the location of economic activities. Econo-
metrica, pages 53–76.
Bernardini, F., Mittleman, J., Rushmeier, H. E., Silva, C. T.,
and Taubin, G. (1999). The ball-pivoting algorithm
for surface reconstruction. IEEE Trans. Vis. Comput.
Graph., (4):349–359.
Bertsekas, D. P. (1988). The auction algorithm: A dis-
tributed relaxation method for the assignment prob-
lem. Ann. Oper. Res., (1–4):105–123.
Bogo, F., Romero, J., Pons-Moll, G., and Black, M. J.
(2017). Dynamic FAUST: registering human bodies
in motion. In CVPR 2017, pages 5573–5582.
Bruna, J., Zaremba, W., Szlam, A., and LeCun, Y. (2014).
Spectral networks and locally connected networks on
graphs. In ICLR 2014.
Burkard, R. E. (1984). Quadratic assignment problems.
European Journal of Operational Research, (3):283–
289.
Chen, S., Duan, C., Yang, Y., Li, D., Feng, C., and Tian, D.
(2020). Deep unsupervised learning of 3d point clouds
via graph topology inference and filtering. IEEE
Trans. Image Processing, 29:3183–3198.
Deprelle, T., Groueix, T., Fisher, M., Kim, V. G., Russell,
B. C., and Aubry, M. (2019). Learning elementary
structures for 3d shape generation and matching. In
NIPS 2019, pages 7433–7443.
Edmonds, J. and Karp, R. M. (1972). Theoretical improve-
ments in algorithmic efficiency for network flow prob-
lems. J. ACM, (2):248–264.
Fan, H., Su, H., and Guibas, L. J. (2017). A point set gen-
eration network for 3d object reconstruction from a
single image. In CVPR 2017, pages 2463–2471.
Feydy, J., S
´
ejourn
´
e, T., Vialard, F.-X., Amari, S.-i., Trouv
´
e,
A., and Peyr
´
e, G. (2019). Interpolating between op-
timal transport and mmd using sinkhorn divergences.
In The 22nd International Conference on Artificial In-
telligence and Statistics, pages 2681–2690.
Gietzen, T., Brylka, R., Achenbach, J., zum Hebel, K.,
Sch
¨
omer, E., Botsch, M., Schwanecke, U., and
Schulze, R. (2019). A method for automatic foren-
sic facial reconstruction based on dense statistics of
soft tissue thickness. PLOS ONE, pages 1–19.
Girdhar, R., Fouhey, D. F., Rodriguez, M., and Gupta, A.
(2016). Learning a predictable and generative vector
representation for objects. In ECCV 2016, pages 484–
499.
NeuralQAAD: An Efficient Differentiable Framework for Compressing High Resolution Consistent Point Clouds Datasets
821

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In
Advances in neural information processing systems,
pages 2672–2680.
Groueix, T., Fisher, M., Kim, V. G., Russell, B., and Aubry,
M. (2018). AtlasNet: A Papier-M
ˆ
ach
´
e Approach to
Learning 3D Surface Generation. In CVPR 2018.
Jonker, R. and Volgenant, T. (1986). Improving the
hungarian assignment algorithm. Oper. Res. Lett.,
(4):171–175.
Kingma, D. P. and Ba, J. (2015). Adam: A method for
stochastic optimization. In ICLR 2015.
Kingma, D. P. and Welling, M. (2014). Auto-encoding vari-
ational bayes. In ICLR 2014.
Klambauer, G., Unterthiner, T., Mayr, A., and Hochreiter,
S. (2017). Self-normalizing neural networks. In NIPS
2017, pages 971–980.
Kuhn, H. W. (1955). The Hungarian Method for the Assign-
ment Problem. Naval Research Logistics Quarterly,
(1–2):83–97.
Liu, M., Sheng, L., Yang, S., Shao, J., and Hu, S. (2020).
Morphing and sampling network for dense point cloud
completion. In EAAI 2020, pages 11596–11603.
Maturana, D. and Scherer, S. A. (2015). Voxnet: A 3d con-
volutional neural network for real-time object recog-
nition. In IROS 2015, pages 922–928.
Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S.,
and Geiger, A. (2019). Occupancy networks: Learn-
ing 3d reconstruction in function space. In CVPR,
pages 4460–4470.
Park, J. J., Florence, P., Straub, J., Newcombe, R. A., and
Lovegrove, S. (2019). Deepsdf: Learning continu-
ous signed distance functions for shape representa-
tion. CoRR.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017a). Point-
net: Deep learning on point sets for 3d classification
and segmentation. In CVPR 2017, pages 77–85.
Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017b). Point-
net++: Deep hierarchical feature learning on point sets
in a metric space. In NIPS 2017, pages 5099–5108.
Ranjan, A., Bolkart, T., Sanyal, S., and Black, M. J. (2018).
Generating 3D faces using convolutional mesh au-
toencoders. In ECCV 2018, pages 725–741.
Roveri, R., Rahmann, L.,
¨
Oztireli, C., and Gross, M. H.
(2018). A network architecture for point cloud clas-
sification via automatic depth images generation. In
CVPR 2018, pages 4176–4184.
Sabour, S., Frosst, N., and Hinton, G. E. (2017). Dynamic
routing between capsules. In NIPS 2017, pages 3856–
3866.
Sharma, A., Grau, O., and Fritz, M. (2016). Vconv-dae:
Deep volumetric shape learning without object labels.
In ECCV 2016 Workshops, pages 236–250.
Su, H., Maji, S., Kalogerakis, E., and Learned-Miller, E. G.
(2015). Multi-view convolutional neural networks for
3d shape recognition. In ICCV 2015, pages 945–953.
Tatarchenko, M., Park, J., Koltun, V., and Zhou, Q. (2018).
Tangent convolutions for dense prediction in 3d. In
CVPR 2018, pages 3887–3896.
Wang, P., Sun, C., Liu, Y., and Tong, X. (2018). Adap-
tive O-CNN: a patch-based deep representation of 3d
shapes. ACM Trans. Graph., 37(6):217:1–217:11.
Wu, J., Zhang, C., Xue, T., Freeman, B., and Tenenbaum,
J. (2016). Learning a probabilistic latent space of ob-
ject shapes via 3d generative-adversarial modeling. In
NIPS 2016, pages 82–90.
Xu, Y., Fan, T., Xu, M., Zeng, L., and Qiao, Y. (2018).
Spidercnn: Deep learning on point sets with param-
eterized convolutional filters. In ECCV 2018, pages
90–105.
Yang, Y., Feng, C., Shen, Y., and Tian, D. (2018). Fold-
ingnet: Point cloud auto-encoder via deep grid defor-
mation. In CVPR 2018, pages 206–215.
Zadeh, A., Lim, Y.-C., Liang, P. P., and Morency, L.-
P. (2019). Variational auto-decoder: Neural gen-
erative modeling from partial data. arXiv preprint
arXiv:1903.00840.
Zhao, Y., Birdal, T., Deng, H., and Tombari, F. (2019). 3d
point capsule networks. In CVPR 2019, pages 1009–
1018.
Zhou, Y. and Tuzel, O. (2018). Voxelnet: End-to-end learn-
ing for point cloud based 3d object detection. In CVPR
2018, pages 4490–4499.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
822
