Probabilistic Envelope based Visualization for Monitoring Drilling Well

Data Logging

Kishansingh Rajput and Guoning Chen

University of Houston, Houston, U.S.A.

Keywords:

Drilling Well Logs, Anomaly Detection, Casing Wear, Visual Analysis.

Abstract:

In oil and gas industries, to monitor the drilling well status and take actions when needed to prevent damage,

different logs are recorded and compared with the reference logs of the nearby existing wells. The deviation

of the log of the current well from the majority of the reference logs may indicate potential issues of drilling.

Currently, the standard methods used in the industry are line/scatter plots. Due to limitations such as clutter

and lack of quantitative information, these plots are not effective. In this paper, a probabilistic envelope based

technique is proposed for the visualization and anomaly detection of drilling data. This technique provides

quantitative information, is able to avoid the outliers in the reference data and works well even with a large

number of reference sequences. This technique is applied to the detection of anomalies from drilling well logs

to demonstrate its effectiveness. It is also adapted to the detection of over/under gauge during drilling.

1 INTRODUCTION

In oil and gas industry, well drilling is a process of

cutting through rock (and other) formations. Dur-

ing drilling, many logs (or signals), such as, Rate

of Penetration (ROP), Weight on Bit, Torque, are

recorded and monitored in real-time by engineers dur-

ing drilling to detect potential abnormal behaviors of

the drilling. For example, ROP is the speed at which

a drill bit is proceeding further, normally measured in

feet per minute. ROP depends on the formations, the

drill bit is penetrating through. ROP increases when

it enters the sand formation and decreases in Shale (a

type of rock) formations. Another reason of increase

in ROP could be well kick, a condition in drilling

when the pressure within the drilled rock is more than

the mud pressure acting on the rock face, which forces

the formation ﬂuid to the well-bore (Eren, 2018). In

such situation, well engineers need to stop drilling

and perform bottom-up (i.e., entire mud volume is

pumped to the surface from bottom of a well-bore).

The drilling creates bore-hole. The raw sides of

the bore-hole cannot support themselves. If the drilled

well is to become a production well, engineers put a

casing (tubing) inside the drilled well to protect and

support the well-stream, it is called completion pro-

cess. In the process of casing a well, steel pipes are

https://orcid.org/0000-0003-0581-6415

run down the recently drilled bore-hole. This pro-

cess is also called setting pipe. The space between

the raw formation and the casing is ﬁlled with cement

to attach the casing and make it stronger. In addi-

tion to providing stability and keeping the sides of the

well from caving in the bore hole, casing protects the

well-stream from outside contaminants, as well as any

other reservoirs from the oil or gas that is being pro-

duced. Casing wear (damage) occurs as a result of the

drill string rubbing against the casing, high pressure,

and temperature conditions. The wear depends upon

the contact forces, the wear track length (distance of

one surface moved across the other), the nature of the

surfaces in contact, the material strength and hard-

ness, and the presence of third bodies or lubricants

between the wearing surfaces. The main generator of

wear track length is drill string rotation. In addition

to this, bore-holes are not always vertical and some-

times they are inclined or even horizontal. In such

wells there is more chance of wear at the bends.

Figure 1 (e) shows a typical example of casing

wear (over/under gauge) in bore-hole. Casing wear is

a critical problem in oil wells. If not treated on time,

it may lead to severe damage and ultimately abandon-

ment of bore hole, causing huge loss. To prevent this

damage, the geometry information of the cross sec-

tion of the well in different depth is measured via the

Caliper log data (Figure 1 (f)).

Rajput, K. and Chen, G.

Probabilistic Envelope based Visualization for Monitor ing Drilling Well Data Logging.

DOI: 10.5220/0010774900003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 3: IVAPP, pages 51-62

ISBN: 978-989-758-555-5; ISSN: 2184-4321

Figure 1: In oil and gas industry (a), well drilling signals (e.g., some 1D signals as shown in (b)) are actively monitored to

identify potential drilling issues. Anomalies in the trend of the live streaming signals when compared with the signals of the

same property of the existing nearby wells (small plots on the top) may be the early sign of some damage. Current practice

(c) overlaps the live signals on top of the reference signals to identify obvious deviation, resulting in clutter. Our probabilistic

envelope representation of the reference signals enables an effective detection of the anomalies with the indication of the

amount of deviation (> 75% of the reference signals) (d). After the drilling is completed and the well becomes a production

well, casing is put to support the bore-hole (e). To detect the potential casing wear, caliber logs are measured and stored

(f). Caliber logs measure the diameter of the casing at a speciﬁc depth in a number of pre-deﬁned directions (e.g., 8 in the

illustration). These 1D logs are then used to discover over and under gauge sections along the casing manually. The over and

under gauge sections are usually visualized in the 3D representation of the casing (g). This 3D rendering does not intuitively

show the amount of over and under gauge and their orientation.

Despite measuring different properties, most

drilling and well data are represented as 1D signals.

The Y axis represents the depth of drilling (with 0

in the top) and X axis corresponds to the value of a

speciﬁc property (Figure 1 (b)). Because the depth

increases when the drilling time increases, drilling

signals share some similarity with time series data.

Thus, time series data visualization techniques are of-

ten used to show the drilling signals. Among them,

line plots are the most common representation.

To identify the possible anomaly in the live

streaming signal during drilling, current practice of-

ten overlaps it with a few reference signals of the

nearby wells, as shown in Figure 1 (c). This easily

results in cluttering if multiple references are used.

Also, even an anomaly can be spotted, it is hard to

approximate the amount of deviation the live signal is

from the references.

To show casing wear (i.e., over/under gauge), cur-

rent practice uses 3D rendering to visualize the sec-

tions where wear occurs (Figure 1 (g)). This ap-

proach has limitations like obstruction and lack of de-

tails (e.g., amount of wearing and shape of cross sec-

tions at wearing). Although 3D rendering highlights

regions of over/under gauge with colors, user needs to

manually rotate and shift the 3D scene to ﬁnd out the

interesting sections.

To address the above challenges and improve the

efﬁciency in processing drilling log data for decision

making, we introduce a probabilistic envelope (PE-)

based visualization technique (Figure 2) adapted from

the curve box plot technique (Mirzargar et al., 2014),

which provides control over different level of details

and focuses on new observations to effectively com-

pare trends of the real time signal with those of multi-

ple reference signals to quickly detect the anomalies.

The envelope like plots are created from the reference

signals with the help of probability theory and the real

time temporal signal is being visualized over the en-

velopes. More importantly, after some modiﬁcation,

the PE-based visualization technique can be adapted

for the summary visualization of the caliber logs for

IVAPP 2022 - 13th International Conference on Information Visualization Theory and Applications

the detection and analysis of casing wear. In sum-

mary, we make the following contribution.

• We introduce a probabilistic envelope (PE-) based

visualization that can provide an adjustable sum-

mary representation of a set of similar drilling log

data (i.e., some 1D data sequences). This PE-

based technique can be applied to both the open-

ended 1D data sequences and sets of closed 1D

data sequences with small modiﬁcation (e.g., the

circular envelopes).

• Based on the above PE-based summary represen-

tation, we develop two visual analytics systems

for anomaly detection for drilling log monitoring

using nearby reference logs and casing wear visu-

alization and analysis, respectively.

Our PE-based representation is simple to construct

and robust to outliners. It is adjustable by the user

via a couple intuitive parameters. We have applied

the two visual analytics systems developed based on

the PE technique to a number of drilling log data

demonstrate their effectiveness.

2 RELATED WORK

Time series data visualization is very important in dif-

ferent applications, and it becomes crucial in real time

applications where quick decision making is depen-

dent on the provided data. Our work is closely related

to topics from time series data visualization, trend de-

tection and ensemble time series data visualization.

We provide a brief review of the previous work done

in these topics.

Standard Time Series Data Visualization. Time

primitives, type of data and application speciﬁc repre-

sentation need to be considered when visualizing and

interacting with time series data (Aigner et al., 2007;

Aigner et al., 2008). In interactive exploration of tem-

poral data such as time series signals, time mask can

be used to detect one or more disjoint time intervals

in which certain metric is followed by the time series

data (Andrienko et al., 2017). The concept of time

mask and metrics matching is also called rule discov-

ery. Apart from time mask, classiﬁcation, summariz-

ing and clustering are also widely used techniques in

time series data mining (Fu, 2011).

Temporal trend is important for time series data.

The detection of trends at different granularity level

helps to get an overview of data and its structure (Van

To protect the credentials of the data source as required

by the data owner, these data were modiﬁed from the origi-

nal data through small perturbation and resampling.

et al., 2017). But when there are multiple overlapping

sub-trends, it is difﬁcult to separate them via simple

visualization techniques. More advanced techniques

such as animation (Robertson et al., 2008) may be em-

ployed to address this challenge. To address visualiz-

ing long time series with screen-size limitations, Sig-

nalLens technique (Kincaid, 2010) is proposed that

utilizes the Focus+Context techniques. Another sim-

ilar lens technique called ChronoLens (Zhao et al.,

2011) presents a more generalized multi-level lensing

technique for visualization and analysis of large time

series data. Timenotes (Walker et al., 2015) intro-

duces an interactive tool for stack zooming and over-

lays for effective visualization of time series data. All

these techniques focus on the effective visualization

of one time series data and/or the comparison of two

time series sequences, which are not sufﬁcient for our

problem that requires to compare one signal with N

( 2) other signals.

Ensemble Time Series Data Visualization. Our

problem of using a set of reference time series data

to help identify the abnormal behaviors in the tar-

get sequence shares some similarity to the ensemble

time series data visualization, in which a concise vi-

sual representation of a large set of data members is

sought to reduce visual clutter. For an ensemble set of

curves, spaghetti plots (Wilks, 2011) are usually used

to provide an overview of the conﬁguration of the en-

semble, which may result in clutter. Generalization

of box plots for ensembles of curves is a recent tech-

nique to visualize and compare different curves us-

ing the concept of data-depth (Mirzargar et al., 2014).

An extension of contour box-plots to 3D is used to

evaluate shape alignments (Raj et al., 2016). A visu-

alization and exploration approach for modeling and

characterizing the relationships and uncertainties in

the context of a multidimensional ensemble dataset is

proposed in (Chen et al., 2015). Hao proposed a new

ensemble visualization approach for network security

analysis (Hao et al., 2015) and a new visualization for

temporal ensembles (Hao et al., 2016). Potter et al.

proposed a framework for statistical visualization of

ensemble data (Potter et al., 2009). A more compre-

hensive review of ensemble visualization techniques

can be found in a recent survey (Wang et al., 2018).

In this work, we seek for a representation that

can convey the probability information of the distri-

bution of the samples on the reference sequences for

anomaly detection with certain quantitative feedback

(e.g., the target sequence is different than 75% of the

reference in a speciﬁc time period). To address that,

we introduce a probabilistic envelop technique. In

fact, our technique can be considered a special case

of the curved box plot (Mirzargar et al., 2014) with a

Probabilistic Envelope based Visualization for Monitoring Drilling Well Data Logging

(a) (b)

Figure 2: (a) Pipeline to compute the probabilistic envelope boundaries. (b) Illustration of the Probabilistic Envelope based

Visualization technique. Number of layers and probability values assigned to each layer are user controllable.

few major differences. First, our reference signals are

naturally aligned in time axis, enabling a simple and

efﬁcient envelope construction. Second, we construct

our envelope representation enclosing all samples of

the references, while curve box plot need not. Third,

we provide a parameter to the user to control the level

of the detail of the constructed envelope (Figure 4).

3 ENVELOPE-BASED

VISUALIZATION

In this section, we introduce our probability envelope

based (or PE) technique, which constructs a probabil-

ity envelope representation with multiple likelihood

(or probabilistic) layers from a set of reference 1D

signals. The current signal can then be visualized over

the envelope representation to effectively reveal ab-

normal behaviors. The likelihood distribution resem-

bles envelope structure with multiple layers as shown

in Figure 2 (b). The layers (shown with different color

shading) in the envelope structure represents different

likelihood of the reference signals, that is, how likely

a certain percentage of the reference signals falling

within the given layer. In the following, we describe

how to construct the probabilistic envelope with dif-

ferent probability levels.

We estimate the likelihood of a given sample on

a reference falling within a given layer by comput-

ing the proportion of points from the reference signals

falling within the speciﬁc layer. The user can decide

these proportions based on the need of their speciﬁc

application and tasks.

Input Parameters: List of reference signals, num-

ber of layers (m) along with their probability values.

Step-size for clustering.

Method: Firstly, all the reference signals are merged

into a single signal while preserving their time axis

(Figure 2 (a)). Then, the observations are clustered

using a step-size over time axis. Step-size can either

be provided by the user or a default value can be used.

For each cluster, likelihood of the observations falling

at certain magnitude is computed using the probabil-

ity theory. For each cluster, the algorithm starts from

the central/median point and gradually moves away

in both directions until it encloses the desired number

of points to fulﬁll the probability constraint. For ex-

ample, if a cluster consists of 20 points and the prob-

ability value for the central envelope, provided by the

user, is 50%, then starting from the central point the

algorithm will keep moving outwards in both direc-

tions until it encloses 10 points (10 is 50% of 20), and

the algorithm will mark the enclosing region as the

central envelope. Similarly, to deﬁne other envelope

regions, the algorithm will start from both the bound-

aries of the previous envelope in the opposite direc-

tion and follow the similar procedure. This process

will be repeated until all the envelopes are deﬁned.

Algorithm 1 provides a pseudo-code for the compu-

tation of envelopes. For a likelihood distribution with

m layers, we need 2m boundaries. In the algorithm

we call these boundary arrays as boundary

lower

and boundary upper

, representing lower and upper

bounds of envelope

, respectively.

Like the curve box plot technique (Mirzargar

et al., 2014), we start with the median point (or center

position) to grow the envelope. This is different from

techniques that construct envelope around the average

(or mean) curve (Wang et al., 2018), which may not

have equal number of curves (or samples) on the two

sides of the average curve for the subsequent proba-

bility estimation. Different from the curve box plot,

we provide the user the ﬂexibility to specify different

levels of probability (see Figure 3). More importantly,

IVAPP 2022 - 13th International Conference on Information Visualization Theory and Applications

we allow the user to control the level of the details

of the features of the envelope (Figure 4). Finally,

our envelope encloses all reference signals, while the

curve box plot need not, and we apply our envelope

to detect anomalies of the target signal based on the

user-speciﬁed probability level (Figure 7).

To visualize the obtained envelopes, darker shades

for the envelopes with high probability values are

used while gradually decreasing the darkness of the

shades for the envelopes with lower probability values

(Figure 2 (b)). In Figure 2 (b), the envelope structures

consist of 3 layers with the probability values of 50%,

75% and 100%, respectively. Intuitively, the most in-

ner (or central) layer of the envelope encloses 50% of

the points/observations from reference signals, mid-

dle envelope layer encloses 75% of the observations

and the outer envelope layer encloses all the observa-

tions in the reference signals.

Algorithm 1: Algorithm to calculate boundaries for en-

velope structure.

1: Initialize P with list of percentage values

, P

, ...P

for all the m envelopes and D

as step-

size for clustering

2: From all the reference signals group signal points

falling within each D

step (based on depth) as a

cluster

3: for each cluster do

4: Put all the points of the cluster to a list L

5: Find Median M of the list L

6: length ← length of L

7: Initialize m temporary empty lists as

t p

,t p

, ..., t p

8: for each P

in P do

9: Find number of points N

in the envelope i us-

ing N

= int(

length×P

100

)

10: for j in range 1...N

11: X ← A point nearest to M in L

12: Add X to t p

13: Remove X from L

14: Stop if L is empty

15: Append all the element of t p

i−1

to t p

16: for i=1 to len(P) do

17: Add min(t p i) to boundary lower

18: Add max(t p i) to boundary upper

19: return { boundary lower

, boundary upper

, ....

boundary

lower

, boundary upper

}

4 EVALUATION OF PE

REPRESENTATION

In this section, we provide a brief evaluation of the

proposed PE-based visualization technique in terms

of its time complexity, robustness to the outliers in

Figure 3: Examples of outlier mitigation. (a) Line plots for

5 references, 2 of which have outliers. Probabilistic En-

velopes: (b) 5 references, 2 with outliers, probability values

used to construct the envelops are 50%,70%, 100%, respec-

tively; (c) References same as (b), two layers with probabil-

ity 40% and 60%; (d) 10 reference signals, 3 with outliers,

probability values for envelop construction are 50%, 60%,

and 70%, respectively; (e) 15 reference signals, 3 with out-

liers, probability values are 50%, 70%, and 90%, respec-

tively.

Figure 4: Effect of step size on envelopes: (a) step-size 5,

(b) step-size 10, (c) step-size 20, (d) step-size 30.

the reference signals, and the effect of the step size

parameter for the control of the level-of-details in the

envelope representation.

Time Complexity. Consider r reference signals each

consisting of n observations (or samples). To compute

the likelihood with m layers, the run-time complexity

of the above described Algorithm 1 is a function of r

and n, i.e., O(A) = O(r × n). Note that the time com-

plexity does not depend on the number of layers or

the probability values assigned to each layer. There-

fore, the time complexity of likelihood computation is

proportional to the number of aggregate data points in

all the references. It is observed that sometimes, time

series data are described in terms of length of time

axis (T ) and length of time step (S) at which obser-

vations are repeated. In this case, the time complexity

is O(A) = O



r ×



. As the run-time complexity de-

pends on the number of references, the computation

will be slow if the number of references is very large.

As the quality of the envelope structures are enhanced

with increase in number of reference signals, there is

a trade-off between accuracy and speed.

Probabilistic Envelope based Visualization for Monitoring Drilling Well Data Logging

Robustness to Outliers. The standard method does

not have signiﬁcant difference on outlier visualization

with small or large number of references as shown in

Figure 3 (a). In contrast, our PE-technique can miti-

gate the effect of outliers with an appropriate number

of layers and probability values, but this mitigation is

more effective when the number of references is large,

provided the majority of them do not have many out-

liers as shown in Figure 3 (b–e). Reducing the prob-

ability of outermost layer can avoid the outliers, but

with a smaller number of references where the pro-

portion of outliers is large, it needs a large decrease

in probability value which affects the sections with

no outliers. On the other hand, with a large number

of references and less proportion of outliers, it works

well with slight decrease in probability as can be un-

derstood from Figure 3.

Effect of the Step-size for Clustering. The step-size

parameter is used to control the width of the individ-

ual time intervals used to compute the probabilistic

of the observations falling within these intervals. The

smaller the step size the ﬁner (or more detailed) the

temporal trend of the constructed envelopes reveal;

the larger the step size, the smoother the obtained en-

velopes will be. Figure 4 illustrates the effect of dif-

ferent step sizes to the obtained envelope.

5 APPLICATIONS

We apply the envelope based aggregated visualization

technique to two drilling well applications, i.e., the

anomaly detection in drilling logs data based on ref-

erence signals (Section 5.1) and casing wear detection

and visual analysis (Section 5.2).

5.1 Anomaly Detection from Drilling

Well Logs with References

To apply the introduced PE representation for the

anomaly detection in drilling logs, we develop a sim-

ple web-based visualization system based on Dash

and plotly. Figure 5 shows the interface for the PE-

based visualization. We have a control panel with

some parameters along which are set to their default

values based on earlier suggestions from the experts.

Our system allows the user to select a portion of the

signals to have a closer look. The control panel al-

lows the user to specify the step size parameter to con-

trol the detail of the envelop shape and the probability

value for each envelope. The user can also specify

which level of the envelope is used to detect anomaly

(75% is the default threshold). To avoid noise being

Figure 5: Interface of our visualization system. The left

panel shows different control parameters for different visu-

alizations. It currently shows the parameters to set rules to

detect anomaly with the PE technique. The signal shown on

the right plots is the DMSE (downward mechanical speciﬁc

energy). 24 references with step-size 10 are used to gener-

ate the envelope. Three probability layers, 50%, 70%, and

100%, are used. The current signal is shown in green. The

red sections indicate places where the signal goes outside

the speciﬁed likelihood threshold. Middle envelope with

70% probability is used a threshold for anomaly detection.

detected as anomaly, our approach does not mark the

signal being anomalous until it is out of the threshold

envelope for at least x-feet, where x is Offset Range

for Detection on the control panel. The change in

the envelope structures and step-size have a near real-

time effect on the visualization, hence users have a

ﬂexibility to change the envelope structure and off-

set range on the go. During the drilling process engi-

neers want to focus more on the latest portion of the

incoming signal. To allow the engineers to focus on

the latest portion of the signal, the earlier portion of

the signal will be simpliﬁed and faded out.

In some cases, reference signals are not available

or not useful (e.g., the reference wells are too far

away). In such cases, a rigid boundary based anomaly

detection technique can be used. This can be eas-

ily accomplished using simple line plots with bound-

aries that follow certain function enclosing the normal

value range. This function may be according to the

seasonality (if any) or any other factor depending on

the application, generally these boundaries are ﬂat as

shown in Figure 6 (a) with blue color.

The sections of the signal are marked with red

color which has magnitude outside the boundaries.

To provide the quantitative measure of the consis-

tency of the signal, results shown in Figure 6 (a) are

summarized in Figure 6 (b) in the form of histogram.

Histogram shows the proportion of signal data points

falling inside and outside the boundaries, respectively.

We apply our PE-technique to help detect anoma-

lies from the drilling logs. To do so, the user needs

IVAPP 2022 - 13th International Conference on Information Visualization Theory and Applications

(a)

(b)

366

1800

200

400

600

800

1000

1200

1400

1600

2000

4000

0 5 10

Speed (Rot/sec)

Depth (Feet)

Good

Bad

Number of Observations

Figure 6: Hard boundary based signal monitoring.

Figure 7: PE based visualization (with 15 references and

step-size 6) for drilling signal monitoring. Three probabil-

ity layers, 50%, 75%, and 100%, are used. The current sig-

nal is shown as the green line. The red sections indicate

places where the signal goes outside of the speciﬁed likeli-

hood threshold. (a) , (b), and (c) uses the 50%, 75%, and

100% layers as threshold, respectively.

to ﬁrst mark a layer (based on probability values

given initially for the computation of the envelopes)

as threshold and offset depth. Threshold layer is the

outer most layer enclosing valid magnitude range for

the current signal, and all the observations falling out-

side of this envelope will be considered as anomaly.

Figure 7 shows some representative results of the de-

tected sections with anomalies using different proba-

bility levels on a few synthetic ROP signal logs with

15 references for depth up to 470 feet with ROP ob-

servations taken at each 0.5 feet. The envelopes there

are constructed with step-size 6, offset 20 feet, based

on the 15 reference signals. In Figure 7 (a), the outer-

most layer (with 100% probability) is used, in which

no anomaly is found. For Figure 7 (b) and (c), 75%

and 50% layers are used for anomaly detection, re-

spectively. Speciﬁcally, Figure 7 (b) marks ROP as

abnormal in depth interval between 210 feet and 240

feet since the ROP magnitude is higher than its mag-

nitude in at least 75% of the reference logs. Since

the ROP value in this depth range is still very close

to the boundary of 75% layer (i.e., not deviating too

much from the majority), the engineers may consider

its behavior still in the normal range. Our framework

also marks sections between 380 feet and 470 feet be-

cause the ROP magnitude is lower than at least 75%

of the reference logs. The decrease of ROP can indi-

cate the change of the rock formation (e.g., becoming

harder to cut through). In addition, the ROP seems

continuously dropping, even though it remains within

the 100% envelope layer. The engineers will need to

keep a close eye on the behavior of this drill and may

need to stop the drilling if ROP drops out of the out-

ermost layer later.

Figure 5 shows the application of PE-technique

on DMSE logs during drilling. DMSE is amount

of work needed to be done to excavate unit volume

of rock. Drilling through hard rocks require higher

DMSE while sand formations need lower DMSE to

maintain certain ROP. Nearby wells are expected to

have similar surface formations at same depth with

small margin. The envelops shown in Figure 5 are

constructed with 24 reference signals. Both refer-

ences and live signals are for depth 0-7500 feet where

each observation is 0.5 feet apart (total 15000 data

points per signal). Our framework marks live signal

after 7140 feet as abnormal as the observations fall

outside 70% probability range continuously for more

than 20 feet (offset range for detection). The red sec-

tion indicates live DMSE deviates for long duration

from the references. Depending on other logs, this

could indicate a formation transition or a potential

fault in machines (since there are ﬂuctuation in live

signal), well engineers could decide to stop drilling

and perform corrective measures.

Discussion. A popular automatic, machine learn-

ing based technique for time series data is Recurrent

Neural Network (RNN). In some applications one-

dimensional convolutional layers based neural net-

works also perform reasonably well. But these tech-

niques work as a black-box, meaning that the com-

putations behind the inferences (or predictions by the

model) are not intuitive to the end user. In our ap-

plications, the engineers wish to know what leads the

models to classify a time-series as anomalous. On the

other hand, our technique is very intuitive, ﬂexible,

and easy to use. The engineers have complete control

over the parameters, and they have very high conﬁ-

Probabilistic Envelope based Visualization for Monitoring Drilling Well Data Logging

dence in what is being done to mark a certain portion

of the signal as anomalous.

5.2 Visual Analysis of Bore-hole Gauge

with Circular Probability Envelop

In this section, we describe how the above PE-based

representation can be adapted to support the visualiza-

tion and detection of casing wear in bore-hole gauge.

First, we brieﬂy describe the current approach to pro-

vide more background about the caliber log data col-

lected for bore-hole gauge monitoring.

Casing

Caliper

Radius Measuring

Fingers

Observer

(a) (b)

4950

5000

5050

5100

5150

5200

5250

0 55

(a)

22.5

𝑜

& 202.5

𝑜

& 225

𝑜

67.5

𝑜

& 247.5

𝑜

& 270

𝑜

112.5

𝑜

& 292.5

𝑜

135

𝑜

& 315

𝑜

157.5

𝑜

& 337.5

𝑜

180

𝑜

& 360

𝑜

(b)

Figure 8: (a) Top-down view of casing and demonstration

of Caliper Log data collection (b) Conversion of Caliper log

data to vertical casing view (one plot per diameter). Bottom

row shows the conventional vertical casing views from dif-

ferent directions. Directions are represented in the form of

rotation of the two radii from the reference in degrees.

The current approach to visualize gauge (casing

wear) with caliper log data is to use multiple con-

nected area plots providing vertical casing view from

different angles (directions). This is demonstrated in

Figure 8. Radius measurements in opposite directions

are plotted together as an area plot to create a verti-

cal casing view (Figure 8 (b)). Each plot shows cas-

ing from a particular direction as described in Figure

8. Depth ranges within which over/under gauge ex-

ists can be easily captured with these plots along with

their direction information.

For caliper having many measuring ﬁngers (typi-

cally 20-80 ﬁngers), this approach will generate many

plots. Manually analyzing and establishing correla-

tion between such a large number of plots is labor

intensive. To address that, we devise a visual ana-

lytic strategy based on a circular probabilistic enve-

lope – the extension of the previously introduced PE-

technique described next.

5.2.1 Circular Probabilistic Envelope

The envelope based representation introduced in Sec-

tion 3 can be applied to a set of 1D closed sequences

(e.g., closed curves) that have the same center and

the same number of sample directions (e.g., diame-

ter measures), which leads to the circular probabilis-

tic envelope. Speciﬁcally, starting from the center and

along each sample direction, a median point is ﬁrst

found based on the distributions of the samples from

different sequences in this direction. Then, the inter-

val for 50%, 75%, ..., 100% probability of distribution

can be constructed with the same process as described

in Algorithm 1. Note that different from the original

PE-technique, there is no need to specify a step-size

for the circular envelope computation as the circle is

naturally sub-divided into segments based on the in-

dividual sample directions of the diameter measures.

To apply the circular envelope representation for

the caliper log, we connect the diameter measure-

ments in different directions in order at a given depth

to form a closed curve (illustrated by Figure 9 (a)).

We then construct the circular envelope representa-

tion described above. Figure 9 (b) illustrates a circular

envelope representation, which provides a summary

view and a qualitative evaluation of the well for a spe-

ciﬁc depth range. At the center of envelopes an angle

is provided to show the overall orientation of the well

(i.e., the orientation of the summary elliptical shape

of the circular envelope). If all the diameter measure-

ments at different depth are perfect (i.e., identical to

an ideal diameter), there is no orientation information

that can be extracted.

The time complexity of the computation of these

circular envelopes is similar to that discussed in Sec-

tion 4. As explained in Section 4, time-complexity

does not depend on the number of layers or probabil-

IVAPP 2022 - 13th International Conference on Information Visualization Theory and Applications

(a) (b)

Well Circumferences

83.68 degrees

All cross sections

75% cross sections

50% cross sections

Figure 9: Summarized visualization using the circular prob-

abilistic envelopes for bore hole cross sections.

Well Circumferences

unwrapped

Circumference measurements

(inches) divided from central axis

Depth (feet)

1000

800

600

400

200

0 20

Well

Figure 10: The circumference is computed based on the ra-

dius measurements and is unwound to create a vertical heat-

map. The magnitude of circumference is compared with the

ideal circumference and over gauge segments are marked

with red color. Under gauge are marked with blue color.

ity values assigned to each layer. Nonetheless, there

is a trade-off between speed and accuracy because

the run-time complexity is proportional to the number

of diameter measurements at each observation while

having large number of radius measurements at each

observation also enhances the visualization and accu-

racy of well structure.

5.2.2 Detection of over/under Gauge

To detect over/under gauge, we ﬁrst compute a new

heat-map based on the circumferences of the individ-

ual cross sections of the well (Figure 10). Speciﬁ-

cally, we unwrapped the well by choosing one par-

ticular direction and compute a vertical discrete heat-

map based on the difference between the circumfer-

ence of each cross section with the circumference of

the speciﬁed ideal circle of the well. If the difference

is beyond a threshold, ±ε (also speciﬁed by the user),

an over or under gauge event occurs.

(a) (b)

All cross sections

75% cross sections

50% cross sections

Ideal cross sections range

Over gauge

Under gauge

83.68 degrees

Figure 11: Over/Under gauge visualization with the help of

circular envelopes (a) and a summary radial bar chart (b).

The circular envelope indicates the over gauge occurs in

this section of well and it happens in near 90

◦

, which is

supported by the radial bar chart.

Due to measurement error and background noise

during sensing, over/under gauge may occur in a very

short period of time (or in depth) – which is usually

an artifact, as in practice over/under gauge event usu-

ally persists for a longer period in time and depth. To

ﬁlter out this artifact, we use a depth range thresh-

old M, similar to the Offset Range described for the

anomaly detection. Speciﬁcally, we only consider a

depth range as an over/under gauge portion if it is

larger than M feet. Users have an option to select

the median circumference of the circumferences at all

depths as the ideal circumference instead of specify-

ing one explicitly. Users can also modify the depth

range threshold M. When an over gauge event oc-

curs, the corresponding depth range will be colored

in red in the circumference heat-map. Similar, the

depth range with an under gauge event is colored in

red, while purple indicates both over and under gauge

occur in a depth range (Figure 10).

Note that although in theory an over/under gauge

cross section may have the circumferences identical

to the circumference of the ideal circle, in practice

this rarely occurs. In bare-hole application, if there

is wear it is most likely to have difference in two

semi-circumference because the chances of it form-

ing a symmetric ellipse are low.

Once the heat-map is obtained and the depth

ranges where over/under gauge occurs are detected,

we use the above envelope visualization to plot the

statistics of the circumvents within each of these

depth ranges to represent the amount and orienta-

tion of the over/under gauge in that depth range. To

provide the quantitative evaluation of the over/under

gauge along with directional information, we also

construct a radial bar chart connected to the enve-

lope plot, as shown in Figure 11 (b). The red bars out-

Probabilistic Envelope based Visualization for Monitoring Drilling Well Data Logging

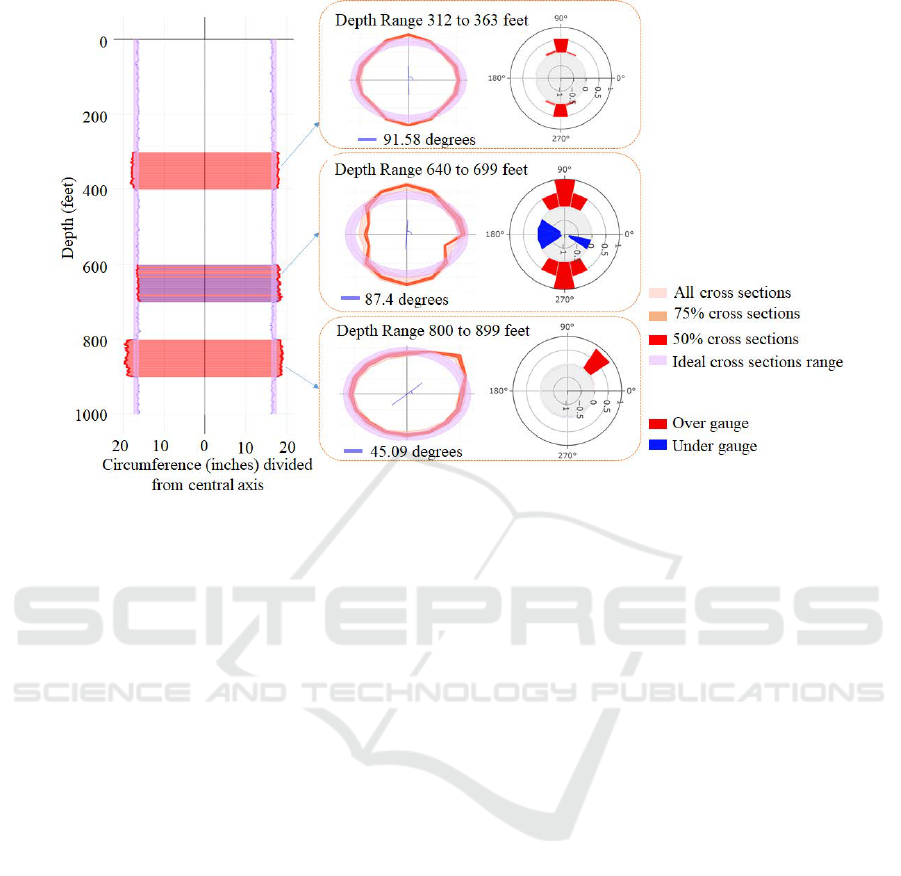
Figure 12: Detection of depth ranges of Over/Under gauges and their detailed evaluation. Detected depth Ranges with

over/under gauge from the heatmap, are all individually plotted with envelope plot for detailed evaluation.

side the casing represents over gauge and the blue bars

inside casing represents under gauge. The lengths of

the bars represent the amount of over/under gauge in

terms of physical length measurement, and the color

shows the amount of observations (i.e., the percent-

age) causing the over/under gauge in that direction.

The more saturated the color, the more observations

with over/under gauge.

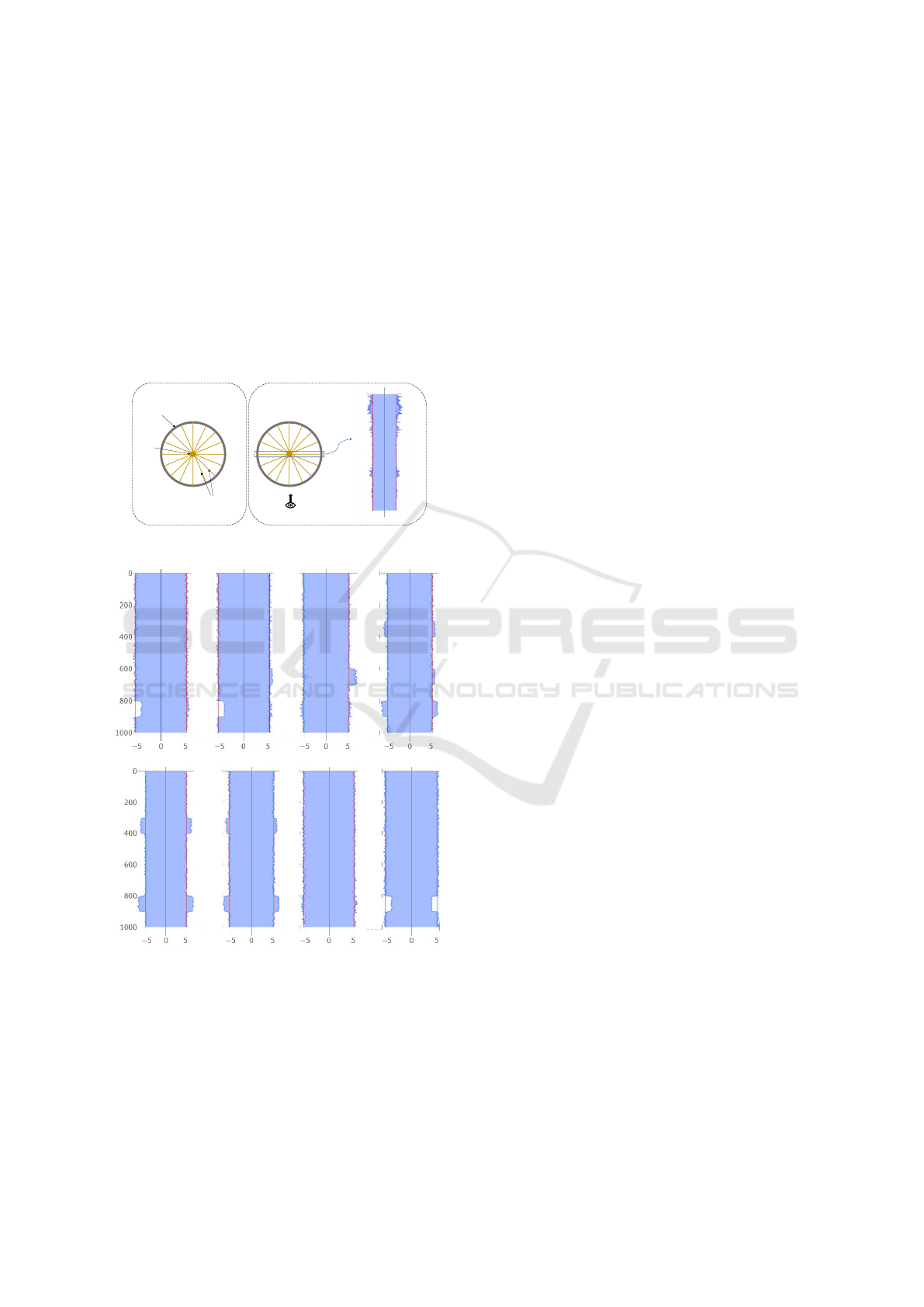
5.2.3 Use Cases

We apply the above visualization techniques to help

provide a detailed study of a section of the bore-hole

conﬁguration on caliper log data of a well with depth

of 1000 feet. A caliper with 16 ﬁngers was used,

providing diameter measurements in 8 different direc-

tions, measurements were taken with a ﬁxed interval

of a feet (total 16000 data points), Figure 12 demon-

strates this. In this case, three depth ranges with dif-

ferent over/under gauge conﬁgurations are automati-

cally detected with M = 5 f t in the heat-map shown in

the left with ideal radius of 5 ± 0.5 inches. For each

of the detected depth ranges, the corresponding cross

sections of the well are used to construct the circu-

lar envelopes. Here, the envelopes with three differ-

ent probability levels (with probability values 50%,

75%, and 100%) are shown. The summary radial bar

charts are also visualized alongside the circular en-

velopes, facilitating a detailed inspection of the re-

spective over/under gauge conﬁgurations.

For the depth range between 312ft to 363ft, over

gauge is detected along the vertical direction (i.e.,

along 91.58

◦

and −91.58

◦

). The conﬁguration of this

over gauge is almost symmetry along the vertical di-

rection as indicated by the radial bar chart. The over-

all deviation of this over gauge is about 1 inch from

the ideal conﬁguration and about 0.5 inch from the

boundary of the ideal margin, indicating small thin-

ning as well as deformation of the casing wall in

the 90

◦

direction. For the depth range from 800ft

to 899ft, another over gauge is detected. Different

from the above over gauge, this over gauge exhibits a

non-symmetry conﬁguration primarily along 45.09

◦

direction. This is clearly indicated in both the circu-

lar envelope representation and the radial bar chart.

The amount of over gauge is about 0.9 inch from the

boundary of the ideal radius margin, suggesting the

wear of the casing wall in the 45

◦

direction. For the

depth range starting 640ft and ending at 699ft, both

over gauge and under gauge are detected within it.

While the over gauge occurs in a much wider angle

range and with a roughly symmetry conﬁguration, the

under gauge occurs in a much narrower angle range

with a non-symmetry conﬁguration. Nonetheless, the

over/under gauge is increasing in this depth, which

may indicate the casing wear is getting worse due to

the rubbing of drillstring against the casing wall be-

comes more severe when drilling down deeper into

the well. The existence of the under gauge also indi-

IVAPP 2022 - 13th International Conference on Information Visualization Theory and Applications

(a)

Effect of Number of Radial measurements on Visualization

Entire Bore Hole 0 feet to 1000 feet

(b)

83.68

degreesAll cross

sections

75% cross

sections

50% cross sections

Ideal cross sections range

0 2 4

246

(d)

Bore Hole 800 feet to 899 feet

(c)

All cross sections

75% cross

sections

50% cross sections

Ideal cross sections range

87.5 degrees

0 2 4

246 0

246

Figure 13: Bore Hole gauge visualization with the help of circular probabilistic envelopes. (a) and (b) show the entire bore

hole, while (c) and (d) show the detected depth range 800 to 899 feet depth where sever wear occurred. (a) and (c) have the

radius measurements in 8 directions whereas (b) and (d) has radius measurements in 16 directions with uniform angle interval,

at each depth level.

cates the casing in this depth is not only worn but may

also be deformed due to higher pressure and tempera-

ture(Lejano et al., 2010), requiring further inspection.

From this example, we show that compared to the

existing practice (Figure 8), our circular envelopes

can help the user intuitively identify the amount of

over/under gauge (based on the distance between the

red circle and the purple/ideal circle) and the orien-

tation of the bore hole gauge. In the meantime, the

radial bar chart provides a concise summary of the

statistics of the over/under gauge conﬁgurations.

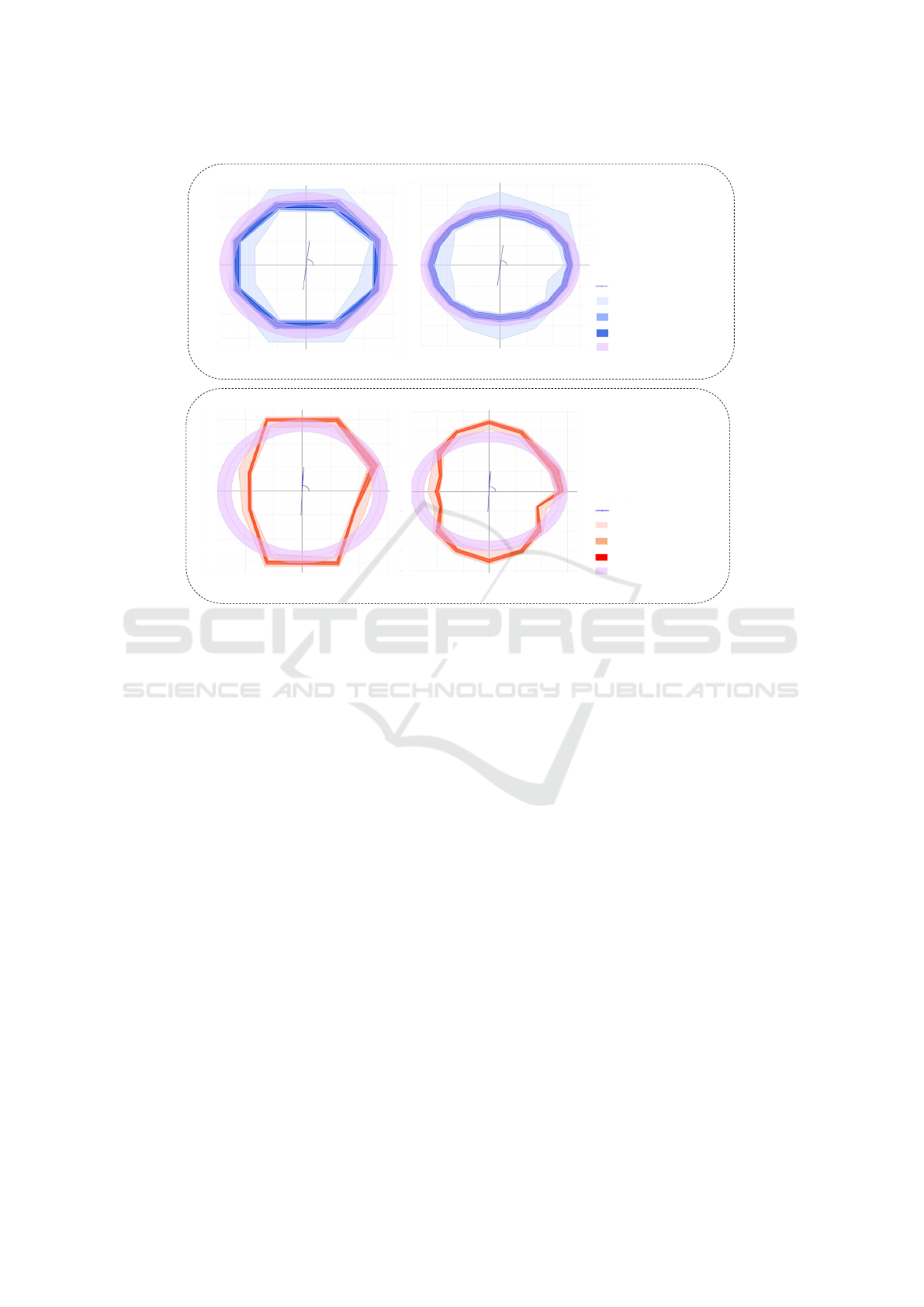
Impact of the Number of Directions (or Fingers) in

the Bore-hole Measures. Figure 13 shows proba-

bilistic envelope plots for the data having radius mea-

surement for 8 and 16 directions at each depth level.

The plots with more radial directions can more accu-

rately represent the actual wear in the casing as shown

in Figure 13 (b)(d) compared to Figure 13 (a)(c).

Nonetheless, with more directions more data need to

be stored and processed. A good trade off needs to be

made to achieve sufﬁcient accuracy in the envelope

representation while having reasonable storage space

and processing time for the data.

Feedback from the Experts. Our visualization sys-

tems have been used by several well engineers in their

daily tasks of monitoring the live drilling of a new

well as well as analyzing a casing wear of a produc-

tion well to decide when to start the repair. Two of

these engineers provide us the feedback on the use of

the systems introduced above. One of them remarks

that “they have very good potential...when properly

used and relevant data are fed to it, can be of great

help to the well engineers and geophysicists”. The

other engineer comments “ in the presence of a caliper

or similar log measuring the internal diameter of a

casing that has been installed in a well, the tool can ef-

fectively reveal casing wear for that casing. ” The tool

can effectively reveal “damage caused to the internal

of casing caused by the drillstring (or other downhole

equipment) rubbing against the casing while drilling

the well”. The summary information conveyed by the

envelope-based representation is “intuitive and thus is

more effective than the custom tools provided by the

service provider (who did the logging work).” The

“utilization of plotly dash makes the tools immensely

interactive...the user does not need to be trained, but

can use the tools easily.” The engineers also sug-

Probabilistic Envelope based Visualization for Monitoring Drilling Well Data Logging

gested us “to try to increase the use cases and trials of

the app to better identify any room for improvement.”

6 CONCLUSION

In this work, we have developed a new probability

and envelope (layers) based visualization, called the

probabilistic envelope based (PE-) technique, for the

summary representation and visualization of differ-

ent drilling log data. Our PE-based representation is

easy to construct and support adjustable visualization

to provide quantitative information about the statis-

tics of the data. We have developed two visual anal-

ysis systems based on this representation to support

the anomaly detection from drilling log signals and

the casing wear analysis, both of which are impor-

tant tasks in oil and gas industries. We have applied

our systems to a number of drilling log data sets to

demonstrate their effectiveness.

Even though our results show that the PE-

technique performs much better than the standard

methods in the anomaly detection and provides a con-

cise and effective representation of various casing

wear, it is yet to assess how easily the proposed PE-

technique can be adapted to other more challenging

situations. In addition, the proposed PE-technique is

computed based on the probabilistic information. In

the future, other statistics information can be used to

aid the design of the visualization to address different

needs of speciﬁc applications.

REFERENCES

Aigner, W., Miksch, S., M

uller, W., Schumann, H.,

and Tominski, C. (2007). Visualizing time-oriented

data—a systematic view. Computers & Graphics,

31(3):401 – 409.

Aigner, W., Miksch, S., M

uller, W., Schumann, H., and

Tominski, C. (2008). Visual methods for analyzing

time-oriented data. IEEE transactions on visualiza-

tion and computer graphics, 14(1):47–60.

Andrienko, N., Andrienko, G., Camossi, E., Claramunt, C.,

Garcia, J. M. C., Fuchs, G., Hadzagic, M., Jousselme,

A.-L., Ray, C., Scarlatti, D., et al. (2017). Visual ex-

ploration of movement and event data with interactive

time masks. Visual Informatics, 1(1):25–39.

Chen, H., Zhang, S., Chen, W., Mei, H., Zhang, J., Mer-

cer, A., Liang, R., and Qu, H. (2015). Uncertainty-

aware multidimensional ensemble data visualization

and exploration. IEEE Transactions on Visualization

and Computer Graphics, 21(9):1072–1086.

Eren, T. (2018). Kick tolerance calculations for drilling op-

erations. Journal of Petroleum Science and Engineer-

ing, 171:558–569.

Fu, T.-c. (2011). A review on time series data min-

ing. Engineering Applications of Artiﬁcial Intelli-

gence, 24(1):164–181.

Hao, L., Healey, C. G., and Bass, S. A. (2016). Effective vi-

sualization of temporal ensembles. IEEE Transactions

on Visualization and Computer Graphics, 22(1):787–

796.

Hao, L., Healey, C. G., and Hutchinson, S. E. (2015). En-

semble visualization for cyber situation awareness of

network security data. In 2015 IEEE Symposium on

Visualization for Cyber Security (VizSec), pages 1–8.

Kincaid, R. (2010). Signallens: Focus+ context applied to

electronic time series. IEEE Transactions on Visual-

ization and Computer Graphics, 16(6):900–907.

Lejano, D., Colina, R., Yglopaz, D., Andrino, R., Malate,

R., and Ana, F. S. (2010). Casing inspection caliper

campaign in the leyte geothermal production ﬁeld,

philippines. In Thirty-Fifth Workshop on Geothermal

Reservoir Engineering.

Mirzargar, M., Whitaker, R. T., and Kirby, R. M. (2014).

Curve boxplot: Generalization of boxplot for ensem-

bles of curves. IEEE transactions on visualization and

computer graphics, 20(12):2654–2663.

Potter, K., Wilson, A., Bremer, P., Williams, D., Dou-

triaux, C., Pascucci, V., and Johnson, C. R. (2009).

Ensemble-vis: A framework for the statistical visual-

ization of ensemble data. In 2009 IEEE International

Conference on Data Mining Workshops, pages 233–

240.

Raj, M., Mirzargar, M., Preston, J. S., Kirby, R. M., and

Whitaker, R. T. (2016). Evaluating shape alignment

via ensemble visualization. IEEE Computer Graphics

and Applications, 36(3):60–71.

Robertson, G., Fernandez, R., Fisher, D., Lee, B., and

Stasko, J. (2008). Effectiveness of animation in trend

visualization. IEEE transactions on visualization and

computer graphics, 14(6):1325–1332.

Van, G. A., Staals, F., L

ofﬂer, M., Dykes, J., and Speck-

mann, B. (2017). Multi-granular trend detection for

time-series analysis. IEEE transactions on visualiza-

tion and computer graphics, 23(1):661–670.

Walker, J., Borgo, R., and Jones, M. W. (2015). Timenotes:

a study on effective chart visualization and interaction

techniques for time-series data. IEEE transactions on

visualization and computer graphics, 22(1):549–558.

Wang, J., Hazarika, S., Li, C., and Shen, H.-W. (2018). Vi-

sualization and visual analysis of ensemble data: A

survey. IEEE transactions on visualization and com-

puter graphics, 25(9):2853–2872.

Wilks, D. S. (2011). Statistical methods in the atmospheric

sciences, volume 100. Academic press.

Zhao, J., Chevalier, F., Pietriga, E., and Balakrishnan,

R. (2011). Exploratory analysis of time-series with

chronolenses. IEEE Transactions on Visualization and

Computer Graphics, 17(12):2422–2431.

IVAPP 2022 - 13th International Conference on Information Visualization Theory and Applications