Analysis of the Future Potential of Autoencoders in Industrial Defect

Detection

Sarah Schneider

1,2

, Doris Antensteiner

, Daniel Soukup

and Matthias Scheutz

High-Performance Vision Systems, Center for Vision, Automation and Control,

AIT Austrian Institute of Technology, Vienna, Austria

Human-Robot Interaction Lab, Tufts University, Medford, MA, U.S.A.

Keywords:

Autoencoder, Anomaly Detection, Computer Vision, One-class Learning.

Abstract:

We investigated the anomaly detection behaviour of three convolutional autoencoder types - a “standard” con-

volutional autoencoder (CAE), a variational convolutional autoencoder (VAE) and an adversarial convolutional

autoencoder (AAE) - by applying them to different visual anomaly detection scenarios. First, we utilized our

three autoencoder types to detect anomalous regions in two synthetically generated datasets. To investigate

the convolutional autoencoders’ defect detection performances “in the industrial wild”, we applied the models

on quality inspection images of non-defective and defective material regions. We compared the performances

of all three autoencoder types based on their ability to detect anomalies and captured the training complexity

by measuring the time needed for training them. Although the CAE is the simplest model, the trained model

performed nearly as well as the more sophisticated autoencoder types, which depend on more complex train-

ing processes. For data that lacks regularity or shows purely stochastic patterns, all our autoencoders failed to

compute meaningful results.

1 INTRODUCTION

The detection of defective material is an essential

component in the industrial manufacturing process.

Yang et al. (2020) describe how the detection of de-

fective material represents a complex problem due to

the elusive nature and immense diversity of the de-

fects. Pang et al. (2021) elaborate in much detail how

anomalies deviate from what is deﬁned as usual or re-

garded as normal and explain the process of anomaly

detection - the detection of data instances that differ

from the majority of samples.

An autoencoder (Rumelhart and McClelland, 1987)

consists of an encoder and a decoder model. The en-

coder network encodes data into a compressed ver-

sion, the decoder network decodes it back such that it

is as similar as possible to the original input. Due to

this underlying principle of learning and compressing

normal data into a latent vector by minimizing the re-

construction error, the autoencoder is an appropriate

tool for anomaly detection. By training an autoen-

coder model purely on normal data, it will learn the

proﬁle of non-anomalous data and the resulting re-

construction error for normal data will be lower than

the reconstruction error for anomalous data.

Normal Anomalous Reconstruction Residual map

Figure 1: Principle of autoencoder based anomaly detec-

tion: The autoencoder is trained exclusively on normal im-

ages. If that trained model is applied on an anomalous im-

age, the input is reconstructed by using the mapping the

model learned from the non-anomalous data. The recon-

struction then deviates from the anomalous image at pixel

positions where the anomalies appear, see the residual map.

By considering non-defective material as normal

and defective material as anomalous, the detection of

defects on material surfaces can be formulated as an

anomaly detection problem. Autoencoders have been

previously used to detect defects, e. g., Essid et al.

(2018) demonstrated how autoencoders can be uti-

lized to localize defects on metal boxes and Kholief

et al. (2017) used autoencoders for the detection of

surface defects on steel strips.

We compared three convolutional versions of

autoencoders - a “standard” autoenocoder (CAE)

(Gondara, 2016), a variational autoencoder (VAE)

(Kingma and Welling, 2014) and an adversarial au-

282

Schneider, S., Antensteiner, D., Soukup, D. and Scheutz, M.

Analysis of the Future Potential of Autoencoders in Industrial Defect Detection.

DOI: 10.5220/0010777000003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

282-289

ISBN: 978-989-758-555-5; ISSN: 2184-4321

toencoder (AAE) (Makhzani et al., 2016).

First, we used two datasets we generated syntheti-

cally. Both consist of a ground structure considered

as normal or non-defective. In the corresponding

anomalous images, the ground structure was changed

in order to create anomalous regions. The pixel-wise

reconstruction error can be used to localize anoma-

lous regions. We can quantify the quality of our

anomaly detection algorithm because the location of

anomalous pixels are exactly known.

To investigate the anomaly detection behaviour of

autoencoders in the “industrial wild”, our models are

utilized to detect defects in quality inspection images

of two different manufactured materials, namely ma-

terial 1 and material 2.

Our investigations show scenarios in which a con-

volutional autoencoder leads to meaningful results,

but we also present a situation where a convolutional

autoencoder fails to detect anomalies. To capture

the “cost-beneﬁt ratio” of our different autoencoder

types, we evaluated the quality of their anomaly

detection results alongside with their measured

training times.

Our contribution comprises:

• a thorough review and suggestions for improved

designs based on the given evidence,

• a quantitative and qualitative comparison of dif-

ferent convolutional autoencoder types (CAE,

VAE, AAE) based on their anomaly localization

performances on two synthetic datasets,

• a qualitative evaluation of the performances of

different convolutional autoencoder types (CAE,

VAE, AAE) on two industrial datasets.

2 AUTOENCODERS FOR

ANOMALY DETECTION

The underlying principle of autoencoders is to en-

code an input sample x ∈ R

C×H×W

into a compressed

representation z ∈ R

×H

×W

and then decoding this

representation back such that it is as similar to the

original input as possible. Typically, the dimen-

sions of the so-called bottleneck layer C

× H

×W

are signiﬁcantly smaller than the input dimensions

C × H × W . This enforces a compression of data.

By training the autoencoder purely on normal sam-

ples, it will learn the proﬁle of these normal images.

A normal image region will be reconstructed more

accurately than an anomalous region. The residual

map R(x,

x) ∈ R

C×H×W

formulates the squared pixel-

wise difference of the input x and its reconstruction

x computed by the trained network and can be uti-

lized to decide between normal and anomalous pixels

(Bergmann et al., 2019; Bank et al., 2020; Manakov

et al., 2019).

R(x,

x) = (x −

(1)

2.1 “Standard” Convolutional

Autoencoder

A “standard” convolutional autoencoder as described

in Bergmann et al. (2019) and Manakov et al. (2019)

consists of a convolutional encoder network E

CAE

which compresses the data x into a latent representa-

tion z and another convolutional network, the decoder

CAE

, which outputs a reconstruction

x of the com-

pressed version of the data:

x = D

CAE

(x)) = D

CAE

(z). (2)

The autoencoder should be forced to reconstruct

the input image, therefore the mean squared error

(MSE) function is used as the guiding loss func-

tion. The MSE-loss is the squared l

-norm between

each pixel of the input x and the reconstructed im-

age

x, where x(m,n) and

x(m,n) denote the intensity

at the pixel locations (m, n) with m ∈ [1, ...,H] and

n ∈ [1,...,W ] of image x and

x, respectively (Rumel-

hart and McClelland, 1987; Bergmann et al., 2019;

Bank et al., 2020; Manakov et al., 2019):

MSE

(x,

x) =

∑

m= 1

∑

n= 1

(x(m,n) −

x(m,n))

(3)

2.2 Variational Autoencoder

Similarly to the CAE, the variational autoencoder

(VAE) as described in Kingma and Welling (2014),

Rocca (2019) and Pereira and Silveira (2018) con-

sists of an encoder E

VAE

, which learns a latent rep-

resentation of the input, and a decoder D

VAE

, which

generates an output based on the latent variables. The

network is trained to encode and decode the input x

in such a way that the reconstructed input

x is as sim-

ilar as possible to x. In contrast to the CAE, the VAE

not only compresses the input to a lower dimensional

representation, but encodes it as a distribution over

the latent space. More precisely, the latent represen-

tation z of an input is now constrained to be a ran-

dom variable distributed according to a prior distribu-

tion p

(z), which is typically a Gaussian distribution

N (µ,σ). For a continuous latent space, the true pos-

terior p

(z|x) is intractable. A deterministic approx-

imation q

(z|x) can be found by applying the vari-

ational inference technique, a technique to approxi-

mate complex distributions. Loosely speaking, the

Analysis of the Future Potential of Autoencoders in Industrial Defect Detection

283

idea is to set a parametrised family of distributions

and to look for the best approximation of the target

distribution among this family, i.e. the element of the

family that gives the least approximation error. To

learn the autoencoder’s parameters, we optimise the

following:

L(θ,φ,x) = E

(z|x)

(x|z)]−D

(z|x)||p

(x)).

(4)

The ﬁrst term of this loss function is the recon-

struction loss, which measures how well the input

was reconstructed. The second term is the Kull-

back–Leibler divergence. It evaluates how much in-

formation is lost if p

is approximated by q

(z|x).

It makes sure that the learned distribution stays close

to the prior distribution. The reconstruction loss can

be simpliﬁed to the MSE loss (given previously in

equation 3) if q

(z|x) is following a Gaussian distri-

bution. Kingma and Welling (2014) show how the

Kullback–Leibler divergence can be simpliﬁed when

both prior and posterior approximations are assumed

to be distributed according to a Gaussian distribution.

Variance σ and mean µ will be learned according to

the following equation, where J is the number of ele-

ments in vectors σ and µ:

− D

(z|x)||p

) =

∑

j=1

(1 + log((σ

)

) − (µ

)

− (σ

)

(5)

2.2.1 Re-parametrization Trick

As the decoder samples randomly from z ∼ q

(z|x),

we need to backpropagate through this random sam-

pling operation in order to train the network. How-

ever, backpropagation can not ﬂow through a random

node. The re-parametrization trick was proposed by

Kingma and Welling (2014) and is commonly used

(Rocca, 2019; Pereira and Silveira, 2018) to bypass

this problem by describing the random variable z as a

differentiable transformation of another random vari-

able ε.

The distribution of ε is independent of z, and

Φ and z are given. If one assumes q

(z|x) =

N (z; µ, diag(σ

)), then, after parametrization with

ε ∼ N (0,I), the latent representation can be com-

puted as in eq. 6. µ and log(σ) are outputs of the

encoder network.

z = µ + σ  ε (6)

2.3 Adversarial Autoencoder

Similarly to the VAE, the adversarial autoencoder

(AAE) proposed by Makhzani et al. (2016) imposes

a prior distribution on the latent vector z. Both prob-

abilistic autoencoders match the aggregated posterior

of the hidden code vector with a prior distribution.

While the VAE does this by applying the Kullback-

Leibler divergence, the AAE uses Generative Adver-

sarial Networks (GAN) (Goodfellow et al., 2014).

The AAE is a composite of a “standard” convolu-

tional autoencoder and an adversarial network which

regularizes the encoded vector. The autoencoder at-

tempts to minimize the reconstruction error. Addi-

tionally, the encoder E

AAE

of the autoencoder is the

generator of the adversarial network and ensures that

the discriminative adversarial network C

AAE

can be

“fooled into thinking” that the hidden code comes

from the true prior distribution.

Both the autoencoder and the adversarial network are

trained jointly in two phases - a reconstruction phase

and a regularization phase.

During the reconstruction phase, E

AAE

and D

AAE

are

optimised in the exact same way as E

CAE

and D

CAE

- the parameters are updated to minimize the recon-

struction error as given in Eq. 3.

In the regularization phase, the adversarial net-

work is trained. The discriminative model C

AAE

this network does not directly discriminate between

“real” and “fake” data but acts as a critic. It esti-

mates the distance between training data distribution

and the distribution generated by E

AAE

by comput-

ing the Wasserstein distance as described in Arjovsky

et al. (2017). To enforce the Lipschitz constraint,

the weights are clipped to a ﬁxed box after each gra-

dient update. The discriminative network is trained

to distinguish between “true samples” z, generated

based on the prior, and the hidden representation of

input data

z computed by E

AAE

. Then the adversar-

ial network updates its generator E

AAE

to confuse the

discriminator C

AAE

(Makhzani et al., 2016; Arjovsky

et al., 2017).

3 COMPARISON OF DIFFERENT

AUTOENCODER TYPES FOR

ANOMALY DETECTION

In order to compare the CAE with the VAE as well

as the AAE, their architectures are chosen to be in an

identical manner. Detailed information about the net-

works’ architectures are given in the appendix. The

encoders of CAE, VAE and AAE are implemented

in an identical manner. Their computed latent rep-

resentations are mapped back to the image domain

by identical decoders for CAE, VAE and AAE (Tab.

2). The bottleneck architecture of the VAE is imple-

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

284

mented based on the exact same architecture as for the

CAE and AAE, except that there are not just one but

two innermost linear layers for σ and µ, respectively

(Tab. 3). These values are then reparametrized for the

VAE. The architecture of the C

AAE

is given in Tab. 4.

The size of the convolutional kernels was chosen to

be 3 × 3.

All networks were trained on the same images for

the same number of epochs, with the same architec-

ture parameters and with the same learning rate and

minibatch size. The Adam algorithm as proposed in

Kingma and Ba (2014) was used to optimize the pa-

rameters of the models.

3.1 Experiments on Synthetic Datasets

Both synthetic datasets include four non-anomalous

images with a ground structure considered as nor-

mal and four images where the ground structure was

changed in order to create anomalies (Fig. 2). The

anomalous regions of the ﬁrst dataset, which we

will refer to as the chess-dataset, are composed of

repetitive sequences of black and white squares of

the same size. The anomalous regions were gener-

ated by applying elastic deformations as described by

Simard et al. (2003): displacement vector ﬁelds were

computed by randomly selecting values from a uni-

form distribution and a subsequent convolution with

a Gaussian kernel.

The non-anomalous images of the second dataset

will be referred to as noise-dataset. It consists of four

images with intensity values drawn from a Gaussian

distribution. The anomalous regions were induced by

plotting a noisy linear function on top of it (Fig. 2).

All three autoencoder types were trained on the

non-anomalous images. The trained model was then

applied to the anomalous examples, R(x,

x) was used

to locate the anomalies. In order to compute a binary

detection mask R

(x,

x), R(x,

x) was thresholded by a

constant t, which was chosen s.t. the IoU (see para-

graph 3.1.1) was maximized.

(a) (b) (c) (d)

Figure 2: Examples of non-anomalous images (Fig. 2a and

Fig. 2c) and their corresponding anomalous images (Fig. 2b

and Fig. 2d) of our synthetic datasets.

3.1.1 Evaluation Metrics

As the anomalies were induced by ourselves, we had

an accurate two-dimensional ground truth available.

We consider how accurately the residual maps capture

the anomalous regions by means of accuracy A and

intersection over union IoU. A is the average number

of correctly classiﬁed pixels. If we denote the binary

segmentation result as R

(x,

x) ∈ R

H×W

and the cor-

responding ground truth as y ∈ R

H×W

, we can com-

pute A as follows (Ulku and Akagunduz, 2019):

A(R

(x,

x),y) =

∑

m,n

δ(R

(m,n), y(m,n)),

with δ(i, j) =

(

1 if i = j = 1

0 else

(7)

where (m,n) denote the pixel positions with m ∈

[1,H] and n ∈ [1,W ]. The variable k represents the

total amount of pixels with an intensity value equal to

1 in the ground truth image y. The IoU is the “over-

lapping” area of R

(x,

x) and ground truth y divided

by the area of union between R

(x,

x) and y and can

be written as follows (Rezatoﬁghi et al., 2019):

IoU(R

(x,

x),y) =

∩ y|

∪ y|

. (8)

Both A and IoU scale between 0 and 1. For a

perfect result, A = 1 and IoU = 1.

3.2 Experiments on Industrial Datasets

Images of two different industrial materials, namely

material 1 and material 2, were used to investigate

our three convolutional autoencoders with respect to

their quality inspection capability. The autoencoders

were trained on defect-free images of the materials,

the trained autoencoders were then applied to im-

ages showing erroneous regions. The pixelwise re-

construction error was used to locate defects in the

images.

Material 1. is an aluminium plate with a translu-

cent riblet foil attached. A riblet foil is a functional

three dimensional surface (“shark skin”), which can

be attached to different materials in order to reduce

drag on surfaces such as wind turbines or airplane

wings. They are frequently used in bionics (Bechert

and Hage, 2006) and hence a highly relevant indus-

trial application. We acquired ten albedo images of

rather defect free regions of the riblet material and

four albedo images of defective riblet material. Addi-

tionally, three surface normal images of non-damaged

Analysis of the Future Potential of Autoencoders in Industrial Defect Detection

285

material and two images of defective material were

generated. The albedo images A ∈ R

1×H×W

have one

intensity value per channel. The surface normal im-

ages are three-channel images, N ∈ R

3×H×W

. The

surface normal components along x- and y-direction

are stored in the ﬁrst and second colour channel, re-

spectively. The z-component is stored in the third

channel. Patches of size 128 × 128 pixel were sam-

pled randomly from the images of size 5496 × 3672

pixel during training (Fig. 3).

Material 2. is a steel plate with a surface of a

speciﬁc granularity texture. Steel products are em-

ployed in various manufacturing sectors (Hidalgo and

Kami

nski, 2011) and a detection of defective material

is highly applicable. For this material, one pair of gra-

dient and corresponding curvature image of defect-

free and an image pair with gradient and curvature

image of defective material were acquired with a pho-

tometric stereo set-up. The images have dimensions

2336 × 4000 pixel. We used 128 × 128 pixel patches

as input images (Fig. 3).

Material 1 Material 2

A N Gradient Curvature

Full view

Patch

Figure 3: Examples of an albedo image A and a surface

normal image N of material 1 and a gradient and curva-

ture image of material 2 are shown. We sampled patches as

shown in the second row for model training.

4 RESULTS

In this section, we demonstrate the quantitative and

qualitative performance of our three autoencoder

types as introduced in Sec. 2 on the datasets we in-

troduced in Sec. 3.

4.1 Synthetic Datasets

First, we present the quantitative and qualitative au-

toencoder performance on our synthetic ground truth

datasets. We evaluate how accurate our models de-

tects anomalous regions and how long the training

takes.

4.1.1 Qualitative Results

All of our three autoencoder types detected the

anomalous regions for both datasets well, but espe-

cially for our noise dataset, there were several non-

anomalous pixels insufﬁciently well reconstructed,

see Fig. 4.

CAE VAE AAE

x y R

(x,

x) R

(x,

x) R

(x,

ChessNoise

Figure 4: Illustration of R

(x,

x) of all our autoencoder

types on both synthetic datasets. The anomalous regions

of images are highlighted in their corresponding ground

truth images. R

(x,

x) of the different networks capture the

anomalous regions.

4.1.2 Quantitative Results

By computing A(R

,y) and IoU(R

,y), we can eval-

uate the anomaly detection performance in a quanti-

tative manner. Both scale between 0 and 1, a higher

value represents superior results.

The values given in Tab. 1 show that, while all mod-

els perform quite well, the AAE performs best for

both datasets. The performance differences are only

marginal for the chess dataset. For the more complex

noise dataset, both CAE and VAE are outperformed

signiﬁcantly by the AAE. The anomalous region in

the chess dataset is detected more accurately than the

anomalous region in the noise dataset.

We measured the training times time

for all

three autoencoder types and for both datasets. The

last column in Tab. 1 shows that the training of the

CAE is faster than training the VAE and the AAE.

This is of course reasonable, the training procedure

of the CAE is the simplest and the least computation

steps are necessary. The VAE needs more compu-

tations due to the re-parametrization of the latent

variables. Training the AAE is the most expensive

procedure since we do not only train an encoder and a

decoder, but also the adversarial network component.

4.2 Industrial Datasets

In this subsection, we evaluate our three autoencoder

types on our self-acquired industrial datasets. For this

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

286

Table 1: Evaluation of the anomaly detection on our syn-

thetic datasets using A and IoU. The last column shows the

time needed for training the models (in seconds).

Type

Metric

A(R

(x,

x),y) IoU(R

(x,

x),y) Time

chess

CAE 0.9487 0.7975 212

VAE 0.9492 0.7995 213

AAE 0.9499 0.7998 1223

noise

CAE 0.9093 0.7594 216

VAE 0.8797 0.7698 220

AAE 0.9218 0.7743 1227

purpose, we generated image samples of two different

materials, namely material 1 and material 2.

Material 1. is a riblet foil mounted on a metal plate,

see section 3.2 for more detailed information. Fig. 5

show that the convolutional autoencoder is able to

learn that albedo images (see Sec. 3.2) consist of al-

ternating dark and bright horizontal tracks. When the

trained model is applied to images with defects, the

model fails to reconstruct the defective regions. The

autoencoder reconstructs these anomalous regions as

if they were normal.

Unfortunately, there is no ground truth available

which clearly states where defective regions are. As

we wanted to get an idea of how well we are able

to distinguish defective patches from non-defective

patches, bounding boxes were drawn around defec-

tive regions. Fig. 6 shows histograms computed by

averaging the reconstruction error of defective and

non-defective patches. The histogram correspond-

ing to the albedo images suggests that signiﬁcantly

higher reconstruction errors are computed for anoma-

lous patches and that our model could potentially

distinguish between defective and non-defective im-

age regions rather well. A distinction between nor-

mal and defective patches is more difﬁcult for surface

normal images. Although some anomalous patches

were reconstructed signiﬁcantly worse than most non-

anomalous patches, there are several non-anomalous

patches which were reconstructed nearly as poorly as

the “most anomalous” (highest reconstruction error)

patches.

Fig. 7 shows qualitative results of an albedo image

with defective regions. Both vertical defects lead to

high reconstruction errors. There are several notably

darker areas in the albedo image, one is highlighted in

Fig. 7. These regions were not considered as anoma-

lous and similar structures were present in the images

the autoencoder was trained on. One can observe,

that although the reconstruction loss is slightly higher

at these image regions, because the regions were not

present on all images, the reconstruction loss is sig-

niﬁcantly higher at the pixel positions of the vertical

defects the model has never seen during training.

Non-defective Defective

Input

Reconstruction

Figure 5: Illustration of normal and anomalous patches of

an albedo image and their reconstructions computed by our

trained CAE. The model reconstructs non-anomalous and

anomalous patches in the exact same way.

Albedo Surface Normals

Figure 6: The histograms show the averaged reconstruction

loss per patch for patches sampled of non-anomalous and

anomalous regions of albedo and surface normal image.

Albedo Residual Map

Figure 7: Illustration of an albedo image with a defective

region and the corresponding residual map. The defective

regions are highlighted with red boxes in the input image.

The region highlighted with a green box was not catego-

rized as anomalous, similar structures were present during

training.

Material 2. is a steel plate with a speciﬁc granular-

ity texture we describe in more detail in paragraph

3.2. We utilize it to investigate the training process

on one of our autoencoder types. For this demonstra-

tion we chose the CAE. Both other types computed

comparable outcomes. Fig. 8 shows how the output

of our CAE model develops during training. One can

see that the model is not able to capture any regular-

ity in the images and starts to just put the averaged

intensity value on all pixel positions for both gradi-

ent and curvature image. As the model did not learn

to reconstruct the normal structure properly, it also

fails to detect the anomalous image regions since both

Analysis of the Future Potential of Autoencoders in Industrial Defect Detection

287

non-defective and defective regions are reconstructed

poorly, see Fig. 9.

Input Epoch 0 Epoch 2 Epoch 15

Figure 8: Illustration of the reconstruction of an input patch

of the gradient image computed by the CAE at different

epochs. The training of the CAE on the curvature image

showed the same “averaging” behaviour.

Input Reconstruction Residual map

Figure 9: Illustration of a gradient input patch with a defec-

tive region marked in red, its reconstructions and residual

map.

5 CONCLUSIONS

In this paper we investigated the autoencoder in dif-

ferent anomaly detection scenarios. To this end, we

compared convolutional versions of the CAE, the

VAE and the AAE.

On our synthetic and industrial datasets, we demon-

strated that the autoencoders can be used effectively

to locate defects by computing the two-dimensional

residual map, but only if there is enough regular geo-

metric structure. All of our autoencoders were capa-

ble to compute an accurate detection of the anoma-

lous image regions. For the anomaly detection in

the albedo and surface normal images of the ﬁrst in-

dustrial dataset material 1, the autoencoders achieved

good results as well. However, the autoencoder mod-

els did not compute any reasonable reconstructions

for material 2. The autoencoders can not identify a

regular pattern in the data and the least costly result

they can reconstruct is an image with intensity val-

ues equal to the averaged value of the input image

(see Fig. 8). If there is no accurate reconstruction

of the normal image structure computed, the residual

map does not include any reasonable anomaly detec-

tion information, see Fig. 9. Interestingly, the model

seems to ﬁnd a pattern in the synthetically generated

noise pattern. We argue that the reason for this lies

in its partial regularity in structure due to its com-

putational generation process. The CAE is the sim-

plest model demanding the simplest training proce-

dure. This is reﬂected in the measured training times,

which are the shortest compared to VAE and AAE.

The training of the VAE model takes longer due to

the re-parametrisation step. Training the AAE takes

the longest, because the adversarial component needs

to be trained additionally. For the synthetic datasets,

the AAE detects the anomalous regions best for both

noise and chess dataset. However, one could argue

that the increase in performance is too subtle to jus-

tify the use of a more complex model.

Although we ﬁnd the autoencoders versatility partic-

ularly convincing, we could also get an insight on ap-

plications where it is not suitable as a tool for anomaly

detection. Namely, if the data lacks any kind of reg-

ularity, the model can not identify a meaningful com-

pression of the data. Additionally we want to men-

tion that although the autoencoder is trained in an un-

supervised manner, compiling a training set with im-

ages of purely non-defective material can be demand-

ing. Even for experts it is challenging to tell if certain

structures should be considered as normal for indus-

trial datasets.

Remarks. In order to examine and compare the de-

fect detection capabilities of autoencoders further, we

strongly depend on the annotation of our industrial

datasets. Such industrial annotation comparison will

be a part of the scope of our future work. Also we are

aware that model architecture parameters, such as the

size of the latent layer, may have a signiﬁcant impact

on results. However, the same parameters were used

for each “session of experiments” and their compari-

son can still be considered to be fair.

ACKNOWLEDGEMENTS

This work was partly funded by the Austrian Re-

search Promotion Agency (FFG) within the project

RiSPECT (874163).

REFERENCES

Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-

stein generative adversarial networks. Proceedings of

the 34th International Conference on Machine Learn-

ing, 70:214–223.

Bank, D., Koenigstein, N., and Giryes, R. (2020). Autoen-

coders. CoRR, abs/2003.05991.

Bechert, D. W. and Hage, W. (2006). Drag reduction with

riblets in nature and engineering. Flow Phenomena in

Nature Volume 2: Inspiration, Learning and Applica-

tion.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

288

Bergmann, P., L

owe, S., Fauser, M., Sattlegger, D., and Ste-

ger, C. (2019). Improving unsupervised defect seg-

mentation by applying structural similarity to autoen-

coders. Proceedings of the 14th International Joint

Conference on Computer Vision, Imaging and Com-

puter Graphics Theory and Applications.

Essid, O., Samir, C., and Hamid, L. (2018). Automatic de-

tection and classiﬁcation of manufacturing defects in

metal boxes. PLOS ONE.

Gondara, L. (2016). Medical image denoising using con-

volutional denoising autoencoders. 2016 IEEE 16th

International Conference on Data Mining Workshops

(ICDMW), pages 241–246.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial networks. Ad-

vances in Neural Information Processing Systems, 3.

Hidalgo, I. and Kami

nski, J. (2011). The iron and steel

industry: A global market perspective. Mineral Re-

sources Management.

Kholief, E., Darwish, S., and Fors, M. (2017). Detection of

steel surface defect based on machine learning using

deep auto-encoder network. 7th International Confer-

ence on Industrial Engineering and Operations Man-

agement( IEOM).

Kingma, D. and Ba, J. (2014). Adam: A method for

stochastic optimization. International Conference on

Learning Representations.

Kingma, D. P. and Welling, M. (2014). Auto-encoding vari-

ational bayes. CoRR, abs/1312.6114.

Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., and

Frey, B. (2016). Adversarial autoencoders. ArXiv,

abs/1511.05644.

Manakov, I., Rohm, M., and Tresp, V. (2019). Walking

the tightrope: An investigation of the convolutional

autoencoder bottleneck. ArXiv, abs/1911.07460.

Pang, G., Shen, C., Cao, L., and Hengel, A. V. D. (2021).

Deep learning for anomaly detection. ACM Comput-

ing Surveys, 54(2):1–38.

Pereira, J. and Silveira, M. (2018). Unsupervised anomaly

detection in energy time series data using variational

recurrent autoencoders with attention. 2018 17th

IEEE International Conference on Machine Learning

and Applications (ICMLA), pages 1275–1282.

Rezatoﬁghi, H., Tsoi, N., Gwak, J., Sadeghian, A., Reid,

I., and Savarese, S. (2019). Generalized intersection

over union: A metric and a loss for bounding box re-

gression. 2019 IEEE/CVF Conference on Computer

Vision and Pattern Recognition (CVPR), pages 658–

666.

Rocca, J. (2019). Understanding variational autoencoders

(vaes) - building, step by step, the reasoning that leads

to vaes.

Rumelhart, D. E. and McClelland, J. L. (1987). Learning

internal representations by error propagation. Paral-

lel Distributed Processing: Explorations in the Mi-

crostructure of Cognition: Foundations, pages 318–

362.

Simard, P., Steinkraus, D., and Platt, J. (2003). Best prac-

tices for convolutional neural networks applied to vi-

sual document analysis. Seventh International Con-

ference on Document Analysis and Recognition, 2003.

Proceedings., pages 958–963.

Ulku, I. and Akagunduz, E. (2019). A survey on deep

learning-based architectures for semantic segmenta-

tion on 2d images. arXiv: Computer Vision and Pat-

tern Recognition.

Yang, J., Li, S., Wang, Z., Dong, H., Wang, J., and Tang,

S. (2020). Using deep learning to detect defects in

manufacturing: A comprehensive survey and current

challenges. Materials, 13:5755.

APPENDIX

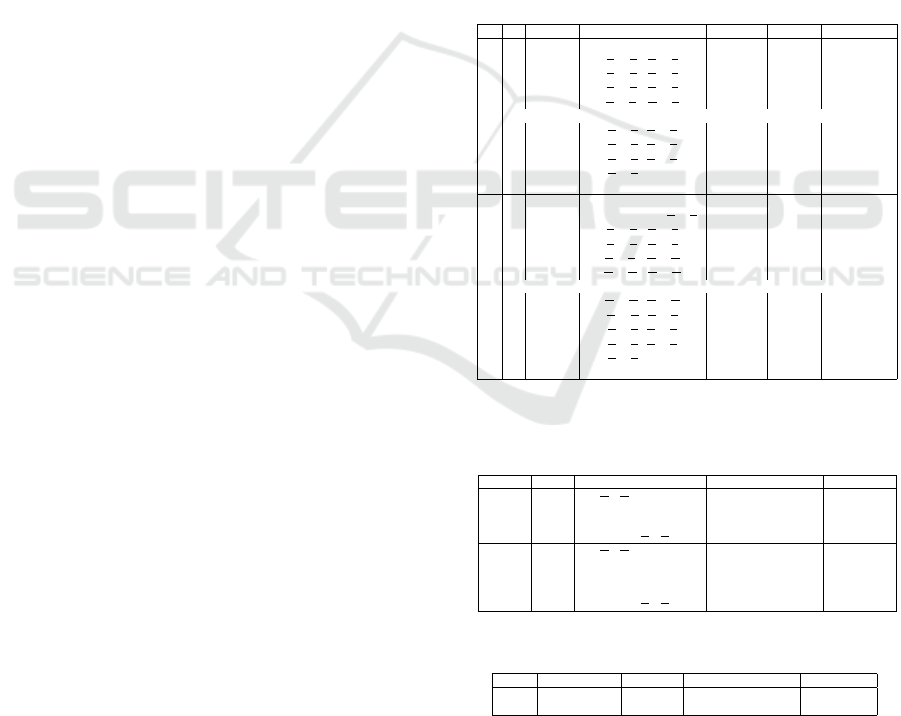
Table 2: Encoder and decoder architecture used for our syn-

thetic datasets (d = 16) and the industrial datasets. n

= 3

for the surface normal images of material 1 and n

= 1 for

the albedo images of material 1 and gradient and curvature

images of material 2.

Layer Resolution Channels Input Activ. func.

Synthetic dataset

Encoder

conv1 W × H/W × H 1/16 Image Leaky ReLU

conv2

16/32 conv1 Leaky ReLU

conv3

32/64 conv2 Leaky ReLU

conv4

64/64 conv3 Leaky ReLU

conv5

64/16 conv4 Leaky ReLU

Bottleneck

Decoder

deconv1

16/64 lin4 Leaky ReLU

deconv2

64/64 deconv1 Leaky ReLU

deconv3

64/32 deconv2 Leaky ReLU

deconv4

/W × H 32/16 deconv3 Leaky ReLU

deconv5 W × H /W × H 16/1 deconv4 Sigmoid

Industrial dataset

Encoder

conv1 W × H/W × H n

/16 Image Leaky ReLU

conv2 W × H/W × H /

16/32 conv1 Leaky ReLU

conv3

32/64 conv2 Leaky ReLU

conv4

64/64 conv3 Leaky ReLU

conv5

64/64 conv4 Leaky ReLU

conv6

64/16 conv5 Leaky ReLU

Bottleneck

Decoder

deconv1

16/64 lin4 Leaky ReLU

deconv2

64/64 deconv1 Leaky ReLU

deconv3

64/64 deconv2 Leaky ReLU

deconv4

64/32 deconv3 Leaky ReLU

deconv5

/W × H 32/16 deconv4 Leaky ReLU

deconv6 W × H /W × H 16/n

deconv5 Sigmoid

Table 3: Bottleneck architectures used for our synthetic

datasets (conv

= conv5, r = 1024, n

= 100) and the in-

dustrial datasets (conv

= conv6, r = 1024, n

= 100).

AE type Layer Resolution Input Activ. func.

CAE/AAE

lin1 1 ×

∗

∗ 16 / 1 × 1024 conv

(ﬂattened) Leaky ReLU

lin2 1× r / 1 × n

lin1 -

lin3 1× n

/ 1 × r lin2 Leaky ReLU

lin4 1 × r / 1 ×

∗

∗ 16 lin3 Leaky ReLU

VAE

lin1 1 ×

∗

∗ 16 / 1 × 1024 conv

(ﬂattened) Leaky ReLU

lin21 1×r / 1 × n

lin1 -

lin22 1×r / 1 × n

lin1 -

lin3 1× n

/ 1 × r lin21, lin22 (reparam.) Leaky ReLU

lin4 1 × r / 1 ×

∗

∗ 16 lin3 Leaky ReLU

Table 4: Architecture of the C

AAE

used for all our datasets.

Layer Resolution Channels Input Activ. func.

lind1 1 × n

/ 1 × 10 - lin2 Leaky ReLU

lind2 1 × 10 / 1 × 1 - lind1 Leaky ReLU

Analysis of the Future Potential of Autoencoders in Industrial Defect Detection

289