DeepPupil Net: Deep Residual Network for Precise Pupil Center

Localization

Nikolaos Poulopoulos

and Emmanouil Z. Psarakis

Department of Computer Engineering & Informatics, University of Patras, Greece

Keywords:

Eye Localization, Eye Tracking, Deep Neural Networks, Deep Learning, Fully Convolutional Network (FCN).

Abstract:

Precise eye center localization constitutes a very promising but challenging task in many human interaction

applications due to many limitations related with the presence of photometric distortions and occlusions as well

as pose and shape variations. In this paper, a Fully Convolutional Network (FCN), namely DeepPupil Net is

proposed to localize precisely the eye centers by performing image-to-heatmap regression between the eye

regions and the corresponding heatmaps. Moreover, a new loss function is introduced in order to incorporate

into the training process the predicted eye center positions and penalize inaccurate localizations. The proposed

method achieves real-time performance in a general-purpose computer environment and outperforms in terms

of accuracy the state-of-the-art eye center localization techniques.

1 INTRODUCTION

Nowadays, human-computer interaction (HCI) is of

growing interest due to the penetration of computer

systems in every aspect of everyday life. This

progress requires new input modalities except from

the traditional devices (keyboards, mousses, touch

surfaces, sensors, etc.) with the eye gaze to constitute

a revolutionary approach to interact without physical

contact. The most characteristic features of the hu-

man face constitute the eyes as they provide signiﬁ-

cant information for the emotional and cognitive hu-

man state. Moreover, eye centers’ location per se can

be exploited in applications such as face alignment,

face recognition, control devices for disabled people,

user attention and gaze estimation (e.g., driving and

marketing) (Kar and Corcoran, 2017; Krafka et al.,

2016).

Despite the active research in this ﬁeld, the accu-

racy of such eye center localization systems has room

for improvement and usually downgraded by many

limitations. The main challenges are related to the

wide variety of human eye colors and shapes, the eye

states (open or closed), the facial expressions and ori-

entations etc. Moreover, the presence of occlusions

from hair and glasses, reﬂections and shadows as well

as poor lighting and low image resolution further de-

https://orcid.org/0000-0002-8341-9805

https://orcid.org/0000-0002-9627-0640

grades the localization accuracy. Accurate eye center

localization becomes even more challenging where

the low complexity is substantial for incorporating

in real-time applications (Poulopoulos and Psarakis,

2018).

End-to-end deep neural network learning consti-

tutes a state-of-the-art approach for solving several

problems and has attracted recently the interest of sci-

entiﬁc community. In this paper, we introduce a novel

network, called DeepPupil Net, that tries to solve the

eye localization problem in an end-to-end way. An

encoder-decoder based architecture is proposed to lo-

calize precisely the eye centers by performing image-

to-heatmap regression between the eye regions and

the corresponding heatmaps. Moreover, a new loss

function is introduced in order to incorporate into the

training process the predicted positions of the corre-

sponding eye centers. In this way we succeed to im-

prove the accuracy of the eye center localizer, over-

coming the aforementioned limitations. The main

contributions of this work are summarized as follows:

• A novel end-to-end architecture for precise eye

center localization.

• A new loss function that penalizes inaccurate lo-

calizations during training.

• Enhanced accuracy over the state-of-the-art meth-

ods in three publicly available databases.

Poulopoulos, N. and Psarakis, E.

DeepPupil Net: Deep Residual Network for Precise Pupil Center Localization.

DOI: 10.5220/0010777900003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages

297-304

ISBN: 978-989-758-555-5; ISSN: 2184-4321

297

2 RELATED WORK

Eye center localization methods working under chal-

lenging conditions can be categorized into the follow-

ing broad classes:

• Feature based methods and

• Appearance based methods.

Feature-based methods exploit the special form of the

eye structure and detect the eye centers by applying

appropriate ﬁlters based on shape, geometry, sym-

metry and color. The obtained features are robust to

shape and scale variances and don’t require any ma-

chine learning techniques. Valenti et al. (Valenti and

Gevers, 2008) introduced a voting process based on

isophote curvatures for localizing the eye centers. Ra-

dial symmetry operators, trying to highlight the cir-

cularity of the iris, have also attracted much popu-

larity for the automatic eye center localization (Loy

and Zelinsky, 2003; Skodras and Fakotakis, 2015).

In (Poulopoulos and Psarakis, 2017; Poulopoulos and

Psarakis, 2018) a Modiﬁed Fast Radial Symmetry

Transform (MFRST) was proposed. It emphasizes on

the shape of the iris and combines the edge informa-

tion that results from an edge-preserving ﬁltering and

the intensity information, in order to ﬁnd shapes with

high radial symmetry.

Appearance-based methods incorporate the holis-

tic eye and its surrounding appearance to a prior

model and perform eye center localization by ﬁt-

ting this trained model. For this purpose, many ma-

chine learning algorithms have been proposed such as

Bayesian (Everingham and Zisserman, 2006), support

vector machines (SVM) (Campadelli et al., 2009) and

AdaBoost (Niu et al., 2006). Deep CNNs have also

achieved several improvements over the last years.

U-Net (Ronneberger et al., 2015) is a Fully Convo-

lutional Network (FCN) with an encoder-decoder like

architecture and skip connections between the encod-

ing and decoding parts, developed for biomedical im-

age segmentation. ResNet (He et al., 2016) introduces

the idea of “identity connections” that skip one or

more layers and ensures that deeper networks don’t

produce training errors higher than their shallower

counterparts. Xia et al. (Xia et al., 2019) proposed

a heatmap based approach to localize the eye centers

using a properly trained shallow FCN with a large ker-

nel convolutional block. In (Choi et al., 2020) and

(Lee et al., 2020) a deep FCN pipeline is proposed

using heterogenous CNN models trained to detect the

face, remove the eye glasses, extract the facial land-

marks and ﬁnally localize the eye centers. PupilTAN

(Poulopoulos et al., 2021) is a few-shot adversarial

training framework that performs image-to-heatmap

translation for precise eye localization.The main idea

is to train this model using an adversarial loss be-

tween the model outputs and random heatmaps sam-

pled from a prior distribution which is learned from

only few ground-truth. This adversarial loss aligns the

output and prior distributions, thereby enabling “un-

supervised” pupil localization.

3 PROPOSED TECHNIQUE

In this section, we describe in detail the proposed

CNN architecture as well as the training scheme used

for achieving our goal. To this end let us consider the

following set of training images:

= {I

)}

k=1

. (1)

with each member of this set constituting a realization

of a random variable with known pd f , i.e. I ∼ f

3.1 Preprocessing

The conversion of an eye center localization to an

image-to-heatmap regression problem requires an ap-

propriate preprocessing of the input images and the

ground-truth. To this end, in every image of the

training set, ﬁrstly the face is detected and the two

eye Regions of Interest (RoIs) are selected based on

the face geometry (Poulopoulos and Psarakis, 2017;

Poulopoulos and Psarakis, 2018). Then, every eye

RoI is resized to 64x96 pixels and transformed to

grayscale in order to feed the input of the proposed

network. Moreover, we transform the ground-truth

coordinates into a Gaussian kernel based heatmap

with equal size as the input image I, i.e:

(x, I) = e

−

||x−x

(I)||

2σ

(2)

where, x the image pixel coordinates, x

(I) the

ground-truth eye center coordinates of the image I of

the training set, ||x||

the l

norm of vector x and σ

the standard deviation of the kernel that determines

the width of the heatmap. We set the hyperparameter

σ = 7, which achieves the best results in our experi-

ments.

3.2 Network Architecture

The proposed network can fully exploit hierarchi-

cal feature representations and reconstruct the corre-

sponding spatial heat maps. The entire network ar-

chitecture summarized in Figure 1, consists of the en-

coding and decoding parts. The encoder comprises

a pyramid structure of residual blocks to extract dis-

tinct geometry information in various scales. Resid-

ual blocks are used to prevent accuracy degradation

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

298

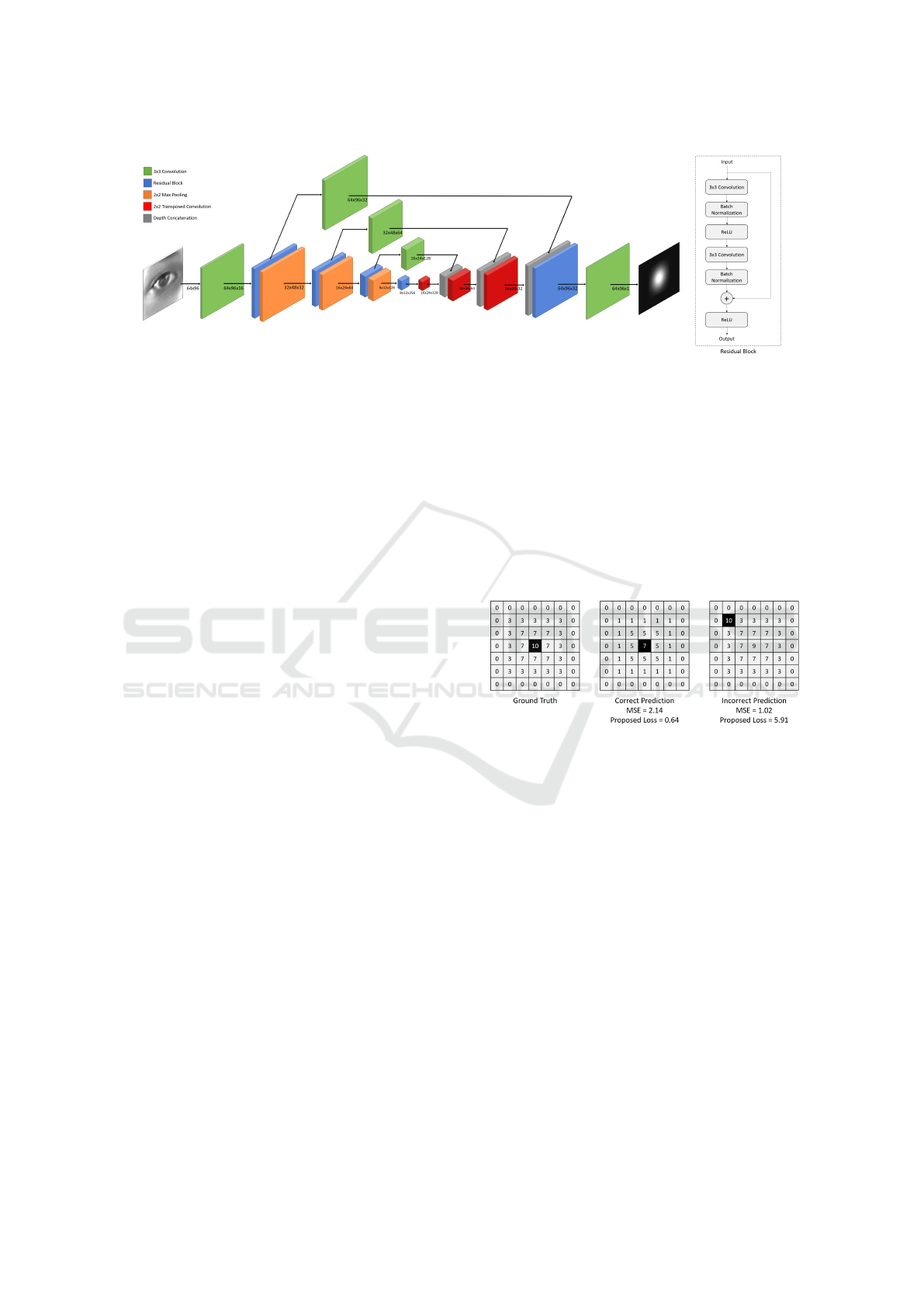
Figure 1: DeepPupil Net (a) and Residual block (b) architecture.

when the network gets deeper. Each block consists of

two convolutional layers followed by a batch normal-

ization and a rectiﬁed linear layer as shown in Figure

1.(b). In order to down-sample the feature maps and

increase the receptive ﬁeld of the net, each residual

block is followed by a max-pooling layer. The num-

ber of kernels after each stage doubles in order the net

to be able to learn the complex structures effectively.

The decoder up-samples the feature maps on differ-

ent scales using transposed convolutions. The num-

ber of kernels after each stage is reduced by a factor

of two and the layers are concatenated with the cor-

responding ones from the encoder. Skip connections

with convolutional layers are used between each stage

of the encoder and decoder, allowing feature maps

from the expanding part to be fused with the sym-

metric feature maps from the down-sampling part.

This helps the model to produce a very accurate re-

sult by combining the semantic information from the

deeper layers with the appearance information from

the shallower layers and compensate the information

loss caused by the max-pooling operations. Finally,

the decoding part is followed by a one-channel con-

volution layer in order to aggregate better multi-scale

information and obtain the ﬁnal regression map. The

network predicts a heat map for every input image

that corresponds to the per-pixel conﬁdence of the lo-

cation of the eye center. The resulting output will

have equal spatial dimensions as the original image.

The position of the maximum of the prediction corre-

sponds to the predicted eye center coordinates.

3.3 Proposed Loss Function

Mean-square-error (MSE) loss, which is the most

common loss function used in heatmap matching, op-

timizes the pixel-wise similarity between the network

predictions and the ground-truth heatmaps. However,

MSE constitutes an indirect way to optimize the pre-

dicted eye center positions because the model ignores

the fact that the coordinate predictions ﬁnally result

from the positions of the maximum heatmap values.

Thus, minimizing the MSE between the predictions

and the ground-truth heatmaps doesn’t guarantee an

improvement in the localization accuracy. Such a case

is illustrated in Figure 2, where the MSE improve-

ment leads to a heavy degradation of the localization

accuracy. It is clear that, the prediction with the cor-

rect maximum location has worse MSE than an al-

most perfectly matching heatmap with the brightest

pixel placed incorrectly.

Figure 2: MSE reduction may worsen the localization. Pro-

posed Loss addresses this by penalizing the inaccurate lo-

calizations.

To overcome this problem, we penalize inaccurate

localization results during training by introducing the

proposed Loss function which is composed by two

terms deﬁned as follows:

(I, θ) = ||H

(x, I)− H

(x, I, θ)||

(3)

(I, θ) = ||x

(I) − argmax

x∈X

(x, I, θ)||

(4)

where H

(x, I) and H

(x, I, θ) the ground truth and

predicted heatmaps respectively, θ the network pa-

rameter vector and argmax

x∈X

f (x) the operator that re-

turns the location where function f (x) attains its

maximum value. Thus, the term L

(I, θ) forces the

network to learn the real heatmaps, while the term

(I, θ) forces the network to correct the inaccurate

localizations derived from the estimated heatmaps.

Then, we can use the convex combination of the

above deﬁned terms to deﬁne the following loss func-

DeepPupil Net: Deep Residual Network for Precise Pupil Center Localization

299

tion:

L (I, θ) = αL

(I, θ) + (1 − α)L

(I, θ) (5)

where α a gain factor that controls the contribution of

each term to the total loss. This factor is set empiri-

cally to 0.3 as this value provides the best results.

However, the operator argmax is not a differen-

tiable function of the parameter vector θ and thus

it cannot be used to backpropagate and update the

parameters of the network. In order to make the

pipeline trainable, we adopt instead its soft counter-

part (Chapelle and Wu, 2010):

(I, θ) =

∑

x∈X

(x, I, θ)x (6)

where:

(x, I, θ) = softargmax

x∈X

(x, I, θ) =

βH

(x,I,θ)

∑

y∈X

βH

(y,I,θ)

(7)

can be interpreted as the probability of H

(x, I, θ) to

be the maximum value of the heatmap produced by

the DeepPupil Net for a given input image I, and hy-

perparameter β is an arbitrarily big constant used to

raise the maximum value and lower the rest of the val-

ues of the heatmap. Note that when the accuracy pa-

rameter β tends to ∞ and the location where the max-

imum value of H

(I(x), θ) is attained is unique, the

(x, I, θ) converges to the following indicator func-

tion:

lim

β→∞

(x, I, θ) =

∞

(x,I,θ)= max

x∈X

(x, I, θ)}

. (8)

Thus, the loss function deﬁned in Eq. (4) can be

redeﬁned as:

(I, θ) = ||x

(I) −

(I, θ)||

(9)

Finally, we deﬁne the following total average loss

function:

L (θ) =

I∼ f

[L (I, θ)] (10)

that we would like to minimize with respect to the

network parameters vector θ.

3.4 Training Details

The network architecture consists of a pyramid struc-

ture with T = 3 stages with the number of kernels

at each stage to increase or decrease by a factor of

two in encoder and decoder respectively. The pro-

posed network was trained using the ADAM opti-

mizer (Kingma and Ba, 2015) for 15 epochs, with

initial learning rate of 10

−3

and batch size of 30 im-

ages. Moreover, we employ two types of regulariza-

tion during training in order to prevent the network

from overﬁtting. We use L

regularization of weights

with coefﬁcient of 10

−4

as well as dropout with a rate

of P

drop

= 0.4 before and after the last residual block

of the encoder.

4 EXPERIMENTS

4.1 Experimental Setup

Experiments were carried out on three publicly avail-

able face databases for fair comparison and the perfor-

mance of the proposed method was extensively eval-

uated and compared with the state-of-the-art. Specif-

ically, the selected MUCT (Milborrow et al., 2010) ,

BioID (Jesorsky et al., 2001) and Gi4E (Villanueva

et al., 2013) databases were widely used by well-

known in the literature eye center localization tech-

niques while they were regarded as extremely chal-

lenging in terms of degradations. The images where

the face detector failed to detect the face due to ex-

treme poses, were excluded for the experiments. The

MUCT database comprises 3755 color images of low

resolution (640 × 480 pixels) with frontal or near

frontal faces. These images include a wide variety

of degradations related to pose and lighting variations

as well as occlusions from hair, glasses and reﬂec-

tions. The BioID database consists of 1521 grayscale

images of low resolution (384 × 288 pixels) includ-

ing 23 subjects taken at different times of the day

in different positions. This database is regarded a

one of the most challenging databases as it contains

wide scale and pose variations while many subjects

are wearing glasses or their eyes were closed or hid-

den by strong reﬂections on glasses. In order to ex-

plore the eye center localization task, 29 images that

contain totally closed eyes were manually removed.

The Gi4E dataset comprises 1380 high resolution

(800 × 600 pixels) color images of 103 individuals,

captured at indoor environment with illumination and

background variations. A variety of head poses and

gaze angles also resulted by asking the subjects to

look at speciﬁc points on their screen. Their head and

eye movements, the eyelid occlusions as well as the

lighting changes simulate realistic conditions for the

task of eye center localization.

The accuracy of the proposed technique and other

relative methods is evaluated adopting the normalized

error, which represents the worst eye center estima-

tion of the two eyes.The normalized error (e) is de-

ﬁned as (Jesorsky et al., 2001):

e =

max{||

−C

, ||

−C

}

||C

−C

(11)

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

300

Figure 3: Precise eye center localization results on MUCT (a), BioID (b) and Gi4E (c) databases.

where,

are the estimated left and right eye

center coordinates respectively, while C

, C

are the

manually labeled corresponding coordinates. The re-

sulting accuracy is expressed as the percentage of the

eye center localizations that fall below the assigned

error threshold. Points with e ≤ 0.25 belong to a disk

area that extends from the eye center to the eye cor-

ners (lacrimal caruncle), points with e ≤ 0.1 belong

to the iris area while points withe ≤ 0.05 belong to

the pupil area.

4.2 Experimental Results

The evaluation of the proposed method demonstrates

that it is highly accurate and robust under many chal-

lenging conditions including shadows, pose and scale

variations as well as occlusions by hair, glasses and

strong reﬂections (please see Figure 3).

The accuracy of the proposed method was evalu-

ated adopting a 5-fold cross validation. This proce-

dure refers to splitting the dataset randomly into ﬁve

(5) subsets and using each single subset for testing

and the remaining ones for training. The accuracy

curves representing the percentage of the eye center

localizations in respect to the corresponding normal-

ized errors, were evaluated for each database and de-

picted in Figure 4. These curves reveal the enhanced

localization accuracy of the proposed method even

under the ﬁne level (e ≤ 0.05).

Figure 4: Accuracy vs. normalized error in all under com-

parison databases.

The proposed method was compared with the

state-of-the-art techniques and the results are pre-

sented in the sequel.

Table 1 contains the accuracy achieved by the

proposed method and the state-of-the-art rivals in

the MUCT database. It is evident that on the de-

graded images of this database, the proposed method

achieves an improvement of 1.25% in performance

over the best method.

DeepPupil Net: Deep Residual Network for Precise Pupil Center Localization

301

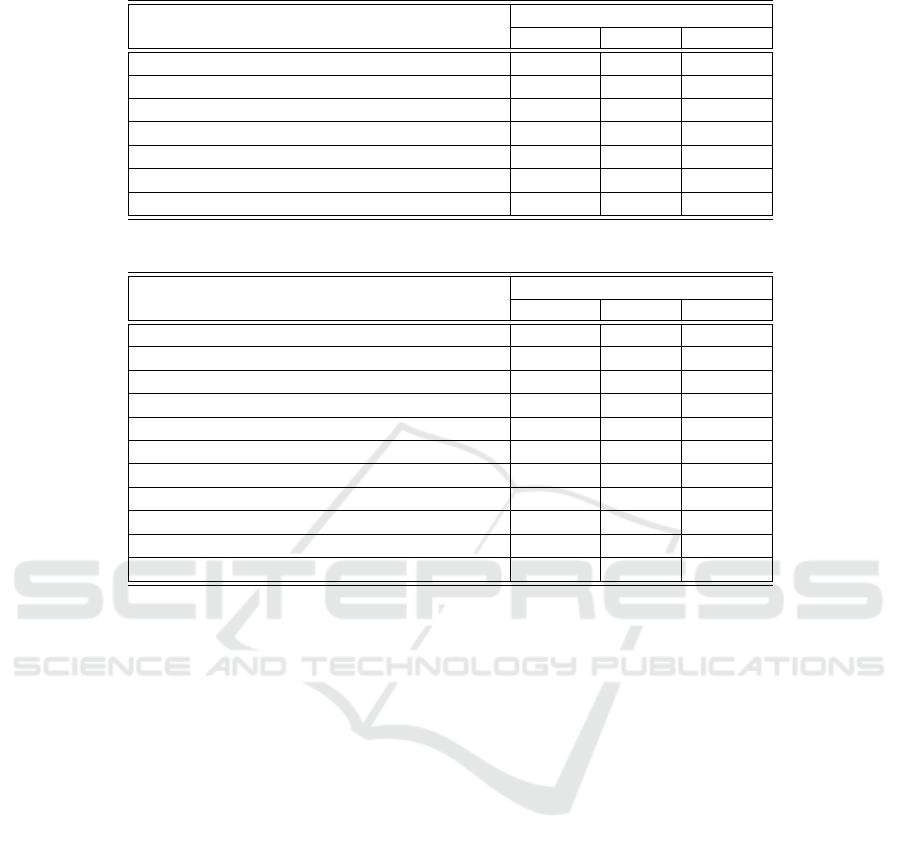
Table 1: Accuracy vs. normalized error in the MUCT database.

Method Accuracy (%)

e ≤ 0.05 e ≤ 0.1 e ≤ 0.25

DeepPupil Net 98.40 99 .97 100

PupilTan

2021

(Poulopoulos et al., 2021) 97.15 99.32 100

MFRST

2017

(Poulopoulos and Psarakis, 2017) 94.75 98.67 99.76

Skodras

2015

(Skodras and Fakotakis, 2015) 92.90 97.20 99.00

Timm

2011

(Timm and Barth, 2011) 78.60 94.90 98.60

Valenti

2008

(Valenti and Gevers, 2008) 63.10 76.70 94.10

Yang

2004

(Yang et al., 2004) 81.60 89.50 94.50

Table 2: Accuracy vs. normalized error in the BioID database.

Method Accuracy (%)

e ≤ 0.05 e ≤ 0.1 e ≤ 0.25

DeepPupil Net 98.00 100 100

PupilTan

2021

(Poulopoulos et al., 2021) 96.86 99.71 100

Lee

2020

(Lee et al., 2020) 96.71 98.95 100

Choi

2020

(Choi et al., 2020) 93.30 96.91 100

Xia

2019

(Xia et al., 2019) 94.40 99.90 100

Xiao

2018

(Xiao et al., 2018) 94.35 98.75 99.80

2018

(Li and Fu, 2018) 85.60 95.90 99.50

Wang

2018

(Wang et al., 2018) 82.15 98.70 100

MFRST

2017

(Poulopoulos and Psarakis, 2017) 87.10 98.15 100

Cai

2017

(Cai et al., 2017) 86.80 96.60 99.90

Anjith

2016

(Anjith and Routray, 2016) 85.00 94.30 -

The performance of the proposed method in the

low resolution images of BioID face database is pre-

sented in Table 2 and compared with state-of-the-art

techniques. The superiority of the proposed method is

obvious in all error categories resulting an outstand-

ing precision accuracy and an increment of 1.14%

higher than the best method.

In Table 3, the accuracy achieved by the proposed

method in Gi4E database is also shown. In this case,

due to the higher resolution images and absence of

strong degradations, we presented also the accura-

cies for the normalized threshold 0.025. Note that

the accuracies denoted with

∗

were estimated from

the accuracy curves. The proposed method not only

achieves almost perfect localization for every error

category, but also outperforms the state-of-the-art for

up to 5.37% for the case of e ≤ 0.025. Moreover, we

explored the impact of training the proposed method

on MUCT and testing on Gi4E database. In this case,

the accuracy decrease was less than 1%, achieving

99.05% and 99.91% for the cases of e ≤ 0.05 and

e ≤ 0.1 respectively, demonstrating robustness of the

proposed technique to unseen images. The above

mentioned results lead us to the conclusion of a sig-

niﬁcant improvement of the proposed method over the

state-of-the-art.

4.3 Ablation Study

In this section we analyze the impact of changing

the stages of the network architecture to the accuracy

and the processing time of the proposed method in

the BioID database. Each stage consists of a residual

block as well as the corresponding transposed convo-

lutional block and the skip connection between them

(please see Figure 1). Speciﬁcally, as shown in Table

4, decreasing the network architecture to two stages

also leads to an accuracy decrease up to 3, 49%. How-

ever, the resulting network with only 0.43M parame-

ters still provides comparable accuracy to the other

state-of-the-art methods. The optimum architecture

in terms of accuracy is the one with three stages and

thus it was selected for the experiments. Note that

the performance after adding more stages saturates.

Therefore, in terms of network complexity, Deep-

Pupil Net contains only 1.65M parameters, which is

signiﬁcantly reduced in comparison with other deep

networks. Speciﬁcally, the U-Net contains 7.7M pa-

rameters, while the architectures proposed in (Lee

et al., 2020) and (Choi et al., 2020) contain 13.6M

and 4.9M respectively only for the face detection and

glasses removal networks, without considering the

eye localization network. Moreover, the selected net-

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

302

Table 3: Accuracy vs. normalized error in the Gi4E database.

Method Accuracy (%)

e ≤ 0.025 e ≤ 0.05 e ≤ 0.1

DeepPupil Net 98.37 99.91 100

Lee

2020

(Lee et al., 2020) 93.00

99.84 99.84

Choi

2020

(Choi et al., 2020) 90.40 99.60 99.84

Xia

2019

(Xia et al., 2019) 70.00

99.10 100

Xiao

2018

(Xiao et al., 2018) 70.00

97.90 100

Levinshtein

2018

(Levinshtein et al., 2018) 88.34 99.27 99.92

Cai

2018

(Cai et al., 2018) 85.70 99.50 -

Table 4: DeepPupil Net performance for different architectures in the BioID database.

Network Stages Number of Parameters Time Accuracy (%)

e ≤ 0.05 e ≤ 0.1 e ≤ 0.25

2 0.43M 13.2ms 94.51 99.50 100

3 1.65M 15.0ms 98.00 100 100

4 6.57M 18.0ms 97.86 100 100

work achieves real-time performance as it requires

only 15ms, in Matlab implementation, to process both

the eyes for every input image.

5 CONCLUSIONS

In this paper, the DeepPupil Net, a FCN that solved

in an accurate and robust manner the eye center lo-

calization problem is introduced. This network con-

sists of an encoder-decoder based architecture and

was trained end-to-end to localize precisely the eye

centers even in the most challenging circumstances.

An extensive evaluation of the proposed method on

three publicly available databases demonstrated a sig-

niﬁcant improvement in accuracy over state-of-the-art

techniques. Moreover, due to its reduced processing

time, DeepPupil Net can be incorporated in low-cost

eye trackers, where the real-time performance is pre-

requisite.

REFERENCES

Anjith, G. and Routray, A. (2016). Fast and accurate al-

gorithm for eye localization for gaze tracking in low

resolution images. arXiv preprint arXiv:1605.05272.

Cai, H., Liu, B., Ju, Z., Thill, S., Belpaeme, T., Vander-

borght, B., and Liu, H. (2018). Accurate eye center

localization via hierarchical adaptive convolution. In

British Machine Vision Conference (BMVC). British

Machine Vision Association.

Cai, H., Liu, B., Zhang, J., Chen, S., and Liu, H. (2017).

Visual focus of attention estimation using eye center

localization. IEEE Systems Journal, 11.

Campadelli, P., Lanzarotti, R., and Lipori, G. (2009). Pre-

cise eye and mouth localization. Int. Journal of Pat-

tern Recognition and Artiﬁcial Intelligence, 23:359–

377.

Chapelle, O. and Wu, M. (2010). Gradient descent opti-

mization of smoothed information retrieval metrics.

Information retrieval, 13:216–235.

Choi, J., Lee, K., and Song, B. (2020). Eye pupil localiza-

tion algorithm using convolutional neural networks.

Multimedia Tools and Applications, 79:32563–32574.

Everingham, M. and Zisserman, A. (2006). Regression and

classiﬁcation approaches to eye localization in face

images. In International Conference on Automatic

Face and Gesture Recognition, pages 441–446. IEEE.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In International

Conference on Computer Vision and Pattern Recogni-

tion, pages 770–778. IEEE.

Jesorsky, O., Kirchbergand, K. J., and Frischholz, R.

(2001). Robust face detection using the hausdorff dis-

tance. In Audio and Video Biom. Pers. Authentication,

pages 90–95.

Kar, A. and Corcoran, P. (2017). A review and analysis

of eye-gaze estimation systems, algorithms and per-

formance evaluation methods in consumer platforms.

IEEE Access, 5:16495–16519.

Kingma, D. and Ba, J. (2015). Adam: A method for

stochastic optimization. In IEEE International Con-

ference on Learning Representations. IEEE.

Krafka, K., Khosla, A., Kellnhofer, P., Kannan, H., Bhan-

darkar, S., Matusik, W., and Torralba, A. (2016). Eye

tracking for everyone. In International Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 2176–2184. IEEE.

Lee, K., Jeon, J., and Song, B. (2020). Deep learning-based

pupil center detection for fast and accurate eye track-

ing system. In European Conference on Computer Vi-

sion (ECCV), pages 36–52. Springer.

DeepPupil Net: Deep Residual Network for Precise Pupil Center Localization

303

Levinshtein, A., Phung, E., and Aarabi, P. (2018). Hybrid

eye center localization using cascaded regression and

hand-crafted model ﬁtting. Image and Vision Comput-

ing, 71.

Li, B. and Fu, H. (2018). Real time eye detector with cas-

caded convolutional neural networks. Applied Com-

putational Intelligence and Soft Computing.

Loy, G. and Zelinsky, A. (2003). Fast radial symmetry for

detecting points of interest. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 25:959–973.

Milborrow, S., Morkel, J., and Nicolls, F. (2010). The muct

landmarked face database. Pattern recognition asso-

ciation of South Africa, 201.

Niu, Z., Shan, S., Yan, S., Chen, X., and Gao, W. (2006).

2d cascaded adaboost for eye localization. In Interna-

tional Conference on Pattern Recognition. IEEE.

Poulopoulos, N. and Psarakis, E. Z. (2017). A new high pre-

cision eye center localization technique. In IEEE In-

ternational Conference on Image Processing (ICIP),

pages 2806–2810. IEEE.

Poulopoulos, N. and Psarakis, E. Z. (2018). Real time

eye localization and tracking. In 27th International

Conference on Robotics in Alpe-Adria Danube Region

(RAAD), pages 560–571. Springer.

Poulopoulos, N., Psarakis, E. Z., and Kosmopoulos, D.

(2021). Pupiltan: A few-shot adversarial pupil local-

izer. In International Conference on Computer Vision

and Pattern Recognition Workshops (CVPRW), pages

3128–3136. IEEE.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-

net: Convolutional networks for biomedical image

segmentation. In International Conference MICCAI,

pages 234–241. Springer.

Skodras, E. and Fakotakis, N. (2015). Precise localization

of eye centers in low resolution color images. Image

and Vision Computing Journal, Elsevier, 12:537–543.

Timm, F. and Barth, E. (2011). Accurate eye centre lo-

calization by means of gradients. In VISAPP, pages

125–130.

Valenti, R. and Gevers, T. (2008). Accurate eye center lo-

cation and tracking using isophote curvature. In Inter-

national Conference on Computer Vision and Pattern

Recognition (CVPR’08), pages 1–8. IEEE.

Villanueva, A., Ponz, V., Sesma-Sanchez, L., Ariz, M.,

Porta, S., and Cabeza, R. (2013). Hybrid method

based on topography for robust detection of iris cen-

ter and eye corners. ACM Transactions on Multimedia

Computing, Communications and Applications, 9.

Wang, Z., Cai, H., and Liu, H. (2018). Robust eye center

localization based on an improved svr method. In Int.

Conf. on Neural Information Processing, pages 623–

634. Springer.

Xia, Y., Yu, H., and Wang, F. (2019). Accurate and ro-

bust eye center localization via fully convolutional

networks. IEEE/CAA Journal of Automatica Sinica,

6:1127–1138.

Xiao, F., Huang, K., Qiu, Y., and Shen, H. (2018). Ac-

curate iris center localization method using facial

landmark, snakuscule, circle ﬁtting and binary con-

nected component. Multimedia Tools and Applica-

tions, 77:25333–25353.

Yang, P., Du, B., Shan, S., and Gao, W. (2004). A novel

pupil localization method based on gaboreye model

and radial symmetry operator. In International Con-

ference on Image Processing (ICIP’04), pages 67–70.

IEEE.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

304