
Segmentation Improves 3D Object Classification in Graph Convolutional
Networks
Clara Holzh
¨
uter
a
, Florian Teich
b
and Florentin W
¨
org
¨
otter
c
III. Physikalisches Institut, Georg-August University, Friedrich-Hundt Platz 1, G
¨
ottingen, Germany
Keywords:
3D, Computer Vision, Classification, Point Clouds, Segmentation, Graph Convolution.
Abstract:
3D object classification is involved in many computer vision pipelines such as autonomous driving or robotics.
However, the irregular format of 3D data makes it challenging to develop suitable deep learning architectures.
This paper proposes CompointNet, a graph convolutional network architecture, which performs 3D object
classification by means of part decomposition. Our model consumes a 3D point cloud in the form of a part
graph which is constructed from segmented 3D shapes. The model learns a global descriptor by hierarchically
aggregating neighbourhood information using simple graph convolutions. To capture both local and global
information, a global classification method processing each point separately is combined with our part graph
based approach into a hybrid version of CompointNet. We compare our approach to several state-of-the art
methods and demonstrate competitive performance. Particularly, in terms of per class accuracy, our hybrid
approach outperforms the compared methods. The proposed hybrid variants achieve a high classification
accuracy, while being much more efficient than those benchmark models with a comparable performance.
The conducted experiments show that part based approaches levering structural information about a 3D object,
indeed, can improve the classification performance of 3D deep learning models.
1 INTRODUCTION
Computer Vision applications are more prevalent in
our everyday lives than ever before. From Vir-
tual Reality applications (Kharroubi et al., 2019) on
our smartphones to Just-Walk-Out-Shopping (Pfeiffer
et al., 2020) and autonomous driving (Arnold et al.,
2019), Computer Vision is aiming to improve our
quality of life in multiple aspects. 3D object clas-
sification is an essential ingredient to various of the
mentioned pipelines. In many of these systems, ap-
proaches are required to categorize the perceived ob-
jects in order to interact with them. With increasing
3D scanner quality as well as decreasing hardware
prices, 3D data becomes more abundant and easier
to access (Mart
´
ınez et al., 2015; Straub and Kerlin,
2014). However, as 3D data is more complex than
traditional 2D image data, specialized approaches
are necessary to realize classification pipelines on
this input modality. Most popular representations
for 3D data nowadays include voxels, point clouds,
a
https://orcid.org/0000-0001-8365-5544
b
https://orcid.org/0000-0001-6708-7233
c
https://orcid.org/0000-0001-8206-9738
meshes or implicit surfaces. Many of the current
3D classification methods can be categorized into two
archetypes: global 3D classification such as PointNet
(Qi et al., 2017a), where each point of the point cloud
is processed individually, not considering its neigh-
borhood. Subsequently, in these global methods, in-
formation from all entities is aggregated by primi-
tive operations such as sum or max. This aggrega-
tion behaviour may thus neglect local information and
therefore does not fully acknowledge that an objects’
surface varies locally. The second archetype of 3D
classification methods are more advanced approaches
such as PointNet++ (Qi et al., 2017b) that work with
grouping or clustering of input entities in order to
hierarchically create the shape descriptor and subse-
quently classify the overall object. However, these
methods are typically using very primitive clustering
mechanisms which do not fully leverage the under-
lying shape topology. A side effect of all these ap-
proaches is that when faced with out-of-distribution
samples, correct class prediction becomes challeng-
ing: if the methods are only trained on e.g. mugs with
one handle and at evaluation, a mug with four han-
dles is queried, many methods may confuse the shape
with instances of other object classes. On the other
290
Holzhüter, C., Teich, F. and Wörgötter, F.
Segmentation Improves 3D Object Classification in Graph Convolutional Networks.
DOI: 10.5220/0010778100003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
290-298
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Four object point clouds and their part instance segmentation. The part graphs are displayed on the bottom left
corner of each image. The red node in the the leftmost image corresponds to an occluded leg of the chair and the green node
in the middle right figure indicates the almost fully occluded leg of the table. The node features are learned from the part’s
point cloud representations.
hand, when parts of an object are occluded, current
approaches may again misclassify the object in ques-
tion.
In this work, we are proposing a bottom-up clas-
sification approach by means of part decomposi-
tion. The approach is inspired by the Recognition-by-
components theory developed by (Biederman, 1987).
It states that humans recognize objects as an assembly
of their parts. Based on the object’s components and
their arrangement, humans are able to identify its cat-
egory. In this paper, we are exploring the possibility
of using segmentation information about the objects
in order to create part-graphs. Leveraging these part-
graphs has two theoretical advantages. First, shape
variance across a single part is usually lower than
across the entire object. Second, using graph sim-
ilarity methods, objects with redundant or occluded
parts may be easier to predict correctly based on their
part-graphs compared to global approaches. More im-
portantly, we are trying to identify the potential of
such bottom-up approach by means of ground-truth
segmentation. For the part graph classification, we
are employing Graph Convolutional Neural Networks
(GCNs).
The rest of the paper is structured as follows:
Chapter 2 provides overview on current 3D classi-
fication approaches, in Chapter 3 the classification
pipeline and its components are explained in more de-
tail. Chapter 4 describes multiple setups to test differ-
ent part based 3D pointcloud classifiers. The results
are presented in Chapter 5. Chapter 6 summarizes the
overall results and discusses possible improvements
for future extensions of the presented method.
2 RELATED WORK
Approaches to 3D object classification can be divided
into two categories: traditional, hand-engineered fea-
ture extraction and subsequent classification thereof
and end-to-end classification pipelines via deep learn-
ing.
The first of these two categories is often em-
ployed in robotics applications or embedded devices
that have limited resources. As a first step, the input
object, i.e. the point cloud is passed into an extrac-
tion module that collects statistics on predefined fea-
tures such as angle between triplets of points from the
cloud, distance between points of the clouds, etc. This
information is discretized into histograms, resulting
in a descriptor for each queried object. Subsequently,
these descriptors are passed to the final classifier (of-
ten SVM or MLP) that is trained on this data and -
during evaluation - is able to predict the target class
of a queried point cloud, based on its extracted fea-
ture descriptor.
For methods of the second category, i.e. deep
learning classifiers, the extracted features are usually
learned implicitly from the training data. In 2015,
VoxNet (Maturana and Scherer, 2015) pushed the ca-
pabilities of such 3D classifiers to new limits with its
CNN architecture that uses a voxelized representation
of the 3D object as input. This CNN design was in-
spired by architectures that proved to be successful
in 2D classification tasks (Krizhevsky et al., 2017)
and could directly be adopted to the 3D scenario -
thanks to the discrete input modality. However, dis-
cretizing the input space leads to the neglection of de-
tails. Sparse and very big input objects which need
to be stored, lead to a high computational cost in-
side the architecture itself, which, in turn, results in
long training and evaluation times. The widely em-
ployed PointNet (Qi et al., 2017a) architecture en-
abled classification on point clouds sampled from the
objects surface. The key of their approach is to utilize
a symmetric function in order to tackle the permu-
tation problem: the network’s output should not de-
pend on the order of the points inside the input cloud.
Segmentation Improves 3D Object Classification in Graph Convolutional Networks
291

By using an MLP with shared weights for all points,
PointNet extracts a high dimensional feature vector
from each point individually. The global aggregation
method (max-operator) then reduces these features to
a single global shape descriptor which is in turn fed
into the classification head (MLP). Similar to Point-
Net, Momen
e
t (Joseph-Rivlin et al., 2019) is based on
MLP layers and max pooling as well, but as a key ad-
vantage it augments the point coordinates using sim-
ple polynomial functions. The products are concate-
nated to the original point features before the features
are passed to a classification MLP. Successors to the
PointNet method started to incorporate the concept of
locality into the pipeline. By grouping points (e.g. us-
ing kNN) and evaluating PointNet on each of these
clusters, PointNet++ (Qi et al., 2017b) manages to
create a hierarchy of point clusters that ultimately su-
perseded PointNet on several classification datasets.
However, PointNet++’s notion of clusters has no se-
mantic base but is just a spatial aggregation of points
at arbitrary regions inside the 3D object. Another
architecture exploring local regions is PointCNN (Li
et al., 2018), which applies discrete convolutions. The
convolutional layer identifies the neighbourhood of a
point using kNN and subtracts the coordinates of the
target point from each of its neighbours to store their
relative positions. Subsequently, an MLP learns high
level features for each point in the local region and
concatenates these feature to the original ones. To
weight and permute the features into a more canonical
order a so-called χ-transformation is applied, which
is implemented using an MLP. Afterwards, a standard
convolution can be applied. Similar to PointNet++,
Sim2Real (Weibel et al., 2019) developed a Graph
Neural Network (GNN) (Kipf and Welling, 2016) that
segments query objects into eight fixed regions that
are then evaluated by a PointNet architecture. Re-
sults of the eight parts are later aggregated and lever-
aged for the final class prediction. Again, this method
neglects high-level part-boundaries as the segmenta-
tion method that is employed often results in segments
that do not contain specific semantic meaning. Never-
theless, these segment based approaches demonstrate
that considering part-wise point clusters of the in-
put may boost classification performance compared
to point-wise methods. In contrast to these methods,
we focus on semantically meaningful segmentation.
Another approach is to represent a point cloud as
a graph, in which each node corresponds to one 3D
point and adjacency is determined by the point’s dis-
tance. A graph convolutional method, which aims to
improve PointNet is the so-called kernel correlation
proposed by (Shen et al., 2018). Similar to a convo-
lutional filter in 2D, a set of learnable points serves as
kernel to apply it to a local region of the kNN graph of
a 3D shape. The similarity of the kernel and the input
is measured by a Gaussian kernel such that regions,
which are similar to the kernel point set produce high
activations. The activations within a certain neigh-
bourhood are aggregated using max pooling. Another
popular kNN graph based method is DGCNN (Wang
et al., 2019), which enables non-local information dif-
fusion via a changing graph topology during the for-
ward pass. It performs edge convolutions, which learn
features for a target node by applying an MLP to all
edges originating from that node and aggregating the
computed features. Initial edge features are computed
from the input points using an MLP. After each con-
volutional layer, the kNN graph is updated such that
each node can have a new set of neighbours in the next
layer. A GNN based on mathematically substantiated
rotation invariance is ClusterNet (Chen et al., 2019),
which defines a representation of a point cloud that
contains all relevant information except the rotation
of the 3D object such that the output for a point cloud
and its rotated version are the same. The mapping is
determined by the norm of a point and its neighbours
and several properties defined by the angle between a
point and its neighbours. This representation is used
to encode the node of a kNN graph of the point cloud,
which can be processed using an MLP. The neigh-
bourhood of a target point is aggregated using max
pooling. To reduce the dimension of the point cloud
and merge clusters in order to obtain a global feature
descriptor in the end, agglomerative hierarchical clus-
tering is applied. Additionally, similar to DGCNN,
MLPs are used to extract edge features. However, in-
stead of the difference between points the above de-
scribed rotation invariant mapping is used.
Recently, several transformer methods such as
(Zhao et al., 2020) and (Guo et al., 2021) have been
proposed. These methods are applied on a sequence
of points and learn relationships between these points
using a self attention mechanism, which estimates the
importance of one point to another. As self attention
mechanisms operate on an input set, they can deal
with the unorderedness of point clouds. The layers
of the Point Transformer classification network (Zhao
et al., 2020) perform self-attention on a local neigh-
bourhood of a 3D point in a vectorized manner. To
encode the location of a 3D point, an MLP learns a
position embedding which is added to the transformed
input feature and the learned attention vectors. To re-
duce the dimension of the point cloud during the for-
ward pass, max pooling within a spatial region is ap-
plied (Zhao et al., 2020). In (Guo et al., 2021) the
input point clouds are transformed to a higher dimen-
sional feature space and passed to several attention
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
292

modules, which are based on MLPs. Features are
computed as the matrix product of the input features
and the computed attention values. Before applying
an MLP to obtain class scores, the authors perform
offset attention, which refers to subtracting the input
feature from the self-attended features.
3 METHODS
3.1 Overview
This paper proposes CompointNet, a bottom-up clas-
sification method for 3D objects based on part graphs,
which are constructed from 3D objects segmented
into their components. Each component of an object
serves as a node in the part graph. Examples for 3D
objects and their corresponding part graphs are shown
in Figure 1. In order to classify 3D shapes Com-
pointNet learns a global representation from their part
graphs in a bottom-up manner. Two basic variants of
CompointNet have been developed, one is based on
the 1-WL proposed by (Morris et al., 2019) and the
other applies the graph attention layer presented in
(Veli
ˇ
ckovi
´
c et al., 2018). To learn a more robust latent
representation, which fuses local and global informa-
tion, two extensions of CompointNet are proposed.
They combine a global Pointnet approach with the
GAT and WL based CompointNet respectively, such
that each input shape is processed by both, the global
and the local model, in parallel. The vector repre-
sentation computed by both methods are concatenated
and further processed to produce a latent representa-
tion from which the final class scores can be inferred.
3.2 Feature Extraction and Part Graph
Construction
The part graph for a 3D object is constructed using
k-nearest neighbour and requires a point cloud seg-
mented into its components. Each node of the part
graph represents a component of the 3D shape and
an edge between two nodes indicates that the corre-
sponding object parts are spatially connected. This
connectivity identified by searching for neighbouring
points with different segmentation labels using kNN.
The resulting part graph is undirected and does not
contain edge labels. Each node comprises a feature
representation, which describes the corresponding ob-
ject part. For this purpose, a PointNet model is ap-
plied to the 3D coordinates of each component to pro-
duce per-node features.
3.3 Part Graph Learning using a GCN
Architecture
To learn a global representation from which the ob-
ject classes can be inferred, two different Compoint-
Net variants have been developed. The simpler vari-
ant is based on the 1-WL layer proposed by (Morris
et al., 2019), which aggregates the neighbourhood of
a node in a learnable way. The hidden representation
h
0
i
of node i is computed as:
h
0
i
= σ(W
1
h
i
+W
2
∑
j∈N(i)
h
j
), (1)
where h
i
is the feature vector of node i, W
1
and W
2
are learnable weights and N(i) is the neighbourhood
of node i. σ refers to a non-linear activation func-
tion. Several of these layers sequentially applied
to an input graph define a convolutional neural net-
work architecture, which (Morris et al., 2019) refer
to as 1-GNN. It implements a basic message pass-
ing scheme, in which a node aggregates the informa-
tion of its neighbours. This way information is propa-
gated across the part graph across the edges. The WL
based CompointNet sequentially applies three convo-
lutional blocks consisting of several WL layers de-
scribed above. The hidden representation computed
by each block are concatenated and further processed
by a set of fully connected layers with softmax acti-
vation in the end.
The other version of CompointNet is based on the
graph attention layer proposed by (Veli
ˇ
ckovi
´
c et al.,
2018). The proposed layer computes the hidden rep-
resentation of a target node as the weighted sum of the
features of its neighbours including itself. For each
target node an attention mechanism assigns attention
coefficients to the adjacent nodes to aggregate their
information based on the importance of each node to
the target node. The coefficient e
i j
for a pair of nodes
i and j is computed as follows:
e
i j
= a(W h
i
, W h
j
) = a
T
[W h
i
kW h
j
], (2)
where h
i
and h
j
correspond to the features of node i
and j respectively. W is a weight matrix and k refers
to the concatenation operation. e
i j
is only computed if
node i and node j are adjacent. The attention mecha-
nism is implemented as multiplication with the learn-
able weight vector a and the coefficients are normal-
ized using a softmax function. The hidden represen-
tation h
0
i
of a target node i is computed as
h
0
i
= σ(
∑
j∈N
i
α
i j
W h
j
). (3)
σ refers to a non-linear activation function applied
to the linear combination of the neighbour of target
Segmentation Improves 3D Object Classification in Graph Convolutional Networks
293

5 1 2 x n p
1 2 8
1 2 8
P o i n t n e t
P o i n t n e t
M L P
M L P
K N N
G l o b a l P o o l
3 x n
3 2 * 8 x n p
1 2 8 x n p 1 2 8 x n p
n c l a s s e s
P a r t f e a t u r e s
P o i n t
c o o r d i n a t e s
G A T
6 4 x n p
6 4 x n p
1 2 8 x n p
6 4 x n p
6 4 x n p
6 4 x n p
6 4 x n p
W L - A l t e r n a t i v e t o G AT
2 5 6
C o n c a t e n a t e
D r o p o u t
C o n v
E L U
B a t c h n o r m
Figure 2: Hybrid CompointNet Architecture using graph attention. The input point cloud is passed to a PointNet architecture
as raw 3D coordinates (lower branch). The corresponding part graph is constructed using kNN, and node features are extracted
from the point cloud of each part using a PointNet model. Subsequently, the graph based GCN (GAT) followed by an MLP is
applied to the part graphs (upper branch). In the end the learned representations are combined using another MLP. The GAT
based GCN can be replaced with the WL based GCN shown on the right.
node i. Accordingly, the feature of a target is com-
puted by summing the transformed features of adja-
cent nodes, which are weighted according to their im-
portance to the target node. To increase the model’s
capacity, (Veli
ˇ
ckovi
´
c et al., 2018) further introduce
multi-head attention, which separately applies several
attention mechanism in the same layer and concate-
nates the resulting feature representations. The cor-
responding variant of CompointNet sequentially ap-
plies a set of GAT layers with multi head attention,
of which the last layer computes only one attention
head. The obtained feature vector is passed to a set of
fully connected layers for final classification.
3.4 Combining Local and Global
Features
Both variants of CompointNet are extended to a hy-
brid version, which combines the above described lo-
cal CompointNet with the global MLP based method
PointNet. The resulting architecture fuses local in-
formation extracted from the part graphs with global
information obtained by individually processing each
point of the entire shape by a PointNet model. The
network is composed of two branches, which are
combined in the end. The PointNet based branch
takes the entire point cloud as input and produces a
feature vector, whilst the part graph based methods
learns a representation from the corresponding part
graph. Both representations are concatenated and fur-
ther transformed an MLP to predict the class scores.
The architecture is shown in Figure 2. The hybrid
CompointNet extends the strictly part graph based
version by the information about the rough overall
input shape learned from the keypoints extracted by
PointNet.
4 EXPERIMENTS
The proposed classification methods are applied to the
PartNet dataset (Mo et al., 2019), which comprises
about 27 000 distinct three-dimensional CAD mod-
els of 24 different object categories. PartNet provides
different levels of segmentation granularity, of which
the most fine-grained one is used in the conducted ex-
periments. To process the 3D objects of PartNet, only
few preprocessing is required and no data augmenta-
tion is applied. As input to all models 1024 points
are dynamically sampled from the point cloud during
training and the entire shape is normalized into a unit
sphere. The performance of the proposed methods is
evaluated using 5-fold cross validation using the en-
tire PartNet dataset.
The configuration of the PointNet model, which
computes the node feature for each component of a
3D shape follows the configuration proposed by the
authors of PointNet with the alteration that the last
two fully connected layers are removed. The resulting
feature vector has a size of 512.
The WL based CompointNet consists of three
convolutional blocks and the output of each block
serves as input to the next block to increase the re-
ceptive field with increasing network depth. In the
first block three convolutional layers transform the
node features of the part graphs from size 512 to 64
via three convolutional layers. The next two convo-
lutional blocks consist of two convolutional layers of
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
294
output size 64. Each of the layers applies ELU ac-
tivation and Layernorm and before each convolution
block dropout with a probability of 0.5 is applied. To
aggregate the per node features global pooling is ap-
plied on the output of the three convolutional blocks
to obtain one vector per graph and per block. The re-
sulting feature representation, accordingly, consists of
three concatenated vector of size 64 produced by the
three convolutional blocks.
In the GAT based CompointNet two subsequent
GAT layers are applied to the part graphs, of which
the first layer computes eight attention heads of 32
features each and the second a single attention head
with 128 features. In both layers attention coefficients
are dropped out with a probability of 0.5. ELU is used
as non-linear activation and Layernorm is applied af-
ter each convolutional layer. The output of the GAT
layers is a vector of size 128 per node, which is mean
pooled into a single feature vector per graph. Deeper
versions of both GCNs with more convolutional lay-
ers have been tested without significant performance
improvements, therefore only the configurations de-
scribed above are considered here.
The obtained feature representations for both vari-
ants and passed to a three-layer MLP with ELU acti-
vation and Layernorm and a log softmax activation in
the end to make the final class predictions.
The GCN applied in the hybrid CompointNet
models are configured as described above except that
the fully connected layers, which are applied in the
end, are removed. The PointNet model integrated into
the hybrid CompointNet is configured as described
in the corresponding paper with the alteration that
the last three fully connected layers are removed as
well. The feature representation obtained by the two
branches are concatenated and passed to three-layer
MLP equally to the non-hybrid variants.
The training procedure for all proposed variants of
CompointNet includes a validation set, which com-
prises 20% of the training data to monitor the valida-
tion error and accuracy. Based on that, early stopping
with terminates the training if the overall validation
accuracy did not increase within the last 15 epochs.
The models are optimized on the negative log likeli-
hood loss using Adam with a learning rate of 0.001.
Every second epochs the learning rate is decayed to
0.9 of its original value. The training is performed on
GPU with a batch size of eight.
5 RESULTS
We compare our model to four benchmark methods:
Vanilla PointNet (Qi et al., 2017a), PointNet++ (Qi
et al., 2017b) and two very recent transformer meth-
ods, which are PCT: Point Cloud Transformer (Guo
et al., 2021) and Point Transformer (Zhao et al., 2020)
described in section 2. The implementation of Point-
Net is provided by (Xia, 2017), which is referred to
by the authors of PointNet. PointNet++ is provided
by Pytorch Geometric and the transformer methods
have been implemented by (You, 2021).
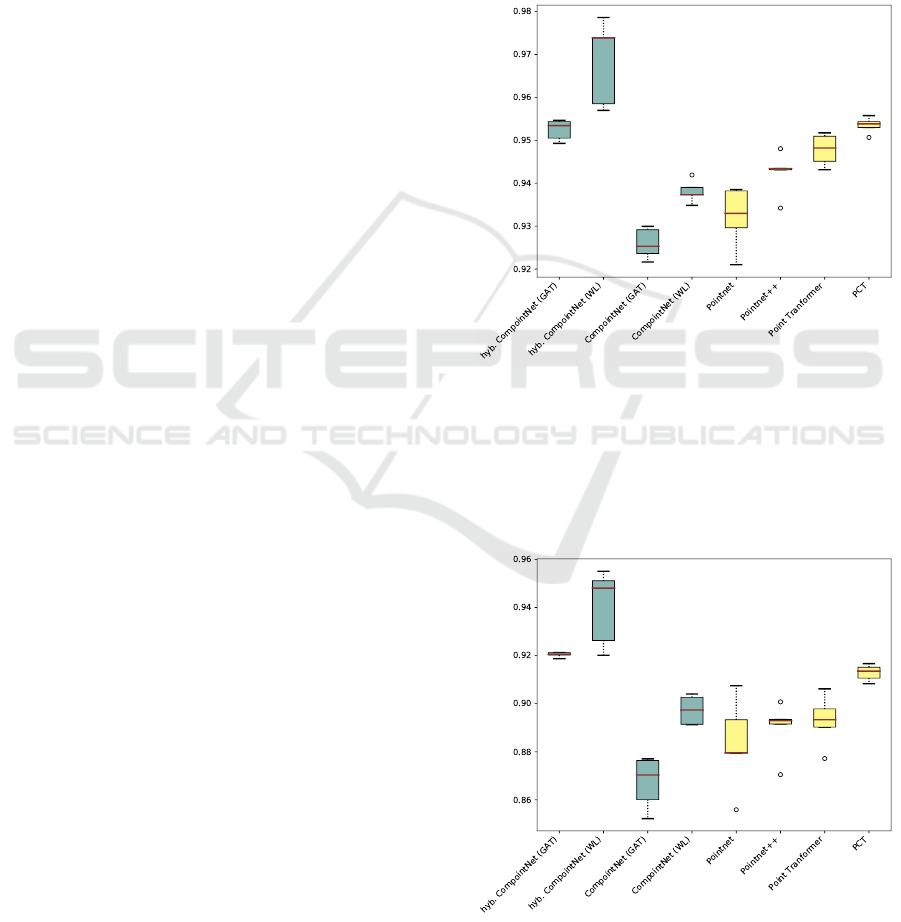
Figure 3 shows a boxplot of the mean overall
accuracy across the different folds for our different
CompointNet variants and the benchmark models. It
Figure 3: Overall Accuracy on PartNet. The hybrid ver-
sions of CompointNet perform consistently well, whereas
the non-hybrid variants reach lower accuracies. PointNet++
performs better than PointNet, however it does not achieve
the accuracy of the hybrid CompointNet. The transformer
methods (right) outperform the PointNet methods and the
non-hybrid variants of CompointNet, but cannot keep up
with the hybrid WL based CompointNet.
Figure 4: Average Class Accuracy on PartNet. The hybrid
variants of CompointNet consistently outperform the com-
pared methods.
Segmentation Improves 3D Object Classification in Graph Convolutional Networks
295

Figure 5: Overall accuracy of our approach vs. number of nodes in the part graph of an object. Different colors indicate the
amount of test samples with n nodes. The darker the color the higher the number of objects with that amount of nodes. The
red line indicates the mean accuracy.
Table 1: Classification results on PartNet. Our approach
achieves state-of-the-art performance. The hybrid WL
based CompointNet outperforms all other compared meth-
ods in terms of average per class and overall accuracy.
Model overall per class
GAT CompointNet 0.93 0.88
WL CompointNet 0.94 0.90
Hybrid GAT CompointNet 0.95 0.92
Hybrid WL CompointNet 0.97 0.94
PointNet(Qi et al., 2017a) 0.93 0.88
PointNet++(Qi et al., 2017b) 0.94 0.89
PCT(Guo et al., 2021) 0.95 0.91
Point Transformer (Zhao et al., 2020) 0.95 0.90
can be observed that our approach achieves com-
petitive performance among the benchmark architec-
tures. Amongst the variants of CompointNet, the
hybrid methods perform significantly better than the
strictly part-graph based models, particularly the WL
based hybrid CompointNet achieves a high accuracy
of 97% on the test dataset. It outperforms Point-
Net and PointNet++ by 3% and 4% respectively and
achieves a 2% improvement over the transformer ar-
chitectures. In general the WL based variants achieve
higher accuracy than the GAT based models, however
the GAT based hybrid model has significantly fewer
variation across different cross validation runs simi-
lar to the transformer based approaches. The average
per class accuracy shown in Figure 4 indicates that
our approach does not only perform well on frequent
classes, but is able to generalize to new objects of
classes with fewer training data as well. Both hybrid
versions of CompointNet outperform all compared
methods and also the non-hybrid WL based Com-
pointNet can keep up with the PointNet models and
PCT in terms of per class accuracy. The GAT based
CompointNet reaches the same per class accuracy as
PointNet. Since the PartNet dataset is very unbal-
anced, the per class accuracy is of particular impor-
tance. Thus, the improvement of 3% and 4% achieved
by the hybrid WL based CompointNet models over
the two compared transformer methods is a promis-
ing result. The exact performance in terms of overall
accuracy and average per class accuracy is shown is
Table 1. Extending the part-graph based model by
including global information using a PointNet archi-
tecture enhances the performance of both, the GAT
based and the WL based model.
Figure 5 illustrates the overall accuracy across
objects with a certain number of nodes. It can be
observed that the hybrid models improves the pure
part graph based models, particularly for objects with
more nodes, i.e. more complex objects. The reason
might be that many nodes usually imply a fine-grained
segmentation into tiny parts, which might be more
difficult to detect for the GCN, since finer segmen-
tation tends to result in geometrically more similar
parts. Additionally, the information diffusion across
the graph is limited locally by the number of convo-
lutional layers in the GCN. Thus, for large graphs the
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
296

0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07
Inference Time in seconds
Pointnet
Pointnet++
PT
PCT
Hybrid GAT
CompointNet
Hybrid WL
CompointNet
GAT
CompointNet
WL
CompointNet
Figure 6: Inference times of our approach and the com-
pared models. The inference times are averaged over the
full PartNet dataset using a batch size of one.
neighbourhood of a node covered by the GCN is small
compared to the size of the graph. This might affect
the performance of CompointNet on larger graphs. As
indicated by the colors a large fraction of objects is
composed of less than 30 nodes. Accordingly, the hy-
brid approach can improve the accuracy of Compoint-
Net on graph classes that are rather rare.
Figure 6 shows the inference times of the vari-
ants of our approach and the compared approaches.
PointNet is by far the fastest method, while Point-
Net++ and the CompointNet models show similar in-
ference times. The transformer methods are drasti-
cally slower. Accordingly, their superior performance
over the PointNet models comes with a significant in-
crease of computational complexity. This does not
apply for our models, which are much more effi-
cient than the transformer methods. Even the hybrid
approach, which show equal or better performance
than the transformer methods are significantly faster.
Since PointNet is included as feature extractor in each
part graph based model, it is clear that our approach
cannot keep up with the inference time of PointNet.
However, the computational complexity of the strictly
part graph based CompointNet is lower than for Point-
Net++. The hybrid versions of CompointNet require
a similar amount of time for the forward pass despite
the per part feature extraction and the global shape
processing, both performed separately using a Point-
Net model. The GCN applied in our approach ac-
counts only for a small fraction of the inference time,
since the per part feature extraction requires one for-
ward pass through the PointNet model for each part.
6 CONCLUSION
This paper investigates the potential of a part graph
based bottom-up approach to improve the classifica-
tion of 3D objects by means of ground truth segmen-
tation. It could be applicable for 3D search engines
or for cataloging of CAD models to improve their
accuracy and robustness. The proposed architecture
variants of CompointNet successfully leverage part
decomposition of 3D objects to learn local 3D fea-
tures using two different graph convolutional network
architectures. Particularly, the hybrid approach inte-
grating both, a global approach and a part graph based
approach in parallel, achieves state-of-the art results.
The experiments have shown that a very basic GCN,
which computes node features as the sum over adja-
cent nodes multiplied with a learnable weight matrix,
is sufficient to learn high-level features for object clas-
sification. It even outperforms the more sophisticated
GAT based GCN. The hybrid methods outperform
Vanilla PointNet and PointNet++ and can keep up
with the compared transformer architectures. In the
conducted experiments the hybrid WL based Com-
pointNet even outperforms the transformer methods,
while being much more efficient. The hybrid models
achieved the highest per class accuracy amongst all
compared architecture, which is of particular impor-
tance for unbalanced datasets such as PartNet. The
proposed models leverage that the variation across
a single part is usually lower than across the entire
object, which is expected to make the application of
PointNet as feature extractor more effective. Further-
more, using GCN to extract 3D features makes use of
the structure of an object, which is a theoretical ad-
vantage compared to global approaches. The applica-
tion of CompointNet on automatic instead of ground
truth segmentation to further investigate the poten-
tial of such bottom-up approaches is left for future
work. To enable CompointNet to capture non-local
relationships between object components, the integra-
tion of deeper GCNs should be further investigated
to enhance the performance of the strictly part graph
based models on larger graphs. Furthermore, different
approaches for the per part feature extraction could
be explored to accelerate this task. By replacing the
PointNet model by a hand-engineered feature extrac-
tion, the inference time would be reduced drastically.
This might open up new application opportunities. Fi-
nally, the WL based CompointNet, which applies a
so-called 1-GNN proposed by (Morris et al., 2019),
could instead apply their 2- or 3-GNN, which operates
on k-sets of nodes instead of single nodes. This might
lead to further improvements regarding the classifica-
tion performance.
Segmentation Improves 3D Object Classification in Graph Convolutional Networks
297

REFERENCES
Arnold, E., Al-Jarrah, O. Y., Dianati, M., Fallah, S., Ox-
toby, D., and Mouzakitis, A. (2019). A survey on
3d object detection methods for autonomous driving
applications. IEEE Transactions on Intelligent Trans-
portation Systems, 20(10):3782–3795.
Biederman, I. (1987). Recognition-by-components: A the-
ory of human image understanding. Psychological Re-
view, 94(2):115–147.
Chen, C., Li, G., Xu, R., Chen, T., Wang, M., and Lin, L.
(2019). ClusterNet: Deep Hierarchical Cluster Net-
work With Rigorously Rotation-Invariant Represen-
tation for Point Cloud Analysis. In 2019 IEEE/CVF
Conference on Computer Vision and Pattern Recog-
nition (CVPR), pages 4989–4997, Long Beach, CA,
USA. IEEE.
Guo, M.-H., Cai, J.-X., Liu, Z.-N., Mu, T.-J., Martin, R. R.,
and Hu, S.-M. (2021). PCT: Point cloud transformer.
Computational Visual Media, 7(2):187–199.
Joseph-Rivlin, M., Zvirin, A., and Kimmel, R. (2019).
Momen
e
t: Flavor the Moments in Learning to Clas-
sify Shapes. In 2019 IEEE/CVF International Confer-
ence on Computer Vision Workshop (ICCVW), pages
4085–4094, Seoul, Korea (South). IEEE.
Kharroubi, A., Hajji, R., Billen, R., and Poux, F. (2019).
Classification and integration of massive 3d points
clouds in a virtual reality (vr) environment. Interna-
tional Archives of the Photogrammetry, Remote Sens-
ing and Spatial Information Sciences, 42(W17):165–
171.
Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-
sification with graph convolutional networks. arXiv
preprint arXiv:1609.02907.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). Im-
agenet classification with deep convolutional neural
networks. Commun. ACM, 60(6):84–90.
Li, Y., Bu, R., Sun, M., Wu, W., Di, X., and Chen,
B. (2018). Pointcnn: Convolution on x-transformed
points. In Proceedings of the 32nd International Con-
ference on Neural Information Processing Systems,
NIPS’18, page 828–838, Red Hook, NY, USA. Cur-
ran Associates Inc.
Mart
´
ınez, J. L., Morales, J., Reina, A. J., Mandow, A.,
Pequeno-Boter, A., and Garc
´
ıa-Cerezo, A. (2015).
Construction and calibration of a low-cost 3d laser
scanner with 360 field of view for mobile robots.
In 2015 IEEE International Conference on Industrial
Technology (ICIT), pages 149–154. IEEE.
Maturana, D. and Scherer, S. (2015). Voxnet: A 3d convolu-
tional neural network for real-time object recognition.
In 2015 IEEE/RSJ International Conference on Intel-
ligent Robots and Systems (IROS), pages 922–928.
Mo, K., Zhu, S., Chang, A. X., Yi, L., Tripathi, S., Guibas,
L. J., and Su, H. (2019). PartNet: A large-scale bench-
mark for fine-grained and hierarchical part-level 3D
object understanding. In The IEEE Conference on
Computer Vision and Pattern Recognition (CVPR).
Morris, C., Ritzert, M., Fey, M., Hamilton, W. L., Lenssen,
J. E., Rattan, G., and Grohe, M. (2019). Weisfeiler
and Leman Go Neural: Higher-Order Graph Neural
Networks. Proceedings of the AAAI Conference on
Artificial Intelligence, 33(01):4602–4609.
Pfeiffer, J., Pfeiffer, T., Meißner, M., and Weiß, E.
(2020). Eye-tracking-based classification of informa-
tion search behavior using machine learning: evidence
from experiments in physical shops and virtual real-
ity shopping environments. Information Systems Re-
search, 31(3):675–691.
Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017a). Point-
net: Deep learning on point sets for 3d classification
and segmentation. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition,
pages 652–660.
Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017b). Point-
net++: Deep hierarchical feature learning on point sets
in a metric space. arXiv preprint arXiv:1706.02413.
Shen, Y., Feng, C., Yang, Y., and Tian, D. (2018). Mining
Point Cloud Local Structures by Kernel Correlation
and Graph Pooling. In 2018 IEEE/CVF Conference
on Computer Vision and Pattern Recognition, pages
4548–4557, Salt Lake City, UT. IEEE.
Straub, J. and Kerlin, S. (2014). Development of a large,
low-cost, instant 3d scanner. Technologies, 2(2):76–
95.
Veli
ˇ
ckovi
´
c, P., Cucurull, G., Casanova, A., Romero, A.,
Li
`
o, P., and Bengio, Y. (2018). Graph Attention Net-
works. International Conference on Learning Repre-
sentations.
Wang, Y., Sun, Y., Liu, Z., Sarma, S. E., Bronstein, M. M.,
and Solomon, J. M. (2019). Dynamic Graph CNN
for Learning on Point Clouds. ACM Transactions on
Graphics, 38(5):1–12.
Weibel, J.-B., Patten, T., and Vincze, M. (2019). Addressing
the sim2real gap in robotic 3-d object classification.
IEEE Robotics and Automation Letters, 5(2):407–413.
Xia, F. (2017). Pointnet.pytorch .
https://github.com/fxia22/pointnet.pytorch.
You, Y. (2021). Point-transformers .
https://github.com/qq456cvb/Point-Transformers.
Zhao, H., Jiang, L., Jia, J., Torr, P., and Koltun, V. (2020).
Point Transformer. arXiv:2012.09164 [cs]. arXiv:
2012.09164.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
298
