Neural Network PET Reconstruction using Scattered Data in

Energy-dependent Sinograms

Gabrielle Fontaine

, Peter Lindstrom

and Stephen Pistorius

1,2

Department of Physics and Astronomy, University of Manitoba, 30A Sifton Road, Winnipeg, MB R3T 2N2, Canada

CancerCare Manitoba Research Institute, 675 McDermot Ave, Winnipeg, MB R3E 0V9, Canada

Keywords: Positron Emission Tomography, Medical Imaging, Neural Network, Deep Learning, Scattered Coincidences,

Direct Reconstruction.

Abstract PET image reconstruction largely relies on pre-reconstruction data correction, which may add noise and

remove information. This loss is particularly notable when correcting for scattered coincidences, which are

useful for image reconstruction, though algorithmic scatter reconstructions require a detector energy

resolution that exceeds the current state-of-the-art. Preliminary research has demonstrated the feasibility of

using convolutional neural networks (CNNs) to reconstruct images directly from sinogram data. We have

extended this approach to reconstruct images from data containing scattered coincidences. Monte Carlo

simulations were performed to simulate PET data from digital phantoms. Data were modeled using 15%

FWHM energy resolution detectors. Energy-dependent sinograms (EDSs), containing true and scattered

coincidences, were constructed from the data. After data augmentation, 210,000 sinograms were obtained. A

CNN was trained on the EDS-activity pairs for image reconstruction. A second network was trained on

sinograms containing only photopeak coincidences. Images were also reconstructed using FBP, and MLEM

approaches. The EDS trained network outperformed the photopeak trained network, with a higher mean

structural similarity index (0.69 ± .05 vs. 0.63 ± .05) and lower average mean square error (0.16 ± .04 vs. 0.20

± .04). Our work demonstrates that CNNs have the potential to extract useful information from scattered

coincidences, even for data containing significant energy uncertainties.

1 INTRODUCTION

Typical positron emission tomography (PET) image

reconstruction techniques make corrections to the raw

data prior to image reconstruction. These include

corrections for dead time, attenuation, random and

scattered coincidences, and normalization. Such

corrections are imperfect. As such, they introduce

noise and can remove valuable data (Cherry, 2012;

Bai & Asma, 2016). The former is evident from the

decreased noise equivalent counting rate (NECR) that

results from scatter and random correction (Cherry,

2012, p. 340). Additionally, any alteration of the data

destroys its Poisson nature (Bai & Asma, 2016, p.

266).

Scattered coincidences, in particular, contain

information that is beneficial for image

reconstruction. Such information may increase

sensitivity due to a lower energy window threshold

(Conti et al., 2012), and when used in image

reconstruction, has been shown to improve contrast

recovery and decrease noise (Sun & Pistorius, 2013a,

2013b). Furthermore, scattered coincidences contain

information about the electron density of the

scattering medium, thereby allowing attenuation

maps to be estimated from scatter data (Berker et al.,

2014; Brusaferri et al., 2020; Sun et al., 2015).

To date, scatter reconstruction studies have

primarily focused on iterative approaches. These take

advantage of the physics of Compton scattering to

constrain annihilation positions to within areas or

volumes in a 2-D or 3-D image space. Both time-of-

flight (TOF) (Conti et al., 2012) and non-TOF (Conti

et al., 2012; Sun, 2016; Sun et al., 2015; Sun &

Pistorius, 2013a, 2013b) methods have been

implemented. Though most approaches have focused

on coincidences where only one photon is scattered,

it has also been demonstrated that even when both

photons are scattered, this is sufficient to constrain the

annihilation position (Sun, 2016).

In the absence of high-resolution TOF

information, detector energy resolution must be

Fontaine, G., Lindstrom, P. and Pistorius, S.

Neural Network PET Reconstruction using Scattered Data in Energy-dependent Sinograms.

DOI: 10.5220/0010782100003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 2: BIOIMAGING, pages 35-42

ISBN: 978-989-758-552-4; ISSN: 2184-4305

sufficient to extract useful spatial information (Conti

et al., 2012). Given current detector energy

resolutions, coincidence timing resolution (CTR)

values must be significantly better than 58-80ps,

which is challenging to achieve (Meikle et al., 2021,

p. 22).

1.1 Deep Learning in Image

Reconstruction

Deep-learning (DL) networks have been applied to

PET imaging. To date, most published studies focus

on networks working entirely in image-space, taking

as an input an image, and producing another image as

output. A common application is generating

attenuation-corrected (AC) PET images from non-

attenuation corrected (NAC) PET images (Dong et

al., 2019, 2020; Shiri et al., 2019). These approaches

do not make use of scatter. Another PET image-space

application is the so-called “super-resolution”

problem, wherein a network attempts to derive a high-

resolution image from a low-resolution one. Song et

al. (Song et al., 2020) provide a particularly thorough

example of this technique. Lastly, CNNs have been

employed to denoise images (Tian et al., 2019). A

comprehensive list of PET image-space studies can

be found in (Lee, 2021).

There is an alternative approach. So-called direct

reconstruction approaches perform a domain

transform to reconstruct images directly from binned

data. These typically employ convolutional neural

networks (CNNs). Compared to algorithmic or

combined algorithmic/DL approaches, certain

advantages are present. First, direct reconstruction is

generally simpler. Second, DL approaches offer a

possible solution to the ill-posedness of the PET

inverse problem (Bai & Asma, 2016, p. 269). This

solution takes the form of a non-linear filter that

approximates regularization or image smoothing and

is learned directly from the data. This may be thought

of as similar to maximum a-posteriori (MAP)

estimation where, from among images of similar

likelihood values, one is chosen that is most probable

given the prior (Bai & Asma, 2016, p. 270). As DL

approaches are data-driven, the prior may be

conceptualized as being learned implicitly from

thousands of training examples.

Another probable advantage of direct

reconstruction is the implicit incorporation of point-

spread functions (PSFs). For iterative reconstruction

methods, incorporating PSFs has been shown to

improve image quality (Tong et al., 2010). A DL

network may implicitly learn a spatially variant PSF

from the data, thereby improving image quality.

In earlier work on direct reconstruction

(Häggström et al., 2019; Liu et al., 2019; Zhu et al.,

2018), scatter was not employed. In the present

context, the primary advantage of using direct

reconstruction is—as we demonstrate—the ability of

CNNs to make use of low-energy resolution scatter

data to improve image quality.

2 METHODS

2.1 Simulation Parameters

Twelve XCAT digital phantoms (Segars et al., 2010)

were obtained, ranging in sex, weight, race and age.

Each phantom was modified ten times by varying the

activity uptake ratios, organ scaling and rotation,

yielding a total of 120 phantoms. From each phantom,

250 transverse slices were obtained, spaced every 3

mm. Thus, 30,000 2-D activity distributions (images)

were generated. Slice dimensions were 40 x 40 cm

(71 x 71 pixels).

Monte Carlo simulations were performed on the

XCAT phantoms. The Geant4 Application for

Tomographic Emission (GATE) (Jan et al., 2004) was

used to simulate positron emission and annihilation,

photon propagation, and detection of coincidences. A

three-dimensional cylindrical array of detectors was

created around the phantoms. The dimensions of the

crystal detectors were 3 mm x 3 mm x 20 mm. The

height and radius of the cylinder were set to 750 mm

and 150 mm, respectively, and the coincidence

window was set to 10 ns.

The GATE source code was modified so that

annihilation and scattered photon propagation were

constrained to within the transverse polar plane. As

this study focused on 2-D image reconstruction,

doing so reduced the number of photons that needed

to be simulated and thus reduced computation time.

Although the simulated acquisition was performed in

3D mode, constraining the photons had the effect of

simulating 2D acquisition.

The detector energy resolution was set to 15%

FWHM in order to represent realistic PET photon

detectors.

2.2 Data Acquisition

Data were recorded in list mode. Approximately 10

counts were recorded per slice. Scatter fractions ranged

from 30% to 50%, depending upon the size of the slice

(torso, head, etc.). Three bins were established

according to photon energy: 456 – 506 keV (bin 1), 478

– 528 keV (bin 2), and 486 – 536 keV (bin 3). Where,

BIOIMAGING 2022 - 9th International Conference on Bioimaging

for a single coincidence, both photon energies fell into

bin 1, the coincidence was assigned to bin 1. Where

one photon energy fell into bin 1, and the other fell into

bin 2, the coincidence was assigned to bin 2. Similarly,

where one photon energy fell into bin 1, and the other

fell into bin 3, the coincidence was assigned to bin 3.

Coincidences that could be placed into two bins, due to

the overlapping energy ranges, were placed into both.

Therefore, the binning of the data was accomplished

via a sliding window.

Coincidences in bin 1, centered about 511 keV,

were more likely true coincidences, relative to those

in bins 2 and 3. Coincidences in bin 2 were likely due

to a singly scattered coincidence. The likely scattered

photons in this bin had energies centered about 503

keV, which corresponds to a 10-degree Compton

scatter. Bin 3 had a central energy of 481 keV, which

corresponds to a 20-degree Compton scatter. The

binning of the data therefore structures it

approximately according to scattering angle, binning

coincidences mainly where only a single photon is

scattered, which constitute most scattered

coincidences (Conti et al., 2012). Due to the energy

uncertainty of the detectors, however, some

coincidences may have been improperly binned.

2.3 Sinogram Construction

Two categories of sinograms were constructed from

the binned data: energy-dependent sinograms (EDSs)

and photopeak sinograms. Photopeak sinograms were

created from bin 1 data only. To construct the EDSs,

individual sinograms were created from the data in

each bin and then combined into a single 3-D array

with dimensions s , ɸ and bin number, where s and ɸ

are the polar coordinates of a 2-D sinogram.

An attenuation correction that assumed that the

simulated phantoms were composed entirely of water

was performed for both types of sinograms. The

average total distance travelled in matter for the

photons in each scattered coincidence was calculated

for all possible singly scattered travel paths. Only the

section of each path which intersected with the

volume of the phantom counted towards the average.

This average distance, together with the Compton

cross-section for water, was used to calculate the

average attenuation coefficient for each scattered

coincidence. Future studies will take an attenuation

map as an additional input to the network to account

for variations in electron density.

As doubly scattered photons were confined to the

transaxial plane by the alteration to the GATE source

code, an attenuated coincidence (that is, one in which

more than one scatter event occurred) could still be

binned, so long as the scattered photon energy was

not below 456 keV (the threshold for bin 3). While

the coincidence would then effectively be counted

twice, we relied on the network to learn corrections

for this. However, it would also be possible to employ

a more sophisticated energy-dependent attenuation

correction factor, which depends on a restricted

Compton cross-section, to deal with this complication

(Sun, 2016, p. 58).

No dead time, random, arc, or normalization

corrections were performed; we relied on the network

to learn these.

Data augmentation was performed to efficiently

increase the number of training examples. Each 2-D

activity image was randomly flipped and rotated, with

the corresponding sinograms modified appropriately.

This was done six times for every image-sinogram

pair, yielding a total of 210,000 image-sinogram pairs.

2.4 Network and Training

A detailed representation of the network we

employed is depicted in Fig. 1. Similar to (Häggström

et al., 2019), we implemented an encoder-decoder

architecture, but as in (Whiteley et al., 2020) we used

fully connected (dense) layers in the center of the

network. These ensured that each pixel in the image

space had as its receptive field the entire input

sinogram, which was desirable due to the presence of

scatter in the data.

Two different networks (which employed the

same network architecture) were trained on the two

different types of sinograms and are referred to as the

EDS network and the photopeak network. Therefore,

the dimensions of the input data—and thus also the

dimensions of the first set of filters—varied

depending upon the sinogram type. EDSs were of size

101 x 180 x 3 (the last digit comes from the three

energy bins), whereas photopeak sinograms were of

size 101 x 180 x 1.

The encoding portion of the network began with a

convolutional layer followed by a ReLu activation.

Next, a max-pooling layer contracted the data. This

was followed by two more convolutional + ReLu

layers. The data were then reshaped (flattened),

passed through two dense layers, and then was

reshaped into an 83 x 83 array. Lastly, the decoding

portion of the network was composed of four

convolutional + ReLu layers and one convolutional +

softmax layer. The output was an image of size 71 x

71 pixels. Due to the final layer of the network being

a softmax layer, each 2D activity image in the training

and test sets was normalized so that the total activity

per slice equaled 1.

Neural Network PET Reconstruction using Scattered Data in Energy-dependent Sinograms

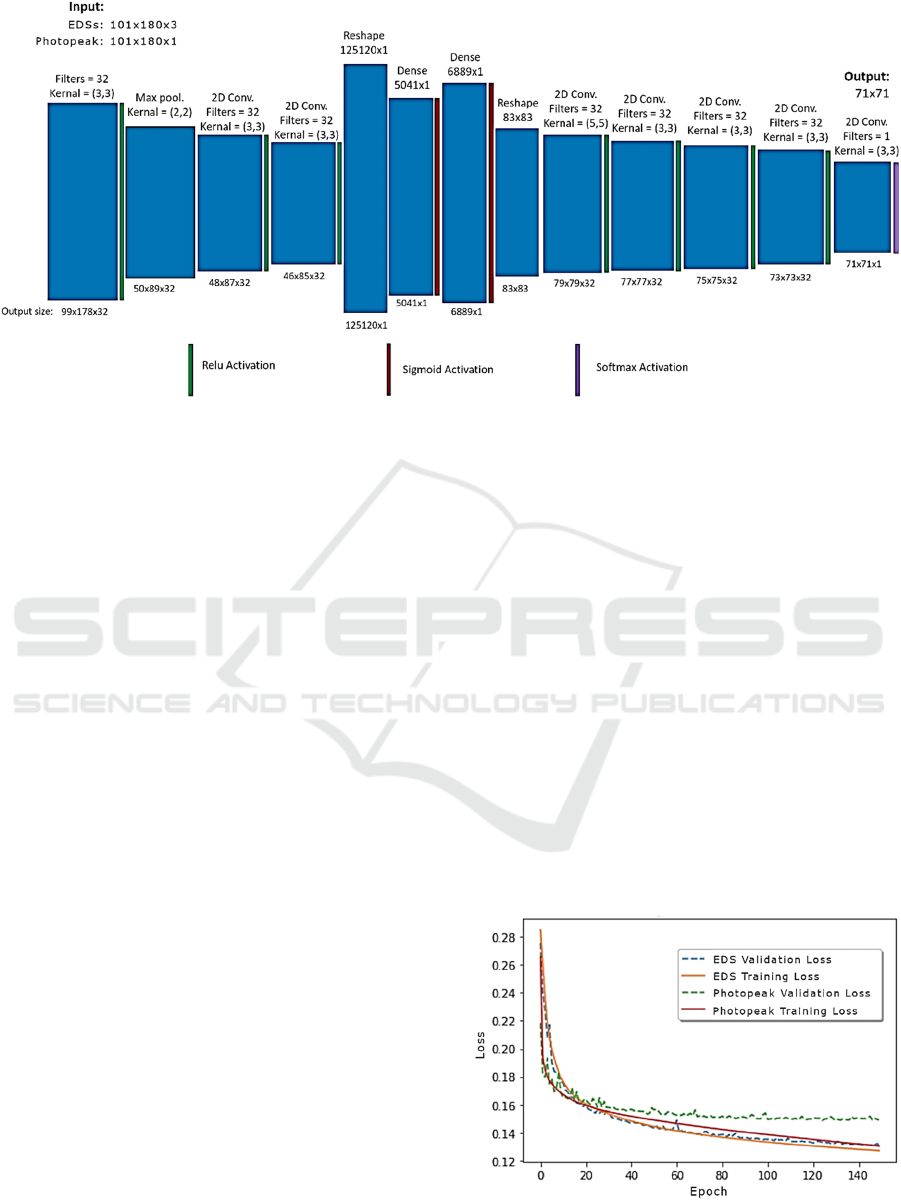
Figure 1: The network takes either energy-dependent sinograms (EDSs) or photopeak sinograms as input. The photopeak

sinograms are 2-D arrays composed of 101 x 108 elements. By contrast, the EDSs have a 3

dimension which contains the

scattered coincidences, arranged according to the energy of the scattered component. Thus, the filter size of the first layer is

different depending upon the input type. Multiple convolutional layers, as well as dense layers in the middle of the network,

ensure that the receptive field for every pixel in the output image comprises the entire input sinogram. This guarantees that

the full scatter data is utilized.

For each 2-D activity image, two sinograms were

created: one energy-dependent, and one photopeak.

From the 210,000 image-sinogram pairs, 180,000

photopeak sinograms and their corresponding activity

distributions were used to train the photopeak

network. The same number of energy-dependent

sinograms (with the same 2-D activity distributions)

were used to train the EDS network. In each case, this

left 30,000 sinogram-image pairs for use as a

validation set. As the validation sets were not used to

tune network parameters, they also functioned as test

sets.

Each network was trained for 150 epochs. During

each epoch, the loss function of the training set and

validation set were computed (Fig 2). Three loss

functions were investigated for network training:

Kullback-Leibler (KL), mean squared error (MSE),

and Poisson. KL was chosen due to the superiority of

images generated; these had less noise than those

generated by a network trained with MSE and had

higher contrast.

Network weights were optimized with an Adam

optimizer using a learning rate equal to 10

-5

. Training

was implemented within Python using the

TensorFlow library.

2.4.1 Transfer Learning

Monte Carlo simulations limit the practical size of

training sets. We, therefore, investigated transfer

learning as a possible method to train the network

more thoroughly.

We began by training a network with sinograms

calculated analytically from the activity distributions

and subsequently corrupted by Poisson noise. The

first 8 layers of the model were then frozen, and the

remainder trained on Monte Carlo-derived data sets.

However, this network underperformed relative to

networks trained only on Monte Carlo data sets, even

though the latter had relatively few training examples.

The authors hypothesize that, as the analytic

sinograms did not include energy-dependent

components, initial network layers did not learn to

take full advantage of the sinogram data and

discarded the scattered components. If transfer

Figure 2: Training and validation losses for the EDS and

photopeak networks.

BIOIMAGING 2022 - 9th International Conference on Bioimaging

learning were to be performed in future efforts, the

3rd dimension of the analytically computed

sinograms should represent the energy-dependent

scatter component more accurately.

3 RESULTS

3.1 Network Performance

Once training of the EDS and photopeak networks

was completed, these were tested with separate sets

of 30,000 sinogram-image pairs. For comparison

purposes, reconstructions of the photopeak sinograms

were made using filtered back projection (FBP) and

maximum likelihood expectation maximization

(MLEM). The latter was terminated at 13 iterations.

No additional scatter corrections were performed on

the data before reconstruction. These, therefore, are

illustrative and should not be taken as examples of the

best possible analytic or algorithmic reconstructions.

Rather, the most relevant comparison is between the

EDS network and the photopeak network. Sample

image reconstructions using all four methods may be

found in Fig. 3.

Figure 3: Images for each reconstruction method are shown;

note that the cold artifacts in images reconstructed from

photopeak sinograms are absent or attenuated in the images

reconstructed from EDSs.

The average mean squared error (MSE) and

structural similarity (SSIM) (Zhou Wang et al., 2004)

were determined from the validation set for each

reconstruction method, relative to the ground truth

images. Contrast values were also determined for all

four methods relative to the EDS-network. This was

done by averaging the intensity of a region of interest

of a hot spot feature (I

), as well as the background

area (I

). The contrast for a single image is then given

by: (I-I

)/I

The average contrast value was computed for a

10-image subset for each reconstruction method.

Then the relative contrast values for the photopeak

network, MLEM and FBP were determined relative

to the EDS network. Figure 4 shows the image quality

metrics for each reconstruction method.

The computation times for each reconstruction

method were also determined. The CNN

reconstruction times were approximately 3 and 92

times faster than FBP and MLEM methods,

respectively.

Figure 4: Evaluation metrics are shown for the four

reconstruction methods employed. Of particular interest are

the metrics for the two CNNs. The network trained on

energy-dependent sinograms (EDSs) outperforms the

network trained on photopeak sinograms, as evidenced by

the structural similarity index metric (SSIM) and mean

square error (MSE). However, for both SSIM and MSE, the

difference between the metrics is less than the standard

deviation of the metric values for images generated by each

network; this is apparent from the error bars in the figure.

3.2 Discussion

For each image metric, the mean performance of the

EDS network exceeded that of the photopeak

network, though the difference was within the

uncertainty for all metrics. However, the uncertainties

are given by the standard deviation of the metric

values, and as each metric value depends on the

particular image considered, comparing differences

in the mean metric values with their uncertainties has

limited utility. For example, it may be possible that

every EDS network image has a higher SSIM than the

equivalent photopeak network image, and yet the

uncertainties may overlap. A more thorough analysis,

to be undertaken in future work, will examine this

problem in greater detail.

Differences in the quality of the reconstructed

images can also be observed by visual inspection.

Figure 3 depicts reconstructions of four different 2-D

Neural Network PET Reconstruction using Scattered Data in Energy-dependent Sinograms

activity distributions using the four reconstruction

methods. The photopeak network generates distinct

cold artifacts that are less visible or absent in the EDS

network images. Noise within constant-activity areas

is also higher in the photopeak network generated

images. Lastly, the contrast between proximal areas

with different activity levels appears higher in the

EDS network generated images. Both CNN-

reconstructed images share broad agreement with

images reconstructed via FBP and MLEM.

Learning curves for the two CNNs are displayed

in Fig. 3. The training and validation loss of the

photopeak network shows slight overfitting, whereas

the energy-dependent network does not. This may be

due to the training set for the EDS network containing

three times the amount of data as the training set for

the photopeak network, whereas the number of

weights—except for the first layer—was equal. This

indicates that the EDS network was appropriately

sized, given the size of its training set.

4 APPLICATIONS AND

IMPROVEMENTS

4.1 3D and Total-body PET

Improved image metrics demonstrate that including

the information contained in the scatter has the

potential to increase image quality, even with 15%

FWHM energy resolution detectors. Given this,

image reconstruction with data containing higher

scatter fractions, such as occurs with 3-D acquisition

or with large patients, is likely to benefit most.

However, 3-D PET rebinning approaches, such as the

Fourier rebinning algorithm (Defrise et al., 1997),

typically only consider true coincidences. To make

full use of scatter data, either fully 3-D reconstruction

must be pursued, or else rebinning algorithms must be

developed which accurately rebin scattered

coincidences. The former approach will require a

much larger CNN with many more weights, which

will require many more training examples. The

computational requirements for such an approach are

likely to be prohibitive. The authors believe the latter

approach to be more reasonable.

The highest scatter fractions occur with total-

body PET (TB-PET). Due to the increased sensitivity

possible with TB-PET, reducing injected activity by

a factor of 20 or more is attainable. However, if a CT

scan must be performed for the purpose of attenuation

correction, this offsets the benefit. Attenuation

corrected emission maps may be constructed with

deep learning methods, even in the absence of CT,

though this may be difficult using the sparse data

from low-dose scans (Meikle et al., 2021, p. 25). In

such cases, using scattered data for attenuation

correction and/or activity estimation looks promising,

especially as scatter fractions—and thus the

information contained in the scatter—are increased

for total-body PET.

4.2 Additional Data Types

If attenuation maps are available, these have the

potential to increase the utility of scatter imaging.

Photons are more likely to be scattered in volumes

with high electron density. Therefore, attenuation

maps contain statistical information about likely

scattering locations. The use of attenuation maps as

prior information for determining scatter locations

may therefore increase the available spatial

information scatter coincidences provide for

determining annihilation positions. Similarly, TOF

information also increases the spatial information that

can be gleaned from scattered coincidences, as

demonstrated by Conti et al. (Conti et al., 2012).

Therefore, networks that use attenuation or TOF data,

together with scatter data, seem promising.

4.3 Future Work

The current study focused on a single network. Future

work will explore various network configurations,

including CycleGan, which often outperforms Unet-

type architectures. In this network type, a cycle-

consistent loss is added, which penalizes projection

functions for not being injective (Wang et al., 2020).

Different binning schemes may also be compared.

Lastly, verification of the reconstruction method

using physical phantoms is necessary to guarantee

that the improvements seen in simulations translate to

real-world applications.

5 CONCLUSION

Two convolutional neural networks sharing the same

network architecture were trained and tested with two

different sets of data: one with coincidences where

both photons fell within a 511(±25) keV photopeak

window, and one which also included coincidences

where one of the photons had a lower detected

energy. The network trained with the energy-

dependent scatter sinograms was observed to have a

lower mean-square-error and larger structural

similarity index than the network trained with only

BIOIMAGING 2022 - 9th International Conference on Bioimaging

the photopeak sinograms. Images generated by the

photopeak network also contained more severe

artifacts.

These results suggest that including scattered

coincidences in the data has the potential to increase

image quality. The authors hypothesize that by

utilizing coincidences outside the photopeak energy

bin, the patient dose may be lowered while

maintaining the same image quality, thus improving

patient care.

ACKNOWLEDGEMENTS

This work is supported by the Natural Sciences and

Engineering Research Council of Canada,

CancerCare Manitoba Foundation, and the University

of Manitoba.

REFERENCES

Bai, B., & Asma, E. (2016). PET Image Reconstruction:

Methodology and Quantitative Accuracy. In M. M.

Khalil (Ed.), Basic Science of PET Imaging (pp. 259–

284). Springer International Publishing.

https://doi.org/10.1007/978-3-319-40070-9_11

Berker, Y., Kiessling, F., & Schulz, V. (2014). Scattered

PET data for attenuation‐map reconstruction in

PET/MRI. Medical Physics (Lancaster), 41(10),

102502-n/a. https://doi.org/10.1118/1.4894818

Brusaferri, L., Bousse, A., Emond, E. C., Brown, R., Tsai,

Y.-J., Atkinson, D., Ourselin, S., Watson, C. C., Hutton,

B. F., Arridge, S., & Thielemans, K. (2020). Joint

Activity and Attenuation Reconstruction From Multiple

Energy Window Data With Photopeak Scatter Re-

Estimation in Non-TOF 3-D PET. IEEE Transactions

on Radiation and Plasma Medical Sciences, 4(4), 410–

421. https://doi.org/10.1109/TRPMS.2020.2978449

Cherry, S. R. (2012). Physics in nuclear medicine (4th ed.).

Elsevier/Saunders.

Conti, M., Hong, I., & Michel, C. (2012). Reconstruction of

scattered and unscattered PET coincidences using TOF

and energy information. Physics in Medicine &

Biology, 57(15), N307–N317. https://doi.org/10.1088/

0031-9155/57/15/N307

Defrise, M., Kinahan, P. E., Townsend, D. W., Michel, C.,

Sibomana, M., & Newport, D. F. (1997). Exact and

approximate rebinning algorithms for 3-D PET data.

IEEE Transactions on Medical Imaging, 16(2), 145–

158. https://doi.org/10.1109/42.563660

Dong, X., Lei, Y., Wang, T., Higgins, K., Liu, T., Curran,

W. J., Mao, H., Nye, J. A., & Yang, X. (2020). Deep

learning-based attenuation correction in the absence of

structural information for whole-body positron

emission tomography imaging. Physics in Medicine &

Biology, 65(5), 055011–055011. https://doi.org/

10.1088/1361-6560/ab652c

Dong, X., Wang, T., Lei, Y., Higgins, K., Liu, T., Curran,

W. J., Mao, H., Nye, J. A., & Yang, X. (2019).

Synthetic CT generation from non-attenuation

corrected PET images for whole-body PET imaging.

Physics in Medicine & Biology, 64(21), 215016–

215016. https://doi.org/10.1088/1361-6560/ab4eb7

Häggström, I., Schmidtlein, C. R., Campanella, G., &

Fuchs, T. J. (2019). DeepPET: A deep encoder–decoder

network for directly solving the PET image

reconstruction inverse problem. Medical Image

Analysis, 54, 253–262. https://doi.org/10.1016/

j.media.2019.03.013

Jan, S., Santin, G., Strul, D., Staelens, S., Assié, K., Autret,

D., Avner, S., Barbier, R., Bardiès, M., Bloomfield, P.

M., Brasse, D., Breton, V., Bruyndonckx, P., Buvat, I.,

Chatziioannou, A. F., Choi, Y., Chung, Y. H., Comtat,

C., Donnarieix, D., Morel, C. (2004). GATE: A

simulation toolkit for PET and SPECT. Physics in

Medicine & Biology, 49(19), 4543–4561.

https://doi.org/10.1088/0031-9155/49/19/007

Lee, J. S. (2021). A Review of Deep-Learning-Based

Approaches for Attenuation Correction in Positron

Emission Tomography. IEEE Transactions on

Radiation and Plasma Medical Sciences, 5(2), 160–

184. https://doi.org/10.1109/TRPMS.2020.3009269

Liu, Z., Chen, H., & Liu, H. (2019). Deep Learning Based

Framework for Direct Reconstruction of PET Images.

In D. Shen, T. Liu, T. M. Peters, L. H. Staib, C. Essert,

S. Zhou, P.-T. Yap, & A. Khan (Eds.), Medical Image

Computing and Computer Assisted Intervention –

MICCAI 2019 (pp. 48–56). Springer International

Publishing. https://doi.org/10.1007/978-3-030-32248-

9_6

Meikle, S. R., Sossi, V., Roncali, E., Cherry, S. R., Banati,

R., Mankoff, D., Jones, T., James, M., Sutcliffe, J.,

Ouyang, J., Petibon, Y., Ma, C., Fakhri, G. E., Surti, S.,

Karp, J. S., Badawi, R. D., Yamaya, T., Akamatsu, G.,

Schramm, G., … Dutta, J. (2021). Quantitative PET in

the 2020s: A roadmap. Physics in Medicine & Biology,

66(6), 06RM01. https://doi.org/10.1088/1361-6560/

abd4f7

Segars, W. P., Sturgeon, G., Mendonca, S., Grimes, J., &

Tsui, B. M. W. (2010). 4D XCAT phantom for

multimodality imaging research. Medical Physics

(Lancaster), 37(9), 4902–4915. https://doi.org/

10.1118/1.3480985

Shiri, I., Ghafarian, P., Geramifar, P., Leung, K. H.-Y.,

Ghelichoghli, M., Oveisi, M., Rahmim, A., & Ay,

M. R. (2019). Direct attenuation correction of brain

PET images using only emission data via a

deep convolutional encoder-decoder (Deep-DAC).

European Radiology, 29(12), 6867–6879.

https://doi.org/10.1007/s00330-019-06229-1

Song, T.-A., Chowdhury, S. R., Yang, F., & Dutta, J.

(2020). PET image super-resolution using generative

adversarial networks. Neural Networks, 125, 83–91.

https://doi.org/10.1016/j.neunet.2020.01.029

Neural Network PET Reconstruction using Scattered Data in Energy-dependent Sinograms

Sun, H. (2016). An improved positron emission tomography

(PET) reconstruction of 2D activity distribution using

higher order scattered data [Masters]. University of

Manitoba.

Sun, H., & Pistorius, S. (2013a). Evaluation of the

Feasibility and Quantitative Accuracy of a Generalized

Scatter 2D PET Reconstruction Method. ISRN

Biomedical Imaging, 2013, 1–11. https://doi.org/

10.1155/2013/943051

Sun, H., & Pistorius, S. (2013b). Evaluation of Image

Quality Improvements When Adding Patient Outline

Constraints into a Generalized Scatter PET

Reconstruction Algorithm. ISRN Biomedical Imaging,

2013, 1–8. https://doi.org/10.1155/2013/326847

Sun, H., Teimoorisichani, M., McIntosh, B., Zhang, G.,

Ingleby, H., Goertzen, A., & Pistorius, S. (2015).

Simultaneous estimation of the radioactivity

distribution and electron density map from scattered

coincidences in PET: A project overview. In D. A.

Jaffray (Ed.), World Congress on Medical Physics and

Biomedical Engineering, June 7-12, 2015, Toronto,

Canada (pp. 150–153). Springer International

Publishing. https://doi.org/10.1007/978-3-319-19387-

8_36

Tian, C., Xu, Y., Fei, L., & Yan, K. (2019). Deep Learning

for Image Denoising: A Survey. In Genetic and

Evolutionary Computing (pp. 563–572). Springer

Singapore. Https://arxiv.org/abs/1810.05052

Tong, S., Alessio, A. M., & Kinahan, P. E. (2010). Noise

and signal properties in PSF-based fully 3D PET image

reconstruction: An experimental evaluation. Physics in

Medicine & Biology, 55(5), 1453–1473.

https://doi.org/10.1088/0031-9155/55/5/013

Wang, T., Lei, Y., Fu, Y., Curran, W. J., Liu, T., & Yang,

X. (2020). Machine Learning in Quantitative PET

Imaging. https://arxiv.org/abs/2001.06597

Whiteley, W., Luk, W. K., & Gregor, J. (2020). DirectPET:

Full-size neural network PET reconstruction from

sinogram data. Journal of Medical Imaging, 7(3).

https://doi.org/10.1117/1.JMI.7.3.032503

Zhou Wang, Bovik, A. C., Sheikh, H. R., & Simoncelli, E.

P. (2004). Image quality assessment: From error

visibility to structural similarity. IEEE Transactions on

Image Processing, 13(4), 600–612. https://doi.org/

10.1109/TIP.2003.819861

Zhu, B., Liu, J. Z., Cauley, S. F., Rosen, B. R., & Rosen,

M. S. (2018). Image reconstruction by domain-

transform manifold learning. Nature (London),

555(7697), 487–492. https://doi.org/10.1038/nature25

988

BIOIMAGING 2022 - 9th International Conference on Bioimaging