
Physics based Motion Estimation to Improve Video Compression
James McCullough
1a
, Naseer Al-Jawad
1b
and Tuan Nguyen
2c
1
School of Computing, University of Buckingham, Hunter Street, Buckingham, U.K.
2
School of Computing & Mathematical Sciences, University of Greenwich, Old Royal Naval College, Park Row, London, U.K.
Keywords: Video Compression, Optical Flow, Physics, Mechanics, Acceleration, Velocity, Segmentation.
Abstract: Optical flow is a fundamental component of video compression as it can be used to effectively compress
sequential frames. However, currently optical flow is only a transformation of one frame into another. This
paper considers the possibility of representing optical flow based on physics principles which has not, to our
knowledge, been researched before. Video often consists of real-world events captured by a camera, meaning
that objects within videos follow Newtonian physics, so the video can be compressed by converting the motion
of the object into physics-based motion paths. The proposed algorithm converts an object’s location over a
series of frames into a sequence of physics motion paths. The space cost in saving these motion paths could
be considerably smaller compared with traditional optical flow, and this improves video compression in
exchange for increased encoding/decoding times. Based on our experimental implementation, motion paths
can be used to compress the motion of objects on basic trajectories. By comparing the file sizes between
original and processed image sequences, effective compression on basic object movements can be identified.
1 INTRODUCTION
The goal of video compression is to minimise the size
of digital video files. This area has been studied
extensively, focusing on compressing the data in
several different ways, which can be divided into two
categories: intra-frame and inter-frame compression.
Intra-frame compression is applied within individual
frames without concern of surrounding frames; this is
equivalent to regular image compression. Inter-frame
compression, however, focuses on how similar
consecutive frames can be compressed, such as
saving vectors to transform one frame into the next if
the two are similar enough to achieve this. However,
given a large quantity of video produced contains
objects from real life, it may be possible to
retroactively apply physics movement to objects
captured on camera. The aim of this paper is to
propose a method to transform object motion into
physics-based motion paths which can be used to
compress this information.
Currently available methods for video
compression are inbuilt into video codecs (the
a
https://orcid.org/0000-0002-8422-0347
b
https://orcid.org/0000-0002-4585-6385
c
https://orcid.org/0000-0003-0055-8218
formats for how video is stored on digital devices)
such as H.264 and HEVC (also called H.265) which
are the two most adopted at the time of writing. Both
example codecs use optical flow / motion estimation
to generate motion vector arrays to trace the
movement of groups of pixels (termed micro
blocks/coding tree units) from one frame to another.
To clarify, motion estimation is the term relating to
estimating motion in the world, whereas optical flow
refers specifically to estimating motion of pixels with
the video frame (Sellent et al., 2012). These two are
not always equal, but in most cases are. This allows
them to compress the information by storing the pixel
values of only one frame and then only the motion
vectors used to transform that frame to the next;
however, this process is only ever used to convert one
frame to another. This paper proposes the possibility
of using physics to transform these individual motion
vector arrays into motion paths defined by physics
principles, thus adding an additional layer onto the
already existing compression.
As this concept is in its early stages, the
experimental setup applies physics to the movement
of individual segmented objects from the DAVIS
364
McCullough, J., Al-Jawad, N. and Nguyen, T.
Physics based Motion Estimation to Improve Video Compression.
DOI: 10.5220/0010811900003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
364-371
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2016 dataset (Perazzi et al., 2016). Then, the file sizes
of the original image sequence can be compared with
the extracted object and background sequences along
with the new generated physics motion path data.
Video compression is a beneficial field of study as
video is stored digitally almost exclusively. At high
resolutions such as 4K, reducing the file sizes should
enable faster video file transfers, and reduce hardware
and energy costs. The aim is that applying physics to
object motion within videos would allow increased
compression rates and a new branch of potential
research is discovered.
2 LITERATURE REVIEW
There is, to the author’s knowledge, no current
research into using physics to improve video
compression, so this research focuses on relevant
existing video compression methods that could be
used as a base to build on. Optical flow is a key
component in video compression, and there are a
wide variety of different approaches and methods
available to calculate it. One key method is block
matching/motion blocking, which is compared with
other methods by Philip et al. (2014). Optical flow is
saved in the form of a motion vector array, which is a
transformation from one frame into another, and this
makes it a possible input for our proposed physics
estimation algorithm. Each frame’s optical flow
encodes the translation of all applicable pixels within
the video, which can be further compressed using
physics-based motion paths in our proposed method.
Further research was carried out on the variety of
different optical flow methods (Barron et al., 1994),
and more specifically using segmentation with optical
flow as the objects would need to be extracted from
the videos. DeepFlow (Weinzaepfel et al., 2013)
effectively adapted optical flow to handle larger
displacements, while ObjectFlow (Tsai et al., 2016)
builds on it and other similar methods to use optical
flow to segment objects and would be useful as a
segmentation process before physics estimation.
Currently, the two most commonly used codecs
(H.264, H.265) each use a version of motion blocking
to generate the optical flow used, with the only
difference being the sizes of the motion blocks used,
and thus the number of motion vectors stored
(Rajabai & Sivanantham, 2018). Our proposed
method is to build upon the output of these created
motion vectors to apply physics estimation to their
movement throughout the video.
Many related studies were included within the
research involving components of optical flow and
segmentation in order to inform this study. Tsai et al.
(2016) uses optical flow to discern object boundaries
which would be a useful basis to then apply physics
to. Motion Blocking also could be expanded upon, for
example Gao et al. (2020) develops upon the method
by breaking down motion blocks into a large number
of possible polygons. This resulted in 82 options,
which allowed motion blocks to be divided
effectively along object edges. By improving the
accuracy of how motion blocks represent objects, this
would allow for semi-segmentation within the motion
blocking process and the proposed physics process
could then be applied more effectively. Being able to
detect and recognise camera movements will also be
important for adjusting the axis that the physics is
measured against, so authors such as Sandula &
Okade (2019) suggesting methods of detecting such
camera movements were also researched. These
issues could also be corrected with some inversion of
motion stabilization where the axis measured against
is stabilized to the camera movement. This can also
be achieved during the motion blocking stage of
compression (Wang et al., 2017), which analyses the
global motion parameters to stabilize the video.
To keep it simple for this proof-of-concept, we
use a segmented dataset and track object movement
via its centre point without regarding any rotation or
other transformation. These will be areas that require
more investigation if this proof-of-concept indicates
a value to physics-based compression.
While physics/mechanics has been widely
explored in areas such as computer vision and object
tracking, the authors have not seen any examples of
an attempt to implement it into video compression.
3 METHODOLOGY
This paper aims to build a process that can compress
videos by segmenting each video frame into objects,
and then analysing the object’s motion in terms of
physics equations which allows this motion data to be
compressed. Firstly, the paper will outline some
physics concepts, then these will be used to convert
object location data into motion paths based on these
concepts, and finally this will be implemented into a
basic video compression process.
As this is a proof-of-concept, this paper is solely
concerned with a physics-based representation of
motion. This means rotation, scaling and
complex/non-rigid objects are disregarded at present.
We also use a segmented dataset to perform an
intuitive test without needing to solve the complicated
issues behind object tracking, but do not suggest
Physics based Motion Estimation to Improve Video Compression
365
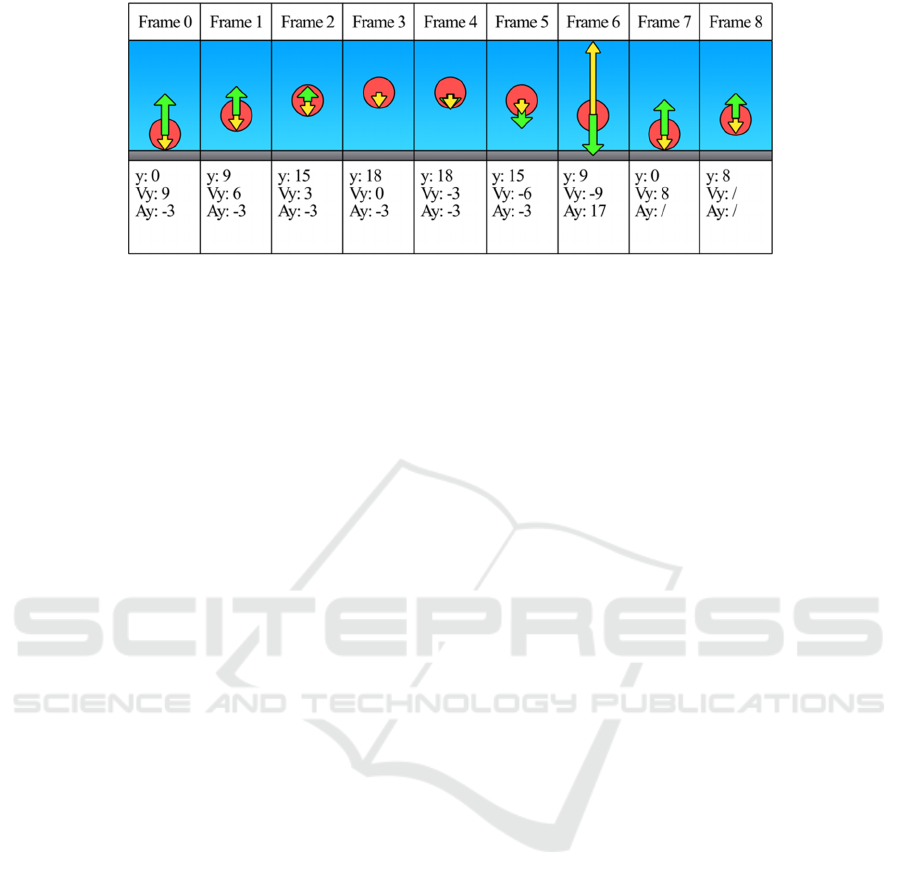
Figure 1: A conceptual video sequence of a ball bouncing with the calculated values of location (y), velocity (Vy) and
acceleration (Ay) for each frame. The values for Vy and Ay are calculated using Equations (1) & (2). The arrows are visual
representations of the velocity (green) and acceleration (yellow). For simplicity, only the y dimension is specified.
segmentation as a method for tracking objects in
future as it is a more intensive process than video
compression requires.
3.1 Physics Concepts
To explain our proposed video compression
technique, it is important to first outline the basic
physics concepts used to achieve it. All object
interactions can be modelled by many different
physics frameworks. For example, the theory of
relatively could be used (Einstein, 2010), but this was
created to update the previous framework’s
interpretation of particles interacting in extreme cases
(such as close to light speed). Newtonian physics
however is what is more typically used to simulate
object interactions at the time of writing, and it is
more mathematically simple to model. As such,
Newtonian physics will be used to build this
modelling of object movement.
Movement in Newtonian physics relies on the
basic concepts of location, velocity and acceleration.
Location is the place where an object is, at a set time
or frame. Velocity is the difference between the
location of the object over a set gap in time (for video
purposes, one frame to the next). Acceleration is the
difference between the velocity of an object at one
point in time, and the velocity of an object at the next
point in time. For an object in motion while no new
force acts upon it, the object’s acceleration will
remain constant, manipulating its velocity which in
turn influences its location (Raine, 2013). These
concepts are formalised in equations (1) and (2)
below, which are then demonstrated visually in
Figure 1. Newtonian Physics concepts can be
demonstrated more clearly using Figure 1, which is a
ball bouncing sequence accompanied by values for its
distance, velocity and acceleration, as would be
calculated using the definitions of location, velocity
and acceleration stated.
𝑉𝑥
,𝑉𝑦
=
𝑥
𝑥
,𝑦
𝑦
(1)
𝐴
𝑥
,
𝐴
𝑦
=
𝑉𝑥
𝑉𝑥
,𝑉𝑦
𝑉𝑦
(2)
where [x
n
, y
n
] is the object’s location within frame n
For simplicity, the y values are measured as the
distance from the ground, however in implementation
they are calculated vertically from the top of the
frame. Figure 1 demonstrates this Newtonian physics
concept as acceleration remains constant as the ball
bounces, until it impacts with the ground on frame 7
where the ball’s gravitational force is combined with
the impulse force from the ground causing the ball’s
acceleration to spike in the other direction for a single
frame. Because of the discrete nature of frame by
frame video, this acceleration is observed on frame 6
because of the large change in velocity.
This approach may seem over-simplified given
that there appear to be many forces acting upon the
ball over time. For example, the ball is affected by the
force of gravity permanently pulling it downwards,
and an occasional impulse force from the ground.
However, this method calculates the acceleration
from the movement of the ball, and as such does not
need to concern itself with the individual forces. Any
combination of forces creates a set acceleration for as
long as those forces continue to act on the object, and
as the process can calculate the acceleration from the
observed movement, individual forces are catered for.
This indicates that no matter the object or the
motion, be it a boat sailing along a river or clouds
moving across the sky, the motion of any object can
be simplified into only the acceleration, velocity and
location of the object over a sequence of frames.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
366

3.2 Optical Flow into Motion Paths
Optical flow is the vector array to transform one
frame into the next. Finding optical flow is a complex
task. There are many differing methods, along with
numerous extensions, to calculate optical flow.
Our proposed method is that the optical flow field
has some underlying redundancy which can be
extracted through the process of physics modelling,
allowing for further compression. Because the optical
flow field is representative of object movements
between only two frames, considering a series of
optical flow frames together, it is likely possible to
group objects together and apply physics to model the
object movements. This is because the motion of
objects does not vary randomly between each frame,
but instead follows a defined path in relation to the
object’s movement in the world. As such, it should be
possible to save optical flow data in the form of
physics equations, and this may have a smaller file
size than the optical flow data itself. This is quite a
complex problem, especially transforming an optical
flow field into distinct objects and maintaining their
persistence throughout a video sequence. This kind of
segmentation has been studied before (Kim et al.,
2003, p. 2; Kung et al., 1996) and indicates that the
proposed method has potential. For example, if
vectors of a similar direction and amplitude can be
clustered together, objects within the video should be
determinable. The same objects movements over the
course of multiple frames can then be converted into
physics motion paths.
Figure 2: Optical flow field example.
Figure 2 shows a depiction of optical flow where the
frame is broken down into blocks, and the arrows
represented the how the pixels are transformed from
one frame into the next. The vast majority of pixels
shift only a small amount, but there are a number of
outlier vectors that have been mismatched with a
similar but different section of the image.
However, the conversion of this optical flow data
into objects is quite a complex problem, so it would
be sensible to determine if saving data into a motion
path format will improve the compression ratio before
attempting to solve it. As such, this paper proposes a
simple proof-of-concept test using pre-segmented
video to extract object coordinates, from which to
determine object motion.
3.3 Converting Filmed Object
Coordinates into Motion Paths
To achieve the video compression, a process has been
constructed to transform a series of coordinates into
motion paths based on physics. This process is
outlined in the flow chart in Figure 3. The input to this
flow-chart is a series of coordinates, and the output is
the corresponding series of motion paths. It is
possible to demonstrate the process with the ball
bouncing sequence from Figure 1.
To begin with, the counter n is used to count
frames through the sequence. A threshold must also
be determined to register a change in acceleration.
Given the discretisation caused by video having a
limited frame rate, a small threshold value should be
chosen to discern big jumps in acceleration, as there
will likely be minor changes detected throughout. In
this case, 1 is a suitable value. It is initialised to the
start of the sequence: frame 0. As there are more than
3 frames in the sequence, the details of that first frame
are saved as the first motion path according to
equations (1) and (2): M[y = 0, Vy = 9, Ay = -3] as
location (y), velocity (Vy) and acceleration (Ay)
respectively. The counter is now increased by 3,
because the first three frames are always accurately
represented as they were used to calculate the motion
path’s values. Then, the new frame’s acceleration is
calculated, and as it is also -3, it is within a threshold
distance from the path’s acceleration (also -3), so the
counter is increased again. This loop will continue
until the counter is equal to 6, as here the calculated
acceleration is now 17 which is outside the threshold
accepted radius around -3 (-4 to -2 are acceptable for
a threshold of 1), so this concludes that motion path.
As there are no longer 3 frames remaining, but only
2, a dummy motion path is generated with no
acceleration to store the location information for the
final two frames, and the process is completed.
In order to generate the original coordinates back
from these motion paths, the following function can
be used.
𝑀
𝑗
=
𝑘,
𝑗
=0
𝑀
𝑗
1
+𝑉𝑘,
𝑗
=1
𝑀
𝑗
1
+𝑉𝑘+
𝑗
1
𝐴𝑘,
𝑗
1
(3)
where j = n – m for a path starting at frame m and n
is the frame in the sequence, and k is x and y,
performed on the [x, y] vector.
Physics based Motion Estimation to Improve Video Compression
367

Figure 3: A flowchart showing the coordinate to motion path process, where Ax
n
is the acceleration on frame n in the x axis,
and M
Ax
is the acceleration of the current motion path in the x axis, and so forth.
For example, to gain the value from frame 3 using
the saved motion paths, j = 3 as the motion path
begins at frame 0, the function can then be solved
recursively for M
k
(3).
The remaining issue is how to determine the
threshold value that detects a change in acceleration
effectively. The value of 1 works for the example, but
from sequence to sequence the optimum threshold is
likely to change. If the threshold is set too low, then
motion paths will be unnecessarily created which will
negate compression. If the threshold is too high, then
the object will veer off its intended path because a
new path is not created when it should be.
𝐹
𝑛
=
1,
|
𝑥
𝑀
𝑛
|
𝑡 ∩ 𝑦
𝑀
𝑛
𝑡
0, 𝑂𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
(4)
where [x,y] is the object’s location, t is a tolerance
and M is the function specified in (3)
𝐴
=
∑
(5)
where N is the total number of frames in the sequence
To solve this issue, a function is proposed defined
in equations (4) and (5) to test every frame. Equation
(5) returns a percentage of frames where the object’s
location has been placed correctly by the algorithm,
using a small value for t to allow for acceptable
displacement. This displacement of the object within
the image is the only change to video quality
introduced by the proposed method, and while this
can be set to 0 to ensure no change/lossless
compression, this would also limit the compression
achievable. The target accuracy can now be set to 1
to ensure the algorithm’s recreations do not vary from
the true locations of the objects and the process could
then be run repeatedly to generate and test object
paths while shifting the threshold up and down until
A = 1 . This method allows for some variation in
acceleration so long as the motion path tracks the
object accurately.
3.4 Video Compression using Physics
Paths
Here is a proposed test to determine the effectiveness
of the process discussed in section 3.3. While physics
motion paths should eventually be implemented on
top of current optical flow methods, it was decided to
keep these initial proof-of-concept tests simple by
using a segmented dataset to extract the object from
each frame and track its motion. Figure 4 shows the
encoding process. Each video sequence contains one
segmented object of focus. This object is extracted
from the background image for each frame and a list
of the object’s centre points is generated using the
centre point, described in equation (6).
𝐶
𝑥,𝑦
=
,
(6)
Where x
max
is the largest x coordinate within the
object, x
min
is the smallest x coordinate within the
object, y
max
is the largest y coordinate within the
object and, y
min
is the smallest y coordinate within the
object.
These centre points are then passed into the
previously discussed physics estimation function
specified in section 3.3 and then the resulting motion
paths, as well as the background and object image
sequences are saved into an encoded file. For a single
object video, this file will consist of a background
plate, an object sequence and the motion paths for the
object. For multiple-object videos, the file will consist
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
368

Figure 4: A flowchart breaking down the video.
of a background plate and several object sequences
each with their own motion paths. Each motion path
consists of three vectors, one for initial location, one
for initial velocity and one for acceleration; an object
may have many of these throughout the sequence. To
decode, the object need only be added to the
background frame at the coordinate retrieved from the
motion path, which is very easy to read consecutively
because of the recursive nature of equation (3). A
possible implementation could be: at the start of each
motion path, load the values of location, velocity and
acceleration into some temporary variables; then for
each frame add the velocity to the location; and add
the acceleration to the velocity; repeat this until the
start of the next motion path where the variables are
overwritten, and this process can continue being
repeated until the end of the image sequence.
4 EXPERIMENTATION AND
RESULTS
4.1 Dataset
This process has been tested using a pre-segmented
dataset and using the coordinates set by taking the
centre of the segmented object in each frame using
equation (6). The DAVIS 2016 Dataset has been used
for the featured tests (Perazzi et al., 2016). This
Figure 5: Example frames from the DAVIS 2016 dataset.
dataset was chosen as it only segments one object per
sequence and contains a wide variety of movement
types with stationary and moving camera angles, as
well as objects overlapping and complicated
segmentation. In particular, three sequences with
simplistic motion (‘soccerball’, ‘boat’ and ‘car-
roundabout’) and three sequences with complicated
motion (‘bus’, ‘bmx-trees’ and ‘hockey’) were
selected to test. The ‘soccerball’ is the simplest
sequence in that the camera is stationary and the ball
rolling along is a smooth deceleration, although the
ball does roll behind some trees which renders the
currently implemented centre tracker inaccurate in
places. The ‘boat’ sequence has a smooth panning
camera and a boat which is not overlapped by any
objects resulting in a simple motion of the boat
moving only slightly horizontally, and ‘car-
roundabout’ also has a smooth camera and no
overlapping elements in its environment.
The ‘bus’ sequence involves the bus driving
behind several signs and a tree, where the overlap
segmentation becomes very detailed, while the
motion is simple as with the car. This sequence was
included to indicate if the complexity of the
segmentation has an effect on the file-size of the
separated images. The ‘bmx-trees’ sequence is also
complex in that the camera shakes quite considerably
and the object is also a human riding a bike, making
its motion more erratic and less consistent. Finally,
‘hockey’ was included as an example of entirely
human movement where the human and the hockey
puck are tracked together as a very complicated and
unpredictable shape moving also unpredictably. This
was included to identify how the system would
handle incorrectly segmented objects, as the human
and puck’s centre point together is not representative
of a real object’s movement.
4.2 Experiments
The current implementation is only focused on the
centre-point of these objects and tracking that point’s
movement. The tested implementation makes no
attempt to break them up into individual components,
even though they may have their own individual
motion such as the BMX bike’s wheels.
In order to test the effectiveness of the proposed
process as a compression algorithm, it was going to
be compared against H.264. The comparison would
have been the size of the raw video file in .mp4
format, against the size of the two separated video
files and the saved motion path information.
However, the results of this test were that the
background plate (with the object removed) was
Physics based Motion Estimation to Improve Video Compression
369

larger in size than the original base image for every
test. We theorise this is because the empty space is
more costly when compressed by the H.264 codec
than when the object is present in the scene.
So, instead, the size of the original frames was
compared with the size of the segmented frames and
the motion data, which has been generated using the
processes described in section 3.3. The dynamic
threshold was used for the experiment to test the
different sequences on a comparable playing ground,
with a target accuracy of 1 (see equation (5)). A target
of 1 ensures each and every frame in the sequence is
accurately represented, while ensuring the minimum
number of motion paths to enable compression.
This experiment was run in Python 3.7 using
OpenCV to read and process the images, Numpy for
matrix manipulation and Pickle for saving the motion
path data. The threshold value was initialised at 1.0
and was stepped up or down by 0.05 until the target
accuracy was reached. If the threshold was lowered to
0, then the test would proceed automatically, but this
would result in an accuracy of 1, as it is equivalent to
saving all the coordinates. The tolerance t (see
equation (4)) was set to 3 pixels, as we were unable
to identify that level of displacement with a visual
inspection of the footage.
𝑆𝑖𝑚𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑇𝑜𝑡𝑎𝑙=𝐵𝑎𝑐𝑘𝑔𝑟𝑜𝑢𝑛𝑑 𝐼𝑚𝑎𝑔𝑒 𝑆𝑖𝑧𝑒 +
𝑂𝑏𝑗𝑒𝑐𝑡 𝐼𝑚𝑎𝑔𝑒 𝑆𝑖𝑧𝑒+ 𝑀𝑜𝑡𝑖𝑜𝑛 𝐷𝑎𝑡𝑎 𝑆𝑖𝑧𝑒
(7)
𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝐷𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑒=
𝑆𝑖𝑚𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑇𝑜𝑡𝑎𝑙
𝐵𝑎𝑠𝑒 𝐼𝑚𝑎
𝑔
𝑒 𝑆𝑖𝑧𝑒
(8)
4.3 Results
These tests revealed a substantial amount about the
proposed process. The simplest clip ‘soccerball’
performed the best with a percentage difference of
64% in comparison to the size of original image
sequence. The ‘boat’ sequence, however, performed
less well with only a 98% percentage difference, so
only 2% smaller than the original file. The surprising
result was the ‘bmx-trees’ sequence, which had a
reduction to 74% its original file size despite the
complexity of the motion in the sequence. As
expected, the more complicated sequences performed
less well, actually expanding the file size by up to
150% of their original size for the very complicated
overlapping ‘bus’ sequence. ‘bmx-trees’ and ‘car-
roundabout’ sequences were an exception,
performing in opposition to our prediction. The
results confirmed the hypothesis that image
sequences can be compressed using motion paths.
4.4 Discussion
Results from the testing show the file size is
unfortunately affected far more by the segmented
image sizes than by the motion data. This reaffirms
that applying segmentation in this way may be more
costly than it is advantageous in many cases,
especially where overlapping causes the
segmentation to be very complex. This is also
reflected in the increase in the background size when
in video format, which could be attributed to the
background plate containing a large empty area with
no details to save and track, using motion blocking.
While the motion paths themselves appear to be
working effectively, the segmentation can greatly
increase the file size which may far outweigh the
compression advantages of the motion paths on more
complicated objects and movements. This aligns with
our initial understanding as segmentation is not
suggested to replace traditional optical flow methods.
Object size also has an effect as larger objects that
take up more of the frame have a more complex
segmentation, even without considering overlapping.
A more relevant possible contributing factor is
that video is discrete in terms of having a limited
number of frames per second, whereas these physics
Table 1: Comparing the size of the original frames of the image sequence, and the separated frames of the image sequence.
Image
Sequence
Background
Image Size
(Bytes)
Object Image
Size (Bytes)
Motion Data
Size (Bytes)
Simulation
Total (Bytes)
Base Image
Size (Bytes)
Percentage
difference (%)
soccerball 5,381,742 606,487 411 5,988,640 9,316,723 64.28
bmx-trees 5,631,113 1,686,822 604 7,318,539 9,871,661 74.14
Boat 4,244,962 3,532,093 610 7,777,665 78,954,803 98.51
hockey 3,810,400 3,659,393 592 7,470,385 7,336,290 101.8
car-roundabout 4,866,468 6,461,275 498 11,328,241 9,535,231 118.8
bus 4,438,933 9,575,051 571 14,014,555 9,340,244 150.0
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
370

concepts are assumed to exist in a continuous
timeline. While they still function on a discrete frame-
by-frame basis, there may be minor information lost
from this discretisation of the object’s movement.
This process could also be improved by breaking
down complicated objects into numerous more
simple objects, and then tracking those components.
While this seems a challenging prospect, all objects
within reality obey the laws of physics. Complex
objects may not display a constant acceleration; it is
likely parts of a complex object may display a
constant acceleration in relation to other parts of the
same object. This could be achieved by developing on
top of the optical flow already in place within most
codecs, which is the next logical area of focus for
study. Lucas & Kanade (1981) already differentiate
between slow and fast object movement, and this is a
useful feature to develop within the proposed method.
Additionally, the ongoing areas we disregarded for
this proof of concept, such as rotation, scaling and
camera movement, will also need to be investigated
and integrated into an overall system for peak
compression to be achieved using this method.
5 CONCLUSION
This paper proposes a physics-based process to
convert object movement into motion paths, as well
as a rudimentary implementation using the DAVIS
2016 segmented dataset. This is not a completed work
but a proof-of-concept that requires further study.
Based on the testing, the system currently
performs well only in basic scenarios with small
objects and a static camera view, as this is the best
scenario it can use to recreate physics paths
accurately. Motion in the camera will affect the
object’s perceived movement away from its true
movement and thus does not strictly comply to the
physics rules being applied without some algorithmic
stabilization. Based upon the testing, the final aim of
this should be a hybrid method: the proposed physics
estimation being applied onto a form of optical flow,
like those used in the H.264 and HEVC codecs. If this
process could be combined with or added after the
pre-existing optical flow section of a codec to further
compress these motion vector arrays, this could
improve the observed compression ratio.
REFERENCES
Barron, J. L., Fleet, D. J., & Beauchemin, S. S. (1994).
Performance of Optical Flow Techniques. 60.
Einstein, A. (2010). Relativity: The Special and the General
Theory.
Gao, H., Liao, R., Reuzé, K., Esenlik, S., Alshina, E., Ye,
Y., Chen, J., Luo, J., Chen, C., Huang, H., Chien, W.,
Seregin, V., & Karczewicz, M. (2020). Advanced
Geometric-Based Inter Prediction for Versatile Video
Coding. 2020 Data Compression Conference, 93–102.
https://doi.org/10.1109/DCC47342.2020.00017
Kim, J.-W., Kim, Y., Park, S.-H., Choi, K.-S., & Ko, S.-J.
(2003). MPEG-2 to MPEG-4 transcoder using object-
based motion vector clustering. 2003 IEEE
International Conference on Consumer Electronics,
2003. ICCE., 32–33.
Kung, S. Y., Tin, Y.-T., & Chen, Y.-K. (1996). Motion-
based segmentation by principal singular vector (PSV)
clustering method. 1996 IEEE International
Conference on Acoustics, Speech, and Signal
Processing Conference Proceedings, 3410–3413 vol. 6.
Lucas, B. D., & Kanade, T. (1981). An Iterative Image
Registration Technique with an Application to Stereo
Vision. Proceedings of Imaging Understanding
Workshop, 10.
Perazzi, F., Pont-Tuset, J., McWilliams, B., Van Gool, L.,
Gross, M., & Sorkine-Hornung, A. (2016). A
Benchmark Dataset and Evaluation Methodology for
Video Object Segmentation. 2016 IEEE Conference on
Computer Vision and Pattern Recognition, 724–732.
Philip, J. T., Samuvel, B., Pradeesh, K., & Nimmi, N. K.
(2014). A comparative study of block matching and
optical flow motion estimation algorithms. 2014
Annual International Conference on Emerging
Research Areas: Magnetics, Machines and Drives, 1–
6.
Raine, D. (2013). Newtonian Mechanics: A Modelling
Approach.
Rajabai, C., & Sivanantham, S. (2018). Review on
Architectures of Motion Estimation for Video Coding
Standards. International Journal of Engineering and
Technology, 7, 928–934.
Sandula, P., & Okade, M. (2019). Camera Zoom Motion
Detection in the Compressed Domain. 2019
International Conference on Range Technology, 1–4.
Sellent, A., Kondermann, D., Simon, S., Baker, S.,
Dedeoglu, G., Erdler, O., Parsonage, P., Unger, C., &
Niehsen, W. (2012). Optical Flow Estimation versus
Motion Estimation. 8.
Tsai, Y.-H., Yang, M.-H., & Black, M. J. (2016). Video
Segmentation via Object Flow. 2016 IEEE Conference
on Computer Vision and Pattern Recognition, 3899–
3908.
Wang, Y., Huang, Q., Zhang, D., & Chen, Y. (2017).
Digital Video Stabilization Based on Block Motion
Estimation. 2017 International Conference on
Computer Technology, Electronics and
Communication, 894–897.
Weinzaepfel, P., Revaud, J., Harchaoui, Z., & Schmid, C.
(2013). DeepFlow: Large Displacement Optical Flow
with Deep Matching. 2013 IEEE International
Conference on Computer Vision, 1385–1392.
Physics based Motion Estimation to Improve Video Compression
371
