
Applying Center Loss to Multidimensional Feature Space in Deep Neural
Networks for Open-set Recognition
Daiju Kanaoka
1 a
, Yuichiro Tanaka
2 b
and Hakaru Tamukoh
1,2 c
1
Graduate School of Life Science and Systems Engineering, Kyushu Institute of Technology,
2-4 Hibikino, Wakamatsu-ku, Kitakyushu-shi, Fukuoka, Japan
2
Research Center for Neuromorphic AI Hardware, Kyushu Institute of Technology,
2-4 Hibikino, Wakamatsu-ku, Kitakyushu-shi, Fukuoka, Japan
Keywords:
Open-set Recognition, Neural Networks, Image Classification, Unknown Class.
Abstract:
With the advent of deep learning, significant improvements in image recognition performance have been
achieved. In image recognition, it is generally assumed that all the test data are composed of known classes.
This approach is termed as closed-set recognition. In closed-set recognition, when an untrained, unknown class
is input, it is recognized as one of the trained classes. The method whereby an unknown image is recognized
as unknown when it is input is termed as open-set recognition. Although several open-set recognition methods
have been proposed, none of these previous methods excel in terms of all three evaluation items: learning cost,
recognition performance, and scalability from closed-set recognition models. To address this, we propose
an open-set recognition method using the distance between features in the multidimensional feature space of
neural networks. By applying center loss to the feature space, we aim to maintain the classification accuracy
of closed-set recognition and improve the unknown detection performance. In our experiments, we achieved
state-of-the-art performance on the MNIST, SVHN, and CIFAR-10 datasets. In addition, the proposed ap-
proach shows excellent performance in terms of the three evaluation items.
1 INTRODUCTION
With the advent of deep learning, image recognition
performance has improved dramatically and has also
been reported to surpass the image recognition per-
formance of a human (He et al., 2016). When tested,
most existing image recognition methods assume that
all the input images belong to known classes. Thus,
they can classify the known classes; however, when
an unknown class is input, these methods classify it as
one of the known classes. This type of image recog-
nition is called closed-set recognition. By contrast,
when an unknown class is input, the image recog-
nition method that recognizes it as an unknown is
termed as open-set recognition (Scheirer et al., 2013).
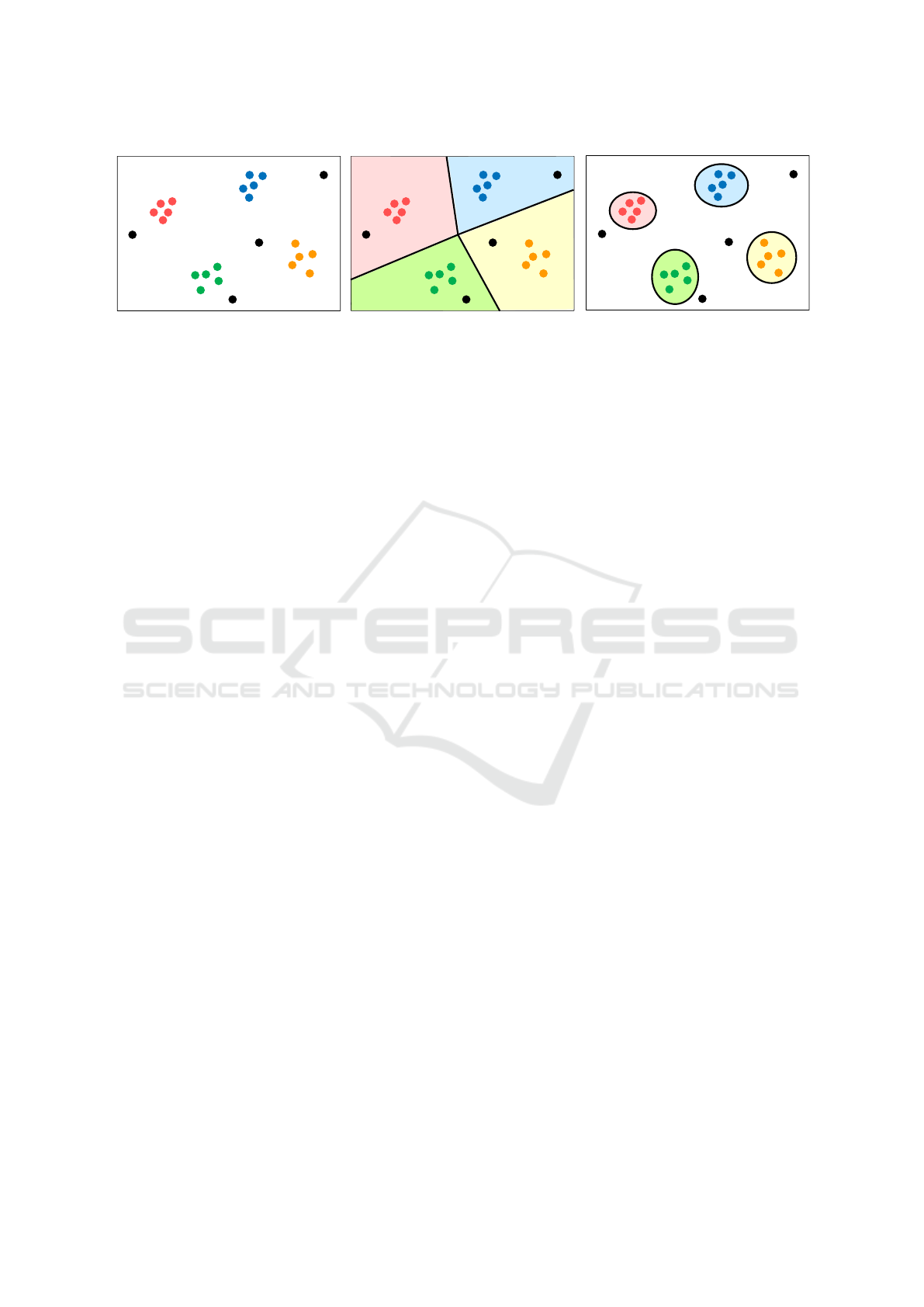
Figure 1 shows the difference between closed-
set recognition and open-set recognition. For the
dataset distribution shown in (a), closed-set recogni-
tion, shown in (b), calculates a hyperplane that sepa-
rates each class suitably. However, in open-set recog-
a
https://orcid.org/0000-0003-2300-4189
b
https://orcid.org/0000-0001-6974-070X
c
https://orcid.org/0000-0002-3669-1371
nition, shown in (c), an exact region for each class
is set; the region that does not belong to any class,
termed as the open space, is also set. The features
that appear in this open space are recognized as an
unknown class.
Deep learning-based open-set recognition can be
classified into two categories: discriminative model-
based methods and reconstruction model-based meth-
ods. The discriminative model-based method in-
volves low learning costs and is easily scalable as
its architecture remains the same as that of closed-
set recognition models; nevertheless, its recognition
performance is low. By contrast, the recognition
performance of reconstruction model-based meth-
ods is higher than that of the discriminative model-
based methods; however, the learning costs are higher
and the architecture differs significantly from that of
closed-set recognition methods. This makes it diffi-
cult to develop an open-set recognition method that
employs closed-set recognition models. Image recog-
nition is often used in embedded systems, where it be-
comes necessary to train additional unknown classes.
Therefore, an open-set recognition model with low
Kanaoka, D., Tanaka, Y. and Tamukoh, H.
Applying Center Loss to Multidimensional Feature Space in Deep Neural Networks for Open-set Recognition.
DOI: 10.5220/0010816600003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
359-365
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
359
Class:1
Class:2
Class:3
Class:4
Unknown
Class:1
Class:2
Class:3
Class:4
Unknown
Class:1
Class:2
Class:3
Class:4
Unknown
(a) Distribution of a dataset
(b) Closed-set recognition
(c) Open-set recognition
Figure 1: Comparison of closed-set recognition and open-set recognition.
training costs and high recognition performance is
required. In addition, if the pre-trained closed-set
recognition models can be scaled up to open-set
recognition via fine tuning, the learning costs can be
reduced. Consequently, it is necessary to develop an
open-set recognition method with low learning costs,
high recognition performance, and scalability from
closed-set recognition.
Anomaly detection is a research topic similar to
open-set recognition. In a previous study on anomaly
detection, a method using the feature space of a recog-
nition model pre-trained on ImageNet (Deng et al.,
2009), which is a large-scale image dataset, was pro-
posed (Rippel et al., 2020). This study confirmed that
normal images and anomaly images appear at differ-
ent positions in a multidimensional feature space.
Deep metric learning is generally used for face
recognition (Wang and Deng, 2021). In face recog-
nition, there are few changes in the features be-
tween classes; therefore, deep metric learning gener-
ates a feature space with a bias between the classes
by imposing constraints on a feature space, such
that features of the same class are located near each
other, whereas features of different classes are lo-
cated far away. Deep metric learning methods such as
contrastive-loss (Chopra et al., 2005) and triplet-loss
(Wang et al., 2014) are well known. However, the dis-
advantage of these methods is that they require a pair
of classes to be created from the dataset during train-
ing; this results in high learning costs as the number
of classes increases. Center loss (Wen et al., 2016)
is a loss function used in face recognition. Center
loss acts as a constraint to keep features of the same
class close in a given batch during training. Center
loss is not classified as deep metric learning based
on its properties. It has achieved high performance
in the field of face recognition. In addition, unlike
contrastive loss, center loss does not require a pair of
classes to be created from the dataset during training.
Thus, it is easier to incorporate into problems other
than face recognition.
In this paper, we propose an open-set recogni-
tion method that focuses on the multidimensional fea-
ture space formed in the middle layer of neural net-
works. Using center loss for a multidimensional fea-
ture space during training, the distance between fea-
tures of each class in a feature space is made vacant.
In the multidimensional feature space of the trained
classifier, clusters are formed at a certain distance for
each class. When an unknown class is input, it is ex-
pected to appear at a different location from the clus-
ters of each class within the multidimensional feature
space. Thus, we propose a method that calculates the
distance between each cluster and a feature of the in-
put image; this approach estimates a class if the dis-
tance is within a set threshold and recognizes as un-
known class if it exceeds the threshold.
2 RELATED STUDIES
2.1 Open-set Recognition
Open-set recognition can be realized via tradi-
tional machine learning-based methods using SVM
(Scheirer et al., 2013) and the nearest neighbor meth-
ods (Mensink et al., 2013) or via deep learning-based
methods (Geng et al., 2020). In this paper, we dis-
cuss deep learning-based methods, which are the most
popular approaches and exhibit high recognition per-
formance.
2.1.1 Discriminative Model (DM)-based
Methods
Discriminative model-based methods generally use
the probability distribution of each class output from
the classifier (Hendrycks and Gimpel, 2017; Bendale
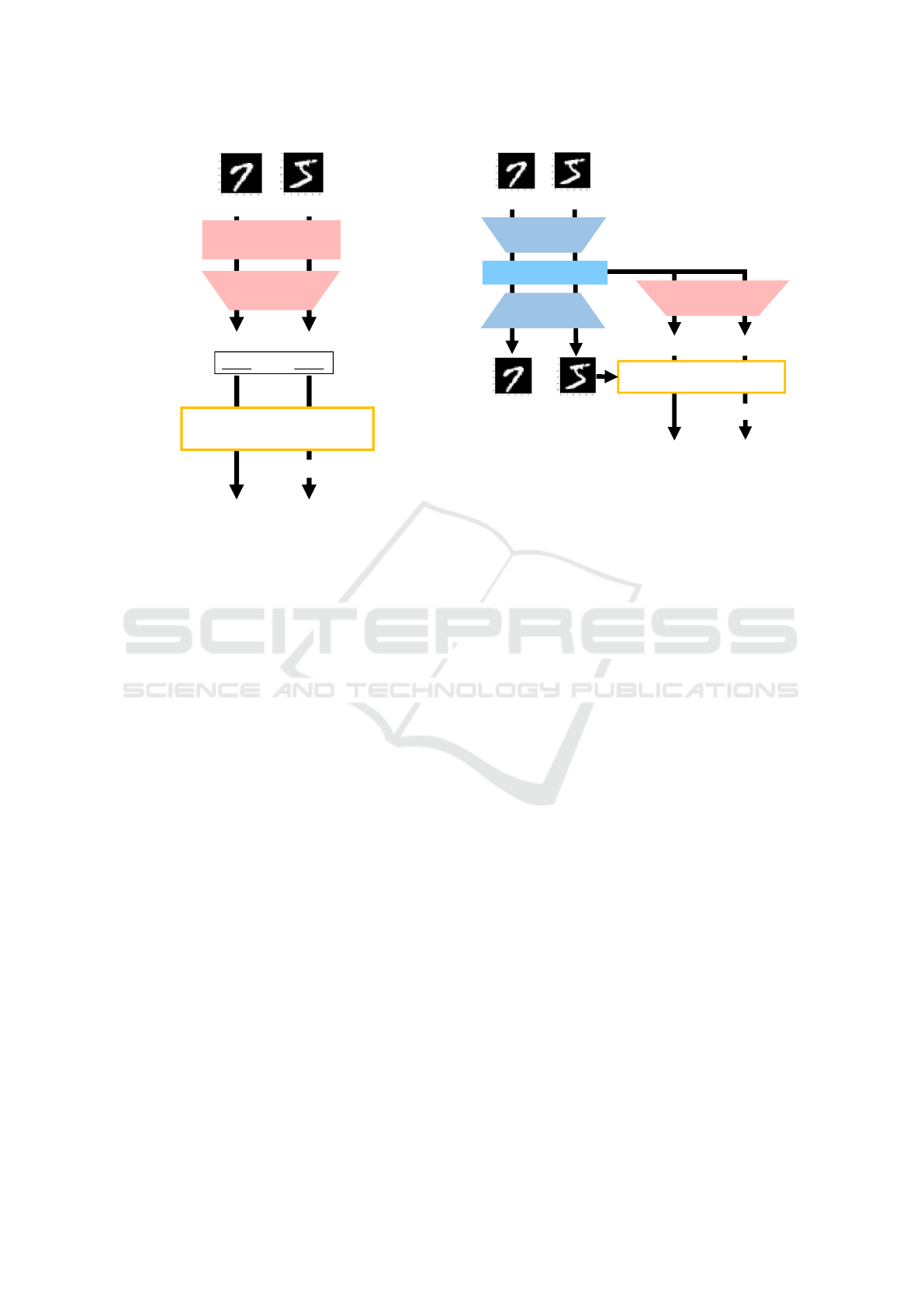
and Boult, 2016). Figure 2 presents a block diagram
of discriminative model-based methods. For example,
softmax-threshold recognizes an unknown class if the
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
360
Unknown Known
Classifier
Feature
Extraction
Class:5
0.76
Class:5
0.98
>Threshold
Unkown Class:5
Maximum
Probability
Maximum
Probability
condition is satisfied
Figure 2: Block diagram of discriminative model-based
methods.
maximum probability of the output probability distri-
bution of each class exceeds a set threshold; alterna-
tively, it estimates a class if this maximum probabil-
ity is less than the threshold (Hendrycks and Gimpel,
2017). The structure of this method is almost identi-
cal to that of closed-set recognition models; it offers
the advantage of low learning costs but suffers from
the disadvantage of a low recognition performance.
2.1.2 Reconstructive Model (RM)-based
Methods
In reconstruction model-based methods, a decoder is
installed in the model to reconstruct the input im-
age and calculate the reconstruction error (Yoshihashi
et al., 2019; Perera et al., 2020; Sun et al., 2020).
Figure 3 depicts the block diagram of reconstruction
model-based methods. If the calculated reconstruc-
tion error exceeds a set threshold, a classifier recog-
nizes it as an unknown; however, if this error is lower
than the threshold, the classifier estimates it as a class.
Although this method affords higher recognition per-
formance than discriminative model-based methods,
it suffers from the disadvantage of higher learning
costs because the reconstruction network needs to be
added to the closed-set recognition model.
Unknown Known
Classifier
Class:5 Class:5
< Threshold
Unknown
Class:5
Latent Features
Encoder
Reconstruct Images
Decoder
Reconstruct
Error
condition is satisfied
Figure 3: Block diagram of reconstructive model-based
methods.
2.2 Anomaly Detection using
Multidimensional Feature Space
The anomaly detection method proposed by Rip-
pel et al. focuses on the multidimensional feature
space obtained from each middle layer of Efficient-
Net (Tan and Le, 2019) pre-trained using ImageNet
(Deng et al., 2009) (Rippel et al., 2020). Figure
4 presents the block diagram of the anomaly detec-
tion method. This method is performed without re-
training the pre-trained model. First, the multivariate
Gaussian distribution of normal images is obtained
by applying Gaussian fitting to the multidimensional
features obtained from the middle layer, when nor-
mal images of the training data are input. During
testing, the Mahalanobis distance between the mul-
tidimensional features when the image is input and
the multivariate Gaussian distribution obtained from
the normal images of the training data are calculated.
If the Mahalanobis distance is within the set thresh-
old, the image is classified as a normal image; how-
ever, if it exceeds the threshold, it is classified as an
anomaly image. During verification using MVTec-
AD (Bergmann et al., 2021), which is a dataset for
anomaly detection, a higher score was achieved, as
compared to previous anomaly detection methods.
2.3 Center Loss
Center loss is a loss function used for face recogni-
tion. A model with center loss learns the center point
of each class of features in a multidimensional feature
space and penalizes the distance between features and
the center point of the class. In this manner, a biased
Applying Center Loss to Multidimensional Feature Space in Deep Neural Networks for Open-set Recognition
361

Anomaly Normal
Classifier
Feature
Extraction
Gaussian distribution
of normal
Multidimensional
Feature Space
Multidimensional
Features
EfficientNet pre-trained
with ImageNet
Anomaly
Normal
Distance<Threshold
condition is satisfied
Figure 4: Block diagram of anomaly detection using multi-
dimensional feature space.
feature space is formed for each class. Equation 1
shows the loss function of the center loss, where m is
the batch size, x
x
x
i
denotes the features of the input data
in the feature space, and c
c
c
y
i
is the center point of class
y
i
in the feature space.
L
c
=
1
2
m
∑
i=1
kx
i
− c
y
i
k
2
2
(1)
Equation 2, 3 shows the update formula for the
center point c
j
of class j, Where t is a learning step,
and α is a hyperparameter. Further, δ(condition) = 1
if the condition is satisfied; otherwise, δ(condition) =
0.
c
t+1
j
= c
t
j
− α · ∆c
t
j
(2)
∆c
j
=
∑
m
i=1
δ(y
i
= j) · (c
j
− x
i
)
1 +
∑
m
i=1
δ(y
i
= j)
(3)
Accordingly, the loss is calculated using Equa-
tion 1, and the center point of each class is up-
dated based on Equation 2, 3. Based on the bench-
marks conducted by the authors on face recognition
datasets, high performance was confirmed even on
small datasets. This also proves that the loss func-
tion is easier to optimize, as compared to the previous
loss functions used for face recognition.
3 PROPOSED METHOD
In this paper, we propose an open-set recognition
method using the multidimensional feature space of
neural networks. We train the neural network on a
dataset comprising only known classes, as in the case
of closed-set recognition. During training, center loss
is applied to the middle layer, immediately before the
output layer of the neural network. In a multidimen-
sional feature space, features of the unknown class are
expected to appear at different positions from features
of the trained classes. By applying center-loss to the
multidimensional feature space, the distance between
features of the trained classes can be shortened, so
that features of the unknown class appear farther from
features of the trained classes compared to the case
where center-loss is not applied. We also calculate
the cross-entropy loss for the probability distributions
of each class, which is the final output. The sum of
these values is used in training as the loss of the neu-
ral network. Next, the training data are input to the
trained neural network, and multivariate Gaussian fit-
ting is performed on the clusters of each class that
appear in the feature space.
Figure 5 shows the block diagram for testing.
First, the test data are input, and the classes are es-
timated. Next, we calculate the Mahalanobis dis-
tance between the multivariate Gaussian distribution
of the estimated classes and the test data. Equation 4
presents the formula for calculating the Mahalanobis
distance d(x
x
x). Here, x
x
x is a feature in the multidimen-
sional feature space, and µ
µ
µ
i
and Σ
i
are the mean and
covariance matrix of the multivariate Gaussian distri-
bution of an estimated class i, respectively.
d(x
x
x) =
q
(x
x
x − µ
µ
µ
i
)
T
Σ
i
(x
x
x − µ
µ
µ
i
) (4)
When the distance of the 95% confidence interval
of the multivariate Gaussian distribution is set as the
threshold, the model recognizes class as an unknown
if the distance exceeds this threshold.
4 EXPERIMENT
We verified the performance of the proposed
method on three datasets: MNIST (LeCun et al.,
2010), SVHN (Netzer et al., 2011), and CIFAR-10
(Krizhevsky, 2012). All of these are 10-class datasets.
In open-set recognition, the model is only trained on
certain classes of the dataset; the untrained classes are
then tested as unknown classes, and the performance
is evaluated using macro-F1 scores. Similarly, in this
experiment, we trained the model on 6 randomly se-
lected classes out of the 10 classes in each dataset; the
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
362
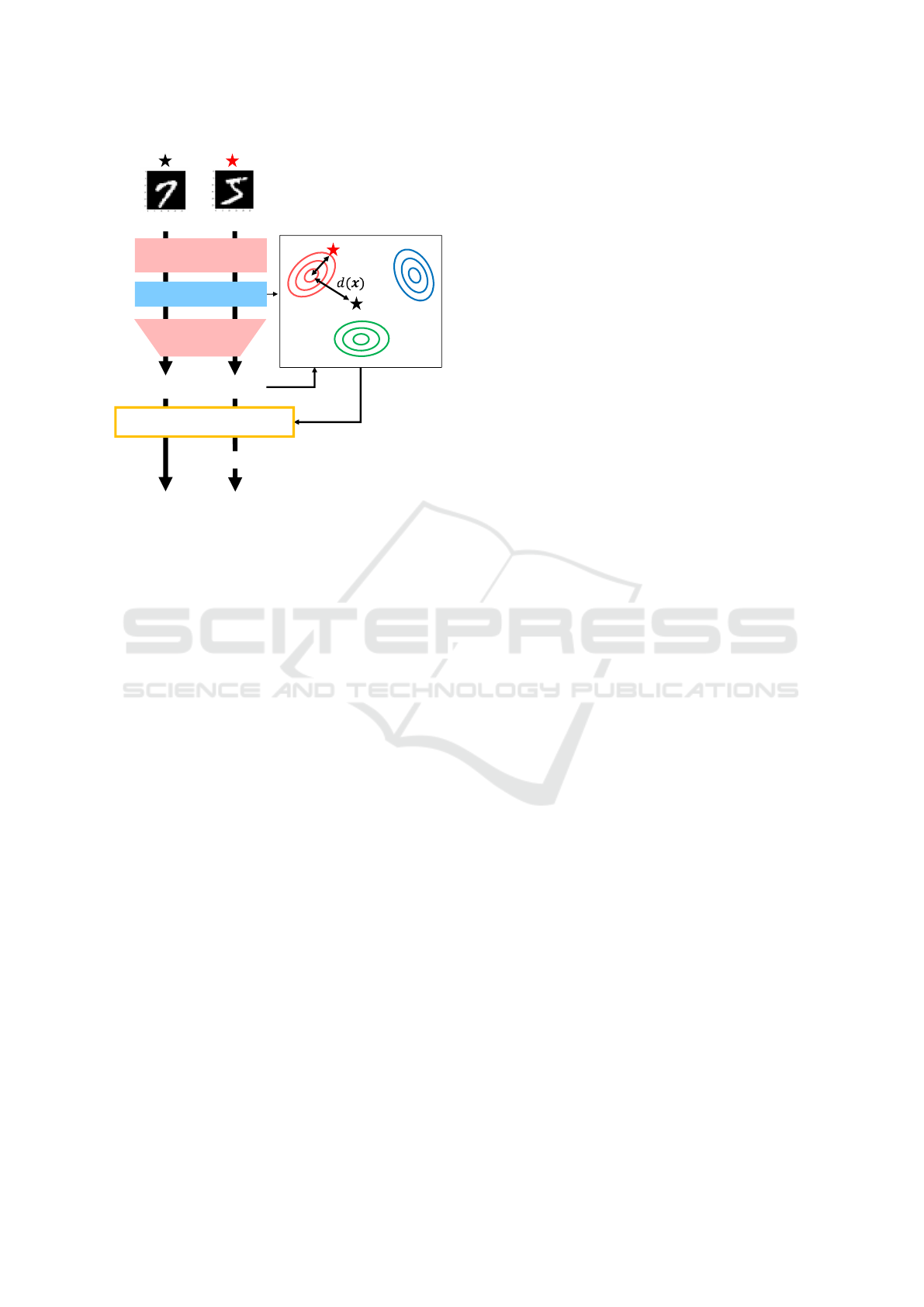
Unknown
Known
Classifier
Feature
Extraction
Class:5 Class:5
Class:5
Class:4
Class:6
Unknown
Class:5
Feature
Multidimensional
Feature Space
Distance>Threshold
condition is satisfied
Figure 5: Block diagram of proposed method.
remaining 4 classes were used as unknown classes.
We calculated the mean and standard deviation of
the scores after five trials. All of our experiments
were conducted using AI Bridging Cloud Infrastruc-
ture provided by National Institute of Advanced In-
dustrial Science and Technology. The model was
trained for about 2 hours using 8 cores of Intel Xeon
Platinum 8360Y Processor 2.4 GHz, NVIDIA A100
with 40GB and 32GB RAM. The experimental con-
ditions are shown in Table 1.
Table 2 presents the experimental results. The
scores of the comparison methods were obtained from
(Sun et al., 2020). The experimental results indicate
that the proposed method achieves better scores than
the previous methods on all the datasets.
5 DISCUSSION
The proposed method outperformed the previous
methods on all the datasets; compared to the pre-
vious methods, it achieved 6 points higher on the
MNIST dataset but only 2 points higher on the SVHN
and CIFAR-10 datasets. MNIST is a grayscale hand-
written character dataset; hence, there is little differ-
ence in the shapes of the recognition targets within
the same class; moreover, the color surrounding the
recognition targets remains constant. By contrast,
SVHN and CIFAR-10 are datasets created from ac-
tual environments; hence, the shapes of the recogni-
tion targets vary within the same class, and the sur-
roundings of the recognition targets are also different.
Hence, the low score is attributed to the large variance
in the multidimensional feature space of the neural
network. This suggests that center loss is not as effec-
tive as MNIST for these datasets. Therefore, chang-
ing the method to apply the multidimensional feature
space may be effective for these datasets. Therefore,
we conclude that the proposed method is highly ef-
fective when the recognition target is simple.
Table 3 presents the evaluation results of the pro-
posed method in terms of three evaluation items:
learning cost, recognition performance, and scalabil-
ity from previous closed-set recognition. The learn-
ing cost is expected to be affected by the multivariate
Gaussian fitting and the center loss computation that
were additionally introduced to the network. Multi-
variate Gaussian fitting involves low computational
costs because it can be performed by inputting all the
training data into the model just once. On introduc-
ing center loss to the network, the number of addi-
tional trainable parameters was only 5,120; by con-
trast, the number of trainable parameters in ResNet34
used in the experiment was approximately 20 mil-
lion. Therefore, we concluded that the effects of in-
troducing these additional computations on the learn-
ing cost were significantly small. With regard to the
recognition performance, we achieved a score exceed-
ing those of all the previous methods. Finally, the
extension from the closed-set recognition models is
highly effective because it only employs the multidi-
mensional feature space formed in the middle layer
of the classifier and does not alter the structure of the
classifier. To summarize, the proposed method is su-
perior to the previous approaches in terms of the three
evaluation items.
6 FUTURE WORKS
In the future, we aim to improve the recognition per-
formance of the proposed method and to further re-
search incremental learning for open-world recogni-
tion.
In this study, we applied center loss to the mid-
dle layer. However, in the field of facial recognition,
several loss functions have been proposed that do not
require the creation of class pairs on datasets, simi-
lar to the center loss (Deng et al., 2019; Liu et al.,
2017; Wang et al., 2018). A model with center loss
learns to locate features of the same class near each
other; however, a model with these methods can learn
to locate features of different classes situated far away
in the multidimensional feature space. Therefore, by
changing the loss function applied in the middle layer,
Applying Center Loss to Multidimensional Feature Space in Deep Neural Networks for Open-set Recognition
363

Table 1: Experiment condition.
Network ResNet34(He et al., 2016)
Training epochs 300
Number of dimensions of multidimensional feature space 512
Optimization method for cross-entropy loss Adam
Optimization method for center loss SGD
Table 2: Macro-F1 scores.
Method MNIST SVHN CIFAR-10
DM-based
methods
Softmax (Hendrycks and Gimpel, 2017) 0.768 ± 0.008 0.725 ± 0.012 0.600 ±0.037
Openmax (Bendale and Boult, 2016) 0.798 ± 0.018 0.737 ± 0.011 0.623 ±0.038
RM-based
methods
CROSR (Yoshihashi et al., 2019) 0.803 ± 0.013 0.753 ± 0.019 0.668 ±0.013
GDFR (Perera et al., 2020) 0.821 ± 0.021 0.716 ± 0.010 0.700 ±0.024
CGDL (Sun et al., 2020) 0.837 ± 0.055 0.776 ± 0.040 0.655 ±0.023
Proposed method 0.901 ± 0.021 0.780 ± 0.006 0.715 ±0.019
Table 3: Performance in terms of three evaluation items.
DM model-based methods RM model-based methods
Proposed method
Learning cost Low High Low
Recognition performance Low High High
Scalability from
closed-set recognition models
×
the recognition performance can be improved. The
threshold for recognition as an unknown class was
determined based on the confidence interval. There-
fore, the unknown recognition performance can be
improved by using a different threshold determination
method, instead of the traditional anomaly detection.
The open-set recognition proposed herein does
not learn the additional classes recognized as un-
known classes. The recognition method that in-
cludes incremental learning, whereby classes recog-
nized as unknown in open-set recognition are addi-
tionally learned, is termed as open-world recognition
(Bendale and Boult, 2015). In the future, we aim to
study and apply incremental learning for the proposed
open-set recognition.
7 CONCLUSION
In this work, we developed and verified an open-set
recognition method using the Mahalanobis distance in
the multidimensional feature space formed at the mid-
dle layer of a neural network. We applied center loss
to the middle layer during training; consequently, fea-
tures of the same class were located near each other in
the multidimensional feature space. The experimental
results show that the proposed method achieves bet-
ter scores than state-of-the-art methods on all datasets
(i.e., MNIST, SVHN, and CIFAR-10). In addition,
the proposed method achieves better results than the
previous methods in terms of three metrics: learning
cost, recognition performance, and scalability from
closed-set recognition models. In the future, we plan
to further improve the recognition performance and
research open-world recognition.
ACKNOWLEDGMENT
This paper is based on results obtained from a
project, JPNP16007, commissioned by the New En-
ergy and Industrial Technology Development Organi-
zation (NEDO).
REFERENCES
Bendale, A. and Boult, T. (2015). Towards open world
recognition. In The IEEE Conference on Computer
Vision and Pattern Recognition (CVPR).
Bendale, A. and Boult, T. E. (2016). Towards open set
deep networks. In Proceedings of the IEEE conference
on computer vision and pattern recognition (CVPR),
pages 1563–1572.
Bergmann, P., Batzner, K., Fauser, M., Sattlegger, D., and
Steger, C. (2021). The mvtec anomaly detection
dataset: a comprehensive real-world dataset for un-
supervised anomaly detection. International Journal
of Computer Vision, 129(4):1038–1059.
Chopra, S., Hadsell, R., and LeCun, Y. (2005). Learning
a similarity metric discriminatively, with application
to face verification. In 2005 IEEE Computer Society
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
364

Conference on Computer Vision and Pattern Recogni-
tion (CVPR), volume 1, pages 539–546.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-
Fei, L. (2009). Imagenet: A large-scale hierarchical
image database. In 2009 IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
248–255.
Deng, J., Guo, J., Xue, N., and Zafeiriou, S. (2019). Ar-
cface: Additive angular margin loss for deep face
recognition. In Proceedings of the IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 4690–4699.
Geng, C., Huang, S.-J., and Chen, S. (2020). Recent ad-
vances in open set recognition: A survey. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence
(TPAMI).
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition (CVPR), pages 770–778.
Hendrycks, D. and Gimpel, K. (2017). A baseline for de-
tecting misclassified and out-of-distribution examples
in neural networks. In 5th International Conference
on Learning Representations (ICLR).
Krizhevsky, A. (2012). Learning multiple layers of features
from tiny images. University of Toronto.
LeCun, Y., Cortes, C., and Burges, C. (2010). Mnist hand-
written digit database. ATT Labs [Online]. Available:
http://yann.lecun.com/exdb/mnist, 2.
Liu, W., Wen, Y., Yu, Z., Li, M., Raj, B., and Song, L.
(2017). Sphereface: Deep hypersphere embedding for
face recognition. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition
(CVPR), pages 212–220.
Mensink, T., Verbeek, J., Perronnin, F., and Csurka, G.
(2013). Distance-based image classification: Gener-
alizing to new classes at near-zero cost. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence
(TPAMI), 35(11):2624–2637.
Netzer, Y., Wang, T., Coates, A., Bissacco, A., Wu, B., and
Ng, A. Y. (2011). Reading digits in natural images
with unsupervised feature learning.
Perera, P., Morariu, V. I., Jain, R., Manjunatha, V.,
Wigington, C., Ordonez, V., and Patel, V. M.
(2020). Generative-discriminative feature representa-
tions for open-set recognition. In Proceedings of the
IEEE/CVF Conference on Computer Vision and Pat-
tern Recognition (CVPR).
Rippel, O., Mertens, P., and Merhof, D. (2020). Model-
ing the distribution of normal data in pre-trained deep
features for anomaly detection. In 2020 25th Inter-
national Conference on Pattern Recognition (ICPR),
pages 6726–6733.
Scheirer, W. J., de Rezende Rocha, A., Sapkota, A., and
Boult, T. E. (2013). Toward open set recognition.
IEEE Transactions on Pattern Analysis and Machine
Intelligence (TPAMI), 35(7):1757–1772.
Sun, X., Yang, Z., Zhang, C., Ling, K.-V., and Peng, G.
(2020). Conditional gaussian distribution learning for
open set recognition. In Proceedings of the IEEE/CVF
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 13480–13489.
Tan, M. and Le, Q. (2019). Efficientnet: Rethinking model
scaling for convolutional neural networks. In Inter-
national Conference on Machine Learning (CIML),
pages 6105–6114.
Wang, H., Wang, Y., Zhou, Z., Ji, X., Gong, D., Zhou, J.,
Li, Z., and Liu, W. (2018). Cosface: Large margin co-
sine loss for deep face recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition (CVPR), pages 5265–5274.
Wang, J., song, Y., Leung, T., Rosenberg, C., Wang, J.,
Philbin, J., Chen, B., and Wu, Y. (2014). Learning
fine-grained image similarity with deep ranking. Pro-
ceedings of the IEEE Computer Society Conference on
Computer Vision and Pattern Recognition (CVPR).
Wang, M. and Deng, W. (2021). Deep face recognition: A
survey. Neurocomputing, 429:215–244.
Wen, Y., Zhang, K., Li, Z., and Qiao, Y. (2016). A discrim-
inative feature learning approach for deep face recog-
nition. In Leibe, B., Matas, J., Sebe, N., and Welling,
M., editors, European conference on computer vision
(ECCV), pages 499–515. Springer International Pub-
lishing.
Yoshihashi, R., Shao, W., Kawakami, R., You, S., Iida, M.,
and Naemura, T. (2019). Classification-reconstruction
learning for open-set recognition. In Proceedings of
the IEEE/CVF Conference on Computer Vision and
Pattern Recognition (CVPR), pages 4016–4025.
Applying Center Loss to Multidimensional Feature Space in Deep Neural Networks for Open-set Recognition
365
