Animating and Adjusting 3D Orthodontic Treatment Objectives

Maxime Chapuis

1,2 a

, Mathieu Lafourcade

1 b

, William Puech

1 c

, G

erard Guillerm

and Noura Faraj

1 d

LIRMM, Universit

e de Montpellier, CNRS, Montpellier, France

Groupe Orqual, Pau, France

Keywords:

Interactive System, 3D Models, Animation, Scripting.

Abstract:

In this paper, we present an interactive system to adjust and animate 3D orthodontic treatment objectives, the

main goal is to improve the communication tools used by orthodontists to exchange with their patients. Given

a 3D pathological patient model and a treatment objective, we propose to automatically generate intermedi-

ate steps using script-like treatment scenarios. The intermediate steps can then be adjusted using intuitive

manipulators, and used to produce an animation of the treatment. The resulting animation is a useful tool

to help patients visualize the potential evolution of their dentition and accept the treatment. The proposed

system relies on the registration of a reference model on both the treatment objective and the patient-speciﬁc

3D segmented mesh, to automatically position key feature points and create control curves. These primitives

are used to both, guide teeth movements during the animation, and provide manipulators to allow for user

interactions. The key contributions of this work are (a) the use of a registered reference model to position and

create intuitive control primitives, and (b) the introduction of script-like treatment scenarios to facilitate and

minimize user interactions during the creation of intermediate treatment steps.

1 INTRODUCTION

Computer aided orthodontic treatment planning is

now the standard way of designing a treatment as it

improves its outcome and allows for a 3D preview of

the patient’s dentition with the desired alignment and

occlusion. This preview, called a treatment objective,

is also a communication tool between the practitioner

and the patient. By viewing the expected outcome,

patients are able to better understand the proposed

treatment, and are more likely to adhere to it. To take

it a step further, an animation of the treatment can be

proposed to illustrate the different states of their den-

tition at different stages of the treatment. However,

doing a simple interpolation between the initial state

and the objective is not correct, as it does not reﬂect

the different steps of a treatment. Indeed, to be use-

ful, a treatment animation should include intermedi-

ate steps. The question is then, how to deﬁne them?

One way to do it, is to manually place each tooth in

the desired position at each step. However, this so-

https://orcid.org/0000-0003-0876-8711

https://orcid.org/0000-0003-2832-2143

https://orcid.org/0000-0001-9383-2401

https://orcid.org/0000-0001-6637-0336

lution is a tedious time consuming process. To ad-

dress this issue, we propose to use a set of instructions

(called actions) to allow the user to deﬁne a treatment

scenario, and automatically generate the intermediate

steps. A scenario contains the collection of actions

for each step of the treatment. Theses actions (similar

to a scripting language) reﬂect the intention of the or-

thodontist during the treatment (extract, level, align,

rotate, etc.). In this paper, we propose a method that

can take any 3D treatment objective as an input, and

allows to easily create an animation of the treatment

with clearly deﬁned intermediate steps. To guide the

movements during the animation, our method relies

on a set a parametric curves automatically positioned

on the input models, which can be modiﬁed through

the use of control points. Manipulators are also pro-

vided in the case the user wants to adjust the generated

intermediate steps or the treatment objective.

The rest of the paper is organized as follows. First

we present related work in Section 2. Then, our pro-

posed method is detailed in Section 3. The results

of our method applied to real patient models are pre-

sented and discussed in Section 4. Finally, in Sec-

tion 5 we conclude and present future work.

Chapuis, M., Lafourcade, M., Puech, W., Guillerm, G. and Faraj, N.

Animating and Adjusting 3D Orthodontic Treatment Objectives.

DOI: 10.5220/0010822100003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

60-67

ISBN: 978-989-758-555-5; ISSN: 2184-4321

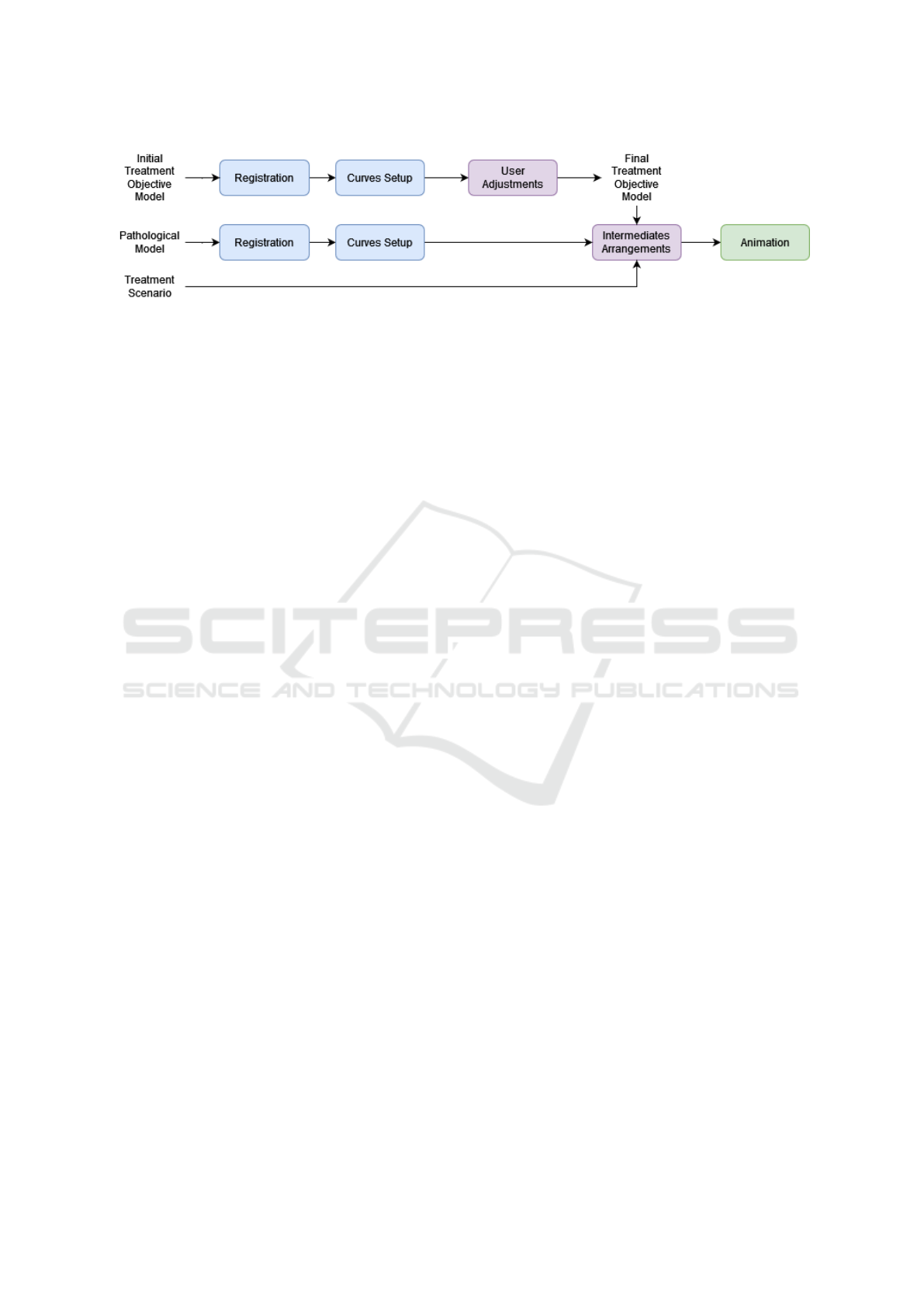
Figure 1: Overview of the system.

2 RELATED WORK

Automatic tooth arrangement is the task of predict-

ing a proper tooth arrangement given a pathological

dental model (i.e a plausible result of the orthodon-

tic treatment). Different types of methods have been

developed for such a task. Kumar et al. proposed a

simulation-based approach, minimizing the energy of

a spring-mass system, where the springs represent or-

thodontic constraints (Kumar et al., 2013b). Cheng

et al. based their approach on satisfying geomet-

ric constraints, by positing feature points on different

planes and curves (Cheng et al., 2015). More recently,

Wei et al. and Li et al. proposed two deep-learning

based methods for automatic tooth arrangement (Wei

et al., 2020; Li et al., 2020a). Deep-learning based

methods offer good-quality tooth alignment on com-

mon cases, but require large data-sets of pre- and post-

treatment orthodontic cases.

When producing a treatment animation, the goal

is, given an initial and a target arrangement, to show

the evolution of the dentition over time. When the

two arrangements are close, using a simple interpola-

tion to compute the intermediate states is reasonable.

In the context of invisible appliances, Li et al. use a

more elaborate strategy. They formulate the problem

as a path planning problem (Li et al., 2020b). The

objective is to ﬁnd, for each tooth, a path going from

the initial situation to the target, while minimizing the

translation distance, the rotation angle, and avoiding

collisions with surrounding teeth. To solve this opti-

mization problem, they ﬁrst initialize the solution us-

ing the interpolated values, and then reﬁne it using an

artiﬁcial bee colony algorithm. Another paper, by Li

et al., suggests that genetic algorithms can be used to

ﬁnd proper paths, but the authors only present partial

results, and it is unclear how the teeth transformations

are coded in their method (Li et al., 2009).

3 PROPOSED METHOD

Given a 3D visual treatment objective, we propose

a method allowing for the automatic creation of in-

termediate treatment steps using a script-like sce-

nario. We also provide manipulators, allowing for

three levels of user interactions, to adjust the gener-

ated steps and the treatment objective. During the

generation process and the interactions, teeth move-

ments are guided by a set of control points and para-

metric curves automatically positioned on the input

models. To achieve this our method relies on the reg-

istration of a reference model onto the input arrange-

ments. The registration data allows us to transfer the

control points of the reference model on the input

models. The whole process is illustrated in Fig. 1.

In Section 3.1 and Section 3.2, we ﬁrst detail the

registration process and the curves setup. Then in

Section 3.3 we detail the different manipulators, and

ﬁnally we present the process for creating the ani-

mation with a user-deﬁned treatment scenario in Sec-

tion 3.4.

3.1 Registration Process

The goal of the registration process, is to automati-

cally position key control points on both the patho-

logical arrangement and the target arrangement. This

process is applied on each input model independently.

The reference model R, shown on Fig. 2a, is a

generic adult dentition with its teeth in a standard

conﬁguration, and control points placed at the center

of the teeth vestibular faces, in the fashion of braces

(Fig. 2b). The vestibular side of a tooth faces the lips

and cheeks. Here, the use of a registered reference

model gives the ability to transfer properties from the

reference model to the input models, and to recon-

struct potential missing information (such as occluded

mesh parts or roots). Each control point has a refer-

ence frame computed using the up vector and the vec-

tor tangent to the arch at the point position. These

reference frames are used to deﬁne the reference ori-

Animating and Adjusting 3D Orthodontic Treatment Objectives

entations of the teeth. Throughout the registration and

the interactions, the control points are subject to the

same transformations as to their corresponding tooth.

The registration process is composed of two steps,

a rigid registration (Section 3.1.1), and a non-rigid

registration (Section 3.1.2).

3.1.1 Rigid Registration

The main algorithm used to carry out the rigid regis-

tration is the Iterative Closest Point (ICP) (Besl and

McKay, 1992; Chen and Medioni, 1992). This al-

gorithm iteratively constructs a rigid transformation

which minimizes the difference between two point-

clouds by ﬁnding point correspondences in the two

data-sets. As the ICP algorithm is sensitive to the ini-

tial alignment, the rigid registration (Fig. 3) starts by

an initialization step. Its purpose is to place the ref-

erence model R in a good enough starting position to

perform an ICP on each tooth. This initialization is

done by scaling and centering R on the input model

P (Fig. 3b and Fig. 3c). These operations are done

“model-wise”, meaning that every tooth is scaled by

the same ratio and translated by the same vector. The

scaling ratio is estimated by averaging the ratios be-

tween the incisors of P and R. The incisors are well

suited for this purpose as they are almost always en-

tirely visible in patient models. The two models are

then roughly aligned by a model-wise ICP (Fig. 3d).

Then “tooth-wise” operations are performed: each

tooth of R is scaled to match its corresponding tooth in

P. To end the initialization process, the teeth bound-

ing boxes P and R are aligned. Mandibular bounding

boxes

are aligned on their upper center, and max-

illary bounding boxes

on their lower center. The

choice to align the top of the crowns is motivated

by the fact that patient teeth are not always entirely

visible. Therefore, centering them on their bounding

boxes centers would result in a poor initialization for

the ICP (Fig. 4).

Finally, each tooth in R is registered to the cor-

responding tooth in P by a tooth-wise ICP (Fig. 3e).

Figure 2: a. Front view of our reference model, b. Control

points are placed at the center of the teeth vestibular faces.

Mandibular refers to the lower arch.

Maxillary refers to the upper arch.

(a)

(b) (c) (d)

(e)

Figure 3: Reference model rigid registration (blue) on the

patient model (red): a. Initial alignment, b. Uniform scal-

ing, c. Centering, d. Model-wise ICP, e. Tooth-wise scal-

ing, centering and ICP.

Only the vertices contained in the bounding boxes of

the patient’s teeth are considered during the ICP. The

result of the rigid registration is a modiﬁed version of

R called P

, with the same tooth arrangement as the

patient.

3.1.2 Non-rigid Registration

The teeth of the reference model are generic teeth

and thus, do not match the patients teeth geometry.

These differences are mitigated by projecting the ref-

erence crowns vertices onto the patient’s crowns using

the projection method APSS (Guennebaud and Gross,

2007). To avoid unwanted deformations, care should

be taken to only project overlapping vertices. The re-

sult of this ﬁnal registration step is shown on Fig. 5a

and Fig. 5b.

3.2 Curves Setup

On each arch, two curves are created, the reference

curve Cr, and the arch curve Ca. The former is used to

translate and orient teeth along the arch, and the latter

to adjust the shape of the arch with the appropriate

manipulator (Section 3.3.3).

3.2.1 Reference Curve and Patient Curve

The control points of the teeth of the reference model

R are used as the control points of a parametric curve

Cr(t), called the reference curve. This reference curve

is a Catmull–Rom spline (Catmull and Rom, 1974).

The choice to use a Catmull–Rom spline is moti-

vated by its interpolating properties (the curve goes

exactly through the control points), and its relatively

low computational cost. This curve gives the ability

Figure 4: a. The bounding boxes of a mandibular reference

tooth (blue) is centered on the bounding box of its corre-

sponding patient tooth (red), b. The same teeth are aligned

on the upper center of their bounding boxes.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

(a) (b)

Tooth-wise ICP

APSS

Projection

Figure 5: a. Views of the lower arches of the patient model

P (red) and the fully registered reference model P

(blue),

b. Comparison of the right lower ﬁrst molar before APSS

(top) and after (bottom).

to deﬁne a reference position and orientation at any

parameter t. It also has the beneﬁt of being an in-

tuitive primitive for orthodontists, as it resembles an

orthodontic wire with braces. The orientation used for

each control point corresponds to its initial reference

frame multiplied by the rotation part of the transfor-

mation computed during the registration.

The patient curve Cp is constructed in a similar

way using the control points of the registered refer-

ence P

. The positions and orientations along Cp re-

ﬂect the dental disorders of the patient.

3.2.2 Arch Curve

Following the method proposed by Kumar et al. (Ku-

mar et al., 2013a), cusps and incisal edges are com-

puted on the treatment objective (R). Theses features

are then transferred to the pathological model (P

) us-

ing the previously computed registration transforma-

tions. Since we transfer the feature points, we en-

sure that they are the same on both models. Their re-

spective arch forms can then be derived as the curves

passing through the distobuccal cusps of the ﬁrst mo-

lars, the canines cusps and the midpoint of the incisors

of each arch as illustrated on Fig. 6. The arch forms

are represented by Catmull–Rom splines made of ﬁve

control points each (blue spheres on Fig. 6).

3.3 Manipulators

The manipulators available allow the users to express

their domain expertise by adjusting the treatment ob-

jective and the generated intermediate steps. To make

sure they were relevant to the domain, the different

manipulators were developed in collaboration with an

orthodontist. We propose several manipulators, of in-

creasing sophistication, permitting the adjustment at

different levels: individual teeth, groups of teeth, or

arch-forms. The usage of the different manipulators

is demonstrated in the companion video.

3.3.1 Teeth Manipulators

The simplest manipulator allows to freely translate

and rotate the individual teeth around their local axes.

The local axes of a given tooth are deduced using

the local frame of its corresponding control point. If

needed, this frame can be adjusted with the dedicated

manipulator. The selection of multiple teeth is possi-

ble, and allows the user to apply a translation to every

teeth of the selection. Note that there is a dedicated

manipulator to level a group of selected teeth. This

has the action of setting every control point of the se-

lection to the same level on the vertical axis (based on

the vertical position of the ﬁrst tooth of the selection).

Finally, the extraction manipulator removes a tooth

from the arrangement. Tooth extraction is a typical

way to make room when the teeth are too cluttered to

be aligned properly.

3.3.2 Space Corrections

The spaces manipulator can be used to close inter-

dental spaces on a given range of teeth. This action

is done by moving each ill-positioned tooth along the

reference curve Cr, going from the incisors to the mo-

lars. The induced collisions are resolved along the

way, as if the moving tooth was pushing its neighbors,

as illustrated on Fig. 7.

When included in the range, the pair of central in-

cisors have to be treated ﬁrst then, the left and right

side can be processed independently.

3.3.3 Arch Form Deformation

Each arch form is represented by a Catmull–Rom

spline made of ﬁve control points Ca. The arch defor-

mation manipulator allows, by moving one of point

of Ca, to move every teeth accordingly (every control

point of Cr). The procedure is the following. When

an arch point is moved, the arch curve Ca is modiﬁed

(slightly) and produces Ca

. To propagate this mod-

iﬁcation to the teeth, we compute the translation to

apply to each control point Cr

as the difference in po-

sition between Ca

(t) and Ca(t) (where t is the curve

parameter corresponding to the projection of Cr

Ca). The teeth collisions induced by the translations

are resolved as described is Section 3.3.2. Once the

teeth are in their correct positions, their orientation

are adjusted to match the reference orientations of the

newly formed Cr (the reference orientations are com-

puted as described in Section 3.2 .)

Animating and Adjusting 3D Orthodontic Treatment Objectives

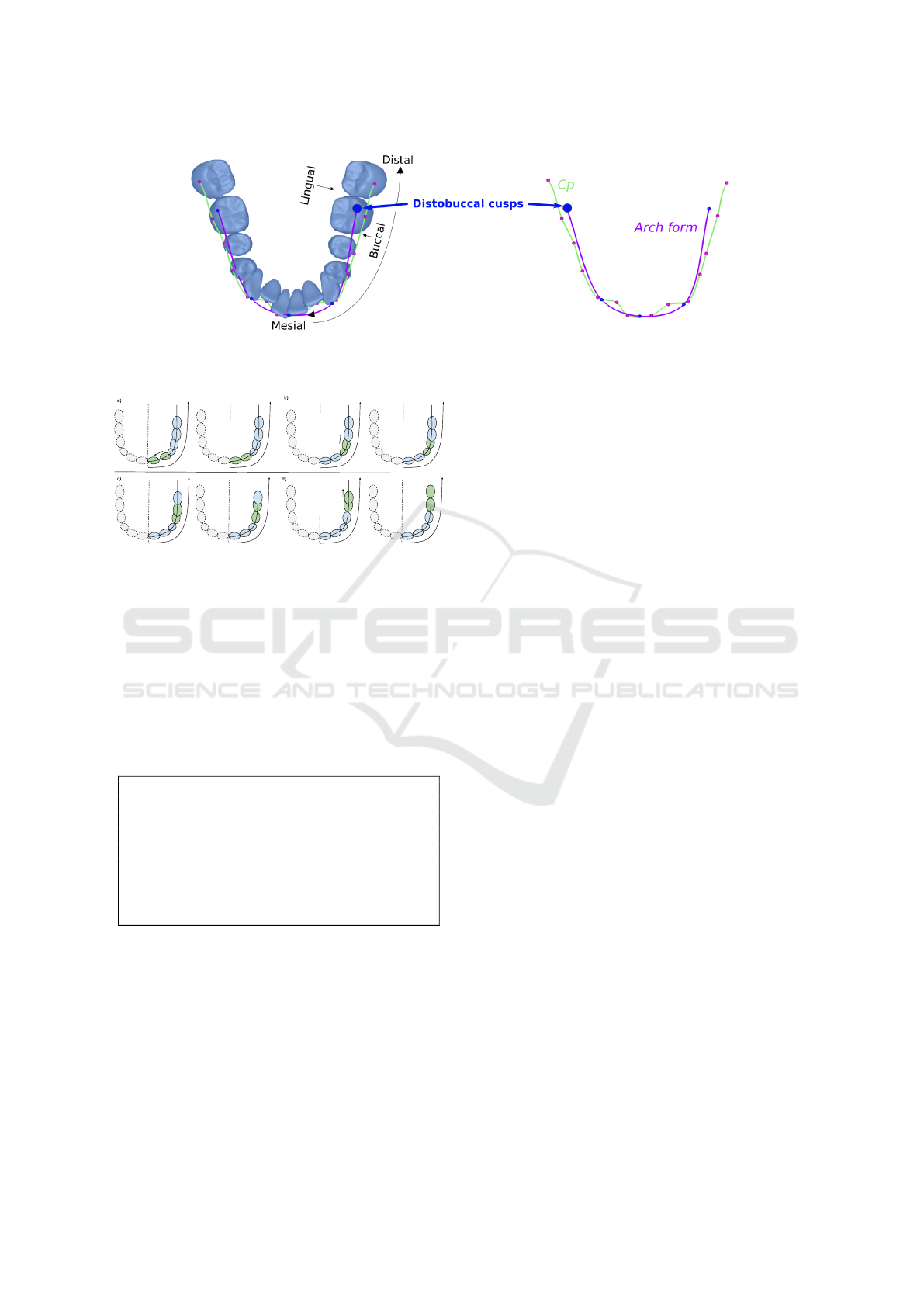
Figure 6: The main features extracted on the lower arch of P

. In green, Cp made of the registered control points. In purple,

the arch form going through the distobuccal cusps of the ﬁrst molars, the canines cusps and the midpoint of the incisors.

Figure 7: The space between each ill-positioned pair

(green) is adjusted. The spaces can either be closed (a) or

opened to de-intersect teeth (b),(c),(d).

3.4 Animation

To create the intermediate treatment steps necessary

for the animation, our method relies on user-deﬁned

treatment scripts.

3.4.1 Treatment Script

step :

ex t rac t l o we r f ir st p rem o lar s

ex t rac t u p pe r se c on d p r emo lar s

step :

lev e l te e th

step :

ali g n te e th

Listing 1: Example of treatment script deﬁning

intermediate steps.

Given a target arrangement, and an initial pathologi-

cal one, the user deﬁnes for each step, the set of ac-

tions to execute in order to get to the objective. These

actions take the form of verbs, reﬂecting the intention

of the orthodontist, and can be applied to a particu-

lar tooth, a group of teeth, or every tooth of an arch.

An example of treatment script is shown in Listing 1.

In this example, three intermediate steps are deﬁned.

The ﬁrst one contains two extract actions, applied on

two groups of teeth (the lower ﬁrst premolars and the

upper second premolars). Actions applied to a group

of teeth are applied to each tooth of the group. The

second step applies the action level on every tooth,

which has the effect of putting the teeth on the same

horizontal plane (based on what is deﬁned in the ob-

jective). The third one, positions the teeth in their tar-

get position using the action align. There is a fourth

implicit step which is, getting to the objective.

3.4.2 Actions

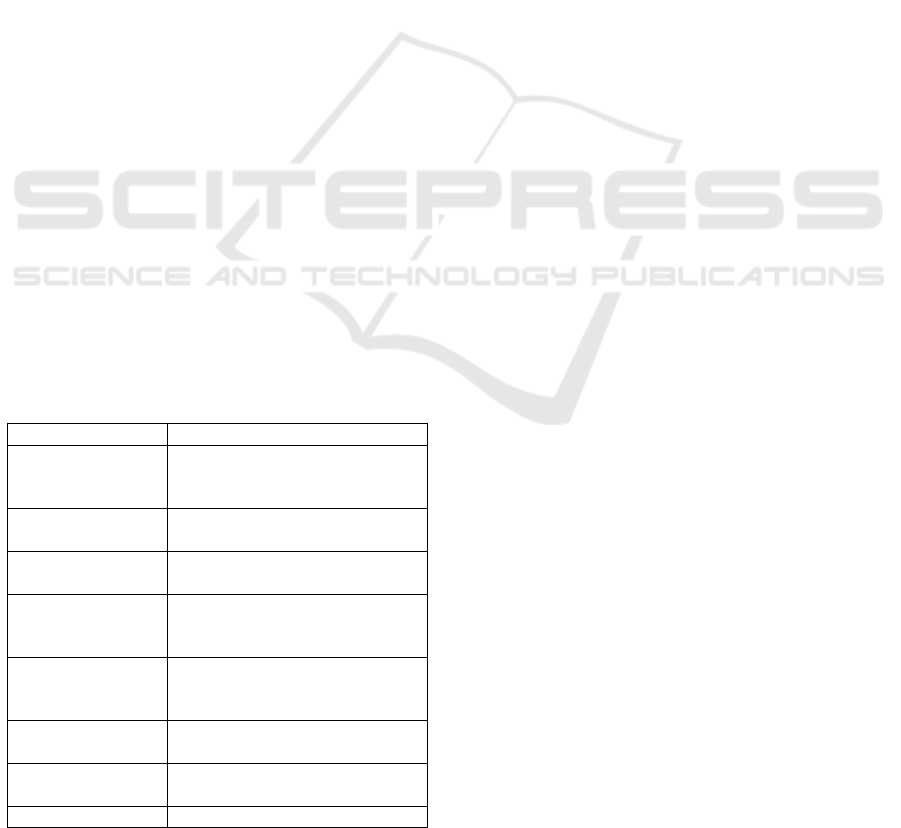
The set of currently available actions is described in

Table 1. Every action is implemented using the con-

trol points or the curves computed in Section 3.2.

The process used to generate the steps is the fol-

lowing. Starting from the initial arrangement, every

time a new step is declared in the script with the step

action: copy the current arrangement and apply the

actions of the step. The application of an action de-

pends on its implementation. Most of the time, it is

done by computing the transformation difference be-

tween the current arrangement and the target arrange-

ment, and only applying a particular component of

the resulting transformation (the component relevant

to the action).

3.4.3 Arrangements Interpolation

The animation between two given dental arrange-

ments is done by linearly interpolating the positions

and orientations of the teeth. Let Pi

and Oi

be the

position and orientation of the tooth j in an initial ar-

rangement, and Pt

and Ot

be the position and orien-

tation of the tooth j in a target arrangement, then for a

given interpolation value t (with 0 6 t 6 1):

(t) = lerp(Pi

, Pt

, t)

(t) = slerp(Oi

, Ot

, t),

(1)

where the lerp function is the regular linear interpola-

tion and the slerp function is the quaternion spherical

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

interpolation (Shoemake, 1985). Here, the slerp func-

tion is used to produce constant-speed rotations. Note

that we have a t value for the position t

and a sec-

ond one for the orientation t

. This gives the ability to

deﬁne different interpolation speeds for the position

and the orientation. Similarly to Li et al., we limit

the amount of rotation and translation possible for a

tooth during one animation step (2° of rotation, and

0.2mm of translation) (Li et al., 2020b). These em-

pirical values are here to represent the limits of the

alveolar bone reconstruction process.

Given every intermediate steps of a treatment, the

resulting animation is the interpolation between the

successive arrangements.

4 EXPERIMENTAL RESULTS

To illustrate our method, we show our pipeline ap-

plied to two representative patient cases, and compare

the resulting animation with the simple linear interpo-

lation between the initial and target arrangement.

Case A (the red model on Fig. 9) presents mod-

erate disorders. The main issues are its upper right

second premolar position (tooth 15), and its anterior

teeth inclination. The treatment scenario for this case

is: ﬁrst level the teeth, then re-position tooth 15 and

ﬁnally align and rotate the remaining teeth. The an-

imation is illustrated on the maxilla in Fig. 9. The

objective is shown in blue, the produced intermediate

steps are in green. The top part of the ﬁgure shows

the linear interpolation for the same animation times

and t

(in grey), and the bottom part is our complete

animation.

Case B (the red model on Fig. 10) illustrates a case

where the provided treatment objective needs to be

adjusted. This can happen when using an automatic

teeth arrangement method to generate the objective

(Section 2). These methods don’t usually predict teeth

extractions or arch expansion. The real treatment plan

for this case suggests the extraction of the premolar.

Therefore, as a preliminary step, the ﬁrst premolars

are extracted and the anterior teeth are re-positioned

using the manipulators described in Section 3.3. The

edited objective is shown on Fig. 8. The treatment

script used to produce the animation is same as List-

ing 1. The resulting animation on the mandibula is

shown on Fig. 10.

The linear interpolation animation is shown in

grey for both cases at the top of Fig. 9 and Fig. 10.

Due to the fact that the interpolation corrects the ro-

tation and position of every teeth simultaneously, we

observe multiple differences. On case A, at t

, our an-

imation only straightens up the teeth to position them

on a same horizontal plane, whereas in the interpo-

lation animation, the teeth moved uniformly closer

to the objective. The difference is clear on tooth 15

(zoomed in). Similar differences are be observed on

case B. The companion video includes the animations

of both cases.

Figure 8: Adjustment of the initial treatment objective by

extracting the premolars, and re-positioning the anteriors.

5 CONCLUSION

In this paper, we present a method allowing to intu-

itively adjust a 3D treatment objective, and to gener-

ate intermediate treatment steps given a user-deﬁned

treatment scenario. The resulting animation is a

more faithful representation of the intended treatment

hence is a better illustration than the simple interpo-

lation between the initial situation and objective, and

may improve the patient’s understanding of his treat-

ment.

In future work, we plan on providing arch-wire

actions to mimic the use of arch-wires of differ-

ent shapes (round, rectangular, squared) and stiffness

(low, medium, high). This requires the use of ad-

ditional patient data such as roots and surrounding

cranio-facial structures. One considered solution is

the registration of a dental cone beam computed to-

mography on our 3D model.

REFERENCES

Besl, P. J. and McKay, N. D. (1992). A method for regis-

tration of 3-d shapes. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 14(2):239–256.

Catmull, E. and Rom, R. (1974). A class of local interpo-

lating splines. In BARNHILL, R. E. and RIESEN-

FELD, R. F., editors, Computer Aided Geometric De-

sign, pages 317–326. Academic Press.

Chen, Y. and Medioni, G. (1992). Object modelling by reg-

istration of multiple range images. Image and Vision

Computing, 10(3):145 – 155. Range Image Under-

standing.

Cheng, C., Cheng, X., Dai, N., Liu, Y., Fan, Q., Hou, Y.,

and Jiang, X. (2015). Personalized Orthodontic Accu-

rate Tooth Arrangement System with Complete Teeth

Model. Journal of Medical Systems, 39(9):84.

Animating and Adjusting 3D Orthodontic Treatment Objectives

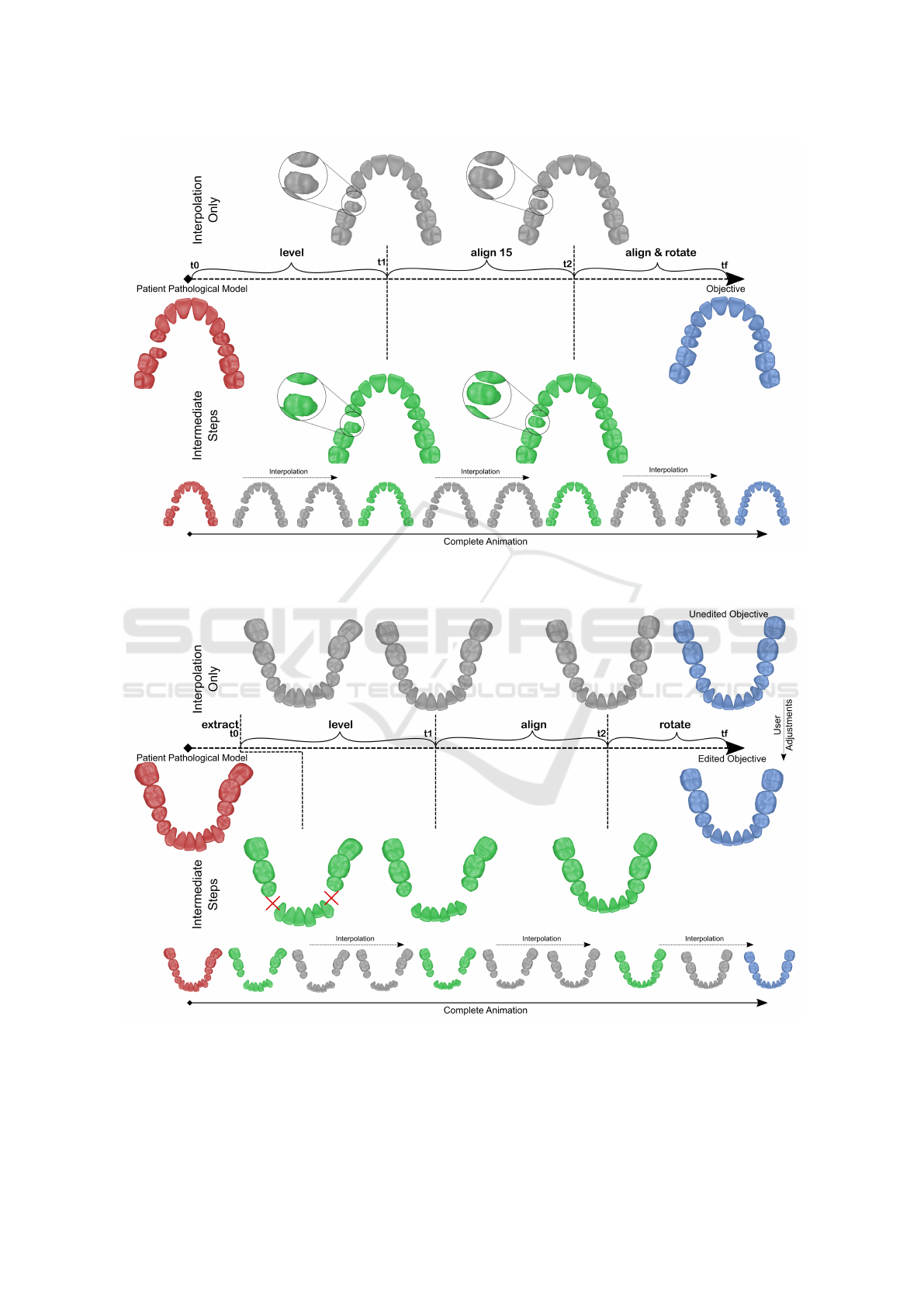
Figure 9: Animation for Case A: Given the initial pathological model (in red) and the objective (in blue), each step produces

an intermediate arrangement (in green). At the top, the linear interpolation in shown for the same animation times t

and t

Our complete animation is shown at the bottom.

Figure 10: Animation for Case B: Given the initial pathological model (in red) and the edited objective (in blue), each step

produces an intermediate arrangement (in green). The red crosses indicate the extraction of two premolars. At the top, the

linear interpolation between the initial situation and the unedited objective is shown. Our complete animation is shown at the

bottom.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

Guennebaud, G. and Gross, M. (2007). Algebraic point set

surfaces. ACM Trans. Graph., 26(3):23–es.

Kumar, Y., Janardan, R., and Larson, B. (2013a). Automatic

feature identiﬁcation in dental meshes. Computer-

Aided Design and Applications, 9:747–769.

Kumar, Y., Janardan, R., and Larson, B. (2013b). Automatic

virtual alignment of dental arches in orthodontics.

Computer-Aided Design and Applications, 10:371–

398.

Li, X., Bi, L., Kim, J., Li, T., Li, P., Tian, Y., Sheng, B., and

Feng, D. (2020a). Malocclusion treatment planning

via pointnet based spatial transformation network. In

Martel, A. L., Abolmaesumi, P., Stoyanov, D., Ma-

teus, D., Zuluaga, M. A., Zhou, S. K., Racoceanu,

D., and Joskowicz, L., editors, Medical Image Com-

puting and Computer Assisted Intervention – MICCAI

2020, pages 105–114, Cham. Springer International

Publishing.

Li, Z., Li, K., and Li, B. (2009). Research on path plan-

ning for tooth movement based on genetic algorithms.

In 2009 International Conference on Artiﬁcial Intel-

ligence and Computational Intelligence, volume 1,

pages 421–424.

Li, Z., Liu, T., Li, H.-A., and Sun, Z. (2020b). Orthodon-

tic path planning method based on optimized artiﬁcial

bee colony algorithm. Journal of Physics: Conference

Series, 1544(1):012017.

Shoemake, K. (1985). Animating rotation with quaternion

curves. SIGGRAPH Comput. Graph., 19(3):245–254.

Wei, G., Cui, Z., Liu, Y., Chen, N., Chen, R., Li, G., and

Wang, W. (2020). TANet: Towards Fully Automatic

Tooth Arrangement. In Lecture Notes in Computer

Science (including subseries Lecture Notes in Artiﬁ-

cial Intelligence and Lecture Notes in Bioinformatics),

volume 12360 LNCS, pages 481–497.

APPENDIX

Table 1: Currently available actions.

Action Effect

step Declare a new step, and initial-

ize it with the current conﬁgura-

tion.

extract Extract a tooth from the current

conﬁguration.

level Position the teeth on the same

horizontal plane.

rotate Correct the orientation of a

tooth on its up axis (local y

axis).

incline Correct the orientation of a

tooth on its mesio-distal axis

(local z axis).

lock /unlock Prevent the tooth from moving

move.

align Position the teeth at their target

position on the arch.

close spaces Close inter-dental spaces.

Animating and Adjusting 3D Orthodontic Treatment Objectives