
SPD Siamese Neural Network for Skeleton-based Hand Gesture
Recognition
Mohamed Sanim Akremi
1
, Rim Slama
2
and Hedi Tabia
1
1
Paris Saclay University, IBISC, Univ Evry, Evry, France
2
LINEACT Laboratory, CESI Lyon, France
Keywords:
SPD Learning Model, Siamese Network, Deep Learning, Hand Gesture Recognition, Skeletal Data.
Abstract:
This article proposes a new learning method for hand gesture recognition from 3D hand skeleton sequences.
We introduce a new deep learning method based on a Siamese network of Symmetric Positive Definite (SPD)
matrices. We also propose to use the Contrastive Loss to improve the discriminative power of the network.
Experimental results are conducted on the challenging Dynamic Hand Gesture (DHG) dataset. We compared
our method to other published approaches on this dataset and we obtained the highest performances with up
to 95,60% classification accuracy on 14 gestures and 94.05% on 28 gestures.
1 INTRODUCTION
Hand gesture recognition is an important topic that
can be used in many fields such as sign language
recognition, robot control, virtual game control, hu-
man computer interaction, etc. Consequently, im-
provement in hand gesture interpretation is becom-
ing an active research area for the past 20 years.
The development of recent sensors such as Microsoft
Kinect or Intel Real Sense brought great opportu-
nities for this domain. In fact, many approaches
have emerged using hand skeletal data that can be
acquired with good precision using these sensors.
Among the various proposed approaches to represent
and recognize hand sequences, SPD networks showed
most reliable methods using skeleton representations
and deep neural network approaches using manifold
based-learning. Besides, they provide powerful sta-
tistical representations for the skeletal data. Several
researches were conducted in this field, and new net-
works were proposed, such as the SPD network pro-
posed by (Huang and Van Gool, 2017) and in turn
was developed by (Nguyen et al., 2019) in order to
improve the performances. Motivated by this obser-
vation, we have decided to continue improving these
proposed models. For this, we have decided to inte-
grate an SPD network in a Siamese network for sev-
eral reasons among those we cite the great success of
the adoption of the Siamese network in many com-
puter vision and machine learning applications such
as; face recognition, handwriting recognition, and vi-
sual tracking. One more advantage of the Siamese
networks is their ability to handle the issue of the lack
of training data. On the other hand, the SPD repre-
sentation has been employed in many areas includ-
ing shape retrieval (Tabia et al., 2014), medical imag-
ing (Jayasumana et al., 2013), and pedestrian detec-
tion and tracking (Tuzel et al., 2008). Recently a Rie-
mannian network for SPD matrix learning has been
introduced by (Huang and Van Gool, 2017). The
proposed network opens new directions to explore, in
particular the application of the deep learning on Rie-
mannian representations with SPD matrices. In this
article, we explore the usage of Siamese networks on
SPD matrices for hand gesture recognition.
A positive symmetric matrix network is adopted
as a starting point for the Siamese network. To the
best of our knowledge, this is the first approach that
combines a positive symmetric matrix network with a
Siamese network. This paper has two main contribu-
tions:
• It focuses on symmetric positive matrix networks
and it develops candidate networks to get the best
accuracy.
• It combines the properties of this network with
the Siamese approximate properties of similarity
in order to improve the efficiency of our network
The rest of this paper is structured as follows. In
section 2, related work on hand gesture recognition
and deep learning manifold-based approaches are re-
viewed. In Section 3, our proposed approach is de-
394
Akremi, M., Slama, R. and Tabia, H.
SPD Siamese Neural Network for Skeleton-based Hand Gesture Recognition.
DOI: 10.5220/0010822500003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
394-402
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

scribed. In section 4, experimental evaluations are re-
ported. Finally, the last section is dedicated for the
conclusion.
2 RELATED WORKS
In order to examine the subject of hand gesture recog-
nition particularly and action recognition generally,
several approaches have been devised to mainly two
groups in order to obtain better architecture. In one
hand, there are traditional methods based on po-
sition detection, dense trajectories such as method
based on video modeling by combining dense sam-
pling with feature tracking and calculating boundary
features along dense trajectories (Chen et al., 2015).
On the other hand, several new vision-based methods
and new deep learning networks have been invoked,
such as: recognition via sparse spatio-temporal fea-
tures based on CNN and LSTM using RGB se-
quences (Sukthanker et al., 2020), convolutional Two-
Stream Network Fusion for video action recogni-
tion (Feichtenhofer et al., 2016) Deep 3D CNN (Wang
et al., 2016), reduction of hierarchical characteris-
tics and deep learning (HFR-DL) proposed by (Suk-
thanker et al., 2020)
In addition, there are many methods proceeding
skeletal data captured by the depth sensing cameras.
As illustrated Figure 1, this skeletal data is com-
posed of a set of 3D joints. They deal generally
with non-Euclidean spaces such as elastic functional
coding of Riemannian trajectories (Anirudh et al.,
2016). Some approaches focus on Lie groups meth-
ods such as the deep learning neural network on
Lie groups for skeleton-based action recognition pro-
posed by (Huang et al., 2017) and based on the suc-
cession of the proposed RotMap + RotPooling block.
The RotMap layer transforms the input rotation ma-
trices and the RotPooling and the RotPooling layer
pools the resulting rotation matrices temporally and
spatially. The proposed network is finalized by a
LogMap Layer. In the same field, Vemulapalli et
al. proposed in (Vemulapalli and Chellapa, 2016)
a neural network. It starts with a Skeletal represen-
tation using 3D rotations between the body joints.
Then comes the warping layer to compute the nom-
inal curves and warp all the curves to it. Along these
nominal curves, a RollingMap layer are applied on
the Lie group over its lie algebra and the actions are
unwrapped onto this lie algebra. These unwrapped ac-
tions are finally transformed into feature vectors and
are classified using the linear SVM classifier. Oth-
ers studies focus on Grassmann manifolds and pro-
posed new Grassmann network architecture (Huang
(a) (b)
Figure 1: Skeletal hand joints.(a) Hand joints illustration.
(b) The full skeleton returned by the Intel Real Sense.
et al., 2018) composed of 3 major blocks: Projection
block, Pooling block and output block. The Projec-
tion block is intended for the transformation of the
orthonormal input matrices. The Pooling block is de-
signed to map the orthonormal matrices and apply
a mean pooling on them. These outputs are vector-
ized and classified in the output block. However,
the major problem with many of these methods is
that they sometimes distort the nature of the data or
lose some information related to the basic character-
istics of the input data. To deal with this problem,
many studies oriented to the SPD matrices which are
characterized by its advantage in preserving the ba-
sic characteristics of the data. Thanks to their ability
to learn appropriate statistical representations while
respecting Riemannian geometry of underlying SPD
manifolds, SPD matrices have been popular in com-
puter visions researches. Many studies carried out on
SPD matrices have managed to create new approaches
and methods exploiting SPD matrices characteristics.
Among these approaches, we mention the Rieman-
nian network proposed in (Huang and Van Gool,
2017), Riemannian Metric Learning for Symmetric
Positive Definite Matrices (Vemulapalli and Jacobs,
2015) (Lim et al., 2019) which used SPD manifold
geodesic and exploited SPD matrix distances proper-
ties to the images clustering, face matching problems.
(Sukthanker et al., 2020) proposed a neural architec-
ture research which grouped many SPD networks lay-
ers and different SPD methods and choose the optimal
SPD network path.
3 THE PROPOSED APPROACH
In this section, we present our network model re-
ferred to as SPD Siamese Network. Firstly, we give an
overview of the approach. Then, we give a summary
of some previous approaches that we need in build-
ing our network. Finally, we explain our proposed
method.
SPD Siamese Neural Network for Skeleton-based Hand Gesture Recognition
395

Figure 2: An overview of the proposed SPD Siamese network. Our method learns the SPD matrices from skeletal data. Using
the Siamese network, the SPD matrices from different classes are distanced from each others. This distancing is used to
predict hand gestures.
3.1 Overview
Our model, illustrated in Figure 2, aims to improve
the performance of an SPD network for skeleton-
based hand gesture recognition using the Siamese net-
work. Before starting running the model, we have to
make all the sequences the same number of frames
using the interpolation method. The resulting arrays
are normalized in order to facilitate the computing.
The data is then ready to be executed. The pro-
posed network is composed of three principal compo-
nents: SPD learning features component, base SPD
network component, and Siamese component. The
initial input is an array describing the evolution of
the 3D positions of the hand joints throughout the ac-
tion time. For the learning of SPD matrices, we use
two networks: Covariance SPD matrices (Huang and
Van Gool, 2017) and the method called ST-TS-HGR-
NET network proposed by (Nguyen et al., 2019) and
used to learn the input data spatially and temporally
returning an SPD matrix containing first-order infor-
mation and second-order-information.
For the base SPD network component, we use the
SPD network proposed by (Huang and Van Gool,
2017) in two different manners: with the transfor-
mation blocks and without the transformation blocks.
Then, we twin the two previous components and use
the Contrastive Loss function for training the model.
Finally, we use the K-NN algorithm on the learnt
model parameters applied to the base SPD network
component for the classification.
3.2 SPD Matrix Learning
Among the methods to learn an SPD matrix-based
representation from skeletal data, we work with first
covariance matrix method which is easily computed
and essentially with ST-TS-HGR-NET. This network
architecture, as shown in Figure 3, is composed by
four principal components: Convolution network, ST-
GA-NET, TS-GA-NET and SPDC network.
Convolution Network: It highlights the correlation
between the neighboring joints of the hand and learns
the filter weight associated to each neighbor of a given
joint. It takes as input a tensor M
t
∈ IR
5×4×3
describ-
ing 3D position of each joint of each finger. In order
to facilitate the computation, we define N
t
∈ IR
6×5×3
as:
(N
t
)
i+1, j+1
=
(
(M
t
)
i, j
i f 2 ≤ i ≤ 4; 1 ≤ j ≤ 6
0 else
(1)
Then, we apply a convolution operation without bias.
Its kernel size is 3×3, the number of its input channels
is 3 and the number of its output channels is d
l
. The
output of the convolution layer is Y ∈ IR
N×5×4×d
l
.
The ST-GA-Net and the TS-GA-Net take as input the
output of convolution layer and are executed simulta-
neously.
ST-GA-Net: Its principal objective is to learn
spatially the hand joints positions of each frame
and returns an SPD matrix containing first-order-
information and second-order-information about the
mean and the covariance of the spatial repartition of
the frames. For this, we divided the input X coming
out of the Convolution component to 6 sub-sequences
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
396

Figure 3: ST-TS-HGR-NET architecture. The network processes skeletal data spatially and temporally using the sub-networks
ST-GA-NET and TS-GA-NET and returns an SPD matrix.
(X
s
)
{s=0..5}
distributed as: the sub-sequence X
0
which
describes all the frames of Y, each of X
1
and X
2
which
describe one of the halves of all sequences of Y, and
each of X
3
, X
4
and X
5
which describe one third of
all sequences of Y. The first layer, Gauss Aggregation
Layer, returns as output:
Y (s, t, f ) =
cov
s,t, f
+ µ
s,t, f
µ
T
s,t, f
µ
s,t, f
µ
T
s,t, f
1
(2)
Where
µ
s,t, f
= mean
4
th
(
1
4(2t
0
+ 1)
t+t
0
∑
i=t−t
0
X
s,t, f
) (3)
cov
s,t, f
=
∑
j∈J
f
∑
t+t
0
i=t−t
0
(X
s,i, j
− µ
s,t, f
)(X
s,i, j
− µ
s,t, f
)
T
4(2t
0
+ 1)
(4)
The ReEig Layer takes as input
X =
X
0
X
1
X
2
X
3
X
4
X
5
T
∈ IR
B
,
B = 3N × 5 × (d
l
+ 1) × (d
l
+ 1)
(5)
where (X
s
)
s=0..5
are the outputs of the previous
layer. It returns :
Y = U max(εI, S) U
T
(6)
where X = USV is the eigen-decomposition, I is the
identity tensor (the same size as Z) and ε is a rec-
tification threshold. This output is mapped into Eu-
clidean space by the LogEig layer (Y = log(X)) and
the VecMat layer (It takes the upper triangle part of an
input X and vectorize them row by row and the out-
put Y ∈ IR
B
, B = 3N × 5 ×
d
l
(d
l
+1)
2
× 1). The second
Gauss aggregation layer returns the last output Y ∈
IR
B
, where B = 6 ×5 × (
d
l
(d
l
+1)
2
+1)×(
d
l
(d
l
+1)
2
+1))
of the ST − GA − NET component, given by:
Y (s) =
cov(s) + µ
s
µ
T
s
µ
s
µ
T
s
1
(7)
Where N
s
is the number of frames of X
s
, mean(s)
and cov(s) are defined as:
µ
s
= mean
2
nd
(X
s
) (8)
cov
s
= cov
2
nd
(X
s
) (9)
TS-GA-Net: Its role consists to capture temporal in-
formation of each hand joint. Each sequence Y (out-
put of the convolution layer) is divided to 6 sub-
sequences {X
s
} in the same manner as in the previ-
ous component. Each sub-sequence is divided into K
sub-sequences. We obtain the set of sub-sequences
{Z
s,k
}
s=0...5,k=0...K−1
where Z
s,k
refers to k
th
the sub-
sequence of X
s
. The outputs of the first Gauss Aggre-
gation Layer are in IR
B
, B = 6 ×5 ×K ×4×(d
l
+1)×
(d
l
+ 1) and are estimated as:
Y (s, k) =
cov
s,k, f
+ µ
s,k, f
µ
T
s,k, f
µ
s,k, f
µ
T
s,k, f
1
(10)
Where:
µ
s,k, f
= mean
2
nd
(Z
s,k
) (11)
cov
s,k, f
= cov
2
nd
(Z
s,k
) (12)
The outputs of the ReEig, the LogEig and the Vec-
Mat Layers are computed in the same manner as that
of ST-HGR-Net. For the second Gauss Aggregation
Layer, the output Y ∈ IR
6×5×(
d
l
(
d
l
+1
)
2
+1)×(
d
l
(
d
l
+1
)
2
+1)
of the ST-GA-NET component, given by:is computed
as:
Y =
cov + µ µ
T
µ
µ
T
1
(13)
Where:
µ = mean
2
nd
,4
th
(Y ) (14)
cov = cov
2
nd
,4
th
(Y ) (15)
SPDC NET: In the first Layer, SPD Aggre-
gation takes both outputs of ST−GA−NET and
TS−GA−NET and returns as output
Y =
∑
W
i
X
i
W
T
i
(16)
Where its parameter W
i
∈ IR
d
c
×(
d
l
(
d
l
+1
)
2
+1)
is a
Stiefel weight parameter.
SPD Siamese Neural Network for Skeleton-based Hand Gesture Recognition
397
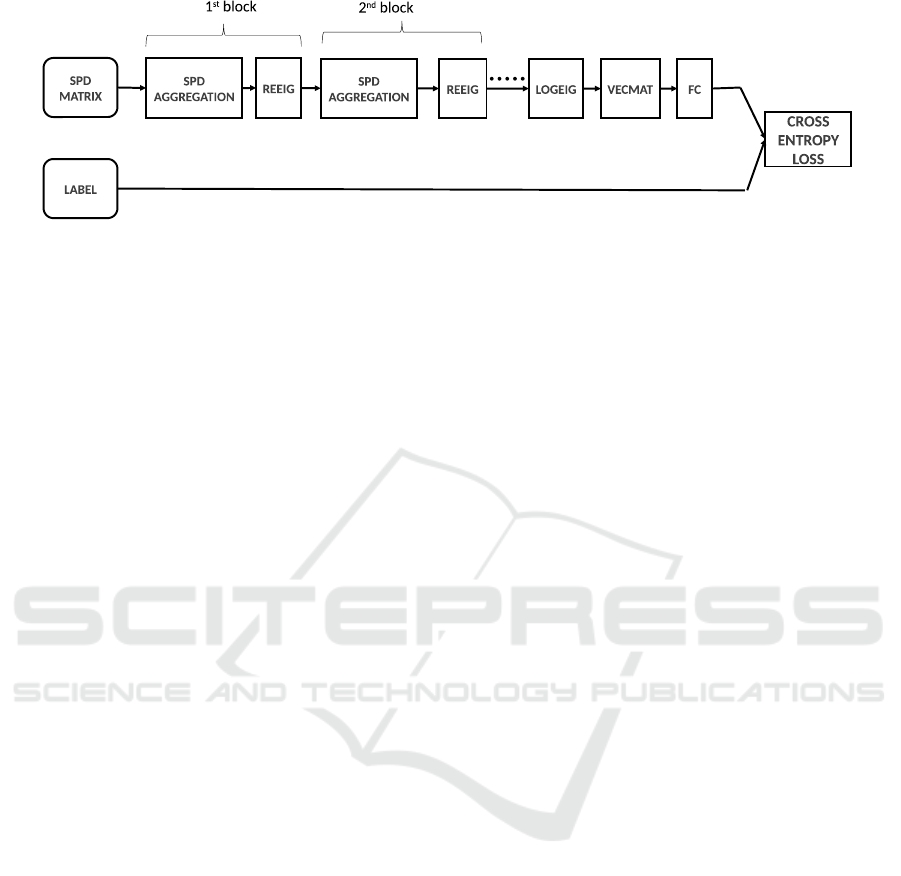
Figure 4: SPDNET architecture. The model is used to process the input SPD matrices, map them and predict the actions of
the hand.
Then, we map the SPD Aggregation output using
a LogEig layer and VecMat layer. Besides, we apply
a fully connected layer and a SoftMax layer. Finally,
we use the Cross Entropy Loss to calculate the loss
function.
For details, we refer readers to (Nguyen et al., 2019).
3.3 Classification using SPD NET
After learning the SPD matrices, comes the step of
classification using the learnt features in gesture clas-
sification. Wherefore, we use the architecture model
proposed by (Huang and Van Gool, 2017) and illus-
trated in Figure 4. It created a neural SPD network
based on succession of SPD transformation blocks
which aims to generate more compact and discrim-
inative SPD matrices, each block is composed of a
BiMap layer (equivalent to SPD Aggregation layer)
and a Rectified layer and finalized his SPD architec-
ture by mapping to a flat space with the matrix loga-
rithm operation log(·) on the SPD matrices. Then, we
utilize a fully connected layer for the classification.
3.4 SPD Siamese Network
This SPD Siamese network, illustrated in Figure 5,
consists of two identical SPD sub-networks joined at
their outputs. During training the two sub-networks
extract features from two signatures, while the joining
neuron measures the distance between the two feature
vectors (Bromley et al., 1993). That’s why, before
starting the execution of the Siamese model, we need
to create an equal number of positive pairs SPD ma-
trices (from the same class) and negative pairs (from
different classes) out of the total learnt SPD matrices.
SPD Siamese network input takes as an input target
the binary label BL defined as:
BL = δ
m,n
(17)
Where m is the class of the first input and n is the class
of the second one. Let Y
1
and Y
2
be the outputs of
the two twin SPD sub-networks and m be the margin
parameter. The Contrastive Loss function is given by
the following expression:
L
Siamese
(Y
1
, Y
2
, BL) = BL
k
Y
1
−Y
2
k
2
+ (1 − BL) max (0, m −
k
Y
1
−Y
2
k
2
)
(18)
The interest of using Contrastive Loss function is
her discriminative properties since it minimizes dis-
tance between positive pair and makes negative pairs
m distant from each other. That improves discrimi-
native performance and helps in gesture recognition.
That’s why, the SPD Siamese network perfor-
mances depend heavily on the SPD sub-network
taken as a base classification model and the conve-
nient choice of the margin parameter of the Con-
trastive Loss function.
3.5 Hand Gesture Recognition
We are going to use the learnt weights of the SPD
network after training the SPD Siamese network. Let
N be the number of gesture classes. Since Siamese
Network doesn’t give a direct prediction of data class,
we are going to use K-Nearest Neighbor algorithm (K
=1) for classification. We choose randomly N items
(X
(k)
rep
)
k=1..N
: one item per class. Let X be an item
with unknown class, Y be the output of the SPD net-
work with X as input, Y
(k)
rep
the output of the SPD Net-
work with X
(k)
rep
as input. The class of item x is deter-
mined using the following formula:
class (X) = min
k ∈[1..N]
Y −Y
(k)
rep
2
(19)
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
398
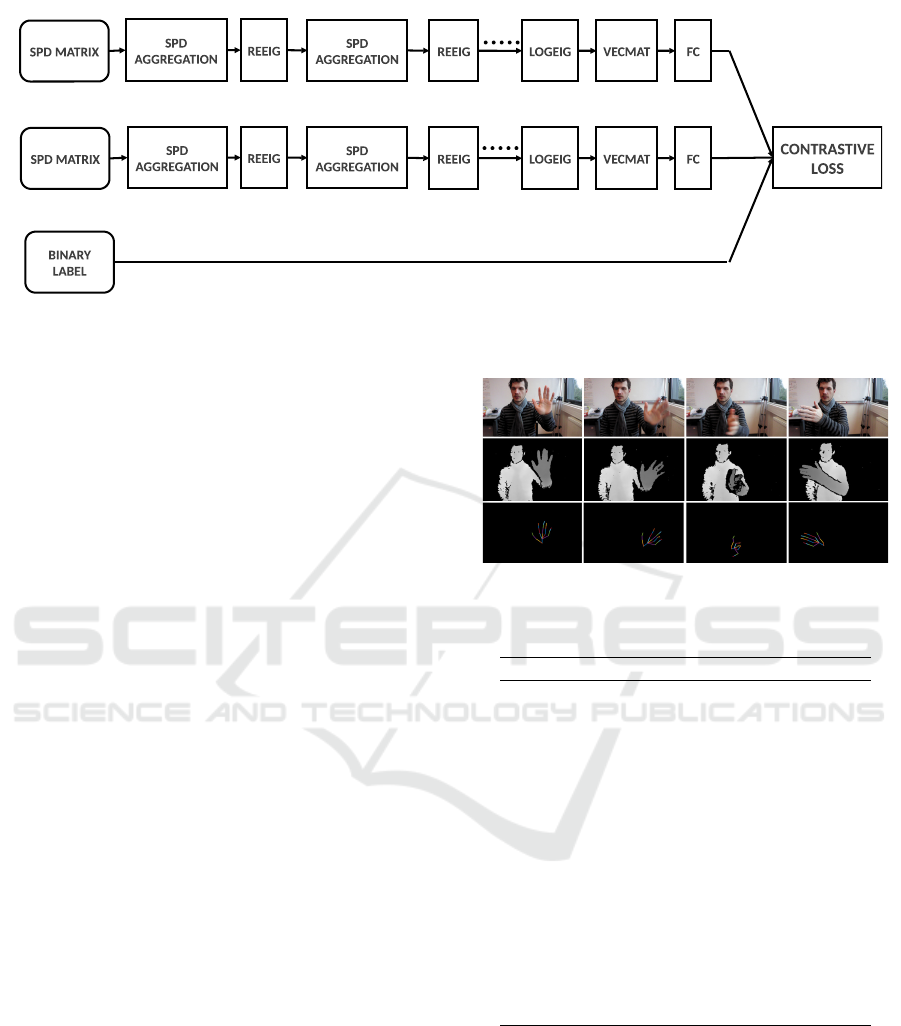
Figure 5: Siamese Network architecture using SPDNET as a sub-network.
4 EXPERIMENTS AND RESULTS
We have implemented and evauated SPD Siamese
network in DHG dataset. For the SPD learning net-
work using ST-TS-HGR-NET architecture (Nguyen
et al., 2019), the sequences are normalized, interpo-
lated into 500 frames. We set t
0
= 1, K=15, ε = 1e-4,
d
l
= 9, t
0
= 1, K=15, d
l
= 9 and d
c
= 200 (For more
details,we refer readers to (Nguyen et al., 2019) and
(Huang and Van Gool, 2017)).
We presented results with the SPD model
ST−TS−HGR−NET. The optimizer used is Adam
optimizer with learning rate lr = 1e-4 (after train-
ing the model with various learning rates, we found
that using a learning rate lr = 1e-4 gives a rapid con-
vergence) . We trained this network for 15 epochs
(24 min/epoch). For the Siamese Network and the
SPDNet network, we used Adam optimizer with
learning rate lr = 7e-4. We trained this network
for 500 epochs (1min/epoch). We evaluated the ap-
proaches mentioned in this paper using DHG dataset
2017 with 14 classes and 28 classes.
All the results are available in the Github reposi-
tory as well as the code to reproduce our method at:
https://github.com/Mohamed-Sanim300/SPD_
Siamese_Network.
4.1 Dataset
DHG dataset (De Smedt et al., 2017) contains depth
images and hand skeletons captured by "the Intel Re-
alSense short range depth camera" (30 frames per sec-
ond). The dataset contains sequences of 14 hand ges-
tures performed in two ways: using one finger and the
whole hand.
The gestures are listed in Table 1. An example a
swipe left gesture is illustrated in Figure 6.
We can consider the dataset to have 14 gestures
regardless of how they are performed. It can be con-
Figure 6: Example of a swipe left gestures from the training
dataset.
Table 1: List of the gestures included in the dataset.
Reference Name Type
1 Grab Fine
2 Tap Coarse
3 Expand Fine
4 Pinch Fine
5 Rotation Clockwise Fine
6 Rotation Counter Fine
Clockwise
7 Swipe Right Coarse
8 Swipe Left Coarse
9 Swipe Up Coarse
10 Swipe Down Coarse
11 Swipe X Coarse
12 Swipe + Coarse
13 Swipe V Coarse
14 Shake Coarse
sidered as having 28 gestures, considering that each of
the two ways of accomplishing each gesture is an in-
dependent action. Each frame of sequences contains
a depth image, the coordinates of 22 joints both in
the 2D depth image space and in the 3D world space
forming a full hand skeleton.
We are going to use the 3D skeletal world space.
It has been split into 1960 train sequences (70% of
the dataset) representing the gestures performed by
the subjects 2, 3, 4, 7, 8, 9, 10, 11, 12, 13, 14, 15,
SPD Siamese Neural Network for Skeleton-based Hand Gesture Recognition
399

16, 19, 20, 21, 22, 25, 26, 27 and 840 test sequences
captured with the help of the other volunteers (30%
of the dataset). The DHG dataset is well balanced.
For train sequences of DHG-14, We have between
130 and 150 skeleton sequences per gesture and for
DHG-28 training items, we have between 64 and 74
skeleton sequences per gesture.
4.2 Experimental Settings
As mentioned in section 3.4, SPD Siamese depends
on the given margin and the SPD network i.e., the
weights parameters of the SPD transformation block.
First of all, we are going to compare the network be-
fore and after introducing Siamese network. Then we
are going to examine the influence of margin variation
and to choose the most efficient SPD network struc-
ture.
4.2.1 Importance of the Introducing of Siamese
Network
In this experiment, we execute, without introducing
Siamese network, the SPD learning networks: ST-TS-
HGR-NET. Then, we try the execution with Siamese
model and compare the obtained accuracy results.
The SPD network is SPDNET without transforma-
tion blocks. According to Table 2, it’s obvious that
the performance of the model has been improved
even though it has already achieved a very high score
(>91%). This explains the importance of our new ap-
proach.
Table 2: Recognition accuracy with/without Siamese Net-
work introducing.
Dataset Without Siamese With Siamese
(%) (%)
DHG-14 91.07 95.60
DHG-28 87.62 94.05
4.2.2 SPD Network
We study the behavior of Siamese network towards
different depth of SPD network (depth = 0,1,3) and
we evaluate the performance of each network. The
results of this experiment illustrated in Table 3 shows
that it’s more efficient to use the SPDNET without
any transformation block while working with Siamese
because the SPD matrix, output of the SPD learning
model, the best for representing gestures since it con-
tains various information(mean, covariance...) about
the gesture performance in different states over time.
Table 3: Recognition accuracy for different SPD networks
on DHG dataset using 14 gestures. TB is an abbreviation of
transformation block.
SPD Network Accuracy on DHG-14(%)
SPDNET + 3 TB 85.59
SPDNET + 1 TB 89.40
SPDNET + 0 TB 95.60
4.2.3 Margin of the Contrastive Loss Function
In this experiment, we vary the margin m and keep
other components of our network unchanged (ST-
TS-HGR-NET for the SPD learning network and
SPDNET + 0 block for the SDP network). Table 4
shows the variation of performance as a function of
the margin m used in the Contrastive Loss function
(m = 1, 2, 5, 7, 8, 10, 20). According to the given
results, the performance of our model is constantly
improving until it reaches its maximum at margin = 7
and then begins to decline gradually.
Table 4: Recognition accuracy for different settings of the
margin.
Margin Accuracy on Accuracy on
DHG-14(%) DHG-28(%)
1 91.78 87.62
2 92.02 88.45
5 92.5 90.48
7 95.60 94.05
8 93.09 91.78
10 93.09 88.45
20 91.54 85.48
For the following section, we report results given
by the SPDNET+0 block with margin = 7.
4.3 Comparison with State-of-the-Art
The Table 5 summarizes the other approaches using
3D skeletal hand sequences of DHG-14/28 dataset
and the performance obtained by each of them. The
given results confirm the effectiveness of the proposed
network architecture for hand gesture recognition. We
get the higher results compared to other methods.
Based on the presented results, it can be concluded
that our approach which can be considered as a com-
bination between the SPDNET invented by (Huang
and Van Gool, 2017), the ST−TS−HGR−NET pro-
posed by (Nguyen et al., 2019) and Siamese network
explained in (Koch et al., 2015), provides an advan-
tage compared to previous works. This can be ex-
plained as follows:
• This approach is robust for the class imbalance:
using the base model, a single data per class
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
400

Table 5: State-of-the-art methods on DHG dataset.
Method Accuracy on DHG-14(%) Accuracy on DHG-28(%)
RNN (Chen et al., 2017) 84.68 80.32
SoCJ + HoHD + HoWR (De Smedt et al., 2016) 88.24 81.9
STA-Res-TCN (Hou et al., 2018) 93.57 90.7
TCN-Summ (Sabater et al., 2021) 93.57 91.43
ST-TS-HGR-NET (Nguyen et al., 2019) 94.29 89.4
DD-Net (Yang et al., 2019) 94.6 91.9
Our SPD Siamese Network 95.60 94.05
is enough for the network to recognize the data
classes in the future.
• Due to the feature of distinguishing between the
differences and bringing the similarities closer, it
gives a very high accuracy result (95.60%)
Thanks to these characteristics, we succeed to pro-
pose a new approach that outperforms even the ap-
proaches that were the basis of our approach.
5 CONCLUSION
In this work, we presented a new approach for hand
gesture recognition using skeletal data. The pro-
posed method consists of learning SPD matrix cou-
pled to the use of Siamese network. We have evalu-
ated the proposed approach on DHG 14/28 Dataset.
The achieved results show high accuracy outperform-
ing state-of-the-art methods.
As future work, we plan to study the impact of
using geodesic distance on the SPD matrix within
Siamese network. Besides, we intend to focus on
online recognition systems using short time sliding
windows where we could recognize gestures. Finally,
applying our approach on different datasets and dif-
ferent applications such as human action recognition
could be interesting to study its performance on dif-
ferent context.
REFERENCES
Anirudh, R., Turaga, P., Su, J., and Srivastava, A. (2016).
Elastic functional coding of riemannian trajectories.
IEEE transactions on pattern analysis and machine
intelligence, 39(5):922–936.
Bromley, J., Guyon, I., LeCun, Y., Säckinger, E., and Shah,
R. (1993). Signature verification using a" siamese"
time delay neural network. Advances in neural infor-
mation processing systems, 6:737–744.
Chen, L., Shen, J., Wang, W., and Ni, B. (2015). Video ob-
ject segmentation via dense trajectories. IEEE Trans-
actions on Multimedia, 17(12):2225–2234.
Chen, X., Guo, H., Wang, G., and Zhang, L. (2017). Mo-
tion feature augmented recurrent neural network for
skeleton-based dynamic hand gesture recognition. In
2017 IEEE International Conference on Image Pro-
cessing (ICIP), pages 2881–2885. IEEE.
De Smedt, Q., Wannous, H., and Vandeborre, J.-P. (2016).
Skeleton-based dynamic hand gesture recognition. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition Workshops, pages 1–9.
De Smedt, Q., Wannous, H., Vandeborre, J.-P., Guerry, J.,
Le Saux, B., and Filliat, D. (2017). Shrec’17 track:
3d hand gesture recognition using a depth and skeletal
dataset. In 3DOR-10th Eurographics Workshop on 3D
Object Retrieval, pages 1–6.
Feichtenhofer, C., Pinz, A., and Zisserman, A. (2016). Con-
volutional two-stream network fusion for video action
recognition. In Proceedings of the IEEE conference on
computer vision and pattern recognition, pages 1933–
1941.
Hou, J., Wang, G., Chen, X., Xue, J.-H., Zhu, R., and
Yang, H. (2018). Spatial-temporal attention res-tcn
for skeleton-based dynamic hand gesture recognition.
In Proceedings of the European Conference on Com-
puter Vision (ECCV) Workshops, pages 0–0.
Huang, Z. and Van Gool, L. (2017). A riemannian network
for spd matrix learning. In Proceedings of the AAAI
Conference on Artificial Intelligence, volume 31.
Huang, Z., Wan, C., Probst, T., and Van Gool, L. (2017).
Deep learning on lie groups for skeleton-based action
recognition. In Proceedings of the IEEE conference on
computer vision and pattern recognition, pages 6099–
6108.
Huang, Z., Wu, J., and Van Gool, L. (2018). Building deep
networks on grassmann manifolds. In Proceedings of
the AAAI Conference on Artificial Intelligence, vol-
ume 32.
Jayasumana, S., Hartley, R., Salzmann, M., Li, H., and Ha-
randi, M. (2013). Kernel methods on the riemannian
manifold of symmetric positive definite matrices. In
Proceedings of the IEEE conference on computer vi-
sion and pattern recognition, pages 73–80.
Koch, G., Zemel, R., and Salakhutdinov, R. (2015).
Siamese neural networks for one-shot image recog-
nition. In ICML deep learning workshop, volume 2.
Lille.
Lim, L.-H., Sepulchre, R., and Ye, K. (2019). Geometric
distance between positive definite matrices of differ-
ent dimensions. IEEE Transactions on Information
Theory, 65(9):5401–5405.
SPD Siamese Neural Network for Skeleton-based Hand Gesture Recognition
401

Nguyen, X. S., Brun, L., Lézoray, O., and Bougleux, S.
(2019). A neural network based on spd manifold
learning for skeleton-based hand gesture recognition.
In Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 12036–
12045.
Sabater, A., Alonso, I., Montesano, L., and Murillo, A. C.
(2021). Domain and view-point agnostic hand action
recognition. arXiv preprint arXiv:2103.02303.
Sukthanker, R. S., Huang, Z., Kumar, S., Endsjo, E. G.,
Wu, Y., and Van Gool, L. (2020). Neural architec-
ture search of spd manifold networks. arXiv preprint
arXiv:2010.14535.
Tabia, H., Laga, H., Picard, D., and Gosselin, P.-H. (2014).
Covariance descriptors for 3d shape matching and re-
trieval. In Proceedings of the IEEE conference on
computer vision and pattern recognition, pages 4185–
4192.
Tuzel, O., Porikli, F., and Meer, P. (2008). Pedestrian detec-
tion via classification on riemannian manifolds. IEEE
transactions on pattern analysis and machine intelli-
gence, 30(10):1713–1727.
Vemulapalli, R. and Chellapa, R. (2016). Rolling rotations
for recognizing human actions from 3d skeletal data.
In Proceedings of the IEEE conference on computer
vision and pattern recognition, pages 4471–4479.
Vemulapalli, R. and Jacobs, D. W. (2015). Riemannian met-
ric learning for symmetric positive definite matrices.
arXiv preprint arXiv:1501.02393.
Wang, X., Gao, L., Song, J., and Shen, H. (2016). Beyond
frame-level cnn: saliency-aware 3-d cnn with lstm for
video action recognition. IEEE Signal Processing Let-
ters, 24(4):510–514.
Yang, F., Wu, Y., Sakti, S., and Nakamura, S. (2019). Make
skeleton-based action recognition model smaller,
faster and better. In Proceedings of the ACM multi-
media asia, pages 1–6.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
402
