
Weakly Supervised Segmentation of Histopathology Images: An Insight
in Feature Maps Ability for Learning Models Interpretation
Yanbo Feng, Adel Hafiane and H
´
el
`
ene Laurent
INSA CVL, Laboratoire PRISME, Bourges, France
Keywords:
Feature Map, Convolutional Neural Network, Weakly Supervised Learning, Image Processing,
Histopathological Image.
Abstract:
Feature map is obtained from the middle layer of convolutional neural network (CNN), it carries the regional
information captured by network itself about the target of input image. This property is widely used in weakly
supervised learning to achieve target localization and segmentation. However, the traditional method of pro-
cessing feature map is often associated with the weight of output layer. In this paper, the weak correlation
between feature map and weight is discussed. We believe that it is not accurate to directly transplant the
weights of output layer to feature maps, the reason is that the global mean value of feature map loses its
spatial information, weighting scalars cannot accurately constrain the three-dimensional feature maps. We
highlight that the feature map in a specific channel has invariance to target’s location, it can stably activate the
more complete region directly related to target, that is, the feature map ability has strong correlation with the
channel.
1 INTRODUCTION
The annotation has always been a labor-intensive and
time-consuming work in deep learning. Especially for
the digital pathological image, nobody but the pathol-
ogist is able to label the image, making pixel-level
label all the more difficult to obtain. Weakly super-
vised learning (WSL) (Zhou et al., 2016) has there-
fore gained lots of attention. Compared with fully-
supervised learning method, it is originally trained for
the objective of classification using only images-level
annotation.
Since (Zhou et al., 2015) presented that convo-
lutional neural networks (CNNs) are able to carry
object information without supervision on the loca-
tion and boundary of object, most of previous studies
(Choe and Shim, 2019) (Singh and Lee, 2017) (Xue
et al., 2019) employed the feature maps outputted by
convolution layers to produce class activation maps
(CAMs) which indicate the objective area of input
image. Since the completeness and accuracy of the
target indicated in CAM is a key issue, some recent
works are undertaken to solve this problem (Bazzani
et al., 2016) (Kim et al., 2017) (Wei et al., 2017) pro-
viding better performance.
The CAM is generated by a weighted sum of fea-
ture maps. The weights from densely connected layer
are used to do the weighted sum of the outputs of
global average pooling (GAP) to generate final scores.
The link between feature maps and weights is that the
weighted objects are the spatial average values of fea-
ture maps, so there is an assumption that the weights
can be transplanted to feature maps to calculate the
CAM of its corresponding class. However, it is not
accurate, because weights act directly on the high di-
mensional space composed of many variables, their
effects on each dimension are difficult to understand.
The input variable directly acted by each weight is a
scalar, while the feature map is a three-dimensional
variable. The activation values in the feature maps
are not always directly related to the target. To bet-
ter identify the complete extent of object, high quality
feature maps need to be selected.
In this paper, based on the binary classification
task of determining whether there is cancer in liver
pathological image, the weight distribution of fully
connected layer, the relation between feature maps
and weights, the behavior of network and the selec-
tion of high-quality feature maps are studied under
the framework of weakly supervised model. Although
CNN generates a large number of feature maps and
the processing of these feature maps is usually asso-
ciated with weights, through research, it is found that
the weights have weak correlation with the feature
Feng, Y., Hafiane, A. and Laurent, H.
Weakly Supervised Segmentation of Histopathology Images: An Insight in Feature Maps Ability for Learning Models Interpretation.
DOI: 10.5220/0010830400003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
421-427
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
421
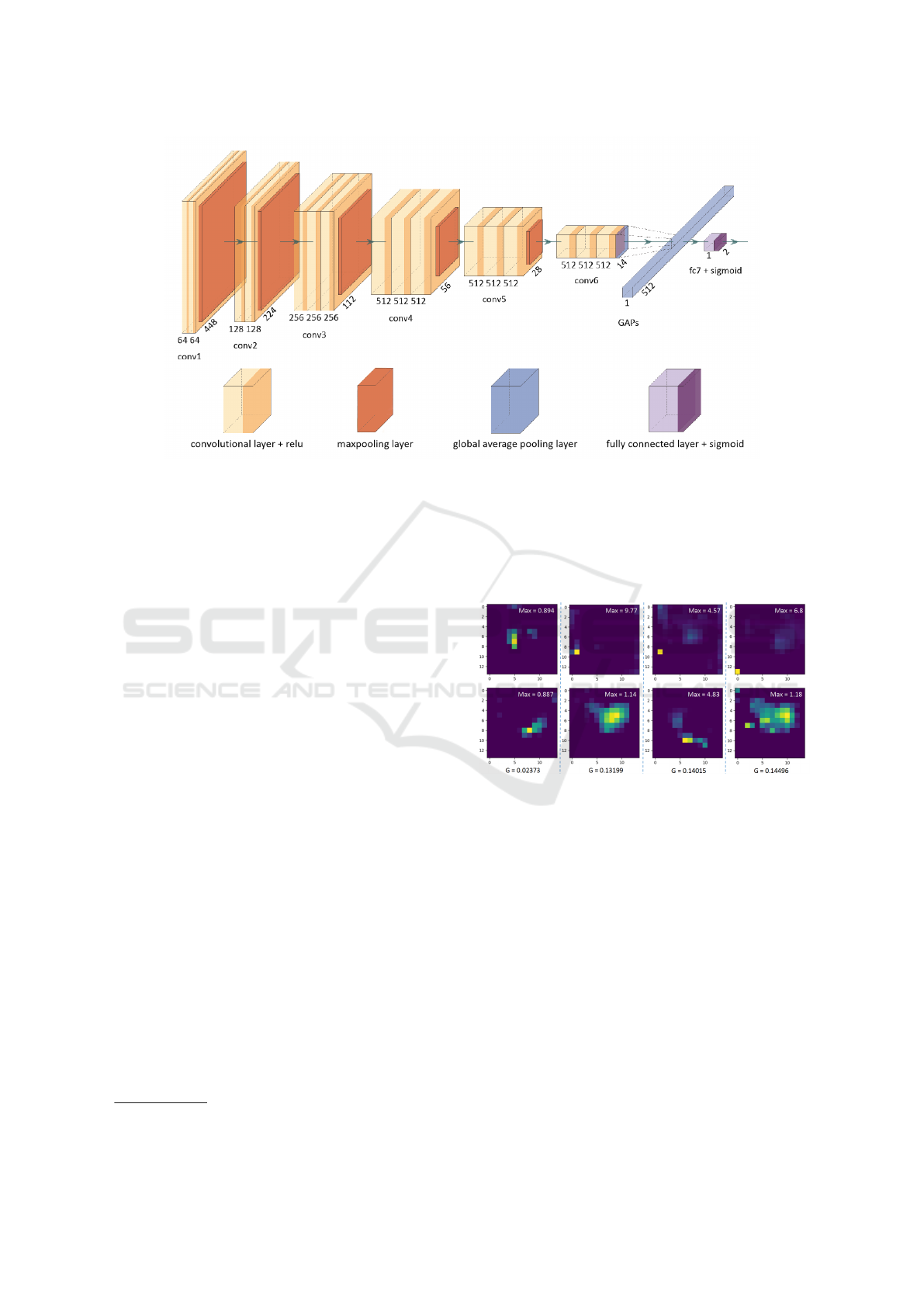
Figure 1: The architecture of weakly supervised learning model based on VGG-16.
maps and it is difficult to accurately select the feature
maps directly related to target region by the weight
value. At the same time, it was found that some fea-
ture maps have the ability to activate the complete ob-
ject and are invariable to the location of target. Fur-
thermore, there exists a strong correlation between
the object-related feature maps and specific channels,
which is instructive for the purpose of feature map se-
lection.
2 METHOD AND EXPERIMENT
2.1 Dataset
The dataset used in this research comes from the 2019
MICCAI PAIP Challenge
1
. The original dataset con-
tains 50 WSIs and ground truths for training, 10 WSIs
and ground truths for validation, 40 WSIs for test.
All WSIs were stained by hematoxylin and eosin and
scanned by Aperio AT2 at x20 200 power. The dataset
used for WSL in this research consists of the patches
cropped from WSIs with the size of 448 x 448 pixels,
the pixel-level and patch-level labels of each cropped
image are kept for further experiments.
2.2 Configuration of Model
As shown in Fig. 1, VGG-16 (Simonyan and Zisser-
man, 2014) was adopted in this study to achieve the
WSL. It could be observed that the main architecture
is maintained as original, but global average pooling
layer is used to replace the maxpooling layer and flat-
1
https://paip2019.grand-challenge.org/dataset/
ten layer, and a densely connected layer composed of
2 elements is used as output layer using Sigmoid as
activation function.
2.3 Global Average Pooling (GAP)
Figure 2: Examples of feature maps with same GAP pre-
sented in column direction. G indicates the GAP value of
that column, Max in images indicates the maximum pixel’s
value of that image.
GAP uses a scalar, which is the average of all the
pixels of feature map to represent it, thus forms an ap-
proximate fully connected layer that can be directly
connected to the output layer. The outputted GAPs
represent the degree to which the feature maps are ac-
tivated, and all spatial information is lost. However,
a feature map has a three-dimensional space, which
consists of the two-dimensional space of pixels and
the pixels’ values. Feature maps are able to indicate
the location, the size and the boundary of object, but
GAPs can not carry these information. As shown in
Fig. 2 on several examples, two feature maps with
same GAP value can correspond to two totally differ-
ent maps.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
422

2.4 Weights in Fully Connected Layer
Fig. 3 shows the structure of the fully connected layer
of model. The weights of this layer directly process
GAPs, meanwhile they are also employed to process
their corresponding feature maps. Each GAP value
has two weights corresponding to class-0 and class-
1, which means that the same GAP value will con-
tribute to the two output units respectively after pro-
cessed by two weights. In the following discussion, it
will be mentioned that the contribution of each GAP
to each output unit will be different by adjusting the
weight. Totally there are 512 GAPs, 1024 weights
and 2 classes, namely: this is a cancer image or this is
not a cancer image.
Figure 3: The fully connected layer of the model in this
research. G
n
represent the GAP values, in this research n
equals 512. W represent the weights. O represent the output
elements corresponding to the 2 classes.
Based on the above structure and constituent el-
ements, the function of the fully connected layer is
realized by the weighted sum of the input variables.
Actually, the weights are fixed after training, the only
variables are GAPs, as described in Eq. 1:
S
c
= Sigmoid(
N
∑
i=0
W
(i,c)
GAP(F
i
) +bias) (1)
where S
c
is the predicted score for class-c; F
i
is the
i
th
feature map; W
(i,c)
is the weight of i
th
feature map
for class-c. After weighted sum, the classification of
input image is realized by comparing S
0
and S
1
. The
rule is that the input image belongs to the category
with the larger value. Therefore, it can be found that
the same set of feature maps will produce different
predicted values on output units to classify the input
image. The corresponding weights are the key point
in this numerical mapping.
2.5 The Numerical Relation of Weights
and the Category of Feature Maps
The weights of the full connection layer are difficult
to interpret, not only because of the large number of
weights, but also the difference in value and sign. As
shown in Fig. 4 (a), (b) and (c), there are 115 GAPs
with two positive weights, 108 GAPs with two neg-
ative weights, 289 GAPs with two weights of oppo-
site signs. Among these last 289 GAPs, there are 150
positive weights for class-0, and 139 positive weights
for class-1. It should be noticed that all the outputs
of GAPs are positive, because feature maps are out-
putted by convolutional block and the Relu layer fil-
ters out the negative values, thus the averages are al-
ways positive.
Figure 4: The weights for class-0 and class-1. (a) 115 same
positive weights. (b) 108 same negative weights. (c) 289
weights with opposite sign.
It can be inferred that the sign of weight deter-
mines whether the corresponding GAP increases or
decreases the predicted value, and the value of weight
determines how much the GAP contributes to the pre-
dicted value. Fig. 4 (a) and (b) show that even the
weights have same sign, their values are different,
which means that GAPs will contribute to the final
predicted scores differently. While the weights with
opposite sign mean that the same GAP could increase
the final predicted score of one class, at the same time,
it will reduce the one of another class. The weights
are fixed after training, the sign and numerical dif-
ferences of weights could be the difference of GAPs,
furthermore be the category of feature maps.
Based on the above observation, the numerical re-
lation between weights belonging to two categories of
the same GAP may carry category information about
Weakly Supervised Segmentation of Histopathology Images: An Insight in Feature Maps Ability for Learning Models Interpretation
423

the feature map. In addition, based on Eq. 1, it is
logical to make the assumption that the feature maps
related to corresponding class will be given a lager
weight of that class for the sake of improving the pre-
dicted score. Thus, it is found that the feature map
can be classified by comparing the weights belonging
to two output units of its corresponding GAP. The
rule of classification is that the feature map belongs
to the class with the larger weight value. As shown
in Fig. 5, the feature maps of three images are firstly
classified according to the above rules, and then the
location of the maximum pixel in each feature map is
selected for drawing.
Figure 5: Three examples of classifying feature maps by
weights. (a) original input images. (b) ground truths. (c) the
maximum value graph of class-1. (d) the maximum value
graph of class-0.
Through comparison, it is found that relatively
more points fall within the cancer area in the graph
belonging to class-1, relatively more points fall within
the normal tissue area in the graph belonging to class-
0. This observation supports the above hypothesis to a
certain extent, the numerical relationship between two
weights of the same GAP value is related to the clas-
sification of corresponding feature graphs. However,
this method cannot classify the feature map exactly,
it can be observed from Fig. 5 that there are points
that don’t belong to the appropriate categories respec-
tively concerned by class-1 and class-0. Applying this
method to classification can only achieve a fuzzy clas-
sification effect, that is, the number of correct points
is higher than the number of wrong points. This re-
sult also proves that the weight is originally weakly
representative of the feature map.
2.6 Correlation between Feature Maps
with Same Weight Value
On the basis of the previous section, the weak rela-
tionship between feature maps and weights is further
explained through experiments in this section. As
shown in Fig. 6, there are four pairs of feature maps
with same weight value for a given class. It can be ob-
served that the activated regions in each feature map
vary greatly. The activated regions in the feature map
have different features, some are continuous pixels,
some are scattered pixels, and some do not output ac-
tivated pixels. Several feature maps have overlapping
areas, such as the 2
th
and 3
th
columns, and their cross
areas are relatively small. Therefore, the correlation
between feature maps is low even though they have
the same weight values.
Figure 6: Examples of feature map with same weight. The
two images in each column have same weight value, W
represents the value of weight with the margin of error
±0.00001.
To prove this point further another experiment is
done in this research. 12 pairs of approximately equal
weights are chosen, their corresponding feature maps
are firstly binarilized by Otsu’s method and then eval-
uated by F1 score. 8000 images are tested, the average
F1 scores are shown in Table. I. According to the data
listed in the table, the activated regions in each pair of
feature maps have almost no correlation. This result
further proves that the value of weight does not repre-
sent the activated features of feature maps, the feature
map has no close relation with the value and the sign
of weight.
2.7 Feature Map Integrity and Specific
Channels
As can be seen from the previous sections, it is diffi-
cult to find feature maps directly related to the target
through weights. In addition to the above reasons, an-
other one is that many feature maps do not activate
the complete target region, and most of them have
scattered irregular pixels. Actually, the weights of
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
424

Table 1: The result of experiment to test the similarity of
feature maps with relatively equal weights.
Channels Weight (±0.00001) F1 score
16 & 167 0.08313 0.00000e+00
21 & 477 0.10225 0.00000e+00
43 & 374 -0.07273 0.00000e+00
47 & 362 -0.05665 0.00000e+00
49 & 50 0.09689 0.00000e+00
56 & 252 -0.06634 0.00000e+00
69 & 256 -0.03166 2.70269e-06
104 & 154 -0.05188 0.00000e+00
124 & 383 0.08003 0.00000e+00
164 & 308 0.07023 1.00540e-04
276 & 312 0.00364 0.00000e+00
329 & 481 0.00089 0.00000e+00
output layer are fixed after training, beyond the nu-
merical level of the weights, the channel in which the
GAP is located is another potentially valuable obser-
vation point. The activated area in feature maps is not
fixed, it changes with the changes of region of interest
(ROI). From this point of view the numerical relation-
ship between weights and GAP is not solid. Weights
are more inclined to a structural distribution in order
to achieve the overall effect, which is specific in this
study. The channel is indeed related to the feature.
Namely some feature maps in fixed channels are able
to capture class-1 and class-0 information. Fig. 7 il-
lustrates this point, four feature map are chosen to be
visualized.
Figure 7: Each column from left to right present (a) in-
put images, (b) ground truths, (c) 51
th
feature maps, (d)
52
th
feature maps, (e) 69
th
feature maps and (f) 70
th
fea-
ture maps.
It is observed that not all of the feature maps ac-
tivate the ROI partially or scatteredly, some of them
present the ROI relatively completely compared with
the ground truth. Among the four channels chosen to
be visualized in Fig. 7, 51
th
and 69
th
feature maps
activate the areas directly related to cancer area and
normal tissue area. Actually, not only the object of
cancer area, but also the normal tissue area is taken
as object for the network. 51
th
and 69
th
position are
chosen particularly to prove that these single feature
maps in fixed position have the ability to capture the
whole object and are shift-invariant for object. 52
th
and 70
th
feature maps are chosen randomly showing
that some feature maps capture the features that have
low comprehensibility. Furthermore, several images
have been tested to check the reproducibility of this
idea. Here, 8000 images are tested to verify the re-
lation between 51
th
, 52
th
, 69
th
and 70
th
feature maps
and their ground truths. Otsu’s method is used to seg-
ment the feature maps firstly, then the similarity be-
tween the binarilized image and their ground truth is
evaluated by F1 score. The result is shown in Table II,
it can be observed that 51
th
and 69
th
feature maps are
strongly correlated with cancer area and normal tissue
area respectively in contrast with 52
th
and 70
th
fea-
ture maps which consistently output image data that
has nothing to do with target areas.
Table 2: The result of experiment to test the similarity be-
tween feature maps in fixed position and corresponding ob-
ject.
Channel F1 score Channel F1 score
51 0.54401 69 0.59972
52 0.00837 70 0.04147
Figure 8: The result of selecting feature maps. (a) the fea-
ture maps directly related to class-1, (b) the feature maps
directly related to class-0. The X-axis is channel position,
and the Y-axis is cumulative score.
Not only 51
th
and 69
th
feature maps are able to
present the complete area of target, there are more fea-
ture maps that activate the area directly related to can-
Weakly Supervised Segmentation of Histopathology Images: An Insight in Feature Maps Ability for Learning Models Interpretation
425

Figure 9: Each column from left to right is (a) 1
th
, (b) 18
th
, (c) 191
th
, (d) 228
th
, (e) 245
th
, (f) 118
th
, (g) 314
th
, (h) 327
th
, (i)
331
th
, (j) 432
th
channel.
cerous and normal tissues. As shown in Fig. 9, there
are ten channels that are able to capture the whole ob-
ject information for the four original images in Fig.
7. Furthermore, 16000 images are used to select out
the channels that reflect the relatively complete tar-
get area in this research. The 512 feature maps of
each image are once again firstly segmented by Otsu’s
method, then the similarity between the binarilized
images and the ground truth is evaluated by F1 score.
If the score is larger than 0.6, that position gets score
1. Fig. 8 presents the cumulative score obtained by
each of the 512 channels over the 16000 images. It
can be observed in the final results that there are spe-
cific channels among the 512 channels that continu-
ously capture feature areas associated with the can-
cerous and normal tissues. This result demonstrates
that the ability of feature maps to activate the com-
plete regions directly related to the target is tied to
particular channels.
3 DISCUSSION
The CNN produces a great number of feature maps
in the middle layers. Since these feature maps are
captured by the network itself, a large part of them
are not able to directly activate the complete target
region, and some of them are unreadable from the hu-
man point of view and irrelevant to the target. Mean-
while, there are feature maps that reflect relatively
complete target area. The complete extent of object
is the key point in weakly supervised learning for the
tasks of segmentation and localization. If the feature
maps with complete activated regions directly related
to the target can be selected from numerous feature
maps, the accuracy of subsequent processing will po-
tentially be improved.
The trained model has fixed weight for each fea-
ture map. It was expected to extract the feature map
with complete target area based on these weights, but
the experiments above have proven that it is inaccu-
rate. In addition to the reasons presented in Section
2. 5 and Section 2. 6, the randomness of the GAPs
with same values also indicates the inefficiency of the
weight’s dependence on the values of GAPs. Since
GAPs are the spatial average of feature map, same
GAPs emerge randomly with the position and size of
the target changing, but their weights are discrimina-
tive. The same scalar values are treated with different
weights, this suggests that the difference is due to the
channel.
The classification of feature map realized by com-
paring the weights of two classes numerically is not
accurate. Note that a phenomenon appeared in the
observation and analysis of 512 feature maps and 512
pairs of weights that, among the two weights of a
feature map related to class-1, the weight belonging
to class-0 category is sometimes larger. This phe-
nomenon means that the feature map related to class-
1 will contribute more to class-0. The opposite case
also exists, which is also reflected in the points that
are misclassified in Fig. 5. However, it can be ob-
served in Fig. 5 that the number of misclassified
points is relatively small compared to the number of
correctly classified points. The reason could be ex-
plained by the stability of high dimensional systems,
since the original processing object of weights is a
high-dimensional space made up of 512 scalars. It is
not the features belonging to a single class that deter-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
426

mine the final classification, which makes the system
robust. From this point of view, the method of classi-
fying feature maps using numerical relationships be-
tween weights is inherently flawed. The numerical
relationship of weights can not clearly represent the
category of feature maps.
The ability to activate complete target regions of
feature maps is found in fixed channels. This prop-
erty of neural networks applies to both cancerous and
normal tissue areas, treating both classes as targets
and activating the corresponding area completely. At
the same time, specific channels are invariant to tar-
get changes in the input image, they can stably output
the complete active area. In addition, this capability is
closely tied to channels from which feature maps can
be obtained once the channels are identified. There-
fore, after the training of neural network, the channels
can be screened with a small amount of data to deter-
mine the needed channels.
4 CONCLUSION
In this paper, we have taken an insight into the neu-
ral network. we have explained the weak correlation
between feature map and the weight of output layer.
The feature map directly related to target cannot be
selected out through the numerical characteristics of
weights. It was also found that the feature map in
specific channel has the ability to capture fixed fea-
ture. The conducted experiments prove that the fea-
ture maps which activate the more complete target re-
gion are output in fixed channels. This work can aid
other researchers in understanding and designing net-
works for image processing.
ACKNOWLEDGEMENTS
The authors gratelfully acknowledge financial support
from China Scholarship Council.
REFERENCES
Bazzani, L., Bergamo, A., Anguelov, D., and Torresani, L.
(2016). Self-taught object localization with deep net-
works. In 2016 IEEE Winter Conference on Applica-
tions of Computer Vision (WACV), pages 1–9.
Choe, J. and Shim, H. (2019). Attention-based dropout
layer for weakly supervised object localization. In
2019 IEEE/CVF Conference on Computer Vision and
Pattern Recognition (CVPR), pages 2214–2223.
Kim, D., Cho, D., Yoo, D., and Kweon, I. S. (2017). Two-
phase learning for weakly supervised object localiza-
tion. In 2017 IEEE International Conference on Com-
puter Vision (ICCV), pages 3554–3563.
Simonyan, K. and Zisserman, A. (2014). Very Deep Con-
volutional Networks for Large-Scale Image Recogni-
tion. arXiv e-prints, page arXiv:1409.1556.
Singh, K. K. and Lee, Y. J. (2017). Hide-and-seek: Forc-
ing a network to be meticulous for weakly-supervised
object and action localization. In 2017 IEEE Interna-
tional Conference on Computer Vision (ICCV), pages
3544–3553.
Wei, Y., Feng, J., Liang, X., Cheng, M.-M., Zhao, Y., and
Yan, S. (2017). Object region mining with adversarial
erasing: A simple classification to semantic segmen-
tation approach. In 2017 IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
6488–6496.
Xue, H., Liu, C., Wan, F., Jiao, J., Ji, X., and Ye, Q. (2019).
Danet: Divergent activation for weakly supervised ob-
ject localization. In 2019 IEEE/CVF International
Conference on Computer Vision (ICCV), pages 6588–
6597.
Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., and Tor-
ralba, A. (2016). Learning deep features for discrimi-
native localization. In 2016 IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), pages
2921–2929.
Zhou, B., Khosla, A., Lapedriza, g., Oliva, A., and Tor-
ralba, A. (2015). Object detectors emerge in deep
scene cnns. In International Conference on Learning
Representations.
Weakly Supervised Segmentation of Histopathology Images: An Insight in Feature Maps Ability for Learning Models Interpretation
427
