
Voronoi Diagrams and Perlin Noise for Simulation of Irregular
Artefacts in Microscope Scans
Atef Alreni
1a
, Galina Momcheva
1,2 b
and Stoyan Pavlov
2,3 c
1
Department of Computer Science, Varna Free University “Chernorizets Hrabar”, Varna, Bulgaria
2
Department of Advanced Computational Bioimaging, Medical University “Prof. Dr Paraskev Stoyanov”, Varna, Bulgaria
3
Department of Anatomy and Cell Biology, Medical University “Prof. Dr Paraskev Stoyanov”, Varna, Bulgaria
Keywords: Artefacts, Perlin Noise, Voronoi Diagrams, ANN.
Abstract: Artefacts are a common occurrence in microscopic images and scans used in life science research. The
artefacts may be regular and irregular and arise from different sources: distortions of the illumination field,
optical aberrations, foreign particles in the illumination and optical path, errors, irregularities during the
processing and staining phases, et cetera. While several computational approaches for dealing with patterned
distortions exist, there is no universal, efficient, reliable, and facile method for removing irregular artefacts.
This leaves life scientists within cumbersome predicaments, wastes valuable time, and may alter the analysis
results. In this article, the authors outline a systematic way to introduce synthetic irregular artefacts in
microscopic scans via Perlin Noise and Voronoi Diagrams. The reasoning behind such a task is to produce
pairs of “successful” and manufactured “failed” image counterparts to be used as training pairs in an artificial
neural network tuned for artefact removal. At the moment, the outlined method only works for grayscale
images.
1 INTRODUCTION
Numerous differing sub-cellular structures can be
mimicked via computation (Abdolhoseini, Kluge,
Walker & Johnson, 2019). Various such approaches
have recently been fathomed (for a thorough review,
refer to (Ulman, Svoboda, Nykter, Kozubek &
Ruusuvuori, 2016)). Within all these methods, two
steps fall as being a commonality in all: firstly, the
desired image is realised with objects of wanted
number and shape, and secondly, background and
foreground textures are created, which are later added
to the respective ideal image to create a realistic noisy
representation (Abdolhoseini et al., 2019).
Abdolhoseini et al. demonstrated a neuron image
synthesiser in which Perlin noise (Perlin, 1985) and
Gaussian mixture models (GMM (Reynolds, 2009))
were implemented, and akin characteristics in (Ulman
et al., 2016) were utilized. Deformed elliptical shapes
are created with spline interpolation (Unser, 1999) for
single nuclei. Following this, foreground and
a
https://orcid.org/0000-0001-6548-8156
b
https://orcid.org/0000-0003-0726-2022
c
https://orcid.org/0000-0002-9322-2299
background textures are created via Perlin noise
(Perlin, 1985). Xiong et al. generated images of
healthy Giemsa-stained red blood cell populations
using deformation models and unbiased average
shapes (Xiong, Wang, Ong, Lim & Jiang, 2010).
Diffeomorphic demons (Vercauteren, Pennec,
Perchant & Ayache, 2007), a non-parametric image
registration, is used to deploy the model which maps
one image to another. Successively, using histogram
distribution models to conceive a proper texture,
colour models were learned. Peng et al. (2009)
applied an instance-based technique to model the
shape space of 2D images of Hela cell nuclei using
kernel distribution (Wasserman, 2004), but with this
method, some of the simulated shapes do not match
the original images, and the method requires large
training datasets (Abdolhoseini, 2019).
Nonetheless, imaging artefacts vary in
abstractness and reason for appearance. They mainly
can be classified into three categories. Firstly,
regularly patterned artefacts appear due to
Alreni, A., Momcheva, G. and Pavlov, S.
Voronoi Diagrams and Perlin Noise for Simulation of Irregular Artefacts in Microscope Scans.
DOI: 10.5220/0010833000003123
In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 2: BIOIMAGING, pages 117-122
ISBN: 978-989-758-552-4; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
117
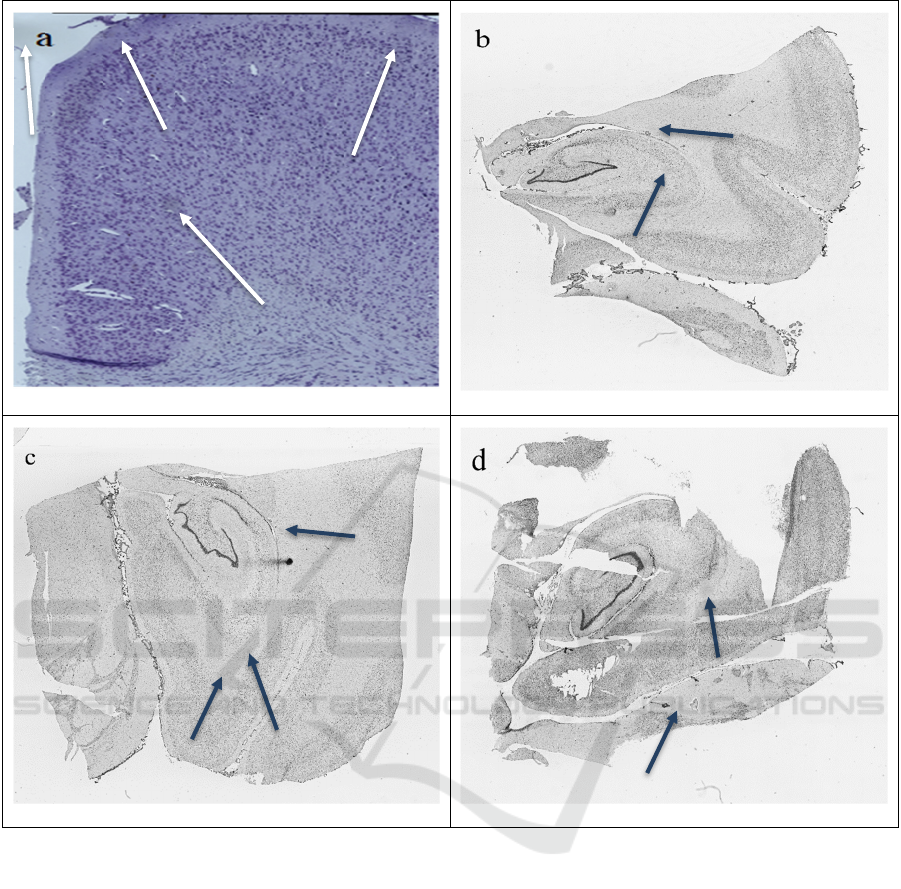
Figure 1: Examples of microscope scans with actual (arrowheads in a) and synthetically generated (arrowheads in b, c and d)
artefacts. The artefacts in b, c and d are generated using the method described in Section 2.
unevenness within the illumination field during
scanning. The centre is brighter than the peripheral
area around it (vignetting), which leads to a grid-like
structure (seams) after the reconstruction. There are
methods for removing this type of distortion;
however, they either require recording the
illumination field before the experiment or rely on
computed estimates, leading to biases and errors in
the result. Contrastingly, irregular artefacts (Figure
1a) have no method for reliable removal. They occur
due to foreign particles or defects within the optical
path, or form due to unstable tissue processing
conditions, especially in areas with non-specific
staining. These latter types are hard to predict and
treat and are thus of most interest. The outlined
innovative method for the generation of synthetic
failed microscope scans focuses on imitating them.
In this paper, we utilise Perlin Noise and Voronoi
diagrams through non-canonical means of original
use for the sake of replicating the abstract shape and
appearance of optical path artefacts in microscope
scans. Subsequently, an aptly sized dataset, consisting
of successful and unsuccessful microscope scans, can
be produced due to both algorithms’ mass versatility
and leniency (their ability to have various parameters
altered for specific desired outcomes). Generating
such a dataset is paramount. The large dataset will be
appropriate as input data to train a neural network to
remove such artefacts in natural microscope scans.
Thus, the authors have explored and identified a
BIOIMAGING 2022 - 9th International Conference on Bioimaging
118

method for realising such artificial artefacts on
microscope scans within this article. The rest of the
article is organised as follows: Section 2 outlines the
method in detail, Section 3 focuses on the results and
their outcome, Section 4 highlights the technique’s
versatility and leniency, and Section 5 discusses the
results’ implications. A note of caution, in the
subsequent paragraphs, a “cell” should be understood
as “Voronoi cell” and not the biological entity.
2 METHOD
2.1 Voronoi Generation Mixed with
Perlin Noise
Perlin noise and Voronoi diagrams have previously
been used in parallel for achieving very concentrated
and desired results (e.g., generating 3D digital
phantoms of colon tissue (Svoboda, Homola &
Stejskal, 2011) and generation of infinite virtual
terrain, a common use case (Choros & Topolski,
2016)).
This step uses Voronoi diagrams, a data structure
extensively investigated in computational geometry
(Ferrero, 2011; Berg, Krevald, Overmars &
Schwarzkopf, 1997), and Perlin noise, a type of
gradient noise (Perlin, 1985; Bae, Kim, Kim, Park,
Kim, Seo & Lee, 2018), coherently to create patches
resembling image artefacts. The authors utilized
Voronoi diagrams with the Euclidean distance
calculating function. However, diverse desired results
may be achieved using other distance metrics. A few
additional parameters were deployed to aid in
increasing the variance and prospect in results: these
parameters are “noisiness”, “excluded cells”, and
“desired cell(s)”, where “noisiness” affects the
noisiness of the Voronoi diagram (higher values
results in smaller artefacts), “excluded cells” defines
what parts of the Voronoi diagram will be removed
and “desired cell(s)” defines what patch(es) will be
used as the final artificial artefact(s).
Firstly, we define the number of cells (higher
values produce better results but increase the number
of computations), their locations (which are
arbitrarily chosen) and an “excluded” value (a label
with a value between 0 and 1, can be defined twice).
The “desired cell(s)” value is defined later since
potentially the “desired cell(s)” could be excluded if
they are above, or below if “excluded cell(s)” is
defined twice, the “excluded cell(s)” value. Also, the
authors constrained the maximum and minimum
value of each Voronoi cell’s x and y coordinates to
enhance efficacy, refer to Table 1 for more
information.
Secondly, we iterate through each pixel within the
image and identify the closest points to each cell
through calculating their Euclidian distance as thus:
𝑑𝑝,𝑞 √
∑
𝑞
𝑝
(1)
where n defines the number of dimensions, and p and
q represent the points within Euclidean space.
Moreover, the closest points for the chosen cell are
computed using the following formula:
𝑅
𝑥 ∈𝑿 | 𝑑𝑥,𝑃
𝑑𝑥,𝑃
∀ 𝑗 𝑘 (2)
such that X is a metric space with the distance
function d, (2); K is a set of indices and (Pk) k∈K is
a tuple of non-empty subsets within the space X; and
Rk, which is associated with the site Pk, is the set of
all points within X whose distance to Pk is not higher
than their distance to the remaining sites Pj Such that
j is any index that differs from k.
Thirdly, once the closest points are decided and
each Voronoi cell is calculated, we normalise each
distance value by dividing them by the maximum-
distance value, allowing the distance values to range
between 0 and 1. Following this, a “noisiness” value
is generated (the value is a floating point number and
ideally is below 2.0), then a Perlin noise value is
generated for each pixel, which then is normalised to
a value between 0 and 1 by dividing each value by 2
and adding 1.
Mathematically, Perlin noise is defined as:
𝑝
𝑥,𝑦
∑
,
, 𝑥 𝛽
𝑥, 𝑦 𝛽
𝑦 (3)
where n defines the number of wanted ‘octaves’, p(.)
represents a simple Perlin noise function defined by
Perlin (1985), 𝛾 and 𝛽 are parameters that regulate
and control the octave magnitude and noise
smoothness. The higher 𝛽 is, the less smooth is the
noise (1), refer to Table 1.
Fourthly, we combine each normalised distance
value with its respective Perlin noise value and the
noisiness value through utilisation of equation (4):
𝑓 𝑣 𝑛 ∗ 𝑝 (4)
where 𝑣 is the normalised distance value, n is the
noisiness parameter and p is the generated and
normalised Perlin noise value, refer to Table 1.
Voronoi Diagrams and Perlin Noise for Simulation of Irregular Artefacts in Microscope Scans
119

Figure 2: Examples of images produced in the intermediate steps of the algorithm: a. Result of 2.1; b. Result of 2.2; c. Result
of 2.2 after repetition.
Finally, we exclude all the undesired cells by
checking whether their final normalised value is ≥
“excluded cell(s)” (excluded if the expression
evaluates to TRUE). In this article, cells that were too
light, i.e., cells which have become non-visible and/or
do not resemble the shading of a natural artefact were
removed. The “excluded cell(s)” value allows the
programmer to control the accepted shading of their
artefact. Therefore, the criterion for estimating if a
cell is excluded can be manipulated, depending on the
desired outcome: if too light and dark artefacts are not
desired, then normalised values ≥ “excluded cell(s)”
value one and normalised values ≤ “excluded cell(s)”
value two will be excluded. Then, we multiply all the
non- removed cells’ final distance values by 255 and
set each Voronoi cell’s pixel value to the final result,
respectively. Also, a “desired cell(s)” value (which is
between 1 and the number of cells, excluding any
cells that have been removed) is generated and it will
determine what cell(s) will be used as the final
artefact(s). In the examples used in this article, the
“desired cell(s)” value was manually chosen, but it
can be assigned randomly.
2.2 Blended (Optionally Can Be
Repeated)
Within this step, we merge the original successful
microscope scan with the image generated in 2.1.
This allows an image with lighter Voronoi cells,
which fade naturally into the image to be generated.
This is essential as the periphery of actual artefacts
shows similar seamless fading into the microscope
scan. Moreover, the central color of the artefact is
lightened as well, which is vital as ideally the artefact
should not be too dark.
Both images are combined using equation (5):
𝑚
𝐴, 𝐵
𝐴
𝐵 (5)
where A represents a two-dimensional matrix of the
pixel values of the successful microscope scan, and B
represents a two-dimensional matrix of the pixel
values of the image from 2.2.
BIOIMAGING 2022 - 9th International Conference on Bioimaging
120

Table 1. Parameters used to generate the synthetic failed microscope scan demonstrated in Figure 1b.
Perlin noise n
𝜸 𝜷
scale Other parameters (Voronoi)
2.1 5 0.5 2.0
(image width,
image height)
C = 500, CL = random (x = 112-1957, y =
712-1877), EC = 0.85, DC = 183 & 186
Discretionally, this step can be repeated where the
newly blended image from this step is blended again
with the original successful microscope scan,
depending on what type of artefacts are wanted. If the
programmer wants to generate lighter artefacts that
are more subtle in appearance, then this step should
be repeated to achieve such an artefact. The authors
have repeated this step to illustrate what artefacts are
generated from such an approach (Figure 1a). Figure
1d shows artefacts from only one iteration of this step;
they are darker and more visible, generally the better
approach in most cases.
2.3 Extrapolation
Finally, for the final result generation, we use the
“desired cell(s)” parameter, defined in 2.1, to extract
the wanted cells from the image generated in 2.3 onto
the successful microscope used initially. Specifically,
this is achieved by iterating over the Voronoi section
of the image from 2.3 and checking whether it is part
of the desired cell(s). If it is, we alter the pixel value
of the original image to that of the one from 2.3. Upon
completion artefacts analogous to those in Figure 1b
are created, depending on what values were inputted
for the parameters and if 2.2 was repeated. Artefacts
in Figure 1c and 1d were generated without repetition
of 2.2.
3 RESULTS
The described algorithm generates a synthetic
artefact(s) on a successful microscope scan, as shown
in “Figure 1b and 1c”. The perceptual similarity
between both artefacts, artificial and “natural”,
pertaining to human-eye estimation, is high and
desirable: the artefacts synthetically generated within
Figure 1b, 1c and 1d naturally blend into the image
without seeming far too artificial, i.e., a massive
colour-contrast difference between the exterior of the
artefact and the pixels around it, is not present,
allowing the artefact to fade into the image and to
seem non-artificial. Also, the artefact(s) is aptly sized
and has the necessary shaping mechanism. The
method does not force the artefact(s) to be
specifically shaped; therefore, with every artefact a
somewhat abstract/realistic shape can be generated,
as seen in Figure 1b and 1c. This proves to be useful
as actual artefacts cannot be identified as having
specific shapes. Moreover, the locations and quantity
of artefacts can be controlled, meaning one successful
input image can be utilised to generate numerous
successful microscope scans with artificial artefacts.
Also, artefacts of distinctive shade can be generated
through repetition or non-repetition of step 2.2, as
seen in Figure 1b when compared to Figure 1c and
1d.
4 VERSATILITY & LENIENCY
The potency laid in a programmer’s hand regarding
achievable artefacts via the authors’ method is
immense, since the method supplies the programmer
with various parameters that can be altered for
attaining specific results, depending on what is
desired. For instance, the Perlin noise function
(Perlin, 1985) has over six parameters and directly
affects the size and shade of artefacts, enabling the
programmer to alter the respective Perlin noise
parameters to achieve lighter artefacts with smother
transitions or darker artefacts with less-smooth
transitions.
Furthermore, by manipulating the number of
Voronoi cells the programmer can alter effectively
the shape and size of the generated artefacts. The
function used for calculating the distance between
Voronoi points can be altered as numerous distance-
calculation functions exist (e.g., Euclidean (Gomathi
& Karthikeyan, 2014; Ranjitkar & Karki, 2016) and
Manhatton distance (Gomathi & Karthikeyan, 2014;
Ranjitkar & Karki, 2016)). This enables further
manipulation opportunities for the programmer; the
Voronoi Diagrams and Perlin Noise for Simulation of Irregular Artefacts in Microscope Scans
121

noisiness parameter allows to increase the roundness
of each artefact and their size, which proves to be as
artefacts vary in roundness and size.
Lastly, the parameters ‘excluded cell(s)’ and
‘desired cell(s)’ allow the programmer to deduct a
chosen proportion of cells. This controls the
generation of certain types of artefacts (lighter
artefacts, darker artefacts or artefacts of generic
shade). Visually appropriate cells can be selected
manually or automatically. The latter increases the
speed of artificial-failed microscope scan generation.
5 CONCLUSION
Within this article, the authors have described a
method for synthetic generation of “failed”
microscope scans for later use as augmented input
data within a neural network. The method outlined
within this article is promising as the generated and
the actual artefacts are very similar in visual
appearance. The artificial image distortions created
with this method naturally blend in microscope scans.
Furthermore, the method is easy to use and is
exceptionally versatile and lenient, i.e., it provides the
programmer with numerous parameters which all can
be slightly or massively tweaked to achieve
distinctive results. Finally, due to the method’s
versatility and leniency, it can synthetically generate
numerous “failed” microscope scans by only being
provided with one successful microscope scan,
allowing massive datasets to be produced for training
an artificial neural network to eliminate these
tiresome artefacts.
Although the quandaries above are intimidating to
the approach regarding restoration, the authors within
this article have developed and outlined the
foundation for solving this reoccurring and unabating
problem. The final solution will be achieved through
using a dataset generated from collecting numerous
and various successful microscope scans and their
synthetically generated failed counterparts, using the
method described within this article.
REFERENCES
Abdolhoseini, M., Kluge, M.G., Walker, F.R., & Johnson,
S.J. (2019). Neuron Image Synthesizer Via Gaussian
Mixture Model and Perlin Noise. 2019 IEEE 16th
International Symposium on Biomedical Imaging (ISBI
2019), 530-533. doi: 10.1109/ISBI.2019.8759471
Bae, H.J., Kim, C.W., Kim, N., Park, B., Kim, N., Seo,
J.B., & Lee, S.M. (2018). A Perlin Noise-Based
Augmentation Strategy for Deep Learning with Small
Data Samples of HRCT Images. Scientific Reports,
8(1). doi: 10.1038/s41598-018-36047-2
Berg, M.D., Cheong, O., Kreveld, M.V., Overmars, M., &
Schwarzkopf, O. (1997). Computational Geometry:
Algorithms and Applications. Springer-Verlag.
Choros, K., & Topolski, J. (2016). Parameterized and
Dynamic Generation of an Infinite Virtual Terrain with
Various Biomes using Extended Voronoi Diagram. J.
Univers. Comput. Sci., 22, 836-855.
Ferrero, M.M.A. (2011). Voronoi Diagram: The Generator
Recognition Problem. Computing Research Repository
- CORR.
Gomathi, V.V., & Karthikeyan, S. (2014). Performance
Analysis of Distance Measures for Computer
tomography Image Segmentation.
Peng, T., Wang, W., Rohde, G.K., & Murphy, R.F. (2009).
Instance-Based Generative Biological Shape
Modeling. Proceedings. IEEE International
Symposium on Biomedical Imaging, 5193141, 690–
693. doi: 10.1109/ISBI.2009.5193141
Perlin, K. (1985). An image synthesiser. SIGGRAPH
Comput. Graph., 19, 287-296. doi:
10.1145/325165.325247
Ranjitkar, H.S., & Karki, S. (2016). Comparison of A*,
Euclidean and Manhattan distance using Influence map
in MS. Pac-Man.
Reynolds, D. (2009). Gaussian Mixture Models. In: Li, S.Z.
& Jain, A. (eds.) Encyclopedia of Biometrics. Springer,
Boston, MA. doi: 10.1007/978-0-387-73003-5_196
Svoboda, D., Homola, O., & Stejskal, S. (2011). Generation
of 3D Digital Phantoms of Colon Tissue. In: Kamel, M.
& Campilho, A. (eds.) Image Analysis and
Recognition. ICIAR 2011. Lecture Notes in Computer
Science, 6754. Springer, Berlin, Heidelberg. doi:
10.1007/978-3-642-21596-4_4
Ulman, V., Svoboda, D., Nykter, M., Kozubek, M., &
Ruusuvuori, P. (2016). Virtual cell imaging: A review
on simulation methods employed in image cytometry.
Cytometry Part A, 89(12), 1057-1072. doi:
10.1002/cyto.a.23031
Unser, M. (1999). Splines: a perfect fit for signal and image
processing. IEEE Signal processing Magazine, 16(6),
22-38. doi: 10.1109/79.799930
Vercauteren, T., Pennec, X., Perchant, A., & Ayache, N.
(2007). Non-parametric diffeomorphic image
registration with the demons algorithm. Medical image
computing and computer-assisted intervention:
MICCAI ... International Conference on Medical Image
Computing and Computer-Assisted Intervention, 10(Pt
2), 319–326. doi: 10.1007/978-3-540-75759-7_39
Wasserman, L. (2004). All of Statistics: A Concise Course
in Statistical Inference. Springer, New York, NY. doi:
10.1007/978-0-387-21736-9
Xiong, W., Wang, Y., Ong, S.H., Lim, J.H., & Jiang, L.
(2010). Learning cell geometry models for cell image
simulation: An unbiased approach.
2010 IEEE
International Conference on Image Processing, 1897-
1900. doi: 10.1109/ICIP.2010.5652455
BIOIMAGING 2022 - 9th International Conference on Bioimaging
122
