Unsupervised Learning to Understand Patterns of Comorbidity in

633,330 Patients Diagnosed with Osteoarthritis

Marta Pineda-Moncusi

, Victoria Y. Strauss

, Danielle E. Robinson

, Daniel Prieto-Alhambra

and Sara Khalid

Centre for Statistics in Medicine, Nuffield Department of Orthopaedics,

Rheumatology and Musculoskeletal Sciences (NDORMS), University of Oxford, Oxford, U.K.

Keywords: Cluster Analysis, Electronic Healthcare Records, Osteoarthritis, Comorbidity Pattern, Data Mining.

Abstract: With the advent of big data in healthcare, machine learning has rapidly gained popularity due to its potential

to analyse large volumes of complex data from a variety of sources. Unsupervised learning can be used to

mine data and discover patterns such as sub-groups within large patient populations. However challenges with

implementation in large-scale datasets and interpretability of solutions in a real-world context remain. This

work presents an application of unsupervised clustering techniques for discovering patterns of comorbidities

in a large dataset of osteoarthritis patients with a view to discover interpretable and clinically-meaningful

patterns.

1 INTRODUCTION

Electronic health records present a wealth of routinely

collected patient care information that can be used for

data-driven health research (Binder and Blettner

2015), (Ehrenstein, Kharrazi et al. 2019).

Machine learning has shown potential for analysis

of large volumes of complex, multi-modality health

data, including pattern recognition to unravel sub-

groups of patients within a large population (Cohen,

Vawdrey et al. 2015, Pinedo-Villanueva, Khalid et al.

2018, Windgassen, Moss-Morris et al. 2018, Khalid

and Prieto-Alhambra 2019, Agrawal and Prabakaran

2020). A variety of algorithms, clustering strategies,

and evaluation criteria exist, as these choices are

largely dataset- and application- dependent (Liao, Li

et al. 2016, Grant, McCloskey et al. 2020).

In this paper we demonstrate the application of

unsupervised learning methods for the task of

identifying patterns of comorbidities within a large

cohort of osteoarthritis and methods for evaluating an

optimal clustering solution.

https://orcid.org/0000-0003-0567-0137

https://orcid.org/0000-0002-5172-512X

https://orcid.org/0000-0002-0940-9211

https://orcid.org/0000-0002-3950-6346

https://orcid.org/0000-0002-2845-5731

1.1 Clinical Context

Osteoarthritis (OA) is a musculoskeletal disorder that

occurs when joint cartilage deteriorates, causing

inflammation, stiffness, reduction of the mobility and

pain on joins. The most commonly affected areas

include knees, hands, hip and spine. OA is considered

the most common type of arthritis and it is estimated

to affect one of ten adults just in the UK (Swain,

Sarmanova et al. 2020). Patients diagnosed with OA

can experience considerable deterioration of their life

quality and severe cases can require a joint

replacement to reduce pain and restore joint function.

In addition to the personal and social implications

of the disease, OA has an important economic impact.

The National Joint Registry estimate that more than

90% of hip, knee and ankles replacements, and 59%

of shoulder replacements in 2019 at the UK were

caused by OA (NJR Report 2020). Moreover, patients

with OA are more likely to have other comorbidities

such as hypertension, dyslipidaemia and back pain

(Swain, Sarmanova et al. 2020).

Pineda-Moncusi, M., Strauss, V., Robinson, D., Prieto-Alhambra, D. and Khalid, S.

Unsupervised Learning to Understand Patterns of Comorbidity in 633,330 Patients Diagnosed with Osteoarthritis.

DOI: 10.5220/0010833500003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 3: BIOINFORMATICS, pages 121-129

ISBN: 978-989-758-552-4; ISSN: 2184-4305

121

The study of comorbidity patterns in OA patients

at the time of OA diagnosis can help to identify sub-

groups of patients e.g., individuals who might require

additional care. This can in turn aid patient care

decision-making and healthcare resource allocation.

1.2 Contribution in This Paper

Unsupervised machine learning methods such as

cluster analysis are well-suited to the problem of

patient sub-group identification (Pinedo-Villanueva,

Khalid et al. 2018, Violan, Roso-Llorach et al. 2018,

Grant, McCloskey et al. 2020, Hansen, Angquist et al.

2020, Wartelle, Mourad-Chehade et al. 2021).

In this work, we demonstrated the application of

cluster analysis methods to a large routinely collected

dataset representative of patients diagnosed with OA

to unravel patterns of OA comorbidities.

Although cluster analysis methods are widely

known, their use for detecting comorbidity patterns in

a large and representative database of OA patients is

presented for the first time in this work, and we

describe key methodological challenges in

implementing cluster analysis with a large sample

size using an open-source software.

2 METHODS

2.1 SIDIAP Database

The Information System for Research in Primary

Care (SIDIAP) is a healthcare database that contains

de-identified patients records from more than 370

primary care teams in Catalonia (Spain), covering

approximately 80% of the Catalan population

(https://www.sidiap.org/).

2.2 Data

Participants aged ≥18 years with at least one

physician-recorded diagnosis of OA for hip, knee,

ankle/foot, wrist/hand, or site recorded as

‘unspecified’ from 1

of January 2006 to 31

of June

2020 in SIDIAP database were included in the study

cohort. Incident cases i.e., first-ever diagnoses of OA

cases were identified, and individuals were followed-

up from the first diagnosis date (index date).

Patients with data recorded for less than a year

before index date were excluded. Exclusion criteria

also included any record of specific non-OA

diagnosis (soft-tissue disorders, other bone/cartilage

diseases) at the same joint in the 12 months before or

after the recorded OA/joint pain consultation.

For the OA cohort, a total of 58 comorbidities of

OA, identified by clinical experts and literature, were

available in the dataset. Patient characteristics

included socio-demographics, medical history,

clinical procedures, laboratory tests, and treatments.

2.3 Pre-processing

Prevalence of the 58 OA comorbidities was

measured. Comorbidities with less than 1%

prevalence in the dataset were excluded. Highly

correlated variables were identified using Pearson

correlation: if a pair of comorbidities had a

correlation coefficient > ±0.6, clinical expert opinion

was used to consolidate the two comorbidities.

2.4 Cluster Analysis

Cluster analysis was used to split the dataset based on

patterns of comorbidities and identify sub-groups of

individuals with similar comorbidities.

The choice of clustering technique can be guided

by the nature of data (e.g., categorical or continuous

distribution) and the goal of the clustering task.

Hard clustering may be preferred where it is desirable

to assign each individual to a single group (non-

overlapping clusters). Conversely, soft clusters

generate cluster membership probabilities for each

individual, such that an individual may have

membership in more than one cluster (overlapping-

clusters).

2.4.1 K-means

K-means is one the most popular hard clustering

approaches, perhaps for being one of the simplest and

less computational demanding. Ideally, it is meant for

continuous data, but it can be applied to binary

variables not highly correlated (Henry, Dymnicki et

al. 2015).

In k-means we must pre-specify the desired

number of clusters (k). Then, k randomly selected

points from the d-dimensional space are assigned to

be the cluster centroids (in our case, k random

individuals became centroids). The distance between

each individual and the centroids is computed, and

each individual is assigned with its closest centroid.

After that, clusters centroids are re-calculated based

on the values within each group, and individuals are

re-allocated to the new closest centroid.

Re-calculation and re-allocation steps are repeated

until position of cluster centroids stops changing.

Since k-means is sensitive to initial random

selection of centroids, the obtained solution might

become trapped in a local minimum. To prevent this

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

122

limitation, the algorithm should be repeated with

random initialisation and the results pooled.

Cluster Evaluation in K-means

The choice of the optimal number of clusters (𝑘



) can

be subjective, but we can use a set of internal and

external evaluation criteria to assist us in the decision.

Additionally, both evaluations can provide us a better

understanding of the performance of the cluster

algorithm, and the existing grouping behaviour of the

data.

The internal evaluation aims to find the solution

of k clusters that maximizes the homogeneity of

individuals within a cluster, while enhances the

heterogeneity between different clusters. The

simplest criteria to evaluate this is based on

measuring the variance or scatter within a cluster: the

within-cluster sum of squares (WCSS).

𝑊𝐶𝑆𝑆  Σ





∈







𝑥



𝑥̅







(1)

where S

is the subset of individuals assigned in

the k

cluster, x

represents the cluster mean, and k is

the candidate number of clusters, k = 1:K. K is the

maximum numbers of clusters considered.

Other methods that are well described in the literature

and are frequently used are Calinski-Harabasz

(Caliński and Harabasz 1974), Gap (Tibshirani,

Walther et al. 2001), and Silhouette (Rousseeuw

1987). The 𝑘



is the k solution where all or most of the

criteria concur, but when the results are not clear, the

best is to select few models and assess them through

an external and clinical evaluation.

The external evaluation uses independent

variables (i.e., external, not included in the

clusterization, but related to cluster features) to

describe the cluster solutions, and therefore externally

validating it. It can be especially useful when there is

no clear consensus of 𝑘



using the internal evaluation.

In our example, we have included age (< 50 years,

between 50 and 70 years, and > 70 years), index of

deprivation (rural areas, socioeconomic status > 3),

and current smoking status.

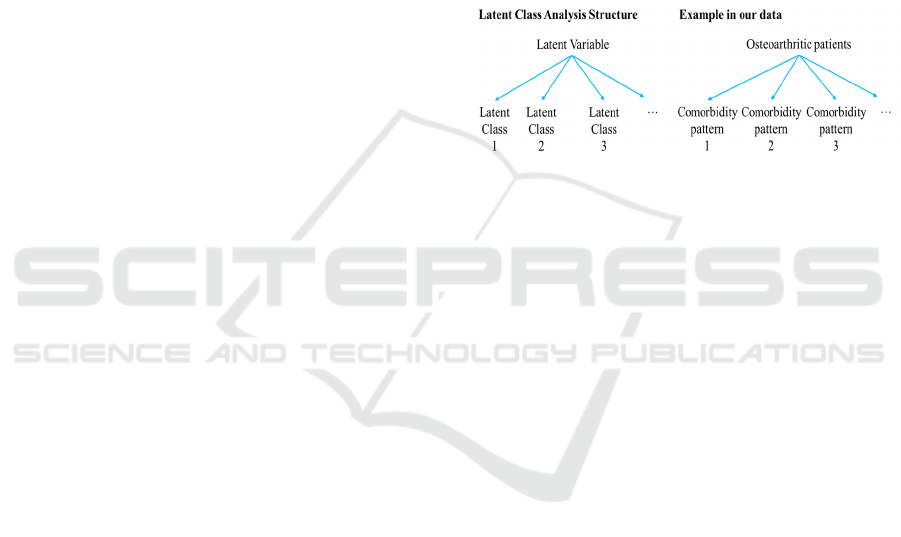
2.4.2 Latent Class Analysis

Latent Class Analysis (LCA) is a type of soft

clustering that explains the heterogeneity between

individuals regarding a particular compilation of

measured items. LCA is a finite mixture model:

instead of measuring the distance between

individuals, LCA uses a mix of distributions to

determine the most likely model that describes the

heterogeneity of the data as a finite number of groups

(latent classes) (figure 1). In other words, it produces

an estimate of how likely is for an individual to

belong to a cluster by summarizing their patterns of

characteristics into a pre-specified number of latent

classes.

In fact, the larger number of features involved in

the analysis, the higher number of patterns can be

found in the data (the increment is exponential),

which increases the difficulty of the results

interpretation. But LCA can reduce the total number

of possible patterns by compressing them into

subsets, showing us the most prevalent of them at the

cost of losing certain amount of specificity.

Nonetheless, the provided patterns will be more

comprehensible and practical while still

parsimonious.

Figure 1: Structure of latent class analysis and application

in our data. A latent variable can be represented by latent

classes (i.e., groups/subgroups of the latent variable that

cannot be measured). In our example, we want to represent

patients with osteoarthritis into groups according to their

combination of comorbidities (i.e., patterns).

LCA was originally designed for discrete

variables, which is the case of the assessed variables

presented in this work, but there is an extension for

dealing with longitudinal data (Jung and Wickrama

2008). As with k-means, LCA requires the

introduction of the expected number of k classes, but

in this case we can statistically determine the

performance of the proposed models in representing

the studied population.

Cluster Evaluation in Latent Class Analysis

The 𝑘



in LCA is obtained by comparing the

performance of the models from k = 1 or 2, to a

reasonable number of subgroups. For example, we

will analyse up to k = 10. We can calculate different

criteria methods to compare the models, such as the

likelihood and its logarithm, the entropy, entropy R

the Akaike's Information Criteria (AIC), Bozdogan's

Criterion (CAIC), the Bayesian Information Criteria

(BIC, as well known as Schwartz's Bayesian

Criterion) and the Akaike's Bayesian information

criterion (ABIC).

In this paper, we have used the entropy R2, the

ABIC, BIC, CAIC criteria methods and log-

likelihood ratio.

Unsupervised Learning to Understand Patterns of Comorbidity in 633,330 Patients Diagnosed with Osteoarthritis

123

Entropy in cluster analysis explains the amount of

disorder (dispersion) in the data, and points how good

the prediction of the cluster membership can be. The

score ranges from 0 to 1, where low values represent

less different characteristics/patterns; and high

numbers represent greater disorder, where is more

likely for the model to be distributed correctly across

different groups. A common desired threshold to set

a good entropy is > 0.7. Boeschoten et al. (2017) fully

report the methodology to calculate the entropy R

LCA models (Boeschoten, Oberski et al. 2017).

The AIC criteria measures of the goodness of fit

of the proposed model derived from frequentist

probability (Akaike 1987), while BIC is derived from

Bayesian probability (Schwarz 1978). Compared to

BIC, complex models are less penalized in AIC. The

CAIC is an extension of the AIC procedure with a

stronger penalty for overparametrized models

(Bozdogan 1987), and ABIC is a sample-sized

adjusted BIC (Sclove 1987). In all these parameters,

the lowest value reflects the best model. In mixed

models, we can measure these parameters as follows:

𝐴𝐼𝐶  2Λ  2Φ (2)

𝐶𝐴𝐼𝐶  2Λ  Φ



1𝑙𝑛𝑁



(3)

𝐵𝐼𝐶  2Λ  Φln𝑁 (4)

𝐴𝐵𝐼𝐶  2Λ  ln









(5)

Where Λ

is the maximum log-likelihood and Φ is

the total number of estimated parameters (degrees of

freedom) of the model, and N is the number of

participants in the subset.

Ideally, the optimal LCA model will be the one

with the lowest value obtained in CAIC, BIC and

ABIC criteria, and the highest entropy R

, but it might

happen that criteria values keep decreasing and

entropy increasing. Like the strategy of selecting the

𝑘



in K-means, we choose few models for a manual

evaluation to unravel the underlying patterns of

comorbidities from each cluster by observing the

posterior probabilities (i.e., probability from patients

to be allocated to one cluster).

2.5 Software Used

All the analysis were conducted using R 4.1.1 for

Windows.

3 RESULTS

We identified 633,330 patients diagnosed with OA in

SIDIAP database, and from the total 58

comorbidities, only 36 were present in more than 1%

of the population (Table 1). No correlations equal or

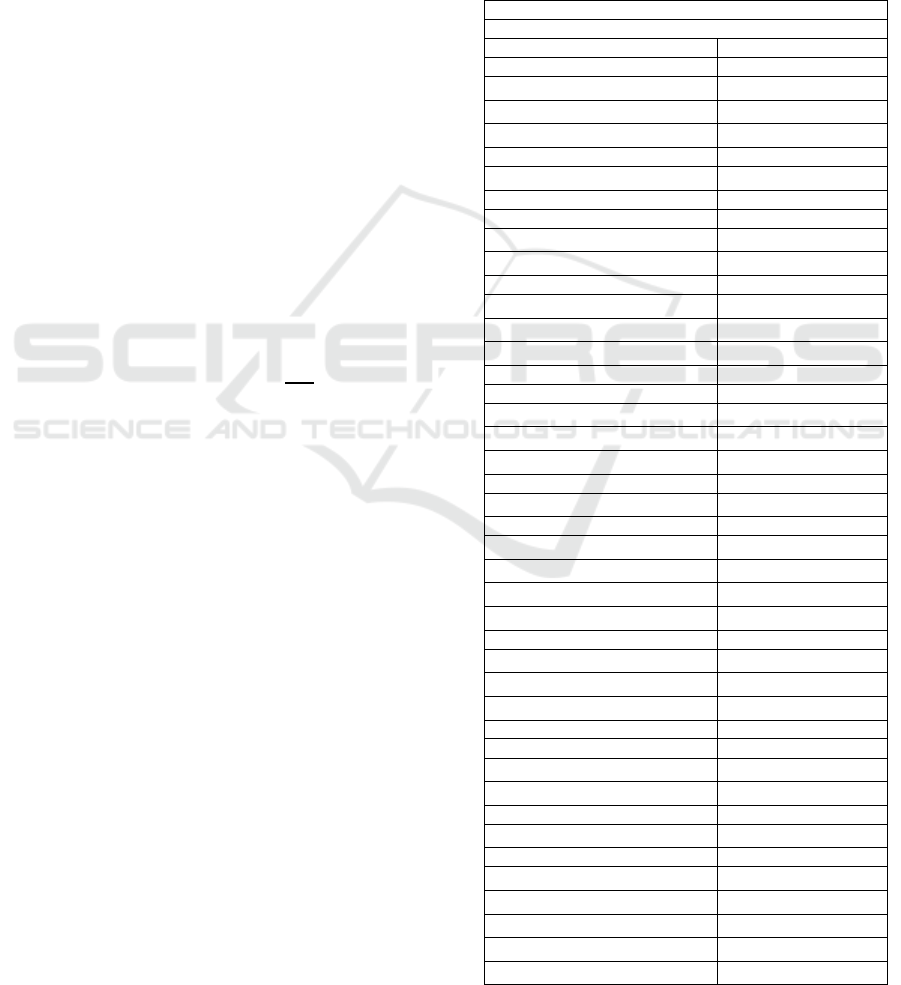
above 0.6 were found.

Table 1: Prevalence of OA patients’ comorbidities. In bold:

comorbidities excluded in the analysis (<1.0% of

prevalence). Abbreviations: BHP, benign prostate

hypertrophy; COPD, chronic obstructive pulmonary

disease; GERD, gastroesophageal reflux disease; IBD,

inflammatory bowel disease; PVD, peripheral vascular

disease; SLE, Systemic lupus erythematosus.

Comorbidities

(

total = 58

)

N=633330

Anaemia 48281

(

7.62%

)

Ank

losin

ond

litis 550

(

0.09%

)

Anxiet

80554 (12.7%)

Arrythmia 32605 (5.15%)

Asthma 15960 (2.52%)

Autism 24

(

0.00%

)

Back/neck pain 212986 (33.6%)

BHP 33560

(

5.30%

)

Cateract 0

(

)

Chronic heart disease 34300 (5.42%)

Chronic heart failure 15850 (2.50%)

Sinusitis 2675

(

0.42%

)

Chronic Kidney disease 36098 (5.70%)

COPD 23961 (3.78%)

Vitamin D deficienc

7569 (1.20%)

Dementia 12467

(

1.97%

)

ression 48757

(

7.70%

)

Diabetes 57498 (9.08%)

Hyperlipidemia 11602 (1.83%)

Eczema 21924 (3.46%)

ile

2671

(

0.42%

)

Fatigue 16852 (2.66%)

Fibrom

ia 10008

(

1.58%

)

Gall

ladde

stone

21346 (3.37%)

GERD

6474 (1.02%)

Gout 12388 (1.96%)

Hearing impairment 41563 (6.56%)

atitis 455

(

0.07%

)

oth

roidis

22153 (3.50%)

HIV/AIDs

252 (0.04%)

ertension

149092 (23.5%)

erth

roidism 4789

(

0.76%

)

IBD 14810

(

2.34%

)

Insomnia 44278 (6.99%)

Irritable bowel syndrome 4520 (0.71%)

Leukaemia 915

(

0.14%

)

Liver 2336 (0.37%)

homa 948

(

0.15%

)

Migrane 10401 (1.64%)

Multiple sclerosis 248 (0.04%)

Obesity 80387 (12.7%)

Osteoporosis 45261 (7.15%)

Other vessel diseases 9621 (1.52%)

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

124

Table 1: Prevalence of OA patients’ comorbidities. In bold:

comorbidities excluded in the analysis (<1.0% of

prevalence). Abbreviations: BHP, benign prostate

hypertrophy; COPD, chronic obstructive pulmonary

disease; GERD, gastroesophageal reflux disease; IBD,

inflammatory bowel disease; PVD, peripheral vascular

disease; SLE, Systemic lupus erythematosus (cont).

Parkinson 3872 (0.61%)

PVD 2773 (0.44%)

Polymyagia rheumatica 3408 (0.54%)

Psoriasis 8179 (1.29%)

Psoriatic arthritis 580 (0.09%)

Rheumatoid arthritis 3250 (0.51%)

Schizo

hrenia 985 (0.16%)

Allergy 80449 (12.7%)

Sjogen’s syndrome 2070 (0.33%)

SLE 504 (0.08%)

Solid malignancy 23946 (3.78%)

Stroke 20986 (3.31%)

Substance abuse 40423

(

6.38%

)

Thrombotic diseases 823 (0.13%)

Tuberculosis 1321 (0.21%)

3.1 Internal Evaluation

Figure 2 shows the results for internal validation of k-

means using WCSS, and figure 3 for LCA using

Entropy R

, goodness of fit tests and likelihood

values. Other metrics (e.g., Gap, Silhouette and

Calinski-Harabasz) were unable to converge given

the sample size. Running times for LCA were larger,

especially for higher numbers of k (up to three weeks

when k = 10 in LCA vs. one day in K-means). WCSS

did not change by more than ±1 std after k=6, and

similar effect was observed in curves from internal

validation of LCA analysis. Therefore, to determine

an optimal number of clusters, cluster visualisation

was performed for k=4, 5, and 6 in both methods.

Figure 2: Representation of the Within-Cluster-Sum-of-

Squares (WCSS) for each number of k.

Figure 3: Representation of A) entropy R

values and, B)

goodness of fit tests and likelihood ratio for each LCA when

k ranges from 1 to 10.

When using k = 4, k-means (figure 4A) show a

generally healthy cluster, a back/neck pain cluster, an

anxiety cluster with half of the patients experiencing

back/neck pain, and a hypertension cluster with

around forty percent of patients experiencing

back/neck pain. In LCA (figure 5A), first 2 clusters

present the same main comorbidities: relatively

healthy group and back/neck pain. Back/neck pain

cluster is also linked with mental disorders (anxiety

and depression), migraine, insomnia, and/or other

pain conditions (fatigue and fibromyalgia). Third and

fourth clusters present a main prevalence of

hypertension and back/neck pain. However, third

cluster is linked to more comorbidities, including

mental disorders, insomnia, anaemia, diabetes, and/or

set of different cardiovascular disorders (arrythmia,

stroke, chronic heart disease and chronic heart

failure), among others.

When using k = 5, k-means (figure 4B) distinguish

patients in back/neck pain, back/neck pain plus

hypertension, anxiety with half of them experiencing

back/neck pain, hypertension, and healthy clusters.

LCA (figure 5B) distinguish patients among

hypertension and back/neck pain plus many other

comorbidities; hypertension and back/neck pain, but

less presence of other comorbidities; back/neck pain,

combined with mental disorders and/or allergy;

hypertension; and healthy clusters.

When using k = 6, k-means (figure 4C) stratify

patients into back/neck pain, healthy, anxiety,

obesity, hypertension and back/neck pain, and

hypertension clusters. LCA results (figure 5C) show:

a cluster with prevalence of hypertension followed by

Unsupervised Learning to Understand Patterns of Comorbidity in 633,330 Patients Diagnosed with Osteoarthritis

125

back/neck pain, obesity and diabetes; second cluster

with hypertension followed by back/neck pain, plus

different cardiovascular disorders, anaemia and/or

diabetes; third cluster with back/neck pain followed

by hypertension, plus allergy, mental disorders and/or

obesity; forth cluster with back/neck pain and low

presence of other comorbidities; fifth cluster with

hypertension followed by back/neck pain, and low

occurrence of other comorbidities; and last, a

generally healthy cluster.

Figure 4: Distribution of comorbidity patterns within a

cluster using K-means: A) k = 4, B) k = 5, and C) k=6.

Number of patients in each cluster is described. External

variables not included in the cluster algorithm: smoke, rural

area, SES, male and age groups. Abbreviations: SES, urban

socioeconomic status where >3 are more deprived areas.

3.2 External Evaluation

In k-means graphs, we included the external features

along with the 10 most prevalent comorbidities

(figure 4). In k = 4, clusters 1 and 4 are older patients.

These clusters were annoted as healthy and

hypertension groups, respectively. Cluster 3, the

anxiety group, has the lower proportion of men.

When k = 5, cluster 4 had the oldest population,

followed by cluster 5 and 2 (identified as

hypertension, healthy and hypertension plus

back/neck pain, respectively). Cluster 3, once again

anxiety group, had the lowest proportion of males.

When k = 6, clusters 3 and 4 (anxiety and obesity,

respectively) had lower male patients, and clusters 1

and 4 (back/neck pain and obesity, respectively) tend

to have younger patients.

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

126

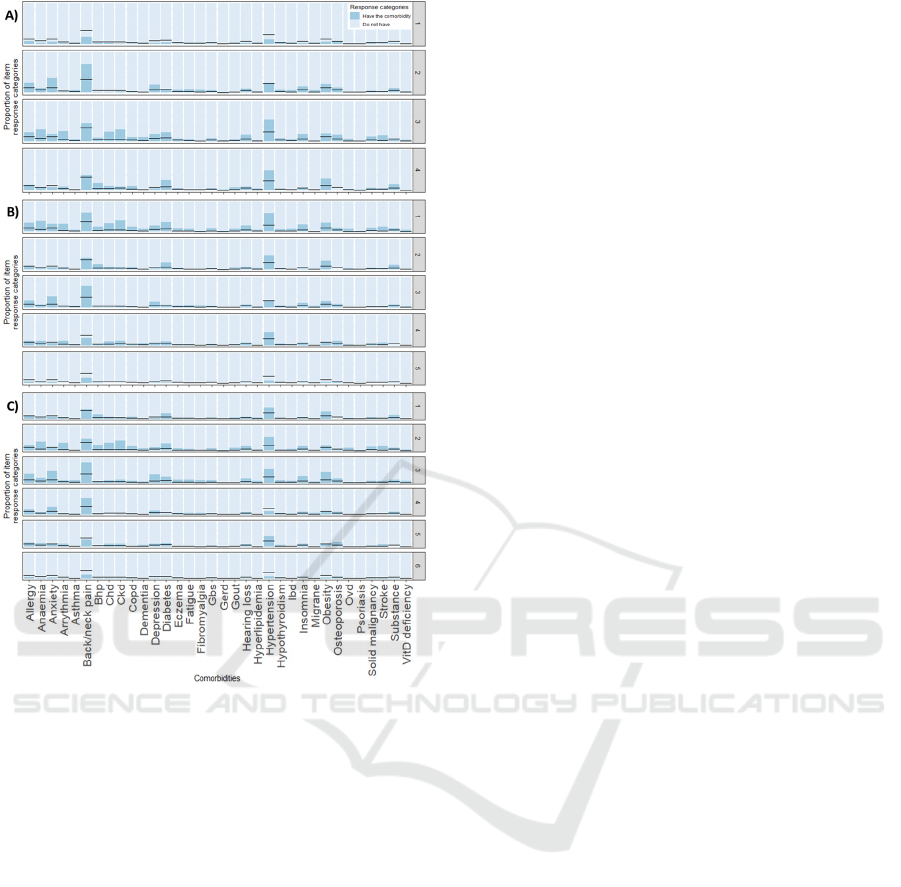
Figure 5: Distribution of comorbidity patterns within a

cluster using LCA: A) k = 4, B) k = 5, and C) k=6.

Black horizontal lines represent the prevalence of the

comorbidity before the clusterization. Abbreviations: Bhp,

benign prostate hypertrophy; Chd, chronic heart disease;

Ckd, chronic kidney disease; Copd, chronic obstructive

pulmonary disease; Gbs, gall bladder stone; Gerd,

gastroesophageal reflux disease; Ibd, inflammatory bowel

disease; Ovd, other vessel diseases; Substance, substance

abuse.

4 DISCUSSION

Cluster analysis is a type of unsupervised learning

methods and therefore, we cannot test in absolute

terms whether the number of groups and the obtained

grouping is accurate or the most optimal. The general

practice is to include more than one method and to

compare the subsequent solutions.

In terms of the limitations of each cluster method,

we have observed that large datasets imply

difficulties in calculating the internal validation

methods based on distance matrix in K-means, and

larger running times in LCA. In terms of

interpretability, results from k-means are easier to

interpret than LCA. Distinct clusters are assigned to

patients, and therefore, highly distinguishable groups

are created. Despite this, soft classification by LCA

allows us to detect more complex patterns that

possibly represents better the behaviour and

interaction of comorbidities among the OA patients.

Comparing the composition of the different

clusters across both methods, similar clusters can be

found: a healthy group, patients with high prevalence

of back/neck pain and hypertension (alone or

combined), mental disorders (i.e., anxiety and/or

depression), etc. Observing the evolution of clusters

when incrementing the k, higher number of groups in

k-means seems to enhance patients’ differences. But

in LCA, clustering patients in 6 different groups

obscures the interpretability rather than show more

hidden patterns. In this method, our proposed

optimum number of stratification is 5, where we can

distinguish a cluster of patients with high complex

comorbidities profiles (cluster 1: hypertension and

back/neck pain plus many other comorbidities) from

a cluster of patients with hypertension and back/neck

pain but less prevalence of other complications

(cluster 2), and from patients with not only back/neck

pain but also mental disorders (cluster 3).

Simultaneous comorbidities exacerbate pain and

diminish the physical function (Calders and Van

Ginckel 2018). Differentiation of individuals from

cluster 1 and 2 leaded us to identify a sub-group of

patients that potentially require further supervision.

To confirm that, next steps will include an evaluation

of the obtained clusters with an external outcome

such as 10-years death or a change in a quality of life

index.

Another limitation to note is that this work

included all OA patients regardless of site. The

location of the affected joint (e.g., OA in knee or hip)

might have a different impact in the clinical profile of

OA patients (and therefore their respective

comorbidity patterns). Thus, examination of site-

specific OA cohorts, such as knee OA, is part of the

on ongoing work.

5 CONCLUSIONS

In this work, patterns of co-morbidities within a large

OA population were examined and sub-groups

identified. We have shown some of the challenges

and strategies of unsupervised machine learning

applied to a large dataset from a representative

primary care database, including lack of convergence

of several methods in K-means and the alternatives to

Unsupervised Learning to Understand Patterns of Comorbidity in 633,330 Patients Diagnosed with Osteoarthritis

127

overcome it, large running times in LCA, and the

complexity of interpreting the results.

ACKNOWLEDGEMENTS

This research was founded by the Foundation for

Research in Rheumatology (FOREUM).

Further acknowledgements were removed for

review purposes.

DISCLAIMER

This paper presents independent research funded by

the Foundation for Research in Rheumatology

(FOREUM) that currently is ongoing. Views

expressed are those of the author(s) and not necessary

those of all partners involved in FOREUM study.

REFERENCES

Agrawal, R. and S. Prabakaran (2020). "Big data in digital

healthcare: lessons learnt and recommendations for

general practice." Heredity 124(4): 525-534.

Akaike, H. (1987). "Factor analysis and AIC."

Psychometrika 52(3): 317-332.

Binder, H. and M. Blettner (2015). "Big data in medical

science--a biostatistical view." Dtsch Arztebl Int

112(9): 137-142.

Boeschoten, L., D. Oberski and T. d. Waal (2017).

"Estimating Classification Errors Under Edit

Restrictions in Composite Survey-Register Data Using

Multiple Imputation Latent Class Modelling (MILC)."

Journal of Official Statistics 33(4): 921-962.

Bozdogan, H. (1987). "Model selection and Akaike's

Information Criterion (AIC): The general theory and its

analytical extensions." Psychometrika 52(3): 345-370.

Calders, P. and A. Van Ginckel (2018). "Presence of

comorbidities and prognosis of clinical symptoms in

knee and/or hip osteoarthritis: A systematic review and

meta-analysis." Semin Arthritis Rheum 47(6): 805-813.

Caliński, T. and J. Harabasz (1974). "A dendrite method for

cluster analysis." Communications in Statistics 3(1):1-

27.

Cohen, B., D. K. Vawdrey, J. Liu, D. Caplan, E. Y. Furuya,

F. W. Mis and E. Larson (2015). "Challenges

Associated with Using Large Data Sets for Quality

Assessment and Research in Clinical Settings." Policy

Polit Nurs Pract 16(3-4): 117-124.

Ehrenstein, V., H. Kharrazi, H. Lehmann and C. O. Taylor

(2019). Chapter 4 Obtaining Data From Electronic

Health Records. Tools and Technologies for Registry

Interoperability, Registries for Evaluating Patient

Outcomes: A User’s Guide, 3rd Edition, Addendum 2

[Internet]. R. E. Gliklich, M. B. Leavy and N. A.

Dreyer, Rockville (MD): Agency for Healthcare

Research and Quality (US).

Grant, R. W., J. McCloskey, M. Hatfield, C. Uratsu, J. D.

Ralston, E. Bayliss and C. J. Kennedy (2020). "Use of

Latent Class Analysis and k-Means Clustering to

Identify Complex Patient Profiles." JAMA Netw Open

3(12): e2029068.

Hansen, N. S., L. Angquist, P. Lange and R. Jacobsen

(2020). "Comorbidity Clusters and Healthcare Use in

Individuals With COPD." Respir Care 65(8): 1120-

1127.

Henry, D., A. B. Dymnicki, N. Mohatt, J. Allen and J. G.

Kelly (2015). "Clustering Methods with Qualitative

Data: a Mixed-Methods Approach for Prevention

Research with Small Samples." Prev Sci 16(7): 1007-

1016.

Jung, T. and K. A. S. Wickrama (2008). "An Introduction

to Latent Class Growth Analysis and Growth Mixture

Modeling." Social and Personality Psychology

Compass 2(1): 302-317.

Khalid, S. and D. Prieto-Alhambra (2019). "Machine

Learning for Feature Selection and Cluster Analysis in

Drug Utilisation Research." Current Epidemiology

Reports 6(3): 364-372.

Liao, M., Y. Li, F. Kianifard, E. Obi and S. Arcona (2016).

"Cluster analysis and its application to healthcare

claims data: a study of end-stage renal disease patients

who initiated hemodialysis." BMC Nephrol 17: 25.

Pinedo-Villanueva, R., S. Khalid, V. Wylde, R.

Gooberman-Hill, A. Soni and A. Judge (2018).

"Identifying individuals with chronic pain after knee

replacement: a population-cohort, cluster-analysis of

Oxford knee scores in 128,145 patients from the

English National Health Service." BMC Musculoskelet

Disord 19(1): 354.

NJR Report. (2020). "National Joint Registry 17th Annual

Report 2020.", from https://reports.njrcentre.

org.uk/downloads.

Rousseeuw, P. J. (1987). "Silhouettes: A graphical aid to

the interpretation and validation of cluster analysis."

Journal of Computational and Applied Mathematics 20:

53-65.

Schwarz, G. (1978). "Estimating the dimension of a

model." The annals of statistics: 461-464.

Sclove, S. L. (1987). "Application of model-selection

criteria to some problems in multivariate analysis."

Psychometrika 52(3): 333-343.

Swain, S., A. Sarmanova, C. Coupland, M. Doherty and W.

Zhang (2020). "Comorbidities in Osteoarthritis: A

Systematic Review and Meta-Analysis of

Observational Studies." Arthritis Care Res (Hoboken)

72(7): 991-1000.

Swain, S., A. Sarmanova, C. Mallen, C. F. Kuo, C.

Coupland, M. Doherty and W. Zhang (2020). "Trends

in incidence and prevalence of osteoarthritis in the

United Kingdom: findings from the Clinical Practice

Research Datalink (CPRD)." Osteoarthritis Cartilage

28(6): 792-801.

BIOINFORMATICS 2022 - 13th International Conference on Bioinformatics Models, Methods and Algorithms

128

Tibshirani, R., G. Walther and T. Hastie (2001).

"Estimating the number of clusters in a data set via the

gap statistic." Journal of the Royal Statistical Society:

Series B (Statistical Methodology) 63(2): 411-423.

Violan, C., A. Roso-Llorach, Q. Foguet-Boreu, M.

Guisado-Clavero, M. Pons-Vigues, E. Pujol-Ribera and

J. M. Valderas (2018). "Multimorbidity patterns with

K-means nonhierarchical cluster analysis." BMC Fam

Pract 19(1): 108.

Wartelle, A., F. Mourad-Chehade, F. Yalaoui, J. Chrusciel,

D. Laplanche and S. Sanchez (2021). "Clustering of a

Health Dataset Using Diagnosis Co-Occurrences."

Applied Sciences 11(5): 2373.

Windgassen, S., R. Moss-Morris, K. Goldsmith and T.

Chalder (2018). "The importance of cluster analysis for

enhancing

clinical practice: an example from irritable

bowel syndrome." Journal of Mental Health 27(2): 94-96.

Unsupervised Learning to Understand Patterns of Comorbidity in 633,330 Patients Diagnosed with Osteoarthritis

129