Syncrack: Improving Pavement and Concrete Crack Detection through

Synthetic Data Generation

Rodrigo Rill-Garc

ıa

1,2 a

, Eva Dokladalova

1 b

and Petr Dokl

adal

3 c

LIGM, Univ Gustave Eiffel, CNRS, ESIEE Paris, Marne-la-Vall

ee, France

Laboratoire Navier, Univ. Gustave Eiffel, CNRS, ENPC, Marne-la-Vall

ee, France

Center for Mathematical Morphology, MINES Paris – PSL Research University, Fontainebleau, France

Keywords:

Transfer Learning, Image Generation, Crack Detection, Inaccurate Labels.

Abstract:

In crack detection, pixel-accurate predictions are necessary to measure the width – an important indicator

of the severity of a crack. However, manual annotation of images to train supervised models is a hard and

time-consuming task. Because of this, manual annotations tend to be inaccurate, particularly at pixel-accurate

level. The learning bias introduced by this inaccuracy hinders pixel-accurate crack detection. In this paper

we propose a novel tool aimed for synthetic image generation with accurate crack labels – Syncrack. This

parametrizable tool also provides a method to introduce controlled noise to annotations, emulating human

inaccuracy. By using this, ﬁrst we do a robustness study of the impact of training with inaccurate labels. This

study quantiﬁes the detrimental effect of inaccurate annotations in the ﬁnal prediction scores. Afterwards, we

propose to use Syncrack to avoid this detrimental effect in a real-life context. For this, we show the advantages

of using Syncrack generated images with accurate annotations for crack detection on real road images. Since

supervised scores are biased by the inaccuracy of annotations, we propose a set of unsupervised metrics to

evaluate the segmentation quality in terms of crack width.

1 INTRODUCTION

For structural monitoring, crack inspection plays an

important role. For many constructions, such as roads

(Coquelle et al., 2012) or concrete structures (Yang

et al., 2018), the cracks’ width is one of the indicators

of the damage severity and future durability. Measur-

ing the width requires a pixel-accurate crack detection

(Escalona et al., 2019; Gao et al., 2019; Sun et al.,

2020; Yang et al., 2020), which is still a challenging

task (Bhat et al., 2020).

Many methods for crack detection rely on man-

ual labels. However, image annotation is a tedious

and highly time-consuming task. Moreover, it is

prone to human error for many reasons: low reso-

lution images, bad lighting conditions, fuzzy transi-

tions between cracks and background, intrusive ob-

jects, non-constant crack width, inappropriate label-

ing tools, etc. Because of this, manual annotations

tend to be inaccurate. More precisely, it is usual that

https://orcid.org/0000-0003-4726-6538

https://orcid.org/0000-0003-1765-7394

https://orcid.org/0000-0002-6502-7461

manual annotations are wider than the actual cracks.

Because of this inaccuracy in the annotations, ex-

isting works usually allow a tolerance margin to eval-

uate the detected cracks: “a pixel predicted as crack

is considered as true positive as long as it is no

more than X pixels away from an actual crack pixel”

(Escalona et al., 2019; Amhaz et al., 2016; Zou et al.,

2012; Shi et al., 2016; Ai et al., 2018). Using these

tolerance margins, state-of-the-art methods achieve

overwhelming F-scores, as high as 95%.

However, tolerance margins are lax and tolerant

to errors on the pixel level, and they have shown to

create huge score gaps: from Precision=47.1% and F-

score=56.7% (0-pixels tolerance) to Precision=90.7%

and F-score=87.0% (2-pixels) (Ai et al., 2018). Thus,

tolerance allows predicted cracks to be wider than

reality, artiﬁcially preserving high precision scores.

While this is sufﬁcient for counting and locating

cracks, it is not for measuring their width.

Rather than allowing tolerant evaluations, we pro-

pose to deal with the inaccuracies of manual anno-

tations. Towards this goal, our contributions can be

summarized as:

Rill-García, R., Dokladalova, E. and Dokládal, P.

Syncrack: Improving Pavement and Concrete Crack Detection through Synthetic Data Generation.

DOI: 10.5220/0010837300003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

147-158

ISBN: 978-989-758-555-5; ISSN: 2184-4321

147

1. The Syncrack generator. We developed this open-

source tool to generate parametrizable synthetic

images of cracked pavement/concrete-like tex-

tures. It provides both accurate annotations to al-

leviate the crack labeling task and parametrizable

noisy annotations to study the robustness of crack

detection methods.

2. A robustness study of the impact of inaccurate la-

bels. We studied the detrimental impact of train-

ing under different background and label noise

conditions, with accurate annotations for evalua-

tion. We measure the impact on prediction using

supervised and unsupervised scores. To the best

of our knowledge, we are the ﬁrst to perform this

type of study for crack detection.

3. An improved crack width detection. By training

solely with Syncrack-generated images, we pro-

duced predictions competitive with those obtained

by training with real-life images. Moreover, these

predictions exhibit an improved crack width with

respect to the ones obtained using real images.

The rest of the paper is organized as follows. In

section 2, we provide a literature review of crack de-

tection under the context of inaccurate manual anno-

tations. In section 3, we describe our proposed tool:

Syncrack. The experimental setup used to validate

our results with Syncrack is described in section 4.

In section 5, we use Syncrack to quantify the detri-

mental effect of inaccurate annotations in the predic-

tion scores. There, we analyze the ability of unsuper-

vised scores to assess the quality of crack detection.

In section 6, we show the promising scores of mod-

els trained on Syncrack when evaluated on real data.

Finally, section 7 concludes the paper.

2 RELATED LITERATURE

Automatic crack detection has been a topic of interest

for many years in the ﬁeld of construction. Beginning

by traditional image processing, strategies like Mini-

mal Path Selection (Amhaz et al., 2016) and Crack-

Tree (Zou et al., 2012) are fundamental works in the

area. However, such methods were overperformed

and displaced by machine learning approaches. In

this domain, we can cite representative examples such

as CrackIt (Oliveira and Correia, 2014) and CrackFor-

est (Shi et al., 2016).

Nonetheless, crack detection has been dominated

in recent years by deep learning. At ﬁrst, predictions

were done at binary patch classiﬁcation level (Zhang

et al., 2016; Kim and Cho, 2018). However, with

the increasing interest of pixel-accurate crack detec-

tion, the proposed methods progressively moved from

convolutional to fully convolutional neural networks.

Particularly, auto-encoders (Escalona et al., 2019; Liu

et al., 2019; Sun et al., 2020) allowed pixel-level pre-

diction using deep learning.

The success of generative models motivated more

complex networks. For example, there has been a re-

cent interest for using generative adversarial networks

(Gao et al., 2019; Zhang et al., 2020a). While these

complex models achieve impressive results in paper,

they rely on tolerance margins for evaluation. More-

over, as the complexity of the models increase, the

risk of overﬁtting to noisy annotations does to.

Inaccurate annotations are a particular case of

noisy labels. Learning in presence of noise is a

highly studied topic, proposing different approaches

such as noise-robust algorithm design, noise ﬁltering,

and noise-tolerant methods (Fr

enay and Verleysen,

2013; Zhou, 2017). However, these approaches are

not properly suited for severe class imbalance, which

is precisely the case of crack detection. In fact, the

problem of inaccurate annotations for crack detection

is barely discussed in the literature beyond the use of

tolerance margins for evaluation.

However, a common practice to avoid overﬁtting

in deep learning is data augmentation. This is particu-

larly useful when available labeled data is scarce. Mo-

tivated by the difﬁculty to obtain annotated images for

crack detection, ofﬂine data augmentation has been

used too (Mazzini et al., 2020; Kanaeva and Ivanova,

2021). However, these approaches rely on inaccurate

annotations, carrying the bias introduced by manual

annotation.

Unlike those approaches, our proposed tool –

Syncrack– provides a way to create datasets with ac-

curate labels. This avoids the necessity of using toler-

ance margins for evaluation of crack detection meth-

ods. It also allows quantifying the effect of training

with inaccurate annotations on prediction scores. Fur-

thermore, since Syncrack is parametrizable, it allows

tuning to approach (visually) a real-life distribution of

interest. In this way, it is possible to perform transfer

learning from the Syncrack domain to the real one.

3 SYNCRACK GENERATOR

Our tool consists of 4 main modules for 1) Creat-

ing a background image, 2) Creating crack shapes,

3) Adding cracks to the background, and 4) Creating

noisy annotations from pixel-accurate crack masks.

These modules are described in the next subsections.

To ensure diversity among images, each module

uses random values for its internal parameters. Some

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

148

Figure 1: Illustration of the Syncrack’s background generation steps.

of these values are obtained based on user-provided

parameters, allowing user customization of the out-

put. To ensure reproducibility, the random value se-

lection is done with a ﬁxed seed.

The user parameters relevant for our experiments

are described in this paper. For further information

about all the user parameters, as well as the random

value selection for internal parameters, we invite the

reader to visit our repository (provided at the end of

this article).

3.1 Background Generation

Our method (illustrated in Fig. 1) consists of 5 main

steps:

1. Creating a 2D Perlin Noise. By using the noise

module (Duncan, 2018), we create a noise map

based on Perlin noise (Perlin, 1985). The ‘scale’

parameter for the Perlin noise follows a normal

law deﬁned by the background average smooth-

ness and standard deviation provided as user pa-

rameters to run the program.

2. Converting to color image. Public crack datasets

contain RGB images; even though the material

generally looks gray, the hue is not strictly zero.

To emulate the appearance of real materials, two

random, low saturated, colors are chosen to repre-

sent the darkest and the lightest regions in the Per-

lin noise. We merge these colors together with a

weighted average using the Perlin noise as weight.

3. Adding crack-like noise. Crack-like artifacts are

added to the image to make crack detection a chal-

lenge. To do this, we chose random pixels as cen-

ters to draw arcs of random size ellipses. Then,

we introduce these lines to the image similarly to

how cracks are introduced (see subsection 3.3).

The amount of noise is inversely correlated to the

background average smoothness parameter in 1.

4. Adding additional noise. Real images are prone to

invasive elements. We add salt and pepper noise

with different radii to simulate dirt on the surface

and acquisition artifacts. The amount of this noise

is inversely correlated to the background average

smoothness parameter too.

5. Combining different textures. Stationary textures

are not frequent in real-life constructions (spe-

cially in roads). We create non-stationary back-

ground by joining together two or more textures,

each one generated with steps 1-4. We combine

the textures with a linear gradient ﬁll to create

smooth transitions.

3.2 Crack Shape Generation

Our crack shapes are based on a modiﬁcation of the

1D Perlin noise. First, we calculate a set of ver-

tices using the Perlin noise generator from the noise

module. The domain of these vertices is determined

by a randomly chosen crack length -i.e. 0 ≤ x ≤

crackLength, ∀(x,y) ∈ vertices.

However, these vertices have two problems: 1)

their height scale (y-axis) is blind to the image size

and the crack length, and 2) they use a straight axis

as origin, so the cracks would always tend to straight

lines. To solve this, we normalize the y-coordinates

of the vertices to the range [0, 1] and map them to

the range [0, crackHeight] with a randomly chosen

height. To obtain curve cracks, we displace the y-

coordinates of the vertices using an elliptic function.

These vertices are connected with straight lines to

create a crack skeleton. To provide the crack with

width, we dilate the skeleton by a disk. The diam-

eter is chosen randomly from a normal distribution

centered at 2 with standard deviation 0.5 (default user

parameters). Since real cracks do not have constant

widths, a sliding-window approach is used to intro-

duce dilations and erosions in random crack regions.

To avoid drastic changes, the structuring element is

a 2-pixel long vertical line. Aditionally, a dilation is

never followed by an erosion or vice-versa. An exam-

ple of a ﬁnal crack shape is shown in Fig. 2.

3.3 Crack Introduction

Once a crack shape is obtained, we generate a weight

map (same size as the background image) by creating

Syncrack: Improving Pavement and Concrete Crack Detection through Synthetic Data Generation

149

Figure 2: A synthetic crack shape generated by Syncrack.

an empty white image (weight=1.0) and putting a ran-

domly rotated version of the crack shape in a random

position within the new image (weight=0.0).

An average contrast value is randomly chosen

from a normal distribution with center and standard

deviation provided as user parameters. Then, within

the weight map, we set each crack-labeled pixel to

a new independent value. Per pixel, this value is

obtained from a new Gaussian distribution using the

chosen average contrast value as mean.

Since different crack regions tend to have different

lightning conditions in real life, we change the con-

trast of certain zones within the crack using a sliding

window. Finally, by using disk mean ﬁlters, we cre-

ate a transition region between the actual crack and

near-to-crack background. An example of the result-

ing weight map is shown in Fig. 3.

Figure 3: Example of a weight map used to introduce the

crack shape in Fig. 2 into a background image.

We use this weight map to introduce the crack into

the background by weighting each color channel with

the map. Fig. 4 shows an example of cracks inserted

in different backgrounds with different contrasts.

3.4 Label Noise Generator

To simulate inaccurate labeling, we introduce noise in

the annotations. We divide the annotation image into

tiles. Then, we alter randomly chosen tiles by per-

forming an erosion or a dilation by a disk with a ran-

dom diameter. With default user parameters, the tile

size is 0.05 ∗ imageHeight × 0.05 ∗ imageWidth. The

diameter of the the disk follows a normal law centered

around 3 for dilation and 2 for erosion. In both cases,

the standard deviation is 0.5.

The user parameter ‘noise percentage’ (np from

now on) is the probability, np ∈ (0, 1], for a tile to be

altered. Since the tiles are obtained by dividing the

whole image, and the probability is unconditional, an

altered tile may contain no cracks.

With np < 1, we expect inaccuracy similar to a

manual one: some crack segments wider (a dilation

was applied), some segments thinner (a small ero-

sion), missing crack segments (big erosion), and some

accurate segments. See Fig. 5 for examples.

4 EXPERIMENTAL SETUP

4.1 Evaluation Scores

We use two kind of evaluations: supervised and un-

supervised. The supervised scores compare the ob-

tained predictions and the available ground truth an-

notations. We used Precision (Pr) and Recall (Re), as

commonly done in the crack detection literature. The

harmonic mean of both yields a single metric – the F-

score. We used its equivalent, the Dice score, easily

allowing to add a smoothing factor to avoid division

by zero in images with no cracks (see last term of Eq.

4 below).

However, as discussed in this paper, when annota-

tions are inaccurate, supervised scores are biased. To

validate our results on real images, we propose a set

of metrics used previously for the evaluation of unsu-

pervised segmentation tasks (Zhang et al., 2008).

The ﬁrst one is the crack region entropy H

crack

based on the region entropy (Pal and Bhandari, 1993).

Given the set R

of pixels within a crack-predicted re-

gion, deﬁne a set V

of all the possible pixel intensities

within R

. Deﬁne L

(m) as the amount of pixels with

intensity m ∈ V

within R

. Then

crack

) = −

∑

m∈V

(m)

log(

(m)

) (1)

This is a way to measure the intra-crack uniformity.

Introducing background pixels into R

will increase

crack

). A good crack prediction should reduce

the crack region entropy.

We also use a second-order crack region en-

tropy H

crack

. The second order-entropy relies on co-

occurrence matrices rather than pixel intensities. This

allows inspecting the intra-crack region for textures.

Given p the probability from the co-occurrence ma-

trix calculated in R

crack

) = −

∑

i∈V

∑

j∈V

i j

log(p

i j

) (2)

Similarly to the ﬁrst order entropy, including back-

ground pixels in R

will increase the entropy. A good

segmentation reduces this score.

We assume that cracks and background are two

different distributions. We use the Kolmogorov-

Smirnov test (Smirnov, 1939) to measure the distance

between the distributions of pixels predicted as crack

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

150

Figure 4: Syncrack images generated with different user parameters. The crack mask is the same, but the background

generation and crack-introduction parameter values differ to create different levels of difﬁculty for crack detection.

Figure 5: Examples of different label noise levels for Fig. 4. From left to right, levels 0 to 4 (see Table 2). The second row

shows: Green) Crack pixels; Blue) Crack pixels mislabeled as background; Red) Background pixels mislabeled as crack.

and as background, respectively. If both distribu-

tions differ, the Kolmogorov-Smirnov score (K-S) in-

creases. Therefore, we want to maximize this score.

All our metrics are calculated per image, and the

results shown in the rest of the paper are the averages

over all the analyzed images.

4.2 Synthetic Datasets

In this paper, we use 3 datasets (200 images each)

obtained with the Syncrack generator using different

user parameter values. Particularly, we modiﬁed 2

parameters: the background average smoothness (re-

ferred to as bas) and the crack average contrast (re-

ferred to as cac). The background smoothness in-

tervenes both in the Perlin noise generation and the

amount of added noise (see subsection 3.1). The crack

contrast modiﬁes the relative contrast between the

background and the added crack (see subsection 3.1).

By modifying these two parameters, we create Syn-

crack datasets with 3 difﬁculty levels as described in

Table 1.

Table 1: Parameters used to create the 3 difﬁculty versions.

Difﬁculty level Easy Medium Hard

Background smoothness (bas) 6.0 3.0 1.5

Crack contrast (cac) 0.5 0.7 0.7

The easy difﬁculty has a smooth background and

well-contrasted cracks. The medium difﬁculty (de-

fault values) has rough textures with low-contrast

cracks. The hard example has the same contrast as

the medium one, but the background is rougher. The

3 datasets share the same cracks (see Fig. 4 for exam-

ple).

To study the effect of different label noise levels

in annotations used for training, we create noisy ver-

sions of the 3 above mentioned datasets. Particularly,

we introduce 5 label noise levels from 0 (no noise)

to 4 (the maximum amount of noise) by varying the

values of the np parameter (see subsection 3.4).

An analysis of the generated noise is pre-

sented in Table 2. The crack-to-background and

background-to-crack mislabeling percentages are cal-

Table 2: Label noise levels used for experiments.

Label noise level 0 1 2 3 4

np 0.00 0.25 0.50 0.75 1.00

Crack →

Background

mislabeling (%)

0.00 9.68 19.35 29.03 38.71

Background →

Crack

mislabeling (%)

0.00 12.90 24.19 32.26 43.55

Mislabeling (%) 0.00 22.58 43.55 61.29 82.26

DSC (%) 100 88.93 78.41 68.39 58.94

Pr (%) 100 88.44 77.18 68.53 58.29

Re (%) 100 89.92 80.61 69.41 60.66

Syncrack: Improving Pavement and Concrete Crack Detection through Synthetic Data Generation

151

Figure 6: U-VGG19’s architecture.

culated with respect to the total number of crack

pixels. For example, with 100 crack pixels in

the dataset: if 10 crack pixels were labeled as

background, Crack→Background mislabeling (%) =

10; if 5 background pixels were labeled as crack,

Background→Crack mislabeling (%) = 5. Mislabel-

ing (%) is the sum of both percentages. To understand

better the behavior of these percentages, we show the

DSC, precision and recall with respect to the clean

annotations too. Fig. 5 illustrates the different label

noise levels for Fig. 4.

4.3 Real Road Images

To validate the performance of models trained with

Syncrack on real-life data, we use the CrackForest

Dataset (CFD). This public dataset contains 118 im-

ages collected from urban roads containing perturba-

tions such as shadows, oil spots, and water stains in

Beijing, China (Shi et al., 2016). Similarly to the de-

fault size of the Syncrack generator, the original im-

age size is 480×320. The cracks in this dataset have a

width around 3 pixels, again similarly to the default

Syncrack generator. This dataset provides two an-

notations: borders and segmentation. As suggested

by (Sun et al., 2020), we removed some images with

clear severe annotation errors; we kept 108 images.

4.4 Baseline Model

U-net (Ronneberger et al., 2015), a symmetrical auto-

encoder, has seen success in pavement distress seg-

mentation. Similarly, VGG has been an attractive fea-

ture extractor to detect cracks (Escalona et al., 2019;

Zhang et al., 2020b). Based on this, we built a U-net-

like network using the pre-trained VGG19 (Simonyan

and Zisserman, 2015) as a basis.

This network, referred to as U-VGG19, is used as

a baseline model for our experiments (see Fig. 6).

4.5 Training Setup

We implemented the proposed architecture using Ten-

sorﬂow 2.1.0. For training, input images are cropped

to 256×256 patches and fed as 4-patch batches. We

used the Adam optimizer with a 10

−4

learning rate

and default parameters. The initial weights from

the encoder are the weights from VGG19 pre-trained

on ImageNet; from this starting point, the whole U-

VGG19 is trained together. Each dataset is randomly

split into 50% training and 50% validation.

Our preliminary models trained on synthetic im-

ages failed to detect cracks within color outlier pic-

tures. For example, bluish-looking pavement in con-

trast with the normal grayish colors. Since learning

models are sensitive to color information, we wish to

neglect the effect of color saturation due to the acqui-

sition process. To do this, all images are converted to

grayscale and converted back to 3 channels by con-

catenation.

To avoid overﬁtting to the distributions used by the

Syncrack generator, we trained using data augmenta-

tion. Our data augmentation consisted of randomly

transforming an image (and its corresponding annota-

tion) immediately before feeding it to the neural net-

work for training. To do this, a random value for

each of the 6 following operations is chosen: adding

noise, changing illumination, ﬂipping, zooming, ro-

tating and shearing. Every image undergoes the 6 op-

erations in the given order.

To reﬁne the results at late epochs, we reduce the

learning rate on validation loss plateau (by 2, with

5 epochs tolerance). To avoid overﬁtting, we add

an early stop if the validation loss does not decrease

during 20 consecutive epochs. We report the scores

calculated on the validation split using the network

weights with the minimum validation loss.

The loss is a combination of the binary cross-

entropy loss (BCE) and a DSC-based loss (DICE):

Loss = BCE + α ∗DICE (3)

Here, α is a hyperparameter (Sun et al., 2020) set em-

pirically to 3 to give more importance to DICE, cal-

culated as follows:

DICE = 1 −

2(GT · Pred) + 1

GT + Pred +1

(4)

Here, GT is the set of pixels annotated as crack and

Pred is the set of pixels predicted as crack. The more

similar GT and Pred are, the lower is DICE.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

152

5 EFFECT OF DIFFERENT

NOISE CONDITIONS

To validate the unsupervised segmentation scores pro-

posed in this paper, we analyze their behavior under

controlled conditions. To do this, we use the noisy

annotations obtained with the Syncrack generator.

In this section, we ﬁrst analyze the ability of un-

supervised scores to assess the quality of crack de-

tection using inaccurate annotations as reference. Af-

terwards, we use these inaccurate annotations to train

the baseline model (U-VGG19). Finally, we analyze

the relation between the unsupervised scores and the

prediction quality of trained models (one model per

noise and difﬁculty level).

In Table 3, we summarize the unsupervised scores

calculated on the three difﬁculty versions of Syncrack

using the automatically generated annotations (with

different label noise levels).

Table 3: Unsupervised evaluation of the Syncrack generated

annotations.

Difﬁculty Metric

Label noise level

0 1 2 3 4

Easy

crack

3.58 3.85 4.02 4.11 4.19

crack

6.80 7.11 7.36 7.49 7.65

K-S 0.98 0.89 0.81 0.77 0.73

Medium

crack

3.98 4.06 4.12 4.14 4.16

crack

7.39 7.50 7.59 7.61 7.67

K-S 0.68 0.63 0.58 0.54 0.49

Hard

crack

4.14 4.20 4.24 4.26 4.29

crack

7.57 7.65 7.72 7.74 7.80

K-S 0.54 0.50 0.46 0.43 0.39

With 0 noise in the annotations, when the difﬁ-

culty level increases, both entropies increase too and

the K-S decreases (see Fig. 7). This is natural, since

it becomes harder to tell the difference between crack

and background by looking at the images.

More importantly, we observe a relation between

mislabeling and the unsupervised scores: as the anno-

tations become more inaccurate, the region entropies

increase and the K-S decreases. With this conclu-

sion, we extend our study using unsupervised scores

to evaluate predictions obtained with U-VGG19 (the

proposed baseline model for crack detection).

In this experiment, we trained U-VGG19 with the

different difﬁculty and label noise levels proposed for

Syncrack in this paper. In this way, we can observe 1)

the effect of training with noisy labels when evaluat-

ing with accurate annotations and 2) the relation be-

tween supervised and unsupervised scores when hav-

ing accurate labels for evaluation.

The results of this experiment are shown in Table

Figure 7: Unsupervised evaluation of the Syncrack gener-

ated annotations.

4. By analyzing the 0 noise column, we observe the

impact of the difﬁculty level in the prediction scores.

While the model on easy difﬁculty obtains supervised

scores above 96%, they decrease drastically as the

difﬁculty increases. Just as before, the unsupervised

scores get worse as we increase the difﬁculty level.

Table 4: Prediction scores obtained in the validation splits

of the Syncrack’s 3 difﬁculty levels.

Difﬁculty Metric

Label noise level

0 1 2 3 4

Easy

DSC 96.07 96.21 95.55 91.31 73.50

Pr 96.14 95.69 92.30 84.74 58.39

Re 96.03 96.77 99.07 99.09 99.80

crack

3.57 3.59 3.66 3.84 4.19

crack

6.79 6.82 6.96 7.20 7.86

K-S 0.98 0.98 0.97 0.92 0.76

Medium

DSC 78.43 78.58 77.86 75.49 71.45

Pr 81.17 78.58 71.30 68.44 60.75

Re 76.55 79.36 86.71 85.25 88.12

crack

3.92 3.95 4.01 4.03 4.09

crack

7.29 7.39 7.56 7.60 7.74

K-S 0.73 0.71 0.66 0.64 0.59

Hard

DSC 67.44 65.91 65.29 65.70 62.58

Pr 66.30 63.85 59.54 61.55 53.70

Re 70.17 69.67 74.47 72.21 77.81

crack

4.08 4.09 4.14 4.13 4.20

crack

7.54 7.57 7.71 7.67 7.85

K-S 0.60 0.58 0.54 0.55 0.49

However, it is important to compare the unsuper-

vised scores of the predictions with respect to the an-

notations. When 0 label noise is present, in the easy

difﬁculty, both the annotation and the prediction su-

pervised scores are very close; this is true as well for

the unsupervised scores. Nonetheless, for the other

difﬁculties, the unsupervised scores are slightly better

even though the supervised scores are lower.

Syncrack: Improving Pavement and Concrete Crack Detection through Synthetic Data Generation

153

This kind of behavior can be explained by two fac-

tors. 1) The severe class unbalance; if a few pixel

change in the crack region is numerically measurable

it may be not in the background region (which is by

far more populated). 2) As a consequence of the pre-

vious, the unsupervised scores are blind to false neg-

atives. Missing cracks won’t affect these scores. This

bias emphasizes the predictions when only pixels with

high likelihood of being crack pixels are segmented,

even at the cost of missing cracks or having isolated

false positives. Thus, these unsupervised scores must

be understood under this context and should be paired

with supporting supervised scores to be able to draw

conclusions.

With this in mind, we still observe that both the

supervised and unsupervised scores get worse as we

increase the label noise (see Fig. 8). This suggests

that the unsupervised scores can be used as indicators

of segmentation quality regardless of the annotation

quality.

Figure 8: Prediction scores obtained in the validation splits

of the Syncrack’s 3 difﬁculty levels evaluating with accurate

annotations.

It is interesting to notice that the DSC seems to in-

dicate noise robustness in the trained models: as we

increase the label noise level, the DSC of the predic-

tion (Table 4) tends to be higher than the DSC of the

annotations (Table 2).

However, this apparent robustness is a trade-off

between precision and recall. As the noise increases,

the recall tends to increase too; nonetheless, the pre-

cision decreases more. From this, we can hypothesize

that using noisy annotations may actually help to de-

tect harder cracks at the cost of having a considerable

amount of false positives. The presence of these false

positives is congruent with the behavior of the unsu-

pervised scores: both entropies increase while the K-

S decreases.

When we analyzed the predictions qualitatively,

the conclusion was that the main source of false posi-

tives was having crack predictions wider than the ac-

curate clean annotation (see Fig. 9).

Figure 9: Example of inaccurate prediction training with

label noise level 4. The color code is the same as in Fig. 5.

Taking this into account, when it comes to the

predicted cracks’ width, we observe a relation be-

tween precision and the proposed unsupervised met-

rics. With these preliminary results, we moved to real

road images for evaluation of our synthetic generator.

6 IMPROVING REAL-LIFE

CRACK DETECTION WITH

SYNCRACK

To have a baseline for real data, we trained U-VGG19

with our CFD training split. Table 5 compares our re-

sults with other methods based on deep learning when

no tolerance margins are used for evaluation. The

chosen metric was F-score, since it is the most com-

mon score used in the literature.

Table 5: F-scores on CFD without tolerance margins.

Method F-score

U-net

(Gao et al., 2019)

60.48%

GANs

(Gao et al., 2019)

64.13%

Multi-scale Convolutional Blocks

(Sun et al., 2020)

74.19%

Feature Pyramid and Hierarchical Boosting

(Yang et al., 2020)

70.50%

Distribution equalization learning

(Fang et al., 2021)

54.55%

U-VGG19

–(ours)–

70.27%

Training/Evaluation using a CFD+Aigle-RN dataset.

GT and Pred are thinned to 1-pixel edges for evaluation.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

154

From this table, we conﬁrm that U-VGG19 is a

competitive model with respect to the state of the art

when training with real-life data. Thus we use the

scores of this model as a baseline to compare with the

results obtained by training with Syncrack variants.

Table 6 shows the prediction scores of the mod-

els trained on CFD and on the 3 difﬁculty versions of

Syncrack. For these experiments, we trained on the

training split of each respective dataset and calculated

the scores on the CFD validation split. The models

trained on Syncrack were trained using accurate an-

notations.

Table 6: Scores obtained in the CFD validation set by using

models trained on different datasets.

Metric

Training dataset

CFD

Syncrack

easy

Syncrack

medium

Syncrack

hard

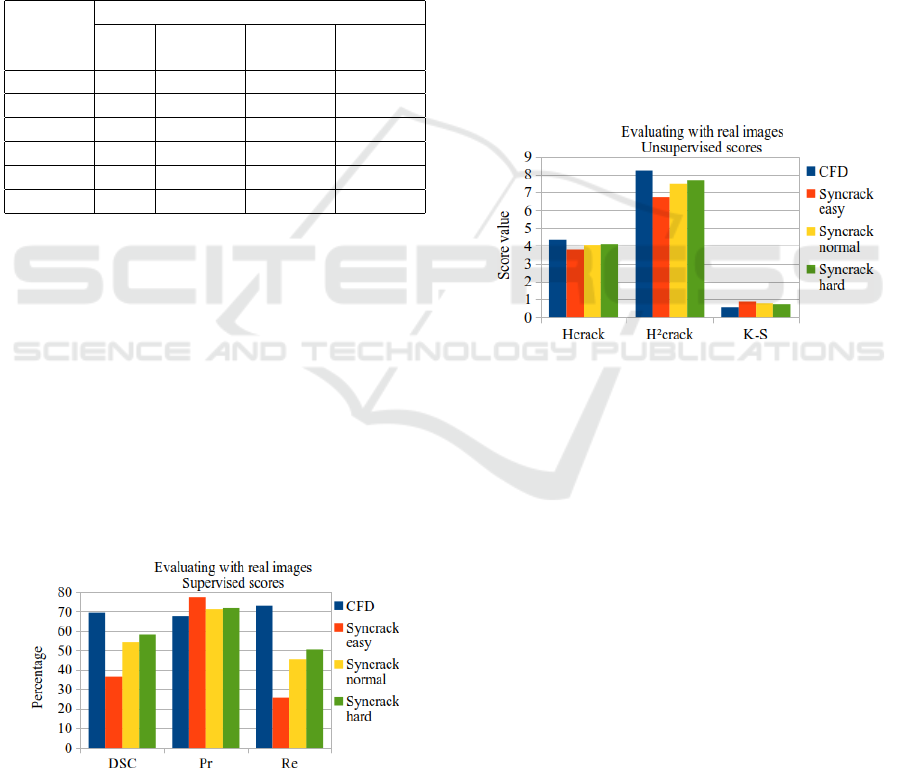
DSC (%) 69.32 36.37 54.26 58.26

Pr (%) 67.71 77.42 70.96 71.98

Re (%) 73.03 25.71 45.37 50.4

crack

4.35 3.79 4.07 4.12

crack

8.22 6.73 7.49 7.67

K-S 0.57 0.87 0.78 0.73

A plot of the supervised scores is shown in Fig.

10. We can see that the models trained with Syn-

crack datasets exhibit a higher precision than the

model trained on real images. However, we see a de-

crease of recall. Since the decrease in recall is higher

than the precision increase, the DSC of the models

trained with synthetic data are lower than the one of

the model trained with CFD. Particularly, the model

trained on the easy Syncrack has both the higher pre-

cision and the lower recall of all the datasets. As

we increase the Syncrack difﬁculty, the precision de-

creases a bit but the recall sees a great increase.

Speciﬁcally, the recall increases as we increase the

Syncrack difﬁculty level.

Figure 10: Supervised scores obtained in the CFD valida-

tion set by using models trained on different datasets.

Since the easy Syncrack has only easy-to-detect

cracks, a model trained with this dataset will strug-

gle to detect cracks with low contrast or rough back-

grounds. Thus, there is a high conﬁdence in the pixels

predicted as cracks but the model will miss hard-to-

detect cracks. As we increase the Syncrack difﬁculty

level, the learned models will detect harder cracks (in-

creasing recall) but will incur in more false positives

(decreasing precision). The model trained with the

hard Syncrack has a better trade-off between preci-

sion and recall, obtaining a DSC of 58.26% in con-

trast with the 69.32% obtained by training with CFD.

This DSC difference is caused only by a decreased

recall. Assuming that manual annotations tend to be

wider than the actual cracks, a more precise segmen-

tation will lead indeed to a lower recall. Fig. 11 shows

the unsupervised scores from the models trained with

the different datasets. We can observe that the mod-

els trained with Syncrack have better scores than the

one trained on CFD. As we increase the Syncrack dif-

ﬁculty level, the entropies in the predicted crack re-

gions increase and the K-S decreases. Even for the

hard difﬁculty, these scores are better than for CFD.

Figure 11: Unsupervised scores obtained in the CFD vali-

dation set by using models trained on different datasets.

The hypothesis is that the decrease in recall is

caused mainly by missing some pixels in the exces-

sively wide annotations. A qualitative analysis of

the predictions conﬁrmed this: as illustrated in Fig.

12, the performance of the models trained with the

medium and hard difﬁculty, respectively, get very

promising results. Not only they do a good job by not

missing cracks, but the predicted width looks more

close to the actual crack that both the annotation and

the prediction of CFD (see Fig. 13).

The model trained on medium Syncrack produces

reﬁned segmentations but prone to contain small dis-

continuities. The model trained on hard Syncrack

tends to ﬁll these gaps, but its predictions look more

coarse. However, using Syncrack generated images

showed their promising potential for supervised crack

detection without requiring labeled real-life images.

Syncrack: Improving Pavement and Concrete Crack Detection through Synthetic Data Generation

155

Figure 12: Example of predictions on a CFD image. The ﬁrst row shows the input image and the provided annotation. The

next rows show the predictions of models trained on the different proposed datasets and its comparison with the manual

annotation (with the color code used in Fig. 5).

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

156

Figure 13: A close-up detailed view of the picture depicted in Fig. 12. The red line is the border of the manual annotation,

the yellow line is the border of the prediction obtained by training on CFD, and the green line is the border of the prediction

obtained by training on Syncrack hard.

7 CONCLUSIONS

In this paper, we introduced the Syncrack generator

–a tool aimed to create synthetic pavement/concrete

images with accurate annotations for crack detection.

By introducing mislabeling, this tool allows generat-

ing noisy versions of the labels to emulate the inaccu-

racy of manual annotations.

With both accurate and noisy labels, we studied

the impact of inaccurate annotations on supervised

segmentation scores as well as a set of proposed un-

supervised scores. These metrics (region entropies

and the Kolmogorov-Smirnov score) were used since

supervised scores are biased by human error in real

data. From these experiments, we found a relation

between the proposed scores and the prediction preci-

sion. However, further work is needed towards met-

rics that are blind to human annotations for this task.

Using these unsupervised scores as a basis, we

evaluated on real-life images the performance of mod-

els trained on Syncrack-generated datasets. Our re-

sults show competitive scores in terms of precision

with respect to real-data training. Although there is

an apparent decrease of recall, this behavior is due

mainly to the excessive width of manual annotations.

This is shown by the unsupervised scores as well as

the qualitative analysis.

Thus, the models trained solely with our syntheti-

cally generated data are competitive with the model

trained on real images; furthermore, they are more

precise in terms of crack width.

The Syncrack generator is available at: https://

github.com/Sutadasuto/syncrack

generator. The code

used to obtain our results is available at: https://

github.com/Sutadasuto/syncrack crack detection

ACKNOWLEDGEMENTS

This work has been supported by the project DiXite.

Initiated in 2018, DiXite (Digital Construction Site) is

a project of the I-SITE FUTURE, a French initiative

to answer the challenges of sustainable city.

REFERENCES

Ai, D., Jiang, G., Siew Kei, L., and Li, C. (2018). Au-

tomatic Pixel-Level Pavement Crack Detection Using

Information of Multi-Scale Neighborhoods. IEEE Ac-

cess, 6:24452–24463. Conference Name: IEEE Ac-

cess.

Amhaz, R., Chambon, S., Idier, J., and Baltazart, V. (2016).

Automatic Crack Detection on Two-Dimensional

Pavement Images: An Algorithm Based on Mini-

mal Path Selection. IEEE Transactions on Intelligent

Syncrack: Improving Pavement and Concrete Crack Detection through Synthetic Data Generation

157

Transportation Systems, 17(10):2718–2729. Confer-

ence Name: IEEE Transactions on Intelligent Trans-

portation Systems.

Bhat, S., Naik, S., Gaonkar, M., Sawant, P., Aswale, S., and

Shetgaonkar, P. (2020). A Survey On Road Crack De-

tection Techniques. In 2020 International Conference

on Emerging Trends in Information Technology and

Engineering (ic-ETITE), pages 1–6.

Coquelle, E., Gautier, J.-L., and Dokl

adal, P. (2012). Au-

tomatic assessment of a road surface condition. In

7th Symposium on Pavement Surface Characteristics,

Surf, Norfolk, Virginia.

Duncan, C. (2018). noise. https://github.com/caseman/

noise.

Escalona, U., Arce, F., Zamora, E., and Sossa Azuela, J. H.

(2019). Fully Convolutional Networks for Automatic

Pavement Crack Segmentation. Computaci

on y Sis-

temas, 23(2):451–460–460. Number: 2.

Fang, J., Qu, B., and Yuan, Y. (2021). Distribution equal-

ization learning mechanism for road crack detection.

Neurocomputing, 424:193–204.

enay, B. and Verleysen, M. (2013). Classiﬁcation in the

presence of label noise: a survey. IEEE transactions

on neural networks and learning systems, 25(5):845–

869.

Gao, Z., Peng, B., Li, T., and Gou, C. (2019). Genera-

tive Adversarial Networks for Road Crack Image Seg-

mentation. In 2019 International Joint Conference on

Neural Networks (IJCNN), pages 1–8. ISSN: 2161-

4407.

Kanaeva, I. and Ivanova, J. A. (2021). Road pavement crack

detection using deep learning with synthetic data. In

IOP Conference Series: Materials Science and Engi-

neering, volume 1019, page 012036. IOP Publishing.

Kim, B. and Cho, S. (2018). Automated Vision-Based De-

tection of Cracks on Concrete Surfaces Using a Deep

Learning Technique. Sensors, 18(10):3452. Number:

10 Publisher: Multidisciplinary Digital Publishing In-

stitute.

Liu, Z., Cao, Y., Wang, Y., and Wang, W. (2019). Com-

puter vision-based concrete crack detection using U-

net fully convolutional networks. Automation in Con-

struction, 104:129–139.

Mazzini, D., Napoletano, P., Piccoli, F., and Schettini, R.

(2020). A Novel Approach to Data Augmentation for

Pavement Distress Segmentation. Computers in In-

dustry, 121:103225.

Oliveira, H. and Correia, P. L. (2014). CrackIT — An im-

age processing toolbox for crack detection and char-

acterization. In 2014 IEEE International Conference

on Image Processing (ICIP), pages 798–802. ISSN:

2381-8549.

Pal, N. R. and Bhandari, D. (1993). Image thresholding:

Some new techniques. Signal Processing, 33(2):139–

158.

Perlin, K. (1985). An image synthesizer. ACM Siggraph

Computer Graphics, 19(3):287–296.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net:

Convolutional Networks for Biomedical Image Seg-

mentation.

Shi, Y., Cui, L., Qi, Z., Meng, F., and Chen, Z. (2016). Au-

tomatic Road Crack Detection Using Random Struc-

tured Forests. IEEE Transactions on Intelligent Trans-

portation Systems, 17(12):3434–3445. Conference

Name: IEEE Transactions on Intelligent Transporta-

tion Systems.

Simonyan, K. and Zisserman, A. (2015). Very Deep Con-

volutional Networks for Large-Scale Image Recogni-

tion. arXiv:1409.1556 [cs]. arXiv: 1409.1556.

Smirnov, N. V. (1939). On the estimation of the discrepancy

between empirical curves of distribution for two inde-

pendent samples. Bull. Math. Univ. Moscou, 2(2):3–

14.

Sun, M., Guo, R., Zhu, J., and Fan, W. (2020). Road-

way Crack Segmentation Based on an Encoder-

decoder Deep Network with Multi-scale Convolu-

tional Blocks. In 2020 10th Annual Computing and

Communication Workshop and Conference (CCWC),

pages 0869–0874.

Yang, F., Zhang, L., Yu, S., Prokhorov, D., Mei, X., and

Ling, H. (2020). Feature Pyramid and Hierarchi-

cal Boosting Network for Pavement Crack Detection.

IEEE Transactions on Intelligent Transportation Sys-

tems, 21(4):1525–1535. Conference Name: IEEE

Transactions on Intelligent Transportation Systems.

Yang, X., Li, H., Yu, Y., Luo, X., Huang, T., and

Yang, X. (2018). Automatic Pixel-Level Crack De-

tection and Measurement Using Fully Convolutional

Network. Computer-Aided Civil and Infrastruc-

ture Engineering, 33(12):1090–1109. https://online

library.wiley.com/doi/pdf/10.1111/mice.12412.

Zhang, H., Fritts, J. E., and Goldman, S. A. (2008). Image

segmentation evaluation: A survey of unsupervised

methods. Computer Vision and Image Understanding,

110(2):260–280.

Zhang, K., Zhang, Y., and Cheng, H.-D. (2020a). Crack-

GAN: Pavement Crack Detection Using Partially Ac-

curate Ground Truths Based on Generative Adversar-

ial Learning. IEEE Transactions on Intelligent Trans-

portation Systems, pages 1–14. Conference Name:

IEEE Transactions on Intelligent Transportation Sys-

tems.

Zhang, L., Shen, J., and Zhu, B. (2020b). A research

on an improved Unet-based concrete crack detec-

tion algorithm. Structural Health Monitoring, page

1475921720940068. Publisher: SAGE Publications.

Zhang, L., Yang, F., Daniel Zhang, Y., and Zhu, Y. J. (2016).

Road crack detection using deep convolutional neural

network. In 2016 IEEE International Conference on

Image Processing (ICIP), pages 3708–3712. ISSN:

2381-8549.

Zhou, Z.-H. (2017). A brief introduction to weakly super-

vised learning. National Science Review, 5(1):44–53.

Zou, Q., Cao, Y., Li, Q., Mao, Q., and Wang, S. (2012).

CrackTree: Automatic crack detection from pavement

images. Pattern Recognition Letters, 33(3):227–238.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

158