
Forecasting Emergency Department Crowding using Data Science
Techniques
Jos
´
e Manuel Domenech Cabrera
1
and Javier Lorenzo-Navarro
2
1
Insular Maternal-Infant University Hospital Complex of Gran Canaria, Avenida Mar
´
ıtima del Sur,
s/n., Las Palmas de Gran Canaria, Spain
2
Inst. of Intelligent Systems and Num. Applic. in Engineering, Univ. of Las Palmas, Las Palmas de Gran Canaria, Spain
Keywords:
Hospital Emergency Department (ED) Predictions, Emergency Department Overcrowding, Time Series
Forecasting, Neural Networks.
Abstract:
The provision of insufficient resources during periods of high demand can lead to overcrowding in emergency
departments. This issue has been extensively addressed through time series forecasting and regression prob-
lems. Despite the fact the increasing number of studies, accurate forecasting of demand remains a challenge.
Thus, the purpose of this study was to develop a tool to predict the future evolution of emergency department
occupancy in order to anticipate overcrowding episodes, avoid their negative effects on health and improve
efficiency. This article presents a novel approach under the premise that the ability of the system to drain
patients is the most determining factor in overcrowding episodes as opposed to previous approaches focused
on patient demand. The forecasts model were based on the hourly number of patients occupying the general
Emergency Department of Insular University Hospital of Gran Canaria Island, mainly given data of the flow of
patients through the emergency department as well as performance indicators from other areas of the hospital
extracted from the information system.
1 INTRODUCTION
The application of information technologies in health-
care during the last decade, mainly the implemen-
tation of Electronic Medical Records, has generated
a large volume of health data, making this field at-
tractive for scientific studies as corroborated by the
growth in the number of scientific publications in re-
cent years (Islam et al., 2018). Data mining is the non-
trivial extraction of implicit, previously unknown in-
formation from the data. Machine learning is a branch
of artificial intelligence whose goal is to give comput-
ers the ability to learn a task without being explicitly
programmed to perform it. We use the term data sci-
ence to include these techniques and their systematic
application to face some of the current challenges of
healthcare management.
Emergency departments (hereinafter referred to as
ED) are an organization of healthcare professionals
that offers multidisciplinary assistance, located in a
specific area of the hospital to attend to emergencies
and urgencies. A complete and precise definition of
acute care can be found in (Hirshon et al., 2013). The
aging of the population (Division, 2019), the chronic-
ity of diseases, together with the sustained increase
over time in the demand for medical care, has aroused
growing concern about the sustainability of the pub-
lic healthcare system (Pammolli et al., 2011). This
situation especially affects emergencies, which is the
fastest growing medical service according to (Min-
istry of Health, 2017), where the provision of insuf-
ficient resources during periods of high demand can
lead to overcrowding. Saturation hinders correct pa-
tient care and causes diagnostic delays, which is re-
lated to an increase in morbidity (Trzeciak and Rivers,
2003), and it also favors human error and increases
mortality (Hoot and Aronsky, 2008). Anticipating
overcrowding would allow us to ensure the quality of
the service, as well as improves efficiency, adjusting
resources to the real demand.
This problem can be analyzed from systems the-
ory for a better understanding, trying to model the
different parts of the emergency system and how
changes in some of these parts affect the others. A
conceptual model of (inputs, throughput, output) of
overcrowding is presented in (Asplin et al., 2003) to
understand its causes and develop potential solutions.
The causes of overcrowding in ED have been exten-
504
Domenech Cabrera, J. and Lorenzo-Navarro, J.
Forecasting Emergency Department Crowding using Data Science Techniques.
DOI: 10.5220/0010840700003123
In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 5: HEALTHINF, pages 504-513
ISBN: 978-989-758-552-4; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

sively studied (Derlet and Richards, 2000). Factors
related to saturation can be external or internal to ED.
External pressure is produced by patients visits, this is
stochastic and unplanned, generating a discontinuous
flow determined by multiple factors, such as working
hours, meals, and days of the week. The flow also
varies in holidays, social events, epidemics, climatic
and atmospheric events. Internal causes include in-
sufficient material and human resources or an inad-
equate physical structure. External causes are delay
of radiology and laboratory tests and time required to
find a bed for admitted patients (Morley et al., 2018).
An internal pressure is caused by patients who remain
in the department pending complementary tests, ad-
mission and discharge. The availability of beds and
the resolution of complementary tests are at the same
time affected by the demand for the scheduled activ-
ity. When hospital occupancy is high, these demands
compete and the scheduled activity is usually priori-
tized.
Increases in external and internal pressure are the
triggers for overcrowding. Therefore, studying the
historical evolution of these patient flows and their
relationship with previous episodes of overcrowding
can help to predict them. It seems like a suitable
problem for the application of data science techniques
and methods. Measuring the moment in which over-
crowding begins has been object of study, a list of
proposed criteria can be found in (Boyle et al., 2011).
Two of these conditions of overcrowding are the per-
centage of occupancy greater than 100% and the num-
ber of patients waiting for a bed greater than 10%. But
it is not specified how many of these criteria are suf-
ficient. Furthermore, these criteria should be adapted
to the specific characteristics of each location. The
number of patient visits or patient arrivals is mostly
used as an indirect indicator of overcrowding because
the service quality is significantly related to the pa-
tient demand, but as previously stated, it is only one
of the factors involved. In this research we focus on
the internal performance of the hospital, under the hy-
pothesis that it has a greater impact on the overcrowd-
ing than the patients demand. Thus, we explore some
variables of performance from the ED itself and from
other hospital departments as independent variables
and we use the number of patients occupying the ED
as target variable.
This paper is organized as follows. Section 2 will
review the related works. Section 3 contains the for-
mal description of data, models and experimental set-
tings. Section 4 presents the experimental results, sec-
tion 5 the conclusion.
2 RELATED WORKS
Overcrowding in ED appears to be an universal prob-
lem (Pines et al., 2011) evidenced by the large number
of recent articles that address the problem through a
statistical forecasting approach. An exhaustive review
is presented in (G
¨
ul and Celik, 2018) where the works
are classified according to the flow of patients (inputs,
throughput, output), the majority of articles focus on
forecasting patient demand, other researchers have
approached this problem by focusing on the charac-
teristics of particular groups of patients, such as in-
fluenza (Araz et al., 2014) and Asthma (Ram et al.,
2015). The frequent throughput objective is the fore-
cast of the length of stays and the forecast of admis-
sions in the case of outputs. Other application themes
includes crowding, utilisation of resources, patient
waiting time, ambulance diversion and inpatient ad-
missions. Our paper does not seem to fit into one of
these three categories since our target variable is re-
lated to all of them, ED occupancy increases with de-
mand raise, in the same way when patient outflow and
treatment capabilities decline.
The overcrowding of ED has been extensively ad-
dressed through time series forecasting and regression
problems. Regression is a statistical process to esti-
mate the relationships between a dependent variable
called target and one or more independent continuous
variables, called characteristics. These characteristics
are properties of a phenomenon that is observed, over-
crowding in the problem at hand. When making a
prediction, new characteristic values are provided and
a regression model provides an answer for the target
variable.
Time series is a collection of observations mea-
surements over time and time series forecasting us-
ing mathematical models to forecast the future val-
ues of a series based on previously observed values.
Several techniques have been proposed for time se-
ries forecasting (Hamilton, 1994). These techniques
can be univariate or multivariate, depending on how
many variables are analyzed simultaneously. Accord-
ing to the desired time horizon, it can be short and
long term forecasting. Finally, data can be sampled in
lower or higher frequency. Time series can be decom-
posed into three components. The trend component
is a systematic linear increasing or decreasing of the
series over time. The stationary component are cycles
repeated over time. The noise component are unsys-
tematic fluctuations that cannot be explained by the
model. The linear components of time series is well
explained by classical time series models, unlike non-
linear components. For the latter, modern machine
learning techniques have been proposed.
Forecasting Emergency Department Crowding using Data Science Techniques
505

Most researches uses time series forecasting as
supervised learning, using future time step as la-
bels. Auto-regressive Integrated Moving Average
(ARIMA) (Boyle et al., 2011) models and their vari-
ant SARIMA (Jones et al., 2008) are the most used.
In recent years, the use of modern machine learn-
ing methods such as Artificial Neural Networks (Gul
and Guneri, 2016), Support Vector Machine (Zlotnik
et al., 2015), Decision Tree (Nas and Koyuncu, 2019),
Random Forest, and Naive Bayes (Hertzum, 2017)
has been incorporated. In recent works, some re-
searchers explore hybrid models, which are the com-
bination of two or more models, expecting to achive
better results comparing with the single model: (Xu
et al., 2016) combines ARIMA and LR in a sequen-
tial manner, because of its ability to capture seasonal
trend and effects of predictors. This model outper-
forms single models in terms of forecasting accuracy.
(Zhang et al., 2019) use a hybrid ARIMA-SVR ap-
proach to forecast daily radiology emergency patient
flow, the hybrid SARIMA-NARNN model to forecast
daily number of admission inpatients is proporsal by
(Zhou et al., 2018). This approach has encouraged us
to explore the use of new hybrid model, our proposal
is to forecast the components separately and assemble
the predictions and compare the results with previous
proposals to evaluate their performance.
The frequency of the data collected and used for
the study most used is daily, followed by monthly
and hourly. Higher frequency time series usually
have more seasonal patterns. Hourly data has daily,
weekly, monthly and annual patterns. Some re-
searchers have shown complications in predicting
hourly patient arrivals (Wargon et al., 2009). More-
over the daily pattern of arrivals is well known and
hourly data show null values. Managers use daily
measurement because overcrowding episodes are not
usually resolved in a few hours. However when use
the census or occupation variable only hourly data has
sense because occupancy can fluctuate during the day.
In addition, we avoid nulls and our forecast can be
more accurate.
The data collection period varied widely, from 1
year to 7 years. In most situations a larger set of
training improves the results of the model. But this is
not always true, it is possible that when adding older
data we will incorporate noise. In some cases, noise
can be easily eliminated, but in other cases there may
be changes in the physical structure of the location
or in the information system that produce trend fluc-
tuations or null values. The forecast horizon ranges
from 1 to 24 hours, from 1 to 30 days and from 1 to
4 months. Most forecast 1 day ahead, which seems
insufficient for resource planning and to avoid over-
crowding episodes. Forecast error generally increase
with the length of the forecast horizon as can be seen
in (Calegari et al., 2016).
We could categorize the variables into the follow-
ing groups: Calendar, Meteorological, Patient and
Miscellaneous. The most used calendar variables are:
weekday, month, holidays and different categories
of holidays. Some works have incorporated meteo-
rological variables such as maximum and minimum
temperature, humidity, wind speed, isolation, rain-
fall, snowfall and pollution. Other data patient used
are gender, triage level, arrival mode, diversion sta-
tus, laboratory orders and radiography orders. Other
miscellaneous variables are google flu trends, flue test
results.
3 MATERIAL AND METHODS
For this work, we have evaluated classic time series
forecasting and machine learning methods, instead of
building a deterministic simulation model of the sys-
tem. We will use the different variables that we can
identify to train a stochastic forecasting model, which
simplifies the construction of the model and we can
discover new relationships and patterns in the data.
As stated before, overcrowding depends on several
variables, so we have faced the problem as multivari-
ate, we have tried different time horizons and sam-
pling frequencies. The general Emergency Depart-
ment of the Insular University Hospital of Gran Ca-
naria Island has been selected for this work. Data of
the flow of patients through the ED as well as perfor-
mance indicators from other areas of the hospital have
been extracted from the information system.
This initial phase focuses on understanding the
project objectives and requirements. The stakeholders
has many competing objectives and constraints that
must be considered. This stage has carried out by lit-
erature review and through interviews with the hospi-
tal managers and domain experts. As a result of these
interviews, a series of improvement objectives were
identified and a better understanding of the flow of
patients and the care process was obtained, as well as
potential features and data sources were identified. As
result of the previous literature review, some research
questions were established and an initial assessment
of tools and techniques were performed. The major
research questions we investigate are:
• What insights can be obtained from exploratory
data analysis?
• Can we predict the ED occupation without using
the patient demand?
HEALTHINF 2022 - 15th International Conference on Health Informatics
506

• Can we obtain better results using internal hospi-
tal performance variables?
The major research objectives to achieve are:
• To develop a tool to predict the future evolution of
emergency department occupancy.
• To analyze the correlation of the internal hospital
performance variables with ED overcrowding.
3.1 Data Preparation
The first step was to collect the data using Extraction
Transformation and Data Loading (ETL) tools. The
raw data consists of 395.380 rows and 121 columns
that correspond to the patients who have been treated
in the ED from January 1, 2017 to March 1, 2021. As
part of feature engineering process 37 features was
created from raw data grouping by hour and aggre-
gate by the average, resulting 36.933 rows and 38
columns. These features were selected to increase
the predictive power of the learning algorithm, the
full list of features is shown in Table 1. Some of the
attention times have been approximate measured by
taking the time of entry into the information system.
From these features, others are derived by shifting
back rows. This method, called the sliding window, is
used to transform time series into supervised learning
dataset. Count of patients occupying the ED (Census)
is the dependent (target) variable in hourly time se-
ries format. The labels used in the supervised training
were generated by shifting the census series several
hours ahead, the chosen forecast horizon range was
24 to 720 hours. Rows with null values resulting from
shifting were removed and the missing values were
replaced with zeros. other strategies has been tested:
mean, median and k-Nearest Neighbors. Finally, fea-
tures was normalized by scaling each feature between
0 and 1.
Table 1: Features used in the study.
Name Description
time Hourly time stamps.
dayofyear Day of the year from 1 to 365.
dayofweek Day of the year from 1 to 7.
monthofyear Day of the year from 1 to 12.
holiday holiday=1, no holiday=0.
holiday period Laboral=0, christmas=1, sum-
mer=2.
visits Count of arrivals to the ED.
discharge Count of discharges to the ED.
census Count of patients occupying the
ED.
tepcf Minutes elapsed since the patient is
admitted until the first medical con-
sultation.
tpu Minutes elapsed since the patient is
admitted until the patient leaves the
ED.
tss Minutes elapsed since the medical
discharge occurs until the patient
leaves the ED.
tssh Minutes elapsed since the medical
discharge occurs until the patient is
admitted to a hospital bed.
tam Minutes elapsed since the start of
the medical consultation until the
medical discharge occurs.
tta Minutes elapsed since the patient
is admitted until the medical dis-
charge occurs.
trc Minutes elapsed since the patient
is admitted until the beginning of
triage.
tc Minutes elapsed since the begin-
ning until the end of the triage.
tpd Minutes elapsed since the patient is
admitted until the first diagnosis is
made.
tea Minutes elapsed since the begin-
ning of the triage until the start of
the first medical consultation.
tem Minutes elapsed until enter a mod-
ule.
tm Minutes elapsed since the patient
enter a module until the medical
discharge occurs.
tom Minutes elapsed since the patient
enters a module until the patient
leaves the ED.
age Mean age of patients.
level1 level 1 of triage: absolute priority
with immediate attention.
level2 level 2 of triage: very urgent, life-
threatening situations that should
not take more than 10/15 minutes.
level3 level 3 of triage: urgent but clin-
ically stable situation, potentially
life-threatening and with a maxi-
mum delay of 60 minutes.
level4 level 4 of triage: minor urgency
with very low life risk and a max-
imum delay of 120 minutes.
census hosp Count of patients occupying a hos-
pital bed.
sched surg Count of scheduled surgeries.
waiting bed Counting patients waiting for a bed.
traumatology Patient typology.
severe trauma Patient typology.
cardiovascular Patient typology.
gastrointestinal Patient typology.
respiratory Patient typology.
neurologic Patient typology.
codes Patient typology.
psycho social Patient typology.
Forecasting Emergency Department Crowding using Data Science Techniques
507

3.2 Exploratory Data Analysis
Through an exploratory analysis of the data, we can
understand the characteristics of the data which sup-
port the selection of appropriate model. Moreover,
we can also verify our hypothesis about the causes
of overcrowding, concluding if the factors are statis-
tically significant. The tool to perform the data anal-
ysis has been Python with libraries pandas, numpy,
matplotlib and seaborn. The hourly census time serie
shown in Fig.1 presents different patterns and high
fluctuations, a significant decrease in the census can
be observed during the declaration of the state of
alarm and national lockdown of march 14, 2020 due
to the covid-19 pandemic. Before this moment, a year
stationary pattern can be recognized, for example, the
census decreases in summer and increases in winter.
However, the mean, the standard deviation and the
distribution of values of each year are growing each
year (Table 2). It could indicate that the series was
non-stationary, but this is ruled out by performing the
Augmented Dickey-Fuller unit root test (Dickey and
Fuller, 1979) that can be seen in Table 3. The statis-
tic test value of -13.68 is smaller than the 5% critical
value of -2.86 and p-value is also smaller than signifi-
cant threshold level of 0.05, so we can say the census
time series is stationary and the way it changes re-
mains constant, so it is predictable.
Table 2: Census Statistical Summary.
count mean std min 25% 50% 75% max
Time
2017 8759.0 73.0 26.0 13.0 52.0 69.0 90.0 183.0
2018 8759.0 86.0 27.0 21.0 65.0 83.0 105.0 203.0
2019 8759.0 91.0 32.0 18.0 67.0 89.0 113.0 215.0
2020 8783.0 86.0 37.0 14.0 58.0 82.0 110.0 227.0
2021 1933.0 116.0 34.0 39.0 90.0 112.0 139.0 230.0
Table 3: Results of Dickey-Fuller Test for census serie.
Test Statistic -13.68
p-value 1.37601e-25
Lags Used 24
Number of Observations Used 36968
Critical Value (1%) -3.43
Critical Value (5%) -2.86
Critical Value (10%) -2.57
The histogram of values presented in Fig.2, shows
the bell curve-like shape of the Gaussian distribution
with a longer right tail of outliers. Moreover, the
large difference between 75th percentil and max val-
ues suggests that there are extreme values-outliers in
our data set. Therefore, the data is slightly skewed to
the right, and to eliminate this bias a Box-Cox power
transformation (Box and Cox, 1964) has been applied,
verifying that it slightly improves the results.
A Pearson correlation among features is shown in
Fig.3, Pearson’s coefficient, denoted by the letter r, is
the most commonly reported correlation coefficient.
For non-normal distributions correlation coefficients
should be calculated from the ranks of the data, not
from their actual values. The closer correlation coef-
ficient to 1 indicates a strong and positive correlation
between two features and the correlation closer to 0,
indicate a weak correlation. The closer coefficient to
-1 also implies a strong correlation between the two
series variables but in inverse way. The interpreta-
tion and the name of the correlation strength varies ac-
cording to the authors and the research areas (Akoglu,
2018). We find that the correlation rates achieved by
other authors are in ranges similar to ours. The p-
value shows the probability that this strength may oc-
cur by chance, a statistically significant heatmap can
be found in Figure 4. Therefore, there are strong cor-
relations with level3, cardiovascular, respiratory and
waiting bed, there are moderate correlations with gas-
trointestinal, level2, neurologic, traumatology, cen-
sus hosp, level4, visits, level1, discharge and psy-
cho social. We notice a moderate inverse correlation
with scheduled surgeries and day number of the week.
Most of these variables have not been used before by
other authors.
The census shifted ahead variables have stronger
correlation with waiting bed than visits, in addition
census hosp and visits have the same strength. This
fact verifies our hypothesis about the higher influence
of the hospital performance compared to external de-
mand. Other performance variables are strongly cor-
related, especially patient typologies and emergency
levels, we notice that cardiovascular and respiratory
variables are stronger correlated than other categories,
we also notice that level3 is more correlated than other
more critical levels.
Time series can be be analyzed through the de-
composition of its time series components, hourly
census decomposed by the additive model is shown
in Figure 5. The Trend does not show long term pos-
itive or negative tendency in hourly frequency, how-
ever there is an annual growing trend. The Seasonal
indicates a strong hourly pattern that also occurs daily,
weekly and annually. Therefore, we expect that mod-
els suitable for multivariate time series with trend and
multiple seasonal components will reach better re-
sults.
The ACF (Auto-Correlation Function) gives us
auto-correlation measures of the series with its lagged
values and PACF (Partial Auto-Correlation Function)
give us auto-correlation measures of the residuals,
HEALTHINF 2022 - 15th International Conference on Health Informatics
508

Figure 1: ED hourly census time serie.
Figure 2: ED hourly census and normal fit census.
Figure 3: Correlation heatmap.
which remains after removing the seasonally and
trend effects. ACF and PACF in Figure 6 show peaks
that coincide with the seasonality daily period.
3.3 Experimental Design and
Implementation
Several models have been selected from the litera-
ture review. The selection includes the models fre-
quently applied in this problem, and others that have
Figure 4: Statistically significant correlation.
Figure 5: ED hourly census decompose.
exhibited good results applied to other forecasting and
regression problems with time series. Different lin-
ear regression models have been compared to analyze
the correlation of the internal hospital performance
variables with ED overcrowding. Those linear meth-
Forecasting Emergency Department Crowding using Data Science Techniques
509
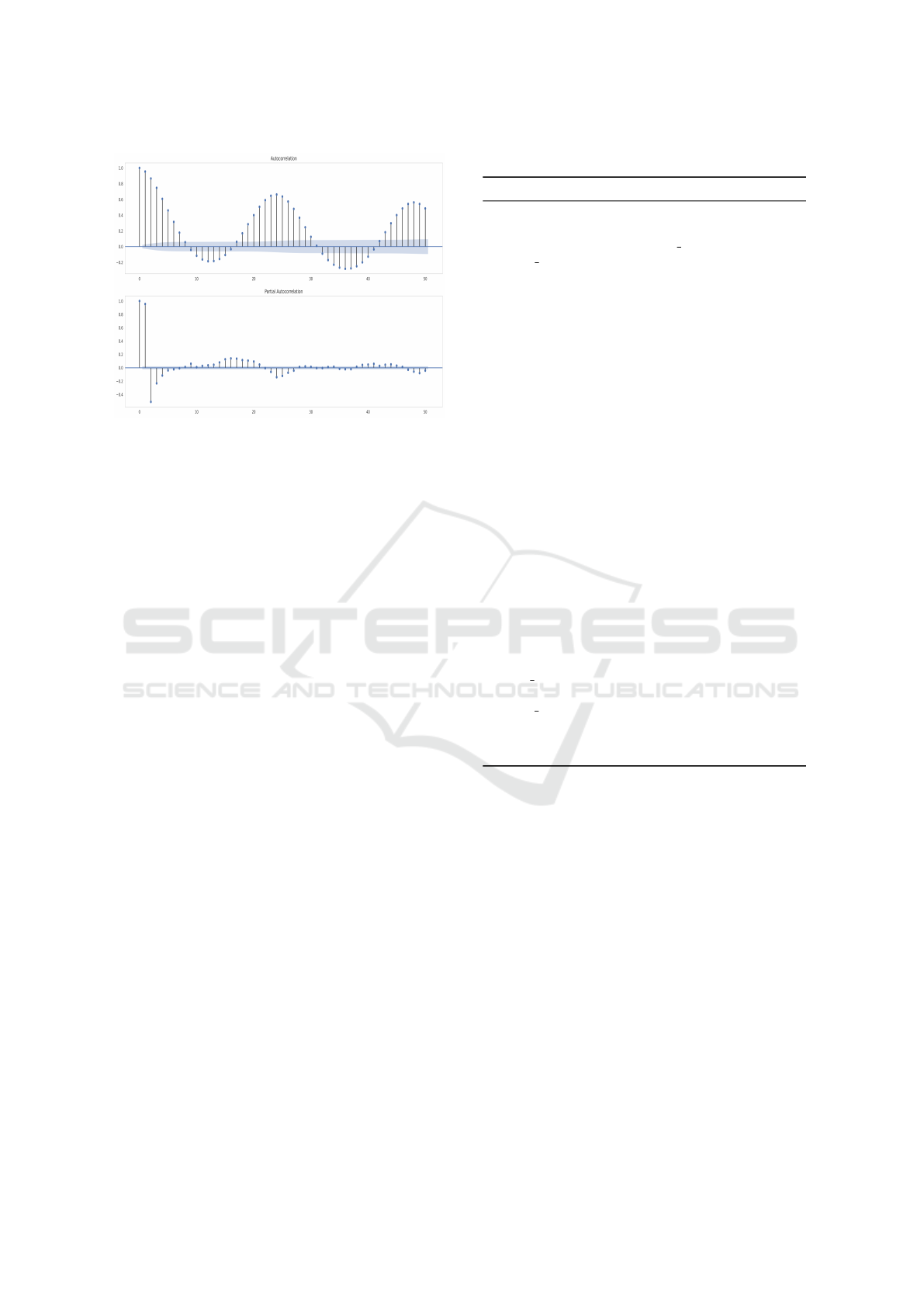
Figure 6: Auto-Correlation function.
ods are: standard linear regression (Standard), Ridge
regression that includes the L2 regularization of the
weights, Lasso optimization that includes the L1 reg-
ularization of the weights increasing the number of
non-zero coefficients, and a combination of Ridge and
Lasso named Elastic-Net that includes L1 and L2 reg-
ularization.
Before the dataset was split into training dataset
(80%) and testing dataset (20%) a process of fea-
ture selection was tested to reduce the number of fea-
tures by selecting the most significant. Feature se-
lection reduces training time and can improve accu-
racy (Piramuthu, 2004). We have implemented fea-
ture selection through SelectFromModel method from
sklearn library, a meta-transformer for selecting fea-
tures based on importance weights. The selection
has been made on the set of variables shown in Ta-
ble1. The inclusion in the set of the variables derived
from these by the sliding window method also has
been tested. All the tests we have performed of au-
tomatic feature selection have generated models with
larger error scores than the exhaustive manual selec-
tion method. This means that the selection method is
leaving out important variables. The set of features
selected by exhaustive process is shown in Table 4.
Different linear time window sizes have been tested
obtaining optimal performance with 168 lags. The
definitive set contains 3024 features derived from pre-
vious inputs of each of these 18 features by the sliding
window method.
4 RESULTS AND DISCUSSION
To assess the performance of the methods, the follow-
ing measures are the most widely used: Mean Abso-
Table 4: Features selected.
Name Description
dayofyear Day of the year from 1 to 365.
dayofweek Day of the year from 1 to 7.
holiday holiday=1, no holiday=0.
holiday period Laboral=0, christmas=1, sum-
mer=2.
discharge Count of discharges to the ED.
visits Count of arrivals to the ED.
census Count of patients occupying the
ED.
tepcf Minutes elapsed since the patient is
admitted until the first medical con-
sultation.
tssh Minutes elapsed since the medical
discharge occurs until the patient is
admitted to a hospital bed.
trc Minutes elapsed since the patient
is admitted until the beginning of
triage.
level1 level 1 of triage: absolute priority
with immediate attention.
level2 level 2 of triage: very urgent, life-
threatening situations that should
not take more than 10/15 minutes.
level3 level 3 of triage: urgent but clin-
ically stable situation, potentially
life-threatening and with a maxi-
mum delay of 60 minutes.
level4 level 4 of triage: minor urgency
with very low life risk and a max-
imum delay of 120 minutes.
census hosp Count of patients occupying a hos-
pital bed.
waiting bed Counting patients waiting for a bed.
cardiovascular Patient typology.
respiratory Patient typology.
neurologic Patient typology.
lute Percentage Error (MAPE), Root Mean Square Er-
ror (RMSE), Mean Absolute Error (MAE), and coef-
ficient of determination (R-squared). Good accuracy
is reached when the differences between the observa-
tions and the predicted values are small and unbiased.
MAPE is the mean of the difference between the ob-
servations and the predicted, expressed as a percent-
age of the observations. Lower values indicate better
model performance. It is used frequently for its easy
interpretation. However, MAPE divides each error by
the demand, so high errors during low-demand peri-
ods have a great impact. It is not a good measure to
optimize a model because it will undershoot the de-
mand. RMSE is the root squared mean of the squared
differences between predicted and actual values. It
gives more importance to the most significant errors,
its version without square root MSE has been selected
as regression loss function. MAE has easy interpre-
tation and is less sensitive to outliers. R-squared is
HEALTHINF 2022 - 15th International Conference on Health Informatics
510

Figure 7: ED hourly census prediction 24 hours ahead with performance variables.
Figure 8: ED hourly census prediction 24 hours ahead without performance variables.
the percentage of explained variability by the model.
Unlike the previous ones, it is unscaled and a higher
R-squared value means a better model accuracy.
Table 5 shows the results obtained with the com-
pared regression methods and it can be observed that
all of them perform similarly. As expected, the fore-
cast accuracy decreases as the time horizon go ahead.
Figure 7 shows the predicted census 24 hours ahead
by standard Linear Regression method and prediction
interval with 95% of confidence.
To assess the significance of the internal hospi-
tal performance variables: census
hosp, waiting bed,
tepcf, tssh, and trc; an ablation study was carried out
removing those variables from the model. Table 6
shows the results and it can be noted a decrease in the
performance in all configurations, except for MAPE
and 1-day ahead horizon, this can be seen in Figure 8,
it can be observed that this model is a worse fit for the
real census.
Table 5: Occupancy forecast using linear models and
performance variables.
Method Horizon Test error
MAERMSE MAPE R
2
Standard 1 day 12.64 15.89 12.70%0.81
1 week 17.42 22.48 17.10%0.62
1 month20.86 26.72 19.52%0.46
Lasso 1 day 12.73 16.03 12.80%0.81
1 week 17.45 22.48 17.13%0.62
1 month20.88 26.74 19.50%0.46
Ridge 1 day 12.64 15.89 12.70%0.81
1 week 17.42 22.48 17.10%0.62
1 month20.86 26.72 19.52%0.46
ElasticNet1 day 12.72 16.03 12.80%0.81
1 week 17.45 22.49 17.13%0.62
1 month20.88 26.74 19.50%0.46
Table 6: Occupancy forecast using linear regression
without performance variables.
Method Horizon Test error
MAERMSE MAPE R
2
Standard1 day 13.45 17.34 12.38% 0.77
1 week 23.90 31.04 20.88% 0.27
1 month29.72 39.60 24.97%-0.18
Forecasting Emergency Department Crowding using Data Science Techniques
511

5 CONCLUSIONS
We can now answer the research questions raised in
section3.
• What insights can be obtained from exploratory
data analysis?: The exploratory analysis of the
data shows us a higher predictive value of the in-
ternal performance variables. The dependent vari-
able has a stronger correlation with waiting bed
than visits, and census hosp and visits have the
same strength. This fact verifies our hypothesis
about the higher influence of the hospital perfor-
mance compared to external demand. Other vari-
ables are stronger correlated, especially patient ty-
pologies and critical levels. We notice that car-
diovascular and respiratory variables are stronger
correlated than other categories, we also notice
that level3 is more correlated than other more crit-
ical levels.
• Can we predict the ED occupation without us-
ing the patient demand? Although the influence
of hospital performance is very important, we
achieved better results by characterizing all fac-
tors related to overcrowding, both external and in-
ternal.
• Can we obtain better results using internal hos-
pital performance variables? Definitely, incorpo-
rating the proposed variables improves the results
of the ED overcrowding forecasting models.This
has been confirmed with the ablation study where
these variables were eliminated and the perfor-
mance of the estimation decreased.
All the research objectives have been reached, the
results show that ED occupation can be predicted
from internal performance variables, even excluding
external demand. A better understanding of the corre-
lation of internal hospital performance variables with
overcrowding in emergency departments has been
reached.
The linear regression models used in the experi-
ments are powerful enough to yield good performance
but not so much complex to mask the influence of the
variables in the results. Thus, they allow us to estab-
lish a baseline for future works to explore the use of
different machine learning models like artificial neu-
ral networks and decisions trees. Another possible fu-
ture work is to explore the use of exogenous variables.
REFERENCES
Akoglu, H. (2018). User’s guide to correlation coefficients.
Turkish Journal of Emergency Medicine, 18(3):91–93.
Araz, O., Bentley, D., and Muelleman, R. (2014). Us-
ing google flu trends data in forecasting influenza-
like–illness related emergency department visits in
omaha, nebraska. The American Journal of Emer-
gency Medicine, 32.
Asplin, B. R., Magid, D. J., Rhodes, K. V., Solberg, L. I.,
Lurie, N., and Camargo, C. A. (2003). A conceptual
model of emergency department crowding. Annals of
Emergency Medicine, 42(2):173–180.
Box, G. E. P. and Cox, D. R. (1964). An analysis of trans-
formations. Journal of the Royal Statistical Society.
Series B (Methodological), 26:211–252.
Boyle, J., Jessup, M., Crilly, J., Green, D., Lind, J., Wal-
lis, M., Miller, P., and Fitzgerald, G. (2011). Predict-
ing emergency department admissions. Emergency
medicine journal : EMJ, 29:358–65.
Calegari, R., Fogliatto, F., Lucini, F., Neyeloff, J., Kuchen-
becker, R., and Schaan, B. (2016). Forecasting daily
volume and acuity of patients in the emergency de-
partment. Computational and Mathematical Methods
in Medicine, 2016:1–8.
Derlet, R. W. and Richards, J. R. (2000). Overcrowd-
ing in the nation’s emergency departments: Complex
causes and disturbing effects. Annals of Emergency
Medicine, 35:63–68.
Dickey, D. and Fuller, W. (1979). Distribution of the esti-
mators for autoregressive time series with a unit root.
JASA. Journal of the American Statistical Association,
74.
Division, P. (2019). World population ageing: highlights.
New York : UN, 2019, page 37.
G
¨
ul, M. and Celik, E. (2018). An exhaustive review and
analysis on applications of statistical forecasting in
hospital emergency departments. Health System.
Gul, M. and Guneri, A. (2016). Planning the future of emer-
gency departments: Forecasting ed patient arrivals by
using regression and neural network models. Inter-
national Journal of Industrial Engineering: Theory,
Applications and Practice, 23:137–154.
Hamilton, J. (1994). Time series analysis. Princeton Univ.
Press, Princeton, NJ.
Hertzum, M. (2017). Forecasting hourly patient visits in the
emergency department to counteract crowding. The
Ergonomics Open Journal.
Hirshon, J., Risko, N., Calvello, E., Ramirez, S., Narayan,
M., Theodosis, C., and O’Neill, J. (2013). Health sys-
tems and services: The role of acute care. Bulletin of
the World Health Organization, 91:386–388.
Hoot, N. and Aronsky, D. (2008). Systematic review of
emergency department crowding: Causes, effects, and
solutions. Annals of emergency medicine, 52:126–36.
Islam, M. S., Hasan, M. M., Wang, X., Noor-E-Alam, M.,
and Germack, H. (2018). A systematic review on
healthcare analytics: Application and theoretical per-
spective of data mining. Healthcare, 6.
Jones, S., Thomas, A., Evans, R. S., Welch, S., Haug, P.,
and Snow, G. (2008). Forecasting daily patient vol-
umes in the emergency department. Academic emer-
gency medicine : official journal of the Society for
Academic Emergency Medicine, 15:159–70.
HEALTHINF 2022 - 15th International Conference on Health Informatics
512

Ministry of Health, S. (2017). Siae emergency activity. Sta-
tistical Portal of the National Health System.
Morley, C., Unwin, M., Peterson, G., Stankovich, J., and
Kinsman, L. (2018). Emergency department crowd-
ing: A systematic review of causes, consequences and
solutions. PLOS ONE, 13.
Nas, S. and Koyuncu, M. (2019). Emergency department
capacity planning: A recurrent neural network and
simulation approach. Computational and Mathemati-
cal Methods in Medicine, 2019:1–13.
Pammolli, F., Riccaboni, M., and Magazzini, L. (2011). The
sustainability of european health care systems: Be-
yond income and aging. The European journal of
health economics : HEPAC : health economics in pre-
vention and care, 13:623–34.
Pines, J., Hilton, J., Weber, E., Alkemade, A., Shabanah,
H., Anderson, P., Bernhard, M., Bertini, A., Gries, A.,
Ferrandiz, S., Kumar, V., Harjola, V.-P., Hogan, B.,
Madsen, B., Mason, S., Ohl
´
en, G., Rainer, T., Rath-
lev, N., Revue, E., and Schull, M. (2011). Interna-
tional perspectives on emergency department crowd-
ing. Academic emergency medicine : official jour-
nal of the Society for Academic Emergency Medicine,
18:1358–70.
Piramuthu, S. (2004). Evaluating feature selection methods
for learning in data mining applications. European
Journal of Operational Research, 156:483–494.
Ram, S., Zhang, W., Williams, M., and Pengetnze, Y.
(2015). Predicting asthma-related emergency depart-
ment visits using big data. IEEE journal of biomedical
and health informatics, 19.
Trzeciak, S. and Rivers, E. (2003). Emergency depart-
ment overcrowding in the united states: An emerging
threat to patient safety and public health. Emergency
medicine journal : EMJ, 20:402–5.
Wargon, M., Guidet, B., Hoang, T., and Hejblum, G.
(2009). A systematic review of models for forecasting
the number of emergency department visits. Emer-
gency medicine journal : EMJ, 26:395–9.
Xu, Q., Tsui, K.-L., Jiang, W., and Guo, H. (2016). A hybrid
approach for forecasting patient visits in emergency
department: Forecasting patient visits. Quality and
Reliability Engineering International, 32:2751–2759.
Zhang, Y., Luo, L., Yang, J., Liu, D., Kong, R., and Feng, Y.
(2019). A hybrid arima-svr approach for forecasting
emergency patient flow. Journal of Ambient Intelli-
gence and Humanized Computing, 10:3315–3323.
Zhou, L., Zhao, P., Wu, D., Cheng, C., and Huang, H.
(2018). Time series model for forecasting the number
of new admission inpatients. BMC Medical Informat-
ics and Decision Making.
Zlotnik, A., Gallardo-Antol
´
ın, A., Cuchi, M., P
´
erez, M.,
and Montero, J. (2015). Emergency department visit
forecasting and dynamic nursing staff allocation us-
ing machine learning techniques with readily available
open-source software. Computers, informatics, nurs-
ing : CIN, 33.
Forecasting Emergency Department Crowding using Data Science Techniques
513
