Subclass-based Undersampling for Class-imbalanced Image

Classiﬁcation

Daniel Lehmann and Marc Ebner

Institut f

ur Mathematik und Informatik, Universit

at Greifswald

Walther-Rathenau-Straße 47, 17489 Greifswald, Germany

Keywords:

Undersampling, Clustering, CNN.

Abstract:

Image classiﬁcation problems are often class-imbalanced in practice. Such a class imbalance can negatively

affect the classiﬁcation performance of CNN models. A State-of-the-Art (SOTA) approach to address this issue

is to randomly undersample the majority class. However, random undersampling can result in an information

loss because the randomly selected samples may not come from all distinct groups of samples of the class

(subclasses). In this paper, we examine an alternative undersampling approach. Our method undersamples

a class by selecting samples from all subclasses of the class. To identify the subclasses, we investigated if

clustering of the high-level features of CNN models is a suitable approach. We conducted experiments on 2

real-world datasets. Their results show that our approach can outperform a) models trained on the imbalanced

dataset and b) models trained using several SOTA methods addressing the class imbalance.

1 INTRODUCTION

Image classiﬁcation datasets are often imbalanced in

practice. Certain classes contain signiﬁcantly less

frequent samples (minority classes) than the other

classes (majority classes). A dataset of images show-

ing healthy plants and plants suffering from a plant

disease, for instance, will be imbalanced if the plant

disease occurs rarely in nature (minority class: plant

with disease, majority class: healthy plant). A Con-

volutional Neural Network (CNN) model trained on

this dataset may not perform well for images of the

less frequent class. During training, the mini-batches

mostly contain images of the majority class as they

occur more frequently in the data. Hence, the result-

ing model may only have learned a proper representa-

tion of the majority class but not of the minority class.

A State-of-the-Art (SOTA) approach to address

this problem is random undersampling (Buda et al.,

2018; Lee et al., 2016; More, 2016). Random un-

dersampling balances a dataset by randomly select-

ing samples of the majority class until the number

of picked majority class samples is approximately as

high as the number of minority class samples. Then, a

model is trained using the minority class samples and

the selected majority class samples. A disadvantage

of this approach, however, is that it can lose infor-

mation about the majority class. A class may con-

tain different groups of images (Nguyen et al., 2016;

Wei et al., 2015) (subclasses). The ImageNet (Rus-

sakovsky et al., 2015) class baseball, for instance, can

be grouped into images showing a baseball player

and images showing only the ball. If samples from

the baseball class are randomly selected, then the se-

lected samples may come mostly from only one of the

2 subclasses. As a consequence, a model trained on

such an undersampled dataset will not have learned

a proper representation of the baseball class as it has

not seen enough samples from both subclasses.

In this work, we examine an alternative approach

to undersample the majority class. Our method se-

lects samples from every subclass. Before we can

select any samples, however, we must ﬁrst ﬁnd the

subclasses within the majority class samples. To iden-

tify the subclasses, we use clustering on the high-level

features of the CNN model. Using this undersam-

pling method, we state 2 research questions: 1) Is

clustering of the high-level image features of a CNN

model beneﬁcial for undersampling, and 2) is our ap-

proach able to outperform a model trained on the im-

balanced dataset as well as models using SOTA meth-

ods addressing the class imbalance? Our experiments

show that both questions can be answered with yes.

Our contributions are as follows: 1) We show that

clustering of the high-level image features of a CNN

model is beneﬁcial for undersampling, 2) we pro-

Lehmann, D. and Ebner, M.

Subclass-based Undersampling for Class-imbalanced Image Classiﬁcation.

DOI: 10.5220/0010841100003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages

493-500

ISBN: 978-989-758-555-5; ISSN: 2184-4321

493

pose a subclass-based undersampling approach that

selects the majority class samples more carefully than

a random undersampling, and 3) we show (on 2 real-

world datasets) that our method can outperform sev-

eral SOTA methods addressing the class imbalance.

2 RELATED WORK

To improve random undersampling, various methods

have been suggested. Kubat and Matwin (Kubat and

Matwin, 1997) introduced one-sided selection, which

identiﬁes redundant samples close to a class bound-

ary. Zhang and Mani (Zhang and Mani, 2003) pro-

posed a method that selects samples according to the

distance between the majority and minority class sam-

ples. Garcia and Herrera (Garc

ıa and Herrera, 2009)

suggested an evolutionary undersampling. Majumder

et. al. (Majumder et al., 2020) proposed a method

based on feature vector angles to pick the samples that

contain the most information. Koziarski (Koziarski,

2020a) introduced a radial-based undersampling. Liu

et. al. (Liu et al., 2009) proposed EasyEnsemble

and BalanceCascade. EasyEnsemble is an ensemble

method that picks different subsets of the majority

class and trains a model for each of them. Balance-

Cascade, in contrast, trains a model sequentially. In

each iteration, the correctly classiﬁed majority class

samples are removed from the training set. However,

the methods most similar to ours are cluster-based

(Agrawal et al., 2015; Sowah et al., 2016; Tsai et al.,

2019; Yen and Lee, 2009) and hashing-based under-

sampling (Ng et al., 2020). Cluster-based undersam-

pling attempts to ﬁnd clusters in the dataset and then

selects samples from each identiﬁed cluster. Hashing-

based undersampling, in contrast, uses hashing to di-

vide the majority class into subspaces. However, both

methods have been suggested for tabular data and can

not be used for image data directly. Our method, in

contrast, is applied to images used for CNN training.

We investigated if clustering of high-level image fea-

tures can be used for undersampling.

Besides undersampling, several other approaches

have been proposed to address model training using

a class-imbalanced dataset. A widely used approach

is oversampling, which creates additional samples for

the minority class to balance the dataset. A sim-

ple method to oversample a class is to duplicate ran-

domly selected samples of that class (More, 2016).

Singh and Dhall (Singh and Dhall, 2018) improved

this method by not selecting samples randomly for

duplication but based on the distance of a sample to

its cluster centroid. Besides duplicating samples, var-

ious methods have been suggested to oversample a

minority class by creating synthetic samples for that

class (Ando and Huang, 2017; Chawla et al., 2002;

Hao et al., 2020; Mullick et al., 2019). Shen et.

al. (Shen et al., 2016) do not create any samples

but uniformly populate the mini-batches with sam-

ples from all classes during model training. Kozarski

(Koziarski, 2020b) introduced a method that com-

bines oversampling and undersampling. Furthermore,

there has been work that addresses the class im-

balance by introducing a special loss function (Cao

et al., 2019; Dong et al., 2017; More, 2016; Sarkar

et al., 2020), a balanced group softmax (Li et al.,

2020), dynamic sampling (Pouyanfar et al., 2018),

dynamic curriculum learning (Wang et al., 2019),

cost-sensitive learning (Khan et al., 2015), a local

embedding (Huang et al., 2016) or category centers

(Zhang et al., 2018). Category centers are also used

in high-level image feature space. However, the cen-

ters are exploited for the classiﬁcation process and not

to undersample the dataset as our method does.

3 METHOD

Our undersampling method can be applied to multi-

class imbalanced image datasets containing several

majority classes. To balance such a dataset, our

method must be applied to each majority class sep-

arately. Thus, in order to explain our method, we

consider a two-class imbalanced dataset containing

only one majority class in the following without los-

ing generality. We undersample the majority class in

2 stages. First, we identify the subclasses of the ma-

jority class (as shown in steps 1 to 4 in Figure 1). Sec-

ond, we select representative samples from each iden-

tiﬁed subclass (as shown in step 5 in Figure 1). The

selected majority class samples and all minority class

samples form the new undersampled dataset. We de-

scribe both stages in more detail below.

In order to identify subclasses of the majority

class C, we use a method similar to that suggested

by Nguyen et. al. (Nguyen et al., 2016). However,

Nguyen et. al. introduced their method to visualize

multifaceted features learned by a CNN. We adapted

their method to ﬁnd representative samples of a class

for undersampling that class. First, we train an ini-

tial model f

using the imbalanced training set (X, Y).

The resulting model f

may not perform well for the

minority class as it is underrepresented in the data.

We assume, however, the model f

learns at least a

sufﬁcient representation of the majority class C. After

we trained the model f

, we use this model to extract

features from each image x

of the majority class C.

We assume C has N

samples x

in the training set

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

494

2) Choose Layer

Pool

1) Feed Images of

and Reduce to 2D

3) Fetch Activations

5) Select

Samples

4) Clustering

the Class to CNN

Figure 1: Our method: 1) Feed majority class images into the initial CNN model (trained on the imbalanced dataset), 2)

choose a layer from which to fetch activations, 3) fetch activations of the images at the chosen layer and reduce activations to

2D, 4) ﬁnd clusters in the activations and 5) select samples from each identiﬁed cluster.

(X, Y ). In order to extract the features, we feed all N

images x

into model f

. At a certain layer L, we fetch

the layer activations of each image x

. The activations

represent the features that layer L extracts from the

images x

. Which layer to pick depends on the classi-

ﬁcation problem to solve. It is important, however, to

choose one of the last layers of the CNN (i.e., closer

to the output layer). The last layers of a CNN extract

high-level features (e.g., object parts), while the ear-

lier layers extract low-level features (e.g., edges, sim-

ple shapes) as shown by Zeiler and Fergus (Zeiler and

Fergus, 2014). In order to identify subclasses repre-

senting different semantic concepts (e.g., the subclass

baseball player and the subclass ball from the Ima-

geNet class baseball), we must use the high-level fea-

tures from one of the last network layers as only these

features are characteristic for the different semantic

concepts. If the chosen layer is a convolutional layer,

the fetched activations of each image x

will be in

cube form. To convert the activations to vector form,

we ﬂatten the activations. If the chosen layer is a lin-

ear layer, however, the fetched activations will be in

vector form already, and we do not need to ﬂatten

them. In either case, we receive N

feature vectors

(one from each image x

) of length M

. Then, we

concatenate all N

vectors a

to a feature matrix A

of size N

× M

In the data of the matrix A

, we try to ﬁnd clus-

ters representing different subclasses of C. Before we

can apply clustering on the data, however, we need to

reduce the dimensions of the feature matrix A

from

× M

down to N

× 2. This preprocessing step is

necessary as clustering is usually more difﬁcult to ap-

ply in high dimensions (Chen et al., 2019). First, we

normalize A

by subtracting the mean and then di-

viding by the standard deviation (prerequisite for di-

mensionality reduction). Then, we project A

from

×M

down to N

×50 using PCA (Pearson, 1901)

followed by a second reduction from N

×50 down to

× 2 using UMAP (McInnes et al., 2018). As a re-

sult, we receive the projected features matrix p(A

)

of size N

× 2. The reason why we use PCA and

UMAP combined is that A

is usually too large to

directly apply a non-linear dimensionality reduction

technique such as UMAP. On the other hand, using

only a linear dimensionality reduction (such as PCA)

did not result in a sufﬁcient data representation in our

experiments. Thus, we use a combination of both

techniques. A similar approach was also suggested

by Ngyuen et. al. (Nguyen et al., 2016). Finally,

we apply k-Means clustering (MacQueen, 1967) on

p(A

) to identify clusters in the feature data. To ﬁnd

the parameter k, we apply k-Means multiple times us-

ing different k (values: 2-9) and compute the Silhou-

ette score (Rousseeuw, 1987) of the resulting clusters

for each k. The Silhouette score is an evaluation met-

ric that measures the cluster quality using the mean

inter-cluster and mean intra-cluster distance (range:

between -1 and 1, a higher score means a better cluster

quality). As Chen et. al. (Chen et al., 2019) pointed

out, this score works well for evaluating clusters in

the layer activations of a CNN. Thus, we choose the k

that obtained the best Silhouette score. As a result, we

receive 1, ..., k clusters, which represent the potential

subclasses of the majority class.

After identifying 1, ..., k clusters in p(A

), we se-

lect a certain number of representative samples x

from each cluster 1, ..., k. For instance, if we need

to select 100 majority class samples, and we found 2

clusters, we will select 50 samples from each identi-

Subclass-based Undersampling for Class-imbalanced Image Classiﬁcation

495

ﬁed cluster. In order to select the samples from each

cluster, we consider 2 options: a) We select the sam-

ples from each cluster that are closest to their cluster

center, and b) we select the samples from each cluster

that are farthest from their cluster center (excluding

outliers). The most representative samples of a clus-

ter should be samples closest to their cluster center.

Therefore, we chose to examine option a). On the

other hand, however, the samples closest to a cluster

center may be quite similar if these samples are close

to each other as well. We would like to select samples

that are as unique as possible when undersampling the

data. Thus, we also examine option b) by selecting

the samples of a cluster that are most far away from

their cluster center. In order to avoid selecting out-

liers (e.g., noise, mislabeled samples), however, we

only consider the 80th percentile of all the samples of

a cluster. After selecting the samples x

from each

cluster 1, ..., k using one of the 2 options, we merge

these samples together with all minority class sam-

ples to obtain the undersampled dataset (X

, Y

). This

dataset can be used to train a new model f

4 EXPERIMENTS

4.1 Experimental Setup

We conducted several experiments to test our method

described in section 3. For each experiment, we

executed the following steps: 1) Training an initial

model, 2) selecting a layer of that model, 3) feeding

all training images of the class that should be under-

sampled to the model and fetching their activations at

the selected layer, 4) ﬁnding clusters in the fetched

activations, 5) picking a certain number of samples

from each cluster, 6) using the picked samples and

all training images from the other classes that should

not be undersampled as the new training set, 7) train-

ing a model using the new undersampled training set,

and 8) comparing this model to a model trained on

the imbalanced training set (baseline) and to models

trained using SOTA methods addressing the class im-

balance (e.g., through random undersampling, over-

sampling, a class-weighted loss) with respect to their

performance on the test set.

For our experiments we used the datasets from 2

image classiﬁcation competitions hosted on the data

science platform Kaggle: a) The Plant Pathology

2020

competition (Thapa et al., 2020) and b) the

https://www.kaggle.com/c/plant-pathology-2020-

fgvc7

Fisheries Monitoring

competition. The Plant Pathol-

ogy dataset has 4 classes. One of the classes con-

tains signiﬁcantly fewer images than the other classes.

The Fisheries Monitoring dataset, in contrast, has 8

classes. One of the classes contains signiﬁcantly more

images than the other classes.

We used the same training setup for all of our

models. Except for our experiments in section 4.4,

we chose a ResNet50 (He et al., 2016) as model ar-

chitecture. All models were pretrained on ImageNet

(Russakovsky et al., 2015). We removed the output

layer (for the ImageNet classes) and replaced it with

the following new layers: A combination of an adap-

tive average pooling layer and an adaptive max pool-

ing layer (output of both are concatenated) - Batch-

Norm - Dropout (p = 0.25) - Linear layer (size: 512)

- ReLU - BatchNorm - Dropout (p = 0.5) - Linear out-

put layer. Each model was ﬁne-tuned using a discrim-

inative ﬁne-tuning strategy (Howard and Ruder, 2018)

in a two-stage process. First, we ﬁne-tuned only the

initial weights of the new layers (which we added)

for 3 epochs. Then, we ﬁne-tuned the weights of all

layers of the network for 8 more epochs. The learning

rate was set to an initial value of 0.01 and was then ad-

justed over the course of training via a cyclical learn-

ing rate schedule (Smith, 2017). We used mixed pre-

cision training (Micikevicius et al., 2018) to be able to

set the batch size to 25. For the Plant Pathology data,

we adopted all data augmentation techniques from

the original winner

of the corresponding competition

(brightness, contrast, blur, shift, scale, rotation, hori-

zontal and vertical ﬂip). For the Fisheries Monitoring

data, we used the same data augmentation techniques

except for the vertical ﬂip. Unlike the Plant Pathol-

ogy images, the images of the Fisheries Monitoring

dataset were always taken from the same vertical ori-

entation. All images of both datasets were resized to

224 × 224 before training.

Each model was evaluated using the Kaggle sub-

mission system. The submission system evaluates the

Plant Pathology competition using the ROC AUC

metric, while it evaluates the Fisheries Monitoring

competition using the multi-class logarithmic loss

(LogLoss). Kaggle splits the test set of a competition

into 2 parts: A public and a private test set. While

the competition is active, the submission system only

shows how a model performed on the public test set.

When the competition is over, the evaluation score on

the private test set will be visible as well. The user

with the best score on the private test set wins the

competition. As the Plant Pathology and the Fish-

https://www.kaggle.com/c/the-nature-conservancy-

ﬁsheries-monitoring

https://github.com/alipay/cvpr2020-plant-pathology

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

496

Table 1: Comparison of our method (selecting closest/farthest samples to cluster center) to the baseline (imbalanced dataset)

and random undersampling on the Plant Pathology data. All models were trained over 6 random seeds. The results are

reported as median ROC AUC scores (a higher value is better) and standard deviations (std) over the 6 seeds.

Method Undersampled Class ROC AUC

median std

Baseline - 0.9387 0.0045

Random Undersampling healthy 0.9375 0.0086

rust 0.9187 0.0092

scab 0.9377 0.0024

healthy, rust, scab 0.9068 0.0233

Ours (closest) healthy 0.9391 0.0058

rust 0.9171 0.0069

scab 0.9425 0.0088

healthy, rust, scab 0.8909 0.0166

Ours (farthest) healthy 0.9353 0.0059

rust 0.9183 0.0098

scab 0.9369 0.0080

healthy, rust, scab 0.9004 0.0054

eries Monitoring competition are both not active any-

more, the evaluation scores on the private test set are

already available for both competitions. Thus, we use

the scores on the private test set to evaluate our mod-

els as these are crucial for winning the competitions.

4.2 Selecting Closest Samples

We conducted an experiment to test whether our un-

dersampling approach using the closest samples to

each identiﬁed cluster center (as described in section

3) is able to improve model performance. As the Plant

Pathology dataset contains 3 majority classes (rust,

scab and healthy), we examined 4 different under-

sampling strategies: 1) Undersampling of the healthy

class only (from 516 to 100 samples), 2) undersam-

pling of the rust class only (from 622 to 100 samples),

3) undersampling of the scab class only (from 592 to

100 samples) and, 4) undersampling of the healthy,

rust and scab class (to 100 samples per class). To be

able to ﬁnd clusters in the data of a majority class,

our method requires choosing a layer whose activa-

tions should be used for clustering. We considered

the last 3 layers before the output layer of the network.

Among these 3 layers, we chose the layer whose ac-

tivations reached the best Silhouette score. For rust

and healthy, we obtained the best Silhouette score us-

ing the activations of the adaptive pooling layer (con-

catenation of average and max pooling), while for

scab the last linear layer before the output layer re-

sulted in the best Silhouette score. For each class, we

picked the same number of samples from each iden-

tiﬁed cluster. For instance, we found 2 clusters in the

data of the healthy class. Therefore, we picked 50

samples closest to each cluster center to obtain 100

samples in total for that class. As a result, we re-

ceived the following datasets: a) One undersampled

dataset from our method for each strategy 1) - 4), b)

the baseline (imbalanced dataset) and c) 6 randomly

undersampled datasets (More, 2016) (using a differ-

ent random seed each time for the random sampling)

for each strategy 1) - 4). With each of these datasets,

we trained 6 models using a different random seed

each time and report the median test performance over

the 6 models. The results are shown in Table 1.

The Fisheries Monitoring dataset contains 1 ma-

jority class (ALB class). As a result, we undersampled

only this class (from 1719 to 734 samples). Again, we

selected the same number of samples from each iden-

tiﬁed cluster. We obtained the best Silhouette score

using the activations of the last ResNet50 layer before

the newly added layers. Thus, we used these layer ac-

tivations to undersample the class. Then, we trained a

model (1 seed) using a) the dataset undersampled by

our method (using the closest samples), b) the base-

line (imbalanced dataset), and c) 5 randomly under-

sampled datasets (More, 2016) (using a different ran-

dom seed each time for the random sampling). The

results of our experiment for the Fisheries Monitor-

ing data are shown in Table 2.

4.3 Selecting Farthest Samples

In another experiment, we tested if our undersam-

pling approach using the farthest samples from each

identiﬁed cluster center is able to improve model per-

formance. The experimental setup was the same as

in section 4.2, except for the method how to pick

the samples. Instead of selecting the closest samples

to each cluster center, we undersampled the data by

Subclass-based Undersampling for Class-imbalanced Image Classiﬁcation

497

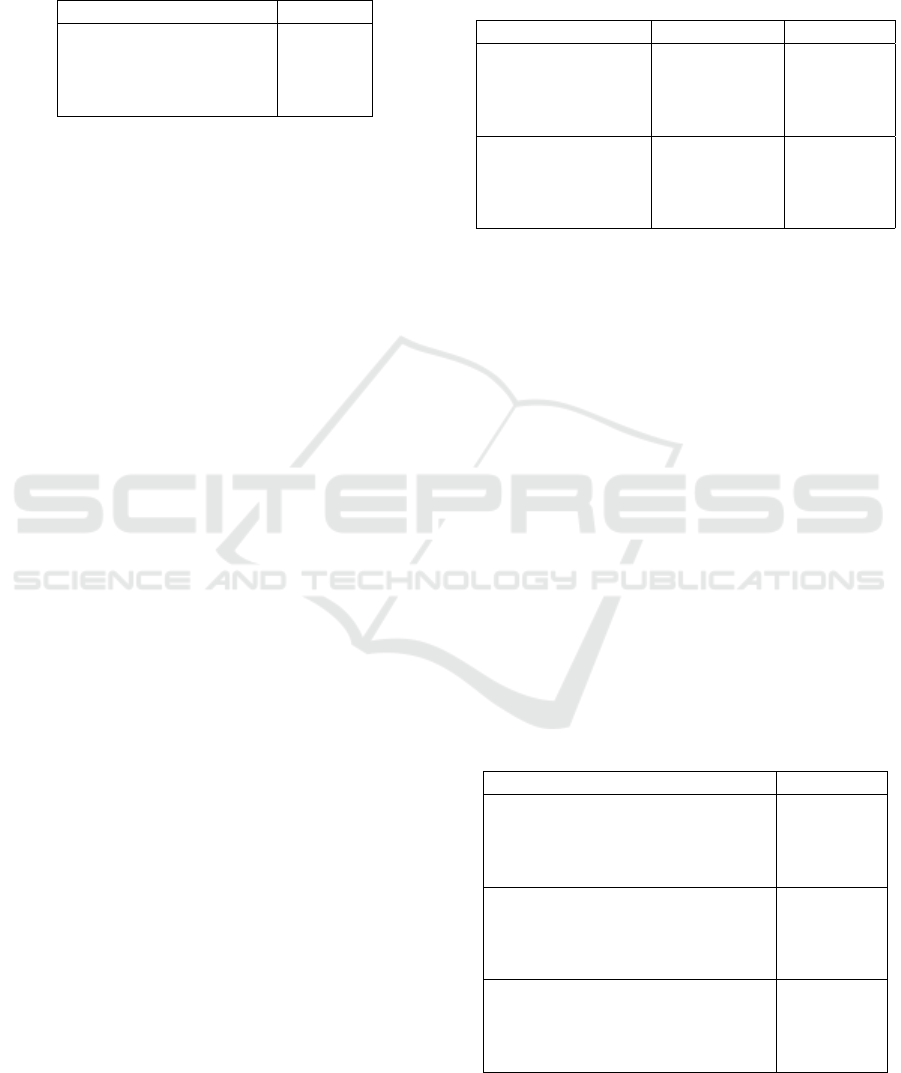
Table 2: Comparison of our method to the baseline (imbal-

anced dataset) and random undersampling (median over 5

random samplings) on the Fisheries Monitoring data (un-

dersampling of class ALB). The results are reported as

multi-class logarithmic loss (a lower value is better).

Method LogLoss

Baseline 5.7333

Random Undersampling 4.0771

Ours (closest) 3.8657

Ours (farthest) 3.9302

picking the farthest samples from each cluster center,

as described in section 3. The results of the experi-

ment for the Plant Pathology data are shown in Table

1, and the results of the experiment for the Fisheries

Monitoring data are shown in Table 2. In contrast to

section 4.2, however, we obtained the best Silhouette

score for the Fisheries Monitoring dataset using the

activations of the adaptive pooling layer. Thus, we

used these layer activations for undersampling.

4.4 Other CNN Architectures

In our experiments in section 4.2 and section 4.3, we

used a pretrained ResNet50 for all our models, as de-

scribed in section 4.1. To examine how our under-

sampling approach performs using other CNN archi-

tectures, we conducted additional experiments for the

healthy class (516 samples) of the Plant Pathology

data. The experimental setup was the same as for the

experiments in section 4.2 and section 4.3, except for

the CNN architecture. We examined 2 additional ar-

chitectures: a) DenseNet121 (Huang et al., 2017) and

b) VGG16 (Simonyan and Zisserman, 2015) (with

BatchNorm (Ioffe and Szegedy, 2015)). A model

was trained (1 seed) for each architecture using a)

the dataset undersampled by our method (to 100 sam-

ples), b) the baseline (imbalanced dataset), and c)

5 randomly undersampled datasets (More, 2016) (to

100 samples using a different random seed each time

for the random sampling). The results of the experi-

ment are shown in Table 3.

4.5 Comparison to SOTA Methods

In our experiments in section 4.2, 4.3 and 4.4 we only

compared our method to the baseline (imbalanced

dataset) and random undersampling (More, 2016). In

another experiment, we examined how our method

performs in comparison to other SOTA methods ad-

dressing data imbalance applied to the Plant Pathol-

ogy dataset: a) oversampling (More, 2016) of the

minority class (multiple diseases class, 91 samples)

and b) a training approach using a class-weighted loss

function (More, 2016). For oversampling, we tested 2

Table 3: Comparison of our method to the baseline (imbal-

anced dataset) and random undersampling (median over 5

random samplings) with respect to different CNN architec-

tures on the Plant Pathology data (undersampling of class

healthy). The results are reported as ROC AUC scores (a

higher value is better).

Method CNN Arch. ROC AUC

Baseline VGG16 0.9435

Rand. Undersamp. 0.9404

Ours (closest) 0.9447

Ours (farthest) 0.9322

Baseline DenseNet121 0.9461

Rand. Undersamp. 0.9384

Ours (closest) 0.9294

Ours (farthest) 0.9465

approaches: 1) duplicating the minority class samples

2 times (resulting in 182 samples), and b) duplicating

the minority class samples 6 times (resulting in 546

samples). For the class-weighted loss function, we set

the weights for each class according to the fraction

of samples of that class among the total number of

samples of the Plant Pathology dataset. Moreover, we

tested 2 additional conﬁgurations for undersampling

the healthy class using our method. First, besides se-

lecting the closest samples to each cluster center and

selecting the farthest samples from each cluster cen-

ter, we also selected samples from each cluster ran-

domly. Second, besides undersampling the healthy

class from 516 to 100 samples, we also undersampled

the healthy class from 516 to 250 samples. We trained

a model (1 seed) for each method. The results of the

experiment are shown in Table 4.

Table 4: Comparison of our method (undersampling of class

healthy) to the baseline (imbalanced dataset), random un-

dersampling, oversampling, and a class-weighted loss ap-

proach on the Plant Pathology data. The results are reported

as ROC AUC scores (a higher value is better).

Method ROC AUC

Baseline 0.9343

Class-Weighted Loss 0.9466

Oversampling (182 samples) 0.9469

Oversampling (546 samples) 0.9268

Rand. Undersamp. (100 samples) 0.9370

Ours (closest, 100 samples) 0.9451

Ours (farthest, 100 samples) 0.9301

Ours (random, 100 samples) 0.9377

Rand. Undersamp. (250 samples) 0.9474

Ours (closest, 250 samples) 0.9488

Ours (farthest, 250 samples) 0.9453

Ours (random, 250 samples) 0.9551

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

498

5 CONCLUSION

In section 1, we stated 2 research questions: 1) Is

clustering of the high-level image features of a CNN

model beneﬁcial for undersampling, and 2) is our

approach able to outperform a model trained on the

imbalanced dataset as well as models using SOTA

methods addressing the class imbalance? Our ex-

periments (section 4) show that our method is able

to obtain a better performance than the baseline and

a random undersampling. Moreover, our method is

also able to surpass the performance of other SOTA

methods addressing data imbalance (oversampling,

class-weighted loss). Selecting the closest samples

to each cluster center for undersampling the majority

class performed best in most cases in our experiments.

However, there were also cases in which selecting the

farthest samples from each cluster center or a ran-

dom cluster sample selection reached a better perfor-

mance. As a result, we have shown that a subclass-

based undersampling is able to surpass the perfor-

mance of a model trained on the imbalanced dataset

(baseline) and models trained using SOTA methods

addressing the class imbalance. This could also be

helpful for other research areas. In medical imag-

ing, for instance, datasets are frequently imbalanced

as well (Larrazabal et al., 2020; Reza and Ma, 2018).

Furthermore, datasets in practice often contain label

noise (Algan and Ulusoy, 2021; Xiao et al., 2015),

i.e., some images of a dataset were inadvertently mis-

labeled. In future work, it could be investigated if we

can identify such noise using our method.

REFERENCES

Agrawal, A., Viktor, H. L., and Paquet, E. (2015).

Scut: Multi-class imbalanced data classiﬁcation using

smote and cluster-based undersampling. In IC3K, vol-

ume 1, pages 226–234, Lisbon, Portugal. IEEE.

Algan, G. and Ulusoy, I. (2021). Image classiﬁcation with

deep learning in the presence of noisy labels: A sur-

vey. Knowledge-Based Systems, 215:106771.

Ando, S. and Huang, C. Y. (2017). Deep over-sampling

framework for classifying imbalanced data. In Ceci,

M., Dzeroski, S., Vens, C., Todorovski, L., and Holl-

men, J., editors, ECML PKDD, Lecture Notes in CS,

pages 770–785. Springer.

Buda, M., Maki, A., and Mazurowski, M. A. (2018). A

systematic study of the class imbalance problem in

convolutional neural networks. Neural Networks,

106:249–259.

Cao, K., Wei, C., Gaidon, A., Arechiga, N., and Ma, T.

(2019). Learning imbalanced datasets with label-

distribution-aware margin loss. In Wallach, H.,

Larochelle, H., Beygelzimer, A., d'Alch

e-Buc, F.,

Fox, E., and Garnett, R., editors, Adv Neural Inf Pro-

cess Syst, volume 32, Vancouver, CA. CAI.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: Synthetic minority over-

sampling technique. Journal of Artif Int Res,

16(1):321–357.

Chen, B., Carvalho, W., Baracaldo, N., Ludwig, H., Ed-

wards, B., Lee, T., Molloy, I., and Srivastava, B.

(2019). Detecting backdoor attacks on deep neu-

ral networks by activation clustering. In Espinoza,

H., h

Eigeartaigh, S.

O., Huang, X., Hern

andez-

Orallo, J., and Castillo-Effen, M., editors, Workshop

on SafeAI@AAAI, volume 2301 of CEUR Workshop,

Honolulu, HI, USA. ceur-ws.org.

Dong, Q., Gong, S., and Zhu, X. (2017). Class rectiﬁcation

hard mining for imbalanced deep learning. In ICCV,

pages 1869–1878, Venice, Italy. IEEE.

Garc

ıa, S. and Herrera, F. (2009). Evolutionary undersam-

pling for classiﬁcation with imbalanced datasets: Pro-

posals and taxonomy. Evol Comput, 17(3):275–306.

Hao, J., Wang, C., Zhang, H., and Yang, G. (2020). An-

nealing genetic gan for minority oversampling. ArXiv,

abs/2008.01967.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In CVPR, pages

770–778, Las Vegas, NV, USA. IEEE.

Howard, J. and Ruder, S. (2018). Universal language model

ﬁne-tuning for text classiﬁcation. In Proc of the ACL,

pages 328–339, Melbourne, Australia. ACL.

Huang, C., Li, Y., Loy, C. C., and Tang, X. (2016). Learning

deep representation for imbalanced classiﬁcation. In

CVPR, pages 5375–5384, Las Vegas, NV, USA. IEEE.

Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger,

K. Q. (2017). Densely connected convolutional net-

works. In CVPR, pages 2261–2269, Honolulu, HI,

USA. IEEE.

Ioffe, S. and Szegedy, C. (2015). Batch normalization:

Accelerating deep network training by reducing in-

ternal covariate shift. In Bach, F. and Blei, D., edi-

tors, ICML, volume 37 of Proc Mach Learn Res, page

448–456, Lille, France. PMLR.

Khan, S. H., Hayat, M., Bennamoun, M., Sohel, F., and

Togneri, R. (2015). Cost sensitive learning of deep

feature representations from imbalanced data. ArXiv,

abs/1508.03422.

Koziarski, M. (2020a). Radial-based undersampling for

imbalanced data classiﬁcation. Pattern Recognition,

102:107262.

Koziarski, M. (2020b). Two-stage resampling for con-

volutional neural network training in the imbal-

anced colorectal cancer image classiﬁcation. ArXiv,

abs/2004.03332.

Kubat, M. and Matwin, S. (1997). Addressing the curse

of imbalanced training sets: One-sided selection. In

ICML, pages 179–186. Morgan Kaufmann.

Larrazabal, A. J., Nieto, N., Peterson, V., Milone, D. H.,

and Ferrante, E. (2020). Gender imbalance in med-

ical imaging datasets produces biased classiﬁers for

computer-aided diagnosis. Proc National Academy of

Sciences, 117(23):12592–12594.

Subclass-based Undersampling for Class-imbalanced Image Classiﬁcation

499

Lee, H., Park, M., and Kim, J. (2016). Plankton classiﬁca-

tion on imbalanced large scale database via convolu-

tional neural networks with transfer learning. In ICIP,

pages 3713–3717, Phoenix, AZ, USA. IEEE.

Li, Y., Wang, T., Kang, B., Tang, S., Wang, C., Li, J., and

Feng, J. (2020). Overcoming classiﬁer imbalance for

long-tail object detection with balanced group soft-

max. In CVPR, pages 10991–11000.

Liu, X.-Y., Wu, J., and Zhou, Z.-H. (2009). Exploratory

undersampling for class-imbalance learning. Trans.

Sys. Man Cyber. Part B, 39(2):539–550.

MacQueen, J. B. (1967). Some methods for classiﬁcation

and analysis of multivariate observations. In Cam,

L. M. L. and Neyman, J., editors, Berkeley Symp on

Math Stat and Prob, volume 1, pages 281–297. Univ

of Calif Press.

Majumder, A., Dutta, S., Kumar, S., and Behera, L. (2020).

A method for handling multi-class imbalanced data

by geometry based information sampling and class

prioritized synthetic data generation (gicaps). ArXiv,

abs/2010.05155.

McInnes, L., Healy, J., and Melville, J. (2018). UMAP:

Uniform manifold approximation and projection for

dimension reduction. ArXiv, abs/1802.03426.

Micikevicius, P., Narang, S., Alben, J., Diamos, G., Elsen,

E., Garcia, D., Ginsburg, B., Houston, M., Kuchaiev,

O., Venkatesh, G., and Wu, H. (2018). Mixed preci-

sion training. In ICLR, Vancouver, CA.

More, A. (2016). Survey of resampling techniques for

improving classiﬁcation performance in unbalanced

datasets. ArXiv, abs/1608.06048.

Mullick, S. S., Datta, S., and Das, S. (2019). Generative

adversarial minority oversampling. In ICCV, pages

1695–1704, Seoul, South Korea. IEEE.

Ng, W. W., Xu, S., Zhang, J., Tian, X., Rong, T., and

Kwong, S. (2020). Hashing-based undersampling

ensemble for imbalanced pattern classiﬁcation prob-

lems. Transactions on Cybernetics.

Nguyen, A., Yosinski, J., and Clune, J. (2016). Multifaceted

feature visualization: Uncovering the different types

of features learned by each neuron in deep neural net-

works. ArXiv, abs/1602.03616.

Pearson, K. (1901). LIII. On lines and planes of closest

ﬁt to systems of points in space. London, Edinburgh

Dublin Philos Mag J Sci, 2(11):559–572.

Pouyanfar, S., Tao, Y., Mohan, A., Tian, H., Kaseb, A. S.,

Gauen, K., Dailey, R., Aghajanzadeh, S., Lu, Y. H.,

Chen, S. C., and Shyu, M. L. (2018). Dynamic sam-

pling in convolutional neural networks for imbalanced

data classiﬁcation. In MIPR, Proc MIPR 2018, pages

112–117. Inst Electrical and Electronics Engineers

Inc.

Reza, M. S. and Ma, J. (2018). Imbalanced histopatholog-

ical breast cancer image classiﬁcation with convolu-

tional neural network. In ICSP, pages 619–624. IEEE.

Rousseeuw, P. J. (1987). Silhouettes: A graphical aid to

the interpretation and validation of cluster analysis. J.

Comput. Appl. Math., 20(1):53–65.

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,

Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-

stein, M., Berg, A. C., and Fei-Fei, L. (2015). Ima-

genet large scale visual recognition challenge. IJCV,

115(3):211–252.

Sarkar, D., Narang, A., and Rai, S. (2020). Fed-focal loss

for imbalanced data classiﬁcation in federated learn-

ing. ArXiv, abs/2011.06283.

Shen, L., Lin, Z., and Huang, Q. (2016). Relay backprop-

agation for effective learning of deep convolutional

neural networks. In Leibe, B., Matas, J., Sebe, N., and

Welling, M., editors, ECCV, volume 9911 of Lecture

Notes in CS, pages 467–482. Springer.

Simonyan, K. and Zisserman, A. (2015). Very deep convo-

lutional networks for large-scale image recognition. In

Bengio, Y. and LeCun, Y., editors, ICLR, San Diego,

CA, USA.

Singh, N. D. and Dhall, A. (2018). Clustering and learning

from imbalanced data. ArXiv, abs/1811.00972.

Smith, L. N. (2017). Cyclical learning rates for training

neural networks. In WACV, pages 464–472. IEEE.

Sowah, R. A., Agebure, M. A., Mills, G. A., Koumadi,

K. M., and Fiawoo, S. Y. (2016). New cluster under-

sampling technique for class imbalance learning. Int

Journal of Mach Learning and Computing, 6(3):205.

Thapa, R., Zhang, K., Snavely, N., Belongie, S., and Khan,

A. (2020). The plant pathology challenge 2020 data

set to classify foliar disease of apples. Appl in Plant

Sciences, 8(9):e11390.

Tsai, C.-F., Lin, W.-C., Hu, Y.-H., and Yao, G.-T. (2019).

Under-sampling class imbalanced datasets by combin-

ing clustering analysis and instance selection. Infor-

mation Sciences, 477:47–54.

Wang, Y., Gan, W., Yang, J., Wu, W., and Yan, J. (2019).

Dynamic curriculum learning for imbalanced data

classiﬁcation. In ICCV, pages 5016–5025, Seoul,

South Korea. IEEE.

Wei, D., Zhou, B., Torrabla, A., and Freeman, W. (2015).

Understanding intra-class knowledge inside CNN.

ArXiv, abs/1507.02379.

Xiao, T., Xia, T., Yang, Y., Huang, C., and Wang, X. (2015).

Learning from massive noisy labeled data for image

classiﬁcation. In CVPR, pages 2691–2699, Boston,

MA, USA. IEEE.

Yen, S.-J. and Lee, Y.-S. (2009). Cluster-based under-

sampling approaches for imbalanced data distribu-

tions. Expert Systems with Applications, 36(3):5718–

5727.

Zeiler, M. D. and Fergus, R. (2014). Visualizing and un-

derstanding convolutional networks. In Fleet, D., Pa-

jdla, T., Schiele, B., and Tuytelaars, T., editors, ECCV,

number PART 1 in Lecture Notes in CS, pages 818–

833, Zurich, CH. Springer.

Zhang, J. and Mani, I. (2003). kNN approach to unbalanced

data distributions: A case study involving information

extraction. In Proc ICML Workshop on Learning from

Imbalanced Datasets, volume 126.

Zhang, Y., Shuai, L., Ren, Y., and Chen, H. (2018). Image

classiﬁcation with category centers in class imbalance

situation. In YAC, pages 359–363.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

500