
Hardware-oriented Algorithm for Human Detection
using GMM-MRCoHOG Features
Ryogo Takemoto
1 a
, Yuya Nagamine
1
, Kazuki Yoshihiro
1
, Masatoshi Shibata
2
, Hideo Yamada
2
,
Yuichiro Tanaka
3 b
, Shuichi Enokida
4 c
and Hakaru Tamukoh
1,3 d
1
Graduate School of Life Science and Systems Engineering, Kyushu Institute of Technology,
2-4 Hibikino, Wakamatsu-ku, Kitakyushu, Fukuoka, 808-0196, Japan
2
AISIN CORPORATION, 2-1 Asahi-machi, Kariya, Aichi, 448-8650, Japan
3
Research Center for Neuromorphic AI Hardware, Kyushu Institute of Technology,
2-4 Hibikino, Wakamatsu-ku, Kitakyushu, Fukuoka, 808-0196, Japan
4
Department of Artificial Intelligence, Faculty of Computer Science and Systems Engineering,
Kyushu Institute of Technology, 680-4 Kawazu, Iizuka, Fukuoka, 820-8502, Japan
Keywords:
Image Processing, Human Detection, HOG, MRCoHOG, GMM-MRCoHOG, FPGA.
Abstract:
In this research, we focus on Gaussian mixture model-multiresolution co-occurrence histograms of oriented
gradients (GMM-MRCoHOG) features using luminance gradients in images and propose a hardware-oriented
algorithm of GMM-MRCoHOG to implement it on a field programmable gate array (FPGA). The proposed
method simplifies the calculation of luminance gradients, which is a high-cost operation in the conventional
algorithm, by using lookup tables to reduce the circuit size. We also designed a human-detection digital
architecture of the proposed algorithm for FPGA implementation using high-level synthesis. The verification
results showed that the processing speed of the proposed architecture was approximately 123 times faster than
that of the FPGA implementation of VGG-16.
1 INTRODUCTION
The demand for home service robots and self-driving
cars has been increasing in response to the recent
acceleration in the aging population and decline in
birthrate. Because t hese robots and cars with artifi-
cial intelligence are expected to operate near humans,
high-precision and high-speed human detection func-
tions are required from the viewpoint of safety. How-
ever, the more accurate the human detection, the more
complex is the computation and the longer the com-
putation time. Parallelization is one of the effective
solutions to accelerate the computation.
A typical device for parallel processing is a graph-
ics processing unit (GPU). However, GPUs are not
suitable for embedded systems such as home service
robots and self-driving cars in terms of power con-
a
https://orcid.org/0000-0002-6795-0794
b
https://orcid.org/0000-0001-6974-070X
c
https://orcid.org/0000-0001-6309-3185
d
https://orcid.org/0000-0002-3669-1371
sumption and heat exhaustion . Instead of software
implementation on GPUs, hardware implementation,
where a dedicated circuit with parallel architecture
for some computation is designed, can achieve a low-
power system with high-speed processing because the
operation on the dedicated circuit can be more effec-
tive than that on GPUs. Therefore, we aim to design a
dedicated circuit for human detection and implement
it on a field-programmable gate array (FPGA). Be-
cause FPGAs have limited physical circuit resources,
we need a hardware-oriented algorithm that reduces
the number of complex operations in the original al-
gorithm to efficiently utilize the limited resources.
For high-accuracy human detection, histograms
of oriented gradients (HOG) features have been pro-
posed (Dalal and Triggs, 2005) and used in multi-
ple applications. This method extracts features of
object shapes from luminance gradients in images,
and represents the features as histograms of the gra-
dients. For higher-accuracy and smaller-memory re-
source implementation of human detection compared
Takemoto, R., Nagamine, Y., Yoshihiro, K., Shibata, M., Yamada, H., Tanaka, Y., Enokida, S. and Tamukoh, H.
Hardware-oriented Algorithm for Human Detection using GMM-MRCoHOG Features.
DOI: 10.5220/0010848100003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
749-757
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
749

with HOG features, the Gaussian mixture model-
multiresolution co-occurrence histograms of oriented
gradients (GMM-MRCoHOG) features that approx-
imate the conventional histogram-based state space
with a mixed Gaussian distribution and optimize the
feature space have been proposed (Higashi et al.,
2018; Nagamine et al., 2019). However, the algorithm
still requires a large number of complex operations
that are not suitable for FPGA implementation.
In this study, we propose a hardware-oriented
algorithm of GMM-MRCoHOG that simplifies the
complex operation in the original algorithm, such
as the calculation of luminance gradients by using a
lookup table (LUT); we then design a dedicated cir-
cuit for human recognition integrating the hardware-
oriented GMM-MRCoHOG with a binarized neural
network (BNN) (Hubara et al., 2016), and implement
it on an FPGA to achieve a high-accuracy, high-speed,
and low-power system.
2 RELATED WORKS
MRCoHOG (Iwata and Enokida, 2014), a derivative
work of HOG, extracts features by down-sampling
an image in two steps; it represents the gradient co-
occurrence between images of three resolutions as a
two-dimensional co-occurrence histogram. Feature
extraction methods using gradient histograms, such
as HOG and MRCoHOG, require a manual determi-
nation of the optimal class width of the histogram to
discretize the luminance gradients. This is difficult
because the discretization error of the gradient infor-
mation and the generalization ability of the features
vary depending on the class width. Moreover, these
methods require many memory resources to represent
gradient histograms.
Conversely , GMM-MRCoHOG constructs an op-
timal state space by approximating the co-occurrence
histogram with a mixed Gaussian distribution, as
shown in Fig. 1 and performs feature extraction based
on the state space. The approximation results in re-
ducing the required memory resources for gradient
histograms in the original algorithm because only a
small number of memories is required to represent the
mixed Gaussian distribution.
Figures 2 and 3 show the processing flow of
GMM-MRCoHOG. First, the co-occurrences of the
luminance gradient pairs (36 gradient directions for
each axis in Fig. 2) of the positive and negative
data of the training images are mapped to the feature
space as continuous values, and each feature is ap-
proximated by a mixture Gaussian distribution. Then,
using the Jensen– Shannon (JS) information content
(Michishita et al., 2018), only features that can ef-
fectively separate the positive and negative data are
extracted from the respective mixed Gaussian distri-
butions and approximated to a mixed Gaussian dis-
tribution using the EM algorithm (Dempster et al.,
1977). The resulting mixed Gaussian distribution is
then used as the feature space, and the responsibility
(described as “resp” in Fig. 3) of each Gaussian dis-
tribution is calculated and used as the feature value.
In GMM-MRCoHOG, the final number of feature di-
mensions is determined by the number of Gaussian
distributions in 2D space, and not by the number of
gradient quantization.
Figure 1: Sample of Gaussian Mixture Model.
Figure 2: Training Process of State Space in GMM-
MRCoHOG.
Figure 3: Feature Extraction Process in GMM-MRCoHOG.
GMM-MRCoHOG has difficulties in hardware
implementation because it includes an arctangent
function for the luminance gradient angle decision
and the responsibility calculation for the feature value
decision, which are complex operations that require
considerable circuit resources. Nagamine et al. pro-
posed a hardware-oriented algorithm that approxi-
mates these calculations to reduce the circuit re-
sources (Nagamine et al., 2019). The algorithm deter-
mines the luminance gradient angles by using a con-
dition branch of the horizontal and vertical luminance
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
750

gradients f
x
and f
y
. Figure 4 shows a first quadrant
in the luminance gradient space of f
x
and f
y
, which is
divided into several areas at intervals of 16 in Manhat-
tan distance. The condition branch determines an an-
gle by subtracting f
x
and f
y
according to the divided
area; therefore, the angle decision does not require
complex operations. For the feature value decision,
the algorithm infers a responsibility from the distance
between the input vector and each Gaussian distri-
bution. The algorithm also approximates the Gaus-
sian distribution width as a power of two and changes
the Gaussian shape as a rectangle so that the compu-
tation can be represented by bit-shift operations and
fuzzy inferences. Although the hardware-oriented al-
gorithm reduces most circuit resources from the orig-
inal algorithm, the condition branch for the angle cal-
culation still requires many LUTs, which worsens the
performance of the algorithm because of the impre-
cise angle approximation .
Figure 4: Condition Branch for Luminance Gradient Angle
Decision in (Nagamine et al., 2019).
3 PROPOSED METHODS
To improve the method proposed by Nagamine et al.,
we propose a novel coarse angle calculation method
using a fixed-point tan θ table. We then construct a
hardware-oriented GMM-MRCoHOG-based human
recognition circuit using the method for a high-speed
and low-power human detection system.
3.1 Coarse Angle Calculation Method
using Fixed-point Tangent Table
In the GMM-MRCoHOG algorithm, the luminance
gradient angle θ is calculated as θ = tan
−1
( f
y
/ f
x
)
and discretized in 36 directions. Here, assuming that
the angle θ appears in the first quadrant of the lumi-
nance gradient space, we calculate tan θ from tan0
◦
to
tan80
◦
in advance, as given by Eq. (1) and discretize
Figure 5: Overview of Discretized tan θ.
it, as shown in Fig. 5.
i f tan 0
◦
≤
f
y
f
x
<tan10
◦
direction = 1(θ : 0
◦
∼ 10
◦
)
eli f tan 10
◦
≤
f
y
f
x
<tan20
◦
direction = 2(θ : 10
◦
∼ 20
◦
)
.
.
.
eli f tan 80
◦
≤
f
y
f
x
direction = 9(θ : 80
◦
∼ 90
◦
)
(1)
Then, we create a tanθ table representing the re-
lationship between the discretized tan θ, f
x
, and f
y
,
which enables us to obtain rough angles of luminance
gradients. By utilizing the symmetry of the trigono-
metric functions, the tan θ table can be applied to the
second through fourth quadrants.
Additionally, we eliminate divisions that require
most circuit resources in the conditional branch in the
tanθ table. As f
x
≥ 0 and f
y
≥ 0, we can replace Eq.
(1) with Eq. (2), where no division is required.
i f f
x
× tan0
◦
≤ f
y
< f
x
× tan10
◦
direction = 1(θ : 0
◦
∼ 10
◦
)
eli f f
x
× tan10
◦
≤ f
y
< f
x
× tan20
◦
direction = 2(θ : 10
◦
∼ 20
◦
)
.
.
.
eli f f
x
× tan80
◦
≤ f
y
direction = 9(θ : 80
◦
∼ 90
◦
)
(2)
The values in the tan θ table are then approximated
with fixed-point numbers that enable faster computa-
tion and fewer circuit resource implementations com-
pared with floating-point numbers.
Hardware-oriented Algorithm for Human Detection using GMM-MRCoHOG Features
751

3.2 Human Recognition Circuit
Integrating Hardware-oriented
GMM-MRCoHOG and BNN
We designed a dedicated human recognition circuit
using the proposed coarse angle calculation algorithm
and the responsibility inference method proposed by
Nagamine et al. (Nagamine et al., 2019), as shown in
Fig. 6.
This circuit receives a 32 × 64 pixels image as in-
put and continuously transfers one pixel at a clock
cycle from the top-left to the bottom-right pixel of
the image to the image buffers. Here, we set the
GMM-MRCoHOG extract features from three reso-
lution images: the original size image, a 1/2-resized
image, and a 1/4-resized image; therefore, we im-
plemented three image buffers for these resolutions.
Each of the buffers is a three-line buffer to calculate
the luminance gradient from 3 × 3 pixels in the im-
age. The derivative filter blocks receive three lines of
pixels and calculate the horizontal and vertical lumi-
nance differences. The angle calculation blocks cal-
culate the angles of the luminance gradients, and the
results are stored in the two-line buffers of the second
stage. Then, the gradient co-occurrence is calculated,
and the GMM-MRCoHOG feature is extracted. The
obtained feature is fed into the BNN, which classifies
the input image as human or not human. The synaptic
weights and activation of the BNN are binarized such
that the circuit requires small memory resources.
Here, the number of mixtures of the Gaussian dis-
tribution used in the GMM-MRCoHOG is 6. The
BNN has three layers: input, hidden, and output lay-
ers, and the number of neurons in the hidden layer is
1.
4 EXPERIMENT
We verified the proposed coarse angle calculation
method, implemented a human recognition circuit
integrating the hardware-oriented GMM-MRCoHOG
and the BNN using high-level synthesis, and esti-
mated the processing speed and circuit size. The ex-
perimental environment is presented in Table 1.
4.1 Coarse Angle Calculation Method
using the Fixed-point Tangent Table
In this experiment, we verified the proposed coarse
angle calculation method with respect to circuit size,
estimated the angle matching rate to true angles, pro-
cessing speed of the circuit, and the approximation
effect on accuracy for human recognition tasks.
First, we verified the circuit sizes of the tanθ table
when the integer part of the fixed-point numbers in
the table was fixed to three bits, and the fraction part
was varied from zero to seven bits. The target device
was a Xilinx Zynq XC7Z020 FPGA on a Zedboard
with a clock frequency of 200 MHz.
Next, we verified the matching rate between
the estimated angles calculated using the proposed
method and the true angle values. The bit width set-
ting of the fixed-point numbers in the table was the
same as the circuit size verification. The true an-
gle values were calculated by feeding f
x
and f
y
into
the atan2 function of the cmath library in C language
and discretized in 36 directions. In addition, we com-
pared the proposed method with the angle approxima-
tion method from a previous study (Nagamine et al.,
2019).
Next, we compared processing speeds of angle
calculations of the following three methods:
1. Software implementation of angle calculation by
atan2 function
2. Software implementation of angle calculation by
the proposed method
3. Hardware implementation of angle calculation by
the proposed method
In the software implementation, the average of the
calculation times of all 261,121 input luminance gra-
dients executed on an Intel Core i7-8700K central
processing unit (CPU) was used as the angle calcu-
lation time for software. In the hardware implemen-
tation, clock cycles to calculate an angle by the circuit
multiplied by the clock cycle time was used as the an-
gle calculation time. Here, the fraction part of the
fixed-point numbers in the table was set to six bits,
and the target board and its clock frequency were the
same as the circuit size verification. Thus, the clock
cycle time was set to 5 ns.
Next, we verified the approximation effect of the
proposed method on the accuracy of human recog-
nition tasks. To avoid the effect of the binarization
of the discriminator using the BNN, we used a sup-
port vector machine (SVM) (Cristianini and Shawe-
Talor, 2000), which is a floating-point number model,
as a discriminator. Here, we compared the accuracy
of three algorithms for GMM-MRCoHOG: the origi-
nal algorithm, the hardware-oriented algorithm of the
previous study (Nagamine et al., 2019), and the pro-
posed algorithm. We set the number of mixtures of
Gaussian distribution as 16 and 32. The datasets used
in this experiment were the Daimler Pedestrian Clas-
sification Benchmark Dataset (Gavrila and Enzweiler,
2008) and INRIA Person Dataset (Dalal and Triggs,
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
752
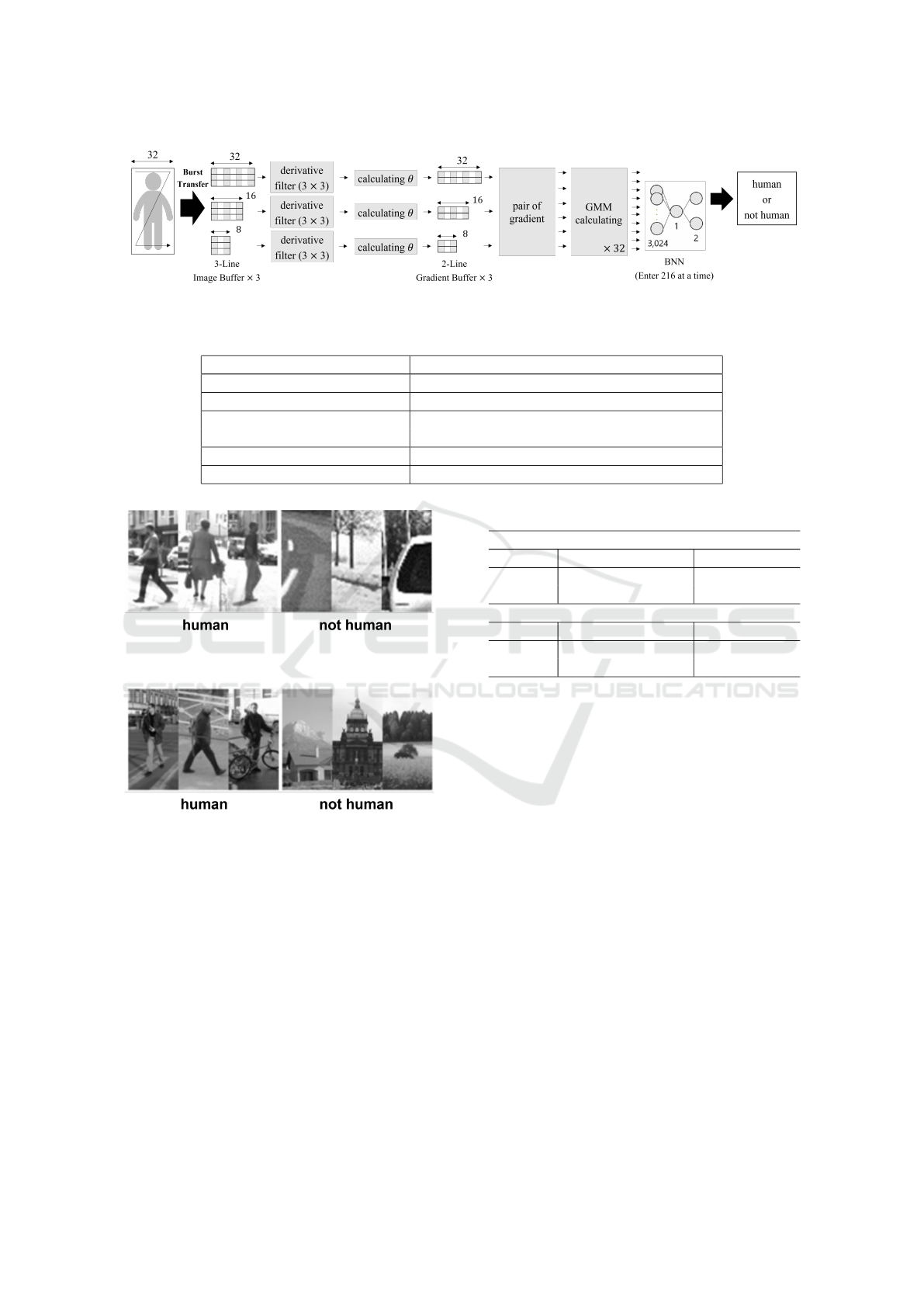
Figure 6: Human Recognition Circuit Integrating Hardware-Oriented GMM-MRCoHOG and BNN.
Table 1: Experimental Environment.
CPU Intel Core i7-8700K 3.70[GHz]
Memory 16GB
OS Windows 10
Circuit Synthesis Environment
Vivado HLS 2018.2
GUINNESS
FPGA Board ZedBoard, XC7Z020CLG484-1 (200[MHz])
FPGA Board ZCU102, XCZU9EG-2FFVB1156 (100[MHz])
Figure 7: Examples of Daimler Pedestrian Classification
Benchmark Dataset.
Figure 8: Examples of INRIA Person Dataset.
2005), which consist of human and non-human im-
ages of size 32 × 64 pixels. The details of these
datasets are summarized in Table 2, and example im-
ages of these datasets are shown in Figs. 7 and 8.
We also verified the accuracy of a human recog-
nition system using the BNN as a discriminator and
compared it with that of a binarized version of the
VGG-16 network (Simonyan and Zisserman, 2015).
Table 2: Dataset.
Train
Dataset Images Resolution
Daimler human: 10,000
32 × 64 pixels
INRIA not human: 10,000
Test
Dataset Images Resolution
Daimler human: 1,126
32 × 64 pixels
INRIA not human: 4,840
4.2 Human Recognition Circuit
Integrating Hardware-oriented
GMM-MRCoHOG and BNN
The designed human recognition circuit was synthe-
sized using Vivado HLS 2018.2, to estimate the pro-
cessing speed and circuit size. The target device was a
Xilinx Zynq UltraScale+ MPSoC XCZU9EG FPGA
on a ZCU102 board with a clock frequency of 100
MHz. For comparison, we also implemented the bina-
rized VGG-16 in the XCZU9EG FPGA using GUIN-
NESS (Nakahara et al., 2019).
For the speed comparison between software and
hardware implementations of the human recognition
systems, the average of the software execution time
to process 5,955 images of size 32 × 64 pixels on an
Intel Core i7-8700K CPU was used as the image pro-
cessing time for the software implementation. For the
hardware implementation, clock cycles to process an
image of 32 × 64 pixels, estimated by C Synthesis of
Vivado HLS 2018.2, multiplied by the clock cycle
time 10 ns, was used as the image processing time.
For the binarized VGG-16, clock cycles to process an
Hardware-oriented Algorithm for Human Detection using GMM-MRCoHOG Features
753

image of 48 × 48 pixels, estimated by GUINNESS,
multiplied by the clock cycle time 10 ns, was used as
the image processing time.
We also estimated the circuit size of the human
recognition system using the Export RTL of Vivado
HLS 2018.2, and the circuit size of the binarized
VGG-16 using GUINNESS. Moreover, we estimated
the power consumption of the circuit using Vivado
2018.2.
5 RESULTS
5.1 Coarse Angle Calculation Method
by using Fixed-point Tangent Table
Figures 9 and 10 show the circuit resource utilization
of the tanθ table. As shown in Fig. 9, both the LUT
and flip-flop (FF) utilization increased almost linearly
while the bit width of the fraction part of the fixed-
point numbers was zero to six bits. However, in the
case of the seven-bit model, the number of resources
was lower than that in the six-bit model. As shown in
Fig. 10, a digital signal processor (DSP) was required
only in the case of the seven-bit model whereas no
DSP was required in the range of zero to six bits.
Figure 9: Circuit Resource Utilization of LUTs and FFs.
Figure 10: Circuit Resources Utilization of DSPs.
Figure 11 shows the angle matching rate between
approximated angles by the proposed method and true
angles obtained by atan2 function. According to a
previous study (Nagamine et al., 2019), the matching
rate was 91Therefore, the matching rate of the pro-
posed method was higher than that of the previous
study when the bit width of the fraction part of the
fixed-point numbers was four or more, and it was ap-
proximately 99 % when the bit width was six or more.
The maximum error of the angle in the figure repre-
sents the maximum absolute difference between the
angles approximated by the proposed method and the
true angles. For example, if some angle is classified
by atan2 function in the third direction while the angle
is classified by the proposed method as the fourth di-
rection, the error is 1. From the figure, the maximum
error of the angle was 1 in cases of more than two bits
for the fraction part of the fixed-point numbers.
Table 3 shows the processing time of the angle
calculation. As shown in the table, the proposed
hardware-oriented algorithm on the CPU required ap-
proximately 14 times longer processing time than
that of the atan2 function. The proposed hardware-
oriented algorithm on the FPGA was approximately
twice as fast as the atan2 function, and approximately
28 times faster than the proposed algorithm on the
CPU.
Table 3: Processing Time of Angle Calculation.
Methods Time [ns]
atan2 (software) 59.6
Proposed (software) 837.7
Proposed (hardware) 30
Figures 12 and 13 show the accuracy of the human
recognition system with 16 and 32 Gaussian mixtures
with the SVM implemented by MATLAB. As shown
in these figures, the proposed method improved the
accuracy of the human recognition task from the pre-
vious study in both mixture cases.
Table 4 presents the human recognition accuracy
of the proposed method with the BNN where the num-
ber of mixtures was set as six, and Table 5 shows the
human recognition accuracy of the binarized VGG-
16. The proposed human recognition system with a
BNN having one neuron in the hidden layer was able
to classify humans with high accuracy and outperform
the binarized VGG-16.
Table 4: Human Recognition Accuracy by Hardware-
Oriented GMM-MRCoHOG with BNN.
Accuracy rate
train 99.4 [%]
test 97.1 [%]
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
754

Figure 11: Angle Matching Rate and Maximum Error between Angles by the Proposed Method and atan2 Function.
Figure 12: Human Recognition Accuracy in the case of 16
Mixtures.
Table 5: Human Recognition Accuracy of Binarized VGG-
16.
Accuracy rate
train 77.4 [%]
test 44.3 [%]
5.2 Human Recognition Circuit
Integrating Hardware-oriented
GMM-MRCoHOG and BNN
Table 6 presents the estimated processing time of hu-
man recognition. The proposed hardware was ap-
proximately 118 times faster than the software im-
plementation and approximately 123 times faster than
the hardware implementation of the binarized VGG-
16.
Figure 13: Human Recognition Accuracy in the case of 32
Mixtures.
Table 6: Processing Time of Human Recognition.
Methods Time[ms]
Proposed (software) 5.2
Proposed (hardware) 0.044
Binarized VGG-16 (hardware) 5.4
Table 7 presents the estimated circuit resource uti-
lization of the proposed human recognition circuit and
Table 8 shows the estimated circuit resource utiliza-
tion of the binarized VGG-16. As presented in Ta-
ble 7, the proposed circuit can be implemented in the
XCZU9EG FPGA, whereas the circuit could not be
implemented in the XC7Z020 FPGA owing to a lack
of resources. The dominant resource in the circuit was
the block random access memory (BRAM), which
was determined by the number of center coordinates
Hardware-oriented Algorithm for Human Detection using GMM-MRCoHOG Features
755

and width of the mixture Gaussian distribution, and
the synaptic weights of the BNN. Compared with the
binarized VGG-16, the proposed human recognition
circuit consumed fewer FFs and LUTRAMs, but more
BRAMs and LUTs.
Table 7: Circuit Resource Utilization of the Proposed Hu-
man Recognition Circuit.
Used Available Utilization [%]
BRAM 154 912 16.9
DSP48E 0 2,520 0
FF 11,529 548,160 2.1
LUT 27,331 274,080 10.0
LUTRAM 111 144,000 0.1
Table 8: Circuit Resource Utilization of the Binarized
VGG-16.
Used Available Utilization [%]
BRAM 148 912 16.2
DSP48E 0 2,520 0
FF 21,751 548,160 3.9
LUT 21,765 274,080 7.9
LUTRAM 1,934 144,000 1.3
Table 9 lists the estimated power consumption of
the circuit. As shown in the table, the power con-
sumption of the proposed circuit is 0.923 [W]. It
is noteworthy that this power was for only the pro-
grammable logic on the XCZU9EG chip, not for the
entire FPGA board, including the processing system
on the chip and dynamic RAMs on the board.
Table 9: Estimated Power Consumption of the Circuit.
Power [W]
Proposed circuit 0.923
Binarized VGG-16 0.949
6 DISCUSSION
6.1 Coarse Angle Calculation Method
by using Fixed-point Tangent Table
As shown in the experimental results (Figs. 9 and
10), the number of LUTs and FFs increased linearly
while the fraction part of fixed-point numbers was in
range from zero to six bits. In the case of the seven-bit
model for the fraction part, the number of LUTs and
FFs decreased, and the number of DSPs increased be-
cause the high-level synthesis compiler estimated us-
ing the DSP was more efficient than using LUTs and
FFs to represent multiplications.
Table 10 is a summary of the comparison of FFs
and LUTs utilization for the tan
−1
function between
the high-level synthesis of atan2 function, the method
of the previous study (Nagamine et al., 2019), and
the proposed method. As presented in the table, the
proposed method, even with six bits for the fraction
part, which was the most resource-intensive method
among the proposed method, required approximately
1/30 of the circuit resources for both FF and LUT of
the high-level synthesis of the atan2 function. More-
over, the number of LUTs in the proposed circuit was
significantly smaller than that in the previous study.
Therefore, the proposed method succeeded in reduc-
ing the size of the circuit.
Table 10: Circuit Resource Utilization of the Original Al-
gorithm, Previous Study, and Proposed Method.
FF LUT
tan
−1
6,000 10,000
Previous study 76 3,087
Proposed (0 bit) 52 97
Proposed (1 bit) 75 112
Proposed (2 bit) 100 167
Proposed (3 bit) 119 197
Proposed (4 bit) 130 236
Proposed (5 bit) 137 266
Proposed (6 bit) 183 297
The accuracy of the proposed method for the
human recognition task was better than that of the
binarized VGG-16, as well as in a previous study
(Nagamine et al., 2019). According to a pre-
vious study, the accuracy for the same task was
92.4whereas, the accuracy of the proposed method
was 97.1Additionally, a discrepancy in the angle cal-
culation of the previous method was 9Therefore, the
proposed method extracted more precise features, re-
sulting in better performance in the human recogni-
tion task.
6.2 Human Recognition Circuit
Integrating Hardware-oriented
GMM-MRCoHOG and BNN
Although there was no significant difference between
the proposed circuit and binarized VGG-16 in terms
of circuit size and power consumption, the proposed
circuit outperformed the binarized VGG-16 for the
human recognition task, and the processing time of
the proposed circuit was significantly faster than that
of the binarized VGG-16 because the proposed cir-
cuit computed the algorithm in parallel using an effec-
tive pipeline architecture with line buffers. Therefore,
we concluded that the proposed circuit is more suit-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
756

able for a human detection system than the binarized
VGG-16.
7 CONCLUSIONS
For robots and self-driving cars operating near hu-
mans, a high-accuracy, high-speed, and low-power
human detection function is required. In this study,
we designed a dedicated circuit of GMM-MRCoHOG
with high human recognition performance and imple-
mented it in an FPGA to realize a high-speed and low-
power human recognition system. Using the tanθ ta-
ble, the proposed hardware-oriented algorithm sim-
plifies the calculation of luminance gradients, which
is a high-cost operation in the original algorithm. The
experimental results show that the proposed method
improves the accuracy and processing speed of the
human recognition task while reducing the circuit re-
sources.
In future work, we plan to implement a human de-
tection system on an FPGA by feeding multiple re-
gions of interest from an image to the proposed circuit
for human recognition. Because the processing speed
of the circuit is high, the realization of a real-time hu-
man detection system can be expected.
REFERENCES
Cristianini, N. and Shawe-Talor, J. (2000). An introduction
to support vector machines. In Cambridge University
Press.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In Proc. IEEE Computer
Vision and Pattern Recognition (CVPR), volume 1,
pages 886–893.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum likelihood from incomplete data via the em
algorithm. Journal of the Royal Statistical Society,
39:1–38.
Gavrila, D. M. and Enzweiler, M. (2008). Monocular pedes-
trian detection: Survey and experiments. In IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence (TPAMI), volume 31, pages 2179–2195.
Higashi, S., Michishita, Y., Enokida, S., Shibata, M., and
Yamada, H. (2018). Pedestiran detection based on
gaussian mixture model multiresolution cohog. In
Proc. 4th World Congress on Electrical Engineering
and Computer Systems and Sciences.
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and
Bengio, Y. (2016). Binarized neural networks. In
Advances in Neural Information Processing Systems
(NIPS), volume 29, pages 4107–4115.
Iwata, S. and Enokida, S. (2014). Object detection based
on multiresolution cohog. In Proc. 10th International
Symposium on Visual Computing, pages 427–437.
Michishita, Y., Higashi, S., Shibata, M., Muramatsu, R., Ya-
mada, H., and Enokida, S. (2018). Autonomous state
space construction method based on mixed normal
distributions for pedestrian detection. In IEEJ Trans-
actions on Electronics, Information and Systems, vol-
ume 138, pages 1100–1107.
Nagamine, Y., Yoshihiro, K., Enokida, S., M. Shibata, H. Y.,
and Tamukoh, H. (2019). Human detection using
hardware oriented gmm-mrcohog. In 35th Fuzzy Sys-
tem Symposium, pages 715–719.
Nakahara, H., Yonekawa, H., Fujii, T., Shimoda, M., and
Sato, S. (2019). Guinness: A gui based binarized deep
neural network framework for software programmers.
In IEICE Transactions on Information and Systems,
volume E102.D, pages 1003–1011.
Simonyan, K. and Zisserman, A. (2015). Very deep con-
volutional networks for large-scale image recognition.
In Proc. International Conference on Learning Repre-
sentations (ICLR).
Hardware-oriented Algorithm for Human Detection using GMM-MRCoHOG Features
757
