Improved MRI-based Pseudo-CT Synthesis via Segmentation Guided

Attention Networks

Gurbandurdy Dovletov

1 a

, Duc Duy Pham

, Josef Pauli

1 b

, Marcel Gratz

2,3 c

and Harald H. Quick

2,3

Intelligent Systems Group, Faculty of Engineering, University of Duisburg-Essen, Duisburg, Germany

High-Field and Hybrid MR Imaging, University Hospital Essen, University of Duisburg-Essen, Essen, Germany

Erwin L. Hahn Institute for MR Imaging, University of Duisburg-Essen, Essen, Germany

Keywords:

Image-to-Image Translation, Pseudo-CT, Attention Mechanism, U-Net, Generative Adversarial Network.

Abstract:

In this paper, we propose 2D MRI-based pseudo-CT (pCT) generation approaches that are inspired by U-Net

and generative adversarial networks (GANs) and that additionally utilize coarse bone segmentation guided

attention (SGA) mechanisms for better image synthesis. We ﬁrst introduce and formulate SGA and its ex-

tended version (E-SGA), then we embed them into our baseline U-Net and conditional Wasserstein GAN

(cWGAN) architectures. Since manual bone annotations are expensive, we derive coarse bone segmentations

from CT/pCT images via thresholding and utilize them during the training phase to guide image-to-image

translation attention networks. For inference, no additional segmentations are required. The performance of

the proposed methods regarding the image generation quality is evaluated on the publicly available RIRE data

set. Since MR and CT image pairs in this data set are not correctly aligned with each other, we also brieﬂy

describe the applied image registration procedure. The results of our experiments are compared to baseline

U-Net and conditional Wasserstein GAN implementations and demonstrate improvements for bone regions.

1 INTRODUCTION

Positron emission tomography (PET) is an imaging

technique that reveals physiological and biochemi-

cal processes of tissue and organs by measuring their

metabolic activity. The technique is based on the de-

tection of radioactivity emitted in opposite directions

after a small amount of a radioactive tracer is injected

into a peripheral vein (Paans, 2006). When traveling

through some tissue or hardware parts such as the pa-

tient table these photons lose their energy and as a

consequence, only a part of them reaches detectors.

In order to compensate for such physical behavior,

an attenuation correction (AC) procedure is required

(Ollinger and Fessler, 1997). In stand-alone PET sys-

tems, AC is performed based on a transmission scan

acquired using external rod sources.

A lack of anatomical information in a pure PET

initiated the development of combined PET and com-

puted tomography (CT) systems in a single gantry,

https://orcid.org/0000-0002-2401-8745

https://orcid.org/0000-0003-0363-6410

https://orcid.org/0000-0001-9723-5233

also known as PET/CT. The additional CT examina-

tion in such systems allows deriving attenuation cor-

rection maps (µ-maps) directly from Hounsﬁeld units

(HU) by scaling the acquired CT image to the energy

level of a PET image (Beyer et al., 2000). Obtained

in such a way µ-maps are later used for attention cor-

rection of PET scans. The main application areas

of PET/CT are cardiology, neurology, and oncology.

According to (Brady et al., 2008), in oncology, it is

by far the most intensively used diagnostic and stag-

ing device.

Being able to provide an excellent soft tissue con-

trast, PET/MR combination was introduced, which

moreover goes without the need of additional radia-

tion as it is the case for PET/CT. Such systems do not

provide a straightforward way to obtain µ-maps for

AC by energy scaling like it is possible in stand-alone

PET or PET/CT combination (Keereman et al., 2013).

Unlike PET and CT, MRI uses physical mechanisms

that do not allow for a direct derivation or correlation

of image intensities with electron density.

Various approaches have been proposed to resolve

this issue. In atlas-based methods, µ-maps are calcu-

lated based on prior registration of atlas images to a

Dovletov, G., Pham, D., Pauli, J., Gratz, M. and Quick, H.

Improved MRI-based Pseudo-CT Synthesis via Segmentation Guided Attention Networks.

DOI: 10.5220/0010849200003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 2: BIOIMAGING, pages 131-140

ISBN: 978-989-758-552-4; ISSN: 2184-4305

131

target image with subsequent utilization of achieved

transformations. (Burgos et al., 2014) propose to gen-

erate synthetic CTs by locally matching target MR

images to a database of MR-CT pairs and deriving

the corresponding µ-maps from them. An alterna-

tive approach is a segmentation-based AC, where dis-

crete linear attenuation coefﬁcients (LACs) are as-

signed to each achieved segmentation class (Berker

et al., 2012). In order to take advantage of both

segmentation- and atlas-based approaches, (Paulus

et al., 2015) propose to ﬁrst derive µ-maps via seg-

menting a Dixon image into air, fat, lung, and soft tis-

sue classes. After that, atlas-based continuous µ-maps

for each of major body bones (femur, hip, spine, and

skull) are derived and fused with the existing µ-maps

from the previous step.

One other possible way to derive µ-maps for PET

AC is to ﬁrst generate a pseudo-CT (pCT) image from

an MRI and then scale it to PET’s energy level in the

same way as it is done for PET/CT machines. This

MRI-based pCT generation task, however, introduces

some challenges, since the MR modality is sensitive

to proton density and thus not capable of distinguish-

ing between air and lungs. Moreover, compact bone

is also indistinguishable as its signal vanishes, due to

the comparably short relaxation time, before it can be

acquired.

Previously proposed methods have already

demonstrated the feasibility of generating pCT from

MR images using deep learning methods. (Liu et al.,

2017) propose a pipeline for PET attenuation correc-

tion, where an encoder-decoder like architecture is

ﬁrst employed to segment an MR image into three

classes, namely, air, bone, and soft tissue. The ob-

tained segmentation is later converted to a pseudo-CT

image via mapping each class ID to its corresponding

statistical HU value. (Nie et al., 2016) propose to

use a 3D fully convolution network (FCN) for a

direct non-linear mapping from MRI to CT domain.

They utilize a patch-based training procedure for

better preservation of the neighborhood information

in predicted pseudo-CT images. Moreover, an

additional image gradient difference loss term was

used to retain the sharpness of synthesized CTs. In

order to generate even more realistic images, (Nie

et al., 2017) extend their existing architecture with an

additional discriminator and employ the adversarial

training approach from (Goodfellow et al., 2014).

(Han, 2017) adapts and modiﬁes the well-known

U-Net (Ronneberger et al., 2015) architecture by

changing the number of convolutional layers in such

a way, that allows to initialize the feature extraction

part of the proposed architecture from a pretrained

VGG-16 model. (Wolterink et al., 2017) propose to

utilize the state-of-the-art Cycle-GAN (Zhu et al.,

2017) image-to-image translation model, which is

the extension of GAN (Goodfellow et al., 2014) and

involves the simultaneous training of two generators

and two discriminator models.

There have been several attempts to improve

the bone quality of generated (synthesized) pseudo-

CT images with the help of additional information.

(Leynes et al., 2018) propose to utilize zero-echo-time

(ZTE) images additionally to fat and water maps de-

rived from a 2-echo Dixon MRI (in-phase and out-

of-phase) sequence to capture bone information, and

thus, generate more accurate pseudo-CT images. The

main limitations of their work, however, are the long

ZTE image acquisition time (Mecheter et al., 2020)

and UTE/ZTE’s limited availability, since they are

not standard clinical sequences. Dixon-type pulse se-

quences, on contrary, are increasingly popular and

are offered, nowadays, by nearly every manufacturer.

To this end, (Torrado-Carvajal et al., 2019) employ a

U-Net architecture with four Dixon images, where fat

and water maps are explicitly used as additional in-

puts to 2-echo Dixon MRI. Alternatively, (Qi et al.,

2020) utilize a stack of images from four different se-

quences (T1, T2, T1C, and T1DixonC-Water) as an

input to their U-Net/GAN-based networks.

This paper makes several contributions. We in-

troduce and formulate segmentation guided attention

(SGA) mechanisms that can be adapted and used for

different image-to-image translation tasks. We utilize

the proposed SGA and its extended version (E-SGA)

for the task of MRI-based pseudo-CT generation. The

proposed attention mechanisms are based on coarse

bone masks, which are derived from CT/pCT im-

ages in a fully automatic manner. These masks are

only used during the training phase and thus are not

required during the inference. We demonstrate that

these attention networks are capable of producing su-

perior quality pCTs, especially for bone regions.

2 METHODOLOGY

In this section, we ﬁrst introduce and formulate the

segmentation guided attention mechanism and its ex-

tended version. After that, we introduce U-Net-

based and conditional Wasserstein GAN-based atten-

tion networks for the MRI-based pseudo-CT genera-

tion task.

2.1 Segmentation Guided Attention

The main goal of the image-to-image translation task

is to transform input images from a source domain

BIOIMAGING 2022 - 9th International Conference on Bioimaging

132

X to a target domain Y via a mapping function

G : X → Y . Neural networks can learn such non-

linear G mapping functions and, thus, can be used to

generate (predict) ˆy from the input image x, as fol-

lows:

ˆy = G(x) (1)

Pixel-wise loss functions, such as L1 or L2 norm, are

playing an essential role while training such image-

to-image translation networks. L1 loss, for example,

can be mathematically formalized as follows:

(y, ˆy) =

M · N

∑

i=1

∑

j=1

i j

− ˆy

i j

(2)

where ˆy denotes the output image of size M × N pre-

dicted by a neural network and y is the corresponding

ground truth (GT) image. This loss function is cal-

culated as the mean absolute error (MAE) between

GT and prediction image over all (i, j) positions. As

a consequence, while training, a neural network pays

attention to the entire input image.

The proposed segmentation guided attention

(SGA) loss, in contrast, focuses speciﬁcally on pro-

vided regions of interest (ROI) and helps image-to-

image translation networks to achieve better perfor-

mance for them. We formulate the SGA loss function

as follows:

SGA

(y, ˆy, seg

) =

γ(seg

) ·

M · N

∑

i=1

∑

j=1

seg

i j

· ky

i j

− ˆy

i j

(3)

where seg

is a binary mask derived from the target

domain image y. Multiplication of seg

i j

with its cor-

responding pixel-wise difference at position (i, j) pe-

nalizes an error only for the provided area of interest.

We propose to use an additional weighting function

γ(.) which is dependent on seg

and can be calculated

as follows:

γ(seg

) =

M · N

(

∑

i=1

∑

j=1

seg

i j

) + ε

(4)

where ε is needed to deal with the cases of division

by 0, when seg

i j

is 0 at each of its positions. This

ensures that L

SGA

stays on approximately the same

range independent of ROI mask properties.

It can be noticed that the SGA loss is a generaliza-

tion of the L

loss from Equation 2. When the ROI

mask contains 1’s at each of its positions L

SGA

is ap-

proximately equal to L

, since γ(seg

) is equal to 1.

The proposed segmentation guided attention loss

can be used as a separate, alternative pixel-wise func-

tion or in combination with existing ones. Moreover,

an alternative SGA loss can also be formulated based

on the L2 norm.

2.2 Extended-SGA

The previously proposed L

SGA

loss deﬁnition can be

extended to L

E-SGA

, which considers two segmenta-

tion masks simultaneously. In addition to seg

, which

is based on a ground truth image, a segmentation seg

ˆy

based on a predicted image ˆy, is utilized. Thus, the

extended-SGA (E-SGA) loss is deﬁned as follows:

E-SGA

(y, ˆy, seg

, seg

ˆy

) = γ

(seg

, seg

ˆy

)

M · N

∑

i=1

∑

j=1

kseg

i j

· y

i j

− seg

ˆy

i j

· ˆy

i j

(5)

where γ

(.) is a weighting function:

(seg

, seg

ˆy

) =

2 · M · N



∑

i=1

∑

j=1

(seg

i j

+ seg

ˆy

i j

)



+ ε

(6)

which is dependent on seg

and seg

ˆy

. In contrast to

SGA, minimization of the extended loss during the

training not only enforces networks to generate better

quality seg

regions but also constrains them to pay

attention to seg

ˆy

regions.

It can be noticed that L

E-SGA

is equivalent to L

SGA

from Equation 3 when seg

and seg

ˆy

are identical.

2.3 U-Nets with Additional SGA/E-SGA

The previously introduced loss functions can be uti-

lized for MRI-based pseudo-CT generation task. Our

proposed network topologies are based on the U-Net

architecture, which was originally proposed to ad-

dress semantic segmentation tasks in the medical im-

age computing domain (Ronneberger et al., 2015). It

is a fully convolutional network (FCN) which con-

sists of a contracting (encoding) path followed by an

expanding (decoding) path with additional skip con-

nections between layers of the same size, as can be

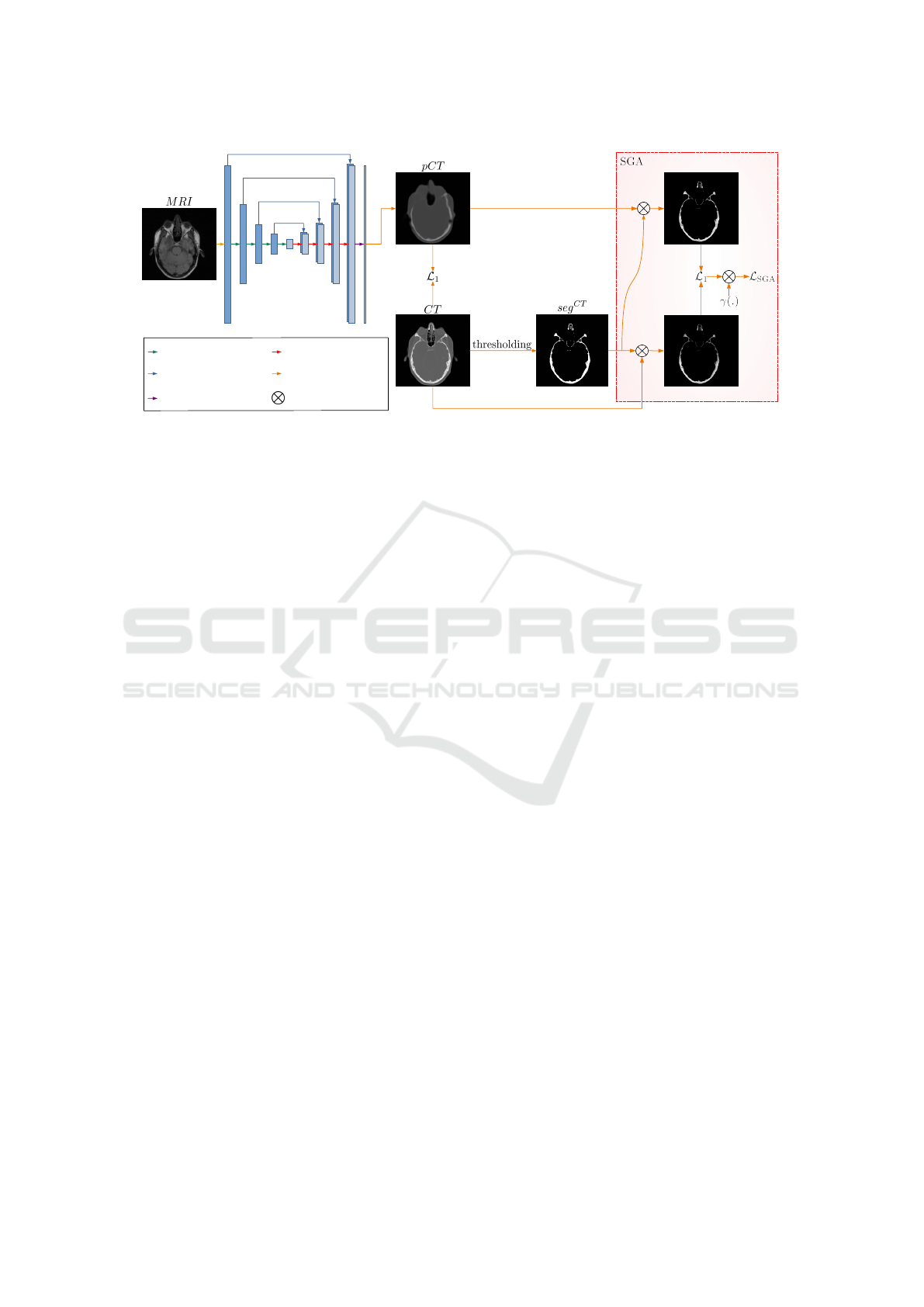
seen on the left part of Figure 1 and Figure 2. While

the encoding path of the network behaves similar to

a traditional convolutional neural network (CNN) and

learns to extract hierarchical features from an input,

the decoding path is responsible for reconstructing an

output image gradually by adding more details at each

following resolution level.

The proposed segmentation guided U-Net

SGA

ap-

proach is schematically shown in Figure 1. By prop-

agating an input MR image through the network we

generate a pCT image. The global L

loss func-

tion (see Equation 2) compares the synthesized pCT

to its corresponding ground truth CT image. In U-

Net

SGA

we enforce the network to pay particular at-

tention to the bone area via utilizing the previously

introduced L

SGA

loss term (see Equation 3). There-

fore, we ﬁrst multiply both generated pCT and its

Improved MRI-based Pseudo-CT Synthesis via Segmentation Guided Attention Networks

133

2xConvolution,

followed by Max-Pooling

Skip Connection

(Concatenation)

Data Flow Arrow

(no operation)

Transposed Convolution,

followed by 2xConvolution

Element-wise multiplication

128

256

512

1x1 Convolution

Figure 1: The proposed segmentation guided U-Net

SGA

approach for MRI-based pseudo-CT generation. While L

loss

considers entire pCT and CT images, L

SGA

loss concentrates exclusively on the bone area from CT images.

corresponding CT images with the binary bone mask

(seg

, in Figure 1), and then calculate the difference

between the resulting images. We propose to derive

the required bone masks from CT via thresholding,

which is described in more detail in Subsection 3.2.

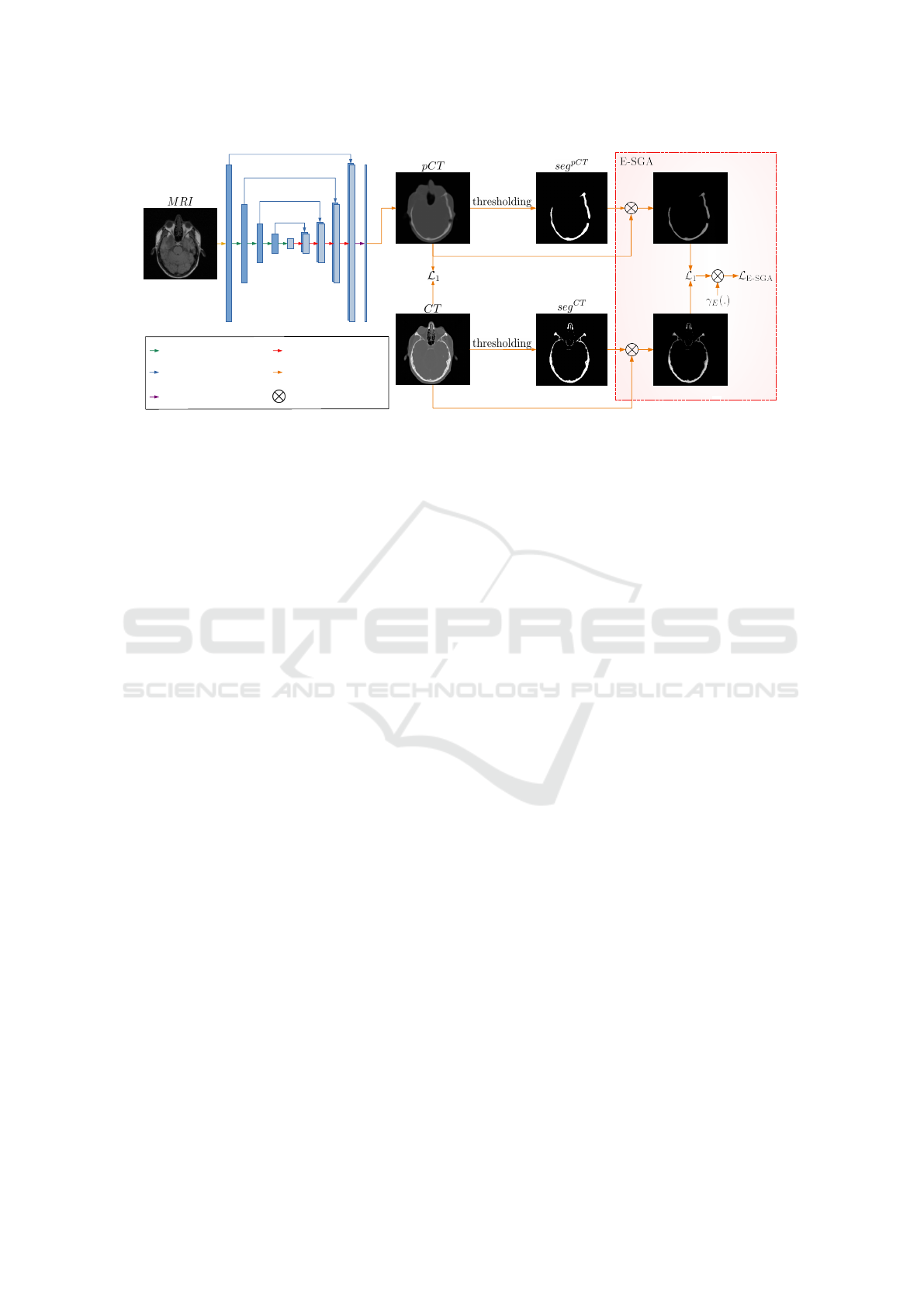
We extend the proposed SGA-based U-Net approach

and introduce U-Net

E-SGA

, which is schematically

shown in Figure 2. This approach uses the additional

E-SGA

loss term (see Equation 6). In comparison

to U-Net

SGA

, this method requires additional seg

pCT

bone masks from predicted pCTs. We propose to de-

rive them in a similar manner as seg

images from

CTs. Thus, the total objective for U-Net

SGA/E-SGA

consists of two loss functions and is deﬁned as fol-

lows:

Unet

SGA/E-SGA

= L

+ αL

SGA/E-SGA

(7)

where α is a hyperparameter and can be used to con-

trol the relative importance of the two objectives.

2.4 Conditional Wasserstein GANs with

Additional SGA/E-SGA

MRI-based pseudo-CT images can also be synthe-

sized by using generative models, such as genera-

tive adversarial networks (GANs) (Goodfellow et al.,

2014). The simplistic GAN framework consists of

generator G and discriminator D networks. While the

generator attempts to create data similar to those in

the training set, the discriminator inspects it and tries

to correctly identify whether it is real (from the train-

ing set) or fake (generated by G). Both networks are

trained together by taking turns and using the adver-

sarial loss function, which is deﬁned as follows:

adv

= E

[log(D(y))] + E

[log(1 − D(G(x)))] (8)

with x and y representing images from source and tar-

get domain, correspondingly. In other words, they are

playing a minimax game against each other: while G

attempts to maximize L

adv

and thus fool D, the latter

one tries to not be fooled by minimizing the adversar-

ial loss.

Our proposed network topologies are based on the

conditional Wasserstein GAN (cWGAN) training ap-

proach, which is an extension of Wasserstein GAN

(Arjovsky et al., 2017). In contrast to traditional

GANs, Wasserstein GAN can improve the stability

of the learning process and can help to get rid of the

mode collapse problem. This is achieved by using

a different adversarial loss function, which approxi-

mates the Earth Mover’s Distance, and changing the

role of the discriminator from a binary classiﬁer into

a critic C, which predicts scores of how real or fake

provided images are looking. For faster convergence

and better preservation of structural information, MR

image-based conditioning on the corresponding critic

is utilized. Conditional Wasserstein GAN objective

can be formalized as follows:

= E

x,y

[C(x, y)]− E

[C(x, G(x))] (9)

with x and y representing MR and CT images, cor-

respondingly. Thus, while G tries to minimize L

against adversarial critic C, the latter one attempts to

maximize the same objective. We use U-Net as the

generator in our baseline cWGAN approach. For the

critic network, CNN architecture is utilized, which is

described in more detail in Subsection 3.2). Anal-

ogously to the U-Net-based extensions, we also in-

troduce two extensions of the cWGAN. The pro-

posed cWGAN

SGA

and cWGAN

E-SGA

approaches

additionally include previously introduced segmenta-

tion guided attention loss terms while training their

corresponding U-Net generator networks. For the

BIOIMAGING 2022 - 9th International Conference on Bioimaging

134

2xConvolution,

followed by Max-Pooling

Skip Connection

(Concatenation)

Data Flow Arrow

(no operation)

Transposed Convolution,

followed by 2xConvolution

Element-wise multiplication1x1 Convolution

128

256

512

Figure 2: The proposed extended segmentation guided U-Net

E-SGA

approach for MRI-based pseudo-CT generation. While

loss considers the entire pCT and CT images, L

E-SGA

loss concentrates exclusively on bone areas from both CT and pCT.

sake of shortness, we only depict cWGAN

E-SGA

ap-

proach in Figure 3. Thus, our ﬁnal objectives for gen-

erators G and critics C of cWGAN

SGA/E-SGA

can be

expressed as:

= (L

+ αL

SGA/E-SGA

) + λL

= λL

(10)

where λ denotes the weighting factor of the condi-

tional Wasserstein GAN objective.

3 EXPERIMENTS

In this section, data set information including utilized

registration procedure and following data preparation

are introduced. After that, implementation details of

proposed architectures and evaluation metrics are out-

lined.

3.1 Data

We evaluated the proposed architecture on the pub-

licly available Retrospective Image Registration Ex-

periment (RIRE) Project data set (West et al., 1997),

that provides different modality images of the head

area for 16 patients. For our experiments, we chose

to use T1-weighted MR images of size 256 × 256

in combination with corresponding CTs of size

512 × 512. Both images ﬁt into 12 bits data represen-

tation, meaning that CT’s intensities range between

−1024 HU and 3071 HU while MR’s are ranging

from 0 and 4095. Some of the CT volumes include

the patient’s table.

The RIRE project was originally designed to com-

pare CT-MR and PET-MR registration techniques.

Since the ground truth data is not provided, we used

Mattes’s mutual-information-based multi-resolution

algorithm (Mattes et al., 2003) implemented in Sim-

pleITK (Lowekamp et al., 2013; Yaniv et al., 2018)

framework to register CT and MR volume pairs. Dur-

ing the registration procedure, CT was chosen as a

ﬁxed volume, while the corresponding MR volume

was considered as a moving one. Optimization of mu-

tual information between MR and CT volumes was

done via gradient descent with a learning rate set to

0.01 value. While solving the optimization task, we

utilized linear interpolation to deform the MR image.

Since ground truth transformations are not available,

we qualitatively inspected the registered MR-CT vol-

ume pairs and validated the utilized registration pro-

cedure.

All registered volumes were ﬁrst brought to

isotropic 1×1 × 1 mm

voxel spacing. After that, de-

pending on the obtained spatial resolution, cropping

from the center point of the image or padding around

its borders was utilized in order to achieve the same

ﬁeld of view. Finally, we resized the achieved MR

and CT slices to the size of 256 × 256 pixels.

After the ﬁnal visual inspection of the data set,

we identiﬁed MR/CT slices that did not have valid

CT/MR counterparts. These image pairs were located

either on the top or at the bottom of the registered

volumes when looking along the longitudinal axis.

The main reason for their occurrence at these spe-

ciﬁc locations is not the low-quality registration, but

rather the different ﬁelds of view of initial (not reg-

istered) MR and CT scans. Thus, we excluded them

and ended up with 553 valid MR-CT image pairs in

total.

3.2 Implementation Details

The experiments were conducted in a 4-fold cross-

validation manner with one set used for each testing

Improved MRI-based Pseudo-CT Synthesis via Segmentation Guided Attention Networks

135

2xConvolution,

followed by Max-Pooling

Skip Connection

(Concatenation)

Data Flow Arrow

(no operation)

Transposed Convolution,

followed by 2xConvolution

Element-wise multiplication

1x1 Convolution

128

256

512

Strided Convolution

128

256

512

Figure 3: The proposed conditional Wasserstein GAN with extended segmentation guided attention (cWGAN

E-SGA

) for MRI-

based pseudo-CT generation.

and three sets used for training and validation. During

our experiments, we increased the number of training

samples via data augmentation by means of random

rotations (in the range of ±7.5 degrees), scaling (with

factors in the range [1; 1.15]), and horizontal ﬂipping

(with the probability of 50%).

3.2.1 U-Nets

Baseline U-Net. In our baseline U-Net implemen-

tation, we started with 32 convolutional kernels in the

ﬁrst resolution level and we used two subsequent con-

volutional layers with zero padding at each resolution

level. We chose to use kernels of size 5 × 5 at each

convolutional layer and windows of size 2×2 for each

following max pooling step. The number of convo-

lutional ﬁlters was doubled at each following image

resolution. In the expanding path, we used transposed

convolutions with kernels of size 2 × 2 with a stride

size of 2 pixels in both directions. At each upsam-

ple step the number of output features was reduced

twice compared to the corresponding number of input

channels. As a ﬁnal layer, we used 1 × 1 convolution

in order to get a single channel output image. We did

not normalize MR and CT images as we did not ob-

serve any performance gain compared to the network

trained with normalized inputs.

U-Nets with SGA/E-SGA. We used the same

U-Net structure, as described previously, for both pro-

posed segmentation guided approaches. For a given

MRI-based pseudo-CT generation task we are partic-

ularly interested in an improved bone quality synthe-

sis. Therefore, regions of interest required for SGA

calculations should also represent bone areas.

Since manual annotation of bones from CTs is

expensive and time consuming, we generated coarse

bone masks by applying global threshold-based seg-

(a) MR. (b) CT. (c) Bone mask.

Figure 4: Exemplary MR, CT and coarse bone mask images

for Patient 002 (slice #7).

mentation approach to ground truth CT images:

seg

i j

(

1 if y

i j

> T

0 otherwise

(11)

where T is a threshold value.

We set the threshold value to 350 HU, which is

approximately in the same range as stated in the liter-

ature (Buzug, 2009; Chougule et al., 2018). Figure 4

shows exemplary MR, CT and the obtained from CT

coarse bone segmentation mask. In a similar man-

ner and with the same threshold value we derived

seg

ˆy

, segmentation masks from synthesized ˆy images,

which are needed for E-SGA loss term calculations.

We set α to 1 when calculating the total loss func-

tions for both U-Net

SGA

and U-Net

E-SGA

approaches.

The intuition behind this choice is that we want to

achieve a better synthesis quality for bone areas, how-

ever, we want to keep a good performance for other

parts of the image as well.

Training U-Nets. We trained our U-Net models for

100 epochs with a learning rate of 0.01 using the

Adam optimizer with β

= 0.9 and β

= 0.999 as sug-

gested by (Kingma and Ba, 2014). Mini-batches of

size 16 were used for all our experiments.

BIOIMAGING 2022 - 9th International Conference on Bioimaging

136

3.2.2 Conditional WGANs

Baseline cWGAN. We used the previously intro-

duced baseline U-Net as a generator in our baseline

conditional Wasserstein GAN architecture. A hyper-

bolic tangent layer was added on top of it as the ﬁ-

nal activation layer. This ensured that the output in-

tensities landed in the range between −1 and 1. In

our critic architecture, we started with 16 convolu-

tional kernels in the ﬁrst resolution level. We chose

to use kernels of size 4 × 4 with a stride of 2 pix-

els and 1 pixel padding in both directions, which al-

lowed us to avoid max pooling layers, as was sug-

gested by (Radford et al., 2015). We applied the

LeakyReLU non-linear activation function after each

convolutional layer. The number of ﬁlters was dou-

bled at each following image resolution. In order to

make the training procedure more stable, we applied

a batch normalization at each resolution level, except

for the ﬁrst one. Strided convolutions were repeated

until we obtained a single scalar value as an output

per input image.

Input images were normalized to the range of −1

and 1 before being fed into our networks. This was

achieved by applying the following min-max normal-

ization equations for MR and CT images:

normalized

= 2 ·

4095

− 1 (12)

normalized

= 2 ·

CT + 1024

4095

− 1 (13)

During the inference, synthesized pseudo-CT images

were mapped back to the original intensity range

based on the same normalization scheme, as in Equa-

tion 13.

CWGANs with SGA/E-SGA. The same baseline

conditional WGAN architecture, as described pre-

viously, was utilized in our segmentation guided

cWGAN

SGA

and cWGAN

E-SGA

approaches. Since

their corresponding generator networks synthesize

normalized pCT images, the previously utilized

350 HU threshold value was also mapped to the range

between −1 and 1 using the Equation 13, which led

to the value of −0.329.

With similar intuition behind as for segmentation

guided U-Nets, we set α to 1 when calculating the

total loss objectives of the generator networks.

Training cWGANs. We used a two times update

rule for training our cWGANs as it was proposed by

(Heusel et al., 2017). Our models were trained for

2000 epochs with learning rates of 0.0002 and 0.0004

for generators and discriminators, correspondingly.

(a) MR. (b) CT. (c) Head mask.

Figure 5: Exemplary MR, CT and head mask from MR im-

ages for Patient 002 (slice #2).

During the training, we utilized an additional gradi-

ent penalty as suggested by (Wu et al., 2018). Net-

works were optimized using the Adam optimizer and

mini-batches of size 16.

3.3 Evaluation Metrics

For evaluation, the obtained 2D pseudo-CT images

were ﬁrst stacked to build 3D volumes, and then only

compared to the desired ground truth CT volumes.

We chose mean squared error (MSE) and mean ab-

solute error (MAE) as pixel-wise quality metrics.

Moreover, we calculated MSE and MAE val-

ues only for speciﬁc regions of interest, such as for

bone and head areas (MSE

bone/head

and MAE

bone/head

Head masks were derived from MR images via Otsu’s

thresholding followed by subsequent morphological

operations. First, a morphological opening with a

disk-shaped structuring element of a 5 px radius was

used to remove small artifacts from initial segmen-

tations. Next, a closing operation (radius of 25 px)

was utilized to ﬁll the holes in nasal areas. Finally, a

morphological dilation (radius of 5 px) was applied to

slightly increase the total shape of the segments. An

exemplary head mask is depicted in Figure 5.

To better evaluate the quality of generated pseudo-

CT images we additionally calculated peak signal-to-

noise ratio (PSNR) as follows:

PSNR(y, ˆy) = 10 · log



MAX

MSE(y, ˆy)



(14)

where MAX

is the maximum possible intensity value.

We also calculated the structural similarity index

measure (SSIM) (Wang et al., 2004) between gener-

ated pCTs and corresponding CTs as follows:

SSIM(y, ˆy) =

(2µ

ˆy

)(2σ

y ˆy

)

(µ

+ µ

ˆy

)(σ

+ σ

ˆy

)

(15)

where µ

ˆy

and µ

denote mean values of pCT and CT

images, respectively; σ

and σ

ˆy

are corresponding

variances; σ

y ˆy

is the covariance between pCT and CT

image; and C

= (k

and C

= (k

are two vari-

ables to stabilize the division with weak denomina-

tors. Here, k

= 0.01, k

= 0.03, and L = MAX

rep-

resents the dynamic range of CT/pCT intensities.

Improved MRI-based Pseudo-CT Synthesis via Segmentation Guided Attention Networks

137

4 RESULTS

Table 1 shows averaged evaluation metrics for

both baseline and segmentation guided architectures.

Baseline U-Net implementation achieved MAE of

101 ± 35 HU and MSE of 69139 ± 27664 HU

when considering entire pseudo-CT images. Re-

garding the quality of image synthesis, it reached a

PSNR of 24.3 ± 1.9 dB and SSIM of 79.6 ± 6.8 %.

The proposed U-Net

SGA

performed signiﬁcantly bet-

ter than baseline U-Net when considering only the

bone regions (column ”Bone Area” in Table 1). With

327 ± 46 HU and 180162 ± 56182 HU

, over 45%

reduction of MAE

bone

and around 66% reduction of

MSE

bone

have been achieved. This improvement is

the expected behavior since the SGA mechanism has

been formulated in a such way, that it pays more atten-

tion to bone regions from ground truth images. How-

ever, U-Net

SGA

’s performance is worse than base-

line when considering the overall MAE and MSE

metrics (columns ”Entire Image” and ”Head Area”

in Table 1). This could be due to the suboptimal

choice of α when calculating the total loss function

of U-Net

SGA

. Although U-Net

E-SGA

was not able

to improve bone metrics as drastically as U-Net

SGA

values still appeared to be better than for the base-

line architecture. Regarding the averaged metrics for

the bone area, U-Net

E-SGA

yield 454 ± 88 HU and

345229 ± 112172 HU

for MAE and MSE, which is

around 141 HU and 187466 HU

gain over the base-

line U-Net implementation. In contrast to the net-

work with SGA, U-Net

E-SGA

was able to pay atten-

tion to bones, however, was still able to retain the im-

age quality for other parts of the image too. MSE

and MAE values for entire images and head areas are

in the same range as for the baseline U-Net. Exem-

plary pseudo-CT generation results for Patient 007

(slice #1) from baseline U-Net, U-Net

SGA

and from

U-Net

E-SGA

are shown in Figure 7 (b-d). Thus,

with regard to the proposed two segmentation guided

mechanisms, U-Net

E-SGA

seems to yield better perfor-

mance than baseline U-Net and U-Net

SGA

. The same

conclusion can be drawn from the difference images,

which are shown in Figure 8 (ﬁrst row).

The baseline conditional Wasserstein GAN per-

formed slightly worse than the baseline U-Net when

comparing the entire pCTs, however, the generated

images are looking qualitatively better. As expected

Table 1: Averaged MAE, MSE, PSNR and SSIM metrics for baselines and segmentation guided networks. While MAE and

MSE values (for entire images, head areas and bone areas) are given in HU and HU

, PSNR and SSIM values are reported in

dB and %, respectively.

Entire Image Head Area Bone Area

Name MAE MSE MAE MSE MAE MSE PSNR SSIM

U-Net 101±35 69139±27664 180±30 131393±38343 595±120 532695±198330 24.3±1.9 79.6±6.8

U-Net

SGA

128±34 83695±28792 257±42 192630±45684 327±46 180162±56182 23.2±1.5 77.5±6.2

U-Net

E-SGA

108±35 67528±27680 191±32 138309±37912 454±88 345229±112172 24.3±1.8 79.3±6.6

cWGAN 113±37 80507±31839 202±34 154101±42147 493±90 408417±131774 23.7±1.9 77.2±7.3

cWGAN

SGA

117±38 81997±31843 206±34 154975±40802 485±95 394859±129604 23.6±1.9 74.8±7.2

cWGAN

E-SGA

110±43 76425±35158 195±39 144978±44869 473±101 377988±133286 24.0±2.2 77.2±8.1

(a) MR (b) U-Net (c) U-Net

SGA

(d) U-Net

E-SGA

(e) CT

(f) cWGAN (g) cWGAN

SGA

(h) cWGAN

E-SGA

Figure 6: Exemplary MR, CT and MRI-based pseudo-CTs from U-Nets (b-d) and cWGANs (f-h) for Patient 007 (slice #1).

BIOIMAGING 2022 - 9th International Conference on Bioimaging

138

Figure 7: Differences images between CTs and correspond-

ing pCTs for Patient 007 (slice #1). From upper left to

bottom right: U-Net, U-Net

SGA

, U-Net

E-SGA

, cWGAN,

cWGAN

SGA

and cWGAN

E-SGA

. Red color represents un-

derestimated regions, while blue one highlights overesti-

mated areas.

and as it can be seen by comparing (b) and (f) im-

ages from Figure 7, cWGAN based approach was able

to preserve more anatomical bone structures and to

generate more realistic pCT images, due to the assis-

tance of an additional critic network. While consid-

ering only ROIs, it improved MAE

bone

and MSE

bone

metrics. Thus, cWGAN yields 493 ± 90 HU and

408417 ± 131774 HU

, which is around 102 HU

and 124278 HU

gain over the baseline U-Net. With

485 ± 95 HU and 394859 ± 129604 HU

for

bone regions, conditional WGAN with SGA per-

formed slightly better than the baseline cWGAN,

while its extended versions improved the metrics even

further. Considering MAE

bone

and MSE

bone

met-

rics, cWGAN

E-SGA

yield approximately 20 HU and

30429 HU

improvement over the baseline cWGAN.

Averaged SSIM values for cWGANs are in general

slightly lower than for U-Nets, due to attempts of gen-

erative models to synthesize the patient’s table. This

can be conﬁrmed by inspecting the difference images

in Figure 8 (second row), where the table partially ap-

pears, although it does not exist in the corresponding

ground truth image from Figure 7. The same reason

lies behind the slightly higher errors for whole im-

ages (compared to the baseline U-Net and U-net

SGA

MAE

head

and MSE

head

values correlate with their cor-

responding metrics when considering the entire pCT

images. Thus, comparing the obtained results to the

desired GTs, signiﬁcant qualitative and quantitative

improvements for bone regions in favor of the E-SGA

approach can be observed. It is worth mentioning

that cWGAN

SGA

delivered slightly better overall re-

sults when compared to the corresponding baseline,

whereas U-Net

SGA

was better only for bone regions.

We argue that this was mainly achieved due to the

contribution of the additional critic network which

did not allow the corresponding generator to pay too

much attention to the regions of interest.

5 CONCLUSION

In this work, we present 2D MRI-based pseudo-CT

generation approaches with the additional segmenta-

tion guided attention mechanisms. We deﬁned our to-

tal loss functions as a combination of global and local

loss terms, whereas the second one enforces networks

to pay particular attention to bone areas while gener-

ating pCT images. From the evaluation results, we

observe that segmentation guided approaches yield

improvements compared to baseline U-Net and con-

ditional Wasserstein GAN architectures. As a re-

sult, more precise µ-maps for attenuation correction

of PET image in PET/MR systems could be derived.

Despite the apparent simplicity, segmentation guided

attention allows networks to focus more on speciﬁc

regions of interest, and as a consequence, achieve

better performances for them. We believe that the

proposed segmentation guidance can also be helpful

when training cycle GAN-based architectures. We are

currently in process of investigating this hypothesis.

REFERENCES

Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-

stein generative adversarial networks. In Interna-

tional conference on machine learning, pages 214–

223. PMLR.

Berker, Y., Franke, J., Salomon, A., Palmowski, M.,

Donker, H. C., Temur, Y., Mottaghy, F. M., Kuhl,

C., Izquierdo-Garcia, D., Fayad, Z. A., et al.

(2012). MRI-based attenuation correction for hy-

brid PET/MRI systems: a 4-class tissue segmen-

tation technique using a combined ultrashort-echo-

time/dixon mri sequence. Journal of nuclear

medicine, 53(5):796–804.

Beyer, T., Townsend, D. W., Brun, T., Kinahan, P. E., Char-

ron, M., Roddy, R., Jerin, J., Young, J., Byars, L.,

Nutt, R., et al. (2000). A combined PET/CT scanner

for clinical oncology. Journal of nuclear medicine,

41(8):1369–1379.

Brady, Z., Taylor, M., Haynes, M., Whitaker, M., Mullen,

A., Clews, L., Partridge, M., Hicks, R., and Trapp, J.

(2008). The clinical application of PET/CT: a contem-

porary review. Australasian Physics & Engineering

Sciences in Medicine, 31(2):90–109.

Burgos, N., Cardoso, M. J., Thielemans, K., Modat, M.,

Pedemonte, S., Dickson, J., Barnes, A., Ahmed, R.,

Mahoney, C. J., Schott, J. M., et al. (2014). Atten-

uation correction synthesis for hybrid PET-MR scan-

ners: application to brain studies. IEEE transactions

on medical imaging, 33(12):2332–2341.

Buzug, T. M. (2009). Computed tomography: from photon

statistics to modern cone-beam CT.

Chougule, V., Mulay, A., and Ahuja, B. (2018). Clini-

cal case study: spine modeling for minimum invasive

Improved MRI-based Pseudo-CT Synthesis via Segmentation Guided Attention Networks

139

spine surgeries (MISS) using rapid prototyping. Bone

(CT), 226:3071.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. Advances

in neural information processing systems, 27.

Han, X. (2017). MR-based synthetic CT generation using a

deep convolutional neural network method. Medical

physics, 44(4):1408–1419.

Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., and

Hochreiter, S. (2017). Gans trained by a two time-

scale update rule converge to a local nash equilibrium.

Advances in neural information processing systems,

30.

Keereman, V., Mollet, P., Berker, Y., Schulz, V., and Van-

denberghe, S. (2013). Challenges and current methods

for attenuation correction in PET/MR. Magnetic Res-

onance Materials in Physics, Biology and Medicine,

26(1):81–98.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Leynes, A. P., Yang, J., Wiesinger, F., Kaushik, S. S.,

Shanbhag, D. D., Seo, Y., Hope, T. A., and Larson,

P. E. (2018). Zero-echo-time and dixon deep pseudo-

ct (ZeDD CT): direct generation of pseudo-CT images

for pelvic PET/MRI attenuation correction using deep

convolutional neural networks with multiparametric

MRI. Journal of Nuclear Medicine, 59(5):852–858.

Liu, F., Jang, H., Kijowski, R., Bradshaw, T., and McMil-

lan, A. B. (2017). Deep learning MR imaging–based

attenuation correction for PET/MR imaging. Radiol-

ogy, 286(2):676–684.

Lowekamp, B. C., Chen, D. T., Ib

nez, L., and Blezek, D.

(2013). The design of SimpleITK. Frontiers in neu-

roinformatics, 7:45.

Mattes, D., Haynor, D. R., Vesselle, H., Lewellen, T. K.,

and Eubank, W. (2003). PET-CT image registration in

the chest using free-form deformations. IEEE trans-

actions on medical imaging, 22(1):120–128.

Mecheter, I., Alic, L., Abbod, M., Amira, A., and Ji, J.

(2020). MR image-based attenuation correction of

brain PET imaging: Review of literature on machine

learning approaches for segmentation. Journal of Dig-

ital Imaging, 33(5):1224.

Nie, D., Cao, X., Gao, Y., Wang, L., and Shen, D. (2016).

Estimating CT image from MRI data using 3D fully

convolutional networks. In Deep Learning and Data

Labeling for Medical Applications, pages 170–178.

Springer.

Nie, D., Trullo, R., Lian, J., Petitjean, C., Ruan, S., Wang,

Q., and Shen, D. (2017). Medical image synthesis

with context-aware generative adversarial networks.

In International conference on medical image comput-

ing and computer-assisted intervention, pages 417–

425. Springer.

Ollinger, J. M. and Fessler, J. A. (1997). Positron-

emission tomography. Ieee signal processing maga-

zine, 14(1):43–55.

Paans, A. M. (2006). Positron emission tomography.

Paulus, D. H., Quick, H. H., Geppert, C., Fenchel, M.,

Zhan, Y., Hermosillo, G., Faul, D., Boada, F.,

Friedman, K. P., and Koesters, T. (2015). Whole-

body PET/MR imaging: quantitative evaluation of a

novel model-based MR attenuation correction method

including bone. Journal of Nuclear Medicine,

56(7):1061–1066.

Qi, M., Li, Y., Wu, A., Jia, Q., Li, B., Sun, W., Dai, Z., Lu,

X., Zhou, L., Deng, X., et al. (2020). Multi-sequence

MR image-based synthetic CT generation using a gen-

erative adversarial network for head and neck mri-

only radiotherapy. Medical physics, 47(4):1880–1894.

Radford, A., Metz, L., and Chintala, S. (2015). Unsu-

pervised representation learning with deep convolu-

tional generative adversarial networks. arXiv preprint

arXiv:1511.06434.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In International Conference on Medical

image computing and computer-assisted intervention,

pages 234–241. Springer.

Torrado-Carvajal, A., Vera-Olmos, J., Izquierdo-Garcia, D.,

Catalano, O. A., Morales, M. A., Margolin, J., Sori-

celli, A., Salvatore, M., Malpica, N., and Catana,

C. (2019). Dixon-VIBE deep learning (DIVIDE)

pseudo-CT synthesis for pelvis PET/MR attenuation

correction. Journal of nuclear medicine, 60(3):429–

435.

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.

(2004). Image quality assessment: from error visi-

bility to structural similarity. IEEE transactions on

image processing, 13(4):600–612.

West, J., Fitzpatrick, J. M., Wang, M. Y., Dawant, B. M.,

Maurer Jr, C. R., Kessler, R. M., Maciunas, R. J., Bar-

illot, C., Lemoine, D., Collignon, A., et al. (1997).

Comparison and evaluation of retrospective inter-

modality brain image registration techniques. Journal

of computer assisted tomography, 21(4):554–568.

Wolterink, J. M., Dinkla, A. M., Savenije, M. H., Seevinck,

P. R., van den Berg, C. A., and I

sgum, I. (2017). Deep

mr to ct synthesis using unpaired data. In Interna-

tional Workshop on Simulation and Synthesis in Med-

ical Imaging, pages 14–23. Springer.

Wu, J., Huang, Z., Thoma, J., Acharya, D., and Van Gool, L.

(2018). Wasserstein divergence for gans. In Proceed-

ings of the European Conference on Computer Vision

(ECCV), pages 653–668.

Yaniv, Z., Lowekamp, B. C., Johnson, H. J., and Beare, R.

(2018). SimpleITK image-analysis notebooks: a col-

laborative environment for education and reproducible

research. Journal of digital imaging, 31(3):290–303.

Zhu, J.-Y., Park, T., Isola, P., and Efros, A. A. (2017).

Unpaired image-to-image translation using cycle-

consistent adversarial networks. In Proceedings of

the IEEE international conference on computer vi-

sion, pages 2223–2232.

BIOIMAGING 2022 - 9th International Conference on Bioimaging

140