LiDAR Dataset Distillation within Bayesian Active Learning Framework

Understanding the Effect of Data Augmentation

Anh Ngoc Phuong Duong, Alexandre Almin, Léo Lemarié and B. Ravi Kiran

Machine Learning, Navya, France

Keywords:

Active Learning, Point Clouds, Semantic Segmentation, Data Augmentation, Label Efﬁciency, Dataset

Distillation.

Abstract:

Autonomous driving (AD) datasets have progressively grown in size in the past few years to enable better

deep representation learning. Active learning (AL) has re-gained attention recently to address reduction of

annotation costs and dataset size. AL has remained relatively unexplored for AD datasets, especially on

point cloud data from LiDARs. This paper performs a principled evaluation of AL based dataset distillation

on (1/4th) of the large Semantic-KITTI dataset. Further on, the gains in model performance due to data

augmentation (DA) are demonstrated across different subsets of the AL loop. We also demonstrate how DA

improves the selection of informative samples to annotate. We observe that data augmentation achieves full

dataset accuracy using only 60% of samples from the selected dataset conﬁguration. This provides faster

training time and subsequent gains in annotation costs.

1 INTRODUCTION

Autonomous driving has witnessed a recent increase

in research and industry-based large-scale datasets

in the point cloud domain such as Semantic-KITTI

(Behley et al., 2019) and Nuscenes (Caesar et al.,

2020). These datasets enable diverse driving scenar-

ios and lighting conditions, along with variation in

the poses of on-road obstacles. The collection pro-

cedure frequently involves recording temporal seg-

ments with key frames that are manually selected.

However, these large-scale point clouds datasets have

high redundancy, especially in training Deep Neu-

ral Network (DNN) architectures. This is mainly

due to the temporal correlation between point clouds

scans, the similar urban environments and the sym-

metries in the driving environment (driving in oppo-

site directions at the same location). Hence, data re-

dundancy can be seen as the similarity between any

pair of point clouds resulting from geometric trans-

formations as a consequence of ego-vehicle move-

ment along with changes in the environment. Data

augmentations (DA) are transformations on the input

samples that enable DNNs to learn invariances and/or

equivariances to said transformations (Anselmi et al.,

2016). DA provides a natural way to model the geo-

https://orcid.org/0000-0002-8641-7530

metric transformations to point clouds in large-scale

datasets due to ego-motion of the vehicle.

Active Learning (AL) is an established ﬁeld that

aims at interactively annotating unlabeled samples

guided by a human expert in the loop. With existing

large datasets, AL could be used to ﬁnd a core-subset

with equivalent performance w.r.t a full dataset. This

involves iteratively selecting subsets of the dataset

that greedily maximises model performance. As a

consequence, AL helps reduce annotation costs, while

preserving high accuracy. AL distills an existing

dataset to a smaller subset, thus enabling faster train-

ing times in production. It uses uncertainty scores ob-

tained from predictions of a model or an ensemble to

select informative new samples to be annotated by a

human oracle. Uncertainty-based sampling is a well-

established component of AL frameworks today (Set-

tles, 2009).

This paper studies the dataset distillation or re-

duction of redundant samples on point clouds from

the Semantic-KITTI dataset. We note that Semantic-

KITTI with 23201 point cloud samples was gener-

ated by continuous motion of the ego-vehicle in ur-

ban environments in Germany. After testing differ-

ent options to evaluate uncertainty, we show that DA

techniques, if carefully chosen and applied, can im-

prove the selection of informative samples in an AL

pipeline. Contributions of the current study include:

Duong, A., Almin, A., Lemarié, L. and Kiran, B.

LiDAR Dataset Distillation within Bayesian Active Learning Framework Understanding the Effect of Data Augmentation.

DOI: 10.5220/0010860800003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

159-167

ISBN: 978-989-758-555-5; ISSN: 2184-4321

159

1. An evaluation of Bayesian AL methods on a large

point cloud dataset for semantic segmentation.

2. Evaluating existing heuristic function, BALD

(Houlsby et al., 2011) for the semantic seg-

mentation task within a standardized AL library

(Atighehchian et al., 2019)(Atighehchian et al.,

2020). The BALD heuristic used in conjunction

with DA techniques shows a high labeling efﬁ-

ciency on a 6000 sample subset of the Semantic-

KITTI dataset.

3. Key ablation studies on informativeness of dataset

samples vs data augmented samples that reﬂect

how DA affects the quality of AL based sam-

pling/acquisition function.

4. A competitive compression over the baseline ac-

curacy while using only 60% of the dataset under

study.

Like many previous studies on AL, we do not explic-

itly quantify the amount of redundancy in the datasets

and purely determine the trade-off of model perfor-

mance with smaller subsets w.r.t the original dataset.

2 RELATED WORK

The reader can ﬁnd details on the major approaches

to AL in the following articles: uncertainty-based

approaches (Gal et al., 2017), diversity-based ap-

proaches (Sener and Savarese, 2018), and a combi-

nation of the two (Kirsch et al., 2019)(Ash et al.,

2020). Most of these studies were aimed at classi-

ﬁcation tasks. Adapting diversity-based frameworks

usually applied to a classiﬁcation, such as (Sener and

Savarese, 2018), (Kirsch et al., 2019), (Ash et al.,

2020), to the point cloud semantic segmentation task

is computationally costly. This is due to the dense out-

put tensor from DNNs with a class probability vector

per pixel, while the output for the classiﬁcation task

is a single class probability vector per image. Var-

ious authors in (Kendall and Gal, 2017)(Golestaneh

and Kitani, 2020), Camvid (Brostow et al., 2009) and

Cityscapes(Cordts et al., 2016) propose uncertainty-

based methods for image and video segmentation.

However, very few AL studies are conducted for point

cloud semantic segmentation. Authors (Wu et al.,

2021) evaluate uncertainty and diversity-based ap-

proaches for point cloud semantic segmentation. This

study is the closest to our current work.

Authors (Birodkar et al., 2019) demonstrate the

existence of redundancy in CIFAR-10 and ImageNet

datasets, using agglomerative clustering in a seman-

tic space to ﬁnd redundant groups of samples. As

shown by (Chitta et al., 2019), techniques like en-

semble active learning can reduce data redundancy

signiﬁcantly on image classiﬁcation tasks. Authors

(Beck et al., 2021) show that diversity-based methods

are more robust compared to standalone uncertainty

methods against highly redundant data. Though au-

thors suggest that with the use of DA, there is no sig-

niﬁcant advantage of diversity over uncertainty sam-

pling. Nevertheless, the uncertainty was not quanti-

ﬁed in the original studied datasets, but were artiﬁ-

cially added through sample duplication. This does

not represent real word correlation between sample

images or point clouds. Authors (Hong et al., 2020)

uses DA techniques while adding the consistency loss

within a semi-supervised learning setup for image

classiﬁcation task.

3 METHOD

In this section, we describe our setup used to eval-

uate the performances of AL for point cloud seman-

tic segmentation, including dataset setup, DNN model

architecture, the chosen DA techniques, and most im-

portantly the setup on our AL experiments.

Dataset. Although there are many datasets for im-

age semantic segmentation, few are dedicated to point

clouds. The Semantic-KITTI dataset & benchmark

by authors (Behley et al., 2019) provides more than

43000 point clouds of 22 annotated sequences, ac-

quired with a Velodyne HDL-64 LiDAR. Semantic-

KITTI is by far the most extensive dataset with se-

quential information. All available annotated point

clouds, from sequences 00 to 10, for a total of 23201

point clouds, are later randomly sampled, and used

for our experiments.

Model. Among different deep learning models

available, we choose SqueezeSegV2 (Wu et al.,

2018), a spherical-projection-based semantic segmen-

tation model, which performs well with a fast infer-

ence speed compared to other architectures, thus re-

duces training and uncertainty computation time. We

apply spherical projection (Wu et al., 2018) on point

clouds to obtain a 2D range image as an input for the

network shown in ﬁgure 1. To simulate Monte Carlo

(MC) sampling for uncertainty estimation (Gal and

Ghahramani, 2016), a 2D Dropout layer is added right

before the last convolutional layer of SqueezeSegV2

(Wu et al., 2018) with a probability of 0.2 and turned

on at test time.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

160

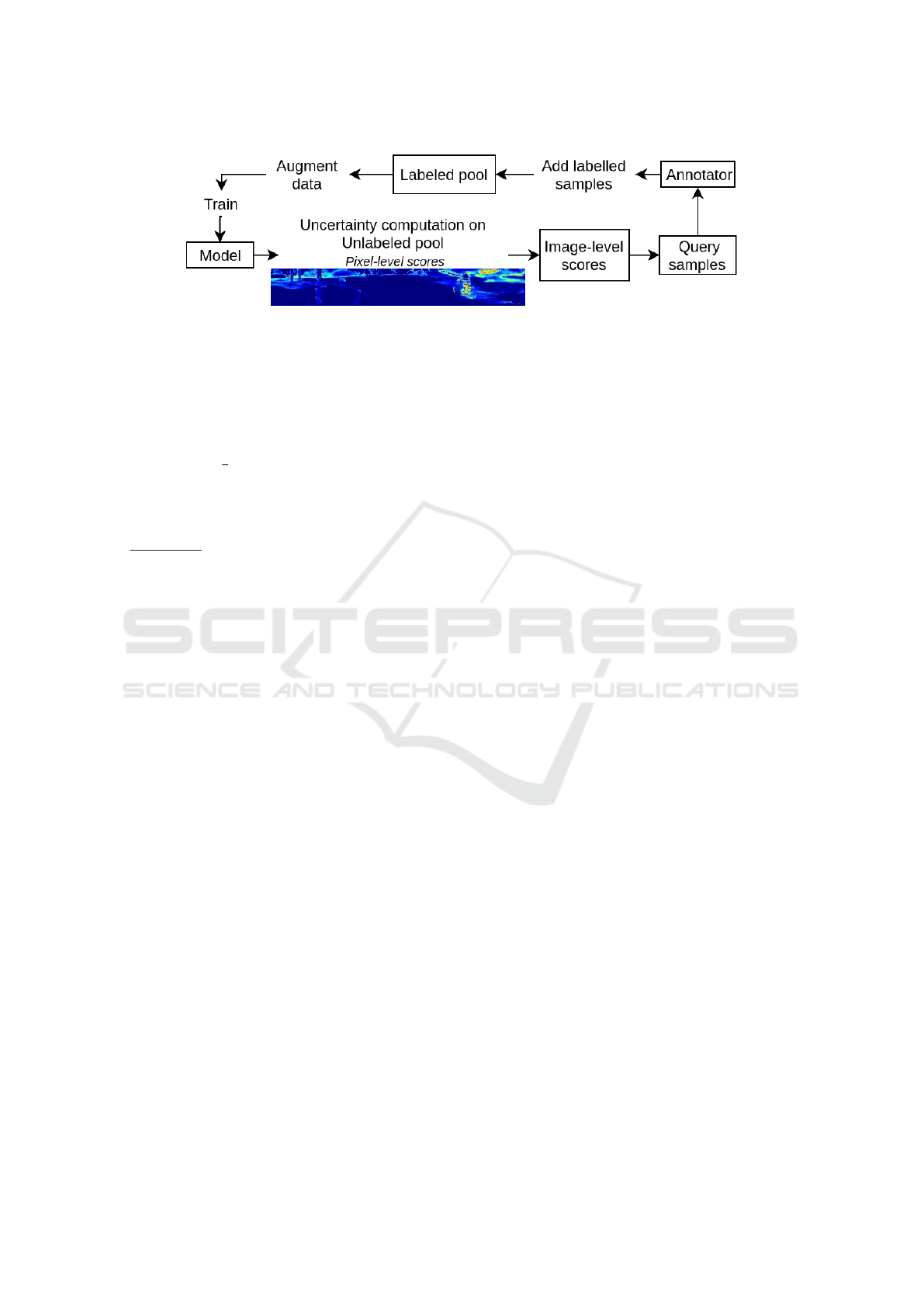
Figure 1: Global ﬂow of active learning on range images from point clouds using uncertainty methods.

Spherical Projection. Rangenet++ architectures by

authors (Milioto et al., 2019) use range image based

spherical coordinate representations of point clouds

to enable the use of 2D-convolution kernels. The re-

lationship between range image and LiDAR coordi-

nates is the following:







[1 − arctan(y,x)π

−1

] × w

[1 − (arcsin(z × r

−1

) + f

) × f

−1

] × h



where (u,v) are image coordinates, (h,w) the height

and width of the desired range image, f = f

down

, is the vertical f ov of the sensor, and r =

+ y

+ z

, range measurement of each point. The

input to the DNNs used in our study are images of size

W × H × 4, with spatial dimensions W,H determined

by the FOV and angular resolution, and 4 channels

containing the x,y coordinates of points, r range or

depth to each point, i intensity or remission value for

each point.

Bayesian Uncertainty-based Approach of AL. In

a supervised learning setup, given a dataset D :=

{(x

),(x

),...,(x

)} ⊂ X × Y , the DNN is

seen as a high dimensional function f

: X → Y with

model parameters ω. A simple classiﬁer maps each

input x to outcomes y. A good classiﬁer minimizes

the empirical risk l : Y × Y → R, which is deﬁned

with the expectation R

emp

( f ) := P

X,Y

[Y 6= f (X)]. The

optimal classiﬁer is one that minimizes the above risk.

Thus, the classiﬁer’s loss does not explicitly refer to

sample-wise uncertainty but rather to obtain a func-

tion which makes good predictions on average.

Predictive uncertainty (Hüllermeier and Waege-

man, 2021) estimates uncertainty over each prediction

ˆy = f

(x) = p(y|x) given its input x. A model’s pre-

dictive uncertainty is a combination of the aleatoric

uncertainty, irreducible uncertainty due to intrinsic

randomness of underlying process, and the epistemic

uncertainty, reducible uncertainty caused due to miss-

ing knowledge, and could be reduced given additional

information.

Authors (Gal and Ghahramani, 2016) propose

generation of MC samples for a given model and in-

put, by activating standard dropout layers at inference

time. This provides an uncertainty estimation by sam-

pling different values of DNN weights. Readers can

consult work by (Gawlikowski et al., 2021) for uncer-

tainty estimation in DNNs.

Key Components of AL Framework. We shall use

the following terminologies to describe our AL train-

ing setup.

1. Labeled dataset D = {(x

)}

i=1

where x

∈ W ×

H × 4 are range images with 4 input channels,

W,H are spatial dimensions, and y

∈ W × H ×C

are one-hot encoded ground truth with C classes.

The output of the DNN model is distinguished

from the ground truth as ˆy

with the same dimen-

sions.

2. Labeled pool L ⊂ D and a unlabeled pool U ⊂

D considered as a data with/without any ground-

truth, where at any AL-step L∪U = D, the subsets

are disjoint and restore the full dataset.

3. Query size B, also called a budget, to ﬁx the num-

ber of unlabeled samples selected for labeling

4. Acquisition function, known as heuristic, provid-

ing a score for each pixel given the output ˆy

of the

DNN model, f : R

W ×H×C

→ R

W ×H

5. Including the usage of MC iterations the output

of the DNN model could provide several outputs

given the same model and input, ˆy

∈ W ×H ×C×

T where T refers to the number of MC iterations.

6. Subset model f

is the model trained on labeled

subset L

7. Aggregation function a : R

W ×H×C×T

→ R

is a

function that aggregates heuristic scores across all

pixels in the input image into a positive scalar

value, which is used to rank samples in the un-

labeled pool.

Heuristic. Heuristic functions are transformations

over the model output probabilities p(y|x) that deﬁne

uncertainty-based metrics to rank and select informa-

tive examples from the unlabeled pool at each AL-

LiDAR Dataset Distillation within Bayesian Active Learning Framework Understanding the Effect of Data Augmentation

161

step. We used the following uncertainty-based met-

rics in our experiments:

1. Certainty heuristic measures the least conﬁdent

class probability across the highest conﬁdent predic-

tion over different MC iterations :

min

max

{ f

(x)}

i=1

where T is the number of MC iterations.

2. Entropy heuristic measures the entropy over

predicted class probabilities

H(y|x,L) = −

∑

p(y = c|x,L)log(p(y = c|x,L))

3. Variance computes the variance of predictions

from model parameters for each class, then averages

all variances from all classes to obtain the aggregated

score for a sample in classiﬁcation, or a pixel in im-

age semantic segmentation. The heuristic selects the

samples having the highest aggregated scores. The

variance for each class σ

(p(y = c|x, L)) is:

∑

i=1

(p(y = c|x, w

|L) − p(y = c|x,L))

(1)

4. BALD (Houlsby et al., 2011) selects sam-

ples maximizing information gain between the pre-

dictions from model parameters, using MC Itera-

tions. The expectation in the equation below is per-

formed over model parameters ω. The information

gain I(y,ω|x,L) is given by

H(y|x,L) − E

p(ω|L)

(H(y|x,ω)) (2)

Data Augmentations on Range Images. We apply

DA directly on the range image projection. We se-

lected known effective transformations: (a) Random

dropout mask on range image and its target by cre-

ating a binary mask with uniform dropout probabil-

ity p ∈ [0.1,0.5]; (b) CoarseDropout which randomly

masks out rectangular regions by applying with the

following parameters: max_height: 16, max_holes:

5, max_width: 64, min_height: 1, min_holes: 2,

min_width: 1; (c) Gaussian noise on depth of range

image by with the following parameters µ = 0,σ

∈

[0.05,0.1] ; (d) Gaussian noise on remission chan-

nel of range image with the following parameters:

µ = 0,σ

∈ [0.5,1.0]; (e) Random cyclic shift on range

image (corresponding to rotations on point cloud) and

its target to left and right, from 0 to 22.5 degrees

around the center; (f) Instance Cut Paste randomly

copying and pasting instances from one scan to an-

other within a batch. More description and experi-

ment setup of these transformations are in ﬁgure 2.

Evaluation Metrics. To evaluate the performance

of our experiments we are using the following met-

rics:

1. MeanIoU Intersection over Union (IoU) (Song

et al., 2016), known as Jaccard index, measures the

number of common pixels between the target and pre-

diction masks over the total number of pixels. Mean-

IoU (mIoU) is mean value of IoU over all classes.

Given T P

, FP

, and FN

as the number of true pos-

itive, false positive, and false negative predictions for

class c, and C is the number of classes, MeanIoU can

be formulated as

∑

c=1

T P

+ FP

+ FN

(3)

2. Labeling efﬁciency Authors (Beck et al.,

2021) use the labeling efﬁciency (LE) to compare

the amount of data needed among different sampling

techniques with respect to a baseline. In our ex-

periments, instead of accuracy, we use MeanIoU as

the performance metric. Given a speciﬁc value of

MeanIoU, the labeling efﬁciency is the ratio between

the number of labeled range images, acquired by the

baseline sampling and the other sampling techniques.

LE =

labeled_others

(MeanIoU = a)

labeled_baseline

(MeanIoU = a)

(4)

The baseline method is usually the random heuristic.

Experimental Setup. As seen in ﬁgure 1 we fol-

low a Bayesian AL using MC Dropout. The heuristic

computes uncertainty scores for each pixel. To obtain

the ﬁnal score per range image, we use sum as an ag-

gregation function to combine all pixel-wise scores of

an image into a single score. At each AL step, the

unlabeled pool is ranked w.r.t the aggregated score.

A new query of samples limited to the budget size is

selected from the ranked unlabeled pool. The total

number of AL steps is indirectly deﬁned by budget

size, n

Based on this pipeline, we made AL runs across

different heuristics: random, BALD (Houlsby et al.,

2011), entropy and certainty, with and without the ap-

plication of DA applied during training time. As men-

tioned in Table 1, we only use 6000 randomly chosen

samples from Semantic-KITTI over the 23201 sam-

ples available, because every experiment is very time-

consuming, and our resources were limited. At each

training step, we reset model weights to avoid biases

in the predictions, as proven by (Beck et al., 2021).

In order to evaluate the performances of our

pipeline over each experiment, on test set we use

LE and MeanIoU as our metrics. Finally, to speed

up the training steps, we use early stopping based

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

162

(a) Random dropout mask (b) CoarseDropout of Albumentations library

(e) Random cyclic shift range image

(f) Instance Cut Paste

Figure 2: Before and after applying transformations on Semantic-KITTI. Each image corresponds to a sample such that inner

images, from top to bottom, are before and after applying transformations, and the error between them. a, b, c, d are directly

used or customized based on Albumentations library (Buslaev et al., 2020).

Table 1: Common experiments settings to each active learning (AL) run.

Data related parameters AL Hyper parameters

Range image resolution Total pool size Test pool size Init set size Budget MC Dropout AL steps Aggregation

1024x64 6000 2000 240 240 0.2 25 sum

Hyper parameters for each AL step

Max train iterations Learning rate (LR) LR decay Weight decay Batch size

Early stopping

Evaluation period Metric Patience

100000 0.01 0.99 0.0001 16 500 train mIoU 15

on the stability of training MeanIoU over patience ∗

evaluation_period iterations.

4 EXPERIMENTS

Based on previously described AL conﬁgurations, we

investigate (A) which heuristic performs the best on

semantic segmentation for point clouds, (B) the im-

pact of DA techniques on LE, (C) the informativeness

of dataset vs data augmented samples across AL steps

and (D) ﬁnally the DNN model’s stability for sample

selection.

A. Heuristic Performances on Dataset Compres-

sion. Firstly, we evaluated the performances of the

random heuristic, which is our baseline method. Each

complete AL run can achieve the goal performance

using fewer number of labeled samples (Figure 3).

BALD outperforms other heuristics, allowing the

model to converge faster with the highest LE ratio.

To focus on our study on DA, we restrict our focus

to the BALD and random heuristics for the rest of the

experiments.

B. Data Augmentation Performances on Dataset

Distillation. In this experiment, DA techniques are

applied at training time. On both random and BALD

heuristics, ﬁgure 5 shows that DA helps the model

to reach the baseline accuracy on test set faster com-

pared to runs without DA. DA provides a signiﬁcant

improvement in the early AL-steps when the subset

size are small, as one expects.

LiDAR Dataset Distillation within Bayesian Active Learning Framework Understanding the Effect of Data Augmentation

163

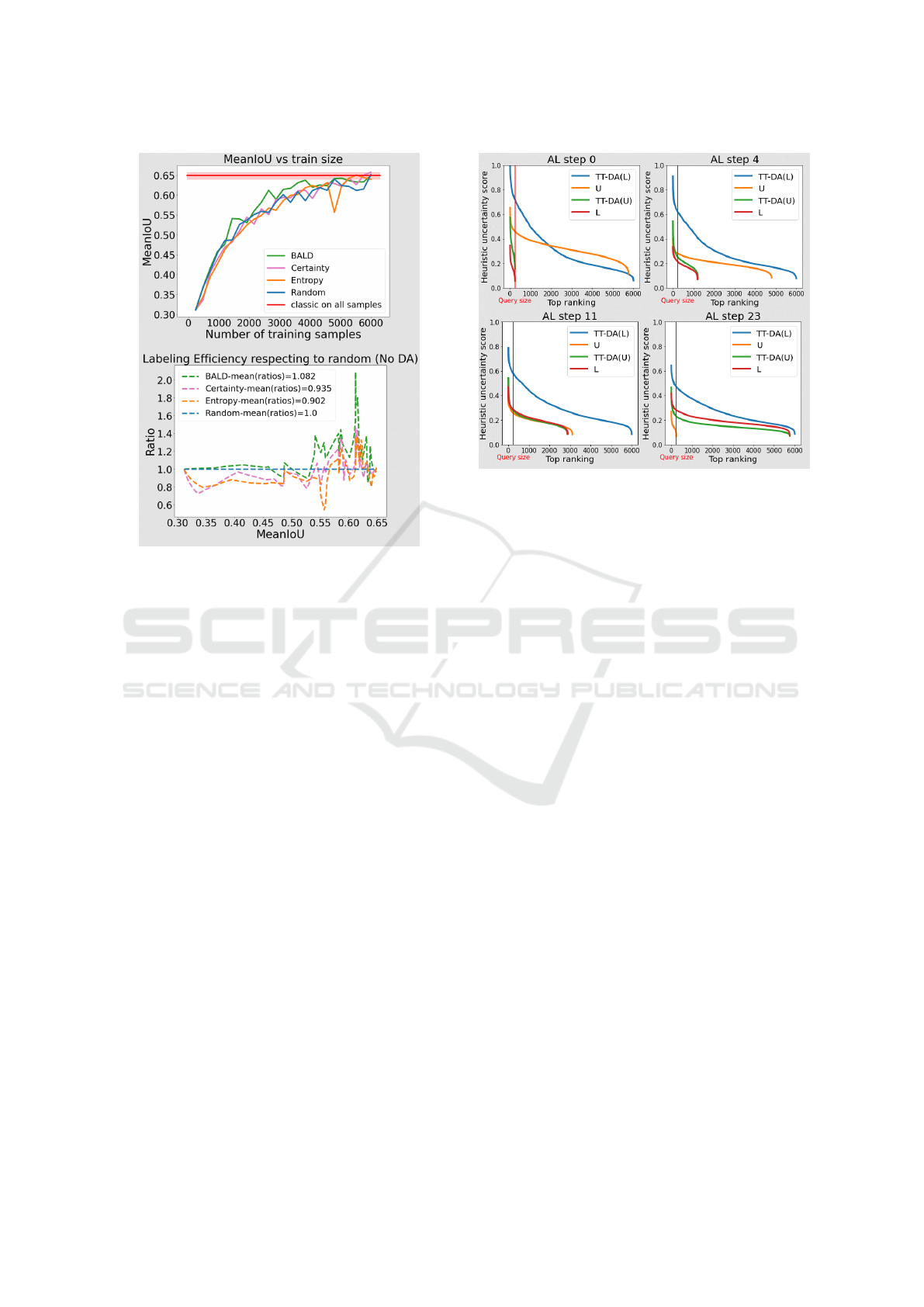
Figure 3: MeanIoU vs number of training samples and la-

beling efﬁciency evaluated on test set. Using 100% of avail-

able samples at the end of each run allows us to deﬁne an

average top performance.

DA provides better generalization by regulariza-

tion. Model output probabilities are conﬁdent for

dataset samples that are similar to DA samples from

the labeled pool. In other words, with DA, the model

tends to select samples different from the trained sam-

ples and their transformations, and thus reduces re-

dundancy. BALD with DA can achieve an important

dataset distillation, by using only 60% of the total

sample pool and still achieving baseline accuracy.

C. Heuristic Evaluation on Data Augmented Sam-

ples. In an effort to understand how data augmented

samples affect the heuristic function we evaluated the

heuristic function using models trained without DA

while predicting on test time augmented images. We

evaluated the aggregated heuristic scores for BALD

over ﬁrstly the labeled and unlabeled pools, secondly

we use Test-Time Data Augmentations (TT-DA) on

both labeled and unlabeled pool samples (Figure 4)

at different AL steps. To be clear, we used models

with no DA during training for this experiment. (TT-

DA(L)) is generated by applying DA at test time on the

Labeled pool (L) at each training epoch. (TT-DA(U))

contains augmented samples from the Unlabeled pool

(U). We ensure that the combined sizes of (TT-DA(U))

and (U) is always equal to 6000 samples.

In ﬁgure 4 the sorted aggregated scores a to the

Figure 4: Aggregated heuristic score of samples sorted by

decreasing value.

left of the red line which deﬁnes the budget of each

AL-step, we notice the following ordering : These re-

sults show that in the early AL steps:

a(T T DA(L)) > a((U )) > a(T T DA(U )) > a((L))

and in ﬁnal AL steps:

a(T T DA(L)) > a(T T DA(U)) > a((L)) > a((U))

We observe that during the initial AL step, the ag-

gregated score is low as expected on (L), which has

been used to train the model. Because the model has

been trained on only 240 samples from (L), the ag-

gregated score is very high on (U), (TT-DA(U)) and

(TT-DA(L)). As the AL step goes on, the aggregated

scores are globally decreasing, this can be explained

by the growing pool of selected data (L) used to train

the model. In the ﬁnal AL step, (U) has the smallest

uncertainty scores as the model is now well trained

and able to correctly generalize on unseen samples.

The highest aggregated scores are related to DA sam-

ples from the labeled (TT-DA(L)) and unlabeled (TT-

DA(U)) pool. This could be because the DA is pro-

viding transformed samples that are now outside the

support of the dataset distribution.

D. Model Stability and Effectiveness for Sample

Selection. In this part, we study the model stability,

based on the mean variance computed on class prob-

abilities across all MC iterations. We also measure

the model sampling effectiveness by computing mean

BALD metric.

Across all AL steps (Figure 6), models with DA

become conﬁdent in earlier AL steps (on account of

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

164

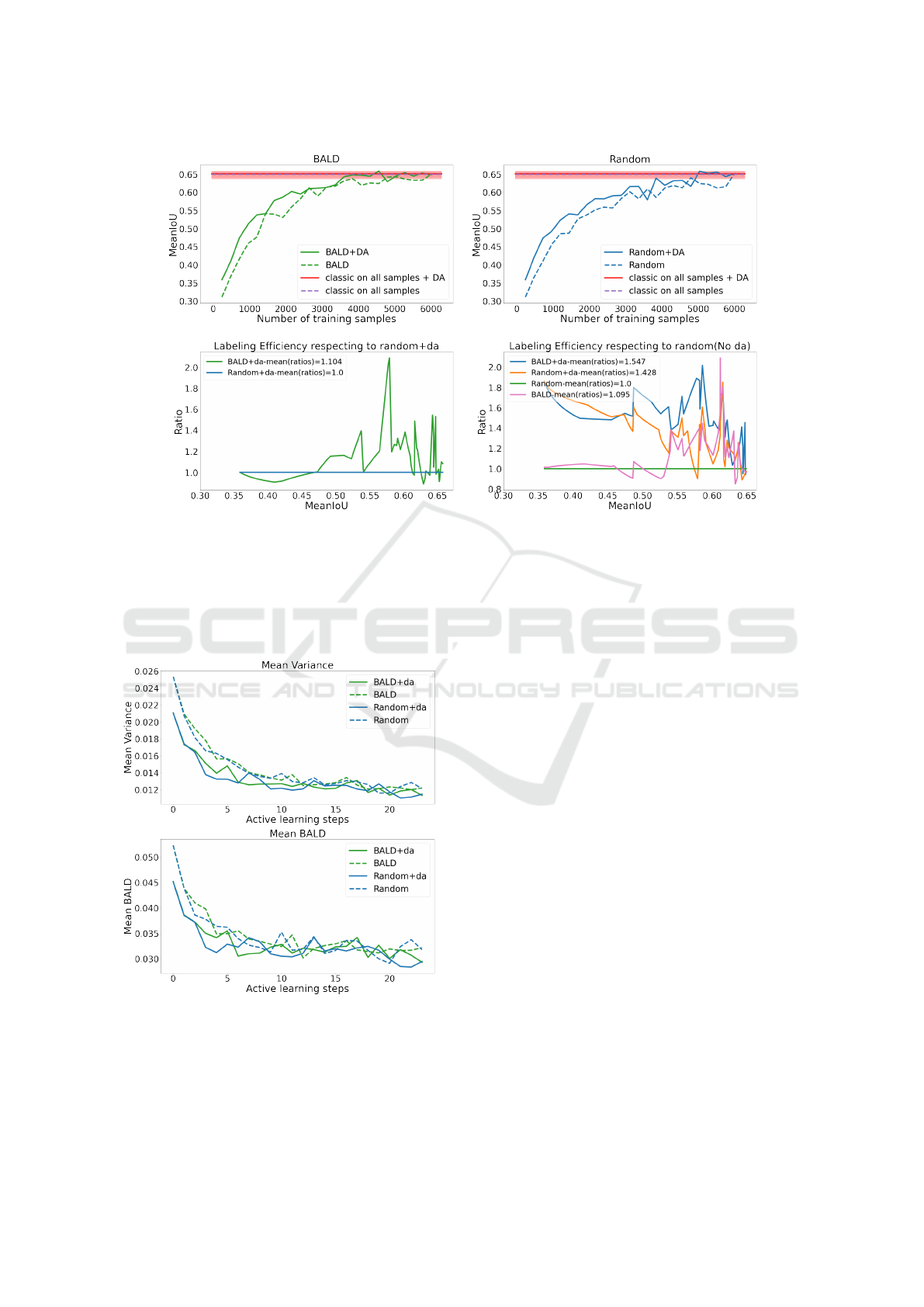
Figure 5: MeanIoU vs number of training samples and labeling efﬁciency evaluated on test set.

dropout), and are able to select samples that max-

imise information gain sooner w.r.t models without

DA. This experiment shows that DA improves the sta-

bility of models and allows a better and faster sample

selection by reducing the uncertainty of the heuristic

functions.

Figure 6: Mean of variances computed on class probabili-

ties over MC predictions (equation 1) and mean of BALD

(equation 2) for all pixels across all samples in the test set.

Key Future Challenges. Quantifying data redun-

dancy shall be investigated in our future study based

on work by authors in (Birodkar et al., 2019), (Guo

et al., 2021). To improve the heuristic function, re-

cent work (Lakshminarayanan et al., 2016) (Alling-

ham et al., 2021) on explicit ensembles shows strong

results for uncertainty computing, and (Aghdam et al.,

2019) show that adding temporal reasoning can be

beneﬁcial for data selection on object detection task.

We aim to further our study by experiment on dif-

ferent budget sizes, while testing on the complete

Semantic-KITTI dataset. Another key issue in in-

dustrial datasets is the ﬁltering or exclusion of cor-

rupted or outlier images/pointclouds from the AL

loop (Chitta et al., 2019) that frequently affect the

ranking of unlabeled pool samples. Finally, the last

but critical step in AL is the stopping criterion to ter-

minate any future input to the AL-pipeline, though

this is highly task and dataset dependent. A simple

rule can be thresholding the change in entropy over

model’s output class probabilities. It could also be

the incremental gain in the performance of the model.

A much more practical limit would be the budget of

human effort allocated to annotation.

5 CONCLUSION

Our work demonstrates the beneﬁts of data augmen-

tation in active learning (AL) for point cloud semantic

segmentation task. It conforms with results by (Beck

et al., 2021) for the image classiﬁcation task on CI-

FAR dataset. We observe that the effect of data aug-

LiDAR Dataset Distillation within Bayesian Active Learning Framework Understanding the Effect of Data Augmentation

165

mentation on BALD heuristic provides a robust and

efﬁcient heuristic for sample selection. It not only

selects more uncertain samples at each AL step, but

also improves the heuristic function’s stability, sub-

sequently leading to improved label efﬁciency. With

only 60% of the samples, we reach the same accuracy

as a supervised training with the full selected subset.

The computing time gained by training the model on

the AL-selected subset from AL w.r.t training on the

original dataset could help gain few days to weeks.

Thus data augmentation within AL frameworks have

helped in reducing annotation costs as well as reduc-

ing training time in production over large datasets.

ACKNOWLEDGEMENTS

This work was granted access to HPC resources

of [TGCC/CINES/IDRIS] under the allocation

2021- [AD011012836] made by GENCI (Grand

Equipement National de Calcul Intensif). It is also

part of the Deep Learning Segmentation (DLS)

project ﬁnanced by ADEME.

REFERENCES

Aghdam, H. H., Gonzalez-Garcia, A., Weijer, J. v. d., and

López, A. M. (2019). Active learning for deep detec-

tion neural networks. In Proceedings of the IEEE/CVF

International Conference on Computer Vision, pages

3672–3680.

Allingham, J. U., Wenzel, F., Mariet, Z. E., Mustafa,

B., Puigcerver, J., Houlsby, N., Jerfel, G., Fortuin,

V., Lakshminarayanan, B., Snoek, J., et al. (2021).

Sparse moes meet efﬁcient ensembles. arXiv preprint

arXiv:2110.03360.

Anselmi, F., Rosasco, L., and Poggio, T. (2016). On

invariance and selectivity in representation learning.

Information and Inference: A Journal of the IMA,

5(2):134–158.

Ash, J. T., Zhang, C., Krishnamurthy, A., Langford, J., and

Agarwal, A. (2020). Deep batch active learning by

diverse, uncertain gradient lower bounds.

Atighehchian, P., Branchaud-Charron, F., Freyberg, J., Par-

dinas, R., and Schell, L. (2019). Baal, a bayesian

active learning library. https://github.com/ElementAI/

baal/.

Atighehchian, P., Branchaud-Charron, F., and Lacoste, A.

(2020). Bayesian active learning for production, a sys-

tematic study and a reusable library.

Beck, N., Sivasubramanian, D., Dani, A., Ramakrishnan,

G., and Iyer, R. (2021). Effective evaluation of deep

active learning on image classiﬁcation tasks.

Behley, J., Garbade, M., Milioto, A., Quenzel, J., Behnke,

S., Stachniss, C., and Gall, J. (2019). Semantickitti:

A dataset for semantic scene understanding of lidar

sequences.

Birodkar, V., Mobahi, H., and Bengio, S. (2019). Seman-

tic redundancies in image-classiﬁcation datasets: The

10don’t need.

Brostow, G. J., Fauqueur, J., and Cipolla, R. (2009). Seman-

tic object classes in video: A high-deﬁnition ground

truth database. Pattern Recognit. Lett., 30:88–97.

Buslaev, A., Iglovikov, V. I., Khvedchenya, E., Parinov, A.,

Druzhinin, M., and Kalinin, A. A. (2020). Albumen-

tations: Fast and ﬂexible image augmentations. Infor-

mation, 11(2).

Caesar, H., Bankiti, V., Lang, A. H., Vora, S., Liong, V. E.,

Xu, Q., Krishnan, A., Pan, Y., Baldan, G., and Bei-

jbom, O. (2020). nuscenes: A multimodal dataset for

autonomous driving.

Chitta, K., Alvarez, J. M., Haussmann, E., and Farabet, C.

(2019). Training data subset search with ensemble ac-

tive learning. arXiv preprint arXiv:1905.12737.

Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler,

M., Benenson, R., Franke, U., Roth, S., and Schiele,

B. (2016). The cityscapes dataset for semantic urban

scene understanding.

Gal, Y. and Ghahramani, Z. (2016). Dropout as a bayesian

approximation: Representing model uncertainty in

deep learning.

Gal, Y., Islam, R., and Ghahramani, Z. (2017). Deep

bayesian active learning with image data.

Gawlikowski, J., Tassi, C. R. N., Ali, M., Lee, J., Humt, M.,

Feng, J., Kruspe, A., Triebel, R., Jung, P., Roscher, R.,

Shahzad, M., Yang, W., Bamler, R., and Zhu, X. X.

(2021). A survey of uncertainty in deep neural net-

works.

Golestaneh, S. A. and Kitani, K. M. (2020). Importance of

self-consistency in active learning for semantic seg-

mentation.

Guo, J., Pang, Z., Sun, W., Li, S., and Chen, Y. (2021).

Redundancy removal adversarial active learning based

on norm online uncertainty indicator. Computational

Intelligence and Neuroscience, 2021.

Hong, S., Ha, H., Kim, J., and Choi, M.-K. (2020). Deep

active learning with augmentation-based consistency

estimation. arXiv preprint arXiv:2011.02666.

Houlsby, N., Huszár, F., Ghahramani, Z., and Lengyel, M.

(2011). Bayesian active learning for classiﬁcation and

preference learning.

Hüllermeier, E. and Waegeman, W. (2021). Aleatoric and

epistemic uncertainty in machine learning: An intro-

duction to concepts and methods. Machine Learning,

110(3):457–506.

Kendall, A. and Gal, Y. (2017). What uncertainties do we

need in bayesian deep learning for computer vision?

Kirsch, A., van Amersfoort, J., and Gal, Y. (2019). Batch-

bald: Efﬁcient and diverse batch acquisition for deep

bayesian active learning.

Lakshminarayanan, B., Pritzel, A., and Blundell, C.

(2016). Simple and scalable predictive uncertainty

estimation using deep ensembles. arXiv preprint

arXiv:1612.01474.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

166

Milioto, A., Vizzo, I., Behley, J., and Stachniss, C. (2019).

Rangenet++: Fast and accurate lidar semantic seg-

mentation. In 2019 IEEE/RSJ International Confer-

ence on Intelligent Robots and Systems (IROS), pages

4213–4220. IEEE.

Sener, O. and Savarese, S. (2018). Active learning for con-

volutional neural networks: A core-set approach.

Settles, B. (2009). Active learning literature survey.

Song, S., Yu, F., Zeng, A., Chang, A. X., Savva, M., and

Funkhouser, T. (2016). Semantic scene completion

from a single depth image.

Wu, B., Zhou, X., Zhao, S., Yue, X., and Keutzer, K. (2018).

Squeezesegv2: Improved model structure and unsu-

pervised domain adaptation for road-object segmenta-

tion from a lidar point cloud.

Wu, T.-H., Liu, Y.-C., Huang, Y.-K., Lee, H.-Y., Su, H.-

T., Huang, P.-C., and Hsu, W. H. (2021). Redal:

Region-based and diversity-aware active learning for

point cloud semantic segmentation.

LiDAR Dataset Distillation within Bayesian Active Learning Framework Understanding the Effect of Data Augmentation

167