Non-planar Surface Shape Reconstruction from a Point Cloud in the

Context of Muscles Attachments Estimation

∗

Josef Kohout

and Martin Cervenka

Faculty of Applied Sciences, University of West Bohemia, Technick

a 8, Plze

n, Czech Republic

Keywords:

Shape Reconstruction, Point Cloud, Multidimensional Scaling, Muscle Attachments Estimation, Fast March-

ing, Scalar Distance Field.

Abstract:

Knowledge of muscle attachments on bones is essential for musculoskeletal modelling. A muscle attachment

is often represented by points (in 3D) obtained by a manual digitisation system during dissection. Although

this representation sufﬁces for many purposes, sophisticated musculoskeletal models commonly require repre-

senting a muscle attachment by a surface patch or at least by a closed boundary curve. In this paper, therefore,

we propose an approach to automatic shape reconstruction from such point sets. It is based on iso-contour

extraction from a scalar ﬁeld of distances to geodetics connecting the pairs of points (from the input set) as

identiﬁed by a state-of-the-art algorithm for 2D curve reconstruction running on the input points transformed

to 2D. We investigated the performance of 15 existing state-of-the-art algorithms with public implementations

on the TLEM 2.0 data set of muscle attachments. The best results were obtained for the lenz algorithm with

just one unacceptable reconstruction when standard projection onto a best-ﬁt plane was used to transform the

input 3D points to 2D. The second algorithm was α-shape with three unacceptable reconstructions, whereas

in this case, the multidimensional scaling technique was exploited to transform the points.

1 INTRODUCTION

Shape reconstruction from a point cloud is an im-

portant computational geometry problem with vari-

ous applications in computer graphics, computer vi-

sion, medical image analysis, pattern recognition,

computer-aided design, cultural heritage, and others.

During the past decades of research, many algorithms

for shape reconstruction have been proposed. Some

work with points sampled on the boundary of an ob-

ject whose shape is to reconstruct, while others work

with the points sampled in its interior . Some algo-

rithms can deal (to some extent) with non-uniform or

sparse sampling, noise or outliers , while others as-

sume a dense uniform sampling Some focus on spe-

ciﬁc kinds of objects, e.g., CAD objects with sharp

edges or terrain data . Some require additional infor-

mation, such as normals in points . However, most

importantly, some work in 2D, processing 2D point

https://orcid.org/0000-0002-3231-2573

https://orcid.org/0000-0001-9625-1872

∗

This Work Was Supported by the Meys of the Czech

Republic, Project SGS-2019-016.

†

Corresponding author

clouds to reconstruct the outlining contour of the ob-

ject, while others work in 3D, processing 3D point

clouds to reconstruct the outlining surface of the ob-

ject. A good survey of algorithms of the former cate-

gory can be found in (Ohrhallinger et al., 2021). For

a survey of the algorithms of the latter category, we

refer the reader to (Berger et al., 2016).

In this paper, we propose a novel algorithm for re-

constructing a space curve from a set of 3D points. It

employs the multidimensional scaling technique (Cox

and Cox, 2008) to transform the points from 3D to 2D

and then uses a suitable algorithm for 2D curve recon-

struction to get the connectivity of the input points.

Motivation for our work lies in muscle attach-

ment estimation. Knowledge of muscle attachments

on bones is essential for musculoskeletal modelling.

A muscle attachment is often represented by points

obtained by a manual digitisation system during dis-

section. Due to the apparent effort associated with

this process, no wonder that the sampling is sparse.

Commonly, the points are unordered and exhibit a

non-uniform distribution because it is natural to sam-

ple the upper side of the attachment area from left to

right, then cut off the muscle-tendon unit and sample

the lower side from left to right. The points are sub-

236

Kohout, J. and Cervenka, M.

Non-planar Surface Shape Reconstruction from a Point Cloud in the Context of Muscles Attachments Estimation.

DOI: 10.5220/0010869600003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

236-243

ISBN: 978-989-758-555-5; ISSN: 2184-4321

ject to various errors, introduced during the dissection

(e.g., movements of the limbs, the ambiguity in deﬁn-

ing the attachment boundary) or during the registra-

tion process. Sometimes a few points are even sam-

pled in the interior of the attachment area. Figure 1

shows an example of such data.

Figure 1: TLEM 2.0 (Carbone et al., 2015) data set con-

taining point clouds deﬁning various muscle attachments on

lower limbs.

It can be seen that the attachment areas are only

slightly curved. Therefore, a naive approach would

be to project the points onto the best-ﬁtted plane (ob-

tained, e.g., by using the least-squares method) and

then proceed with some of the existing state-of-the-art

algorithms for reconstructing 2D curves. This paper

investigates if exploiting the multidimensional scal-

ing (MDS) technique would not improve the obtained

results when comparing them with the ground truth.

We experimented with 15 different algorithms.

Our other contribution is as follows. Since the

3D models of bones are available, we propose an ap-

proach to convert a non-manifold curve, which may

result from the process, into a closed manifold one. It

is based on iso-contour extraction from the scalar ﬁeld

on the surface of the bones that encodes distances to

geodetics connecting the adjacent points of curves.

2 RELATED WORK

The problem of muscle attachments estimation was

addressed in (Fukuda et al., 2017). The authors dis-

sected individual muscles in the hip region of eight

cadaver specimens while tracing the boundary of the

muscle attachments using an optical tracker. The

recorded points were manually reﬁned to remove out-

lier measurements due to tracking noise. In this paper,

we investigate if we could get the boundary of an at-

tachment automatically without the necessity of such

manual reﬁnement.

In their work, (Kohout and Kuka

cka, 2014) de-

scribed a fully automatic algorithm for extraction of

a closed region from a triangular model of a muscle,

where region boundary is speciﬁed by a set of points

lying on the muscle surface or in its vicinity. The

points had to be speciﬁed in an order such that inter-

connecting every pair of adjacent points by a line seg-

ment would produce a closed non-intersecting poly-

line corresponding to the boundary of the region to

extract. However, typical data sets of attachment ar-

eas do not comply with this requirement, as shown

in Figure 1. In this paper, we investigate how to ﬁl-

ter out the input points and order them to satisfy the

requirement of this algorithm.

Approximating or interpolating the input points by

an analytical function may be considered relevant to

this problem. Most suitable seems to be radial ba-

sis function (RBF) approximation since the points are

scattered and unordered. RBF was used for surface

reconstruction of watertight 3D objects by (Carr et al.,

2001). It is also commonly used for scattered data ap-

proximation in general (Cervenka et al., 2019). In this

paper, we address the idea of transforming the input

3D points to 2D, ﬁnding the curve there (by exploit-

ing RBF approximation) and returning to 3D space.

One option for the points dimension reduction is the

multidimensional scaling (MDS) technique (Cox and

Cox, 2008), which is widely used in many different

scientiﬁc ﬁelds.

Recently, (Ohrhallinger et al., 2021) designed a

benchmark for a comprehensive quantitative evalua-

tion of algorithms for 2D curves reconstruction. It

consists of 14 curve reconstruction algorithms, in-

cluding the recent ones, implemented in C++. Most

of these algorithms construct a graph from the points

and then ﬁlter the outline by some criteria. Most of

them are parameterless, but only some are robust to

noise and outliers.

3 OUR APPROACH

Given a set S = (P

) of n points in 3D, sampled on

a smooth curve on a non-planar smooth surface, in-

cluding potentially noise or outliers, our task is to ﬁnd

an ordered set S

⊆ S such that S

represents a closed

non-intersecting space curve. The other points (S \S

)

which do not lie on the curve are considered as out-

liers. Figure 2 shows an example of the input data.

Our basic idea is to exploit the multidimensional

scaling (MDS) technique (Cox and Cox, 2008) to con-

struct n points Q

in 2D such that:

Non-planar Surface Shape Reconstruction from a Point Cloud in the Context of Muscles Attachments Estimation

237

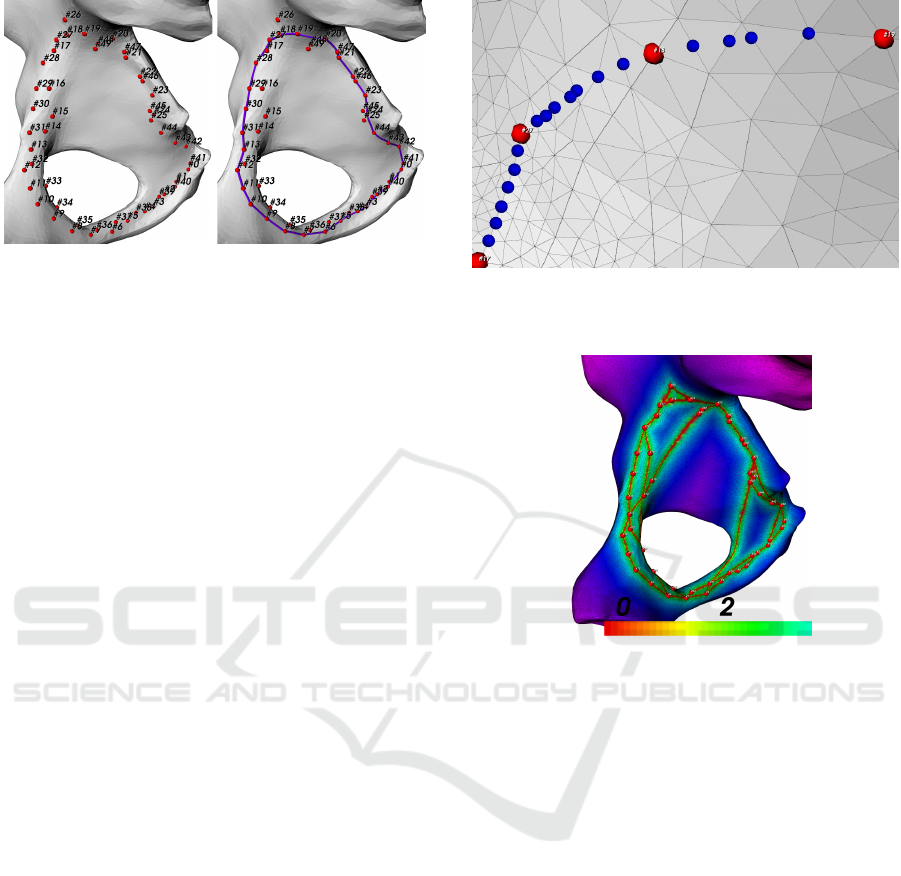
Figure 2: Obturator internus origin data set. Left - the input

point set together with the order in which the points were

sampled, right - the ground truth closed curve we speciﬁed

manually according to anatomical atlases.

• every point Q

is uniquely associated with just one

point P

so we are able to return back to 3D, and

• the distance between a pair of points Q

, Q

are as

close to the distance between a pair of associated

points P

, P

as possible.

Executing a 2D curve reconstruction algorithm on

the set of points Q

produces the sought connectivity

between the points P

. If the output connectivity forms

a single closed curve, we are ready. Otherwise, the

output must be ﬁltered: some edges might need to be

removed, some edges to close the curve might need to

be inserted. We assume that the surface from which

the data were sampled is available and is represented

by a triangular model, or can be reconstructed from

the input points, e.g., by using the RBF approach (see

Section 3.1). It allows us to solve the ﬁltering step in

a rather unorthodox but straightforward approach.

Suppose the points P

and P

should be connected.

At ﬁrst, we subdivide the triangles of the surface mesh

that contain these points in their vicinity, introduc-

ing thus these points as new vertices of the mesh.

Then, we trace the shortest path connecting newly in-

troduced vertices to a set of surface points P

i, j,k

, as

illustrated in Figure 3. The Dijkstra algorithm can be

used for it, providing that the triangular model is ﬁne

enough. Some of the fast marching methods, see, e.g.,

(Peyr

e, 2009), is an alternative suitable in all cases.

We construct a scalar ﬁeld SDF(V ) on the surface

of the mesh such that it returns the geodetic distance

between the given surface point V and the nearest

i, j,k

point – see Figure 4. This ﬁeld can be con-

structed easily using a bread-ﬁrst search algorithm

starting at P

i, j,k

points. We adopt a fast marching

method described in (Peyr

e, 2009) for this purpose.

An algorithm for iso-contours extraction is ex-

ecuted with the iso-value about the average length

of edges P

i, j,k

, P

i, j,k+1

. In our experiments, we

specify this value to 0.5 · (minkP

i, j,k

, P

i, j,k+1

k +

maxkP

i, j,k

, P

i, j,k+1

k). Multiple contours are usually

18,19,0

18,19,1

18,19,2

18,19,3

18,19,4

18,19,5

18,19,0

27,18,0

27,18,6

27,18,7

27,18,8

17,27,0

17,27,1

17,27,2

17,27,3

17,27,4

17,27,5

17,27,6

17,27,7

Figure 3: Reﬁned edges P

, P

, and P

, P

the obturator internus origin data set (see Figure 2) on the

surface of the pelvis bone.

Figure 4: Scalar ﬁeld constructed on the surface of the

pelvis bone for the reﬁned connectivity (obtained by (Lenz,

2006) algorithm) of the obturator internus origin data set.

extracted (e.g., one from the exterior of a closed

curve, the other from the interior). The one with the

largest perimeter is selected as a result – see Figure 5

for an example. We note that the ﬁnal contour does

not go through the input points but providing that the

reﬁnement of the primary edges is sufﬁcient, this does

not stand for a problem in many applications (includ-

ing the muscle attachments estimation).

3.1 Radial Basis Functions (RBF)

Radial basis function interpolation and approximation

is deﬁned as follows:

(x) =

∑

j=1

ϕ(|||x

− x

||), (1)

or also: h = Aλ, A

i, j

= ϕ(||x

− x

||)

The λ

variable is the weight of a single RBF, ϕ de-

notes radial basis function, x

and x

are the positions

of the input vertices (maybe attachment area vertices

in our case), and h

are values in the vertices.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

238

Figure 5: Obturator internus origin closed curve extracted

from the scalar ﬁeld in Figure 4. Compare it with the ground

truth curve in Figure 2 right.

We experimented with a novel RBF described in

(Skala and Cervenka, 2020) deﬁned as:

ϕ(r) = r

− 1) (2)

Variable a is a shape parameter that has to be iden-

tiﬁed accurately to get good results. We also used

a = 1.8 as proposed by the original authors. Fig-

ure 6 shows the surface reconstructed by this ap-

proach from the input points. This surface can be used

as an alternative to the triangulated model of a bone.

Figure 6: The surface of the femur bone reconstructed by

the RBF method from the input points of biceps femoris

origin (top) and vastus intermedius origin (bottom).

4 EXPERIMENTS AND RESULTS

The approach described above was implemented in

C++ 14 using:

• the Visualization Toolkit (VTK)

for loading the

data, curve reconstruction by the α-shape algo-

rithm (see (Edelsbrunner et al., 1983)), iso-lines

extraction , and visualization of results,

• the benchmarking by (Ohrhallinger et al., 2021)

for curve reconstruction by 14 different algo-

https://vtk.org/

rithms – connect2d, hnncrust, ﬁtconnect, stretch-

denoise, discur, vicur, crawl, peel, crust, nncrust,

ccrust, gathan1, gathang, and lenz,

• the code by Yuki Koyama

for the multidimen-

sional scaling,

• the geodesic computation on surfaces by (Krish-

nan, 2013), based on the fast marching method,

• and the Muscle Decomposition by (Kohout and

Kuka

cka, 2014) for extracting the muscle attach-

ment area bounded by the reconstructed curve

from the surface mesh.

We note that the disk radius parameter of the α-shape

algorithm was set to 0.5625 times the maximal short-

est distance between pairs of points, i.e., just enough

to guarantee that the output will have one component

only. The implementations of the other reconstruction

algorithms were used with their default parameters.

We experimented with the point sets representing

muscle attachments of a comprehensive TLEM 2.0

data set of lower limbs (Carbone et al., 2015). Af-

ter performing initial analyses, we selected, more or

less randomly, a couple of representative point sets for

further experiments – see Figure 7. For each of the 27

point sets we ended with, we speciﬁed the ground-

truth connection of the points according to depictions

in anatomical atlases. We note that in some cases, the

task of ﬁnding a proper connection has proven to be

complicated even for a human expert.

We inserted the points into the surface mesh of the

appropriate bone and used the geodesic computation

to obtain the ﬁnal closed ground-truth curve. An ex-

ample of such a curve is in Figure 2, right.

Using the code for the muscle decomposition by

(Kohout and Kuka

cka, 2014), we extracted the part of

the mesh belonging to the attachment area bounded

by the ground-truth closed curve. In three cases (ad-

ductor longus insertion, obturator internus origin and

gluteus maximus inferior origin), the implementation

failed to provide us with an acceptable result. This

was caused by the fact that the input data violated the

assumptions of the original method. Figure 8 shows

examples of extracted ground-truth attachments.

We then ran our implementation. It provided us

with 15 contours for each dataset, one for every curve

reconstruction algorithm. For each output contour,

the surface patch was extracted from the bone model

in the same way as described above. Dice similar-

ity coefﬁcient (DSC) was computed to measure the

dissimilarity between the outcome and the ground

truth. DSC = 1 means a perfect match, while DSC = 0

means that the patches do not intersect. Naturally,

the value of DSC depends on the sampling frequency.

https://github.com/yuki-koyama/multidimensional-

scaling/blob/master/mds.h

Non-planar Surface Shape Reconstruction from a Point Cloud in the Context of Muscles Attachments Estimation

239

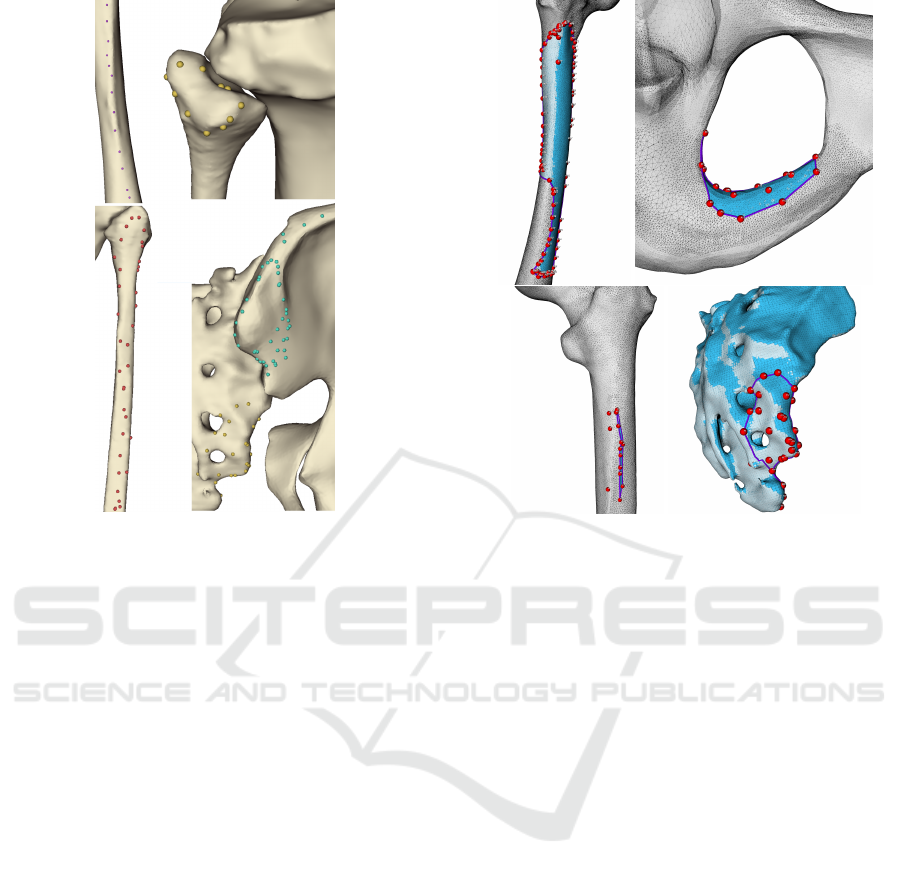
Figure 7: Representative examples of TLEM 2.0 point sets

of muscle attachments. From top to bottom, left to right:

biceps femoris origin, biceps femoris insertion, soleus later-

alis origin, and gluteus maximus superior + inferior origin.

Our samples included all vertices of the bone mesh

triangles plus some points sampled randomly in ev-

ery triangle with an area larger than ε. The num-

ber of samples in such a triangle was determined as

its area divided by ε. In the experiments, we used

ε = π · 0.1 · 0.1, which means our sampling frequency

was about 0.2 mm.

Figure 9 shows the results we obtained. For closed

curves with almost uniform sampling without appar-

ent outliers and noise, represented, e.g., for biceps

femoris insertion, the differences between 2D curve

reconstruction algorithms are negligible. It is also

apparent that only the α-shape algorithm was robust

enough to process every data set. Connect2d, ﬁtcon-

nect, discur, and vicur algorithms could process only

about 70.8% of data sets, stretchdenoise only about

58.3%. The rest failed to process the gluteus medius

posterior insertion, which is not surprising consider-

ing that this data set contains many outliers (see Fig-

ure 10). The poor performance, generally, showed

discur and vicur algorithms.

Further inspection reveals that none of the algo-

rithms could provide acceptable results for the gluteus

maximus inferior insertion and vastus intermedius

origin data sets. In the former case, the reason is

simply that the data contains three outliers outside the

attachment region (probably introduced during an er-

Figure 8: Ground-truth closed curves (purple) for vastus

intermedius origin, obturator externus lateral origin, glu-

teus maximus inferior origin, and gluteus maximus infe-

rior insertion. Surface patches representing the attachment

areas, extracted using the implementation by (Kohout and

Kuka

cka, 2014) are shaded in blue.

roneous registration process) – see Figure 10. In the

latter case, the explanation is more complicated. Al-

though the data of vastus intermedius origin seems

quite OK for a human observer (see Figure 8), the

algorithms yield multiple connections between the

points on the left side with those on the right one.

It might be because the sampling frequency on the

boundary is insufﬁcient, and thus the inﬂuence of the

single apparent outlier is not negligible. As the fe-

mur bone resembles a cylinder, the geodetics com-

puted for these incorrect edges are not on the same

side, but some lie in the front, others in the back. As a

result, the bone is effectively cut into several parts, as

shown in Figure 10 and, therefore, only a part of the

attachment area is extracted.

On average, the best performance reached α-

shape (72.00%), followed by connect2d (69.35%),

and lenz (67.04%). However, it is needed to point

out that the dice similarity coefﬁcient is not a re-

liable indicator for very narrow attachments repre-

sented by slightly curved lines, for which values as

low as 30% are often visually acceptable. This is

the case of adductor longus insertion, adductor mag-

nus mid insertion, adductor magnus proximal inser-

tion, biceps femoris CB origin, iliopsoas superior in-

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

240

Muscle attachment

alpha shape

connect2d

hnncrust

fitconnect

stretchdenoise

discur

vicur

crawl

peel

crust

nncrust

ccrust

gathan1

gathang

lenz

adductor magnus distal insertion 94.64% 87.58% 28.79% 92.49% 92.49% 0.48% 14.31% 34.14% 28.37% 24.80% 93.70% 14.57% 26.01% 26.01% 93.38%

adductor magnus mid insertion 78.88% 51.98% 28.83% 28.83% 28.83% 28.83% 28.83% 25.86% 28.83% 28.83% 28.83% 52.22% 28.83% 72.11%

adductor magnus proximal insertion 85.06% 81.97% 24.83% 24.83% 24.83% 24.83% 24.83% 22.88% 24.72% 21.36% 21.36% 21.36% 81.83% 21.36% 86.38%

biceps femoris origin 84.72% 54.63% 19.09% 19.09% 19.09% 19.09% 19.09% 20.48% 19.58% 20.48% 20.48% 20.48% 54.84% 20.48% 26.02%

biceps femoris insertion 98.44% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.23% 97.95%

gluteus maximus inferior insertion 16.46% 31.96% 28.91% 28.68% 30.09% 27.92% 27.92% 31.64% 35.42% 17.31%

gluteus maximus superior insertion 89.67% 21.92% 33.59% 25.10% 29.46% 91.06% 14.44% 15.27% 18.40% 83.66%

gluteus maximus superior origin 79.92% 87.56% 5.78% 76.52% 76.52% 3.88% 3.55% 94.14% 8.10% 6.89% 81.34% 3.19% 4.26% 7.18% 77.98%

gluteus medius anterior insertion 91.48% 83.15% 7.05% 89.35% 89.35% 16.23% 11.39% 20.65% 12.97% 10.01% 65.61% 14.41% 8.62% 15.88% 84.84%

gluteus medius anterior origin 96.84% 7.22% 13.09% 10.72% 5.59% 93.02% 2.91% 4.24% 5.21% 97.47%

gluteus medius posterior insertion 79.40%

gluteus medius posterior origin 97.31% 98.11% 98.11% 97.98% 97.98% 3.73% 98.08% 98.11% 98.11% 98.11% 98.11% 4.00% 98.11% 98.11% 98.36%

iliopsoas inferior insertion 96.17% 77.17% 8.82% 54.97% 54.97% 0.91% 16.68% 25.79% 17.46% 18.71% 47.84% 11.75% 9.54% 17.81% 95.59%

iliopsoas superior insertion 71.98% 65.20% 49.47% 49.47% 49.47% 49.47% 49.47% 32.39% 32.39% 49.47% 49.47% 49.47% 49.47% 49.47% 66.23%

obturator externus lateral origin 89.09% 62.48% 9.62% 11.78% 5.23% 12.28% 17.84% 10.30% 17.15% 65.52% 7.38% 45.24% 6.08% 78.82%

obturator externus medial origin 97.89% 78.36% 6.40% 80.84% 80.84% 6.48% 4.82% 10.11% 6.14% 6.62% 89.87% 5.68% 1.50% 7.51% 96.77%

sartorius insertion 48.95% 20.88% 61.61% 34.42% 35.86% 74.81% 40.69% 35.02% 48.11% 59.02%

semimembranosus insertion 78.91% 72.93% 34.34% 34.34% 34.34% 34.34% 34.34% 24.14% 34.85% 24.14% 24.14% 24.14% 72.80% 24.14% 78.88%

semimembranosus origin 70.16% 87.90% 12.20% 8.95% 8.95% 1.89% 9.28% 19.69% 12.62% 23.40% 56.29% 8.91% 13.53% 79.03% 73.13%

soleus lateralis origin 71.05% 45.73% 15.31% 15.52% 15.52% 3.64% 7.07% 15.55% 14.89% 11.36% 15.56% 10.60% 51.43% 11.66% 16.24%

soleus medialis origin 15.38% 12.28% 48.25% 46.16% 46.16% 15.54% 47.63% 48.43% 44.07% 45.44% 19.33% 51.41% 12.27% 12.27% 14.24%

vastus intermedius origin 0.06% 6.73% 11.19% 6.42% 10.56% 36.09% 4.49% 22.82% 4.00% 39.64%

vastus medialis inferior origin 36.76% 31.47% 41.63% 42.55% 40.60% 41.45% 41.45% 38.42% 41.45% 33.87%

vastus medialis superior origin 58.85% 34.74% 14.56% 25.18% 20.83% 8.65% 23.99% 13.34% 13.32% 44.78% 12.14% 13.00% 15.50% 53.97%

Figure 9: Dice similarity coefﬁcients of various muscle attachments, obtained for the MDS with different curve reconstruction

algorithms. Missing values mean that the reconstruction algorithm failed. The best performances are marked in bold.

Figure 10: The data sets causing troubles during the pro-

cessing (see the text): gluteus medius posterior insertion

with a lot of internal points (top left), gluteus maximus infe-

rior insertion with three outer points (top right), and vastus

intermedius origin with an insufﬁcient sampling frequency

(bottom). The ground-truth curve is purple, the ﬁnal con-

tour obtained from α-shape curve is light blue, and geodet-

ics computed from the connectivity found by the lenz algo-

rithm are yellow.

sertion, semimembranosus insertion, soleus medialis

origin, and vastus medialis inferior origin. If we ex-

clude the results of these data sets, we get four al-

gorithms whose performance exceeds 70% on aver-

age: α-shape (78.74%), lenz (76.45%), connect2d

(76.36%), and nncrust (70.05%). Considering that

connect2d failed repeatedly, we can recommend only

α-shape or lenz algorithms for the curve reconstruc-

tion in our context.

For the data sets mentioned above, a better indi-

cator might be the difference in the perimeter of the

reconstructed and ground-truth curves. Table 1 shows

that according to this indicator, the best performing

algorithm is connect2d, with the error of 1.25% on

average but one failure, followed by gathan1 (2.60%

on average), α-shape (3.03%), and lenz (3.43%). All

other algorithms exhibited a worse performance with

multiple failures or average errors exceeding 4% (in

absolute values). We note that median errors were

below 4% in all cases. The order of the ﬁve best-

performing algorithms remains the same even when

median errors are considered.

Therefore, it can be concluded that α-shape or

lenz algorithms are universal algorithms suitable for

all cases. This result is also conﬁrmed by a subjec-

tive test, in which a human volunteer assessed all the

reconstructed contours visually, classifying them into

three categories:

• A = no issue or a minor one only without any con-

siderable impact on musculoskeletal modelling,

• B = acceptable but with some issues that might

have some undesirable impacts on musculoskele-

tal modelling, and

• C = unacceptable.

The α-shape and lenz algorithms have almost half

of their contours (48.1% precisely in both cases) in

category A. While hncrust, discur, vicur, peel, crust,

ccrust, gathan1, and gathang algorithms have more

than half of the contours they produced in category

C, α-shape and lenz have there only 4 and 5 contours,

which corresponds to 11.1% and 18.5%, respectively.

Two of these contours belong to gluteus maximus

inferior insertion, and vastus intermedius origin, al-

ready discussed above (see also Figure 10).α-shape

further failed to provide acceptable results for vastus

medialis superior origin, lenz for obturator externus

Non-planar Surface Shape Reconstruction from a Point Cloud in the Context of Muscles Attachments Estimation

241

Table 1: Differences between the perimeters of the reconstructed and ground-truth contours for selected 2D curve reconstruc-

tion algorithms. The best results are bold.

Name α-shape connect2d ﬁtconnect nncrust gathan1 lenz

adductor longus insertion 7.73% 5.82% 7.85% 7.84% 5.82% 8.26%

adductor magnus mid insertion 1.54% 0.00% 1.07% 1.07% 0.00% 0.92%

adductor magnus proximal insertion 2.31% -0.20% 3.79% 3.71% -0.20% 3.11%

biceps femoris origin 1.25% -0.28% 1.37% 0.73% -0.28% 1.41%

iliopsoas superior insertion 6.69% 0.70% 8.35% 8.35% 8.35% 7.05%

semimembranosus insertion 1.85% -0.04% 2.48% 2.68% -0.04% 1.97%

soleus medialis origin -1.31% -2.98% -5.75% -0.22% -2.99% -0.84%

vastus medialis inferior origo 1.59% 7.63% 3.09% 3.86%

Avg(abs(error)) 3.03% 1.25% 3.83% 4.03% 2.60% 3.43%

lateral origin, soleus lateralis origin, and soleus medi-

alis origin. In all four cases, the attachments are much

more stretched in one dimension than in the other.

Due to sparse sampling, the MDS increased further

this ratio, producing points visually lying almost on

a one-dimensional object (see Figure 11). All algo-

rithms then struggled with such data.

Figure 11: Soleus lateralis origin after being transformed

into 2D using projection onto the best ﬁt plane (left) and

using the multidimensional scaling technique (right).

We, therefore, compared the results with those ob-

tained when the input points were projected onto the

plane ﬁtted to the data by the least-squares method

instead of using the multidimensional scaling tech-

nique. Table 2 show that although some algorithms

beneﬁt from the MDS technique (e.g., ﬁtconnect,

stretchdenoise, or peel), others, without any doubt,

perform better without it (e.g., lenz or nncrust). As

for the subjective tests, lenz algorithm came in ﬁrst

with 15 (i.e., 55.6%) muscle attachments in category

A, 11 (i.e., 40.7%) in category B and only vastus

intermedius origin in category C. The second place

was taken by α-shape with 10 (i.e., 37%) muscle at-

tachments in category A, 13 (i.e., 48.1%) in category

B, and 4 (i.e., 14.8%) in category C. Clearly, while

α-shape achieved more acceptable results with the

MDS, lenz demonstrated different behaviour.

However, we must point out that a projection of

points onto a common plane is not suitable when the

curve to be reconstructed bends several times, e.g.,

like in the case of a narrow saddle. Although such

cases are pretty rare in the context of muscle attach-

ments, they seem to be frequent in the aneurysm neck

identiﬁcation problem.

Table 2: Difference of the average performance when using

the MDS and when using the projection onto a common

plane. Positive values mean that the MDS outperforms the

projection. Dice similarity coefﬁcients (DSC) are used as

a performance indicator for the data for which DSC is a

reliable indicator (see the text for explanation). For the rest,

errors in the muscle attachments perimeters (PER) are used.

Algorithm DSC PER

α-shape -0.37% -0.31%

connect2d -8.80% 0.23%

hnncrust 8.83% 0.00%

ﬁtconnect 11.54% 0.25%

stretchdenoise 17.10% -0.26%

discur -8.46% 6.38%

vicur -5.70% -0.01%

crawl -6.69% -0.03%

peel 9.61% 0.05%

crust 4.31% -0.08%

nncrust -6.63% -0.57%

ccrust -0.17% -6.31%

gathan1 3.87% -2.11%

gathang -12.59% -11.09%

lenz -12.66% -0.72%

We also did some preliminary testing of the RBF

approach for ordering the vertices and smoothing the

curve. The primary purpose of this test is to check

whether the RBF approach will be capable of creating

a closed and non-self-intersecting curve in 2D.

If the outliers or apparent nonuniformity are

present, the resulting curve is far from expectations

(e.g. vastus intermedius origin on the left of Fig-

ure 12). Luckily, this approach gives better results

for many other attachment areas (e.g. gluteus medius

posterior on the right of the Figure 12). The polar

coordinate system for the dimension reduction causes

problems in some cases, mainly if there is a wide an-

gle without any vertex (left image of the Figure 12,

bottom part), causing a single or even multiple self-

intersectional loops. Approximating the curve instead

of interpolating may solve these issues.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

242

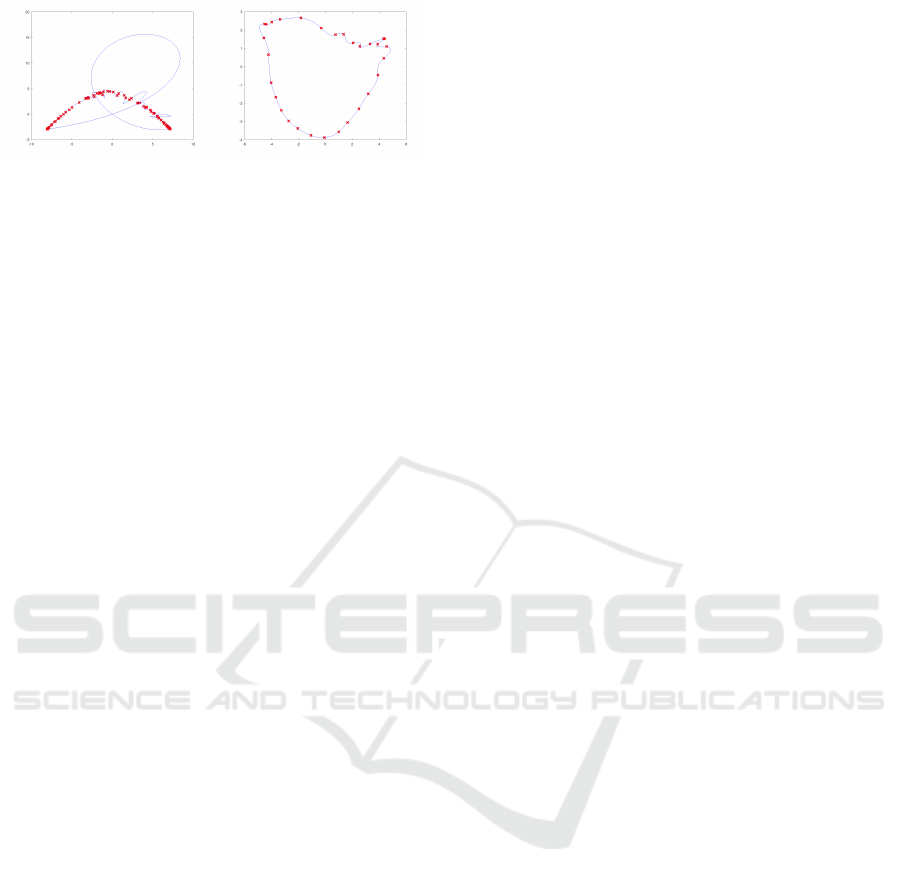
Figure 12: Two radial basis function approximation results.

Vastus intermedius origin is on the left. The connection be-

tween both ends of the attachment area does not turned out

well due to looping the curve. Gluteus medius posterior

origin is on the right. The shape is approximated by expec-

tations.

5 CONCLUSION AND FUTURE

WORK

This paper investigated the options of reconstructing

a closed space curve from the points sampled on that

curve, supporting sparse sampling and noisy data with

multiple outliers. Our extensive experiments, per-

formed on the TLEM 2.0 data sets (Carbone et al.,

2015) in the context of muscle attachments estima-

tion, lead us to the following recommendations. If

the curve to be reconstructed is not expected to have

a shape of a narrow saddle or be otherwise strangely

bent, the points should be projected onto the plane

that best ﬁt the input data. The lenz algorithm (Lenz,

2006) should be used on the projected points to ﬁnd

the primary connectivity between the input points.

Suppose this algorithm is unavailable or the expec-

tations on the curve shape do not hold. In that case,

the input data should be transformed onto the plane

using the multidimensional scaling (MDS) technique

(Cox and Cox, 2008). The α-shape algorithm (Edels-

brunner et al., 1983) should be then used on the trans-

formed points (instead of the lenz algorithm), with the

disc radius being slightly above half of the maximal

shortest distance between pairs of transformed points.

If neither algorithm is available, connect2d or nncrust

(see (Ohrhallinger et al., 2021)) are a decent choice.

Providing that the surface on which the space

curve lies is available, the reconstructed curve can

be reﬁned by tracing the shortest paths between each

pair of points connected by an edge. A non-manifold

curve, i.e., a curve containing vertices of valence

larger than 2, can be converted into a manifold one

using the algorithm proposed in the paper, based on

iso-contour extraction from a scalar ﬁeld describing

for each point on the surface its distance to the curve.

If the object bounded by the curve covers only a tiny

portion of the surface in any direction or the surface

is open, this conversion is reliable.

REFERENCES

Berger, M., Tagliasacchi, A., Seversky, L. M., Alliez, P.,

Guennebaud, G., Levine, J. A., Sharf, A., and Silva,

C. T. (2016). A survey of surface reconstruction from

point clouds. Computer Graphics Forum, 36(1):301–

329.

Carbone, V., Fluit, R., Pellikaan, P., van der Krogt, M.,

Janssen, D., Damsgaard, M., Vigneron, L., Feilkas,

T., Koopman, H., and Verdonschot, N. (2015). TLEM

2.0 – a comprehensive musculoskeletal geometry

dataset for subject-speciﬁc modeling of lower extrem-

ity. Journal of Biomechanics, 48(5):734–741.

Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J.,

Fright, W. R., McCallum, B. C., and Evans, T. R.

(2001). Reconstruction and representation of 3d ob-

jects with radial basis functions. In Proceedings of the

28th annual conference on Computer graphics and in-

teractive techniques. ACM Press.

Cervenka, M., Smolik, M., and Skala, V. (2019). A new

strategy for scattered data approximation using radial

basis functions respecting points of inﬂection. Com-

putational Science and Its Applications.

Cox, M. A. A. and Cox, T. F. (2008). Multidimensional

scaling. In Handbook of Data Visualization, pages

315–347. Springer Berlin Heidelberg.

Edelsbrunner, H., Kirkpatrick, D., and Seidel, R. (1983).

On the shape of a set of points in the plane. Informa-

tion Theory, IEEE Transactions on, 29:551 – 559.

Fukuda, N., Otake, Y., Takao, M., Yokota, F., Ogawa, T.,

Uemura, K., Nakaya, R., Tamura, K., Grupp, R. B.,

Farvardin, A., Armand, M., Sugano, N., and Sato, Y.

(2017). Estimation of attachment regions of hip mus-

cles in CT image using muscle attachment probabilis-

tic atlas constructed from measurements in eight ca-

davers. Int J Comput Assist Radiol Surg., 12(5):733–

742.

Kohout, J. and Kuka

cka, M. (2014). Real-time modelling of

ﬁbrous muscle. Computer Graphics Forum, 33(8):1–

15.

Krishnan, K. (2013). Geodesic computations on surfaces.

The VTK Journal.

Lenz, T. (2006). How to sample and reconstruct curves

with unusual features. In Proceedings of the 22nd

European Workshop on Computational Geometry

(EWCG), pages 29–32.

Ohrhallinger, S., Peethambaran, J., Parakkat, A. D., Dey,

T. K., and Muthuganapathy, R. (2021). 2d points

curve reconstruction survey and benchmark. Com-

puter Graphics Forum, 40(2):611–632.

Peyr

e, G. (2009). Geodesic methods in computer vision

and graphics. Foundations and Trends® in Computer

Graphics and Vision, 5(3-4):197–397.

Skala, V. and Cervenka, M. (2020). Novel rbf approxima-

tion method based on geometrical properties for sig-

nal processing with a new rbf function: Experimental

comparison. 2019 IEEE 15th International Scientiﬁc

Conference on Informatics.

Non-planar Surface Shape Reconstruction from a Point Cloud in the Context of Muscles Attachments Estimation

243