Beyond Global Average Pooling: Alternative Feature Aggregations for

Weakly Supervised Localization

Matthias K

orschens

1 a

, Paul Bodesheim

1 b

and Joachim Denzler

1,2 c

Friedrich Schiller University Jena, F

urstengraben 1, Jena, Germany

DLR Institute of Data Science, M

alzerstraße 3-5, Jena, Germany

Keywords:

Computer Vision, Pooling, Weakly Supervised Object Localization, Weakly Supervised Segmentation.

Abstract:

Weakly supervised object localization (WSOL) enables the detection and segmentation of objects in appli-

cations where localization annotations are hard or too expensive to obtain. Nowadays, most relevant WSOL

approaches are based on class activation mapping (CAM), where a classiﬁcation network utilizing global av-

erage pooling is trained for object classiﬁcation. The classiﬁcation layer that follows the pooling layer is then

repurposed to generate segmentations using the unpooled features. The resulting localizations are usually im-

precise and primarily focused around the most discriminative areas of the object, making a correct indication

of the object location difﬁcult. We argue that this problem is inherent in training with global average pooling

due to its averaging operation. Therefore, we investigate two alternative pooling strategies: global max pooling

and global log-sum-exp pooling. Furthermore, to increase the crispness and resolution of localization maps,

we also investigate the application of Feature Pyramid Networks, which are commonplace in object detection.

We conﬁrm the usefulness of both alternative pooling methods as well as the Feature Pyramid Network on the

CUB-200-2011 and OpenImages datasets.

1 INTRODUCTION

In recent years, most of the basic supervised learning

tasks in computer vision, like image categorization,

semantic segmentation, and object detection, have

been solved to a satisfactory degree on a multitude

of benchmark datasets by using convolutional neural

networks (CNNs). However, the proposed approaches

are often quite data-hungry, and solving the above-

mentioned tasks in a new domain usually requires an

entirely new set of data annotations, with many hours

of labor to label the images depending on the task.

Therefore, the focus recently shifts more in the direc-

tion of weakly supervised approaches, where the label

annotations do not match the target output of the task

but are more imprecise. There are, for example, ap-

proaches that try to solve weakly supervised semantic

segmentation (WSSS) based on bounding box labels

or even class labels only. Moreover, other approaches

try to solve the task of weakly supervised object local-

ization (WSOL), i.e., determining either the bounding

https://orcid.org/0000-0002-0755-2006

https://orcid.org/0000-0002-3564-6528

https://orcid.org/0000-0002-3193-3300

Figure 1: An overview of the differences between the stan-

dard CAM method (top) using GAP, and our method (bot-

tom), which utilizes GMP/GLSEP and optionally an FPN.

box or the segmentation map for an object of a known

class in an image.

Enabling WSSS or WSOL based on images with

class labels only is of great importance, as this kind

of annotation is the easiest one to acquire, either by

180

Körschens, M., Bodesheim, P. and Denzler, J.

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization.

DOI: 10.5220/0010871700003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

180-191

ISBN: 978-989-758-555-5; ISSN: 2184-4321

explicit annotations of domain-experts in specialized

ﬁelds or implicitly annotated images found online.

Hence, requiring only class labels for images mas-

sively reduces the amount of work required to enable

more advanced tasks like segmentation and object lo-

calization in a novel domain.

There already exist many different approaches for

WSOL. Most of the recent ones are based on the class

activation mapping work by Zhou et al. (2016). They

discovered that the weights of a classiﬁcation network

can be repurposed in a convolutional layer to create

a map of class activations, known as class activation

maps (CAMs). When applied at the last layer of a

feature extractor backbone, these CAMs show high

activations in image regions containing features that

correspond to the speciﬁc classes. Hence, CAMs can

also be thresholded and afterward converted into seg-

mentations or bounding boxes, as shown in (Zhou

et al., 2016).

CAMs are typically used with network architec-

tures that are trained for a classiﬁcation task and con-

tain global average pooling. However, training these

networks leads to certain issues. First, the network

primarily focuses on the most discriminative regions

of the objects instead of the complete object, mak-

ing correct localization hard. Second, the averaging

operation does not encourage the network to learn

crisp localizations, but rather fuzzy ones as activa-

tions are often distributed to neighboring pixels to in-

crease the activation and, therefore, also the classi-

ﬁcation score. There have been several WSOL ap-

proaches based on the CAM method to counter these

problems, for example, by introducing certain types

of occluding data augmentations to improve the distri-

bution of the CAMs over the whole object (Yun et al.,

2019; Zhang et al., 2018b; Singh and Lee, 2017).

Other methods try to modify the algorithm for gen-

erating the CAM or the localization map (Selvaraju

et al., 2017; Chattopadhay et al., 2018; Fu et al., 2020;

Wang et al., 2020; Ramaswamy et al., 2020; Muham-

mad and Yeasin, 2020).

We argue that most problems in the outputs of the

CAM method are established during network train-

ing. Hence, if the training is done correctly, i.e., in

a way that such problems do not occur, they do not

require ﬁxing afterward. In this context, we found

that the base method of CAM, i.e., utilizing a classi-

ﬁcation network with a global average pooling layer,

has not been revisited in recent papers. As mentioned

above, global average pooling has several caveats that

lead, in our opinion, to suboptimal performance for

WSOL. Therefore, we investigate two alternatives:

global max pooling (GMP) and global log-sum-exp

pooling (GLSEP). Regarding the former, Zhou et al.

(2016) argued that GMP focuses too much on a single

point in the image and is therefore not a good option

for proper localization. Hence, we also investigate

GMP in the setting of training with occluded inputs,

similar to several approaches mentioned before. In

addition to this, we also consider the second potential

replacement: GLSEP. As the log-sum-exp function is

a fully differentiable approximation of the maximum

function but still aggregates information over multiple

locations in the image similar to GAP, it can be treated

as a compromise between GMP and GAP. Similar

methods to GLSEP have been applied before in classi-

ﬁcation (Zhang et al., 2018a) and in a different WSOL

setting (Pinheiro and Collobert, 2015). However, to

the best of our knowledge, we are the ﬁrst to apply

this kind of pooling method to WSOL in combination

with CAMs. There are also other methods represent-

ing a compromise between GMP and GAP (Christlein

et al., 2019). However, we focus on GLSEP as it is a

comparably simple and parameter-free option.

A recurring problem in WSOL is the small output

resolution of the CAMs caused by the small resolu-

tions of the last layers in the feature extraction back-

bones. This is usually partially resolved by remov-

ing strides in the last layers of the backbones and

thus doubling or quadrupling the output size. How-

ever, this way, the last layers usually merely contain

high-level features but, for example, little informa-

tion about local object borders. Feature Pyramid Net-

works (FPNs) (Lin et al., 2017a) are often used for

object detection and segmentation tasks. However,

they are usually not used in WSOL. We, therefore,

investigate FPNs as an alternative to simply removing

strides in the network, as they provide a simple way to

include low-level features in a rich feature represen-

tation and thus have the potential to improve localiza-

tion even further. An example output of our combined

method can be seen in Figure 1.

Therefore, our contributions are the following: we

revisit the basic CAM method and investigate two al-

ternatives to the commonly used GAP layer: GMP

and GLSEP. We analyze these layers as simple re-

placement of GAP and in combination with FPNs.

By implementing the usage of FPNs in the WSOL

task, we want to determine if it is a viable alterna-

tive to simply removing strides. Therefore, we inves-

tigate different extraction layers of the FPN and ana-

lyze their inﬂuence on the localization performance.

We also incorporate an occlusion augmentation sim-

ilar to those already proposed by others (Singh and

Lee, 2017; Yun et al., 2019; Choe and Shim, 2019).

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization

181

2 RELATED WORK

Weakly Supervised Object Localization. One of the

most prominent approaches in the area of WSOL is

the already mentioned CAM approach (Zhou et al.,

2016). As explained above, this approach uses the

weights of the trained classiﬁcation layer for a convo-

lutional layer applied to the extracted feature map to

generate a map of discriminative regions. This map

is thresholded to generate values that are used as a

basis for calculating bounding boxes or segmentation

maps. Based on CAMs, there have been further de-

velopments in the area of WSOL (Singh and Lee,

2017; Zhang et al., 2018b,c; Choe and Shim, 2019;

Yun et al., 2019). One approach, for example, tack-

les the task by adversarially erasing discriminative re-

gions (Zhang et al., 2018b), while another one tries

to generate additional pseudo-pixel-wise annotations

on the ﬂy via self-produced guidance (Zhang et al.,

2018c). Further approaches apply novel data aug-

mentation techniques to distribute the discriminative

regions over the image more equally, for example, ei-

ther by dropping parts of the images (Singh and Lee,

2017; Choe and Shim, 2019) or cutting and pasting

parts of images (Yun et al., 2019).

However, while on public datasets seemingly bet-

ter results were achieved in the last years using ap-

proaches like those mentioned before, Choe et al.

(2020) analyzed the most recent approaches and

found that most improvements over the original CAM

paper (Zhou et al., 2016) were primarily due to usu-

ally prohibited hyperparameter optimization on the

test set. They found that no signiﬁcant improvement

over the CAM method was achieved when compared

on equal grounds. They also proposed several novel

metrics to evaluate the quality of the localizations dis-

entangled from the classiﬁcation accuracy, which was

commonplace before.

In this work, we will focus on the CAM method

itself, instead of merely building on it, and utilize the

localization metrics proposed by Choe et al. (2020).

We also use a comparably simple occlusion augmen-

tation similar to several methods mentioned above,

namely Cutout (DeVries and Taylor, 2017), primarily

to ﬁnd potential synergies with the pooling methods

investigated in this work.

Improved CAM Methods. Several methods have

been proposed to improve the output of the CAM ap-

proach, either for localization, or for better visual in-

terpretation. To this end, multiple approaches include

gradients into the CAM computation (Selvaraju et al.,

2017; Chattopadhay et al., 2018; Fu et al., 2020),

while others use score weighting (Wang et al., 2020),

ablation techniques (Ramaswamy et al., 2020), or

even principal components (Muhammad and Yeasin,

2020). These approaches, however, aim at improving

the CAMs after training, while we modify the output

of the CAMs indirectly by training the network in a

different way such that it learns better localizations

implicitly.

Log-Sum-Exp Pooling. We found that applying the

log-sum-exp function as a pooling operation has only

been rarely done in previous work. A variation of it,

a log-mean-exp pooling function referred to as Al-

phaMEX, has been successfully applied by Zhang

et al. (2018a) in classiﬁcation, however not in WSOL

as it is the case in our work. In WSOL, the log-sum-

exp function has been investigated by Pinheiro and

Collobert (2015), who applied it to aggregate score

maps into class scores. In contrast, we apply it di-

rectly to the feature maps in place of global aver-

age pooling. We selected log-sum-exp pooling due

to its similarity to global max pooling, which is the

usual alternative to global average pooling. Log-sum-

exp pooling offers a differentiable, parameter-free ap-

proximation to global max pooling and therefore is a

natural choice to use in this place. While there is also

a multitude of other pooling methods previously pro-

posed (Christlein et al., 2019; Gao et al., 2016; Simon

et al., 2017), but not utilized in WSOL, we will leave

the investigation of these methods for future work.

3 OUR APPROACH

Class activation mapping (CAM) introduced by Zhou

et al. (2016) is the basis for our method. In the CAM

method, a CNN is ﬁrst trained on a classiﬁcation task

using the standard network scheme for classiﬁcation.

That is, the network comprises three parts: a back-

bone for extracting features in a pixel-wise manner, a

pooling layer, usually global average pooling (GAP),

and a single classiﬁcation layer, which is typically a

fully connected layer applied on the pooled feature

activations. After training the classiﬁer, the pooling

layer is left out, and the weights learned for the fully

connected classiﬁcation layer are applied directly to

the unpooled activations extracted from the backbone.

This results in a class activation map highlighting

class-relevant regions in the images by high activa-

tions for the respective class.

In contrast to GAP, we investigate the usage of two

alternative pooling methods. We do this as GAP has

certain limitations that can be circumvented with al-

ternative pooling strategies. We also implement Fea-

ture Pyramid Networks (FPNs) (Lin et al., 2017a) as

an alternative way to increase the output resolution of

the CAM. FPNs include features from different stages

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

182

in the network in the ﬁnal feature representation in

contrast to upscaled versions of the last layers. Hence,

FPNs might be advantageous for object localization.

Finally, we also explore the already existing Cutout

augmentation method (DeVries and Taylor, 2017) in

conjunction with our investigated pooling layers, as

it is a simple method to mask out parts of the im-

ages, and the individual pooling methods might ben-

eﬁt from this kind of augmentation.

3.1 Pooling Methods

In this section, we introduce the three pooling meth-

ods we are interested in, and explain the intuitions be-

hind them.

Global Average Pooling (GAP). GAP is deﬁned as

GAP(F) =

W · H

∑

x=1

∑

y=1

x,y

, (1)

with F ∈ R

W ×H×C

representing the input feature map,

and x and y the coordinates for the different spatial

locations. W , H and C represent the width, height

and depth (i.e., the number of channels) of F, re-

spectively. GAP is the pooling layer usually applied

in most classiﬁcation networks. However, we argue

that it is not the optimal choice for localization tasks.

During training for a classiﬁcation task, the network

aims at maximizing the feature score for the target

class while minimizing the scores for the remaining

classes. If we consider that the ﬁnal classiﬁcation

layer contains the weight vector w ∈ R

for a target

class, then the class score s can be calculated as

s = w

f =

∑

· f

, (2)

with f = GAP(F) and f ∈ R

. To maximize this score

for the target class, f has to be maximized in all chan-

nels c that are deemed to be relevant for this class

with respect to the weights w. This results in the net-

work trying to maximize the activations of these rele-

vant channels over all locations in the feature map F.

As most current networks have rather large receptive

ﬁelds, neighboring pixels in F usually have a simi-

lar view on the input image and can hence potentially

extract very similar features. Due to the abovemen-

tioned procedure, the GAP layer encourages the ex-

traction of similar features, which, in the end, can lead

to strongly inaccurate CAMs for localization.

Global Max Pooling (GMP). To counter the above-

mentioned limitation of GAP, we consider GMP as

an alternative. Using the notation introduced before,

GMP can be deﬁned as

GMP(F) = max

x,y

. (3)

As GMP does not contain an averaging operation, the

abovementioned inaccuracy should not be a problem

here. However, GMP has its own issues. As men-

tioned in (Zhou et al., 2016), GMP usually focuses

only on a small number of points in an image, which

is also suboptimal for good localization maps. While

we aim to counter this problem with occlusion aug-

mentations of the input image, namely Cutout (De-

Vries and Taylor, 2017) (see Section 3.3), we investi-

gate log-sum-exp pooling as another alternative.

Global Log-Sum-Exp Pooling (GLSEP). GLSEP is

an approximation of GMP and deﬁned as

GLSEP(F) = log

∑

x=1

∑

y=1

expF

x,y

. (4)

While GLSEP approximates GMP, it still aggregates

information from the entire feature map similar to

GAP. Hence, it can be viewed as a compromise be-

tween GMP and GAP. Moreover, while it aggregates

information over the whole feature map, the detri-

mental effect from GAP should not occur here too

strongly, due to the log-sum-exp function weighting

higher activations stronger than lower ones, which

likely reduces the effect. Hence, GLSEP has the abil-

ity to focus on multiple high activations during train-

ing, instead of only single ones like GMP, while also

not increasing low-activations by the same amount as

high ones, as GAP does.

3.2 Feature Pyramid Networks

Feature Pyramid Networks (FPNs) have been intro-

duced by Lin et al. (2017a). The general idea of

this network architecture is to upscale feature maps

from deeper layers of common classiﬁcation net-

works (e.g., ResNets (He et al., 2016)) and con-

nect them with information from features from earlier

stages of the network, which usually have higher reso-

lution but lower semantic value. These networks gen-

erate very rich feature maps at a high resolution that

contain not only highly meaningful semantic infor-

mation for distinguishing classes, but also low-level

information for object parts and borders, which en-

able more accurate localizations of the objects. For

this reason, FPNs are utilized, for instance, in fully

supervised object detection (Lin et al., 2017a,b) and

instance segmentation (He et al., 2017; Kirillov et al.,

2019). However, while used in their fully supervised

counterparts, to the best of our knowledge, FPNs have

not seen much attention in the area of weakly super-

vised learning. An overview of our combined method

is depicted in Figure 1.

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization

183

3.3 Cutout

Cutout is a data augmentation method introduced by

DeVries and Taylor (2017) in 2017. When applied to

an input image, a random part of the image is masked

out and replaced, e.g., with a black square or rectan-

gle, forcing the network to learn features not lying in

this speciﬁc area. This regularizes the network and

encourages it to learn a wider variety of features, re-

sulting in more robust representations. In the case of

WSOL, this leads to higher class activations in less

discriminative regions of the image and vice versa.

While other augmentation methods apply similar oc-

cluding augmentations (Singh and Lee, 2017; Choe

and Shim, 2019; Yun et al., 2019), we choose this one

due to its simplicity.

4 EXPERIMENTS

We ﬁrst describe the evaluation methods and datasets

for our experiments. Afterwards, we specify our ex-

perimental setup and present results for comparing the

different approaches.

4.1 Evaluation

Our evaluation is based on the recent work of Choe

et al. (2020). They argued that the classiﬁcation abil-

ity of a network should not be included in the evalu-

ation of the WSOL performance and also suggested

that hyperparameter optimization should be done on

an image set independent from the test set. To this

end, they extended three datasets, two of which we

utilize in this work, by adding a validation set with

ground truth localizations. Moreover, they proposed

several novel metrics for evaluating WSOL. It should

be noted that these metrics are gt-known metrics, i.e.,

the identity of the class is known and plays no role

during evaluation.

The ﬁrst metric we use is called MaxBoxAccV2

and was designed for evaluating bounding boxes only.

It analyses the score maps generated by the CAMs

and uses them to create bounding boxes for fur-

ther evaluation. These bounding boxes are selected

based on three different intersection over union (IoU)

thresholds with the ground-truth boxes (0.3, 0.5, 0.7),

and the results of these three thresholds are averaged

to obtain a single value. For details of this metric, we

refer to (Choe et al., 2020).

The second metric is the pixel average precision

PxAP, used for evaluating the quality of single-class

segmentation maps. It is deﬁned as the area under the

precision-recall curve generated by the thresholded

CAM score maps for different thresholds. For the ex-

act deﬁnition of this metric, we again refer to (Choe

et al., 2020).

4.2 Datasets

In our experiments, we utilize the augmented CUB

(Wah et al., 2011) and OpenImages (Benenson et al.,

2019) dataset versions proposed by Choe et al. (2020).

Caltech-UCSD Birds-200-2011 (CUB). CUB (Wah

et al., 2011) is a popular ﬁne-grained classiﬁcation

dataset, which is also commonly used for evaluation

in WSOL. It comprises 200 bird species with 5,994

images for training and 5,794 for testing. Choe et al.

(2020) collected 1,000 additional images as a vali-

dation set, and provide corresponding bounding box

annotations. In our experiments, we use the annota-

tions of the validation set for hyperparameter tuning

only. The results on this dataset are evaluated using

the MaxBoxAccV2 metric.

OpenImages. The OpenImages dataset proposed by

Choe et al. (2020) is a subset of the one introduced

in (Benenson et al., 2019). It encompasses images of

100 general object classes, split into 29,819 images

for training, 2,500 for validating, and 5,000 for test-

ing. In contrast to the CUB dataset, the annotations

are segmentation maps for the objects in the images.

As in the original OpenImages dataset, images often

contain multiple different classes. Choe et al. (2020)

cropped these images such that there is only a single

class contained in each image. For the evaluation on

this dataset, we use the PxAP metric.

4.3 Setup

We use the same basic setup for all our experiments.

For training the networks, we use the SGD optimizer,

a batch size of 32, and an input size for the network

of 224 × 224, which is obtained by random cropping

from an original image size of 256 × 256. We further

use random horizontal ﬂipping and, depending on the

experiment, Cutout as data augmentations. We train

our models similar to the training scheme presented

by Choe et al. (2020), i.e., we train for 50 and 10

epochs on CUB and OpenImages, respectively, and

reduce the learning rate by a factor of 0.1 every 15

and 3 epochs, respectively.

For our training, we have two to three hyperpa-

rameters: learning rate, weight decay, and optionally

the maximum size of Cutout. For each pair of dataset

and pooling method, we determine a suitable combi-

nation of learning rate, weight decay, and maximum

Cutout size. This is done by randomly sampling val-

ues for these parameters 30 times, training the net-

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

184

work for the abovementioned number of epochs, and

selecting the best parameters based on the respective

localization metric evaluated on the validation sets.

This is done for every setup. For more details on

the hyperparameter search, we would like to refer to

the Appendix. Furthermore, in our experiments, we

use a ResNet50 (He et al., 2016) initialized with Ima-

geNet (Russakovsky et al., 2015) weights as provided

by the Pytorch framework (Paszke et al., 2019). As

Choe et al. (2020) mentioned, it is commonplace in

WSOL to increase the output resolution of the net-

work by removing the strides in the last network lay-

ers. Hence, as done in (Choe et al., 2020), for our

experiments on OpenImages we removed the strides

for the last convolutional block, and additionally the

ones of the second-to-last block for the experiments

on CUB, doubling and quadrupling the output reso-

lution, respectively. In addition to this, to also have

a more direct comparison of the effect of a doubled

output resolution between CUB and OpenImages, we

also ran experiments on CUB with only double the

resolution, which was not done in (Choe et al., 2020).

In the experiments with FPN, we use the network in

its original form, using only the FPN to increase the

output resolution to 2, 4, and 8 times the original reso-

lution for the FPN layers P4, P3 and P2, respectively.

A Note on Hyperparameters. In order to repro-

duce our results, it should be noted that the hyper-

parameters for the different methods differ strongly

from each other. Especially notable are the frequent

requirements for strong weight decay for GMP and

GLSEP (partially > 1 exp−2) and the small learning

rate requirements for GLSEP (≈ 1e − 5).

4.4 Impact of Feature Pyramid

Networks

In our experiments, we ﬁrst investigate the potential

beneﬁts of FPNs for WSOL. To this end, we compare

the results of a standard ResNet50 (He et al., 2016)

with an enlarged output feature map and a ResNet50

using an FPN with extraction layers P4, P3, and P2,

as deﬁned in the original paper (Lin et al., 2017a),

using a depth of 512. The results of this comparison

are shown in Table 1.

CUB. As mentioned above, for CUB, we investigated

two different kinds of enlarged output feature maps:

the quadruple enlargement, as done in (Choe et al.,

2020), and a double enlargement, as done in the ex-

periments on the OpenImages dataset. We observe a

positive inﬂuence of the FPN for GMP and GAP, how-

ever, with different best-performing layers for each

pooling method. For example, for GAP, the FPN

layer yielding the best results is the P3 layer, where a

MaxBoxAccV2 of 63.88 and 64.86 is achieved with-

out and with Cutout usage, respectively. For GMP, in

turn, the P4 layer yields the best results, achieving up

to 66.09 MaxBoxAccV2 and hence outperforming all

other combinations. For GLSEP, the doubly enlarged

ResNet50 without FPN yields the best results, while

the quadruply enlarged one performed the worst. The

differences in the top-performing FPN layer for each

method can likely be explained by looking at the lo-

calization performance conditions of the single meth-

ods. As GMP does not aggregate information over

a larger area in contrast to GAP, its localizations are

more accurate for lower-resolution features with more

semantic meaning. The same goes for GLSEP, which

does aggregate information over a larger area, but

only in a reduced amount compared to GAP due to

different implicit weighting in the log-sum-exp func-

tion. Therefore, GMP and GLSEP ﬁnd the optimal

balance between localization features and semantic

features in a lower-resolution layer than GAP. In addi-

tion to this, the results suggest that a lower resolution

of the feature maps synergizes better with GLSEP.

Furthermore, it should be noted that, while the P3

layer has the same output resolution as the ResNet50

with a four times enlarged output feature map for

CUB (28 × 28), the performance using the P3 layer

is greater. This shows that the resolution is not the

most important factor for good localization, but other

factors like the semantics of the features play a signif-

icant role as well.

OpenImages. On the OpenImages dataset, neither

the GAP baseline nor GLSEP shows improvements

when using the FPN, resulting in a top PxAP of 59.00

and 61.76, respectively. In contrast, GMP gains an

increase of PxAP from 61.60 to 62.01.

The good performance of GAP and GLSEP using

only the original network features can be explained

through the bigger objects in the OpenImages dataset,

which strongly differ from the ones contained in the

CUB dataset. For localizing or segmenting the big-

ger objects, ﬁner-grained features are not necessary,

and more coarse-grained localizations are sufﬁcient.

While GMP also achieves good results without FPN,

it appears to also get use out of the very ﬁne-grained

features of the P2 FPN layer, which are likely too

noisy for area aggregation pooling methods like GAP

and GLSEP.

4.5 Pooling Layer Comparison

We now compare the different pooling methods based

on the results shown in Table 1. Overall, we ﬁnd

that the performance of the different pooling layers

depends strongly on the dataset, primarily due to the

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization

185

Table 1: The results of our experiments using a ResNet50 and a Feature Pyramid Network using three different extraction

layers. All experiments are averaged over ﬁve runs. Top results are marked in bold. Experiments marked with (2x) and (4x)

represent models with doubled or quadrupled output resolution by stride removal. The setups with (4x) on CUB and (2x) on

OpenImages are the ones used in (Choe et al., 2020).

Network Pooling

CUB

(MaxBoxAccV2)

OpenImages

(PxAP)

No Cutout Cutout No Cutout Cutout

ResNet50

without FPN (4x)

GAP 62.22 ± 0.19 62.66 ± 0.21 - -

GMP 51.00 ± 0.82 55.67 ± 0.82 - -

GLSEP 43.13 ± 1.79 51.45 ± 1.05 - -

ResNet50

without FPN (2x)

GAP 59.38 ± 0.85 63.09 ± 0.65 59.00 ± 0.28 57.37 ± 0.12

GMP 58.13 ± 0.53 62.14 ± 1.06 61.60 ± 0.15 57.97 ± 1.58

GLSEP 56.86 ± 0.74 59.31 ± 1.06 61.76 ± 0.15 61.45 ± 0.25

ResNet50

+ FPN (P2)

GAP 59.40 ± 0.84 64.33 ± 0.77 57.63 ± 0.29 58.44 ± 0.24

GMP 63.03 ± 0.96 64.04 ± 0.71 62.01 ± 0.33 60.44 ± 0.26

GLSEP 53.26 ± 0.68 55.73 ± 0.43 56.32 ± 0.08 56.26 ± 0.24

ResNet50

+ FPN (P3)

GAP 63.88 ± 0.73 64.86 ± 0.53 56.04 ± 0.13 57.98 ± 0.43

GMP 61.68 ± 1.11 64.79 ± 1.27 59.15 ± 0.57 60.02 ± 0.25

GLSEP 54.58 ± 0.43 56.59 ± 0.31 57.42 ± 0.11 57.44 ± 0.26

ResNet50

+ FPN (P4)

GAP 59.92 ± 1.26 63.25 ± 0.81 57.60 ± 0.30 57.72 ± 0.36

GMP 63.16 ± 1.55 66.09 ± 0.34 59.31 ± 0.32 58.27 ± 0.11

GLSEP 56.16 ± 0.64 57.05 ± 0.69 57.32 ± 0.27 57.88 ± 0.18

granularity and size of the objects, as well as the func-

tionality of the respective pooling method. During

training, CNNs typically focus on the most discrim-

inative parts of the objects. CUB is a typical ﬁne-

grained dataset and therefore only has subtle differ-

ences between the different classes, resulting in the

detected discriminative areas being very small. Open-

Images contains more general objects, for which the

full extent can be viewed as discriminative area. Due

to the functionality of CAM, the network will mainly

mark the areas it considers to be discriminative for

the class in question as localization area. As men-

tioned above, GMP and GLSEP are more precise than

GAP, and therefore mark only the small discrimina-

tive parts of the object during localization. The above-

mentioned impreciseness of GAP leads to it marking

areas larger than the small discriminative regions and

therefore marking a bigger part of the object in the

localization map. This leads to GAP outperforming

the alternative strategies on CUB with no additional

augmentation.

This impreciseness, however, is disadvantageous

on OpenImages, where already most of the object’s

extent is utilized during classiﬁcation and therefore

also localization, leading to both GMP and GLSEP

outperforming GAP with PxAPs of 61.60 and 61.76,

respectively. This assessment is also supported by the

experiments including Cutout (DeVries and Taylor,

2017) usage. Cutout usually leads to a stronger focus

on the complete object instead of only the most dis-

criminative parts. Hence, it leads to an improvement

for all methods only on the CUB dataset, resulting

in GMP outperforming both alternative methods with

FPN layer P4 with a MaxBoxAccV2 of 66.09. On

OpenImages, the effect of Cutout is negligible or even

detrimental, as the focus already lies on the whole ex-

tent of the object. This leads to GMP performing best

using FPN layer P2 without Cutout (PxAP 62.01). An

overview and comparison of qualitative results gener-

ated by the methods can be found in the Appendix.

Comparison with State-of-the-Art Methods. We

also compare our results with the ones presented in

(Choe et al., 2020), as well as the newer methods

from (Bae et al., 2020), (Ki et al., 2020) and (Kim

et al., 2021). The results of the comparison can be

seen in Table 2. We observe that our proposed ap-

proaches result in signiﬁcant improvements over the

GAP baselines from (Choe et al., 2020) and lead to

larger differences compared to competing methods.

On the CUB dataset, besides the baseline, we out-

perform all competing methods, with the exception

of HaS (Singh and Lee, 2017) and IVR (Kim et al.,

2021). On OpenImages, our methods outperform ev-

ery competing approach by a large margin. It should

be noted that GLSEP without bells and whistles leads

to a new state-of-the-art result on OpenImages, which

is only outperformed by the combination of FPN and

GMP, raising the new state-of-the-art even further.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

186

Table 2: Comparison of the relative improvements of the results shown in (Choe et al., 2020) and other previous works with

our best results using GMP and GLSEP. The network used is a ResNet50 in all cases. The topmost values used for comparison

have been taken from (Choe et al., 2020).

Method

CUB

(MaxBoxAccV2)

OpenImages

(PxAP)

GAP (Zhou et al., 2016) 63.0 58.5

HaS (Singh and Lee, 2017) +1.7 -2.6

ACoL (Zhang et al., 2018b) +3.5 -1.2

SPG (Zhang et al., 2018c) -2.6 -1.8

ADL (Choe and Shim, 2019) -4.6 -3.3

CutMix (Yun et al., 2019) -0.2 -0.8

Bae et al.(Bae et al., 2020) - +2.4

Ki et al.(Ki et al., 2020) +0.2 -

IVR (Kim et al., 2021) +3.83 +0.47

GMP + FPN (P4) + Cutout (Ours) +3.09 -0.23

GMP + FPN (P2) (Ours) +0.03 +3.51

GLSEP (No FPN) (Ours) -3.69 +3.26

5 CONCLUSIONS

In this paper, we investigated alternative pooling

strategies as a replacement for global average pool-

ing in neural networks for weakly supervised object

localization, namely global max pooling and global

log-sum-exp pooling. This has been done in conjunc-

tion with adding a Feature Pyramid Network, where

we have been able to increase the output resolution of

the network to obtain more precise localizations and

study the inﬂuence of the different pooling strategies.

We found that on CUB, the Feature Pyramid Network

alone in conjunction with global average pooling can

already bring improvements. However, the combi-

nation of Cutout and global max pooling with the

Feature Pyramid Network outperforms all other alter-

natives by a large margin. On OpenImages, global

log-sum-exp pooling alone already outperforms the

global average pooling baseline by a large margin.

In conjunction with Feature Pyramid Network, global

max pooling improves the results even further, set-

ting a new state-of-the-art. Regarding Cutout, we

found that it primarily improves the results in a ﬁne-

grained setting, where the network’s focus usually lies

on a small discriminative area. Here, at the exam-

ple of CUB, Cutout helped to distribute the network

focus over the complete objects, improving localiza-

tion. However, as seen on the OpenImages dataset, for

objects with more apparent features, its effect on the

performance is either negligible or even detrimental.

All in all, our experiments conﬁrmed that global aver-

age pooling is suboptimal for correct localization, and

global max pooling, as well as global log-sum-exp

pooling, situationally offer better alternatives. Our

approach is a potential basis for the development of

further advanced methods in the area of weakly su-

pervised object localization. In future work, it would

be interesting to study parameterized versions of the

alternative pooling strategies in order to further opti-

mize them concerning dedicated model design objec-

tives.

ACKNOWLEDGEMENTS

Matthias K

orschens thanks the Carl Zeiss Foundation

for the ﬁnancial support.

REFERENCES

Bae, W., Noh, J., and Kim, G. (2020). Rethinking class ac-

tivation mapping for weakly supervised object local-

ization. In European Conference on Computer Vision,

pages 618–634. Springer.

Benenson, R., Popov, S., and Ferrari, V. (2019). Large-scale

interactive object segmentation with human annota-

tors. In Proceedings of the IEEE Conference on Com-

puter Vision and Pattern Recognition (CVPR), pages

11700–11709.

Chattopadhay, A., Sarkar, A., Howlader, P., and Balasub-

ramanian, V. N. (2018). Grad-cam++: Generalized

gradient-based visual explanations for deep convolu-

tional networks. In Proceedings of the IEEE Win-

ter Conference on Applications of Computer Vision

(WACV), pages 839–847.

Choe, J., Oh, S. J., Lee, S., Chun, S., Akata, Z., and Shim,

H. (2020). Evaluating weakly supervised object lo-

calization methods right. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 3133–3142.

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization

187

Choe, J. and Shim, H. (2019). Attention-based dropout

layer for weakly supervised object localization. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition (CVPR), pages 2219–

2228.

Christlein, V., Spranger, L., Seuret, M., Nicolaou, A., Kr

al,

P., and Maier, A. (2019). Deep generalized max

pooling. In 2019 International Conference on Docu-

ment Analysis and Recognition (ICDAR), pages 1090–

1096.

DeVries, T. and Taylor, G. W. (2017). Improved regular-

ization of convolutional neural networks with cutout.

arXiv preprint arXiv:1708.04552.

Fu, R., Hu, Q., Dong, X., Guo, Y., Gao, Y., and Li, B.

(2020). Axiom-based grad-cam: Towards accurate vi-

sualization and explanation of cnns. arXiv preprint

arXiv:2008.02312.

Gao, Y., Beijbom, O., Zhang, N., and Darrell, T. (2016).

Compact bilinear pooling. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 317–326.

He, K., Gkioxari, G., Doll

ar, P., and Girshick, R. (2017).

Mask r-cnn. In Proceedings of the IEEE International

Conference on Computer Vision (ICCV), pages 2961–

2969.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 770–778.

Ki, M., Uh, Y., Lee, W., and Byun, H. (2020). In-

sample contrastive learning and consistent attention

for weakly supervised object localization. In Proceed-

ings of the Asian Conference on Computer Vision.

Kim, J., Choe, J., Yun, S., and Kwak, N. (2021). Normaliza-

tion matters in weakly supervised object localization.

In Proceedings of the IEEE/CVF International Con-

ference on Computer Vision, pages 3427–3436.

Kirillov, A., Girshick, R., He, K., and Doll

ar, P. (2019).

Panoptic feature pyramid networks. In Proceedings of

the IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 6399–6408.

Lin, T.-Y., Doll

ar, P., Girshick, R., He, K., Hariharan, B.,

and Belongie, S. (2017a). Feature pyramid networks

for object detection. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 2117–2125.

Lin, T.-Y., Goyal, P., Girshick, R., He, K., and Doll

ar, P.

(2017b). Focal loss for dense object detection. In

Proceedings of the IEEE International Conference on

Computer Vision (ICCV), pages 2980–2988.

Muhammad, M. B. and Yeasin, M. (2020). Eigen-cam:

Class activation map using principal components. In

2020 International Joint Conference on Neural Net-

works (IJCNN), pages 1–7.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).

Pytorch: An imperative style, high-performance deep

learning library. In Wallach, H., Larochelle, H.,

Beygelzimer, A., d'Alch

e-Buc, F., Fox, E., and Gar-

nett, R., editors, Advances in Neural Information Pro-

cessing Systems 32, pages 8024–8035. Curran Asso-

ciates, Inc.

Pinheiro, P. O. and Collobert, R. (2015). From image-level

to pixel-level labeling with convolutional networks. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition (CVPR), pages 1713–

1721.

Ramaswamy, H. G. et al. (2020). Ablation-cam: Vi-

sual explanations for deep convolutional network via

gradient-free localization. In Proceedings of the IEEE

Winter Conference on Applications of Computer Vi-

sion (WACV), pages 983–991.

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,

Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-

stein, M., et al. (2015). Imagenet large scale visual

recognition challenge. International Journal of Com-

puter Vision, 115(3):211–252.

Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R.,

Parikh, D., and Batra, D. (2017). Grad-cam: Visual

explanations from deep networks via gradient-based

localization. In Proceedings of the IEEE International

Conference on Computer Vision (ICCV), pages 618–

626.

Simon, M., Gao, Y., Darrell, T., Denzler, J., and Rodner, E.

(2017). Generalized orderless pooling performs im-

plicit salient matching. In Proceedings of the IEEE

International Conference on Computer Vision (ICCV),

pages 4960–4969.

Singh, K. K. and Lee, Y. J. (2017). Hide-and-seek: Forc-

ing a network to be meticulous for weakly-supervised

object and action localization. In Proceedings of the

IEEE International Conference on Computer Vision

(ICCV), pages 3544–3553.

Wah, C., Branson, S., Welinder, P., Perona, P., and Be-

longie, S. (2011). The caltech-ucsd birds-200-2011

dataset.

Wang, H., Wang, Z., Du, M., Yang, F., Zhang, Z., Ding, S.,

Mardziel, P., and Hu, X. (2020). Score-cam: Score-

weighted visual explanations for convolutional neural

networks. In Proceedings of the IEEE Conference on

Computer Vision and Pattern Recognition Workshops

(CVPR-WS), pages 24–25.

Yun, S., Han, D., Oh, S. J., Chun, S., Choe, J., and Yoo,

Y. (2019). Cutmix: Regularization strategy to train

strong classiﬁers with localizable features. In Pro-

ceedings of the IEEE International Conference on

Computer Vision (ICCV), pages 6023–6032.

Zhang, B., Zhao, Q., Feng, W., and Lyu, S. (2018a). Al-

phamex: A smarter global pooling method for convo-

lutional neural networks. Neurocomputing, 321:36–

48.

Zhang, X., Wei, Y., Feng, J., Yang, Y., and Huang, T. S.

(2018b). Adversarial complementary learning for

weakly supervised object localization. In Proceedings

of the IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR), pages 1325–1334.

Zhang, X., Wei, Y., Kang, G., Yang, Y., and Huang,

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

188

T. (2018c). Self-produced guidance for weakly-

supervised object localization. In Proceedings of the

European Conference on Computer Vision (ECCV),

pages 597–613.

Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., and Tor-

ralba, A. (2016). Learning deep features for discrim-

inative localization. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 2921–2929.

APPENDIX

Hyperparameter Search

As mentioned in the main paper, our hyperparameter

search was conducted by random sampling pairs or

triples of parameters from certain intervals, depend-

ing on the experimental setting. The hyperparameters

we sampled are learning rate, weight decay, and the

Cutout (DeVries and Taylor, 2017) max size. Dur-

ing training, the size of the Cutout-square was also

sampled from the interval (0.0, maxsize), which rep-

resents sizes relative to the maximum size of the im-

age.

The learning rate and the weight decay were sam-

pled from a log-uniform distribution over the inter-

vals (1e-5, 1.0) and (1e-7, 1e-1), respectively. The

Cutout maximum size was sampled uniformly from

the interval (0.0, 0.5). It should be noted that for

the quadruple enlargement experiment using GLSEP

without Cutout we chose the log-uniform interval of

(1e-7, 0.01), as otherwise the network diverged.

Example Heatmaps

A selection of example heatmaps comparing our

combined approach using global log-sum-exp pool-

ing (GLSEP) and global max pooling (GMP) with

the standard class activation mapping (CAM) (Zhou

et al., 2016) approach using global average pooling

(GAP) is shown in Figure 2 for the CUB dataset and

in Figure 3 for the OpenImages dataset.

In general, we notice that the heatmaps using GAP

are often very accurate already. However, on many

occasions, as mentioned above, it focuses too strongly

on few discriminative areas. In several other exam-

ples from Figure 2, it includes the environmental sur-

roundings of the objects, like water. We also note that

both are not the case for GMP and GLSEP in any of

the images. This leads to GMP generating better lo-

calizations in several cases. GLSEP performs drasti-

cally differently on both datasets, as also seen in the

quantitative results in Table 1. While on CUB, it does

not have the same problems as GAP, its localization

is often widely inexact, strongly focusing on the most

discriminative parts of the object. On OpenImages in

Figure 3, however, it is often more accurate than both

competing methods. Here, it often matches almost the

exact shape of the object. In several instances, it ap-

pears to also focus too strongly on the most discrimi-

native areas, leading to GMP outperforming it.

To summarize, in these qualitative results, we also

observe the beneﬁts of our approach compared to the

standard CAM + GAP approach.

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization

189

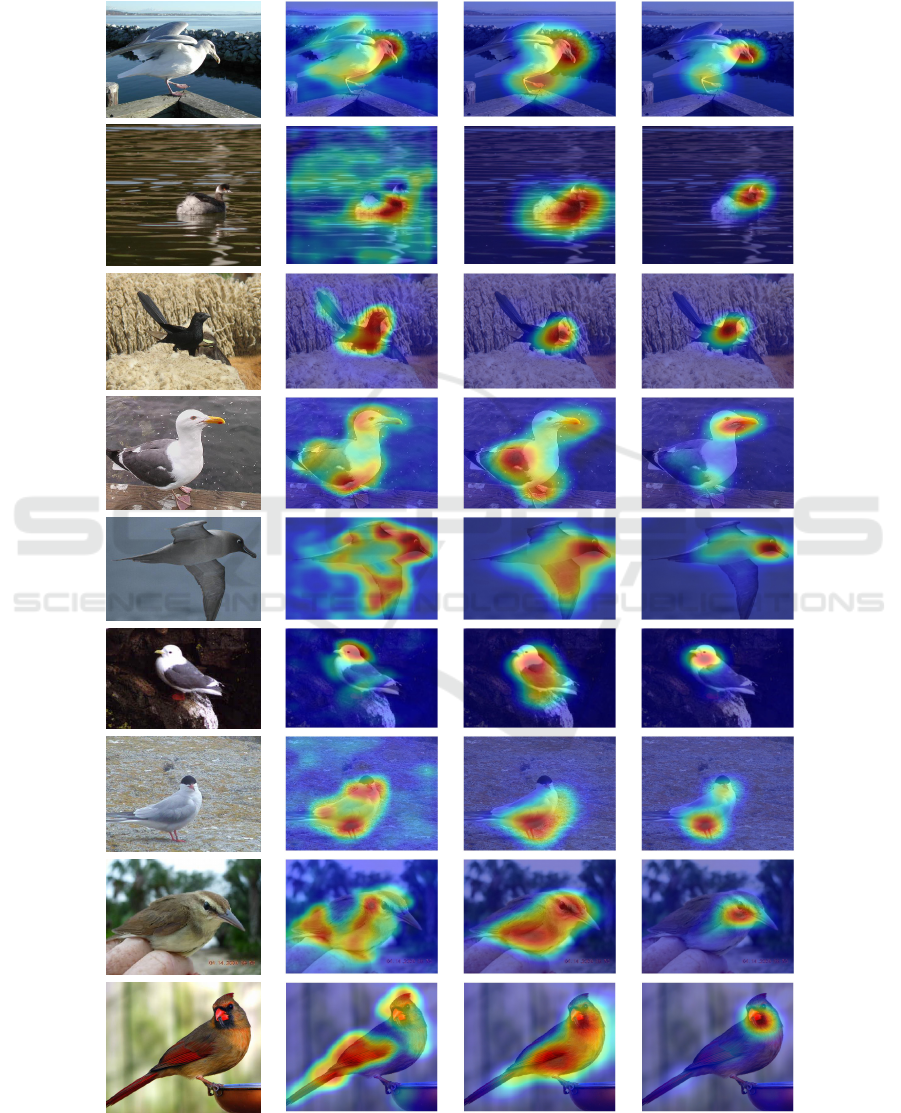
Original

Image

CAM

+ GAP

CAM

+ GMP

+ FPN (P4)

+ Cutout

CAM

+ GLSEP

+ Cutout

Figure 2: Example heatmaps from the CUB dataset using different setups. The CAM + GAP column represents the baseline

approach using vanilla CAM without FPN and Cutout.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

190

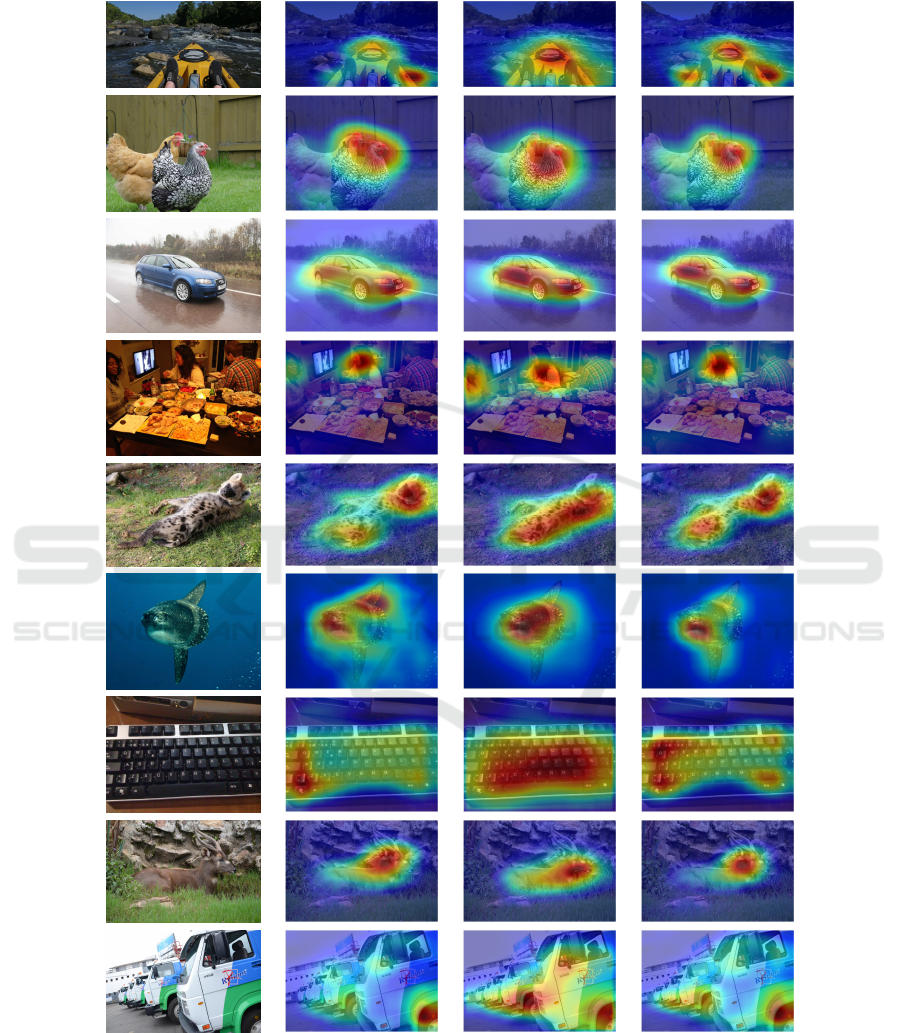
Original

Image

CAM

+ GAP

CAM

+ GMP

+ FPN (P2)

CAM

+ GLSEP

Figure 3: Example heatmaps from the OpenImages dataset using different setups. The CAM + GAP column represents the

baseline approach using vanilla CAM without FPN and Cutout.

Beyond Global Average Pooling: Alternative Feature Aggregations for Weakly Supervised Localization

191