Camera Pose Estimation using Human Head Pose Estimation

Robert Fischer

, Michael H

odlmoser

and Margrit Gelautz

2 a

emotion3D GmbH, Vienna, Austria

Visual Computing and Human-Centered Technology, TU Wien, Vienna, Austria

Keywords:

Camera Networks, Camera Pose Estimation, Head Pose Estimation, Extrinsic Calibration.

Abstract:

This paper presents a novel framework for camera pose estimation using the human head as a calibration

object. The proposed approach enables extrinsic calibration based on 2D input images (RGB and/or NIR),

without any need for additional calibration objects or depth information. The method can be used for single

cameras or multi-camera networks. For estimating the human head pose, we rely on a deep learning based

2D human facial landmark detector and ﬁt a 3D head model to estimate the 3D human head pose. The paper

demonstrates the feasibility of this novel approach and shows its performance on both synthetic and real multi-

camera data. We compare our calibration procedure to a traditional checkerboard calibration technique and

calculate calibration errors between camera pairs. Additionally, we examine the robustness to varying input

parameters, such as simulated people with different skin tone and gender, head models, and variations in

camera positions. We expect our method to be useful in various application domains including automotive in-

cabin monitoring, where the ﬂexibility and ease of handling the calibration procedure are often more important

than very high accuracy.

1 INTRODUCTION

Registering the position and orientation of cameras

relative to each other is called camera pose estimation

or extrinsic calibration. It is a common task in 3D

computer vision, where main application ﬁelds cover

the areas of robotics as well as automotive and virtual

reality (Pajdla and Hlav

ac, 1998; Xu et al., 2021). In

order to calculate the camera pose, some known cali-

bration object is commonly used to ﬁnd proper inter-

relationships (Gua et al., 2015). Prevalent objects are

boards with a checkerboard pattern or a circle grid

pattern on a ﬂat surface (Zhang, 2000; Abad et al.,

2004). Unfortunately, such patterns are not always

easily applicable in different scenes and use cases.

In this paper, we present a novel approach to calcu-

late the extrinsics of multiple cameras using the hu-

man head as a calibration pattern. Figure 1 shows

the application of our camera pose estimation tech-

nique in an automobile cockpit. Given one or mul-

tiple synchronized cameras observing a human head

and one projection for each camera of such a head

allows the extraction of 2D landmarks for each pro-

jection, which, in combination with a given 3D head

model, allows the extraction of both a 3D head pose

https://orcid.org/0000-0002-9476-0865

and all camera poses. The presented method is there-

fore especially suited for camera setups where human

heads are visible or analyzed, such as environments

within a cockpit of a vehicle, train or plane, where

one or more cameras are focusing on the occupants.

By using an underlying 3D head model, the method

does not need depth information as an input and in-

stead only requires 2D input images, such as RGB

or NIR images. Our approach is useful for applica-

tions where an ease of calibration is more important

than a high calibration accuracy. Such applications in-

clude region-based attention monitoring (Lamia and

Moshiul, 2019), robot attention tracking (Stiefelha-

gen et al., 2001) and automated shops (Gross, 2021).

It is infeasible to require users of such systems to cal-

ibrate the cameras extrinsically beforehand.

2 RELATED WORK

Using the human head as a calibration target is a novel

approach for multi-camera pose estimation. Tradi-

tionally, a planar calibration pattern has been applied

for the task of multi-camera pose estimation. Ini-

tially, (Zhang, 1999) proposes to use a plane from

unknown orientations. Later, (Zhang, 2000) propose

Fischer, R., Hödlmoser, M. and Gelautz, M.

Camera Pose Estimation using Human Head Pose Estimation.

DOI: 10.5220/0010879400003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

877-886

ISBN: 978-989-758-555-5; ISSN: 2184-4321

877

Figure 1: Our camera pose estimation framework performs

a multi-camera pose estimation based purely on head pose

estimation.

to use a planar checkerboard-like calibration pattern.

(Abad et al., 2004) adapt this approach to rely on con-

centric cycles. (Ansar and Daniilidis, 2002) propose

an algorithm for camera pose estimation supporting

both point and line correspondences. (Manolis and

Xenophon, 2013) shows a model-based pose estima-

tion technique using general rigid 3D models can be

applied as well. (Camposeco et al., 2018) aim to solve

camera pose estimation by leveraging structure-based

(2D-3D) and structure-less (2D-2D) correspondences.

oll et al., 2010) provide an overview of camera pose

estimation techniques.

Human head pose estimation is the task of esti-

mating the 3D pose of a head in a given input image

(Shao et al., 2020). In some earlier works, head pose

estimation was performed by using manifolds (Chen

et al., 2003; Balasubramanian et al., 2007; Raytchev

et al., 2004). Promising results were also achieved by

applying random forests on RGB and depth images

(z. Qiao and Dai, 2013; Fanelli et al., 2011; Fanelli

et al., 2013; Huang et al., 2010; Valle et al., 2016; Li

et al., 2010). Deep learning based approaches have

also shown to be successful for RGB and depth im-

ages (Venturelli et al., 2016; Ruiz et al., 2018; Wu

et al., 2018; Liu et al., 2016; Patacchiola and Can-

gelosi, 2017).

The need for multi-camera pose estimation in the

absence of a dedicated calibration object is common

in 3D computer vision. (Bleser et al., 2006) use a

CAD model to reconstruct the camera pose. The ap-

proach of (Rodrigues et al., 2010) exploits planar mir-

ror reﬂections in the scene. (H

odlmoser et al., 2011)

rely on pedestrians on a zebra crossing to estimate the

camera pose. Related to our approach are (Puwein

et al., 2014), (Kosuke et al., 2018) and (Moliner et al.,

2020). However, their methods use the whole hu-

man body pose, instead of only the head pose, to cal-

culate the extrinsics of all cameras relative to each

Table 1: Runtimes of head pose estimation on ARM Cortex

A57 (2.035 GHz) per camera.

No. Cores: 1 2 3 4

Runtime 25.1 ms 14.9 ms 12.1 ms 9.9 ms

other. Consequently, these approaches usually require

the full human body to be visible by the cameras.

Such set-ups are convenient in common surveillance

or studio-like environments, but less well suited for

scenarios where the human head is the focus of the

camera setup. Another fundamental difference is that

these approaches use the joint positions as point cor-

respondences, whereas our work relies on pure esti-

mation of a human’s head pose.

3 CAMERA POSE ESTIMATION

Our multi-camera calibration method performs head

pose estimation for each camera independently and

simultaneously, resulting in a set of transformations

from a shared head coordinate system into the respec-

tive camera coordinate systems and vice versa. In this

section, we explain the overall calibration workﬂow

for multi-camera pose estimation using 3D head pose

estimation.

3.1 General Workﬂow

Multi-camera pose estimation is a common problem

in 3D computer vision and can be time-consuming to

perform. Traditionally, it is ﬁrst necessary to phys-

ically prepare some calibration object, for example

print an adequate checkerboard, and then validate that

the calibration object satisﬁes certain conditions, such

as being rigid and unbendable. Afterwards, it is usu-

ally necessary to set up and parametrize the calibra-

tion pipeline. The calibration itself can then be exe-

cuted by placing the calibration object, capturing the

calibration data and ﬁnally performing the calibration.

In contrast, our approach only requires a single person

to be present in the scene in order to calculate the head

pose based camera pose estimation. Calculating the

human head pose is computationally more expensive

than localizing the checkerboard pattern. We counter-

act this problem by running the head pose estimation

algorithm on a graphical processing unit (GPU), re-

sulting in comparable execution times. Table 1 gives

an overview of the runtimes on different numbers of

cores.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

878

3.2 Camera Pose Estimation using 3D

Human Head Pose Estimation

Assuming the camera intrinsics are known, the ﬁrst

step in our novel camera pose estimation pipeline is

the extraction of a human head pose. In principle,

any head pose estimator that returns a proper orien-

tation and translation for a human head can be used

for our method. For the case of cockpits in vehicles,

we can usually assume that the cameras have an un-

obstructed view of the occupant’s face, which allows

for the usage of facial landmarks for head pose esti-

mation. In our work, we ﬁrst detect the face using

an off-the-shelf face detector and then extract the fa-

cial landmarks in the captured 2D image from each

camera. We choose a convolutional neural network

(CNN) architecture to obtain the facial landmarks us-

ing convolutional pose machines (CPMs) based on

(Wei et al., 2016) trained with faces from the COCO

2014 dataset (T.-Y. Lin et al., 2014). The authors of

(Wei et al., 2016) provide a prediction framework for

learning image features and image-dependent spatial

models with long-range dependencies between image

features. In the original paper, the authors applied

CPMs for human pose estimation, but as shown in

Section 4, this can be extended to extracting facial

landmarks as well.

We then use the extracted facial landmarks to ﬁt

a 3D-head model using iterative Perspective-n-Point

(PnP) on the estimated facial landmarks (Lu et al.,

2000). We ﬁrst consider the case of a single camera.

Using PnP, we get a transformation from the head co-

ordinate system to the camera coordinate system. The

accuracy of the PnP-step depends on two main fac-

tors. Firstly, the quality of the facial landmarks. For

example, the nose can usually be predicted relatively

precisely. The same might not be the case for the ears,

as they are often covered by hair or the orientation of

the head itself. Luckily, the CPM architecture we im-

plemented can often still estimate a reasonable loca-

tion for such facial landmarks. Secondly, the degree

to which the 3D-head model actually matches the pre-

dicted facial landmarks is also important for the qual-

ity of the ﬁnal head pose. We assume a predeﬁned

3D-head model for each detection, which might lead

to more inaccuracy if the recorded head does not ﬁt

the assumption. Nevertheless, we found in our exper-

iments that a generic 3D-head model still is applicable

for a broad range of different human heads.

In the following we discuss how to construct the

multi-camera network. Figure 2 visualizes the multi-

camera setup with the corresponding coordinate sys-

tems and transformations.

Figure 2: Schematic overview of the camera network

with the corresponding camera coordinate systems (CCS),

a shared coordinate system (SCS), and the corresponding

transformations between them.

We deﬁne a head pose as a translation and orien-

tation between a camera coordinate system’s origin to

the head’s coordinate system’s origin. To construct a

transformation T from the head pose translation t and

rotation matrix R, which transforms from the head co-

ordinate system into the camera coordinate system,

we use the convention of Equation 1. We deﬁne a

transformation T as a 4x3 matrix in which a 3x3 ma-

trix R deﬁnes the rotation and a 1x3 matrix t speciﬁes

the translation. Equation 2 shows how to perform the

inverse transformation.

T = [R|t] (1)

−1

= [R

| − R

∗t] (2)

In Figure 3, the coordinate system of a camera is de-

noted as CCS

, the shared coordinate system deﬁned

by the head pose is denoted as SCS. Estimating the

head pose in the coordinate system of a camera CCS

gives us a transformation T

, which is a transforma-

tion from the shared coordinate system SCS into CCS

Transforming from CCS

into SCS can be done by ap-

plying the transformation T

−1

SCS

= T

−1

∗t

(3)

SCS

= rot(T

)

−1

∗ R

∗ rot(T

) (4)

rot([R|t]) = R (5)

Equation 3 deﬁnes the transformation of an arbitrary

translation t

from the coordinate system of camera i

CCS

into the shared coordinate system deﬁned by the

head pose SCS, resulting in the transformed transla-

tion t

SCS

. It can be seen that we can transform from

the SCS into CCS

by applying the transformation T

Equation 4 shows how to transform an arbitrary ro-

tation R

from the coordinate system of the camera

Camera Pose Estimation using Human Head Pose Estimation

879

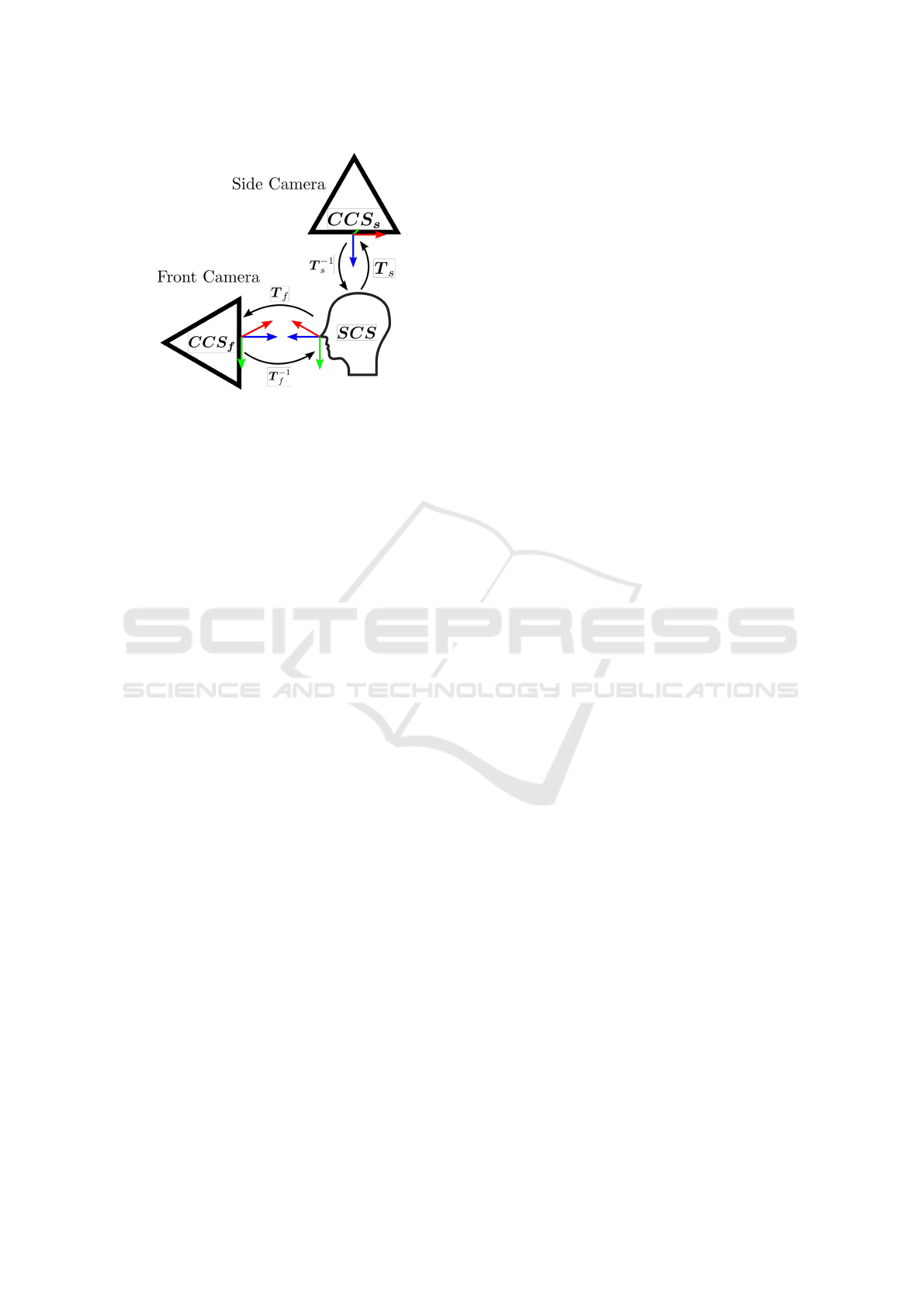
Figure 3: Schematic overview of the proposed camera setup

and the corresponding transformations for the experiments.

See text for more detailed explanations.

i CCS

into the shared coordinate system deﬁned by

the head pose SCS, resulting in the transformed rota-

tion R

SCS

. The function rot(T) returns the 3x3 rotation

matrix R of the transformation T (see Equation 5).

4 EXPERIMENTS

In the following subsections we examine the accu-

racy of our calibration method under multiple modal-

ities: We investigate the overall performance of head

pose based camera pose estimation in Section 4.2. We

compare our approach to a camera pose estimation

based on a checkerboard in Section 4.3. We examine

the bias of our approach towards different groups of

people in Section 4.4. We compare the performance

of our approach with different camera poses relative

to the head pose in Section 4.5. We analyze the im-

pact of different head models 4.6. We carry out a cal-

ibration using real data captured using the Opti-Track

Motive camera system (NaturalPoint Inc., 2021) in

Section 4.7, and we perform a qualitative evaluation

of our head pose based camera calibration in Section

4.8.

4.1 Experiment Setup

The experiments were mainly carried out using a syn-

thetic NIR camera, as we wanted to simulate a typi-

cal setup found in cars. Most of the times, near in-

frared cameras are applied in such environments be-

cause they do not depend on a well-illuminated scene

to deliver high-quality images. Other setups using

RGB cameras are also compatible with our method.

Using synthetically rendered images enables us to test

many different modalities which would have been dif-

ﬁcult to replicate in the real world. In order to ensure

our approach generalizes we also performed experi-

ments using a real-world near infrared camera setup.

Our simulation additionally includes the ground truth

camera pose estimation for all cameras. Thus, we can

compare the results of our multi-camera pose estima-

tion method with the ground truth pose.

We perform our experiments using stereo camera

setups commonly found in vehicle-like cockpits. As

shown in Section 3, adding additional cameras to the

camera network has no impact on the transformation

accuracy of previous cameras. A schematic overview

of the evaluation camera setup is shown in Figure 3.

The setup consists of a front and side camera. The

front camera is placed directly in front of the occupant

and the side camera is placed on the right side of the

occupant. For our experiments we seek to deﬁne eval-

uation metrics that enable us to compare the results in-

tuitively, while also ensuring that the chosen metrics

actually reﬂect the accuracy of our system. First of

all, we split the transformation error into errors result-

ing from the translation and the rotation, in order to

distinguish between inaccuracies relating to rotation

and translation. Given a point in the shared coordinate

system SCS, we transform the point p

SCS

into CCS

and CCS

to p

using corresponding ground truth

camera pose data. Then we transform the point p

us-

ing the estimated camera pose T

−1

for camera 1 into

SCS resulting in p

SCS from 1

. Analogously, we trans-

form p

using the estimated camera pose T

−1

for cam-

era 2 into SCS resulting in p

SCS from 2

. If the estimated

camera poses match the ground truth camera poses

exactly, p

SCS from 1

= p

SCS from 2

= p

SCS

holds, mean-

ing that both points transform to the same position

in the shared coordinate system SCS. Comparing the

two transformed points p

SCS from 1

and p

SCS from 2

with

each other allows us to measure the degree of inaccu-

racy introduced by the camera pose transformation.

We then compare the mean euclidean distance of the

two points.

Similarly, for the rotation errors, given a rotation

in the shared coordinate system SCS, we transform the

rotation R

SCS

into CCS

to R

and CCS

to R

using

ground truth camera pose data. Then we transform

the rotation R

using the estimated camera pose T

−1

for camera 1 into SCS resulting in R

SCS from 1

, anal-

ogously we transform R

using the estimated camera

pose T

−1

for camera 2 into SCS resulting in R

SCS from 2

As in the previous point transformation, if the esti-

mated camera poses match the ground truth camera

pose exactly, R

SCS from 1

= R

SCS from 2

= R

SCS

holds,

meaning that the rotations transform to the same rota-

tion in the shared coordinate system SCS. Afterwards,

we convert the rotation matrices into pitch, yaw and

roll Euler angles in degrees, as they are intuitive to

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

880

Table 2: Quantitative evaluation results for our synthetic dataset. Sequence ID relates to the order of operation in which

we have performed the evaluation and is used for reference. Calibration object refers to the calibration object which has

been used for estimating the camera pose. Skin refers to the skin tone of the person visible. Head Model deﬁnes the head

model which we used for estimating the camera pose. Camera Distance deﬁnes the camera position. Refer to Figure 6 for a

visualization of the different camera positions. Mean Distance refers to the mean euclidean distance in meters between the

estimated camera positions. Mean Euler refers to the mean angle difference of the three Euler angles pitch, yaw and roll in

degrees. Std. Distance and Std. Euler refer to the standard deviation for the respective evaluation metrics. The row with

sequence ID 14 contains the evaluation results for all synthesized camera images from previous experiments.

Seq. Calibration Skin Head Camera Mean Mean Std. Std.

ID Object Model Distance Distance Euler Distance Euler

[m] [deg] [m] [deg]

1 Checkerboard - - Regular 0.103 0.171 0.002 0.178

2 Woman 1 Lighter Default Regular 0.232 10.981 0.051 7.141

3 Woman 2 Darker Default Regular 0.259 14.674 0.088 9.213

4 Woman 3 Darker Default Regular 0.212 10.744 0.059 5.736

5 Man 1 Darker Default Regular 0.279 15.015 0.083 8.88

6 Man 2 Lighter Default Regular 0.295 13.366 0.063 9.568

7 Man 3 Lighter Default Regular 0.272 13.847 0.055 10.500

9 Woman 1 Lighter Exact Regular 0.231 13.305 0.089 8.254

10 Woman 1 Lighter Default Far Side 0.226 10.053 0.121 9.040

11 Woman 1 Lighter Default Far 0.203 9.636 0.119 8.558

12 Woman 1 Lighter Default Near 0.252 10.462 0.0428 6.199

13 Woman 1 Lighter Default Side 0.203 9.636 0.119 8.558

14 All persons All All All 0.239 11.641 0.089 9.856

understand for humans. We then calculate the mean

absolute circle difference of all Euler angles.

As mentioned before, our approach is suited for

applications where an ease of calibration is more im-

portant than a high calibration accuracy. In these cir-

cumstances, we consider a mean distance of 0.3m and

a mean Euler difference below 15 degrees to be ac-

ceptable.

4.2 Core Experiment

The results of our multi-camera pose estimation

method achieved for our entire synthetic dataset can

be seen in Table 2 at sequence Id 14. The mean dis-

tance in this test is 0.24m and the mean of the Euler

angles is 11.64 degrees. Thus, our approach works as

expected and the results are satisfactory for a wide ar-

ray of different settings. We observe some inaccuracy,

but not to a degree that makes the approach inapplica-

ble for various use-cases in cockpits or other similar

environments.

4.3 Comparison with Checkerboard

This experiment compares the head pose based cam-

era pose estimation with a traditional checkerboard

based camera pose estimation workﬂow, establishing

a baseline performance for further comparisons. To

the best of our knowledge, there is no pre-existing

method for camera pose estimation using a human

head which can be compared to our approach in a

meaningful way. Thus, we chose the following ap-

proach of establishing a baseline for the accuracy.

We synthesize a scenario in which a person in

front of a stereo camera setup turns their head from

facing forward to facing 90 degrees to the right. We

sample 46 frames from this motion. In each frame,

the person moves their head slightly towards the ﬁnal

head rotation. This approach captures the inaccura-

cies introduced by different head poses relative to the

two cameras. Afterwards, we capture additional 46

frames, but this time we rotate a checkerboard from

facing forward to facing 90 degrees to the right in-

stead. As the motion and camera setup are essentially

the same, we can compare the accuracy of these two

approaches meaningfully. We calculate the metrics

described in Section 4.1 for both the head pose based

camera pose estimation and the checkerboard based

camera pose estimation. The mean distance of the

checkerboard based camera pose estimation is 0.10m

and the mean Euler is 0.11 degrees (refer to Table 2,

sequence Id 1). The mean distance for our approach

is 0.23m and the mean Euler is 11.64 degrees (refer

to Table 2, sequence Id 14). Figure 4 shows the per-

formance of our calibration method compared to the

checkerboard relative to the head rotation. The x-axis

represents the degree of the rotated head and the y-

axis represents the euclidean distance for two trans-

formed points in Figure 4 (left) and the mean Euler

difference in Figure 4 (right).

Camera Pose Estimation using Human Head Pose Estimation

881

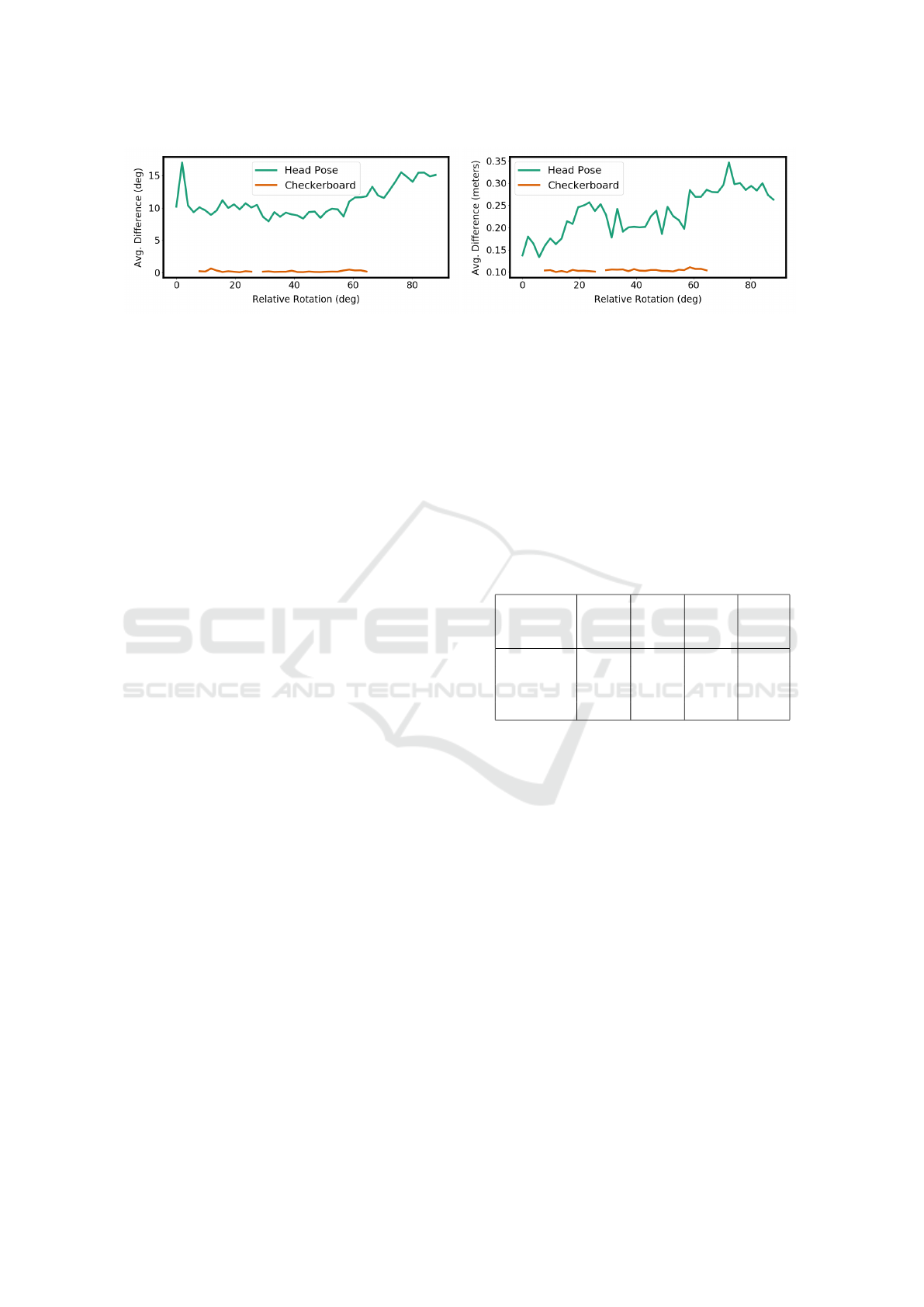
Figure 4: Comparison of the accuracy achieved using the checkerboard calibration object and the head pose based camera

pose estimation in terms of rotation (left) and translation (right) error.

The graphs of Figure 4 show that in our example

for the translation, the most accurate transformations

can be achieved for cases where the head is rotated

approximately 45 degrees. For the rotation no such

observation can be made. Another insight from those

graphs is that the checkerboard is (a) more stable re-

gardless of the rotation of the calibration object it-

self, (b) more accurate for estimating the camera pose

compared with the head pose based camera pose es-

timation and (c) the camera pose estimation fails for

extreme rotations of the checkerboard relative to the

forward-facing camera. Importantly, our approach is

not expected to match the accuracy of the checker-

board pattern. Instead its advantage lies in the ease

of calibration for cases which do not require the most

accurate calibration. Additionally, the accuracy of our

approach is heavily dependent on the quality of the

head pose estimation. Better head pose estimators

most likely result in better camera pose estimations.

However, for a variety of use cases, such as attention

monitoring or early sensor fusion in a multi-camera

setup, the inaccuracies we observe would most likely

be acceptable.

4.4 Bias towards Skin Color and

Gender

In this subsection, we examine a potential bias of our

approach towards different groups of people. In par-

ticular, we focus on the evaluation of the performance

of our model for people with different skin colors and

different genders. Many deep learning based systems

have shown signiﬁcant biases towards people with

lighter skin. In the following, we generate synthetic

datasets with different people. In particular, we create

a total of six datasets with different groups of people

and with 46 frames each, similar to the dataset syn-

thesized for Section 4.3. These datasets contain three

people with darker skin and three people with lighter

skin, as well as three females and three males. Figure

5 shows a rendering of the human models used in the

datasets for this experiment. Table 2 shows the eval-

uation results for the people in rows with sequence Id

2,3,4,5,6 and 7. Table 3 shows the evaluation metrics

for the selected subgroups.

There is no evidence of bias from the data we syn-

thesized. The maximum difference of the mean dis-

tance is 5.4 cm and the maximum difference in mean

Euler is 2.97 degrees. Thus, in our tests we found that

our approach, based on the synthesized dataset, shows

no evidence of bias regarding gender and skin-color.

Table 3: Performance metrics for people with different skin

colors and different genders. The data does not indicate

signiﬁcant bias against any skin color or gender.

Bias Mean Mean Std. Std.

Modality Dist. Euler Dist. Euler

[m] [deg] [m] [deg]

Light skin 0.266 13.4 0.062 9.9

Dark skin 0.240 12.8 0.079 8.1

Female 0.228 11.8 0.068 7.6

Male 0.282 14.7 0.069 10.2

4.5 Comparison of Camera Poses

This subsection examines the impact of different cam-

era poses relative to the head pose. Intuitively, one

would expect that different camera poses do not have

a signiﬁcant impact on the accuracy of the ﬁnal cam-

era poses, as long as the head pose can be accurately

estimated. We selected four different camera poses

for this experiment. In Figure 6, we show a rendering

of the various camera poses used for the evaluation.

Additionally to the regular camera pose (number 4 in

Figure 6), we selected two other poses which have a

smaller distance to the main frontal camera (cameras

with the label Side and Far Side in Table 2). We also

used a setup with a camera that was much closer to

the head of the person, marked with the label Near in

Table 2.

The experiment results indicate that there is no

signiﬁcant loss of performance by changing the cam-

era pose. The mean distances of the various camera

poses listed in Table 2 (Id 2, 10, 11 and 12) differ at

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

882

(a) Man 1. (b) Man 2. (c) Man 3. (d) Woman 1. (e) Woman 2. (f) Woman 3.

Figure 5: Rendering of the six different 3D models we use for data generation of our synthetic data generation pipeline. With

these models we try to cover a broad range of different appearances of humans and their facial land marks.

Figure 6: Visualization of all the camera positions of all the

synthetic experiments. Camera 1 represents the ﬁrst camera

used for all experiment setups. For the second camera, the

speciﬁc location changes: Camera 2 is used for the camera

pose with label Side, camera 3 for Far Side, camera 4 for

Regular, and camera 5 for Near in Table 2.

most 5cm from each other, the mean Euler differ an-

gles 1.3 degrees at most. The standard deviations of

the selected accuracy metrics are in the same orders of

magnitude. Thus, our experiments indicate no signif-

icant decrease of accuracy for various camera poses

relative to the head pose.

Figure 7: Correspondence between 2D facial landmarks and

the 3D head model. Left: 2D facial landmarks on 3D head.

Right: 3D head model ﬁtted according to facial landmarks.

4.6 Impact of Different Head Models

To examine the impact of different head models, we

created a dataset with a different head model. As

our data is synthetically generated, we have access to

the true 3D head model. Figure 7 shows the 2D fa-

cial landmarks (left) and the corresponding 3D head

model (right). Table 2 sequence Id 9 contains the eval-

uation results with the true 3D head model. Sequence

Id 2 shows the results using a generic 3D head model.

The difference of the mean distance is 0.1 cm, and the

difference of the mean Euler angle is 3 degrees for the

generic head model and the exact head model.

Both differences are not signiﬁcant enough to state

that the exact head model performs better (or worse)

compared to the generic head model. It is remarkable

that against our intuition, the default head model does

not perform better than the exact 3D head model. We

reason this might be due to inaccuracies in the anno-

tation of the facial landmark keypoints in the dataset

we chose to train our deep learning network on.

Table 4: Performance using real data captured by using the

Opti-Track Motive camera setup.

Calib. Mean Mean Std. Mean Std.

Object Dist. Euler Dist. Euler

[m] [deg] [m] [deg]

Checker- 0.017 0.3 0.007 0.0

board

Person 0.174 4.8 0.056 3.1

4.7 Real Data

In order to verify that our approach generalizes to real

data, we performed experiments with data captured

by the Opti-Track Motive camera system (Natural-

Point Inc., 2021). We created a setup as similar as

possible to the experiment we describe in Section 4.3.

A person’s head is rotating from the front camera to

the side camera, which is approximately 90 degrees

to the left side of the person. We additionally perform

camera pose estimation using a checkerboard, giving

us a baseline for the performance of the head pose

based camera pose estimation algorithm.

As can be seen in Table 4, the mean distance of the

head pose based camera calibration differs on average

by 17.4cm and the Euler rotation on average by 4.83

degrees. These values show that our approach gener-

Camera Pose Estimation using Human Head Pose Estimation

883

Figure 8: Head pose estimation results from real camera input. As can be seen in the qualitative results on synthetic input

data (see Figure 9), the head pose estimation is signiﬁcantly more stable and accurate on real data than on synthetic data. This

result is expected as the 2D facial landmark detector has been trained on real input data.

(a) Distance: 0.285m

Mean Euler: 14.8°.

(b) Distance: 0.130m

Mean Euler: 22.1°.

Mean Euler: 8.9°.

(d) Distance: 0.137m

Mean Euler: 10.2°.

Figure 9: Qualitative results of the synthetic dataset. The 3D-axis (1) represents the estimated head pose. The 3D axis (2)

represents the estimated camera pose and the 3D-axis with the red outline (3) represents the ground truth camera pose. The

ﬁrst row represents the forward-facing camera and the second row shows the side-facing camera. A nearby-positioned and

similarly-rotated 3D axis (2) of the estimated camera pose relative to the 3D axis (3) of the ground truth camera pose indicates

a more accurate camera pose estimation.

alizes to the real world. Interestingly, the mean Eu-

ler and distance metric is considerably lower for the

real data than the synthetic data. This phenomenon is

most likely due to the fact that the deep learning based

facial landmark extractor is better at extracting the fa-

cial landmarks of real human faces, rather than syn-

thetically rendered human faces. Qualitatively, it can

be seen in Figure 8 that the head pose estimation al-

gorithm provides more stable head rotation estimates

for real data than for the synthetic data.

4.8 Qualitative Evaluation

In this subsection, we evaluate the results of the head

pose based camera pose estimation qualitatively. We

compare the ground truth with the results of our cam-

era pose estimation result in Figure 9. It can be seen

that the main driving factor for a reliable head pose

based camera pose estimation is a proper head pose

estimation. For cases in which the head pose is es-

timated more precisely, the resulting camera pose is

also estimated more accurately. Comparing the syn-

thetic head pose estimation in Figure 9 with head pose

estimations on real data in Figure 8 reveals why the

mean Euler difference and mean distance for the real

dataset are lower. The head pose estimation for the

real image captures is qualitatively superior compared

to the synthetic dataset. There are no unexpected rota-

tions present and the nose is always the origin of the

estimated head coordinate system. Our results indi-

cate that our head pose based camera pose estimation

generalizes to real-world applications. Thus, our ap-

proach will likely perform satisfactory in a real world

application as well.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

884

5 CONCLUSION AND FUTURE

WORK

We have demonstrated the feasibility of a novel

single- and multi-camera pose estimation technique

which relies exclusively on the computed 3D head

pose of a human in the scene. A broad range of ex-

periments were carried out on simulated and real im-

ages of vehicle cockpit scenes with varying camera

conﬁgurations. Our tests on real multi-camera data

have shown an average translational and rotational er-

ror of about 17 cm and less than 5 degrees, respec-

tively. The proposed method can be applied to use

cases where a certain decrease in accuracy compared

to traditional checkerboard calibration is outweighed

by the natural, easy and ﬂexible handling of the head

pose based calibration. Such use cases include camera

setups within the cockpit of a vehicle, train or plane,

where one or more cameras focus on the occupants,

for example, for the purpose of attention monitoring

or early sensor fusion in a multi-camera environment.

Other potential applications include robot attention

tracking or monitoring costumer interest in automated

stores.

In future work, the 2D facial landmarks employed

in our approach and symmetries typically present in

human faces could potentially be used to extend our

approach to estimate the camera intrinsics as well.

This would allow for the extraction of a full camera

calibration from human faces as a calibration object.

Currently, our approach relies on detecting 2D facial

landmarks for head pose calculation. Further research

could try to alleviate the requirements of facial land-

marks detection in order to generalize the head pose

estimation algorithm to viewing conditions where the

human face is not visible to all cameras.

ACKNOWLEDGEMENTS

This work was partly supported by the Synthetic-

Cabin project (no. 884336), which is funded through

the Austrian Research Promotion Agency (FFG) on

behalf of the Austrian Ministry of Climate Action

(BMK) via its Mobility of the Future funding pro-

gram.

REFERENCES

Abad, F., Camahort, E., and Viv

o, R. (2004). Camera

calibration using two concentric circles. In Proc. of

ICIAR, pages 688–696. 1, 2

Ansar, A. and Daniilidis, K. (2002). Linear pose estimation

from points or lines. In Proc. of ECCV, pages 282–

296. 2

Balasubramanian, V., Nallure, Ye, J., and Panchanathan, S.

(2007). Biased manifold embedding: A framework for

person-independent head pose estimation. In Proc. of

CVPR, pages 1–7. 2

Bleser, G., Wuest, H., and Stricker, D. (2006). Online cam-

era pose estimation in partially known and dynamic

scenes. In Proc. of ISMAR, pages 56–65. 2

Camposeco, F., Cohen, A., Pollefeys, M., and Sattler, T.

(2018). Hybrid camera pose estimation. In Proc. of

CVPR, pages 136–144. 2

Chen, L., Zhang, L., Hu, Y., Li, M., and Zhang, H. (2003).

Head pose estimation using ﬁsher manifold learning.

In Proc. of AMFG, pages 203–207. 2

Fanelli, G., Dantone, M., Gall, J., Fossati, A., and v. Gool,

L. (2013). Random forests for real time 3d face anal-

ysis. IJCV, 101(3):437–458. 2

Fanelli, G., Gall, J., and v. Gool, L. (2011). Real time head

pose estimation with random regression forests. In

Proc. of CVPR, pages 617–624. 2

Gross, R. (2021). How the Amazon Go Store’s AI Works.

Towards Data Science (https://bit.ly/3tVHXi2). 1

Gua, J., Deboeverie, F., Slembrouck, M., v. Haerenborgh,

D., v. Cauwelaert, D., Veelaert, P., and Philips, W.

(2015). Extrinsic calibration of camera networks us-

ing a sphere. Sensors, 15(8):18985–19005. 1

odlmoser, M., Micusik, B., and Kampel, M. (2011).

Camera auto-calibration using pedestrians and zebra-

crossings. In Proc. of ICCVW, pages 1697–1704. 2

Huang, C., Ding, X., and Fang, C. (2010). Head pose esti-

mation based on random forests for multiclass classi-

ﬁcation. In Proc. of ICPR, pages 934–937. 2

Kosuke, T., Dan, M., Mariko, I., and Hideaki, K. (2018).

Human pose as calibration pattern: 3d human pose

estimation with multiple unsynchronized and uncal-

ibrated cameras. In Proc. of CVPRW, pages 1856–

18567. 2

Lamia, A. and Moshiul, H. M. (2019). Vision-based driver’s

attention monitoring system for smart vehicles. In In-

telligent Computing & Optimization, pages 196–209.

Li, Y., Wang, S., and Ding, X. (2010). Person-independent

head pose estimation based on random forest regres-

sion. In Proc. of ICIP, pages 1521–1524. 2

Liu, X., Liang, W., Wang, Y., Li, S., and Pei, M. (2016). 3d

head pose estimation with convolutional neural net-

work trained on synthetic images. In Proc. of ICIP,

pages 1289–1293. 2

Lu, C.-P., Hager, G., and Mjolsness, E. (2000). Fast and

globally convergent pose estimation from video im-

ages. TPAMI, 22(6):610–622. 3

Manolis, L. and Xenophon, Z. (2013). Model-based pose

estimation for rigid objects. In Computer Vision Sys-

tems, pages 83–92. 2

Moliner, O., Huang, S., and

Astr

om, K. (2020). Better

prior knowledge improves human-pose-based extrin-

sic camera calibration. In Proc. of ICPR, pages 4758–

4765. 2

Camera Pose Estimation using Human Head Pose Estimation

885

NaturalPoint Inc. (2021). Optitrack motive camera sys-

tem. https://optitrack.com/software/motive/. Ac-

cessed: 2021-07-26. 4, 7

oll, T., Pagani, A., and Stricker, D. (2010). Markerless

camera pose estimation - an overview. In Proc. of

VLUDS, volume 19, pages 45–54. 2

Pajdla, T. and Hlav

ac, V. (1998). Camera calibration and

euclidean reconstruction from known observer trans-

lations. In Proc. of CVPR, pages 421–426. 1

Patacchiola, M. and Cangelosi, A. (2017). Head pose es-

timation in the wild using convolutional neural net-

works and adaptive gradient methods. Pattern Recog-

nition, 71:132–143. 2

Puwein, J., Ballan, L., Ziegler, R., and Pollefeys, M. (2014).

Joint camera pose estimation and 3d human pose es-

timation in a multi-camera setup. In Proc. of ACCV,

pages 473–487. 2

Raytchev, B., Yoda., I., and Sakaue, K. (2004). Head pose

estimation by nonlinear manifold learning. In Proc. of

ICPR, volume 4, pages 462–466. 2

Rodrigues, R., Barreto, J., and Nunes, U. (2010). Camera

pose estimation using images of planar mirror reﬂec-

tions. In Proc. of ECCV, pages 382–395. 2

Ruiz, N., Chong, E., and Rehg, J. (2018). Fine-grained

head pose estimation without keypoints. In Proc. of

CVPRW. 2

Shao, X., Qiang, Z., Lin, H., Dong, Y., and

Wang, X. (2020). A survey of head

pose estimation methods. In Proc. of

iThings,GreenCom,CPSCom,SmartData,Cybermatics,

pages 787–796. 2

Stiefelhagen, R., Yang, J., and Waibel, A. (2001). Track-

ing focus of attention for human-robot communica-

tion. Citeseer. 1

T.-Y. Lin, M. M., Belongie, S., Bourdev, L., Girshick, R.,

Hays, J., Perona, P., Ramanan, D., Zitnick, C. L., and

Doll

ar, P. (2014). Microsoft coco: Common objects in

context. In Proc. of ECCV, pages 740–755. 3

Valle, R., Buenaposada, J., Vald

es, A., and Baumela, L.

(2016). Head-pose estimation in-the-wild using a ran-

dom forest. In Proc. of AMDO, pages 24–33. 2

Venturelli, M., Borghi, G., Vezzani, R., and Cucchiara, R.

(2016). Deep head pose estimation from depth data

for in-car automotive applications. In Proc. of ICPRW,

pages 74–85. 2

Wei, S., Ramakrishna, V., Kanade, T., and Sheikh, Y.

(2016). Convolutional pose machines. In Proc. of

CVPR, pages 4724–4732. 3

Wu, H., Zhang, K., and Tian, G. (2018). Simultane-

ous face detection and pose estimation using con-

volutional neural network cascade. IEEE Access,

6:49563–49575. 2

Xu, Y., Li, Y.-J., Weng, X., and Kitani, K. (2021). Wide-

baseline multi-camera calibration using person re-

identiﬁcation. In Proc. of CVPR, pages 13134–13143.

z. Qiao, T. and Dai, S. (2013). Fast head pose estimation

using depth data. In Proc. of CISP, pages 664–669. 2

Zhang, Z. (1999). Flexible camera calibration by viewing a

plane from unknown orientations. In Proc. of ICCV,

volume 1, pages 666–673. 1

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. TPAMI, 22(11):1330–1334. 1

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

886