
BRDF-based Irradiance Image Estimation to Remove Radiometric
Differences for Stereo Matching
Kebin Peng
a
, John Quarles
b
and Kevin Desai
c
Department of Computer Science, The University of Texas at San Antonio, Texas, U.S.A.
Keywords:
Bidirectional Reflectance Distribution Function, Irradiance, Radiometric Differences, Stereo Matching.
Abstract:
Existing stereo matching methods assume that the corresponding pixels between left and right views have
similar intensity. However, in real situations, image intensity tends to be dissimilar because of the radiometric
differences obtained due to change in light reflected. In this paper, we propose a novel approach for removing
these radiometric differences to perform stereo matching effectively. The approach estimates irradiance images
based on the Bidirectional Reflectance Distribution Function (BRDF) which describes the ratio of radiance to
irradiance for a given image. We demonstrate that to compute an irradiance image we only need to estimate
the light source direction and the object’s roughness. We consider an approximation that the dot product of the
unknown light direction parameters follows a Gaussian distribution and we use that to estimate the light source
direction. The object’s roughness is estimated by calculating the pixel intensity variance using a local window
strategy. By applying the above steps independently on the original stereo images, we obtain the illumination
invariant irradiance images that can be used as input to stereo matching methods. Experiments conducted on
well-known stereo estimation datasets demonstrate that our proposed approach significantly reduces the error
rate of stereo matching methods.
1 INTRODUCTION
Estimating depth from stereo image pairs is one
of the most fundamental tasks in computer vision
(Scharstein and Szeliski, 2002). This task is vital for
many applications, such as 3D reconstruction (Geiger
et al., 2011), robot navigation and control (Song et al.,
2013), object detection and recognition (Chen et al.,
2015). The standard approach is to find accurate pixel
correspondence and recover the depth using epipolar
geometry. Approaches for pixel correspondence work
with a color consistency assumption that the pixels in
the left and right views have similar color intensity
values. However, in real situations, the color intensity
values for a given pixel differs between the left and
right views. These differences are known as radiomet-
ric differences. According to (Heo et al., 2010), light
reflection and camera setting changes are two main
reasons for having radiometric differences. Light re-
flection is determined by the angle between the direc-
tion of incident ray and the direction of the surface
normal (Heo et al., 2010). The same object surface
a
https://orcid.org/0000-0003-4866-786X
b
https://orcid.org/0000-0002-4790-167X
c
https://orcid.org/0000-0002-2964-8981
could show a different color intensity value if this an-
gle is different. Another typical situation is the differ-
ence in the intensity of the light source. Apart from
light reflection, camera settings such as exposure vari-
ations decide the amount of light which reaches the
camera and hence can also cause differences in the
pixel color intensity (Heo et al., 2010).
1.1 Proposed Approach
In this paper, we consider the radiometric differences
in stereo images from the viewpoint of the Bidi-
rectional Reflectance Distribution Function (BRDF)
(Walter et al., 2007a). Commonly used in Computer
Graphics, BRDF considers the micro-structure and
light reflection features of an object’s surface and de-
scribes the ratio of radiance to irradiance for a given
image. We propose a novel BRDF-based irradiance
image estimation technique for removing radiomet-
ric differences. Different from previous approaches
(Tan and Triggs, 2010; Han et al., 2013) for radio-
metric difference removal that focus on radiance, i.e.
reflected light from the object’s surface, we consider
irradiance, i.e. incident light on the object’s surface.
Using mathematical foundations around BRDF,
734
Peng, K., Quarles, J. and Desai, K.
BRDF-based Irradiance Image Estimation to Remove Radiometric Differences for Stereo Matching.
DOI: 10.5220/0010879800003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
734-744
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
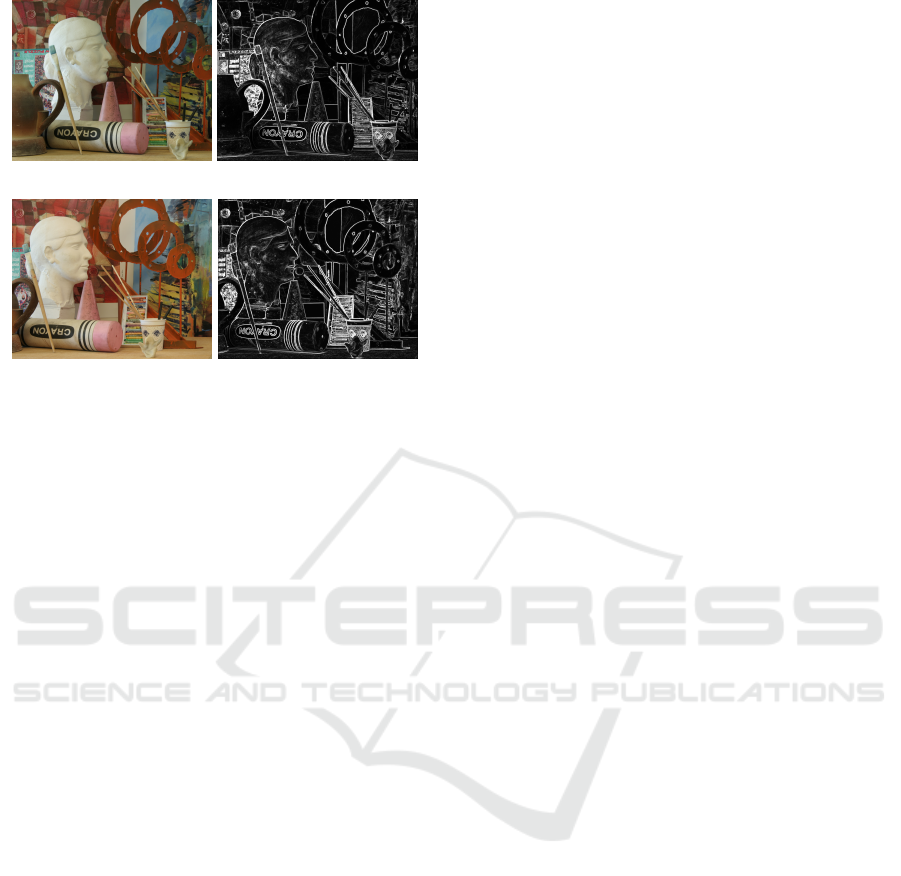
(a) Left image (b) Irradiance image of (a)
(c) Right image (d) Irradiance image of (c)
Figure 1: ArtL example from Middlebury-14 dataset
(Scharstein and Szeliski, 2002) where left (a) and right (b)
stereo images have different light conditions. (b) and (d) are
the illumination invariant irradiance images corresponding
to (a) and (c), that are computed using our radiometric dif-
ference removal approach.
we demonstrate that to compute an irradiance image
we only need to estimate two parameters - light source
direction and object roughness. In our algorithm, we
do not need to estimate the unknown light direction
parameters separately. Rather only the dot products
for these unit direction vectors need to be estimated,
for which we employ an approximation strategy based
on a Gaussian distribution (see section 3.3). To esti-
mate the surface roughness for the objects in the im-
age, we use a local window approach and estimate the
pixel intensity variance (see section 3.4). As the irra-
diance image is decided by light source intensity and
the distance between light sources and objects, it will
not be affected by light reflection, viewing angle and
camera setting changes (see Figures 6(b) and 1(d)).
By using the irradiance image as the input for stereo
matching instead of original stereo image pairs, sig-
nificant performance improvement is obtained for the
state-of-the-art stereo matching methods.
1.2 Contributions
In this paper we make the following contributions:
• A Computer Graphics perspective is provided for
removing the radiometric differences in stereo im-
ages by modeling it with the Bidirectional Re-
flectance Distribution Function (BRDF).
• Irradiance image estimation is proposed for ra-
diometric difference removal, which is robust to
lighting conditions and camera exposure.
• The light source direction is approximated using a
Gaussian distribution and object roughness is es-
timated using local window-based pixel intensity
variance.
• Existing stereo matching methods are signifi-
cantly improved by the use of the estimated irra-
diance images as opposed to the original left and
right stereo images.
2 RELATED WORK
Research in radiometric difference removal can be
broadly classified into the following three categories:
2.1 Matching Cost Function
Methods in this category aim at performing stereo
matching by proposing matching costs that are robust
on images with radiometric differences. Window-
based mutual information methods (Egnal, 2000;
Fookes et al., 2002; Sarkar and Bansal, 2007) do
not require relative ordering and also have similar ef-
fectiveness in removing the radiometric differences.
Another effective way is to perform segment-wise
stereo matching (Zitnick et al., 2004). (Kim et al.,
2003) uses mutual information with iterative global
graph-cuts to compute matching cost. The hierarchi-
cal calculation of pixel-based matching costs, as pro-
posed in (Hirschmuller, 2007), shows the same ac-
curacy results as compared to the window-based ap-
proach (Kim et al., 2003). Even though these methods
work well in removing radiometric differences, they
require a large local-window size to obtain good per-
formance, which results in a high time consumption.
2.2 Pixel Transformation
Pixel transformation methods use a function to remap
the pixel intensity in an image, making the pixel in-
tensity values obey a specific distribution or a curve.
(Khan et al., 2015) uses normalized histogram to
make the pixel intensity values obey a uniform distri-
bution. (Deng, 2016; Changyong et al., 2014) apply
log functions on an image to make the pixel inten-
sity values obey a log curve. (Rahman et al., 2016;
Deng, 2016) make the pixel intensity values obey a
gamma curve by applying gamma correction tech-
niques. These pixel-transformation methods work
well only when the background and foreground have
similar pixel intensity. Many techniques have been
proposed to overcome this drawback. (Zhuang and
Guan, 2017) divides the whole image into sub-images
and then normalizes each sub-image by its mean and
BRDF-based Irradiance Image Estimation to Remove Radiometric Differences for Stereo Matching
735

variance-based histogram. (Campos et al., 2019) pro-
poses a machine-learning based approach for hyper-
parameter selection in order to perform a contrast lim-
ited adaptive histogram equalization. However, be-
cause methods in this category only consider the pixel
intensity and ignore the light condition and object ma-
terial, they have not been able to effectively deal with
radiometric differences. Also, because uniform distri-
bution makes pixel intensity similar, histogram meth-
ods, such as (Khan et al., 2015), are more likely to
create blurry disparity maps.
2.3 Reflectance Estimation
Methods in this category take a more direct approach
and estimate the reflectance from a 2D image, which
is light invariant when objects have the same reflec-
tivity. Usually, this idea depends on an illumination
model, e.g., reflectance-illumination model. (Xie and
Lam, 2006) proposes a local normalization method
by assuming that objects, faces in their case, consist
of a combination of small facets and remove the ra-
diometric differences by performing normalization on
these facets. (Tan and Triggs, 2010) proposes local
ternary patterns to remove the radiometric differences
by using thresholds for neighboring pixels based on
the value of the central pixel. While the above two
methods estimate reflectance indirectly, (Chen et al.,
2006) develops total variation models which consider
a 2D image as the product of light source intensity and
a kernel function. However, selecting a specific kernel
function may not be applicable to images with varying
light conditions. Moreover, these methods do not con-
sider the object’s micro surface structure which could
influence the reflectance.
In this paper, we exploit the advantages of all the
above three categories to design a radiometric dif-
ference removal algorithm that considers image re-
flectance for all pixels in a given window. As op-
posed to matching cost methods, our approach per-
forms a lot faster as it only considers a static-sized
window. Compared with existing pixel transforma-
tion approaches, our reflectance-based method works
on each pixel separately and hence does not result in
a blurry disparity map. Our method performs consis-
tently well on images from a variety of well-known
stereo matching datasets. Our radiometric difference
removal approach is described in Section 3, with the
experiments and results reported in Section 4. We fur-
ther analyze and discuss some of our results in Section
4.7 and provide concluding remarks in Section 5.
3 PROPOSED APPROACH
The overall objective of our approach is to estimate
the left and right irradiance images by removing the
radiometric differences from the stereo image pairs.
Stereo matching is applied on these irradiance im-
ages instead of the original stereo images to obtain
improved disparity map results. As shown in Fig-
ure 2, the proposed radiometric difference removal
algorithm consists of three parts: (1) irradiance im-
age computation, (2) light direction estimation, and
(3) object roughness estimation.
3.1 Assumptions
A given pixel can receive light from two types of
sources - direct light and indirect light. To simplify
our model, we assume that there is a single direct
light source following other BRDF estimation pa-
pers, e.g., (Chung et al., 2006) and we call it single
light source assumption. Indirect light refers to the
reflected light between objects (ambient light). We
Figure 2: Overview of the proposed radiometric difference removal approach for Stereo Matching.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
736

further assume that ambient light comes from all di-
rections except light source direction with nearly the
same lighting brightness and we call it uniform am-
bient light assumption. With such assumptions, we
use order-0 Spherical Harmonics to model the ambi-
ent light (Sloan et al., 2005).
3.2 Irradiance Image Computation
BRDF, denoted by f
r
(i, o), is the ratio of scattered ra-
diance L(i) in the direction i to irradiance E(o) from
the direction o. Based on this definition, we perform
irradiance image estimation using the equation:
E(o) =
L(i)
f
r
(i, o)
(1)
Using Microfacet theory, (Walter et al., 2007b)
shows that a roughness term α can be incorporated
into BRDF for describing an object’s micro-surface.
By applying that formulation to our Equation 1, we
obtain the following:
E(o) =
Z
i∈Ω
L(i)4 |i ·n||o · n|
F
schlick
(F
0
, h, i)G(n, o, α)D(h)
(2)
The integral in the above equation represents all
possible incoming light for the pixel in the upper
hemisphere (Ω in Equation 3). i is the direction of the
reflected light from an object’s surface. o is the direc-
tion of light coming from the light source. n refers to
the direction of the object surface’s normal. h is the
normalized half-vector of i and o. F(i, h) is a Fres-
nel term which describes the reflection and transmis-
sion of light when incident on an interface between
different optical media. It is usually approximated us-
ing Fresnel-Schlick function F
schlick
(F
0
, h, i) (Schlick,
1994) where F
0
is the reflection coefficient for light
incoming parallel to the normal. G(i, o, α) is the Ge-
ometrical Attenuation Factor (Kelemen and Szirmay-
Kalos, 2001) which describes what percentage of the
reflected light will not be blocked by the surface to-
pography (Hao et al., 2019). D(h) is the GGX Distri-
bution Function (Walter et al., 2007a) which describes
the probability distribution of the surface normal.
To solve Equation 3, we first discuss the possi-
ble incoming light directions in the upper hemisphere
for a pixel. According to single light source assump-
tion in Section 3.1, the direct light only has one di-
rection, which is the light source direction. However,
the indirect light has unlimited directions in the upper
hemisphere. Here, we apply uniform ambient light
assumption, as mentioned in Section 3.1. That is,
the ambient light comes in all directions except light
source direction with nearly the same lighting bright-
ness. So the ambient can be viewed as a constant C.
Intuitively, We may set C as the mean value of input
images, or we could use 0-order Spherical Harmonics
function (Sloan et al., 2005), which is
q
1
4π
, to model
the ambient light. So Equation 3 can be simplified as:
E(o) =
L(i)4 |i ·n||o · n|
F
schlick
(F
0
, h, i)G(n, o, α)D(h)
+C (3)
Next, we estimate the reflected light L(i) as received
by the camera by mapping it to image pixel inten-
sity. This is modeled by the camera response function
which, according to (Ng et al., 2007), is assumed to
be a gamma curve that is generally approximated by
a polynomial function. We compared different types
of polynomial approximations (linear, quadratic, etc.)
and found no significant difference between them.
Hence, in our approach we approximate the camera
response function using a linear function which im-
plies that L(i) is the same as image intensity.
After solving for L(i), the only unknown variables
that need to be estimated are i, o, n, h, and α. The
first four parameters are associated with the light di-
rection, whereas the last parameter is the object sur-
face roughness. Considering theoretical foundations
and expansion of the functions in Equation 3, param-
eters i, o, n, and h are never used on their own. Rather,
they are always used in combinations as a dot product.
In Section 3.3, we demonstrate that the dot product
of any of these parameters obeys a Gaussian distribu-
tion, based on which we estimate the light direction.
We estimate the surface roughness α using a local
window-based approach for pixel intensity variance,
shown in Section 3.4.
3.3 Light Direction Estimation
As mentioned above, light source direction can be es-
timated by approximating the dot products of i, o, n,
and h. We demonstrate that any combination of the
dot products of these direction vectors follow a Gaus-
sian distribution.
Assume a and b are any of the four direction vec-
tors i, o, n, and h. The dot product of a and b can
be represented as a · b =
|
a
||
b
|
cosθ. These vectors
are normalized unit direction vectors. Hence, the dot
product is dependent on just the cosine of the angle θ
between a and b i.e. cos θ. As we do not know the
angle between these vectors, we cannot find the value
for cos θ. Considering that θ ∈ [−π, π], by selecting
specific values for µ and σ
2
, we can plot the function
graph for the Gaussian distribution N(µ, σ
2
). Visual
comparison shows that this Gaussian function graph
is very similar to the function graph for cos θ. Hence,
BRDF-based Irradiance Image Estimation to Remove Radiometric Differences for Stereo Matching
737

we use Gaussian distribution to approximate the value
for cosθ.
In Equation 3, we estimate the irradiance value for
each pixel of an image of length l and height h. We
need to obtain a specific dot product value for the four
direction vectors i, o, n, and h. Hence, we generate
a Gaussian distribution N(µ, σ
2
) for l ∗ h values and
pick the value that matches the row and column value
for the corresponding image. This value is used for
the light source direction estimation.
3.4 Roughness Estimation
As mentioned in Section 3.2, we need to estimate
the object surface roughness α in order to compute
the irradiance images. Surface element roughness de-
scribes how flat (low roughness) or how rugged (high
roughness) a surface is at a micro level. It is depen-
dent on the object’s material and is usually set manu-
ally according to a visual understanding of the object
in the image. However, in stereo image pairs consist-
ing of multiple objects, it is not possible to effectively
set an appropriate value manually.
According to BRDF (Walter et al., 2007a), sur-
face roughness has an inverse relationship with local
pixel intensity variance. If the object surface has high
roughness, the reflected light would be more likely to
be scattered into different directions. This difference
in light direction could make the image seem blurry
indicating that it has smaller pixel intensity variance.
We design a local window-based approach to approx-
imate the pixel intensity variance which leads to the
estimation of surface roughness α based on the fol-
lowing equation:
α =
1
V
t
(p)
=
1
∑
t
i=1
∑
t
j=1
(p
i j
− M
t
(p))
2
(4)
where p is the center pixel for which we are trying
to estimate the pixel intensity variance V
t
(p) in a lo-
cal square window of size t (an odd number). M
t
(p)
denotes the mean pixel intensity value in this window.
Based on the approach mentioned above in Sec-
tions 3.2, 3.3, and 3.4, we compute the left and right
irradiance images for the original stereo image pairs.
The radiometric differences are removed in these irra-
diance images which can then be applied to any stereo
matching method.
4 EXPERIMENTS
In this section, we conduct extensive experimental
analysis to evaluate the effectiveness of our radiomet-
ric difference removal algorithm on stereo matching.
Left Image
SGBM2
ELAS
PSMNet
OVOD
SGBM2*
ELAS*
OVOD*
PSMNet*
LocalExp
HSM-Net
AANet++
CRL
RAFT-Stereo
LEAStereo
LocalExp*
HSM-Net*
AANet++*
CRL*
RAFT-Stereo*
LEAStereo*
Right Image
Figure 3: An example image from the test set (so no ground
truth) of KITTI-15 dataset (Scharstein et al., 2014).
*
de-
notes the use of our approach prior to applying the stereo
matching methods.
4.1 Implementation Details
All the experiments are conducted on a computer hav-
ing a 2.6 GHz CPU with an i7 processor and 32 GB
RAM. Our radiometric removal algorithm for con-
verting the original stereo images to irradiance im-
ages is implemented in C++. For the Fresnel-Schlick
function (Schlick, 1994) used in Equation 3, we use
linear base reflectivity and set F
0
= 0.365. We con-
ducted a separate experiment and found that there
were no major differences in our results across dif-
ferent F
0
values. We picked the value which gave
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
738
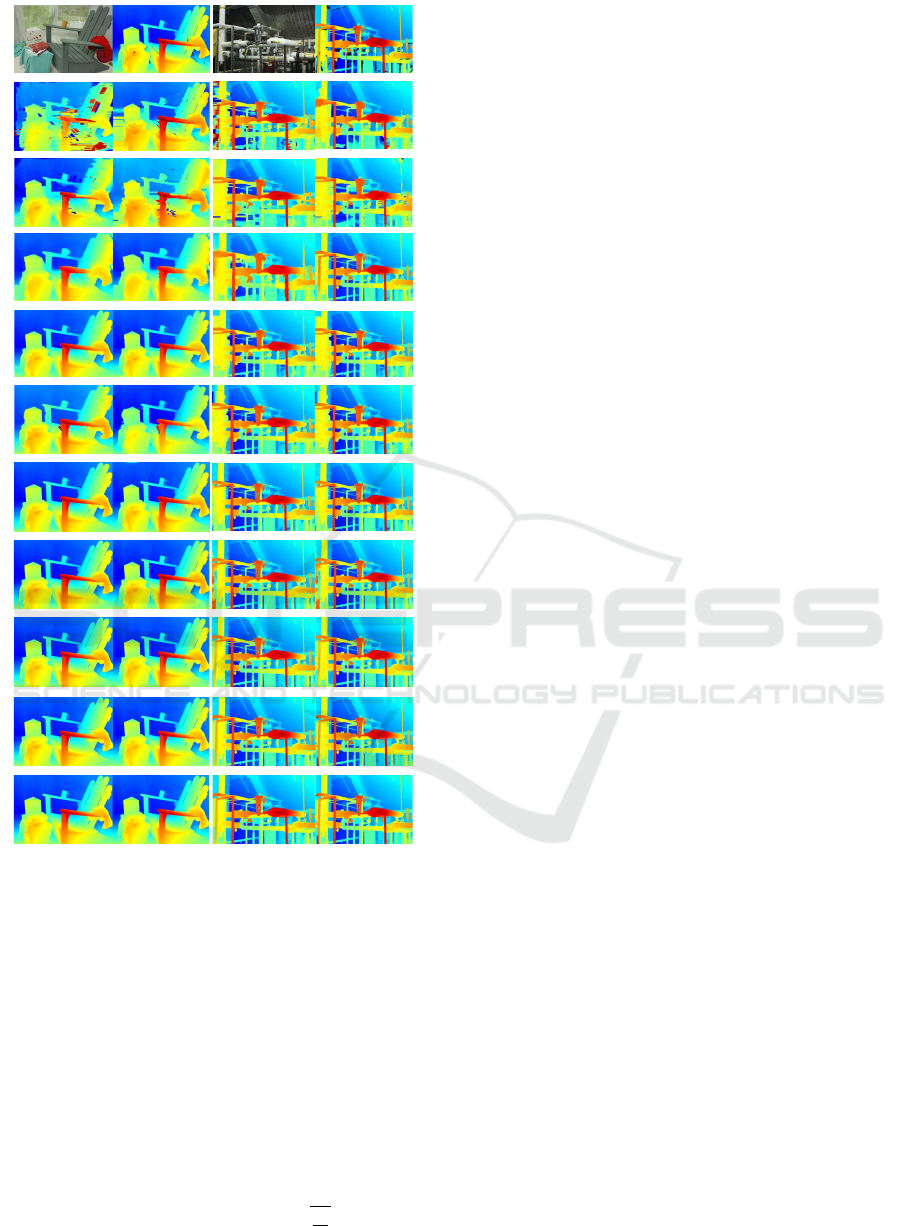
Adirondack
SGBM2
ELAS
PSMNet
OVOD
LocalExp
HSM-Net
AANet++
CRL
RAFT-Stereo
LEAStereo
Ground Truth
SGBM2*
ELAS*
PSMNet
*
OVOD*
LocalExp*
HSM-Net*
AANet++*
CRL*
RAFT-Stereo*
LEAStereo*
Pipes
SGBM2
ELAS
PSMNet
OVOD
LocalExp
HSM-Net
AANet++
CRL
RAFT-Stereo
LEAStereo
Ground Truth
SGBM2*
ELAS*
PSMNet*
OVOD*
LocalExp*
HSM-Net*
AANet++*
CRL*
RAFT-Stereo*
LEAStereo*
Figure 4: Adirondack image and Pipes image from the
Middlebury-14 dataset (Scharstein et al., 2014) along with
the ground truth disparity map. First and third columns
show the disparity maps generated by 10 stereo matching
methods on the original stereo image pairs. Second and
fourth columns show results on the irradiance images esti-
mated by our radiometric difference removal algorithm (de-
noted by
*
).
the best results. We did the same for the Gaussian
distribution N(µ, σ
2
) parameters and set them to be
µ = 10 and σ = 1. The Gaussian distribution is then
used as an approximation of cos θ in estimating the
light direction (see Section 3.3). In Equation 4 we se-
lect the local square window size to be t = 5 because
we find that it results in the best performance. Also,
we set ambient light constant C =
q
1
4π
as it yields
better results. Implementation details of the different
stereo matching methods we use in our experiments
are mentioned in Section 4.3.
4.2 Datasets & Evaluation Metrics
We use three popular stereo matching datasets and the
corresponding evaluation metrics.
• Middlebury-14 (Scharstein et al., 2014) is a high-
resolution two-view dataset that consist of multi-
ple stereo images of indoor scenes. We use the 15
training stereo image pairs and focus only on the
non-occluded pixels during evaluation. avgerr,
bad-0.5, bad-1.0, and bad-2.0 are used as the eval-
uation metrics for this dataset.
• Middlebury-06 (Hirschmuller and Scharstein,
2007) is the older version of the Middlebury-
14 dataset. We use this to evaluate our method
against other pre-processing methods in differ-
ent lighting and exposure conditions. We use the
avgerr metric to graph the comparisons.
• KITTI-15 (Menze et al., 2018) dataset is also
used to evaluate the impact of our proposed
pre-processing method on other stereo matching
methods. We perform analysis on all the 200 low
resolution stereo pairs. The metrics used for this
dataset are D1-all, D1-bg and D1-fg, which refer
to the percentage of outliers for all pixels, back-
ground pixels, and foreground pixels respectively.
For all experiments, we use
*
to denote the use of our
radiometric removal algorithm with the correspond-
ing stereo matching method or evaluation metric.
4.3 Stereo Matching Estimation
Methods Compared
Several pre-processing optimization approaches exist
for improving stereo matching, such as (Heo et al.,
2012) and (Zhou and Boulanger, 2012), which are il-
lumination invariant approaches. However, these ap-
proaches also change the cost function and hence can-
not directly be compared with our approach. Radio-
metric invariant filters such as gradient, census, and
rank filters can also be used for optimizing stereo
matching. These filters also depend on the cost func-
tion. On the other hand, our approach is separate from
the cost function. This is the major advantage of our
method that it can work with any stereo matching al-
gorithms using their individual cost functions.
The irradiance images obtained from our radio-
metric removal algorithm are used as input for 10
representative state-of-the-art stereo matching meth-
ods: SGBM2 (Hirschmuller, 2007), ELAS (Geiger
BRDF-based Irradiance Image Estimation to Remove Radiometric Differences for Stereo Matching
739

et al., 2010), AANet++ (Xu and Zhang, 2020),
PSMNet (Chang and Chen, 2018), HSM-Net (Yang
et al., 2019), LEAStereo (Cheng et al., 2020),Lo-
calExp (Taniai et al., 2017), OVOD (Mozerov and
van de Weijer, 2019),CRL (Pang et al., 2017), RAFT-
Stereo (Lipson et al., 2021). For Figure 4 shows the
disparity maps for the Adirondack image and Pipes
image in the Middlebury-14 dataset. For all meth-
ods, except SGBM2, we directly use implementations
available online on their respective GitHub reposito-
ries. However, we do need to fine-tune specific pa-
rameters in their models to obtain the reported re-
sults on different datasets. We implement SGBM2
(Hirschmuller, 2007) using OpenCV by setting the
following parameter values to accurately replicate re-
sults: SAD window size = 3, truncation value for pre-
filter = 63, P1 = 8 ∗ 3 ∗ 3, P2 = 32 ∗ 3 ∗ 3, uniqueness
ratio = 10, speckle window size = 100, speckle range
= 32, max disparity value = 128. We also set the in-
put image resolution to be half of the original.
Here, we perform experimental analysis on each
of the four datasets and report the results for the same.
Middlebury-14 Dataset (Scharstein et al., 2014):
Figure 4 shows visual disparity map results for the
Adirondack image from the Middlebury-14 dataset
(Scharstein et al., 2014). As visible in the dispar-
ity maps, the results obtained on the stereo matching
methods after applying our radiometric removal algo-
rithm (bottom row) are better compared to the ones
obtained without using our algorithm (top row). The
dataset consists of 15 stereo image pair test cases on
which we conduct our analysis. We conduct exper-
iments for all 10 stereo matching methods on these
image pairs using avgerr, bad-0.5, bad-1.0, and bad-
2.0 as the evaluation metrics.
Table 1 shows the results for our experimental
analysis. In the majority of the cases, we obtain a re-
duction in the error rates indicating the effectiveness
of our algorithm for stereo matching. For example,
we obtain avgerr reduction of 34.43% for SGBM2
and 6.12% for AANet++. The worst performance is
for HSM-Net where avgerr increases by 1.41%.
KITTI-15 Dataset (Menze et al., 2018): We report
results for all the three percentages of outliers metrics
that are generally used for this dataset - D1-all, D1-
bg, and D1-fg. Table 2 shows the results for all the
10 stereo matching methods with and without the use
of our algorithm. As shown in the table, by using our
algorithm, all methods report performance improve-
ment across all metrics. For example, for D1-all, error
reduction is obtained in the range of 1.05%−37.99%.
Figure 3 shows visual disparity map results for an ex-
ample image from the test set in KITTI-15 Dataset.
(a) Aloe (b) Art
Figure 5: Comparison of our approach with other pre-
processing approaches for camera exposure changes on
three images from the Middlebury-06 dataset (Hirschmuller
and Scharstein, 2007).
(a) Aloe (b) Art
Figure 6: Comparison of our approach with other pre-
processing approaches for changes in the light source on
three images from the Middlebury-06 dataset (Hirschmuller
and Scharstein, 2007).
4.4 Robustness to Camera Exposure &
Light Source Changes
We also evaluate the robustness of our approach
across different camera exposure settings as well as
changes to the light source. We use two different im-
ages from the Middlebury-06 dataset (Hirschmuller
and Scharstein, 2007) to compare our approach with
the five other pre-processing approaches. For this
analysis, we use the same experimental setting as in
the ANCC work (Heo et al., 2008). Also, same as in
(Heo et al., 2012), we have included Census(+) in our
evaluation which uses a combined log-chromaticity
color (70% weight) and RGB color (30% weight).
Figure 5 shows the two comparison graphs with
each having four different camera exposure combina-
tions between the left and the right views. Similarly,
Figure 6 shows the comparison graphs for light source
changes. As seen from the graphs, our approach out-
performs most other pre-processing approaches in all
the four combinations for left/right views, for both
camera exposure and light source changes.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
740

Table 1: Results on the Middlebury-14 (Scharstein et al., 2014) training set for 10 stereo matching methods (our algorithm
denoted by
*
). Percentage change in the error values is shown in parenthesis with an arrow indicating increase or decrease.
Method Res avgerr avgerr
*
bad-0.5 bad-0.5
*
bad-1.0 bad-1.0
*
bad-2.0 bad-2.0
*
SGBM2 F 11.15 7.31 (34.43%↓) 56.71 38.60 (31.93%↓) 36.18 24.43 (32.4%↓) 27.52 23.57 (14.35%↓)
ELAS F 7.56 7.62 (0.79%↑) 61.62 60.58 (1.68%↓) 38.73 37.27 (0.65%↓) 27.88 26.18 (0.93%↓)
PSMNet Q 9.92 9.87 (0.50%↓) 89.98 98.90 (9.91%↑) 78.34 77.83 (3.76%↓) 59.11 58.56 (6.09%↓)
OVOD H 1.82 1.79 (1.64%↓) 38.22 37.81 (1.07%↓) 17.91 17.75 (0.89%↓) 9.67 9.53 (1.44%↓)
LocalExp H 1.76 1.74 (1.13%↓) 38.45 38.17 (0.72%↓) 14.32 14.20 (0.83%↓) 6.43 6.31 (1.86%↓)
HSM-Net F 1.41 1.43 (1.41%↑) 50.29 49.61 (1.35%↓) 22.99 23.24 (1.08%↑) 10.78 10.83 (0.46% ↑)
CRL H 1.45 1.43(1.38%↓) 47.35 46.18(2.47%↓) 19.53 19.19(1.74%↓) 12.71 12.54(1.33%↓)
RAFT-Stereo H 1.04 0.98(5.76%↓) 28.61 25.42(11.1%↓) 10.60 10.12(4.52%↓) 5.25 4.92(6.28%↓)
LEAStereo H 1.09 1.03 (5.5%↓) 36.10 35.71 (1.08%↓) 18.40 17.91 (2.7%↓) 2.47 2.52 (2.02% ↑)
AANet++ H 0.98 0.92 (6.12%↓) 33.18 31.95 (3.70%↓) 12.18 11.49 (5.66%↓) 5.65 5.09 (9.91%↓)
Table 2: Results on the KITTI-15 dataset (Menze et al., 2018) with D1-all, D1-bg, and D1-fg evaluation metrics. Superscript
(e.g., D1-all
*
) denotes the use of our algorithm prior to applying the stereo matching methods. Percentage change in the error
values is shown in parenthesis with an arrow indicating increase or decrease.
Method D1-all D1-all
*
D1-bg D1-bg
*
D1-fg D1-fg
*
SGBM2 6.87 4.26 (37.99%↓) 15.29 11.68 (23.61%↓) 5.15 4.27 (17.08%↓)
ELAS 9.78 8.14 (16.85%↓) 19.04 14.93 (21.58%↓) 7.86 5.42 (31.04%↓)
PSMNet 2.32 2.24 (3.44%↓) 1.88 1.64 (12.36%↓) 4.65 4.39 (5.59%↓)
OVOD 4.21 3.9 (7.36%↓) 3.21 3.23 (0.62%↑) 5.94 5.28 (11.11%↓)
LocalExp 4.76 4.71 (1.05%↓) 3.52 3.78 (7.38%↑) 7.47 6.21 (16.86%↓)
HSM-Net 2.19 2.05 (6.39%↓) 1.82 1.76 (3.29%↓) 3.86 3.71 (3.88%↓)
CRL 2.15 2.14(0.46%↓) 2.25 2.21(1.77%↓) 3.41 3.43(0.58%↑)
RAFT-Stereo 1.96 1.73(11.7%↓) 1.75 1.66(5.14%↓) 2.89 2.69 (6.92%↓)
LEAStereo 1.65 1.73 (3.03%↑) 1.40 1.43(2.14 %↑) 2.91 2.93 (0.69%↑)
AANet++ 2.31 2.02 (12.55%↓) 2.10 1.94 (7.61%↓) 5.35 5.22 (2.43%↓)
Table 3: Comparison of our approach with five other pre-processing approaches when used in conjunction with all the 10
stereo matching methods. We report the average error obtained on the Middlebury-14 dataset (Scharstein et al., 2014). Best
result is marked in bold.
Method
No
Pre-processing
Ours Census LoG ANCC Joint Zhou
SGBM2 11.5 7.31 7.96 9.15 15.81 12.64 16.72
ELAS 7.56 7.62 13.06 15.54 7.16 7.14 22.58
PSMNet 9.92 9.87 12.24 12.63 8.40 7.28 18.63
OVOD 1.82 1.79 1.93 2.65 1.73 1.75 5.11
LocalExp 1.76 1.74 2.24 3.43 2.28 2.30 9.98
HSM-Net
1.41 1.43 1.39 4.34 2.45 2.43 7.52
CRL 1.45 1.43 1.47 4.69 2.72 2.30 6.85
RAFT-Stereo 1.04 0.98 1.52 1.31 1.49 1.23 1.77
LEAStereo 1.09 1.03 2.02 1.89 3.15 3.37 3.95
AANet++ 0.98 0.92 1.49 4.07 3.65 3.43 4.84
4.5 Comparison with Other
Pre-processing Methods
As ours is a pre-processing method, we also com-
pare it with five other pre-processing methods that
use radiometric invariant filters, namely ANCC (Heo
et al., 2008) that uses Chromaticity normalization,
Laplacian of Gaussian (LoG) + BT (Birchfield and
Tomasi, 1998), Census (7 × 7) (Zabih and Woodfill,
1994) + Hamming, Joint (Heo et al., 2012) that uses
Log Chromaticity normalization, and Zhou (Zhou and
Boulanger, 2012) that uses Relative Gradients. Be-
cause our approach is separate from the stereo match-
ing algorithm, we use BT (Birchfield and Tomasi,
1998) as our stereo matching algorithm for fair com-
parison. We use GraphCut (GC) to optimize all the
matching costs as the same as (Heo et al., 2012).
In Table 3, we report the avgerr results for ours
and each of the five other pre-processing approaches
when used in conjunction with the 10 state-of-the-
BRDF-based Irradiance Image Estimation to Remove Radiometric Differences for Stereo Matching
741

(a) Origianl Sphare (b) Simulated Sphare
Figure 7: Comparison of our original image and our re-
rendered image. (a) is rendered with the original BRDF
model (b) is re-rendered with our estimated BRDF value.
art stereo matching algorithms. As seen from the re-
sults, our approach improves the performance by re-
ducing the errors significantly for all 10 stereo match-
ing methods, as opposed to the other pre-processing
approaches that use radiometric invariant filters.
4.6 Validation of BRDF Estimation
We evaluated the accuracy of BRDF estimation using
a simulated image, as it is difficult to obtain the ac-
tual BRDF ground truth values. We first use Unity3
to render the original image (a) with our own BRDF
shader, so the ground-truth BRDF values are known.
Then we use our proposed approach to estimate the
BRDF for image (a). At last, we use this estimated
BRDF to render a new reconstructed image, which
we compare with the original image. Figure 7 shows
the results for two different images where we com-
pare the original (a) and the simulated images (b) to
visually validate the accuracy of the proposed BRDF
estimation approach.
4.7 Limitations & Future Work
Our approach for irradiance image computation esti-
mates the light source direction statistically. So there
is a difference between our estimated value and the
real value for the light source direction. We will
investigate such differences in the future. In gen-
eral Computer Graphics, the lighting function is pre-
known and can be used to estimate the ambient light.
However, in our approach the lighting function is un-
known. Hence, we plan to investigate the estimation
of the ambient light constant C by using Monte Carlo
Sampling Methods in the future.
5 CONCLUSIONS
In this paper we propose a novel radiometric dif-
ference removal algorithm for improving the perfor-
mance of stereo matching methods. The approach is
based on the Computer Graphics concept of BRDF
to compute the irradiance images for the original left
and right stereo images. For doing so, we estimate the
light source direction by considering an approxima-
tion that the dot product of the unknown light direc-
tion parameters follows a Gaussian distribution. We
estimate the object’s roughness by employing a lo-
cal window strategy and calculating the pixel inten-
sity variance. The obtained irradiance images are ro-
bust to changes in illumination, exposure, and light
source intensity. These images when used as input
for stereo matching methods improve the quality of
the generated disparity maps as opposed to the ones
obtained while running the methods on the original
stereo images. Results on the experiments performed
on 10 stereo matching methods show significant per-
formance improvement for disparity map generation.
REFERENCES
Birchfield, S. and Tomasi, C. (1998). A pixel dissimilarity
measure that is insensitive to image sampling. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 20(4):401–406.
Campos, G. F. C., Mastelini, S. M., Aguiar, G. J., Manto-
vani, R. G., de Melo, L. F., and Barbon, S. (2019). Ma-
chine learning hyperparameter selection for contrast
limited adaptive histogram equalization. EURASIP
Journal on Image and Video Processing, 2019(1):59.
Chang, J.-R. and Chen, Y.-S. (2018). Pyramid stereo match-
ing network. In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition, pages
5410–5418.
Changyong, F., Hongyue, W., Naiji, L., Tian, C., Hua, H.,
Ying, L., et al. (2014). Log-transformation and its im-
plications for data analysis. Shanghai archives of psy-
chiatry, 26(2):105.
Chen, T., Yin, W., Zhou, X. S., Comaniciu, D., and Huang,
T. S. (2006). Total variation models for variable light-
ing face recognition. IEEE transactions on pattern
analysis and machine intelligence, 28(9):1519–1524.
Chen, X., Kundu, K., Zhu, Y., Berneshawi, A. G., Ma, H.,
Fidler, S., and Urtasun, R. (2015). 3d object propos-
als for accurate object class detection. In Advances in
Neural Information Processing Systems, pages 424–
432.
Cheng, X., Zhong, Y., Harandi, M., Dai, Y., Chang, X., Li,
H., Drummond, T., and Ge, Z. (2020). Hierarchical
neural architecture search for deep stereo matching.
Advances in Neural Information Processing Systems,
33.
Chung, A. J., Deligianni, F., Shah, P., Wells, A., and
Yang, G.-Z. (2006). Patient-specific bronchoscopy vi-
sualization through brdf estimation and disocclusion
correction. IEEE transactions on medical imaging,
25(4):503–513.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
742

Deng, G. (2016). A generalized gamma correction algo-
rithm based on the slip model. EURASIP Journal on
Advances in Signal Processing, 2016(1):69.
Egnal, G. (2000). Mutual information as a stereo correspon-
dence measure.
Fookes, C., Bennamoun, M., and Lamanna, A. (2002). Im-
proved stereo image matching using mutual informa-
tion and hierarchical prior probabilities. In Object
recognition supported by user interaction for service
robots, volume 2, pages 937–940. IEEE.
Geiger, A., Roser, M., and Urtasun, R. (2010). Efficient
large-scale stereo matching. In Asian conference on
computer vision, pages 25–38. Springer.
Geiger, A., Ziegler, J., and Stiller, C. (2011). Stereoscan:
Dense 3d reconstruction in real-time. In 2011 IEEE
intelligent vehicles symposium (IV), pages 963–968.
Ieee.
Han, H., Shan, S., Chen, X., and Gao, W. (2013). A com-
parative study on illumination preprocessing in face
recognition. Pattern Recognition, 46(6):1691–1699.
Hao, D., Wen, J., Xiao, Q., You, D., and Tang, Y.
(2019). An improved topography-coupled kernel-
driven model for land surface anisotropic reflectance.
IEEE Transactions on Geoscience and Remote Sens-
ing.
Heo, Y. S., Lee, K. M., and Lee, S. U. (2008). Illumination
and camera invariant stereo matching. In 2008 IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 1–8. IEEE.
Heo, Y. S., Lee, K. M., and Lee, S. U. (2010). Robust stereo
matching using adaptive normalized cross-correlation.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 33(4):807–822.
Heo, Y. S., Lee, K. M., and Lee, S. U. (2012). Joint depth
map and color consistency estimation for stereo im-
ages with different illuminations and cameras. IEEE
transactions on pattern analysis and machine intelli-
gence, 35(5):1094–1106.
Hirschmuller, H. (2007). Stereo processing by semiglobal
matching and mutual information. IEEE Transac-
tions on pattern analysis and machine intelligence,
30(2):328–341.
Hirschmuller, H. and Scharstein, D. (2007). Evaluation of
cost functions for stereo matching. In 2007 IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 1–8. IEEE.
Kelemen, C. and Szirmay-Kalos, L. (2001). A microfacet
based coupled specular-matte brdf model with impor-
tance sampling. In Eurographics short presentations,
volume 25, page 34.
Khan, M. F., Khan, E., and Abbasi, Z. (2015). Image con-
trast enhancement using normalized histogram equal-
ization. Optik, 126(24):4868–4875.
Kim, J. et al. (2003). Visual correspondence using energy
minimization and mutual information. In Proceed-
ings Ninth IEEE International Conference on Com-
puter Vision, pages 1033–1040. IEEE.
Lipson, L., Teed, Z., and Deng, J. (2021). Raft-stereo: Mul-
tilevel recurrent field transforms for stereo matching.
arXiv preprint arXiv:2109.07547.
Menze, M., Heipke, C., and Geiger, A. (2018). Object scene
flow. ISPRS Journal of Photogrammetry and Remote
Sensing (JPRS).
Mozerov, M. G. and van de Weijer, J. (2019). One-view
occlusion detection for stereo matching with a fully
connected crf model. IEEE Transactions on Image
Processing, 28(6):2936–2947.
Ng, T.-T., Chang, S.-F., and Tsui, M.-P. (2007). Using ge-
ometry invariants for camera response function esti-
mation. In 2007 IEEE Conference on Computer Vision
and Pattern Recognition, pages 1–8. IEEE.
Pang, J., Sun, W., Ren, J. S., Yang, C., and Yan, Q. (2017).
Cascade residual learning: A two-stage convolutional
neural network for stereo matching. In Proceedings of
the IEEE International Conference on Computer Vi-
sion Workshops, pages 887–895.
Rahman, S., Rahman, M. M., Abdullah-Al-Wadud, M., Al-
Quaderi, G. D., and Shoyaib, M. (2016). An adaptive
gamma correction for image enhancement. EURASIP
Journal on Image and Video Processing, 2016(1):1–
13.
Sarkar, I. and Bansal, M. (2007). A wavelet-based multires-
olution approach to solve the stereo correspondence
problem using mutual information. IEEE Transac-
tions on Systems, Man, and Cybernetics, Part B (Cy-
bernetics), 37(4):1009–1014.
Scharstein, D., Hirschm
¨
uller, H., Kitajima, Y., Krathwohl,
G., Ne
ˇ
si
´
c, N., Wang, X., and Westling, P. (2014).
High-resolution stereo datasets with subpixel-accurate
ground truth. In German conference on pattern recog-
nition, pages 31–42. Springer.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. International journal of computer vision,
47(1-3):7–42.
Schlick, C. (1994). An inexpensive brdf model for
physically-based rendering. In Computer graphics fo-
rum, volume 13, pages 233–246. Wiley Online Li-
brary.
Sloan, P.-P., Luna, B., and Snyder, J. (2005). Local, de-
formable precomputed radiance transfer. ACM Trans-
actions on Graphics (TOG), 24(3):1216–1224.
Song, D.-l., Jiang, Q.-l., Sun, W.-c., et al. (2013). A sur-
vey: Stereo based navigation for mobile binocular
robots. In Robot Intelligence Technology and Appli-
cations 2012, pages 1035–1046. Springer.
Tan, X. and Triggs, B. (2010). Enhanced local texture fea-
ture sets for face recognition under difficult lighting
conditions. IEEE transactions on image processing,
19(6):1635–1650.
Taniai, T., Matsushita, Y., Sato, Y., and Naemura, T. (2017).
Continuous 3d label stereo matching using local ex-
pansion moves. IEEE transactions on pattern analysis
and machine intelligence, 40(11):2725–2739.
Walter, B., Marschner, S. R., Li, H., and Torrance, K. E.
(2007a). Microfacet models for refraction through
rough surfaces. In Proceedings of the 18th Eurograph-
ics Conference on Rendering Techniques, EGSR’07,
page 195–206, Goslar, DEU. Eurographics Associa-
tion.
BRDF-based Irradiance Image Estimation to Remove Radiometric Differences for Stereo Matching
743

Walter, B., Marschner, S. R., Li, H., and Torrance, K. E.
(2007b). Microfacet models for refraction through
rough surfaces. Rendering techniques, 2007:18th.
Xie, X. and Lam, K.-M. (2006). An efficient illumination
normalization method for face recognition. Pattern
Recognition Letters, 27(6):609–617.
Xu, H. and Zhang, J. (2020). Aanet: Adaptive aggregation
network for efficient stereo matching. In Proceedings
of the IEEE/CVF Conference on Computer Vision and
Pattern Recognition, pages 1959–1968.
Yang, G., Manela, J., Happold, M., and Ramanan, D.
(2019). Hierarchical deep stereo matching on high-
resolution images. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 5515–5524.
Zabih, R. and Woodfill, J. (1994). Non-parametric local
transforms for computing visual correspondence. In
European conference on computer vision, pages 151–
158. Springer.
Zhou, X. and Boulanger, P. (2012). Radiometric invari-
ant stereo matching based on relative gradients. In
2012 19th IEEE International Conference on Image
Processing, pages 2989–2992. IEEE.
Zhuang, L. and Guan, Y. (2017). Image enhancement
via subimage histogram equalization based on mean
and variance. Computational intelligence and neuro-
science, 2017.
Zitnick, C. L., Kang, S. B., Uyttendaele, M., Winder, S.,
and Szeliski, R. (2004). High-quality video view in-
terpolation using a layered representation. ACM trans-
actions on graphics (TOG), 23(3):600–608.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
744
