
Segregational Soft Dynamic Time Warping and Its Application to Action
Prediction
Victoria Manousaki
1,2 a
and Antonis Argyros
1,2 b
1
Computer Science Department, University of Crete, Heraklion, Greece
2
Institute of Computer Science, Foundation for Research and Technology - Hellas (FORTH), Heraklion, Greece
Keywords:
Soft Dynamic Time Warping, Segregational, Action Prediction, Alignment, Duration Prediction.
Abstract:
Aligning the execution of complete actions captured in segmented videos has been a problem explored by
Dynamic Time Warping (DTW) and Soft Dynamic Time Warping (S-DTW) algorithms. The limitation of
these algorithms is that they cannot align unsegmented actions, i.e., actions that appear between other actions.
This limitation is mitigated by the use of two existing DTW variants, namely the Open-End DTW (OE-DTW)
and the Open-Begin-End DTW (OBE-DTW). OE-DTW is designed for aligning actions of known begin point
but unknown end point, while OBE-DTW handles continuous, completely unsegmented actions with unknown
begin and end points. In this paper, we combine the merits of S-DTW with those of OE-DTW and OBE-DTW.
In that direction, we propose two new DTW variants, the Open-End Soft DTW (OE-S-DTW) and the Open-
Begin-End Soft DTW (OBE-S-DTW). The superiority of the proposed algorithms lies in the combination of
the soft-minimum operator and the relaxation of the boundary constraints of S-DTW, with the segregational
capabilities of OE-DTW and OBE-DTW, resulting in better and differentiable action alignment in the case
of continuous, unsegmented videos. We evaluate the proposed algorithms on the task of action prediction on
standard datasets such as MHAD, MHAD101-v/-s, MSR Daily Activities and CAD-120. Our experimental
results show the superiority of the proposed algorithms to existing video alignment methods.
1 INTRODUCTION
Cameras capture visual information of action and
activity executions from different angles, with dif-
ferent speeds, performed by different subjects, etc.
Temporal video alignment algorithms are powerful
tools for matching action executions in time, de-
spite such differences. Thus, they have been used
to match complete videos in works for action qual-
ity assessment (Roditakis et al., 2021), action co-
segmentation (Papoutsakis et al., 2017a), fine-grained
frame retrieval (Haresh et al., 2021), etc.
Typically, this type of temporal match-
ing/alignment involves a representation of a video
in the form of time series, i.e., a temporal ordering
of frames, each represented as a multidimensional
vector in some feature space
1
. Under such a formula-
tion, a time series representing a test action execution
a
https://orcid.org/0000-0003-2181-791X
b
https://orcid.org/0000-0001-8230-3192
1
For this reason, in this paper we use the term “video”
and “action sequence” or “action execution” interchange-
ably.
needs to be aligned/matched with another time
series, representing a reference action execution. The
Dynamic Time Warping (DTW) algorithm is applied
to such time series representations by establishing an
alignment path of minimum-cost. The Soft Dynamic
Time Warping (S-DTW) algorithm is also applied
to such input and finds the soft-minimum cost of all
possible path-based alignments.
Both DTW and S-DTW align segmented inputs,
i.e., they find the best alignment of different execu-
tions of actions that start and end at known points
in time. However, in many interesting realistic prob-
lems, this is not always the case. For reference actions
we do have complete time series representations. But
the test action to be aligned to the reference ones may
be unsegmented, i.e., we might know its start point
but not its end point, or we may know neither its start
not its end. This happens when we want to match
continuous, unsegmented input to reference actions.
Consider, as an example, a continuous video show-
ing an action that occurs between other, unknown ac-
tions. Matching this action to reference ones requires
not only alignment but also segregation/segmentation
226
Manousaki, V. and Argyros, A.
Segregational Soft Dynamic Time Warping and Its Application to Action Prediction.
DOI: 10.5220/0010882300003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
226-235
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of the input test action.
The problem of aligning partially or fully unseg-
mented test actions is addressed by the Open-End
(OE-DTW) and Open-Begin-End (OBE-DTW) DTW
variants. Specifically, OE-DTW assumes that the test
video has a known starting point but unknown end
point, while in OBE-DTW both the start and the end
of the test video may be unknown.
In this paper, we propose two new DTW variants,
namely the Open-End Soft DTW (OE-S-DTW) and
the Open-Begin-End Soft DTW (OBE-S-DTW). As
their names suggest, these variants combine the dif-
ferentiability of S-DTW with the capability of OE-
DTW and OBE-DTW to handle unsegmented test ac-
tions. Thus, they can be used as temporal alignment
loss to train neural networks in the case of partially
or fully unsegmented input. To the best of our knowl-
edge, OE-S-DTW and OBE-S-DTW are the first soft
DTW variants that segregate the input to be aligned
with the reference action executions.
We use the proposed segregational soft DTW vari-
ants to solve the problem of action prediction. More
specifically, continuous videos are transformed into
time series of certain features. To do so, we either use
features obtained from skeletal data or deep features
extracted by a VGG-16 network on RGB video data.
This partially or fully unsegmented input is matched
with a set of similarly represented reference action
executions and the best match is established. This
means that the label of a partially observed, on-going
action can be predicted before reaching action com-
pletion. As a side effect, the end time of the ongoing
action can also be predicted.
We test the performance of the proposed OE-
S-DTW and OBE-S-DTW algorithms for the prob-
lem of action prediction on four standard benchmark
datasets, namely MSR Daily Activities (Wang et al.,
2012), CAD-120 (Koppula et al., 2013), MHAD (Ofli
et al., 2013) and MHAD101-s/MHAD101-v (Papout-
sakis et al., ). Our proposed OE-S-DTW performs
comparably to OE-DTW in segmented action se-
quences, thus is able to replace OE-DTW in settings
where differentiability is desired. OBE-S-DTW and
OBE-DTW outperform all the other state of the art
algorithms in segmented action sequences. Morover,
OBE-S-DTW outperforms by a great margin OBE-
DTW and other state of the art algorithms in the more
difficult and realistic scenario of action prediction in
unsegmented action sequences.
In summary, the contributions of this work in-
clude:
• The proposal of OE-S-DTW and OBE-S-DTW,
which are the first soft DTW variants that can
align partially/fully unsegmented test time series
to reference ones.
• The extensive evaluation of the two proposed vari-
ants on the problem of short-term human ac-
tion prediction, and action end-time forecasting
in standard datasets and in comparison to existing
state of the art methods.
2 RELATED WORK
Dynamic Time Warping (Sakoe and Chiba, 1978)
aligns segmented sequences by finding a warping path
between them. The warping path is subject to bound-
ary constraints, i.e., it has to start and end at the
known start and end frames of the sequences to be
aligned. The alignment path is established with the
aid of a distance matrix containing all pair-wise dis-
tances of the frames of the two sequences. The align-
ment score is given by the summation of all path-
related values in the distance matrix. DTW has been
used in a plethora of problems and settings. Indica-
tively, in (Papoutsakis et al., 2017b) DTW tempo-
ral alignment has been used to solve the problem of
action co-segmentation by aligning trimmed action
sequences. Recently, (Hadji et al., 2021) proposed
a method for representation learning through DTW
temporal alignment of trimmed videos and cycle con-
sistency. (Dvornik et al., 2021) have proposed a
DTW approximation where outliers in the matching
of sequences are eliminated resulting in a more mean-
ingful alignment.
The Open-End DTW (OE-DTW) (Tormene et al.,
2009) is capable of finding the minimum cost align-
ment path of sequences that contain actions of known
start but unknown end, either due to partially observed
actions or actions followed by an unrelated suffix.
The alignment score is given by the summation of
all minimum-cost path values in the distance matrix.
Such paths start at the top-left point of the distance
matrix (as in DTW). However, unlike DTW, the path
should not necessarily end at the bottom-right cell
of the distance matrix. OE-DTW has been used to
compare motion curves for the rehabilitation of post-
stroke patients (Schez-Sobrino et al., 2019). In Kinect
v2, OE-DTW is used for the evaluation of the user’s
motion in order to provide real-time feedback to the
user (Yang and Tondowidjojo, 2019).
The Open-Begin-End (OBE-DTW) (Tormene
et al., 2009) acquires the minimum-cost alignment by
relaxing both endpoints. The advantage of this vari-
ant is that it makes possible to align unsegmented in-
puts. The warping path of minimum cost does not
have to start and end at the top-left and bottom-right
cells (respectively) of the distance matrix. OBE-DTW
Segregational Soft Dynamic Time Warping and Its Application to Action Prediction
227

has been used in many contexts for unsegmented se-
quence alignment e.g., for the problem of classifying
motion from depth cameras (Kim et al., 2015).
The Soft Dynamic Time Warping (S-DTW) (Cu-
turi and Blondel, 2017) variant of DTW, instead of
taking the minimum-cost alignment, considers the
soft-minimum of the distribution of all costs spanned
by all possible alignments between two time series in
segmented sequences. The S-DTW alignment score
contains the summation of all path-based values. Sim-
ilarly to DTW, S-DTW assumes segmented input.
(Haresh et al., 2021) use the S-DTW algorithm as the
temporal alignment loss in order to train their network
to learn better video representations. (Chang et al.,
2019) use the differentiable alignment of S-DTW for
the alignment and segmentation of actions by using
the videos and the transcripts of the actions.
Segmental DTW (Park and Glass, 2007) seeks for
the minimum-cost sub-sequence alignment of pairs
of unsegmented inputs. Segmental DTW decom-
poses the distance matrix in sets of overlapping ar-
eas and finds the local end-to-end alignments in these
areas resulting in sub-sequence matching. Segmen-
tal DTW has been used in the context of action co-
segmentation (Panagiotakis et al., 2018) in motion-
capture data or video between pairs of actions for the
detecting of commonalities of varying length, differ-
ent actors, etc.
Finally, the Ordered Temporal Alignment Module
(OTAM) (Cao et al., 2020) incorporates a S-DTW-
based alignment method where the soft-minimum op-
erator is used to calculate all possible path-based
alignments in segmented sequences of fixed length.
The alignment score is given by aligning the se-
quences end-to-end using S-DTW, while the align-
ment path is retrieved by an OBE-DTW approxima-
tion. OTAM has been used in (Cao et al., 2020) for
few-shot video classification of fixed-length trimmed
videos.
Temporal sequence alignment has been used ex-
tensively in the context of action recognition and pre-
diction. The work of (Afrasiabi et al., 2019) has been
used for action prediction in trimmed videos where
CNN networks have been used for feature extraction
by using optical flow. The alignment is performed
using DTW and the classification is performed using
the KNN and SVM algorithms. (Manousaki et al.,
2021) have used OE-DTW, and S-DTW to confront
the problem of action prediction in trimmed videos
that show on-going actions observed at different ob-
servation ratios. Also, (Ghoddoosian et al., 2021)
perform action recognition and duration prediction of
incomplete actions by aligning video segments using
object and verb information.
3 ACTION SEQUENCE
ALIGNMENT
Let the test (query) action sequence X be represented
as X = (x
1
,...x
l
) ∈ R
n×l
and the reference video Y
be represented as Y = (y
1
,...,y
m
) ∈ R
n×m
. The Eu-
clidean distance of frames x and y is defined as d(x,y)
and is used to create the distance matrix D(X,Y ) =
[d(x
i
,y
i
)]
i j
∈ R
l×m
containing all pair-wise frame dis-
tances. The cumulative matrix that is based on D and
represents all path-based alignments P of X and Y , is
denoted as C(X,Y ) = {hp,D(X,Y )i, p ∈ P
l,m
} where
P represents all the alignments connecting the upper-
left to the lower-right of the distance matrix. Given
this notation, in the following sections we elaborate
on the existing and proposed action sequence align-
ment algorithms.
3.1 Existing Alignment Methods
The minimum cost of aligning two time series in their
entirety is given by DTW (Sakoe and Chiba, 1978)
at the last index of the cumulative matrix C(X ,Y ).
The alignment score is normalized with the size of
the query. The DTW alignment cost is defined as:
DTW (X,Y ) = min
p∈P
C(X ,Y ). (1)
Open-End Dynamic Time Warping (OE-
DTW) (Tormene et al., 2009): is a variant of
the original DTW (Sakoe and Chiba, 1978). The
query and reference sequences share the same
start but end at different points in time. The
cumulative matrix is calculated using the asym-
metric pattern as follows: C(x
i
,y
j
) = D(x
i
,y
j
) +
min(C(x
i−1
,y
j
),C(x
i−1
,y
j−1
),C(x
i−1
,y
j−2
)). The
alignment can end at any point at the last row of the
cumulative matrix. The values are normalized by the
size of the query. The alignment score is given by the
minimum value in the last row. The alignment cost of
OE-DTW is defined as:
OE − DTW(X,Y ) = min
j=1,...,m
DTW (X,Y
j
). (2)
Open-Begin-End Dynamic Time Warping (OBE-
DTW) (Tormene et al., 2009): OBE-DTW refers to
the DTW variant where the beginning and ending of
the query sequence are unknown. This allows the
matching of one sequence with a part anywhere in-
side the second sequence. To achieve this, a row with
zero values is appended at the beginning of the dis-
tance matrix and the computations are performed as
in OE-DTW. The new cumulative matrix is denoted
as C
0
(X,Y ). The values are normalized by the length
of the query. The back-tracing of the minimum-cost
path starts from the minimum value of the last row
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
228

and ends at the first zero-valued row. The alignment
cost of OBE-DTW is defined as:
OBE − DTW(X,Y ) = min
j=1,...,m
C
0
(X,Y
j
). (3)
Soft Dynamic Time Warping (S-DTW) (Cuturi
and Blondel, 2017): S-DTW is an extension
of the original DTW algorithm. In contrast to
DTW which takes the minimum cost alignment
path, S-DTW takes into account all possible align-
ments. The cumulative matrix C(X,Y ) is cre-
ated by allowing horizontal, diagonal and vertical
moves. More specifically, C(x
i
,y
j
) = D(x
i
,y
j
) +
min
γ
(C(x
i−1
,y
j
),C(x
i−1
,y
j−1
),C(x
i
,y
j−1
)). The cu-
mulative matrix is padded at the top with a row and at
the left with a column so that C
i,0
= C
0, j
= ∞ for all
i, j 6= 0 and C
0,0
= 0.
The alignment cost of S-DTW is defined as:
SDTW
γ
(X,Y ) = min
γ
p∈P
C(X ,Y ), (4)
with
minγ(p
1
,..., p
k
) =
(
min
i≤k
p
i
, γ = 0,
−γlog
∑
k
i=1
e
p
i
/γ
γ > 0,
(5)
where γ ≥ 0 is a smoothing hyper-parameter.
3.2 Proposed Alignment Methods
Open-End Soft DTW (OE-S-DTW): Based on the
OE-DTW and the S-DTW, we propose OE-S-DTW,
where instead of aligning two sequences to their en-
tirety, we align them partially by having them an-
chored at the beginning, while their endpoints are
free. We start by calculating the distance matrix
which contains the pairwise distances of the se-
quences X and Y . The cumulative matrix is calculated
using the min
γ
operator as follows:
C(x
i
,y
j
) = D(x
i
,y
j
)+
min
γ
(C(x
i−1
,y
j
),C(x
i−1
,y
j−1
),C(x
i
,y
j−1
)).
(6)
The alignment path can terminate at any point of the
last row of the C matrix. The scores at the last row are
normalized by the size of the query and the alignment
value is the minimum of the last row. Then, the gra-
dient is calculated from that point backwards to the
common start point to find the alignment between the
two time series. The final OE-S-DTW score is also
normalised by the size of the matched reference. The
alignment cost of OE-S-DTW is defined as:
OE − S − DTW(X,Y ) = min
γ
j=1,...,m
SDTW
γ
(X,Y
j
).
(7)
Open-Begin-End Soft Dynamic Time Warping
(OBE-S-DTW): shares the same alternations as the
OBE-DTW. Upon calculating the distance matrix
D(X,Y ), a row of zero values is appended at the be-
ginning of the distance matrix creating D
0
(X,Y ). The
cumulative matrix C
0
is calculated by using the min
γ
operator as follows:
C
0
(x
i
,y
j
) = D
0
(x
i
,y
j
)+
min
γ
(C
0
(x
i−1
,y
j
),C
0
(x
i−1
,y
j−1
),C
0
(x
i
,y
j−1
)).
(8)
The last row of C
0
is normalized by the size of the
query. The alignment cost is the minimum value of
the last row. Then, the gradient is computed from that
point towards the zero-valued row and ends when it
reaches it. The size of the matched reference corre-
sponds to that range. The gradient gives as the align-
ment matrix, all possible alignments. Once the align-
ment path is obtained, we normalize the alignment
cost with the size of the matching part of the refer-
ence sequence. The alignment cost of OBE-S-DTW
is defined as:
OBE − S − DTW(X,Y ) = min
γ
j=1,...,m
C
0
(X,Y
j
). (9)
3.3 Alignment-based Action Prediction
Action prediction is defined as the problem of infer-
ring the label of a partially executed action. We define
the action observation ratio to be the percentage of the
action that is already observed. In our experiments,
the observation ratio varies in the range [10%,100%].
When the observation ratio equals to 100% then the
whole action has been observed. In this case, the
problem of action prediction becomes identical to the
problem of action classification.
To perform video-based action prediction, we rep-
resent the videos of executed actions as multidimen-
sional time series. Given time series representations
of several prototype executions of certain actions, and
an incomplete video execution of one of these actions,
we cast the problem of action prediction as a problem
of aligning/matching the incomplete action execution
to the prototype ones. The label of the closest match-
ing prototype action is reported as the predicted label
of the incomplete action.
In more detail, the unknown label L(A) of a time
series representation of an incomplete action A is in-
ferred through the alignment/matching of incomplete
and prototype actions. A set of K time series S
i
,
1 ≤ i ≤ K, corresponds to prototype videos with la-
bels L(S
i
). The alignment cost of two time series X,
Y is denoted as Cost(X ,Y ). Thus:
L(A) = L
arg min
1≤i≤K
Cost(A,S
i
)
. (10)
The proposed methodology can infer the label of an
incomplete/query video A by determining which pro-
totype/reference video S
i
has the minimum alignment
Segregational Soft Dynamic Time Warping and Its Application to Action Prediction
229

cost with A. This is is done through the proposed Dy-
namic Time Warping variants. The label of A is set to
L(S
i
).
4 DATASETS
For the evaluation of the proposed methods we em-
ploy four standard benchmark datasets which contain
trimmed and untrimmed action executions of humans
interacting with objects. Action representations en-
code the human body/object pose and the class of the
manipulated object. In general, we test our algorithms
with skeletal (i.e., motion capture) 3-D data and fea-
tures, but also with RGB-based features extracted by
a VGG-16 neural network. We follow the approach
of Manousaki et al. (Manousaki et al., 2021) regard-
ing the fusion of human and object representations for
the computation of the distance matrix of two action
sequences. Specifically, the representation fusion is
done by employing a weighted sum of the individual
distance matrices of the human and object representa-
tions. The weights depend on the class of the manip-
ulated objects. If no objects are present in the scene,
we use only the human pose representations. In case
there are several objects in the observed scene, fol-
lowing (Manousaki et al., 2021), we consider the ob-
ject that is manipulated by and/or closest to the actor.
MHAD Dataset (Ofli et al., 2013): Contains
trimmed executions of 11 human actions. Only one
of them (“throwing a ball”) involves human-object
interaction. The actions are performed by 5 female
and 7 male subjects in different execution styles and
speeds. The actions are: jumping in place, jumping
jacks, bending, punching, waving one hand, waving
two hands, clapping, throwing a ball, sit down and
stand up, sit down, stand up. 3D skeletal data of 30
joints have been acquired from a motion capture sys-
tem that provide 3D positions of 43 LED markers as
well as RGB and depth frames. The first 7 subjects
are used as the reference sequences while the last 5
subjects are used as the test sequences. The same
evaluation split is used as in (Ofli et al., 2013) and
Manousaki et al. (Manousaki et al., 2021).
Skeletal Features: Based on the 3D skeletal data of
the 30 joints provided by the MHAD dataset, we em-
ploy the same human body representation as in (Rius
et al., 2009; Papoutsakis et al., 2017a; Manousaki
et al., 2018). Body-centered and camera-centered fea-
tures are employed resulting in a 60-dimensional vec-
tor. This vector is extended by 4 angles represent-
ing angles encoding the fore- and the back- arms and
upper- and lower legs.
VGG features: For this type of data we opted to utilize
the data provided in (Bacharidis and Argyros, 2020).
From a VGG-16 (Simonyan and Zisserman, 2014)
network, 1-D feature vectors are extracted from the
last fully-connected layer, resulting in a feature vector
of 2048 dimensions for each frame of the sequence.
For the RGB frames the network is not fine-tuned and
the learned weights are maintained from the training
on ImageNet (Deng et al., 2009). In the case of op-
tical flow the VGG-16 layers are fine-tuned starting
from the last 2-D layer and above on optical flow data
from the KTH dataset (Schuldt et al., 2004), freezing
the rest with the weight values from ImageNet (Deng
et al., 2009).
MHAD101 Dataset (Papoutsakis et al., ): Contains
concatenated actions from the MHAD dataset in or-
der to form longer sequences of multiple actions. To
alleviate possible ambiguities, the action labeled as sit
down/stand up is excluded as it is a composition of the
actions sit down and stand up. In the MHAD dataset
each action is repeated five times by each subject but
in this dataset only the first execution of an action
by each subject is used. The skeletal data provided
by the MHAD dataset are used and down-sampled to
30fps. The aforementioned actions (excluding the ac-
tion sit-down/stand-up) are used for creating larger
sequences of actions. The synthesised MHAD101
dataset contains 101 pairs of action sequences. In the
first 50 paired sequences, each sequence consists of 3
concatenated action clips (triplets) and the paired se-
quences have exactly 1 in common. In the rest pairs of
actions sequences, 4 to 7 actions are concatenated in
a long sequence. In all the synthesised sequences the
style and duration variability are promoted by using
different subjects in forming different triplets. The
lengths of the sequences range between 300 to 2150
frames.
Skeletal Features: We use the MHAD101-s version of
MHAD101 which contains skeletal features. We used
only the first 50 pairs of action sequences. By splitting
these 50 pairs, we resulted in 100 action sequences
where each of them contains 3 concatenated actions.
These actions are synthesised from the same features
that are described in Section 4.
VGG Features: We use the MHAD101-v version of
MHAD101 which contains the RGB videos of the
same triplets as in MHAD101-s. We then extract fea-
tures from the VGG-16 network as in (Bacharidis and
Argyros, 2020). We took into account all the available
frames without down-sampling to 30fps.
MSR Daily Activity 3D Dataset (Wang et al.,
2012): Contains 16 trimmed executions of human-
object interactions in two different settings, standing
up and sitting on a sofa. The actions are: eating,
speaking on cellphone, writing on paper, using a lap-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
230

top, using a vacuum cleaner, cheering up, sitting still,
tossing paper, playing a game, walking, lie down on
the sofa, playing the guitar, reading a book, standing
up, drinking and sitting down. The standard evalua-
tion split is used as in (Xia and Aggarwal, 2013; Reily
et al., 2018; Manousaki et al., 2021).
Skeletal Features: Following the work of Manousaki
et al. (Manousaki et al., 2021), we represent the
dataset with 3D joint angles and 3D skeletal joint po-
sitions. The 3D joint angles are based on the work of
(Rius et al., 2009). Due to the noisiness of the lower
body data, only the upper body joints are used thus
resulting in a 30-dimensional feature vector. The 3D
joint angles are augmented with the 3D skeletal joint
position of the upper body that are invariant to the
body center resulting in a 27 + 18 = 45-dimensional
vector. The object class and the 2D object position
are acquired through the YoloV4 (Bochkovskiy et al.,
2020) algorithm as in Manousaki et al. (Manousaki
et al., 2021). The final feature vector per frame is 47-
dimensional.
CAD-120 Dataset (Koppula et al., 2013): Contains
trimmed actions with human-object interactions. The
actions can be performed using different objects by 4
subjects from different viewpoints. The action labels
are: reach, move, pour, eat, drink, open, place, close,
clean, null. The manipulated objects are:cup, box,
bowl, plate, microwave, cloth, book, milk, remote,
medicine box. The standard 4-fold cross validation
split is used as in (Koppula et al., 2013; Manousaki
et al., 2021).
Skeletal Features: The feature vector representing the
CAD-120 dataset contains the 3D location of 8 up-
per body joints, the distance moved by each joint and
their displacement. The objects are represented us-
ing the 3D centroid location, the distance between the
object centroid and each of the 8 human joints. Also,
the distance moved by the object and the displacement
of the object’s centroid. These features are also em-
ployed in (Koppula et al., 2013) and Manousaki et
al. (Manousaki et al., 2021).
4.1 Performance Metrics
The observation ratio of each video is ranging from
10% to 100% with step equal to 10%. The accuracy
of the predicted action label is measured by compar-
ing the partially observed video with the prototype
videos. Action prediction is quantified using stan-
dard metrics such as F1-score, precision, recall and
Intersection-Over-Union (IoU).
5 IMPLEMENTATION ISSUES
For OE-DTW and OBE-DTW we employed a
publicly available implementation
2
. The imple-
mentations of OE-S-DTW and OBE-S-DTW were
based on the S-DTW implementation in the Tslearn
toolkit (R.Tavenard et al., 2020). The parameter γ was
experimentally set equal to 1 for all datasets through
evaluation in the range [0.001 , 1].
The Segmental DTW implementation is provided
by (Panagiotakis et al., 2018; Papoutsakis et al.,
2017b). The parameters of the Segmental DTW algo-
rithm are set according to (Panagiotakis et al., 2018)
where it is recommended the minimum length of a
warping path to be half the length of the smallest ac-
tion. Our experiments showed that if the minimum
length is set too small, the algorithm ends up with
smaller paths that do not represent an alignment. If
the minimum length is very high, the algorithm is un-
able to align videos in the case of small observation
ratios.
For our comparison with the work of Cao et
al. (Cao et al., 2020) we need to stress the fact that
we are not comparing directly with the full OTAM
framework. The comparison is based on the align-
ment algorithm that creates the distance matrices and
finds an alignment path between two sequences and
classifies to the reference video that minimizes the
alignment score. Since there is no code available for
this method, we implemented the alignment compo-
nent based on the details provided in the paper. Also,
the OTAM framework is only tested in trimmed ac-
tion videos of fixed length. In (Cao et al., 2020) a co-
sine distance measure is proposed but in the data used
in the current work the Euclidean distance yields the
best results for this method. So, the reported results
are based on the Euclidean distance and γ value equal
to 1. The key differences are the padding with zeros
at the start and end of the distance matrix and the dif-
ferent computation of the cumulative matrix which is
C(x
i
,y
j
) = D(x
i
,y
j
)+min
γ
(C(x
i−1
,y
j−1
),C(x
i
,y
j−1
)).
The alignment score is given at the last index of the
cumulative matrix which denotes the alignment of the
sequences in their entirety.
6 EXPERIMENTS
To evaluate the proposed OE-S-DTW and OBE-S-
DTW algorithms on the task of human action predic-
tion, we conduct three types of experiments. First,
2
https://github.com/statefb/dtwalign
Segregational Soft Dynamic Time Warping and Its Application to Action Prediction
231
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
Observation Ratio
0
10
20
30
40
50
60
70
80
90
100
Accuracy
MHAD (Skeletal)
OE-DTW
OE-S-DTW
OBE-DTW
OBE-S-DTW
SegmentalDTW
OTAM
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
Observation Ratio
10
20
30
40
50
60
70
80
90
100
Accuracy
MSR Daily Activities (Skeletal)
OE-DTW
OE-S-DTW
OBE-DTW
OBE-S-DTW
SegmentalDTW
OTAM
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
Observation Ratio
0
10
20
30
40
50
60
70
80
90
100
Accuracy
CAD120 (Skeletal)
OE-DTW
OE-S-DTW
OBE-DTW
OBE-S-DTW
SegmentalDTW
OTAM
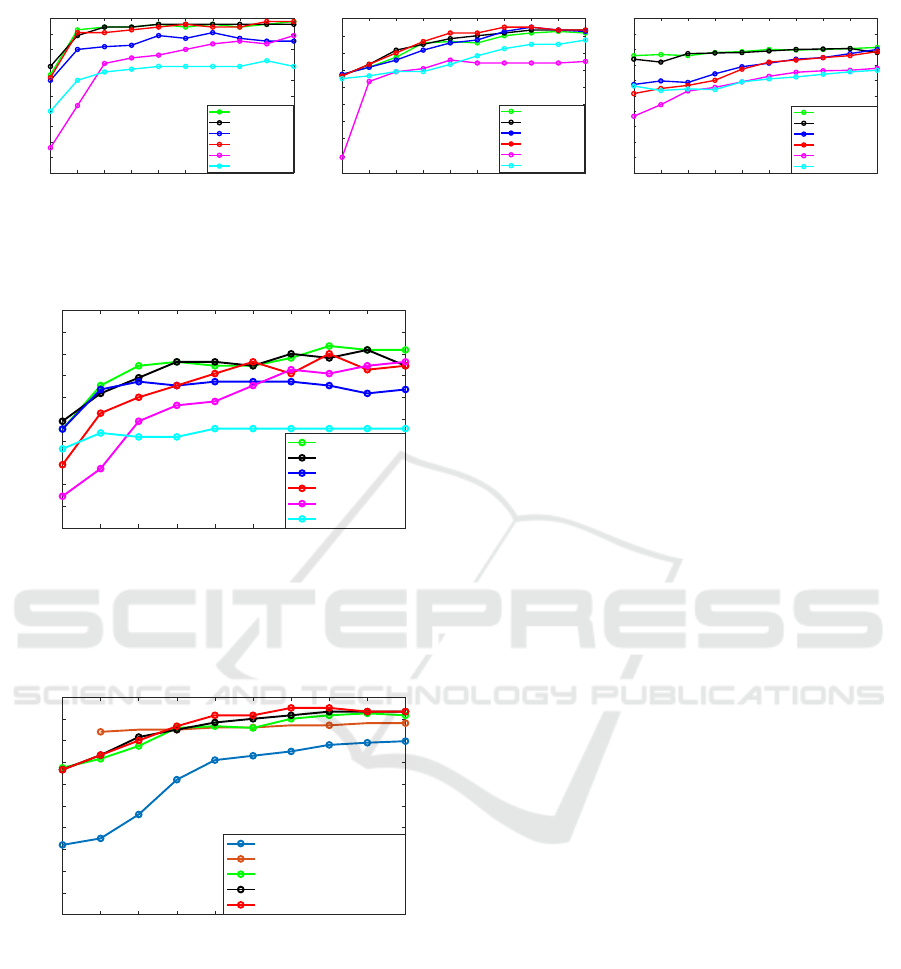
Figure 1: Action prediction accuracy in trimmed videos as a function of observation ratio involving skeletal features in the
MHAD (left), MSR (middle) and CAD-120 (right) datasets.
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
Observation Ratio
0
10
20
30
40
50
60
70
80
90
100
Accuracy
MHAD (VGG Features)
OE-DTW
OE-S-DTW
OBE-DTW
OBE-S-DTW
SegmentalDTW
OTAM
Figure 2: Action prediction accuracy in trimmed videos as
a function of observation ratio involving VGG-16 features
in the MHAD dataset.
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
Observation Ratio
0
10
20
30
40
50
60
70
80
90
100
Accuracy
MSR Daily Activities (Skeletal)
Reily et al. - BIPOD
Alfaifi et al. - 3D-CNN
Manousaki et al. - OE-DTW
OE-S-DTW
OBE-S-DTW
Figure 3: Action prediction accuracy of our methods in
comparison to state of the art methods on the MSR Daily
Activities dataset.
we use these algorithms to perform action prediction
in trimmed action sequences containing one action.
In this setting, the proposed algorithms are used to
align and match an action of known start and variable
observation ratio to a set of prototype actions (sec-
tion 6.1). We also compare the performance of the
proposed algorithms to a number of competing meth-
ods. In a second experiment, the input is a triplet
of actions and the goal is to predict the label of the
middle action under different observation ratios (sec-
tion 6.2). In this untrimmed video/action setting, both
the start and the end of the action are unknown to the
algorithms. Finally, given the capability of the pro-
posed algorithms to predict the label of the on-going
action, we test how accurately they can predict the
end-time of that action (section 6.3).
6.1 Evaluation in Trimmed Actions
In this set of experiments we used the trimmed video
recordings of the MHAD, MSR Daily and CAD-120
datasets. In Fig. 1, we report results on experiments
using skeletal features. We evaluate the proposed OE-
S-DTW and OBE-S-DTW algorithms in comparison
to OE-DTW, OBE-DTW, Segmental DTW (Panagio-
takis et al., 2018) and OTAM (Cao et al., 2020). As
it can be verified, the performance of OE-DTW and
OE-S-DTW is comparable and both achieve very high
accuracy in all datasets. Moreover, OBE-S-DTW out-
performs OBE-DTW by a large margin in the MHAD
and MSR Daily datasets. In the CAD-120 dataset the
performance of OBE-DTW and OBE-S-DTW is prac-
tically the same. Note that OE-DTW and OE-S-DTW
are aware of the common start of the actions while
OBE-DTW and OBE-S-DTW, don’t. Thus, OBE-
DTW and OBE-S-DTW have to deal with a consid-
erably less constrained/more difficult problem.
In the same figure, we can observe the perfor-
mances of the two competitive methods, Segmental
DTW and OTAM. The proposed algorithms outper-
form both Segmental DTW and OTAM by a great
margin in all datasets.
For the MHAD dataset we also experimented with
VGG features. Figure 2 shows the performance of
all evaluated algorithms is such a setting. It can
be observed that even with this type of features, the
proposed OBE-S-DTW outperforms Segmental DTW
and OTAM as well as OBE-DTW for observation ra-
tio greater than 40%. OE-DTW performs comparably
to our proposed OE-S-DTW variant.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
232

1/3
2/3
3/3
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
1/3
2/3
3/3
Observation Ratio
0
10
20
30
40
50
60
70
80
90
100
Accuracy
MHAD101-s Triplets
OE-DTW
OE-S-DTW
OBE-DTW
OBE-S-DTW
SegmentalDTW
OTAM
1/3
2/3
3/3
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
1/3
2/3
3/3
Observation Ratio
0
10
20
30
40
50
60
70
80
90
100
Accuracy
MHAD101-v Triplets
OBE-DTW
OBE-S-DTW
SegmentalDTW
OTAM
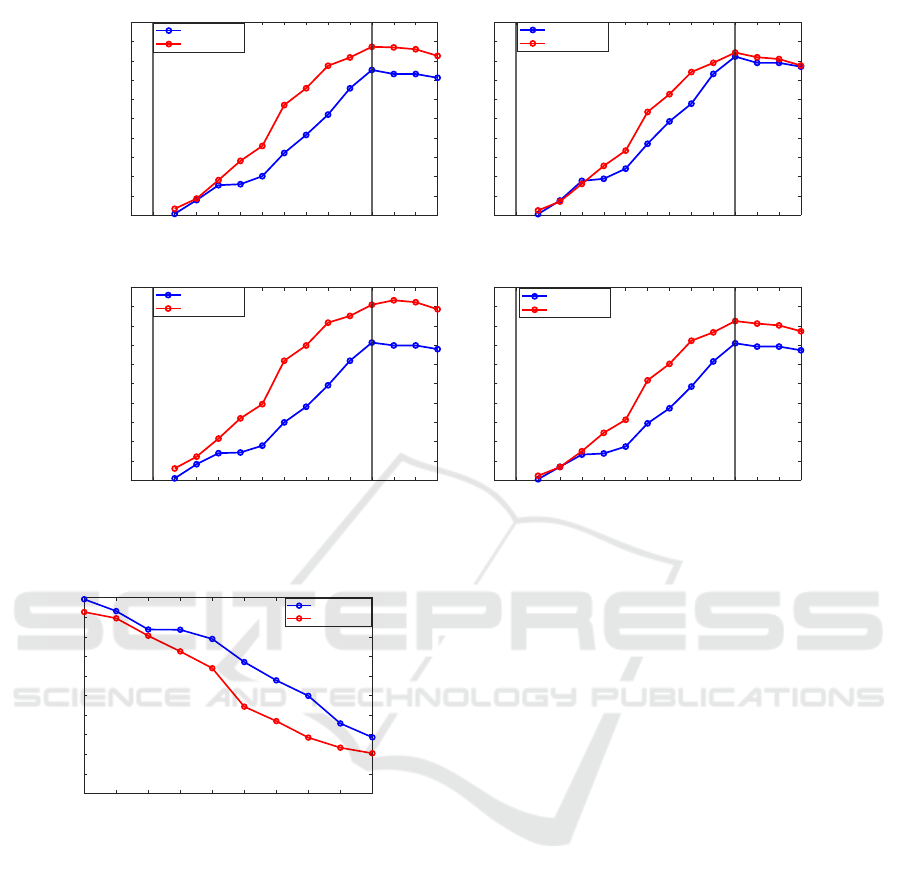
Figure 4: Action prediction accuracy in untrimmed videos (video triplets) of the MHAD101 dataset as a function of observa-
tion ratio involving skeletal features (MHAD101-s, left) and VGG-16 features (MHAND101-v, right).
For the MSR Daily Activities dataset, in Figure 3,
we also compare our approach to the competitive
methods of Reily et al. (Reily et al., 2018), Alfaifi
et al. (Alfaifi and Artoli, 2020) and Manousaki et
al. (Manousaki et al., 2021). As it can be observed,
we outperform (Reily et al., 2018) and Manousaki et
al. (Manousaki et al., 2021) at all observation ratios
and (Alfaifi and Artoli, 2020) for all observation ra-
tions greater than 40%.
6.2 Evaluation in Untrimmed Actions
The proposed methods are also evaluated in the
untrimmed action sequences (action triplets) of
MHAD101-s/-v datasets. In this experiment we ex-
plore whether OBE-S-DTW can recognize an unseg-
mented action that appears between some other prefix
and suffix actions. To do so, the algorithms progres-
sively observe the whole triplet (3 actions in a row)
and aim at segmenting and recognizing the middle ac-
tion. To achieve this, in each triplet that is observed,
we exclude the prefix/suffix actions from the set of
the reference actions. The prefix and suffix actions
are observed in thirds. The middle action is observed
in tenths, so as to have a finer performance sampling
relative to the observation ratio of the test action.
Figure 4 (left) shows the obtained results on the
MHAD101-s dataset (skeletal features). In that plot,
the two vertical black lines denote the ground-truth
start and end of the middle action. High accuracy dur-
ing the prefix denotes the ability of the algorithm to
recognize that the algorithm correctly identifies that
the sought action has not yet started. High accuracy
during the suffix denotes the successful recognition
of the middle action inside the triplet. As it can be
observed, this experiment is not suited for the OE-
DTW and OE-S-DTW variants which fail completely
to segment and identify the middle action. OBE-S-
DTW clearly outperforms OBE-DTW and all other
evaluated algorithms by a large margin.
The same experiment is held using the
MHAD101-v dataset using the VGG-16 features
(Figure 4, right). We observe that overall, the
algorithms perform better with skeletal features than
with VGG ones. However, their ranking and relative
performance does not change. Thus, the superiority
of the proposed OBE-S-DTW is independent of the
type of the employed features.
In Figure 5 we also illustrate the precision, recall,
F1-score and IoU for the two best performing algo-
rithms, OBE-DTW and OBE-S-DTW. In all cases,
OBE-S-DTW produces better action alignments and,
thus, action predictions.
In an effort to gather further experimental evi-
dence, we ran all the experiments reported in this sec-
tion by reversing the videos/action sequences of the
evaluated datasets (i.e., observing them progressively
from the end towards the start). Another reason for
running this additional tests was to check whether the
specific actions that appear as action prefixes or post-
fixes affect the performance of the evaluated algo-
rithms. We report that this change in the observation
order did not affect the performance of the evaluated
algorithms and the conclusions of this study.
6.3 Duration Prediction
Being able to forecast the completion time of an on-
going action is an important piece of information in
many vision applications. Our algorithms can derive
this information by matching a partially observed ac-
tion to the reference ones and by assuming that this
will have the duration of the closest match. In Fig-
ure 6 we can see the performance of OBE-DTW and
OBE-S-DTW in this task. For a given observation ra-
tio, we report the end-frame prediction error which
is defined as the discrepancy of the estimated end of
a certain action from its ground truth end, as a per-
Segregational Soft Dynamic Time Warping and Its Application to Action Prediction
233
2/3
3/3
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
1/3
2/3
3/3
Observation Ratio
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
F1-Score
MHAD101-s
OBE-DTW
OBE-S-DTW
2/3
3/3
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
1/3
2/3
3/3
Observation Ratio
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Precision
MHAD101-s
OBE-DTW
OBE-S-DTW
2/3
3/3
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
1/3
2/3
3/3
Observation Ratio
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Recall
MHAD101-s
OBE-DTW
OBE-S-DTW
2/3
3/3
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
1/3
2/3
3/3
Observation Ratio
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
IoU
MHAD101-s
OBE-DTW
OBE-S-DTW
Figure 5: Performance metrics for OBE-DTW and OBE-S-DTW on the MHAD101-s dataset.
1/10 2/10 3/10 4/10 5/10 6/10 7/10 8/10 9/10 10/10
Observation Ratio
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
End-frame prediction error
MHAD101-s
OBE-DTW
OBE-S-DTW
Figure 6: Percentage of the frames that are lost compared
to the ground truth duration of the action.
centage of the test action length. When an action is
wrongly classified by the algorithm, then a prediction
error of 1.0 (100%) is added. We observe that as the
algorithms see more of a certain action (larger obser-
vation ratio) they predict the action end more accu-
rately. Moreover, the proposed OBE-S-DTW appears
to outperform clearly OBE-DTW.
7 SUMMARY
In this work, we proposed two novel temporal align-
ment algorithms for the matching of incomplete
videos represented as multidimensional time series.
These algorithms proved to be superior to existing
DTW variants on the task of human action prediction
in trimmed and untrimmed videos. The experimental
results on skeletal and deep features show significant
accuracy gain on the human action prediction scenar-
ios by aligning fused human-object action representa-
tions on the MHAD, MSR, CAD-120, MHAD101-s
and MHAD101-v datasets. Moreover, by being soft
and differentiable, the proposed variants can be used
as an integral part of the loss function of Neural Net-
work solutions to a number of related problems. On-
going research work is targeted in this direction.
ACKNOWLEDGEMENTS
The research work was supported by the Hellenic
Foundation for Research and Innovation (HFRI) un-
der the HFRI PhD Fellowship grant (Fellowship
Number: 1592) and by HFRI under the “1st Call for
H.F.R.I Research Projects to support Faculty mem-
bers and Researchers and the procurement of high-
cost research equipment”, project I.C.Humans, num-
ber 91.
REFERENCES
Afrasiabi, M., Mansoorizadeh, M., et al. (2019). Dtw-
cnn: time series-based human interaction prediction in
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
234

videos using cnn-extracted features. The Visual Com-
puter.
Alfaifi, R. and Artoli, A. (2020). Human action prediction
with 3d-cnn. SN Computer Science.
Bacharidis, K. and Argyros, A. (2020). Improving deep
learning approaches for human activity recognition
based on natural language processing of action labels.
In IJCNN. IEEE.
Bochkovskiy, A., Wang, C., and Liao, H. (2020). Yolov4:
Optimal speed and accuracy of object detection.
arXiv:2004.10934.
Cao, K., Ji, J., Cao, Z., Chang, C.-Y., and Niebles, J. C.
(2020). Few-shot video classification via temporal
alignment. In CVPR.
Chang, C.-Y., Huang, D.-A., Sui, Y., Fei-Fei, L., and
Niebles, J. C. (2019). D3tw: Discriminative differ-
entiable dynamic time warping for weakly supervised
action alignment and segmentation. In CVPR.
Cuturi, M. and Blondel, M. (2017). Soft-dtw: a differen-
tiable loss function for time-series. arXiv:1703.01541.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-
Fei, L. (2009). Imagenet: A large-scale hierarchical
image database. In IEEE CVPR.
Dvornik, N., Hadji, I., Derpanis, K. G., Garg, A., and Jep-
son, A. D. (2021). Drop-dtw: Aligning common sig-
nal between sequences while dropping outliers. arXiv
preprint arXiv:2108.11996.
Ghoddoosian, R., Sayed, S., and Athitsos, V. (2021). Ac-
tion duration prediction for segment-level alignment
of weakly-labeled videos. In IEEE WACV.
Hadji, I., Derpanis, K. G., and Jepson, A. D. (2021). Repre-
sentation learning via global temporal alignment and
cycle-consistency. arXiv preprint arXiv:2105.05217.
Haresh, S., Kumar, S., Coskun, H., Syed, S. N., Konin, A.,
Zia, M. Z., and Tran, Q.-H. (2021). Learning by align-
ing videos in time. arXiv preprint arXiv:2103.17260.
Kim, D., Jang, M., Yoon, Y., and Kim, J. (2015). Clas-
sification of dance motions with depth cameras using
subsequence dynamic time warping. In SPPR. IEEE.
Koppula, H., Gupta, R., and Saxena, A. (2013). Learn-
ing human activities and object affordances from rgb-
d videos. The International Journal of Robotics Re-
search.
Manousaki, V., Papoutsakis, K., and Argyros, A. (2018).
Evaluating method design options for action classifi-
cation based on bags of visual words. In VISAPP.
Manousaki, V., Papoutsakis, K., and Argyros, A. (2021).
Action prediction during human-object interaction
based on dtw and early fusion of human and object
representations. In ICVS. Springer.
Ofli, F., Chaudhry, R., Kurillo, G., Vidal, R., and Bajcsy, R.
(2013). Berkeley mhad: A comprehensive multimodal
human action database. In IEEE WACV.
Panagiotakis, C., Papoutsakis, K., and Argyros, A. (2018).
A graph-based approach for detecting common ac-
tions in motion capture data and videos. In Pattern
Recognition.
Papoutsakis, K., Panagiotakis, C., and Argyros, A. (2017a).
Temporal action co-segmentation in 3d motion cap-
ture data and videos. In CVPR.
Papoutsakis, K., Panagiotakis, C., and Argyros, A. A. Tem-
poral action co-segmentation in 3d motion capture
data and videos. In CVPR 2017. IEEE.
Papoutsakis, K., Panagiotakis, C., and Argyros, A. A.
(2017b). Temporal action co-segmentation in 3d mo-
tion capture data and videos. In CVPR.
Park, A. S. and Glass, J. R. (2007). Unsupervised pattern
discovery in speech. IEEE Transactions on Audio,
Speech, and Language Processing.
Reily, B., Han, F., Parker, L., and Zhang, H. (2018).
Skeleton-based bio-inspired human activity prediction
for real-time human–robot interaction. Autonomous
Robots.
Rius, I., Gonz
`
alez, J., Varona, J., and Roca, F. (2009).
Action-specific motion prior for efficient bayesian 3d
human body tracking. In Pattern Recognition.
Roditakis, K., Makris, A., and Argyros, A. (2021). Towards
improved and interpretable action quality assessment
with self-supervised alignment.
R.Tavenard, Faouzi, J., Vandewiele, G., Divo, F., Androz,
G., Holtz, C., Payne, M., Yurchak, R., Rußwurm, M.,
Kolar, K., and Woods, E. (2020). Tslearn, a machine
learning toolkit for time series data. Journal of Ma-
chine Learning Research.
Sakoe, H. and Chiba, S. (1978). Dynamic programming
algorithm optimization for spoken word recognition.
IEEE transactions on acoustics, speech, and signal
processing.
Schez-Sobrino, S., Monekosso, D. N., Remagnino, P.,
Vallejo, D., and Glez-Morcillo, C. (2019). Automatic
recognition of physical exercises performed by stroke
survivors to improve remote rehabilitation. In MAPR.
Schuldt, C., Laptev, I., and Caputo, B. (2004). Recognizing
human actions: a local svm approach. In ICPR. IEEE.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Tormene, P., Giorgino, T., Quaglini, S., and Stefanelli, M.
(2009). Matching incomplete time series with dy-
namic time warping: an algorithm and an application
to post-stroke rehabilitation. Artificial intelligence in
medicine.
Wang, J., Liu, Z., Wu, Y., and Yuan, J. (2012). Mining
actionlet ensemble for action recognition with depth
cameras. In IEEE CVPR.
Xia, L. and Aggarwal, J. (2013). Spatio-temporal depth
cuboid similarity feature for activity recognition using
depth camera. In IEEE CVPR.
Yang, C.-K. and Tondowidjojo, R. (2019). Kinect v2 based
real-time motion comparison with re-targeting and
color code feedback. In IEEE GCCE.
Segregational Soft Dynamic Time Warping and Its Application to Action Prediction
235
