Combining Local and Global Pose Estimation for Precise Tracking of

Similar Objects

Niklas Gard

1 a

, Anna Hilsmann

1 b

and Peter Eisert

1,2 c

Vision and Imaging Technologies, Fraunhofer HHI, Einsteinufer 37, 10587 Berlin, Germany

Institute for Computer Science, Humboldt University of Berlin, Unter den Linden 6, 10099 Berlin, Germany

Keywords:

6DoF Tracking, 6DoF Pose Estimation, Multi-object, Synthetic Training, Monocular, Augmented Reality.

Abstract:

In this paper, we present a multi-object 6D detection and tracking pipeline for potentially similar and non-

textured objects. The combination of a convolutional neural network for object classiﬁcation and rough pose

estimation with a local pose reﬁnement and an automatic mismatch detection enables direct application in

real-time AR scenarios. A new network architecture, trained solely with synthetic images, allows simultaneous

pose estimation of multiple objects with reduced GPU memory consumption and enhanced performance. In

addition, the pose estimates are further improved by a local edge-based reﬁnement step that explicitly exploits

known object geometry information. For continuous movements, the sole use of local reﬁnement reduces

pose mismatches due to geometric ambiguities or occlusions. We showcase the entire tracking pipeline and

demonstrate the beneﬁts of the combined approach. Experiments on a challenging set of non-textured similar

objects demonstrate the enhanced quality compared to the baseline method. Finally, we illustrate how the

system can be used in a real AR assistance application within the ﬁeld of construction.

1 INTRODUCTION

The detection and subsequent registration of 3D rigid

objects in videos are key components in augmented re-

ality (AR) systems. When interacting with real-world

objects, their relative pose with respect to a camera

has to be known to enrich them with additional infor-

mation. Speciﬁcally, there are two subtasks: global

6D pose estimation without prior knowledge of the

pose and local frame-to-frame tracking where an ini-

tial pose is known from the previous frame. This paper

connects current literature on the research areas in a

dynamic system and contributes new ideas to both to

balance them for optimal AR usage.

We target challenging industrial or construction

scenarios, involving manual object assembly or sorting.

They require stable detection and tracking, as well

as real-time capability and occlusion handling. In

addition, the objects are often untextured, similar in

shape and color, and produced in small batches.

This presents particular hurdles for pose estimation.

While convolutional neural network(CNN)-based 6D

pose estimators from single-camera images have ad-

https://orcid.org/0000-0002-0227-2857

https://orcid.org/0000-0002-2086-0951

https://orcid.org/0000-0001-8378-4805

vanced rapidly in recent times, their ability to perform

multi-object pose estimation has received only limited

attention. Often best results for multiple objects are

achieved by training a separate network for each object

(Song et al., 2020; Park et al., 2019; Peng et al., 2019).

Not only does this require more memory than a single-

network solution, but also classiﬁcation is more difﬁ-

cult. Either each network must be tested if an object of

unknown type is visible, or even another network must

be trained to identify the objects. However, knowl-

edge of multiple similar objects helps distinguish them

and prevents false-positive estimates. We extend a

well-known pose estimator PVNet (Peng et al., 2019)

by using object-speciﬁc parameters locally within the

estimated semantic masks. This improves the distin-

guishing of similar objects with a single network and

the handling of shape ambiguities.

Next, objects produced in small batches make the

collection of real-world training images infeasible.

The use of synthetic renderings allows to create unlim-

ited amounts of perfectly labeled data to ﬂexibly add

new objects to the system. We see local reﬁnement as

a key to solving different problems. First, the so-called

domain gap limits the accuracy of CNNs trained on

synthetic data tested on real data (Wang et al., 2020).

Second, a CNN usually processes images with limited

Gard, N., Hilsmann, A. and Eisert, P.

Combining Local and Global Pose Estimation for Precise Tracking of Similar Objects.

DOI: 10.5220/0010882700003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages

745-756

ISBN: 978-989-758-555-5; ISSN: 2184-4321

745

(a) (b) (c) (d)

Figure 1: After the left object is uncovered (a, b) tracking starts immediately. Local tracking keeps active for the right object

also if the CNN detects a wrong (c) or no object (d). Rows from top to bottom: camera image, estimated semantic segmentation,

camera image with rendered overlay.

resolution, limiting also the accuracy of the pose esti-

mates. Contrary to the trend to make the training data

more realistic (Hoda

n et al., 2019), reﬁnement narrows

the domain gap and enables us to use simple domain

randomized training data (To et al., 2018). Even only

single object images are used for training, although

the use in a multi-object system is intended. The lo-

cal edge-based reﬁnement matches the 3D model with

image edges on high-resolution images. Third, false-

positive detections may arise from the CNN due to

shape ambiguities. Object edges provide a cue to sup-

press them. Poses are validated only if it is possible

to accurately match the projected contour of the 3D

model with the image edges, using an edge deviation

error from local pose reﬁnement.

Even though the CNN-based solutions are real-

time capable, we show that it is often beneﬁcial to

prioritize local reﬁnement in video sequences (Fig-

ure 1c,d), e.g. in situations not explicitly modelled in

the training data. Only if local reﬁnement fails due to

occlusion or fast motion, edge-based pose validation

actively triggers reinitialization (Figure 1a,b), so that

otherwise no CNN evaluation is required.

In summary, we present a pipeline for tracking

and 6D detection of multiple similar objects in AR

systems, with automatable training, and evaluate the

individual components with 13 similar objects from

a real AR application. We demonstrate our pipeline

on synthetic images with domain gap and real video

sequences and show beneﬁts and limitations of individ-

ual components and possibilities of the overall system.

2 RELATED WORK

Augmented Reality for Assembly.

Providing guid-

ance e.g. via head-mounted displays during assembly

and construction tasks is an essential AR use case,

motivated by the reduced time needed to complete

a task compared to paper manuals (Henderson and

Feiner, 2010). User acceptance is an important chal-

lenge (Masood and Egger, 2020), and reliable track-

ing is a key factor to achieving immersive, easy-to-

use systems. While stable localization is already in-

tegrated into widely used hardware (Vassallo et al.,

2017), pipelines with easy automatic extendibility for

new objects as well as stable 6D tracking for AR are

still rare. (Zubizarreta et al., 2019) provide a frame-

work based on chamfer matching with conic priors to

detect and register CAD models of machine-made ob-

jects in monocular images. A limitation is that objects

have to consist of conics to be recognized, and it is

unclear whether the system works for geometrically

similar objects. Recognition of subtle differences is

studied in the ﬁeld of assembly state detection (Liu

et al., 2020). Assembly state detection has also been

paired with pose estimation (Su et al., 2019), but with-

out combining it with frame-to-frame pose reﬁnement,

it does not provide stable tracking for AR applications.

Multi-object 6D Pose Estimation.

A common way

to infer the pose of known objects from a monocular

image is to use a CNN to ﬁnd the location of the

2D image projection of 3D points, e.g. object-speciﬁc

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

746

keypoints or dense coordinate maps, and estimate the

pose with a Perspective-n-Point (PnP) algorithm (Peng

et al., 2019; Song et al., 2020; Zakharov et al., 2019;

Tremblay et al., 2018; Li et al., 2019; Park et al., 2019).

As an example, PVNet (Peng et al., 2019) segments

objects and simultaneously predicts unit vector ﬁelds

inside the estimated mask pointing towards the 2D

projections of keypoints. The intersection of two ran-

domly selected points leads to a 2D estimate, which is

validated with a RANSAC-based voting scheme. This

generates a high level of robustness against occlusions.

To detect multiple objects with a single network, they

propose to simply increase the number of classes and

also the number of estimated vector ﬁelds. Neverthe-

less, with PVNet and the other approaches mentioned

above, the best results are achieved when a single

network is trained for every object. In addition, the

amount of GPU memory needed in training drastically

increases with the number of outputs, and training

becomes slower and more difﬁcult.

(Sock et al., 2020) describe a performance drop

due to scalability problems for a backbone that uses a

similar trivial multi-object extension (Rad and Lepetit,

2017). To close this gap, they add object-speciﬁc nor-

malization parameters to the CNN using Conditional

Instance Normalization (CIN) (Dumoulin et al., 2017).

With CIN, the right normalization parameters can only

be selected if the object identity information is known,

e.g. by using a bounding box detector, and only one

pose can be estimated in one inference.

In this work, we improve the PVNet architecture

to choose the correct normalization parameters auto-

matically. Class-adaptive instance (de)normalization

(CLADE) (Tan et al., 2021) selects object-speciﬁc pa-

rameters based on the semantic class of each pixel.

The resulting network can easily be trained for multi-

ple objects, the multi-object gap is narrowed, and all

known objects in one image can be found during one

inference without knowing their identity in advance.

Local Object Tracking.

Although pose estimation

with CNNs has recently developed very rapidly, state-

of-the-art results for model-based frame-to-frame

tracking are still achieved with non-learning-based

methods. For potentially non-textured objects and

image-based tracking, existing approaches can roughly

be separated into edge and region-based methods.

Region-based methods use either global (Prisacariu

and Reid, 2012) or temporary local color (Tjaden et al.,

2018; Zhong and Zhang, 2019) histograms to separate

an object from the background and optimize the pose

to maximize the discrimination. They are best suitable

for objects, which are distinct from the background,

but easily fail for objects, which have a similar color

to the background (Sun et al., 2021).

Edges or contours are suitable visual cues for track-

ing non-textured objects. Based on the RAPID al-

gorithm (Harris and Stennett, 1990), 2D-3D corre-

spondences are searched on scanlines perpendicular

to the object contour. Extensions ﬁlter those corre-

spondences with respect to the contour orientation

(Huang et al., 2020), a global or local color histogram

(Seo et al., 2013; Wang et al., 2015; Huang et al.,

2020) or consider multiple hypotheses per scanline.

Other edge-based algorithms do not explicitly include

point-to-point correspondences, but instead minimize

a pixel-based distance metric directly on the intensity

image (Dong et al., 2020; Wang et al., 2019).

Similarly, analysis-by-synthesis-based methods

(Seibold et al., 2017; Gard et al., 2019) try to syn-

thetically recreate the camera image with a rendered

representation and minimize image distance by mo-

tion compensation with respect to the optical-ﬂow con-

straint. A comparable representation between real and

synthetic images has to be found, either by explicitly

modelling scene or image-parameters such as motion

blur (Seibold et al., 2017), or simpliﬁcation, e.g. by

using robust edge-images (Gard et al., 2019).

Our tracking algorithm combines correspondence

and non-correspondence-based tracking, independent

of color information, and is suitable for textured and

non-textured objects. It bridges larger pose differ-

ences during RAPID-based iterations. A subsequent

analysis-by-synthesis optimization makes ﬁne adjust-

ments and also accounts for inner edges.

3 REGISTRATION PIPELINE

This section covers our multi-object tracking and iden-

tiﬁcation pipeline. Our system should not need any

photos of the real object before being able to recognize

it. In an ofﬂine phase, renderings are generated as train-

ing data for our pose estimation CNN (Section 3.1).

The CNN constantly scans the video stream and esti-

mates an initial pose for each visible, known object

(Section 3.2). After detection, a local reﬁnement step

maps the edges of the 3D model to the image edges

(Section 3.3). A validation step (Section 3.4) evaluates

the quality of these matches and either validates or

invalidates the pose. For objects with validated poses,

it is sufﬁcient to proceed with local reﬁnement for the

next image.

Combining Local and Global Pose Estimation for Precise Tracking of Similar Objects

747

Figure 2: Synthetically rendered training images and the cor-

responding color-coded vector ﬁelds that, within the object

mask, point to the 2D projection of a 3D keypoint.

3.1 Data Generation

The Input of the data generation step is a set of multiple

3D models to be detected and tracked. They may have

similar shapes and may be untextured or from the same

material but should not be rotationally symmetric. The

models are centered at their 3D bounding box and

keypoints, the object center and

k −1

points on the

object surface, are determined using the Farthest Point

Sampling algorithm (Peng et al., 2019).

We create a dataset consisting of synthetic render-

ings using NDDS (To et al., 2018), an Unreal Engine

plugin for generating annotated training images. To

address the domain gap, i.e. the different properties

of real and synthetic images that affect the accuracy

of a CNN trained on synthetic data only, we use do-

main randomization (Tobin et al., 2017). We render

the objects in front of a random background, which

is either a photo or a randomly generated procedural

graphic. In half of the images, the objects are rendered

over a ﬂat surface to introduce shadows. Also, the

position of light sources, the orientation and position

of the object, the texture of the object, and the posi-

tion of the camera are randomized. Randomly placed

distractor objects introduce partial occlusion. In each

image, only one target object is visible, which simpli-

ﬁes the recompilation of new datasets for different sets

of objects.

Contrary to other publications (Hoda

n et al., 2019;

Thalhammer et al., 2021), we do not render near-photo-

realistic images and instead deal with inaccurate pose

estimates by reﬁning the pose locally and ﬁltering

wrong pose estimates by our pose validation step. We

further reduce the domain gap and focus on shape

differences by using grayscale images only. For each

training image, a mask of the visible part of the object,

its pose, and the position of the keypoints in 3D and

2D space are stored (Figure 2).

3.2 6D Detection Network

Our pose estimator ﬁrst establishes 2D-3D correspon-

dences with a correspondence estimation CNN. It pre-

dicts

n + 1

pixel-level masks for the background and

known objects, as well as

joint vector ﬁelds. The

number of keypoints is the same for each object. In

a vector ﬁeld, two coordinate maps form 2D vectors

pointing to the image location of the keypoint belong-

ing to the object a pixel is assigned to in the semantic

segmentation.

As with PVNet (Peng et al., 2019), the intersec-

tions of randomly selected vector pairs within an object

mask result in 2D location estimates that are validated

with a RANSAC-based voting procedure. The object

pose is found with a PnP algorithm. Contrary to them,

the joint vector ﬁeld reduces the number of output

maps for the vector ﬁelds from

2nk

and is in-

dependent of the number of objects. This makes the

network much easier and faster to train, reduces the

required GPU memory during training, and the data

transfer between GPU and CPU after inference. E.g.

for 13 objects with 9 keypoints the number of output

maps are reduced from 248 to 32.

The following modiﬁcations are made to PVNet.

The semantic segmentation and the vector ﬁelds

are predicted with two different decoders con-

nected to the same encoder.

In the keypoint decoder, the batch normaliza-

tion is replaced with a class-adaptive instance

(de)normalization (CLADE) (Tan et al., 2021).

The estimated semantic segmentation is used as a

side input for the CLADE layers to select object-

speciﬁc weights with the Guided Sampling (Tan

et al., 2021) strategy, based on the class a pixel

belongs to.

The object-speciﬁc weights increase the capacity of

the network for multi-object pose estimation. The spa-

tial selection of those weights allows correspondences

for multiple objects to be estimated with one inference.

In the decoder blocks, the semantic mask is downsam-

pled so that its size matches with the output of the.

convolution.

To achieve better convergence during training, the

ground truth mask instead of the estimated mask is

used as side input. During inference, the intermediate

logits of the segmentation are normalized with a scaled

softmax function with high temperature value. Our

CNN architecture is visualized in Figure 3.

3.3 Local Reﬁnement

Poses estimated by the CNN are not stable enough

for AR use, as even small jitter signiﬁcantly reduces

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

748

Figure 3: The input image is processed with a segmentation

branch that guides the vector ﬁeld prediction for 2D-3D

correspondence estimation.

visual quality. Furthermore, a domain gap between

camera images and synthetic training images affects

the accuracy of the tracking. Therefore, we apply an

additional local analysis-by-synthesis reﬁnement to

stabilize the pose estimation. If possible, only the

local reﬁnement is used, since it can bridge the small

frame-to-frame movements.

The reﬁnement starts from an approximate pose

given by

3 ×3

rotation matrix

and translation vector

. This pose is either the output of the global CNN

detection or the output of local reﬁnement at time step

t −1

. A synthetic image

and a depth map

are

generated by an off-screen renderer using meshes of

the detected objects. The goal is to ﬁnd the pose offsets

∆t

∆R

that compensate the difference between camera

image I and

p = [p

, p

]

is a 3D point on the model sur-

face in

, it is transformed to

and projected into

the image point

with the intrinsic matrix

and a

homogenization operation π(p) = [p

, p

]

p = ∆R(

p −t) + t + ∆t (1)

x = π(Kp) (2)

As in (Steinbach et al., 2001), under small motion

assumption, a linearized rotation matrix with three

unknown parameters

∆r = [∆r

,∆r

]

is used and

the displacement error is expressed as a linear equation

using ﬁrst order Taylor expansion. Our optimization

algorithm obtains a two-stage structure of two con-

secutively solved minimization problems. The usage

of an image pyramid and an iteratively reweighted

least squares (IRLS) scheme (Zhang, 1997) stabilize

convergence and reduce the inﬂuence of outliers.

3.3.1 Contour-based Optimization

Inspired by other work (Huang et al., 2020; Harris and

Stennett, 1990), we implement an edge-based registra-

tion algorithm. The depth map

allows generating a

silhouette mask from which

edge points

and the

corresponding 3D points

are extracted.

We extract match hypotheses along

scanlines

, along the unit vector

perpendicular to the pro-

jected contour at a given point. We sample

along

and convolve each sample with pre-computed

5 ×5

rotated Sobel kernels to extract edges with similar ori-

entation to the projected edge. All locations where the

convolved value is a local maximum along the scan-

line and larger than a threshold

, are stored as edge

hypothesis points

i, j

. We minimize the error function

E(∆R,∆t) =

∑

i=0

ω(r

)(s

−π(Kp

))) (3)

whereby the pose delta transforms

(Equa-

tion 1) and

is the hypothesis with the smallest

spatial distance to the observed contour point. By

using the Taylor approximation of the displacement

error, we solve an overdetermined linear equation sys-

tem for the pose parameters. The weighting func-

tion

ω(x) = 1/

√

+ ε

applies the robust Charbon-

nier penalty (Sun et al., 2010) with

ε = 0.001

on the

hypothesis residual

from the previous IRLS iteration.

Two or three weight updates stabilize the estimation

against outliers.

Each pyramid stage consists of four to six repe-

titions. The off-screen renderer and the hypothesis

selection are only executed initially. Consecutively,

only the extracted 3D contour is transformed. More-

over, on the smallest pyramid level, we only solve for

translation and rotation within the 2D image plane.

3.3.2 Dense Reﬁnement

The contour-based optimization may be affected by

mismatches along the scanlines. We use a subsequent

dense optimization minimizing the image distance

with respect to the general optical ﬂow equation (Horn

and Schunck, 1981)

∂

Y s

≈

I −I (4)

which is reformulated to be a linear equation system.

This system is solvable with respect to the unknown

pose parameters using the coefﬁcients

from (Stein-

bach et al., 2001).



∆r

∆t



I −I (5)

Combining Local and Global Pose Estimation for Precise Tracking of Similar Objects

749

Every pixel inside the silhouette of the rendered ob-

ject results in one equation for the iterative reweighted

least squares solution.

Adaptive thresholding (Gard and Eisert, 2018;

Gard et al., 2019) makes the rendered image and the

camera image comparable. First, a thresholded Sobel

ﬁlter extracts edges in the rendered image, then the

threshold for the camera image is adapted over a 2D

grid to reproduce a similar distribution of edge and

non-edge pixels in each grid cell. This also reduces

the inﬂuence of illumination.

Both edge images are smoothed with a box ﬁlter to

introduce smooth gradients around the detected edges

before minimizing the image distance. The optimiza-

tion is suitable for textured and non-textured objects.

Due to the application of simple shading in the off-

screen renderer, sharp geometric edges will be visible

in the Sobel image.

Since all operations are applied pixel-wise, the

processing can be executed on the GPU by custom

compute-shaders. Also, the equation coefﬁcients are

combined on the GPU. The least squares problem is

formulated in

Ax = b

form and each iteration only

needs a transfer of the symmetric

6 ×6

matrix

and the

6 ×1

vector

between GPU and CPU,

where the system is solved.

3.4 Pose Validation

In a single-camera system, objects with small geomet-

ric differences can lead to ambiguities that have to be

ﬁltered reliably. A pose validation ﬁlters wrong pose

estimates due to drift or false-positive detections.

Detection Validation.

The RANSAC-based voting

(Peng et al., 2019) during detection needs a minimum

number of positive samples (e.g.

) to validate a 2D

keypoint hypothesis. After the initial pose estimation,

the reprojection error must be smaller than a threshold

(12 pixels in our experiments) for at least 4 points.

Reﬁnement Validation.

The initial pose can still

be coarse, so pose validation including acceptance

or rejection is performed on the reﬁned poses. It re-

quires the projected contour of the object to match with

the image content. We ﬁnd the error of the RAPID-

inspired local registration suitable to measure this.

Here,

IRLS

is the mean residual value in the last it-

eration in the lowest pyramid level,

Dist

is the mean

distance between points on the projected contour and

the closest correspondence hypothesis, and

valid

the ratio of the number of scanlines to the number of

scanlines on which a correspondence hypothesis was

found. We deﬁne the edge matching score as

edge

= e

IRLS

×e

Dist

×e

valid

. (6)

An initial pose is reﬁned and

edge

of the ﬁrst frame

is stored as initial error

init

. If it is smaller than a

threshold

˜e

init

an initial pose is accepted. Otherwise,

we keep the object as a candidate and further reﬁne

the pose locally for the next frames as long as

edge

decreases. If the error increases compared to the last

frame, a detection is discarded.

Then,

edge

is monitored continuously and the run-

ning mean average

ˆe

edge

is updated as long as the

object remains valid. As long as

edge

is smaller than

a maximum value

˜e

max

and

ˆe

edge

× f

, where

is a pre-

deﬁned factor, an object keeps its validity. If not, the

object is in a borderline state. The pose is not updated

and a mismatch counter increases for every following

invalid frame until either the pose becomes valid again

or two invalid frames appear in a row, which sends the

object to an uninitialized state.

4 IMPLEMENTATION DETAILS

4.1 CNN Training and Architecture

Our training dataset consists of

∼

15000 synthetic im-

ages per object. Our CNN is trained for 125 epochs

using the ADAM optimizer. The initial learning rate

0.002

is divided by two every 25 epochs. The back-

bone of our network provides features for both de-

coders and is connected via skip connections to both

of them. It is a pretrained ResNet-18 (He et al., 2016)

obtaining the same modiﬁcations as in (Peng et al.,

2019). In the keypoint decoder, each convolution is

followed by a CLADE layer. The CLADE layers ex-

tend the CNN by 1024 trainable parameters per object.

In total, the number of trainable weights increases by

about 14% by the second decoder.

Training images have a size of

320

. The images

are augmented by random contrast and brightness, ad-

ditional normally distributed noise, and random rota-

tion and translation variations. The input images are

grayscale. To use the pretrained weights of ImageNet,

the intensities are stacked to form a three-channel im-

age. We use differentiable proxy voting loss (DVPL)

(Yu et al., 2020) and smooth l1-loss to learn the vec-

tor ﬁeld. We use softmax cross-entropy loss to learn

semantic segmentation.

During training, we input the ground truth segmen-

tation to the CLADE layers of the vector ﬁeld decoder.

The numbers given for PVNet are computed with our

Tensorﬂow port of the original code.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

750

4.2 CNN Inference and Live Tracking

The inference in our tracking software uses the

OpenCV DNN module with its CUDA extension. Ini-

tial poses are estimated from 2D-3D correspondences

with EPNP (Lepetit et al., 2009).

The reﬁnement exploits an off-screen OpenGL ren-

derer to compute the intermediate images. While the

contour-based part is fast on CPU, the dense reﬁne-

ment relies on custom GLSL compute shaders for all

image processing and the formation of the equation

system. Only solving the equation system is done on

the CPU, minimizing data transfer.

The resolution of all test images is

1024

, input

size of the CNN is

400

. The local tracking uses three

pyramid levels. The length of the scanlines is 15.

Two tracking modes have been implemented. In

Close-Range mode, the subsampled camera image is

passed to the detection network. Multiple objects are

searched at the same time and objects are tracked in-

dependently. The distance between the objects and the

camera matches the training data.

In Far-Range mode, the distance between object

and camera is much larger than in the training data. We

propose to pass image patches to the CNN in which

the size of the object relative to the patch size matches

the median size of the objects in the training images.

5 EXPERIMENTS

We evaluate our registration pipeline with synthetic

data ﬁrst and then describe general observations on

real data in the scenario of AR-guided construction.

Within that example use case, the evaluation models

are part of a miniaturized model of a grid shell fa-

cade, consisting of 13 node elements (Figure 4) and 42

connector sticks. The node elements are particularly

interesting since they all have similar but not identical

shapes and geometric ambiguities can arise easily.

The

2D projection metric

(Brachmann et al.,

2016) is used to judge the detection accuracy. The

vertices of the models are projected into the image

with the estimated pose and the ground-truth pose. A

pose is correct if the average distance is smaller than 5

pixels and the percentage of correct estimates is listed.

5.1 Beneﬁts of the Multi-object

Detection Network

The objects in commonly used pose estimation

datasets, like Linemod (Hinterstoisser et al., 2012) or

YCB Video (Xiang et al., 2018), are clearly identiﬁable

by varying color and shape. We focus on the beneﬁt of

Figure 4: Renderings of the 13 objects (I01 -I13) used in our

experiments, numbered from top left to bottom right.

Figure 5: Two images from our synthetic evaluation set.

our multi-object model to differentiate between similar

objects.

Our evaluation dataset contains 200 images per

object. Images are generated synthetically but a dif-

ferent render engine is used to introduce a domain

gap between training and testing data. The synthetic

data generator BlenderProc (Denninger et al., 2019)

based on Blender allows rendering nearly-photo real-

istic images. Two examples are shown in Figure 5.

In each image, the object is placed on a ﬂat surface

with varying texture and is surrounded by distractor

objects. The camera, object, and light source poses

vary between the images. First, we compare three

multi-object models:

1. PV-M

uses the trivial multi-object extension of

PVNet. With every added object, 19 channels are

added to the network output.

2. PV-M-C

is a modiﬁcation of the baseline architec-

ture that outputs joint vector ﬁelds.

3. CLADE-PV

uses our proposed network structure,

as described in Section 3.2.

Table 1 lists the results for the different network

structures with respect to the 13 objects. Our model im-

proves the detection accuracy compared to the baseline

model by a large margin. It is important to note that

CLADE-PV

requires much less GPU memory than

PV-M

during training. With

CLADE-PV

, seven times

larger batch sizes were possible on the same hardware,

resulting in much faster training. The

PV-M-C

variant

was designed to be trainable with the same batch size

as CLADE-PV but performed worst.

Combining Local and Global Pose Estimation for Precise Tracking of Similar Objects

751

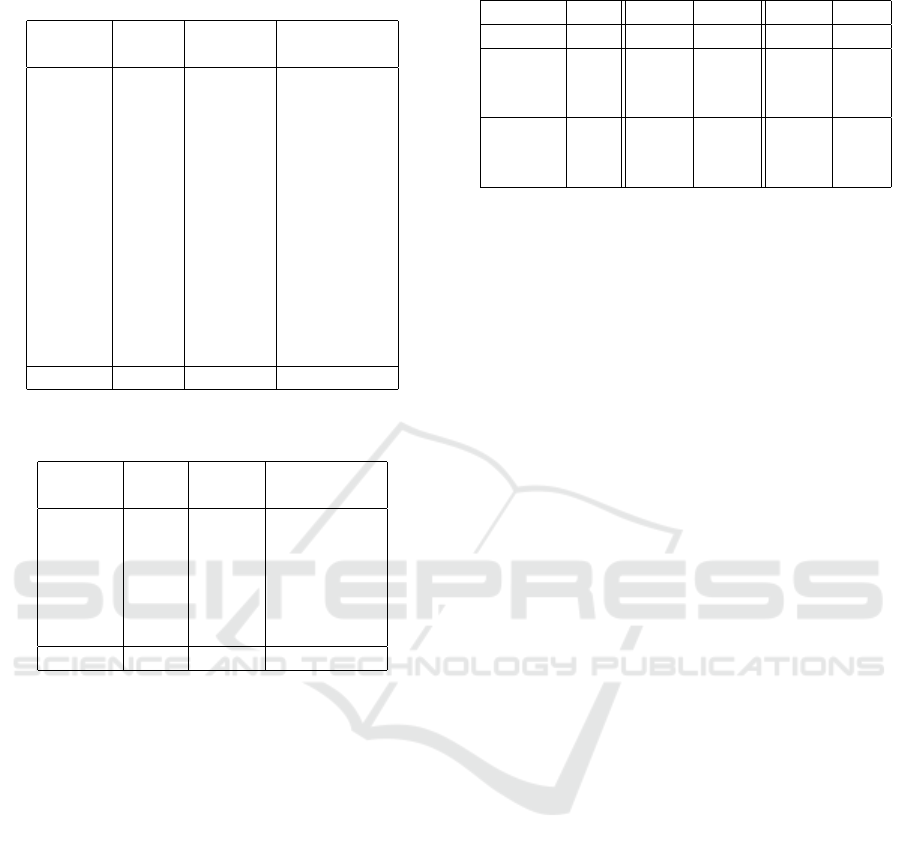
Table 1: Accuracies of our method and the baseline methods

on our evaluation dataset using 2D projection metric.

Method PV-M PV-M-C CLADE-PV

(ours)

I01 75.0 60.0 79.0

I02 78.0 54.5 79.0

I03 71.0 54.0 76.5

I04 82.5 68.0 86.5

I05 93.5 62.5 95.5

I06 66.5 41.5 85.0

I07 80.0 70.0 90.0

I08 73.3 54.2 82.4

I09 53.5 49.5 87.0

I10 75.0 80.0 94.0

I11 85.0 68.5 91.5

I12 69.0 53.5 77.0

I13 84.0 72.5 90.0

Avg. 75.9 60.6 85.6

Table 2: Comparison of single-object models to our multi-

object model using 2D projection metric.

Method PV-S PV-S+ CLADE-PV

(ours)

I01 76.5 80.5 79.0

I02 71.0 70.0 79.0

I03 63.5 61.0 76.5

I04 84.5 77.0 86.5

I05 93.5 87.0 95.5

I06 86.5 78.0 85.0

Avg. 79.3 75.6 83.6

In the next experiment (Table 2), we compare

multi and single-object models. We train two sep-

arate PVNet conﬁgurations for six different objects,

differing in the training data used.

PV-S

sees only the

images of one object. It produces false-positive detec-

tions most of the time for all other objects.

PV-S+

also

sees the same amount of randomly selected images of

other objects to learn to distinguish its own object from

the others. Still, if the identity of the objects present in

the image is unknown, all networks have to be tested

with the input image which will result in computational

overhead. In conclusion, on average the single-object

models perform slightly better than the multi-object

competitors, conﬁrming the multi-object gap, but also

worse than our proposed modiﬁed network.

5.2 Beneﬁts of the Combined Approach

Local Reﬁnement.

We ﬁrst show, how the pose re-

ﬁnement stabilizes the estimations of the CNN. The

raw initial poses are reﬁned using the algorithm from

Section 3.3. While the CNN is limited by the input res-

olution, the reﬁnement uses the full image resolution.

Table 3: Improvement of reﬁnement on initial poses.

Method Iter. 2D

∅R P++

init. − 26.4 0.0 3.50° −

S1 1 76.5 45.7 1.44° 92.3

S2 1 73.8 27.3 1.54° 97.8

S1+2 1 84.3 64.7 0.74° 97.1

S1 3 78.7 52.9 1.20° 90.0

S2 3 83.7 57.8 0.85° 97.7

S1+2 3 86.5 73.9 0.59° 96.5

In Table 3, we list the percentage of valid frames

regarding the 2D projection metric with respect to the

high resolution and use thresholds of 5 (

) and

1 (

) pixel. Also, the average rotational (Tjaden

et al., 2018) error (

∅R

) over all valid frames (5-pixel

threshold), and the percentage of estimates where the

projection error is reduced (

P++

) are listed. The results

for init. correspond to the result from the last section

but refer to the higher resolution. We compare using

contour-based (

) or dense reﬁnement (

) alone

with the combined approach (

S1+S2

), in which the

two processes are alternated in the image pyramid.

We see that one iteration through the image pyra-

mid (

Iter.

) of

S1+S2

improves the accuracy more than

three iterations of

alone.

converges fast, in

the ﬁrst iteration and can potentially bridge larger gaps,

while

is more likely to converge in the right direc-

tion (see

P++

S1+S2

joins both advantages, which

is beneﬁcial for real-time systems. More iterations

further improve the accuracy.

Pose Validation.

During the pose reﬁnement, the er-

ror value

edge

is the criteria for acceptance or rejection

of poses. Ideally, it is larger than

˜e

init

if the estimated

pose is wrong and smaller than

˜e

init

if the estimated

pose is correct.

Table 4 shows the inﬂuence of

˜e

init

. The whole

dataset is passed through the registration pipeline (Sec-

tion 3) and every object is searched in every image.

Three iterations of reﬁnement are allowed. We list the

following percentages: 1) correct estimates (5-pixel

threshold) correctly validated (

Pro j

) (relative to

amount of images), 2) correct estimates correctly vali-

dated (

) (relative to amount of correct detections),

3) wrong estimates correctly declined (

) (rela-

tive to amount of incorrect detections), 4) wrong es-

timates correctly declined using ADD (Hinterstoisser

et al., 2012) to judge pose quality (

ADD

) (relative

to amount of incorrect detections), 5) false-positive

detection of absent object incorrectly validated (

)

(relative to amount of images).

The choice of

˜e

init

is a trade-off, between possibly

declining correct estimates, if too low, or possibly

accepting false detections, if too high. For our test set,

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

752

Table 4: Pose validation results with different initialization

thresholds.

˜e

init

Pro j

ADD

0.08 80.4 94.1 95.2 99.5 0.12

0.10 83.2 96.7 92.6 98.6 0.27

0.12 85.4 98.7 89.3 98.6 0.46

0.14 85.5 99.1 85.5 97.7 0.81

0.16 85.6 99.6 77.5 94.7 0.86

˜e

init

= 0.12

is a good choice.

Pro j

decreases quickly

for smaller values and

decreases quickly for larger

values. Furthermore,

ADD

conﬁrms that most of the

drastically wrong poses are ﬁltered correctly.

False-positively detected objects often provide

strong perspective shape ambiguities, since not only

the wrong object is detected, but also its projected

edges overlap with the image. An interesting observa-

tion is that the CNN partitions the segmentation output

between multiple candidates, when unclear about the

object identity (Figure 8). This may result in multiple

identity/pose estimates for a single object. If a correct

pose cannot be veriﬁed, it is likely that a large part

of the contour is covered or not visible. False pose

detections of present objects can result from false ini-

tial estimates converging to local minima, with large

edge overlap. In both cases, a small object or cam-

era movement is often sufﬁcient in AR applications

with continuous video to ﬁnd a starting position that

converges correctly.

5.3 Beneﬁts in Real Video Sequences

While previous experiments justiﬁed the different com-

ponents of our system under domain gap, we show the

applicability to real-world data on captured sequences.

The recordings come from a live AR demonstrator

guiding a construction scenario in two phases. First,

the objects are sorted in the right order (Close-Range

mode), then they are mounted in that order (Far-Range

mode). Videos showing the sequences including over-

lays are part of the supplementary material.

Close-Range Mode.

We exemplary demonstrate our

pipeline in two sequences, captured with 25 fps and

1024

pixels with an industrial camera. While

Seq. 1

has a white table background,

Seq. 2

has a textured

bubble wrap background with stronger gradients and

light reﬂections. Multiple randomly picked objects are

moved in front of the camera by hand. The sequences

depict fast movements, indirect movements, simulta-

neous movement of multiple objects, occlusion, and

disappearing and reappearing objects.

To evaluate the tracking quality, we apply the multi-

object tracking on the sequences and decide whether

to reﬁne or reinitialize individual objects for the next

frame based on the validation criteria (Section 3.4).

The result conﬁrms our choice of

˜e

init

= 0.12

. Objects

with

edge

< ˜e

init

provide a nearly pixel-accurate over-

lay. The local and global registration beneﬁt from each

other in multiple ways:

During training, the network has never seen multi-

ple objects in an image; during testing, the network

is able to estimate the poses of multiple objects

simultaneously. Accuracy degradations are com-

pensated by local reﬁnement (Figure 6a).

Occlusions between detectable objects were not

seen during training, but even if the network is

unable to ﬁnd the occluded object, tracking will

continue as long as local tracking remains valid

(Figure 7).

Fast movements or heavy occlusions possibly stop

the local tracking, but it continues as soon as the

object is clearly visible again (Figure 1b).

False-positive detections of the network are sup-

pressed since the projected contour does not match

image content well enough.

The textured background in

Seq. 2

has no impact

on the tracking accuracy (Figure 6b). In the course of

the sequence, the objects are also moved on the palm

of a hand, whereby tracking as well as initialization

also succeed in that situation (Figure 6c).

Table 5 shows quantitative results. For each object,

we ﬁrst count the number of frames in which it is

either in motion or partially but no more than half

(three out of six connectors are visible), occluded by a

moving hand/object. We compare two conﬁgurations,

one using the CNN and reﬁnement independent of

the previous pose for every frame (

Init.+Ref.

), and

one dynamically selecting if the CNN is needed by

pose validation (

Init.+Ref.+Valid.

). It can be seen

that the number of correctly validated frames increases

by the latter since the knowledge of the previous pose

is often more meaningful than the result of the CNN.

Nevertheless, on average more than half of the frames

could be used for reinitializing local tracking. Fairly

low values for

I01

and

I06

result from fast movements

with motion blur, possibly under occlusion.

Seq. 1

, ambiguous appearance of an object

during rotation triggers a false-positive detection (Fig-

ure 8). While the network is sure of the correct classi-

ﬁcation in the next frame, local tracking continues at

ﬁrst and only fails after a few frames if the projected

contour deviates too much from the image content.

Far-Range Mode.

We also use the approach to track

objects from a bird’s eye static camera that captures

their assembly in a target structure (Figure 9). Only

Combining Local and Global Pose Estimation for Precise Tracking of Similar Objects

753

Table 5: Evaluation of real-data sequences. For each object, the number of frames with edge error smaller

˜e

init

= 0.12

is listed.

Only frames where interaction with the object (movement or occlusion) happens are considered.

Seq. Method valid I01 I04 I06 I08 I10 I11 FP

1 Init.+Ref. 52.7% 6/34 24/154 17/64 447/646 156/376 72/96 1/1215

1 Init.+Ref.+Valid. 87.5% 16/34 138/154 29/64 614/646 313/376 89/96 3/1215

2 Init.+Ref. 78.0% 371/501 − 311/373 − − − 0/727

2 Init.+Ref.+Valid. 90.4% 460/501 − 330/373 − − − 0/727

(a) Appearing objects.

(b) Movement over textured background.

Figure 6: Tracking and detection of objects in different situations: (a) is from Seq. 1, (b) and (c) are from Seq. 2.

Figure 7: Local tracking remains valid (right), while the

CNN (semantic segmentation, left) would be unreliable.

Figure 8: Geometric ambiguity: For a frame (left) the object

can be identiﬁed (semitransparent mask overlay), while for

the next frame (2nd) the mask is partitioned in two parts,

resulting into two possible object poses (f.l.t.r.).

one object is tracked at a time, so the detection network

is not needed at all, as long as local tracking succeeds.

In the images, the object appears much smaller than

in training data. To compensate for this, the CNN

is applied to the content of a square bounding box

around the last detection or a predeﬁned start position.

In our setup, its side length is half the image size.

Alternatively, it could be scaled dynamically based

on the size of the object in the previous frame. An

additional global detection network is avoided. Of

course, it would also be possible to depict a larger

variation of object-camera distances in the training

dataset. The proposed reconﬁguration should not be

seen as a limitation, but as a way to use the trained

network more ﬂexibly. We found that for more distant

objects only two instead of three pyramid levels and a

lower value of e

init

are preferable.

5.4 Performance

An inference of our CNN with OpenCV requires

∼

ms on an Nvidia GTX 2080 Ti and image size

400

When the network is used for each frame in Close-

Range mode, frame rates of 25-30 frames per sec-

ond are achieved (slightly depending on the size of

the object in the image) when a single object is also

tracked locally. We currently execute the local re-

ﬁnement sequentially, so the performance degrades if

more objects are present. One way to improve that

is to render an extra mask of object IDs and then do

the optimization step for multiple objects simultane-

ously. Thereby, occlusions between known objects

can be explicitly modelled and further improve the

local tracking (Huang et al., 2020). High frame rates

keep the distance between frames small and therefore

stabilize local tracking, with less need for reinitializa-

tion. If, like in the Far-Range mode, the network is

not evaluated for every image and the object is small

compared to the image size, the local reﬁnement runs

at ∼60 fps.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

754

Figure 9: Tracking an object in Far-Range mode. The initialization area is highlighted by a green box.

6 CONCLUSION

We have presented a pipeline for multiple object de-

tection and tracking that combines the advantages of

current CNNs for 6D pose estimation with a local

pose optimizer and a reliable metric for triggering

reinitialization. We use only synthetic training data, al-

lowing fully automatic training without manual image

labeling, and show that local-reﬁnement is suitable to

bridge the domain gap. In addition, we have presented

an extension for a state-of-the-art CNN to better handle

multiple, potentially similar objects, and demonstrate

its beneﬁts using a set of 13 similar, uncolored and

non-textured objects.

In real sequences, difﬁcult situations not encoun-

tered in training can be better handled with a combined

approach that draws on knowledge from previous im-

ages. We argue that such combined approaches are a

very useful option for AR systems. The advantage of

the easy generation of training data outweighs the ex-

tra effort of additional local optimization. The system

is already being used in an AR demonstrator, although

under relatively controlled conditions. In future work,

we will further improve robustness by explicitly mod-

elling occlusions between objects and possibly lift the

self-imposed restriction of using only grayscale im-

ages.

ACKNOWLEDGMENTS

This work is supported by the German Federal Min-

istry of Economic Affairs and Energy (DigitalTWIN,

grant no. 01MD18008B and BIMKIT, grant no.

01MK21001H). We thank Fabian Schmid, Philipp Ko-

priwa, and Gergey Matl (se commerce GmbH) for the

pleasant collaboration and for providing the reference

models.

REFERENCES

Brachmann, E., Michel, F., Krull, A., Yang, M. Y., Gumhold,

S., et al. (2016). Uncertainty-driven 6d pose estimation

of objects and scenes from a single rgb image. In Proc.

CVPR.

Denninger, M., Sundermeyer, M., Winkelbauer, D., Zi-

dan, Y., Oleﬁr, D., Elbadrawy, M., Lodhi, A., and

Katam, H. (2019). Blenderproc. arXiv preprint

arXiv:1911.01911.

Dong, Y., Ji, L., Wang, S., Gong, P., Yue, J., Shen, R., Chen,

C., and Zhang, Y. (2020). Accurate 6dof pose tracking

for texture-less objects. IEEE Transactions on Circuits

and Systems for Video Technology, 31(5):1834–1848.

Dumoulin, V., Shlens, J., and Kudlur, M. (2017). A learned

representation for artistic style. In Proc. ICLR.

Gard, N. and Eisert, P. (2018). Markerless closed-loop pro-

jection plane tracking for mobile projector-camera sys-

tems. In Proc. ICIP.

Gard, N., Hilsmann, A., and Eisert, P. (2019). Projection

distortion-based object tracking in shader lamp scenar-

ios. IEEE Transactions on Visualization and Computer

Graphics, 25(11):3105–3113.

Harris, C. and Stennett, C. (1990). Rapid-a video rate object

tracker. In Proc. BMVC.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep residual

learning for image recognition. In Proc. CVPR.

Henderson, S. and Feiner, S. (2010). Exploring the beneﬁts

of augmented reality documentation for maintenance

and repair. IEEE Transactions on Visualization and

Computer Graphics, 17(10):1355–1368.

Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski,

G., Konolige, K., and Navab, N. (2012). Model based

training, detection and pose estimation of texture-less

3d objects in heavily cluttered scenes. In Proc. ACCV.

Hoda

n, T., Vineet, V., Gal, R., Shalev, E., Hanzelka, J.,

Connell, T., Urbina, P., Sinha, S. N., and Guenter,

B. (2019). Photorealistic image synthesis for object

instance detection. In Proc. ICIP.

Horn, B. K. and Schunck, B. G. (1981). Determining optical

ﬂow. Artiﬁcial intelligence, 17(1-3):185–203.

Huang, H., Zhong, F., Sun, Y., and Qin, X. (2020). An

occlusion-aware edge-based method for monocular

3d object tracking using edge conﬁdence. Computer

Graphics Forum, 39(7):399–409.

Combining Local and Global Pose Estimation for Precise Tracking of Similar Objects

755

Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). Epnp:

An accurate o (n) solution to the pnp problem. Interna-

tional Journal of Computer Vision, 81(2):155–166.

Li, Z., Wang, G., and Ji, X. (2019). Cdpn: Coordinates-based

disentangled pose network for real-time rgb-based 6-

dof object pose estimation. In Proc. ICCV.

Liu, H., Su, Y., Rambach, J., Pagani, A., and Stricker, D.

(2020). Tga: Two-level group attention for assembly

state detection. In Proc. ISMAR.

Masood, T. and Egger, J. (2020). Adopting augmented reality

in the age of industrial digitalisation. Computers in

Industry, 115:103112.

Park, K., Patten, T., and Vincze, M. (2019). Pix2pose: Pixel-

wise coordinate regression of objects for 6d pose esti-

mation. In Proc. ICCV.

Peng, S., Liu, Y., Huang, Q., Zhou, X., and Bao, H. (2019).

Pvnet: Pixel-wise voting network for 6dof pose estima-

tion. In Proc. CVPR.

Prisacariu, V. A. and Reid, I. D. (2012). Pwp3d: Real-time

segmentation and tracking of 3d objects. International

Journal of Computer Vision, 98(3):335–354.

Rad, M. and Lepetit, V. (2017). Bb8: A scalable, accurate,

robust to partial occlusion method for predicting the

3d poses of challenging objects without using depth.

In Proc. ICCV.

Seibold, C., Hilsmann, A., and Eisert, P. (2017). Model-

based motion blur estimation for the improvement of

motion tracking. Computer Vision and Image Under-

standing, 160:45–56.

Seo, B.-K., Park, H., Park, J.-I., Hinterstoisser, S., and Ilic,

S. (2013). Optimal local searching for fast and ro-

bust textureless 3d object tracking in highly cluttered

backgrounds. IEEE Transactions on Visualization and

Computer Galraphics, 20(1):99–110.

Sock, J., Castro, P., Armagan, A., Garcia-Hernando, G.,

and Kim, T.-K. (2020). Tackling two challenges of

6d object pose estimation: Lack of real annotated rgb

images and scalability to number of objects. arXiv

preprint arXiv:2003.12344v1.

Song, C., Song, J., and Huang, Q. (2020). Hybridpose: 6d

object pose estimation under hybrid representations. In

Proc. CVPR.

Steinbach, E., Eisert, P., and Girod, B. (2001). Model-based

3-d shape and motion estimation using sliding textures.

In Proc. VMV.

Su, Y., Rambach, J., Minaskan, N., Lesur, P., Pagani, A.,

and Stricker, D. (2019). Deep multi-state object pose

estimation for augmented reality assembly. In Proc.

ISMAR.

Sun, D., Roth, S., and Black, M. J. (2010). Secrets of optical

ﬂow estimation and their principles. In Proc. CVPR.

Sun, X., Zhou, J., Zhang, W., Wang, Z., and Yu, Q. (2021).

Robust monocular pose tracking of less-distinct ob-

jects based on contour-part model. IEEE Transac-

tions on Circuits and Systems for Video Technology,

31(11):4409–4421.

Tan, Z., Chen, D., Chu, Q., Chai, M., Liao, J., He, M.,

Yuan, L., Hua, G., and Yu, N. (2021). Efﬁcient seman-

tic image synthesis via class-adaptive normalization.

IEEE Transactions on Pattern Analysis and Machine

Intelligence.

Thalhammer, S., Leitner, M., Patten, T., and Vincze, M.

(2021). Pyrapose: Feature pyramids for fast and ac-

curate object pose estimation under domain shift. In

Proc. ICRA.

Tjaden, H., Schwanecke, U., Sch

omer, E., and Cremers,

D. (2018). A region-based gauss-newton approach to

real-time monocular multiple object tracking. IEEE

Transactions on Pattern Analysis and Machine Intelli-

gence, 41(8):1797–1812.

To, T., Tremblay, J., McKay, D., Yamaguchi, Y., Le-

ung, K., Balanon, A., Cheng, J., Hodge, W., and

Birchﬁeld, S. (2018). NDDS: NVIDIA deep learn-

ing dataset synthesizer. https://github.com/NVIDIA/

Dataset Synthesizer.

Tobin, J., Fong, R., Ray, A., Schneider, J., Zaremba, W.,

and Abbeel, P. (2017). Domain randomization for

transferring deep neural networks from simulation to

the real world. In Proc. IROS.

Tremblay, J., To, T., Sundaralingam, B., Xiang, Y., Fox, D.,

and Birchﬁeld, S. (2018). Deep object pose estimation

for semantic robotic grasping of household objects. In

Proc. CoRL.

Vassallo, R., Rankin, A., Chen, E. C., and Peters, T. M.

(2017). Hologram stability evaluation for microsoft

hololens. In Proc. SPIE Volume 10136.

Wang, B., Zhong, F., and Qin, X. (2019). Robust edge-based

3d object tracking with direction-based pose valida-

tion. Multimedia Tools and Applications, 78(9):12307–

12331.

Wang, G., Manhardt, F., Shao, J., Ji, X., Navab, N., and

Tombari, F. (2020). Self6d: Self-supervised monocular

6d object pose estimation. In Proc. ECCV.

Wang, G., Wang, B., Zhong, F., Qin, X., and Chen, B.

(2015). Global optimal searching for textureless 3d

object tracking. The Visual Computer, 31(6):979–988.

Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).

Posecnn: A convolutional neural network for 6d object

pose estimation in cluttered scenes. In Proc. RSS.

Yu, X., Zhuang, Z., Koniusz, P., and Li, H. (2020). 6dof

object pose estimation via differentiable proxy voting

regularizer. In Proc. BMVC.

Zakharov, S., Shugurov, I., and Ilic, S. (2019). DPOD: 6d

pose object detector and reﬁner. In Proc. ICCV.

Zhang, Z. (1997). Parameter estimation techniques: A tuto-

rial with application to conic ﬁtting. Image and Vision

Computing, 15(1):59–76.

Zhong, L. and Zhang, L. (2019). A robust monocular 3d

object tracking method combining statistical and photo-

metric constraints. International Journal of Computer

Vision, 127(8):973–992.

Zubizarreta, J., Aguinaga, I., and Amundarain, A. (2019). A

framework for augmented reality guidance in industry.

The International Journal of Advanced Manufacturing

Technology, 102(9):4095–4108.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

756