Can We Use Neural Regularization to Solve Depth Super-resolution?

Milena Gazdieva

1 a

, Oleg Voynov

1 b

, Alexey Artemov

1 c

, Youyi Zheng

2 d

, Luiz Velho

3 e

and Evgeny Burnaev

1 f

Skolkovo Institute of Science and Technology, Moscow, Russia

State Key Lab, Zhejiang University, Hangzhou, China

Instituto Nacional de Matem

atica Pura e Aplicada, Rio de Janeiro, Brazil

Keywords:

Depth Super-Resolution, Neural Regularization, 3D Deep Learning.

Abstract:

Depth maps captured with commodity sensors often require super-resolution to be used in applications. In

this work we study a super-resolution approach based on a variational problem statement with Tikhonov

regularization where the regularizer is parametrized with a deep neural network. This approach was previously

applied successfully in photoacoustic tomography. We experimentally show that its application to depth map

super-resolution is difﬁcult, and provide suggestions about the reasons for that.

1 INTRODUCTION

Existing research reveals two major classes of state-

of-the-art approaches to depth super-resolution (SR):

data-driven methods based on deep neural net-

works (Riegler et al., 2016; Hui et al., 2016; Voynov

et al., 2019) and variational optimization-based ap-

proaches (Haefner et al., 2018; Haefner et al.,

2020). Among these, learning-based methods bring

the promise of leveraging powerful data-driven priors

by learning these directly from data, which has proven

to achieve impressive quantitative performance; how-

ever, as deep networks are trained by optimizing their

target functions in an averaged sense, they are likely

to produce imperfect estimates for speciﬁc (unseen)

test instances. In contrast, variational approaches

commonly employ sophisticated hand-crafted regu-

larizers and come with theoretical convergence guar-

antees, bounding an error between an estimate and the

true high-resolution depth for individual instances.

Unfortunately, in some instances, the designed regu-

larizer fails to capture image variations present in the

real-world data, leading to suboptimal performance

during variational optimization.

https://orcid.org/0000-0003-0047-1577

https://orcid.org/0000-0002-3666-9166

https://orcid.org/0000-0001-5451-7492

https://orcid.org/0000-0002-9120-9592

https://orcid.org/0000-0001-5489-4909

https://orcid.org/0000-0001-8424-0690

Combining advantages offered by these classes of

approaches represents a natural interest; one partic-

ular variant is to incorporate an informative prior or

a distribution statistic learned from a representative

dataset of high-resolution depth images directly into

the optimization formulation, e.g., as a learned reg-

ularizer. In this approach, a pre-trained neural net-

work aims to provide a data-driven loss term during

the optimization of each individual test instance; we

use this approach in this work. The key intuition of it

is to help alleviate the limitations of either learning-

or optimization-based methods by leveraging the data

distribution information summarized by pre-training

on high-resolution depth images but still optimizing

for each individual test instance.

Image-based tasks have successfully integrated

data-driven loss functions (Gatys et al., 2016; John-

son et al., 2016); inspired by this line of research, in

this paper, we consider the question: “Can we use

learned regularizers to improve depth image super-

resolution?” More speciﬁcally, we opted to use Net-

work Tikhonov (NETT) (Li et al., 2020) framework,

a theoretically sound regularization approach in the

functional analytic sense offering attractive conver-

gence properties, but adapt it to target speciﬁcally

depth images. To this end, we focus on training a

deep convolutional neural network (CNN) to penalize

artifacts found in an input depth image; we further in-

tegrate the norm of feature activations computed in a

pre-trained network as a regularizer into an optimiza-

tion procedure to operate on a per-image basis. To the

582

Gazdieva, M., Voynov, O., Artemov, A., Zheng, Y., Velho, L. and Bur naev, E.

Can We Use Neural Regularization to Solve Depth Super-resolution?.

DOI: 10.5220/0010883500003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

582-590

ISBN: 978-989-758-555-5; ISSN: 2184-4321

best of our knowledge, we are the ﬁrst to investigate

data-driven regularizers in the context of depth SR;

we denote this approach DSRNETT.

We systematically study both theoretical require-

ments and empirical behavior of DSRNETT, where

we are able to meet all theoretical claims (e.g., co-

ercivity), obtain pre-trained regularization models,

and perform optimization using a pre-trained net-

work. However, we discover that it is extremely dif-

ﬁcult for the DSRNETT optimization procedure to

reach a good solution; moreover, the respective tar-

get function is found to correlate weakly with com-

monly used quality measures such as per-pixel RMSE

and perceptually-based RMSE

(Voynov et al., 2019).

These results hold across multiple appropriate data

augmentation strategies, optimization formulations,

and for networks of varying capacity; together, we

believe they indicate limitations of the NETT-type

frameworks for single-image depth SR tasks.

2 RELATED WORK

Depth Super-resolution. Numerous approaches to

deal with depth super-resolution problem were pro-

posed in recent years. One group of approaches fo-

cuses on application of convolutional neural networks

(CNNs) to depth SR (e.g., (Hui et al., 2016; Voynov

et al., 2019; Song et al., 2020)). For instance, (Hui

et al., 2016) proposes a neural architecture that com-

plements low-resolution depth features with high-

frequency features from high-resolution RGB data,

using a multi-scale fusion strategy. (Voynov et al.,

2019) focus on designing a visual-difference based

loss function, aiming to improve the performance

of existing state-of-the-art depth processing methods.

(Song et al., 2020) proposes iterative residual learn-

ing based framework with the use of channel atten-

tion, multi-stage fusion and weight sharing strategies

to tackle both synthetic and real-world degradation

processes of depth maps.

Variational approaches represent another group,

dealing with designing and optimizing an appropriate

target function without relying on learning. (Haefner

et al., 2018) propose a variational functional to jointly

solve single-shot depth SR and shape-from-shading

problems, i.e., inferring high-resolution depth from

color variations in the high-resolution RGB image.

(Haefner et al., 2020) modiﬁes the same approach for

multi-shot depth SR using photometric stereo.

We focus on a combined approach; in contrast to

variational approaches, it does not require to construct

a regularizer manually but inherits their good conver-

gence properties. Unlike purely learning-based meth-

ods, it does not rely on training only but optimizes the

solution for individual samples.

Combined Approaches propose learning a regular-

izer and have been drawing attention recently; these

have not been previously applied to depth SR.

One type of combined approaches corresponds

to bilevel optimization, which incorporates learning

into the deﬁnition of optimal regularizer parameters

(e.g., (De los Reyes et al., 2017; Chen et al., 2013)).

According to this method, optimal parameters are

derived as empirical risk minimizers for supervised

training dataset. In (De los Reyes et al., 2017) bilevel

optimization approach is applied for total variation

(TV) type regularizers. Bilevel optimization with

richer markov random ﬁeld (MRF) parametrization of

regularizer is investigated in (Chen et al., 2013) by ap-

plying it to the image restoration tasks.

Data-driven loss functions have been successfully

applied in the context of image-based tasks such as

style transfer (Gatys et al., 2016) and photo super-

resolution (Johnson et al., 2016) (where they are

known as perceptual losses), reconstruction tasks in

computed and photoacoustic tomography (Li et al.,

2020; Obmann et al., 2019; Arridge et al., 2019; Lunz

et al., 2018), or for feature-based knowledge distilla-

tion (see, e.g., (Gou et al., 2021) for a survey).

Two recent combined approaches (Lunz et al.,

2018; Li et al., 2020) focus on neural network

parametrizations of regularizers in application to

computed and photoacoustic tomography reconstruc-

tion respectively. (Lunz et al., 2018) train a regu-

larizer to discriminate ground-truth and (known) im-

perfect solutions. Another combined approach (Li

et al., 2020) trains a regularizer to penalize solutions

with various kinds of artifacts. (Arridge et al., 2019)

gives an overview of more methods aiming to incor-

porate learning into the variational optimization. In

this work, we parametrize the regularizer using a neu-

ral network; more speciﬁcally, we follow (Li et al.,

2020) that focuses on theoretical foundations, pro-

vides regularizing properties of their method, and de-

rives respective convergence and convergence rates.

3 NETWORK TIKHONOV

VARIATIONAL FORMULATION

FOR DEPTH

SUPER-RESOLUTION

We start with a brief review of the NETT formulation,

rewriting the mathematical relations for our task. The

goal of depth super-resolution is to

estimate x ∈ D from data y

= F(x) + ε

, (1)

Can We Use Neural Regularization to Solve Depth Super-resolution?

583

where F : D ⊂ X → Y is a (known) downsampling

operator, X, Y denote the spaces of high- and low-

resolution depth images, respectively, and ε

is an un-

known data error, s.t., kε

k 6 δ, δ > 0.

Depth super-resolution as formulated by (1) is an

ill-posed inverse problem and admits many possible

solutions. To favor a particular class of solutions,

Tikhonov regularization rewrites the task in an opti-

mization perspective:

D(F(x),y

) + αR (x) → min

x∈D

, (2)

where D : Y ×Y → [0,∞) is a data ﬁdelity term de-

ﬁned on depth images and R : D → [0,∞) is a regu-

larization term. In this work, we focus on the form of

regularizer term, seeking to learn it from data rather

than design it manually. Our DSRNETT draws inspi-

ration from Network Tikhonov framework (Li et al.,

2020), but is redesigned to target speciﬁcally depth

images. Let Φ denote a neural network, which we

view as a composition of afﬁne linear maps V

(x) =

x + b

and non-linearities σ

where l is a layer in-

dex. Many convolutional architectures such as U-

Net (Ronneberger et al., 2015) admit this form. We

indicate a (trainable) afﬁne part V = (V)

in the no-

tion of Φ

(·) and formulate our regularizer as

R (x) = ψ(Φ

(x)), (3)

where ψ : X → [0,∞) is a scalar function.

To effectively guide optimization in (2), network

parameters V must be learned using the available

training data before any optimization may happen (we

assume that non-linearities σ

are not trainable). We

consider the two following pre-training schemes.

Scheme 1: Train the network to predict an arti-

fact component from the input depth image. In this

scenario, we split a set X

of high-resolution train-

ing images x

into two disjoint subsets X

∪X

and

compute approximations

= F

(F(x

)) for each x

∈

, using an upsampling operator F

(a pseudo-

inverse of F). The network then trains to predict a

residual r

= x

−

from the input approximation

for images in X

, or an exactly zero image for im-

ages in X

. A simple regularizer based on this net-

work is a Euclidean norm of the predicted residual:

R (x) = kΦ

(x)k

Scheme 2: An alternative approach, which we ex-

perimentally observed to aid convergence, is to train

the model to directly predict ground-truth depth im-

ages given either an input approximation or a ground-

truth image. In this scenario, the network is trained to

output the same image as input x

for images in X

and an ideal x

from input approximation

for images

in X

. We attribute the advantages of this approach

to the beneﬁt of having inputs of similar scale. A sim-

ilar approach is employed by (Obmann et al., 2019).

We then keep the idea of penalizing images with arti-

facts in the design of regularizer, which is deﬁned as

R (x) = kΦ

(x) − xk

NETT is guaranteed to converge to a unique and

stable solution provided that certain analytic condi-

tions hold (Li et al., 2020). We report a detailed anal-

ysis in the context of our task in the Appendix.

4 EXPERIMENTS

4.1 Toy Examples: GDSR and SimGeo

We start by implementing our approach on sim-

ple synthetic depth images, using the dataset from

(Riegler et al., 2016), that we denote GDSR. It con-

sists of scenes containing randomly placed cubes,

spheres and planes in varying poses and dimensions.

Here and below, we visualize 3D scenes as renderings

of corresponding depth maps, obtaining these using a

simple normals-based method (Voynov et al., 2019).

We train two CNNs to predict residuals in up-

scaled depth images according to Scheme 1 (i.e., the

CNN predicts the artifact part of the training in-

stances): one using the original depth images and an-

other using the noise-augmented depth images, and

perform optimization using the two trained models as

regularizers. To optimize for a ﬁnal depth image, we

minimize a sum of the squared L

-norm data ﬁdelity

term and the squared L

-norm of network output:

kF(x) − yk

+ αkΦ

(x)k

→ min

. (4)

Since the network is trained to output artifact part

of the depth maps for visualization of its performance

we use rendering of sum of network input and net-

work output, which should approximate ground-truth

depth map.

While we are able to train efﬁcient estimators

of residuals using both clean and noise-augmented

images, as shown in Figures 1–2, using the noise

augmentations proves to have a major effect on the

optimization performance (see Figures 3–4). More

speciﬁcally, we ﬁnd that regularizing optimization

in (4) with the network trained on clean synthetic im-

ages leads to a bad solution (see Figures 3 (c)–(d)).

Moreover, we discover that the DSRNETT loss

function correlates poorly with RMSE

, the standard

root-mean-squared (RMS) error capturing per-pixel

differences between depth maps, and perceptual mea-

sure RMSE

(Voynov et al., 2019), deﬁned as the

RMS difference between renderings capturing visual

differences between 3D surfaces represented as depth

maps. Both RMSE

and RMSE

represent measures

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

584

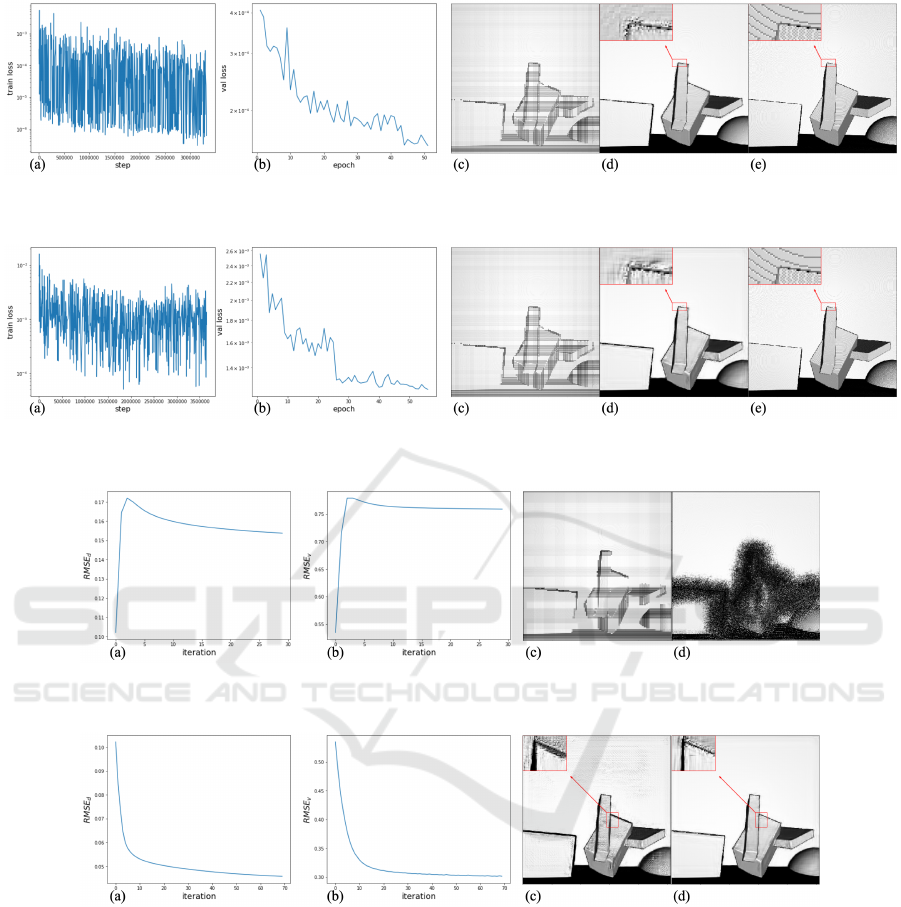
Figure 1: Typical pre-training results using GDSR: (a): train loss dynamics; (b): validation loss dynamics, log-scale; (c):

initial approximation (network input); (d): reconstructed depth image; (e): ground-truth.

Figure 2: Typical pre-training results using noisy GDSR: (a): train loss dynamics; (b): validation loss dynamics, log-scale;

(c): initial approximation (network input); (d): reconstructed depth image; (e): ground-truth.

Figure 3: Typical optimization results using networks pre-trained on GDSR: (a): RMSE

to ground-truth dynamics; (b):

RMSE

to ground-truth dynamics; (c): initial approximation; (d): optimization result (30 iterations).

Figure 4: Typical optimization results using networks pre-trained on noisy GDSR: (a): RMSE

to ground-truth dynamics;

(b): RMSE

to ground-truth dynamics; (c): initial approximation; (d): optimization result (70 iterations).

commonly used in evaluating depth map processing

performance (see inset Figure 5).

Eventually, optimization resulted in only a

marginal improvement for validation samples from

GDSR (see Figures 4 (c)–(d)). We hypothesize that

this stems from a limited capacity in our network, and

seek to increase it in Section 4.2.

Implementation Details. We obtain 128 × 128 high-

resolution training samples by splitting each image

from GDSR dataset into 16 patches. For 50% of

these high-resolution patches, we generate their low-

resolution counterparts, choosing F as a box down-

sampling method with a scaling factor of 4, and ob-

tain approximations

x by applying the pseudo-inverse

as an upsampling operator. In total, we obtained

128K patches for training and 32K for validation.

We employ a U-Net-like architecture (Ron-

neberger et al., 2015). In order to satisfy the co-

ercivity condition for the regularizer term, which is

stated by (Li et al., 2020) to be the most restrictive

one, we replace ReLU activation function in network

architecture with leaky ReLU. We train by optimiz-

ing MSE loss using Adam (Kingma and Ba, 2015)

for ∼70 epochs using a batch size of 2.

Can We Use Neural Regularization to Solve Depth Super-resolution?

585

Figure 5: Pre-training on clean data (a)–(c) leads to op-

timization results where the DSRNETT loss function (4)

does not correlate well with the commonly used RMSE

and RMSE

measures. Pre-training with noise-augmented

data (d)–(f) yields more predictable optimization dynamics.

Figure 6: Performance of NETT approach in compari-

son to underlying network (CNN) and Bilinear interpola-

tion on samples from SimGeo for a network pre-trained on

GDSR with added noise. For each sample - First row:

depth maps in pseudo-colour; Second row: renderings in

grayscale.

We perform optimization in (4) using the in-

cremental gradient descent algorithm following (Li

et al., 2020). Thus, optimization consisted of two

steps: gradient descent step for data ﬁdelity term with

weight s and gradient descent step for regularizer term

with weight s · α, done with the use of backpropaga-

tion algorithm. We also choose the step weights, fol-

lowing (Li et al., 2020). Yet in contrast, we do not use

a zero image as initial approximation, but start op-

timization from approximation of ground-truth depth

map, derived by upsampling y, since the network is

trained on similar train samples.

To train the network with noisy data, we add

Gaussian noise with variance equal to 0.05 to all pix-

els in input depth images.

Due to the low complexity of the training dataset,

network was pre-trained very well and optimization

did not improve network result for validation sam-

ples from GDSR. On the other hand, for geomet-

rically more complex synthetic scenes from Sim-

Geo (Voynov et al., 2019) dataset network, pre-

trained on GDSR, output poor result and NETT ap-

proach was not working correctly; see Figure 6 for

comparison of approach performance with underly-

ing network and bilinear interpolation on simple and

complex synthetic scenes. According to these sugges-

tions we decided to reimplement NETT with stronger

network architecture, using complex synthetic and

real-world scenes for pre-training.

4.2 Complex Synthetic and Real-world

Scenes: MPI Sintel and Middlebury

To study our approach in a full-scale setting, we use

data collections and network architectures with larger

complexity. More speciﬁcally, we use U-MSG-Net, a

U-Net-like version of the MSG-Net architecture (Hui

et al., 2016) that has demonstrated good performance

for depth SR due to the effective use of RGB guid-

ance (see Appendix for more details). For training our

network, we use MPI Sintel (Butler et al., 2012) and

Middlebury 2014 (Scharstein et al., 2014) datasets,

both providing RGB-D images. MPI Sintel contains

complex scenes retrieved from a naturalistic 3D an-

imated short ﬁlm, while Middlebury 2014 consists

of complex high-quality real images captured with a

structured light system.

Due to the difﬁculties with optimization conver-

gence, that we discuss further, in addition to training

the network according to Scheme 1 we experimented

with training according to Scheme 2, where the goal

is to predict a reconstructed image given an input ap-

proximation. We observed that Scheme 2 leads to

better convergence in comparison to Scheme 1 and

further provide results for Scheme 2. For optimiza-

tion, we accordingly set the regularizer to R (x) =

kΦ

(x) − xk

, re-using the general framework de-

scribed previously.

We do not explicitly account for the coercivity

condition of the architecture, since (Li et al., 2020)

provides ways to obtain coercivity for an arbitrary ar-

chitecture, e.g., using skip connection between net-

work input and output, as we discuss further.

Data Augmentation. To aid generalization, we study

a number of data augmentation strategies aiming to

expand the training domain, summarized in Table 1.

Training with noisy inputs. We train the network

on input depth images augmented with different vari-

ations of additive random noise (lines 2, 4-6 in the

table).

Training with both noisy inputs and targets. Aim-

ing to increase network robustness, we train the net-

work to predict noisy ground-truth depth from noisy

ground-truth, keeping target noise variance smaller

than that of input noise (line 7).

Training with input in-between approximation and

ground truth. The regularizer R (x) is designed to

push x to ground-truth data manifold, approximated

by Φ

(x). Based on the derivation in Appendix, we

hypothesize that, in contrast to this desired behaviour,

the optimization of the regularizer also pushes the out-

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

586

Figure 7: Typical pre-training results using Middlebury 2014 / MPI Sintel (test sample from SimGeo): (a): train loss dynamics;

(b): validation loss dynamics, log-scale; (c): input approximation (network input); (d): reconstructed depth image; (e):

ground-truth image.

Figure 8: Typical optimization results using networks pre-trained on Middlebury 2014 and MPI Sintel: (a): RMSE

ground-truth dynamics; (b): RMSE

to ground-truth dynamics; (c): initial approximation; (d): optimization result (30 itera-

tions).

Figure 9: Typical optimization results using networks pre-trained on noisy Middlebury 2014 and MPI Sintel: (a): RMSE

to ground-truth dynamics; (b): RMSE

to ground-truth dynamics; (c): initial approximation; (d): optimization result (70

iterations).

Figure 10: Typical optimization results using networks pre-trained on Middlebury 2014 and MPI Sintel augmented using

linear interpolation between GT and approximation: (a): RMSE

to ground-truth dynamics; (b): RMSE

to ground-truth

dynamics; (c): initial approximation; (d): optimization result (7 iterations).

put of the network in the undesired direction. To pre-

vent that, we additionally train the network on the

samples, where the input is the result of one step of

optimization with small regularizer step size s · α =

0.001. We also try a simpler strategy to train on ran-

dom linear interpolation between the approximation

and the ground truth as the input.

Additionally, in the experiments with MPI Sin-

tel and Middlebury 2014 we randomly rotate the

patches by 90

◦

. We brieﬂy review the results of these

experiments below.

Similarly to results in Section 4.1, training without

data augmentations results in optimization hitting a

bad solution (see Figure 8). Network trained on noisy

data tends to produce over-smooth depth maps (see

Figure 9). Using noisy data with gradually decreas-

Can We Use Neural Regularization to Solve Depth Super-resolution?

587

Table 1: Summary of conducted experiments. Mid./Sint. correspond to Middlebury 2014/MPI Sintel.

Pre-training Net Scheme Input augmentation Optimization Result Opt. RMSE

RMSE

GDSR U-Net 1 — GDSR Noisy X X X

GDSR U-Net 1 Gaussian noise with σ = 0.05 GDSR OK X X X

Mid./Sint. U-MSG-Net 2 — SimGeo Noisy X 7 7

Mid./Sint. U-MSG-Net 2 σ = 0.03 SimGeo Over-smoothed X X X

Mid./Sint. U-MSG-Net 2 σ = 0.03, scaled by 0.7 every 10-th epoch SimGeo Over-smoothed X X X

Mid./Sint. U-MSG-Net 2 Additional input samples (+): GT with gaussian noise with σ = MSE(GT,approximation) SimGeo Same as input X X 7

Mid./Sint. U-MSG-Net 2 + GT with noise ε, and target with noise ε/10 SimGeo Same as input X X 7

Mid./Sint. U-MSG-Net 2 + random linear interpolation between GT and approximation SimGeo Noisy 7 7 7

Mid./Sint. U-MSG-Net 2 + with the result after one step of optimization SimGeo Same as input X 7 7

ing noise variance similarly leads to over-smoothed

network outputs and optimization result. Expand-

ing training data with intermediate optimization re-

sults did not alleviate difﬁculties with optimization

convergence. Moreover, in some instances, this re-

sulted in well trained network, but exploding opti-

mization, yielding extremely noisy results (see Figure

10). Training using noisy targets again led to over-

smoothed network outputs and aggravated artefacts in

optimization results.

Implementation Details. We construct training

dataset similar to the one proposed in (Hui et al.,

2016) for training MSG-Net but appropriate for use

within DSRNETT. We split all images into patches

of size 64 × 64. For all patches we calculate inten-

sity, corresponding to RGB component. For half of

the patches we generate low-resolution depth using

box downsampling method with a scaling factor of

4, and obtain approximations using a bilinear upsam-

pling method instead of pseudo-inverse of box down-

sampling, since the former produces patches that are

more relevant for training MSG-Net. Finally, follow-

ing our Scheme 2, we train the model using the high-

frequency (HF) components of intensity and depth of

generated patches as inputs, and HF components of

ground-truth depth and intensity as targets. For sim-

plicity we further omit the fact that model is trained

on HF components and its inputs and outputs con-

tain not only depth, but also intensity part, since it

is not changed during training or optimization. In to-

tal, training was performed on 75K patches with 15K

patches used for validation. We train by optimizing

MSE loss using Adam for ∼120 epochs with a batch

size of 128.

We experimentally set minimum noise variance to

0.03. In experiment with noisy targets for network

inputs we added Gaussian noise with variance σ =

0.001; each target variance of noise was deﬁned as

MSE(σ,0), divided by 10.

Ensuring Coercivity of Regularizer. According to

remark in (Obmann et al., 2019) in order to ensure

coercivity of regularizer in experiments with U-MSG-

Net, we employed skip-connection between network

input and output and deﬁne regularizer as R (x) =

kΦ

(x)−xk

+kxk

. We have checked, that such reg-

ularizer design does not help to solve optimization

issues and concluded, that optimization convergence

to undesired local minimum was not lead by possible

regularizer non-coercivity.

5 DISCUSSION

In this work, we performed an adaptation of

NETT (Li et al., 2020), an approach to image process-

ing leveraging data-driven regularizers, for the depth

super-resolution (SR) task. We have validated that

our formulation of depth SR meets all theoretical re-

quirements of NETT, including the restrictive coer-

civity condition. Furthermore, we were able to train

an efﬁcient residual estimator deep network in all ex-

perimental cases. Unexpectedly, we have discovered

subsequent optimization to converge to the bad min-

imum in most experiments despite multiple efforts

to increase network stability by varying the training

dataset, applying data augmentations, selecting dif-

ferent models, or considering various formulations of

the optimization task.

Our results raise questions regarding the use of

learned regularizers in the context of depth SR (or

image-based tasks), which may represent promising

future research directions. More speciﬁcally,

1. What is the required form of the regularization

term that would allow effective optimization?

2. What are the characteristic features of image-

based tasks that might prevent optimization meth-

ods such as (Li et al., 2020) from converging to

good solutions?

3. What is the “right” training procedure for the reg-

ularizer?

ACKNOWLEDGEMENTS

This work was supported by Ministry of Science and

Higher Education grant No. 075-10-2021-068. We

acknowledge the usage of Skoltech CDISE supercom-

puter Zhores (Zacharov et al., 2019) for obtaining the

presented results.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

588

REFERENCES

Arridge, S., Maass, P.,

Oktem, O., and Sch

onlieb, C.-B.

(2019). Solving inverse problems using data-driven

models. Acta Numerica, 28:1–174.

Butler, D. J., Wulff, J., Stanley, G. B., and Black, M. J.

(2012). A naturalistic open source movie for optical

ﬂow evaluation. In Fitzgibbon, A., Lazebnik, S., Per-

ona, P., Sato, Y., and Schmid, C., editors, Computer

Vision – ECCV 2012, volume 7577 of LNCS, pages

611–625, Berlin, Heidelberg. Springer Berlin Heidel-

berg.

Chen, Y., Pock, T., Ranftl, R., and Bischof, H. (2013). Re-

visiting loss-speciﬁc training of ﬁlter-based mrfs for

image restoration. In Weickert, J., Hein, M., and

Schiele, B., editors, German Conference on Pattern

Recognition, volume 8142 of LNCS, pages 271–281,

Berlin, Heidelberg. Springer.

De los Reyes, J. C., Sch

onlieb, C.-B., and Valkonen, T.

(2017). Bilevel parameter learning for higher-order

total variation regularisation models. Journal of Math-

ematical Imaging and Vision, 57(1):1–25.

Gatys, L., Ecker, A., and Bethge, M. (2016). A neural algo-

rithm of artistic style. Journal of Vision, 16(12):326–

326.

Gou, J., Yu, B., Maybank, S. J., and Tao, D. (2021). Knowl-

edge distillation: A survey. International Journal of

Computer Vision, 129(6):1789–1819.

Haefner, B., Peng, S., Verma, A., Qu

eau, Y., and Cremers,

D. (2020). Photometric depth super-resolution. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 42(10):2453–2464.

Haefner, B., Qu

eau, Y., M

ollenhoff, T., and Cremers,

D. (2018). Fight ill-posedness with ill-posedness:

Single-shot variational depth super-resolution from

shading. In 2018 IEEE/CVF Conference on Computer

Vision and Pattern Recognition, pages 164–174.

Hui, T.-W., Loy, C. C., and Tang, X. (2016). Depth map

super-resolution by deep multi-scale guidance. In

Leibe, B., Matas, J., Sebe, N., and Welling, M., ed-

itors, European Conference on Computer Vision –

ECCV 2016, volume 9907 of LNCS, pages 353–369,

Cham. Springer International Publishing.

Johnson, J., Alahi, A., and Fei-Fei, L. (2016). Perceptual

losses for real-time style transfer and super-resolution.

In European conference on computer vision, pages

694–711. Springer.

Kingma, D. P. and Ba, J. (2015). Adam: A method for

stochastic optimization. In ICLR (Poster).

Li, H., Schwab, J., Antholzer, S., and Haltmeier, M. (2020).

NETT: Solving inverse problems with deep neural

networks. Inverse Problems, 36(6):065005.

Lunz, S.,

Oktem, O., and Sch

onlieb, C.-B. (2018). Adver-

sarial regularizers in inverse problems. In Proceedings

of the 32nd International Conference on Neural In-

formation Processing Systems, NIPS’18, pages 8516–

8525, Red Hook, NY, USA. Curran Associates Inc.

Obmann, D., Nguyen, L., Schwab, J., and Haltmeier, M.

(2019). Sparse l

-regularization of inverse problems

using deep learning. arXiv:1908.03006 .

Riegler, G., Ferstl, D., R

uther, M., and Bischof, H. (2016).

A deep primal dual for guided depth super-resolution.

In British Machine Vision Conference, United King-

dom. The British Machine Vision Association.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-

net: Convolutional networks for biomedical image

segmentation. In Navab, N., Hornegger, J., Wells,

W. M., and Frangi, A. F., editors, Medical Image Com-

puting and Computer-Assisted Intervention – MICCAI

2015, volume 9351 of LNCS, pages 234–241, Cham.

Springer International Publishing.

Scharstein, D., Hirschm

uller, H., Kitajima, Y., Krathwohl,

G., Ne

c, N., Wang, X., and Westling, P. (2014).

High-resolution stereo datasets with subpixel-accurate

ground truth. In Jiang, X., Hornegger, J., and Koch,

R., editors, German Conference on Pattern Recog-

nition, volume 8753 of LNCS, pages 31–42, Cham.

Springer International Publishing.

Song, X., Dai, Y., Zhou, D., Liu, L., Li, W., Li, H., and

Yang, R. (2020). Channel attention based iterative

residual learning for depth map super-resolution. In

2020 IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR), pages 5630–5639.

Voynov, O., Artemov, A., Egiazarian, V., Notchenko, A.,

Bobrovskikh, G., Zorin, D., and Burnaev, E. (2019).

Perceptual deep depth super-resolution. In Proceed-

ings of the IEEE International Conference on Com-

puter Vision, pages 5653–5663.

Zacharov, I., Arslanov, R., Gunin, M., Stefonishin,

D., Bykov, A., Pavlov, S., Panarin, O., Mal-

iutin, A., Rykovanov, S., and Fedorov, M. (2019).

“zhores”—petaﬂops supercomputer for data-driven

modeling, machine learning and artiﬁcial intelligence

installed in skolkovo institute of science and technol-

ogy. Open Engineering, 9(1):512–520.

APPENDIX

Network Tikhonov Regularization

Assumptions

(Li et al., 2020) prove well-posedness and conver-

gence of NETT regularization, provided that cer-

tain assumptions on regularizer and data ﬁdelity term

hold.

We have tried to ensure fulﬁllment of this condi-

tions in our work. Conditions on data ﬁdelity term are

not restrictive and hold for squared L

-norm distance,

while the conditions on regularizer term include:

1. Regularizer R (x) = ψ(Φ

(x)) is weakly lower

semicontinuous, which is guaranteed by condi-

tions:

• Linear operators A

are bounded;

• Non-linearities σ

are weakly continuous;

Can We Use Neural Regularization to Solve Depth Super-resolution?

589

• Scalar functional ψ is weakly lower-

semicontinuous;

2. R (x) is coercive, i.e. lim

kxk→∞

R (x) = 0.

U-Net-type and U-MSG-Net architectures in-

clude convolution operations and batch normaliza-

tions, that are bounded linear operations, and max

pooling, leaky ReLU and upsampling operations, that

are weakly continuous and coercive non-linearities.

We use squared L

-norm distance as weakly lower

semi-continuous scalar functional ψ. We note that the

number of parameters in the U-Net model is close to

7M, while in the U-MSG-Net it is around 700K.

Several ways to obtain coercivity of the regular-

izer are discussed in (Li et al., 2020). One way is to

ensure layer-wise coercivity, i.e. use coercive non-

linearities σ

and linear operators A

, satisfying the

inequality:

∃c

∈ [0,∞)∀x ∈ X : kxk ≤ c

xk. (5)

We relied on this approach in experiments with U-

Net-type architecture. Since U-MSG-Net contains

non-coercive parametric ReLU non-linearities, we

used another way to obtain network coercivity by ex-

ploiting skip connection between network input and

output, see ”Ensuring coercivity of regularizer” in

Section 4.2.

Speciﬁcally, fulﬁllment of presented conditions

guarantee existence of a solution, stability and con-

vergence for optimization problem (2). Stability of

the method corresponds to continuous dependence of

the solutions x of optimization problem (2) on input

y. Convergence of the method states, that while noise

level δ

in inputs y

decreases to zero, sequence x

of corresponding solutions weakly converges to the

R (·)-minimizing solution x

of F(x) = y

, if it is

unique.

Experiments

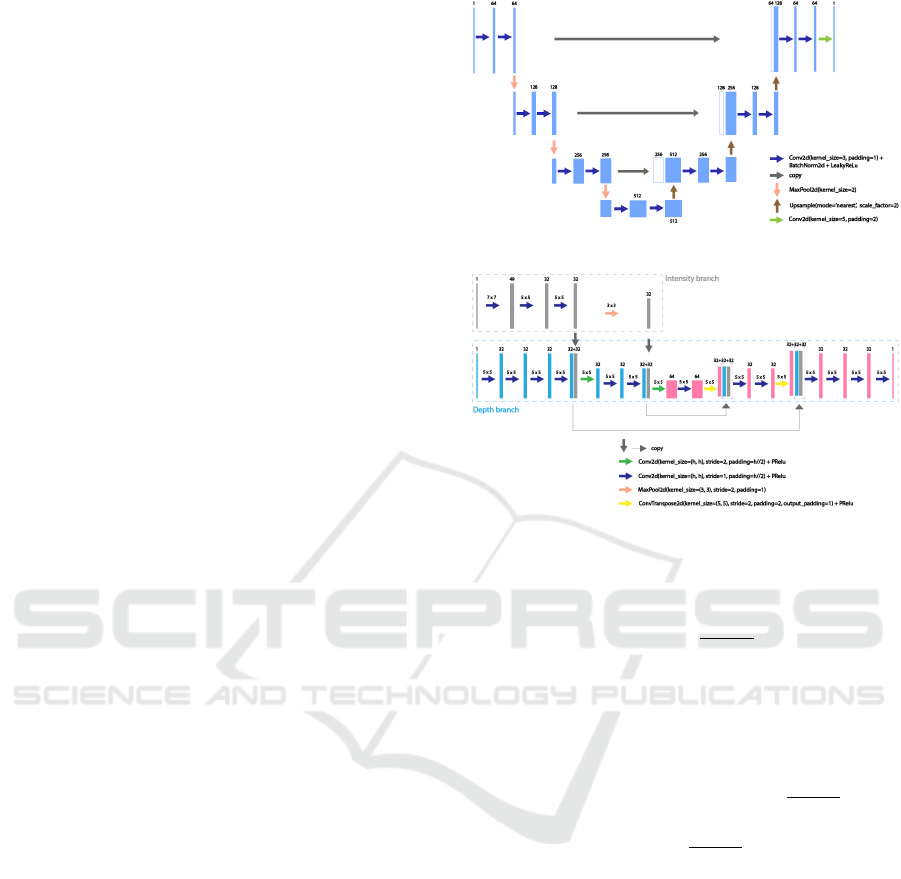
Figures 11 and 12 represent architectures of networks,

used in experiments in Sections 4.1 and 4.2 respec-

tively.

Training on Intermediate Optimization

Results as Input

In our experiments we use approximation

x, i.e.

upsampled low-resolution version of ground-truth

depth, as optimization initial approximation. We sup-

pose, that optimization approximation is not signiﬁ-

cantly changed after the ﬁrst data ﬁdelity gradient de-

scent step and treat

x as its result.

Figure 11: U-Net-type architecture.

Figure 12: U-MSG-Net architecture.

Then after the regularizer gradient descent step we

obtain approximation x

x − s · α ·

dR (x)

(6)

If network is trained to predict ground-truth depth

given both

x or x

, then regularizer gradient descent

step would not move optimization approximation to

the direction of x

kΦ

) − x

= kΦ

(

x) −

x + s · α ·

dR (x)

≥ kΦ

(

x) −

+ ks · α ·

dR (x)

≥ kΦ

(

x) −

Thus, we come to idea to add optimization ﬁrst step

approximation for small s · α = 0.001 to the training

samples.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

590