Transformers in Self-Supervised Monocular Depth Estimation with

Unknown Camera Intrinsics

Arnav Varma

∗

, Hemang Chawla

∗

, Bahram Zonooz and Elahe Arani

Advanced Research Lab, NavInfo Europe, The Netherlands

Keywords:

Transformers, Convolutional Neural Networks, Monocular Depth Estimation, Camera Self-calibration,

Self-Supervised Learning.

Abstract:

The advent of autonomous driving and advanced driver assistance systems necessitates continuous develop-

ments in computer vision for 3D scene understanding. Self-supervised monocular depth estimation, a method

for pixel-wise distance estimation of objects from a single camera without the use of ground truth labels, is

an important task in 3D scene understanding. However, existing methods for this task are limited to con-

volutional neural network (CNN) architectures. In contrast with CNNs that use localized linear operations

and lose feature resolution across the layers, vision transformers process at constant resolution with a global

receptive ﬁeld at every stage. While recent works have compared transformers against their CNN counter-

parts for tasks such as image classiﬁcation, no study exists that investigates the impact of using transformers

for self-supervised monocular depth estimation. Here, we ﬁrst demonstrate how to adapt vision transform-

ers for self-supervised monocular depth estimation. Thereafter, we compare the transformer and CNN-based

architectures for their performance on KITTI depth prediction benchmarks, as well as their robustness to

natural corruptions and adversarial attacks, including when the camera intrinsics are unknown. Our study

demonstrates how transformer-based architecture, though lower in run-time efﬁciency, achieves comparable

performance while being more robust and generalizable.

1 INTRODUCTION

There have been rapid improvements in scene un-

derstanding for robotics and advanced driver assis-

tance systems (ADAS) over the past years. This suc-

cess is attributed to the use of Convolutional Neural

Networks (CNNs) within a mostly encoder-decoder

paradigm. Convolutions provide spatial locality and

translation invariance which has proved useful for im-

age analysis tasks. The encoder, often a convolutional

Residual Network (ResNet) (He et al., 2016), learns

feature representations from the input and is followed

by a decoder which aggregates these features and con-

verts them into ﬁnal predictions. However, the choice

of architecture has a major impact on the performance

and generalizability of the task.

While CNNs have been the preferred architec-

ture in computer vision, transformers have also re-

cently gained traction (Dosovitskiy et al., 2021) mo-

tivated by their success in natural language process-

ing (Vaswani et al., 2017). Notably, they have

∗

Equal contribution

also outperformed CNNs for object detection (Car-

ion et al., 2020) and semantic segmentation (Zheng

et al., 2021). This is also reﬂected in methods for

monocular dense depth estimation, a pertinent task

for autonomous planning and navigation, where su-

pervised transformer-based methods (Li et al., 2020;

Ranftl et al., 2021) have been proposed as an al-

ternative to supervised CNN-based methods (Lee

et al., 2019; Aich et al., 2021). However, super-

vised methods require extensive RGB-D ground truth

collected from costly LiDARs or multi-camera rigs.

Instead, self-supervised methods have increasingly

utilized concepts of Structure from Motion (SfM)

with known camera intrinsics to train monocular

depth and ego-motion estimation networks simultane-

ously (Guizilini et al., 2020; Lyu et al., 2020; Chawla

et al., 2021). While transformer ingredients such as

attention have been utilized for self-supervised depth

estimation (Johnston and Carneiro, 2020), most meth-

ods are nevertheless limited to the use of CNNs that

have localized linear operations and lose feature reso-

lution during downsampling to increase their limited

receptive ﬁeld (Yang et al., 2021).

758

Varma, A., Chawla, H., Zonooz, B. and Arani, E.

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics.

DOI: 10.5220/0010884000003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

758-769

ISBN: 978-989-758-555-5; ISSN: 2184-4321

EMBED

TRANSFORMER

REASSEMBLE

REASSEMBLE FUSION

HEAD

REASSEMBLE

FUSION

HEAD

FUSION

HEAD

FUSION

HEAD

TRANSFORMER

REASSEMBLE

CONV

ReLU

CONV

ReLU

CONV

ReLU

CONV

GLOBAL AVERAGE

POOLING

CONV CONV

SOFTPLUS

, F

, C

EMBED

Target

Source

Ego-motion & Intrinsics Network

Depth Network

View

Synthesis

Source

Target

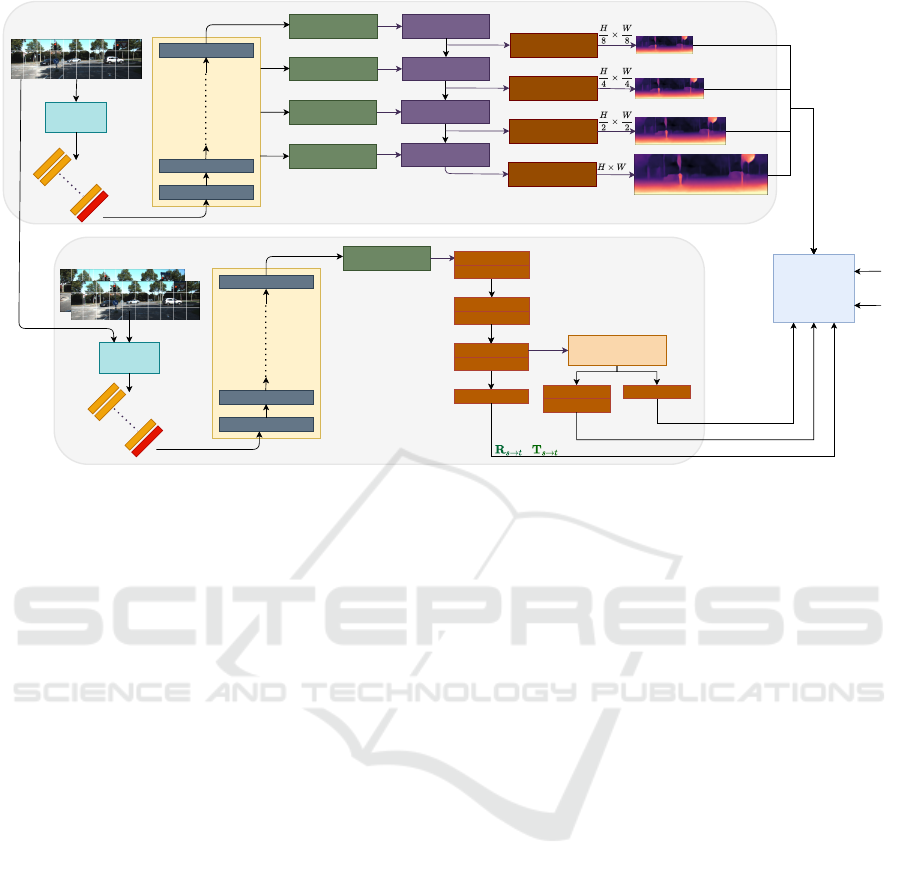
Figure 1: An overview of Monocular Transformer Structure from Motion Learner (MT-SfMLearner) with learned intrinsics.

We readapt modules from Dense Prediction Transformer (DPT) and Monodepth2 to be trained with appearance-based losses

for self-supervised monocular depth, ego-motion, and intrinsics estimation.

On the other hand, transformers with fewer in-

ductive biases allow for more globally coherent pre-

dictions with different layers attending to local and

global features simultaneously (Touvron et al., 2021).

However, transformers require more training data

and can be more computationally demanding (Caron

et al., 2021). While multiple studies have compared

transformers against CNNs for tasks such as image

classiﬁcation (Raghu et al., 2021; Bhojanapalli et al.,

2021), no study exists that evaluates the impact of

transformers in self-supervised monocular depth es-

timation, including when the camera intrinsics may

be unknown.

In this work, we conduct a comparative study

between CNN- and transformer-based architectures

for self-supervised monocular depth estimation. Our

contributions are as follows:

• We demonstrate how to adapt vision transform-

ers for self-supervised monocular depth estima-

tion by implementing a method called Monocular-

Transformer SfMLearner (MT-SfMLearner).

• We compare MT-SfMLearner and CNNs for

their performance on the KITTI monocular depth

Eigen Zhou split (Eigen et al., 2014) and the on-

line depth prediction benchmark (Geiger et al.,

2013).

• We investigate the impact of architecture choices

for the individual depth and ego-motion networks

on performance as well as robustness to natural

corruptions and adversarial attacks.

• We also introduce a modular method that simulta-

neously predicts camera focal lengths and princi-

pal point from the images themselves and can eas-

ily be utilized within both CNN- and transformer-

based architectures.

• We study the accuracy of intrinsics estimation as

well as its impact on the performance and robust-

ness of depth estimation.

• Finally, we also compare the run-time computa-

tional and energy efﬁciency of the architectures

for depth and intrinsics estimation.

MT-SfMLearner provides real-time depth esti-

mates and illustrates how transformer-based architec-

ture, though lower in run-time efﬁciency, can achieve

comparable performance as the CNN-based architec-

tures while being more robust under natural corrup-

tions and adversarial attacks, even when the cam-

era intrinsics are unknown. Thus, our work presents

a way to analyze the trade-off between the perfor-

mance, robustness, and efﬁciency of transformer- and

CNN-based architectures for depth estimation.

2 RELATED WORKS

Recently, transformer architectures such as Vision

Transformer (ViT) (Ranftl et al., 2021) and Data-

efﬁcient image Transformer (DeiT) (Touvron et al.,

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics

759

2021) have outperformed CNN architectures in im-

age classiﬁcation. Studies comparing ViT and CNN

architectures like ResNet have further demonstrated

that transformers are more robust to natural corrup-

tions and adversarial examples in classiﬁcation (Bho-

janapalli et al., 2021; Paul and Chen, 2021). Mo-

tivated by their success, researchers have replaced

CNN encoders with transformers in scene under-

standing tasks such as object detection (Carion et al.,

2020; Liu et al., 2021), semantic segmentation (Zheng

et al., 2021; Strudel et al., 2021), and supervised

monocular depth estimation (Ranftl et al., 2020; Yang

et al., 2021).

For supervised monocular depth estimation,

Dense Prediction Transformer (DPT) (Ranftl et al.,

2020) uses ViT as the encoder with a convolutional

decoder and shows more coherent predictions than

CNNs due to the global receptive ﬁeld of transform-

ers. TransDepth (Yang et al., 2021) additionally uses

a ResNet projection layer and attention gates in the

decoder to induce the spatial locality of CNNs for

supervised monocular depth and surface-normal es-

timation. Lately, some works have inculcated ele-

ments of transformers such as self-attention (Vaswani

et al., 2017) in self-supervised monocular depth esti-

mation (Johnston and Carneiro, 2020; Xiang et al.,

2021). However, there has been no investigation

of transformers to replace the traditional CNN-based

methods (Godard et al., 2019; Lyu et al., 2020) for

self-supervised monocular depth estimation.

Moreover, self-supervised monocular depth esti-

mation still requires prior knowledge of the cam-

era intrinsics (focal length and principal point) dur-

ing training, which may be different for each data

source, may change over time, or be unknown a pri-

ori (Chawla et al., 2020). While multiple approaches

to supervised camera intrinsics estimation have been

proposed (Lopez et al., 2019; Zhuang et al., 2019),

not many self-supervised approaches exist (Gordon

et al., 2019).

Therefore, we investigate the impacts of trans-

former architectures on self-supervised monocular

depth estimation for their performance, robustness,

and run-time efﬁciency, even when intrinsics are un-

known.

3 METHOD

Our objective is to study the effect of utilizing vision

transformers for self-supervised monocular depth es-

timation in contrast with the contemporary methods

that utilize Convolutional Neural Networks.

Given a set of n images from a video sequence,

we simultaneously train depth and ego-motion pre-

diction networks. The inputs to the networks are a se-

quence of temporally consecutive RGB image triplets

−

} ∈ R

H×W×3

. The depth network learns the

model f

: R

H×W×3

→ R

H×W

to output dense depth

(or disparity) for each pixel coordinate p of a sin-

gle image. Simultaneously, the ego-motion network

learns the model f

: R

2×H×W×3

→ R

to output rela-

tive translation (t

) and rotation (r

) form-

ing the afﬁne transformation



0 1



∈ SE(3) between

a pair of overlapping images. The predicted depth

and ego-motion

T are linked together via the perspec-

tive projection model,

∼ K

s←t

−1

+ K

s←t

, (1)

that warps the source images I

∈ {I

−

} to the tar-

get image I

∈ {I

}, with the camera intrinsics de-

scribed by K. This process is called view synthesis,

as shown in Figure 1. We train the networks us-

ing the appearance-based photometric loss between

the real and synthesized target images, as well as

a smoothness loss on the depth predictions (Godard

et al., 2019).

3.1 Architecture

Here we describe Monocular Transformer Struc-

ture from Motion Learner (MT-SfMLearner), our

transformer-based method for self-supervised monoc-

ular depth estimation (Figure 1).

3.1.1 Depth Network

For the depth network, we readapt the Dense Pre-

diction Transformer (DPT) (Ranftl et al., 2020) for

self-supervised learning, with a DeiT-Base (Touvron

et al., 2021) in the encoder. There are ﬁve components

of the depth network:

• An Embed module, which is a part of the en-

coder, takes an image I ∈ R

H×W×3

, and converts

non-overlapping image patches of size p × p into

= H · W /p

tokens t

∈ R

∀i ∈ [1, 2, ...N

where d = 768 for DeiT-Base. This is imple-

mented as a large p × p convolution with stride

s = p where p = 16. The output from this module

is concatenated with a readout token of the same

size as the remaining tokens.

• The Transformer block, that is also a part of

the encoder, consists of 12 transformer layers

which process these tokens with multi-head self-

attention (MHSA) (Vaswani et al., 2017) modules.

MHSA processes inputs at constant resolution and

can simultaneously attend to global and local fea-

tures.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

760

Table 1: Architecture details of the Reassemble modules. DN and EN refer to depth and ego-motion networks, respectively.

The subscripts of DN refer to the transformer layer from which the respective Reassemble module takes its input (see Figure

1). Input image size is H ×W , p refers to the patch size, N

= H ·W /p

refers to the number of patches from the image, and

d refers to the feature dimension of the transformer features.

Operation Input size Output size Function

Parameters

(DN

, DN

, EN)

Read (N

+ 1)× d N

× d Drop readout token −

Concatenate N

× d d × H/p ×W /p Transpose and Unﬂatten −

Pointwise Convolution d ×H/p ×W /p N

× H/p ×W /p N

channels N

= [96,768,1536, 3072,2048]

Strided Convolution N

× H/p ×W /p N

× H/2p ×W /2p k × k convolution, Stride= 2, N

channels, padding= 1 k = [−,−,−,3, −]

Transpose Convolution N

× H/p ×W /p N

× H/s ×W /s p/s × p/s deconvolution, stride= p/s, N

channels s = [4, 8,−,−,−]

• Four Reassemble modules in the decoder, which

are responsible for extracting image-like features

from the 3

, 6

, 9

, and 12

(ﬁnal) transformer

layers by dropping the readout token and concate-

nating the remaining tokens in 2D. This is fol-

lowed by pointwise convolutions to change the

number of channels, and transpose convolution

in the ﬁrst two reassemble modules to upsample

the representations (corresponding to T

and T

Figure 1). To make the transformer network com-

parable to its convolutional counterparts, we in-

crease the number of channels in the pointwise

convolutions of the last three Reassemble mod-

ules by a factor of 4 with respect to DPT. The ex-

act architecture of the Reassemble modules can be

found in Table 1.

• Four Fusion modules in the decoder, based on

ReﬁneNet (Lin et al., 2017). They progressively

fuse information from the Reassemble modules

with information passing through the decoder, and

upsample the features by 2 at each stage. Un-

like DPT, we enable batch normalization in the

decoder as it was found to be helpful for self-

supervised depth prediction. We also reduce the

number of channels in the Fusion block to 96 from

256 in DPT.

• Four Head modules at the end of each Fusion

module to predict depth at 4 scales following

previous self-supervised methods (Godard et al.,

2019). Unlike DPT, the Head modules use 2 con-

volutions instead of 3 as we found no difference

in performance. For further details of the Head

modules, refer to Table 2.

Table 2: Architecture details of Head modules in Figure 1.

Layers

32 3 × 3 Convolutions, stride=1, padding= 1

ReLU

Bilinear Interpolation to upsample by 2

32 Pointwise Convolutions

Sigmoid

3.1.2 Ego-motion Network

For the ego-motion network, we adapt DeiT-Base

(Touvron et al., 2021) in the encoder. Since the input

to the transformer for the ego-motion network con-

sists of two images concatenated along the channel di-

mension, we repeat the embedding layer accordingly.

We use a Reassemble module to pass transformer to-

kens to the decoder. For details on the structure of

this Reassemble module, refer to Table 1. We adopt

the decoder for the ego-motion network from Mon-

odepth2 (Godard et al., 2019).

When both depth and ego-motion networks use

transformers as described above, we refer to the re-

sulting architecture as Monocular Transformer Struc-

ture from Motion Learner (MT-SfMLearner).

3.2 Appearance-based Losses

Following contemporary self-supervised monocular

depth estimation methods, we adopt the appearance-

based losses and an auto-masking procedure from the

CNN-based Monodepth2 (Godard et al., 2019) for

the above described transformer-based architecture

as well. We employ a photometric reprojection loss

composed of the pixel-wise `

distance and the Struc-

tural Similarity (SSIM) between the real and synthe-

sized target images, along with a multi-scale edge-

aware smoothness loss on the depth predictions. We

also use auto-masking to disregard the temporally sta-

tionary pixels in the image triplets. Furthermore, we

reduce texture-copy artifacts by calculating the total

loss after upscaling the depths, predicted at 4 scales,

from intermediate decoder layers to the input resolu-

tion.

3.3 Intrinsics

Accurate camera intrinsics given by

K =





0 c

0 f

0 0 1





, (2)

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics

761

are essential to self-supervised depth estimation as

can be seem from Equation 1. However, the intrin-

sics may vary within a dataset with videos collected

from different camera setups, or over a long period

of time. These parameters can also be unknown for

crowdsourced datasets.

We address this by introducing an intrinsics esti-

mation module. We modify the ego-motion network,

which takes a pair of consecutive images as input, and

learns to estimate the focal length and principal point

along with the translation and rotation. Speciﬁcally,

we add a convolutional path in the ego-motion de-

coder to learn the intrinsics. The decoder features be-

fore activation from the penultimate layer are passed

through a global average pooling layer, followed by

two branches of pointwise convolutions to reduce the

number of channels from 256 to 2. One branch uses

a softplus activation to estimate focal lengths along

x and y axes as the focal length is always positive.

The other branch doesn’t use any activation to esti-

mate the principal point as it has no such constraint.

Note that the ego-motion decoder is the same for both

the convolutional as well as transformer architectures.

Consequently, the intrinsics estimation method can be

modularly utilized with both architectures. Figure 1

demonstrates MT-SfMLearner with learned intrinsics.

4 RESULTS

In this section, we perform a comparative anal-

ysis between our transformer-based method, MT-

SfMLearner, and the existing CNN-based methods

for self-supervised monocular depth estimation. We

also perform a contrastive study on the architectures

for the depth and ego-motion networks to evaluate

their impact on the prediction accuracy, robustness to

natural corruptions and adversarial attacks, and the

run-time computational and energy efﬁciency. Fi-

nally, we analyze the correctness and run-time efﬁ-

ciency of intrinsics predictions, and also study its im-

pact on the accuracy and robustness of depth estima-

tion.

4.1 Implementation Details

4.1.1 Dataset

We report all results on the Eigen Split (Eigen et al.,

2014) of KITTI (Geiger et al., 2013) dataset after re-

moving the static frames as per (Zhou et al., 2017),

unless stated otherwise. This split contains 39, 810

training, 4424 validation, and 697 test images, respec-

tively. All results are reported on the per-image scaled

dense depth prediction without post-processing (Go-

dard et al., 2019), unless stated otherwise.

4.1.2 Training Settings

The networks are implemented in PyTorch (Paszke

et al., 2019) and trained on a TeslaV100 GPU for

20 epochs at a resolution of 640 × 192 with batch-

size 12. MT-SfMLearner is further trained at 2 more

resolutions - 416 × 128 and 1024 × 320, with batch-

sizes of 12 and 2, respectively for experiments in Sec-

tion 4.2. The depth and ego-motion encoders are ini-

tialized with ImageNet (Deng et al., 2009) pre-trained

weights. We use the Adam (Kingma and Ba, 2014)

optimizer for CNN-based networks (in Sections 4.3

and 4.4) and AdamW (Loshchilov and Hutter, 2017)

optimizer for transformer-based networks with initial

learning rates of 1e

−4

and 1e

−5

, respectively. The

learning rate is decayed after 15 epochs by a factor

of 10. Both optimizers use β

= 0.9 and β

= 0.999.

4.2 Depth Estimation Performance

First we compare MT-SfMLearner, where both depth

and ego-motion networks are transformer-based, with

the existing fully convolutional neural networks for

their accuracy on self-supervised monocular depth es-

timation. Their performance is evaluated using met-

rics from (Eigen et al., 2014) up to a ﬁxed range of

80 m as shown in Table 3. We compare the meth-

ods at different input image sizes clustered into cat-

egories of Low-Resolution (LR), Medium-Resolution

(MR), and High-Resolution (HR). We do not compare

against methods that use ground-truth semantic labels

during training. All methods assume known ground-

truth camera intrinsics.

We observe that MT-SfMLearner is able to

achieve comparable performance at all resolutions un-

der error as well as accuracy metrics. This includes

methods that also utilize a heavy encoder such as

ResNet-101 (Johnston and Carneiro, 2020) and Pack-

Net (Guizilini et al., 2020).

Online Benchmark. We also measure the perfor-

mance of MT-SfMLearner on the KITTI Online

Benchmark for depth prediction

using the metrics

from (Uhrig et al., 2017). We train on an image size

of 1024 × 320, and add the G2S loss (Chawla et al.,

2021) for obtaining predictions at metric scale. Re-

sults ordered by their rank are shown in Table 4. The

performance of MT-SfMLearner is on par with state-

of-the-art self-supervised methods, and outperforms

http://www.cvlibs.net/datasets/kitti/eval depth.php?

benchmark=depth prediction. See under MT-SfMLearner.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

762

Table 3: Quantitative results comparing MT-SfMLearner with existing methods on KITTI Eigen split. For each category of

image sizes, the best results are displayed in bold, and the second best results are underlined.

Methods Resolution

Error↓ Accuracy↑

Abs Rel Sq Rel RMSE RMSE log δ < 1.25 δ < 1.25

δ < 1.25

SfMLearner(Zhou et al., 2017) 416×128 0.208 1.768 6.856 0.283 0.678 0.885 0.957

GeoNet (Yin and Shi, 2018) 416×128 0.155 1.296 5.857 0.233 0.793 0.931 0.973

Vid2Depth (Mahjourian et al., 2018) 416×128 0.163 1.240 6.220 0.250 0.762 0.916 0.968

Struct2Depth (Casser et al., 2019) 416×128 0.141 1.026 5.291 0.215 0.816 0.945 0.979

Roussel et al. (Roussel et al., 2019) 416×128 0.179 1.545 6.765 0.268 0754 0916 0.966

VITW (Gordon et al., 2019) 416×128 0.129 0.982 5.230 0.213 0.840 0.945 0.976

Monodepth2 (Godard et al., 2019) 416×128 0.128 1.087 5.171 0.204 0.855 0.953 0.978

MT-SfMLearner (Ours) 416×128 0.125 0.905 5.096 0.203 0.851 0.952 0.980

CC (Ranjan et al., 2019) 832×256 0.140 1.070 5.326 0.217 0.826 0.941 0.975

SC-SfMLearner (Bian et al., 2019) 832×256 0.137 1.089 5.439 0.217 0.830 0.942 0.975

Monodepth2 (Godard et al., 2019) 640×192 0.115 0.903 4.863 0.193 0.877 0.959 0.981

SG Depth (Klingner et al., 2020) 640×192 0.117 0.907 4.844 0.194 0.875 0.958 0.980

PackNet-SfM (Guizilini et al., 2020) 640×192 0.111 0.829 4.788 0.199 0.864 0.954 0.980

Poggi et. al (Poggi et al., 2020) 640×192 0.111 0.863 4.756 0.188 0.881 0.961 0.982

Johnston & Carneiro (Johnston and Carneiro, 2020) 640×192 0.106 0.861 4.699 0.185 0.889 0.962 0.982

HR-Depth (Lyu et al., 2020) 640×192 0.109 0.792 4.632 0.185 0.884 0.962 0.983

MT-SfMLearner (Ours) 640×192 0.112 0.838 4.771 0.188 0.879 0.960 0.982

Packnet-SfM (Guizilini et al., 2020) 1280×384 0.107 0.803 4.566 0.197 0.876 0.957 0.979

HR-Depth (Lyu et al., 2020) 1024×320 0.106 0.755 4.472 0.181 0.892 0.966 0.984

G2S (Chawla et al., 2021) 1024×384 0.109 0.844 4.774 0.194 0.869 0.958 0.981

MT-SfMLearner (Ours) 1024×320 0.104 0.799 4.547 0.181 0.893 0.963 0.982

several supervised methods. This further conﬁrms

that the transformer-based method can achieve com-

parable performance to the convolutional neural net-

works for self-supervised depth estimation.

4.3 Contrastive Study

We saw in the previous section that MT-SfMLearner

performs competently on independent and identically

distributed (i.i.d.) test set with respect to the state-

of-the-art. However, networks that perform well

on an i.i.d. test set may still learn shortcut fea-

Table 4: Quantitative comparison of unscaled dense depth

prediction on the KITTI Depth Prediction Benchmark (on-

line server). Supervised training with ground truth depths is

denoted by D. Use of monocular sequences or stereo pairs is

represented by M and S, respectively. Seg represents addi-

tional supervised semantic segmentation training. The use

of GPS for multi-modal self-supervision is denoted by G.

Method Train SILog↓ SqErrRel↓

DORN (Fu et al., 2018) D 11.77 2.23

SORD (Diaz and Marathe, 2019) D 12.39 2.49

VNL (Yin et al., 2019) D 12.65 2.46

DS-SIDENet (Ren et al., 2019) D 12.86 2x.87

PAP (Zhang et al., 2019) D 13.08 2.72

Guo et al. (Guo et al., 2018) D+S 13.41 2.86

G2S (Chawla et al., 2021) M+G 14.16 3.65

Ours M+G 14.25 3.72

Monodepth2 (Godard et al., 2019) M+S 14.41 3.67

DABC (Li et al., 2018b) D 14.49 4.08

SDNet (Ochs et al., 2019) D+Seg 14.68 3.90

APMoE (Kong and Fowlkes, 2019) D 14.74 3.88

CSWS (Li et al., 2018a) D 14.85 348

HBC (Jiang and Huang, 2019) D 15.18 3.79

SGDepth (Klingner et al., 2020) M+Seg 15.30 5.00

DHGRL (Zhang et al., 2018) D 15.47 4.04

PackNet-SfM (Guizilini et al., 2020) M+V 15.80 4.73

MultiDepth (Liebel and K

orner, 2019) D 16.05 3.89

LSIM (Goldman et al., 2019) S 17.92 6.88

Monodepth (Godard et al., 2017) S 22.02 20.58

tures that are non-robust and generalize poorly to

out-of-distribution (o.o.d.) datasets (Geirhos et al.,

2020). Since self-supervised monocular depth es-

timation networks concurrently train an ego-motion

network (see Equation 1), we investigate the impact

of each network’s architecture on depth estimation.

We consider both Convolutional (C) and Trans-

former (T) networks for depth and ego-motion esti-

mation. The resulting four combinations of (Depth

Network, Ego-Motion Network) architectures are (C,

C), (C, T), (T, C), and (T, T), ordered on the ba-

sis of their increasing inﬂuence of transformers on

depth estimation. To compare our transformer-based

method fairly with convolutional networks, we uti-

lize Monodepth2 (Godard et al., 2019) with a ResNet-

101 (He et al., 2016) encoder. All four combinations

are trained thrice using the settings described in Sec-

tion 4.1 for an image size of 640 × 192. All combina-

tions assume known ground-truth camera intrinsics.

4.3.1 Performance

For the four combinations, we report the best perfor-

mance on i.i.d. in Table 5, and visualize the depth

predictions for the same in Figure 2. The i.i.d. test set

used for comparison is same as in Section 4.2.

We observe from Table 5 that the combination of

transformer-based depth and ego-motion networks i.e

MT-SfMLearner performs best under two of the error

metrics as well as two of the accuracy metrics. The

remaining combinations perform comparably on all

the metrics.

From Figure 2, we observe more uniform esti-

mates for larger objects like vehicles, vegetation, and

buildings when depth is learned using transformers.

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics

763

Table 5: Quantitative results on KITTI Eigen split for all four architecture combinations of depth and ego-motion networks.

The best results are displayed in bold, the second best are underlined.

Architecture

Error↓ Accuracy↑

Abs Rel Sq Rel RMSE RMSE log δ < 1.25 δ < 1.25

δ < 1.25

C, C 0.111 0.897 4.865 0.193 0.881 0.959 0.980

C, T 0.113 0.874 4.813 0.192 0.880 0.960 0.981

T, C 0.112 0.843 4.766 0.189 0.879 0.960 0.982

T, T 0.112 0.838 4.771 0.188 0.879 0.960 0.982

InputC, CC, TT, CT, T

Figure 2: Disparity maps on KITTI for qualitative comparison of all four architecture combinations of depth and ego-motion

networks. Example areas where the global receptive ﬁeld of transformer is advantageous are highlighted in green. Example

areas where local receptive ﬁeld of CNNs is advantageous are highlighted in white.

Transformers are also less affected by reﬂection from

windows of vehicles and buildings. This is likely be-

cause of the larger receptive ﬁelds of the self-attention

layers, which lead to more globally coherent predic-

tions. On the other hand, convolutional networks pro-

duce sharper boundaries, and perform better on thin-

ner objects such as trafﬁc signs and poles. This is

likely because of the inherent inductive bias for spa-

tial locality present in convolutional layers.

4.3.2 Robustness

While the different combinations perform compara-

bly on the i.i.d. dataset, they may differ in robustness

and generalizability. Therefore, we study the impact

of natural corruptions and adversarial attacks on the

depth performance using the following:

• Natural Corruptions. Following (Hendrycks

and Dietterich, 2019) and (Michaelis et al.,

2019), we generate 15 corrupted versions of the

KITTI i.i.d. test set at the highest severity(= 5).

These natural corruptions fall under 4 categories

- noise (Gaussian, shot, impulse), blur (defocus,

glass, motion, zoom), weather (snow, frost, fog,

brightness), and digital (contrast, elastic, pixelate,

JPEG).

• Projected Gradient Descent (PGD) Ad-

versarial Examples. Adversarial attacks

make imperceptible (to humans) changes to

input images to create adversarial examples

that fool networks. We generate adversar-

ial examples from the i.i.d. test set using

PGD (Madry et al., 2018) at attack strength

ε ∈ {0.25,0.5,1.0,2.0,4.0,8.0,16.0,32.0}.

The gradients are calculated with respect to

the training loss. Following (Kurakin et al.,

2016), the perturbation is accumulated over

min(ε + 4, d1.25 · εe) iterations with a step-size of

1. When the test image is from the beginning or

end of a KITTI sequence, the appearance-based

loss is only calculated for the feasible pair of

images.

• Symmetrically Flipped Adversarial Examples.

Inspired by (Wong et al., 2020), we generate

these adversarial examples to fool the networks

into predicting ﬂipped estimates. For this, we use

the gradients of the RMSE loss, where the targets

are symmetrical horizontal and vertical ﬂips of the

i.i.d. predictions. This evaluation is conducted at

attack strength ε ∈ {1.0, 2.0, 4.0}, similar to the

PGD attack described above.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

764

Figure 3: RMSE for natural corruptions of KITTI for all four combinations of depth and ego-motion networks. The i.i.d.

evaluation is denoted by clean.

Figure 4: RMSE for adversarial corruptions of KITTI gen-

erated using PGD at all attack strengths (0.0 to 32.0) for all

four combinations of depth and ego-motion networks. At-

tack strength 0.0 refers to i.i.d. evaluation.

We report the mean RMSE across three training

runs on natural corruptions, PGD adversarial exam-

ples, and symmetrically ﬂipped adversarial examples

in Figures 3, 4, and 5, respectively.

Figure 3 demonstrates a signiﬁcant improvement

in the robustness to all the natural corruptions when

learning depth with transformers instead of convo-

lutional networks. Figure 4 further shows a general

improvement in adversarial robustness when learn-

ing either depth or ego-motion with transformers in-

stead of convolutional networks. Finally, Figure 5

shows an improvement in robustness to symmetri-

cally ﬂipped adversarial attacks when depth is learned

using transformers instead of convolutional networks.

Furthermore, depth estimation is most robust when

both depth and ego-motion are learned using trans-

formers.

Therefore, MT-SfMLearner, where both depth and

ego-motion and learned with transformers, provides

the highest robustness and generalizability, in line

with the studies on image classiﬁcation (Paul and

Chen, 2021; Bhojanapalli et al., 2021). This can be

attributed to their global receptive ﬁeld, which allows

for better adjustment to the localized deviations by ac-

counting for the global context of the scene.

Figure 5: RMSE for adversarial corruptions of KITTI gen-

erated using horizontal and vertical ﬂip attacks for all four

combinations of depth and ego-motion networks.

4.4 Intrinsics

Here, we evaluate the accuracy of our proposed

method for self-supervised learning of camera intrin-

sics and its impact on the depth estimation perfor-

mance. As shown in Table 6, the percentage error for

intrinsics estimation is low for both convolutional and

transformer-based methods trained on an image size

of 640 × 192. Moreover, the depth error as well accu-

racy metrics are both similar to when the ground truth

intrinsics are known a priori. This is also observed in

Figure 6 where the learning of intrinsics causes no ar-

tifacts in depth estimation.

We also evaluate the models trained with learned

intrinsics on all 15 natural corruptions as well as on

PGD and symmetrically ﬂipped adversarial examples.

We report the mean RMSE (µRMSE) across all cor-

ruptions in Table 7. The RMSE for depth estimation

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics

765

Table 6: Percentage error for intrinsics prediction and impact on depth estimation for KITTI Eigen split.

Network Intrinsics

Intrinsics Error(%) ↓ Depth Error↓ Depth Accuracy↑

Abs Rel Sq Rel RMSE RMSE log δ < 1.25 δ < 1.25

δ < 1.25

C,C

Given - - - - 0.111 0.897 4.865 0.193 0.881 0.959 0.980

Learned -1.889 -2.332 2.400 -9.372 0.113 0.881 4.829 0.193 0.879 0.960 0.981

T,T

Given - - - - 0.112 0.838 4.771 0.188 0.879 0.960 0.982

Learned -1.943 -0.444 3.613 -16.204 0.112 0.809 4.734 0.188 0.878 0.960 0.982

Figure 6: Disparity maps for qualitative comparison on KITTI, when trained with and without intrinsics (K). The second and

fourth rows are same as the second and the ﬁfth rows in Figure 2.

Table 7: Mean RMSE (µRMSE) for natural corruptions of

KITTI, when trained with and without ground-truth intrin-

sics.

Architecture Intrinsics µRMSE↓

C, C

Given 7.683

Learned 7.714

T, T

Given 5.918

Learned 5.939

Table 8: Mean RMSE (µRMSE) for horizontal (H) and ver-

tical (V) adversarial ﬂips of KITTI, when trained with and

without ground-truth intrinsics.

Architecture Intrinsics µRMSE↓ (H) µRMSE↓ (V)

C, C

Given 7.909 7.354

Learned 7.641 7.196

T, T

Given 7.386 6.795

Learned 7.491 6.929

on adversarial examples generated by PGD method

for all strengths is shown in Figure 7. The mean

RMSE (µRMSE) across all attack strengths for hor-

izontally ﬂipped and vertically ﬂipped adversarial ex-

amples is shown in Table 8.

We observe that the robustness to natural corrup-

tions and adversarial attacks is maintained by both

architectures when the intrinsics are learned simul-

taneously. Furthermore, similar to the scenario with

known ground truth intrinsics, MT-SfMLearner with

learned intrinsics has higher robustness than its con-

volutional counterpart.

Figure 7: Mean RMSE for adversarial corruptions of

KITTI generated using PGD, when trained with and without

ground-truth intrinsics (K).

4.5 Efﬁciency

We further compare the networks on their computa-

tional and energy efﬁciency to examine their suitabil-

ity for real-time applications.

In Table 9, we report the mean inference speed in

frames per second (fps) and the mean inference en-

ergy consumption in Joules per frame for depth and

intrinsics estimation for both architectures. These

metrics are computed over 10,000 forward passes at

a resolution of 640 × 192 on an NVidia GeForce RTX

2080 Ti.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

766

Table 9: Inference Speed (frames per second) and Energy

Consumption (Joules per frame) for depth and intrinsics es-

timation using CNN- and transformer-based architectures.

Architecture Estimate Speed↑ Energy↓

C,C

Depth 84.132 3.206

Intrinsics 97.498 2.908

T,T

Depth 40.215 5.999

Intrinsics 60.190 4.021

Both architectures run depth and intrinsics esti-

mation in real-time with an inference speed > 30

fps. However, the transformer-based method con-

sumes higher energy and is computationally more de-

manding than its convolutional counterpart.

5 CONCLUSION

This work is the ﬁrst to investigate the im-

pact of transformer architecture on the SfM in-

spired self-supervised monocular depth estimation.

Our transformer-based method MT-SfMLearner per-

forms comparably against contemporary convolu-

tional methods on the KITTI depth prediction bench-

mark. Our contrastive study additionally demon-

strates that while CNNs provide local spatial bias,

especially for thinner objects and around boundaries,

transformers predict uniform and coherent depths, es-

pecially for larger objects due to their global recep-

tive ﬁeld. We observe that transformers in the depth

network result in higher robustness to natural corrup-

tions, and transformers in both depth, as well as the

ego-motion network, result in higher robustness to

adversarial attacks. With our proposed approach to

self-supervised camera intrinsics estimation, we also

demonstrate how the above conclusions hold even

when the focal length and principal point are learned

along with depth and ego-motion. However, trans-

formers are computationally more demanding and

have lower energy efﬁciency than their convolutional

counterparts. Thus, we contend that this work assists

in evaluating the trade-off between performance, ro-

bustness, and efﬁciency of self-supervised monocu-

lar depth estimation for selecting the suitable archi-

tecture.

REFERENCES

Aich, S., Vianney, J. M. U., Islam, M. A., Kaur, M., and

Liu, B. (2021). Bidirectional attention network for

monocular depth estimation. In IEEE International

Conference on Robotics and Automation (ICRA).

Bhojanapalli, S., Chakrabarti, A., Glasner, D., Li, D., Un-

terthiner, T., and Veit, A. (2021). Understanding

robustness of transformers for image classiﬁcation.

arXiv preprint arXiv:2103.14586.

Bian, J., Li, Z., Wang, N., Zhan, H., Shen, C.,

Cheng, M.-M., and Reid, I. (2019). Unsupervised

scale-consistent depth and ego-motion learning from

monocular video. In Advances in Neural Information

Processing Systems, pages 35–45.

Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov,

A., and Zagoruyko, S. (2020). End-to-end object de-

tection with transformers. In European Conference on

Computer Vision, pages 213–229. Springer.

Caron, M., Touvron, H., Misra, I., J

egou, H., Mairal, J., Bo-

janowski, P., and Joulin, A. (2021). Emerging prop-

erties in self-supervised vision transformers. In Pro-

ceedings of the International Conference on Computer

Vision (ICCV).

Casser, V., Pirk, S., Mahjourian, R., and Angelova,

A. (2019). Depth prediction without the sensors:

Leveraging structure for unsupervised learning from

monocular videos. In Proceedings of the AAAI Con-

ference on Artiﬁcial Intelligence, volume 33, pages

8001–8008.

Chawla, H., Jukola, M., Brouns, T., Arani, E., and Zonooz,

B. (2020). Crowdsourced 3d mapping: A combined

multi-view geometry and self-supervised learning ap-

proach. In 2020 IEEE/RSJ International Confer-

ence on Intelligent Robots and Systems (IROS), pages

4750–4757. IEEE.

Chawla, H., Varma, A., Arani, E., and Zonooz, B.

(2021). Multimodal scale consistency and awareness

for monocular self-supervised depth estimation. In

2021 IEEE International Conference on Robotics and

Automation (ICRA). IEEE.

Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-

Fei, L. (2009). Imagenet: A large-scale hierarchical

image database. In 2009 IEEE conference on com-

puter vision and pattern recognition, pages 248–255.

Ieee.

Diaz, R. and Marathe, A. (2019). Soft labels for ordinal

regression. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

4738–4747.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,

M., Heigold, G., Gelly, S., Uszkoreit, J., and Houlsby,

N. (2021). An image is worth 16x16 words: Trans-

formers for image recognition at scale. ICLR.

Eigen, D., Puhrsch, C., and Fergus, R. (2014). Depth map

prediction from a single image using a multi-scale

deep network. In Advances in neural information pro-

cessing systems, pages 2366–2374.

Fu, H., Gong, M., Wang, C., Batmanghelich, K., and

Tao, D. (2018). Deep ordinal regression network for

monocular depth estimation. In Proceedings of the

IEEE Conference on Computer Vision and Pattern

Recognition, pages 2002–2011.

Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).

Vision meets robotics: The kitti dataset. The Inter-

national Journal of Robotics Research, 32(11):1231–

1237.

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics

767

Geirhos, R., Jacobsen, J.-H., Michaelis, C., Zemel, R.,

Brendel, W., Bethge, M., and Wichmann, F. A. (2020).

Shortcut learning in deep neural networks. Nature

Machine Intelligence, 2(11):665–673.

Godard, C., Mac Aodha, O., and Brostow, G. J. (2017). Un-

supervised monocular depth estimation with left-right

consistency. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

270–279.

Godard, C., Mac Aodha, O., Firman, M., and Brostow, G. J.

(2019). Digging into self-supervised monocular depth

estimation. In Proceedings of the IEEE/CVF Interna-

tional Conference on Computer Vision, pages 3828–

3838.

Goldman, M., Hassner, T., and Avidan, S. (2019). Learn

stereo, infer mono: Siamese networks for self-

supervised, monocular, depth estimation. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition Workshops, pages 0–0.

Gordon, A., Li, H., Jonschkowski, R., and Angelova, A.

(2019). Depth from videos in the wild: Unsupervised

monocular depth learning from unknown cameras.

Guizilini, V., Ambrus, R., Pillai, S., Raventos, A., and

Gaidon, A. (2020). 3d packing for self-supervised

monocular depth estimation. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 2485–2494.

Guo, X., Li, H., Yi, S., Ren, J., and Wang, X. (2018). Learn-

ing monocular depth by distilling cross-domain stereo

networks. In Proceedings of the European Conference

on Computer Vision (ECCV), pages 484–500.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Hendrycks, D. and Dietterich, T. (2019). Benchmarking

neural network robustness to common corruptions and

perturbations. Proceedings of the International Con-

ference on Learning Representations.

Jiang, H. and Huang, R. (2019). Hierarchical binary classi-

ﬁcation for monocular depth estimation. In 2019 IEEE

International Conference on Robotics and Biomimet-

ics (ROBIO), pages 1975–1980. IEEE.

Johnston, A. and Carneiro, G. (2020). Self-supervised

monocular trained depth estimation using self-

attention and discrete disparity volume. In Proceed-

ings of the ieee/cvf conference on computer vision and

pattern recognition, pages 4756–4765.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Klingner, M., Term

ohlen, J.-A., Mikolajczyk, J., and

Fingscheidt, T. (2020). Self-Supervised Monocular

Depth Estimation: Solving the Dynamic Object Prob-

lem by Semantic Guidance. In ECCV.

Kong, S. and Fowlkes, C. (2019). Pixel-wise attentional

gating for scene parsing. In 2019 IEEE Winter Con-

ference on Applications of Computer Vision (WACV),

pages 1024–1033. IEEE.

Kurakin, A., Goodfellow, I., Bengio, S., et al. (2016). Ad-

versarial examples in the physical world.

Lee, J. H., Han, M.-K., Ko, D. W., and Suh, I. H. (2019).

From big to small: Multi-scale local planar guid-

ance for monocular depth estimation. arXiv preprint

arXiv:1907.10326.

Li, B., Dai, Y., and He, M. (2018a). Monocular depth es-

timation with hierarchical fusion of dilated cnns and

soft-weighted-sum inference. Pattern Recognition,

83:328–339.

Li, R., Xian, K., Shen, C., Cao, Z., Lu, H., and Hang, L.

(2018b). Deep attention-based classiﬁcation network

for robust depth prediction. In Asian Conference on

Computer Vision (ACCV).

Li, Z., Liu, X., Drenkow, N., Ding, A., Creighton,

F. X., Taylor, R. H., and Unberath, M. (2020). Re-

visiting stereo depth estimation from a sequence-

to-sequence perspective with transformers. arXiv

preprint arXiv:2011.02910.

Liebel, L. and K

orner, M. (2019). Multidepth: Single-

image depth estimation via multi-task regression and

classiﬁcation. In 2019 IEEE Intelligent Transporta-

tion Systems Conference (ITSC), pages 1440–1447.

IEEE.

Lin, G., Milan, A., Shen, C., and Reid, I. (2017). Reﬁnenet:

Multi-path reﬁnement networks for high-resolution

semantic segmentation. In Proceedings of the IEEE

conference on computer vision and pattern recogni-

tion, pages 1925–1934.

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin,

S., and Guo, B. (2021). Swin transformer: Hierarchi-

cal vision transformer using shifted windows. arXiv

preprint arXiv:2103.14030.

Lopez, M., Mari, R., Gargallo, P., Kuang, Y., Gonzalez-

Jimenez, J., and Haro, G. (2019). Deep single image

camera calibration with radial distortion. In Proceed-

ings of the IEEE/CVF Conference on Computer Vision

and Pattern Recognition, pages 11817–11825.

Loshchilov, I. and Hutter, F. (2017). Decoupled weight de-

cay regularization. arXiv preprint arXiv:1711.05101.

Lyu, X., Liu, L., Wang, M., Kong, X., Liu, L., Liu, Y., Chen,

X., and Yuan, Y. (2020). Hr-depth: high resolution

self-supervised monocular depth estimation. CoRR

abs/2012.07356.

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and

Vladu, A. (2018). Towards deep learning models

resistant to adversarial attacks. In 6th International

Conference on Learning Representations, ICLR 2018,

Vancouver, BC, Canada, April 30 - May 3, 2018, Con-

ference Track Proceedings. OpenReview.net.

Mahjourian, R., Wicke, M., and Angelova, A. (2018). Un-

supervised learning of depth and ego-motion from

monocular video using 3d geometric constraints. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition, pages 5667–5675.

Michaelis, C., Mitzkus, B., Geirhos, R., Rusak, E., Bring-

mann, O., Ecker, A. S., Bethge, M., and Brendel, W.

(2019). Benchmarking robustness in object detection:

Autonomous driving when winter is coming. arXiv

preprint arXiv:1907.07484.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

768

Ochs, M., Kretz, A., and Mester, R. (2019). Sdnet: Seman-

tically guided depth estimation network. In German

Conference on Pattern Recognition, pages 288–302.

Springer.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., et al. (2019). Pytorch: An imperative style,

high-performance deep learning library. Advances

in neural information processing systems, 32:8026–

8037.

Paul, S. and Chen, P.-Y. (2021). Vision transformers are

robust learners. arXiv preprint arXiv:2105.07581.

Poggi, M., Aleotti, F., Tosi, F., and Mattoccia, S. (2020). On

the uncertainty of self-supervised monocular depth es-

timation. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition, pages

3227–3237.

Raghu, M., Unterthiner, T., Kornblith, S., Zhang, C., and

Dosovitskiy, A. (2021). Do vision transformers see

like convolutional neural networks? arXiv preprint

arXiv:2108.08810.

Ranftl, R., Bochkovskiy, A., and Koltun, V. (2021). Vision

transformers for dense prediction. ArXiv preprint.

Ranftl, R., Lasinger, K., Hafner, D., Schindler, K., and

Koltun, V. (2020). Towards robust monocular depth

estimation: Mixing datasets for zero-shot cross-

dataset transfer. IEEE Transactions on Pattern Analy-

sis and Machine Intelligence (TPAMI).

Ranjan, A., Jampani, V., Balles, L., Kim, K., Sun, D., Wulff,

J., and Black, M. J. (2019). Competitive collaboration:

Joint unsupervised learning of depth, camera motion,

optical ﬂow and motion segmentation. In Proceed-

ings of the IEEE conference on computer vision and

pattern recognition, pages 12240–12249.

Ren, H., El-Khamy, M., and Lee, J. (2019). Deep robust

single image depth estimation neural network using

scene understanding. In CVPR Workshops, pages 37–

45.

Roussel, T., Van Eycken, L., and Tuytelaars, T. (2019).

Monocular depth estimation in new environments

with absolute scale. In 2019 IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

pages 1735–1741. IEEE.

Strudel, R., Garcia, R., Laptev, I., and Schmid, C. (2021).

Segmenter: Transformer for semantic segmentation.

arXiv preprint arXiv:2105.05633.

Touvron, H., Cord, M., Douze, M., Massa, F., Sablayrolles,

A., and J

egou, H. (2021). Training data-efﬁcient

image transformers & distillation through attention.

In International Conference on Machine Learning,

pages 10347–10357. PMLR.

Uhrig, J., Schneider, N., Schneider, L., Franke, U., Brox,

T., and Geiger, A. (2017). Sparsity invariant cnns.

In 2017 international conference on 3D Vision (3DV),

pages 11–20. IEEE.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

neural information processing systems, pages 5998–

6008.

Wong, A., Cicek, S., and Soatto, S. (2020). Targeted adver-

sarial perturbations for monocular depth prediction. In

Advances in neural information processing systems.

Xiang, X., Kong, X., Qiu, Y., Zhang, K., and Lv, N. (2021).

Self-supervised monocular trained depth estimation

using triplet attention and funnel activation. Neural

Processing Letters, pages 1–18.

Yang, G., Tang, H., Ding, M., Sebe, N., and Ricci, E.

(2021). Transformer-based attention networks for

continuous pixel-wise prediction. In ICCV.

Yin, W., Liu, Y., Shen, C., and Yan, Y. (2019). Enforc-

ing geometric constraints of virtual normal for depth

prediction. In Proceedings of the IEEE International

Conference on Computer Vision, pages 5684–5693.

Yin, Z. and Shi, J. (2018). Geonet: Unsupervised learning

of dense depth, optical ﬂow and camera pose. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 1983–1992.

Zhang, Z., Cui, Z., Xu, C., Yan, Y., Sebe, N., and Yang,

J. (2019). Pattern-afﬁnitive propagation across depth,

surface normal and semantic segmentation. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 4106–4115.

Zhang, Z., Xu, C., Yang, J., Tai, Y., and Chen, L. (2018).

Deep hierarchical guidance and regularization learn-

ing for end-to-end depth estimation. Pattern Recogni-

tion, 83:430–442.

Zheng, S., Lu, J., Zhao, H., Zhu, X., Luo, Z., Wang, Y., Fu,

Y., Feng, J., Xiang, T., Torr, P. H., et al. (2021). Re-

thinking semantic segmentation from a sequence-to-

sequence perspective with transformers. In Proceed-

ings of the IEEE/CVF Conference on Computer Vision

and Pattern Recognition, pages 6881–6890.

Zhou, T., Brown, M., Snavely, N., and Lowe, D. G. (2017).

Unsupervised learning of depth and ego-motion from

video.

Zhuang, B., Tran, Q.-H., Lee, G. H., Cheong, L. F.,

and Chandraker, M. (2019). Degeneracy in self-

calibration revisited and a deep learning solution for

uncalibrated slam. In 2019 IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

pages 3766–3773. IEEE.

Transformers in Self-Supervised Monocular Depth Estimation with Unknown Camera Intrinsics

769