Pose Guided Feature Learning for 3D Object Tracking on RGB Videos

Mateusz Majcher and Bogdan Kwolek

AGH University of Science and Technology, 30 Mickiewicza, 30-059 Krakow, Poland

Keywords:

3D Object Pose, Detection of Object Keypoints, Pose Tracking.

Abstract:

In this work we propose a new approach to 3D object pose tracking in sequences of RGB images acquired

by a calibrated camera. A single hourglass neural network that has been trained to detect ﬁducial keypoints

on a set of objects delivers heatmaps representing 2D locations of the keypoints. Given a calibrated camera

model and a sparse object model consisting of 3D locations of the keypoints, the keypoints in hypothesized

object poses are projected onto 2D plane and then matched with the heatmaps. A quaternion particle ﬁlter

with a probabilistic observation model that uses such a matching is employed to maintain 3D object pose

distribution. A single Siamese neural network is trained for a set of objects on keypoints from the current and

previous frame in order to generate a particle in the predicted 3D object pose. The ﬁlter draws particles to

predict the current pose using its a priori knowledge about the object velocity and includes the predicted 3D

object pose by the neural network in a priori distribution. Thus, the hypothesized 3D object poses are generated

using both a priori knowledge about the object velocity in 3D and keypoint-based geometric reasoning as well

as relative transformations in the image plane. In an extended algorithm we combine the set of propagated

particles with an optimized particle, whose pose is determined by Levenberg-Marguardt.

1 INTRODUCTION

Determining pose between object and camera is a

classical problem in computer vision, but it has re-

cently attracted considerable attention. Although

RGBD-based methods can estimate 6DoF object pose

with high accuracies on popular benchmark data

(Kaskman et al., 2019), considerable research efforts

are devoted to RGB-based methods for 3D object

pose estimation to improve their efﬁciency and usabil-

ity. The RGB-only approaches suffer heavily from in-

herent scale ambiguities (Xiang et al., 2018). Existing

methods can be divided into category level methods

(Pavlakos et al., 2017; Wang et al., 2018; Chen et al.,

2021) and instance level methods (Rad and Lepetit,

2017; Kehl et al., 2017; Tekin et al., 2018; Peng et al.,

2019; Hu et al., 2019). The former group encom-

passes methods that focus more on handling intra-

category variation and aims at estimating poses for an

entire category. In later methods, training set and test

set contain the same objects.

In general, recent methods follow either of two

approaches: (i) keypoint-based approaches that de-

tect a sparse set of keypoints and afterward align a

3D object representation to detections on the image,

(ii) rendering-based approaches utilizing a generative

model, that is built on a 3D mesh representation of an

object undergoing observation. The later methods es-

timate the object pose by reconstructing the input im-

age through rendering-and-comparing (analysis-by-

synthesis) and usually better cope with partial occlu-

sions (Egger et al., 2018).

Recent methods for object pose estimation are

based on convolutional neural networks (CNNs).

They can be divided into indirect and direct meth-

ods. Indirect methods aim at establishing 2D-3D

correspondences between the coordinates in the im-

age plane and object coordinates or learn a pose em-

bedding at an intermediate stage. In contrast, direct

methods determine the ﬁnal 6D pose without using

such an intermediate representation. A ﬁrst attempt

to utilize a CNN for direct regression of 6DoF ob-

ject poses was PoseCNN (Xiang et al., 2018). How-

ever, existing CNN-based methods usually need sep-

arate networks for each object instance (Kehl et al.,

2017; Tekin et al., 2018; Manhardt et al., 2020),

which results in long training times. The current top-

performing deep learning-based methods rely on the

indirect strategies. For instance, in (Rad and Lepetit,

2017) the 2D projections of ﬁxed points, e.g. the 3D

corners of the encapsulating bounding box are deter-

mined. (Hu et al., 2019; Peng et al., 2019) addition-

ally perform object segmentation coupled with vot-

ing for each correspondence in order to improve the

574

Majcher, M. and Kwolek, B.

Pose Guided Feature Learning for 3D Object Tracking on RGB Videos.

DOI: 10.5220/0010886800003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages

574-581

ISBN: 978-989-758-555-5; ISSN: 2184-4321

performance and robustness. Most pf the recent re-

search efforts are directed towards predicting dense

rather than sparse correspondences (Zakharov et al.,

2019; Fan et al., 2021). There are also ﬁrst attempts to

make RANSAC/PnP differentiable (Brachmann and

Rother, 2019).

Although, vast work has been done in the ﬁeld

of 3D object pose estimation, there is comparatively

small number of related works on 3D object tracking

(Fan et al., 2021). Moreover, most existing methods

deliver only a single guess of the object’s pose. In

robotic applications, such approaches can be less use-

ful as robots should be aware of pose uncertainty be-

fore taking an action. Modeling uncertainties through

continuous distributions over 3D object coordinates

or bounding box coordinates have been studied in

(Brachmann et al., 2016) and (Tremblay et al., 2018),

respectively. Recently, (Majcher and Kwolek, 2021)

proposed deep quaternion pose proposals for 3D ob-

ject pose tracking on RGB images. A 3D object

model is rendered and then matched with the object

segmented in advance by a neural network. Object

keypoints detected by a simple neural network are fed

to PnP algorithm in order to calculate an object pose

hypothesis, which is then injected into the probability

distribution, recursively updated in a Bayesian frame-

work.

Inspired by the analysis above and gaps in existing

approaches, in this work we propose a novel approach

to 3D object pose tracking in sequences of RGB im-

ages acquired by a calibrated camera. We trained

a single hourglass neural network in order to detect

ﬁducial keypoints on a set of objects, which delivers

heatmaps representing 2D locations of the keypoints.

Given a calibrated camera model and a sparse object

model consisting of 3D locations of the keypoints,

the keypoints in hypothesized poses of the object are

projected onto 2D plane and then matched with the

heatmaps. A quaternion particle ﬁlter with probabilis-

tic observation model that uses such a matching is em-

ployed to maintain 3D object pose distribution. For a

set of objects, we also trained a single Siamese neu-

ral network on keypoints from the current and previ-

ous frame in order to generate a predicted object pose

on the basis of geometrical relations and motion of

the keypoints in the image plane. The ﬁlter draws

particles to predict the current pose using its a pri-

ori knowledge about the object velocity and includes

the predicted 3D object pose by the neural network in

a priori distribution. Owing to reliable detections of

object keypoints and heatmap-based representation of

keypoint locations, a simpliﬁed keypoint only-based

observation model has been proposed for a Bayesian

ﬁlter, which permits reliable tracking of 3D object

pose. The novelty of this work lies in synergistic

combination of 2D and 3D information about object

motion to generate object pose hypotheses, which are

then veriﬁed on the basis of deep heatmaps, deter-

mined by the learned neural network.

2 METHOD

At the beginning we outline quaternions and explain

the motion model of quaternion particle ﬁlter. In Sub-

section 2.2 we present a neural network for extracting

object keypoints. Subsection 2.3 details the algorithm

for 3D object pose tracking.

2.1 Quaternion Particle Filter

Quaternions can be viewed as numbers with one real

part and three distinct imaginary parts: q = q

i + q

j + q

k, where q

, q

, and q

are real num-

bers, and i, j, k satisfy i

= j

= k

= ijk = −1, and

ij = −ji = k, jk = −kj = i, ki = −ik = j. This implies

that quaternion multiplication is generally not com-

mutative. The quaternion q = q

i +q

j +q

k can

also be viewed as q = w+v, where v = q

i+q

j+q

A unit-length quaternion (|q| = 1) is generated by

dividing each of the four components by the square

root of the sum of the squares of those components.

Every quaternion with unit magnitude enforces the

number of DoF to three, and thus represents a rota-

tion of angle θ about an arbitrary axis. Unit quater-

nions can be represented as a sphere of radius equal

to one unit. The vector originates at the sphere’s cen-

ter, and all rotations take place along its surface. If

the axis passes through the origin of the coordinate

system and has a direction given by the vector n with

|n| = 1, we can parameterize this rotation in the fol-

lowing manner:

q = [q

] =

cos(

θ)

nsin(

θ)

= [w v]

(1)

The set of unit-length quaternions is a sub-group

whose underlying set is named S

. This set of unit

quaternions corresponds to the unit sphere S

in R

As the quaternions q and −q represent identical ro-

tation, only one hemisphere of S

needs to be taken

into account, and thus we choose the northern hemi-

sphere S

with q ≥ 0, which in turn is equivalent to

θ ∈ [0, π].

The quaternion multiplication can be expressed as

follows:

? q

= [w

][w

]

= [w

− v

· v

+ w

+ v

× v

]

(2)

Pose Guided Feature Learning for 3D Object Tracking on RGB Videos

575

where × stands for vector cross product, · is vec-

tor dot product and ? denotes quaternion multiplica-

tion. Quaternion multiplication is noncummutative,

i.e. q

? q

is not the same as q

? q

. The logarithm

of q is deﬁned as follows:

logMap(q) = logMap([cos(α) nsin(α)]) ≡ [0 αn]

(3)

where α =

θ. It is worth noting that the logMap(q)

is not a unit quaternion. The exponential function is

deﬁned as:

expMap(p) = expMap([0 αn]) ≡ [cos(α) nsin(α)]

(4)

where p = [0 αn] = [0 (αx αy αz)] with n as unit

vector (knk = 1). By deﬁnition expMap(p) always

returns a unit quaternion.

Particle ﬁlters (PFs) allow robust estimation of

hidden features of dynamical systems (Kutschireiter

et al., 2017). In this work the unit quaternion is

used as representation of the rotational state space for

a particle ﬁlter. The state vector describing the 6D

object pose comprises two parts: a quaternion as a

description of rotations and translation vector in Eu-

clidean space, which origin is in the camera coordi-

nate system. Let us denote by q the unitary quater-

nion representing the rotation in time t, and by z the

3D translation in time t. The state vector assumes the

following form: x = [q z], where q is a unitary quater-

nion and z is a 3D translation vector. To introduce the

process noise in the quaternion motion of particle i, a

three dimensional normal distribution with zero mean

and covariance matrix C

in the tangential space is ap-

plied as follows (Majcher and Kwolek, 2021):

(t + 1) = expMap(N ([0, 0, 0]

)) ? q

(t) (5)

where q

(t) - orientation of particle i at time t, C

- co-

variance matrix for rotation with standard deviations

(γ

) on the diagonal, ? - quaternion product

(2) and expMap - exponential function (4). The prob-

abilistic motion model for the translation can be ex-

pressed as follows:

(t + 1) = z

(t) + N ([0, 0, 0]

) (6)

In a particle ﬁlter, each sample particle i is represented

as s

(t) = (x

(t), w

(t)), where w

(t) is the particle’s

weight. The weights are calculated on the basis of

a probabilistic observation model and then used in

the resampling of the particles. With the resampling

the particles with large weights are replicated and

the ones with negligible weights are eliminated. The

probabilistic observation model is detailed in Section

2.3.

2.2 Estimation of Object Keypoints

The stacked hourglass model (Newell et al., 2016)

was originally developed for single-person human

pose estimation and designed to output a heatmap for

each body joint of a target person. Every heatmap

represents the likely position of a single joint of the

person. Thus, the pixel with the highest heatmap acti-

vation represents the predicted location for that joint.

Hourglass blocks comprise progressive pooling fol-

lowed by progressive upsampling. The residuals that

were introduced in ResNets are employed as their ba-

sic building blocks. Each residual has three layers:

• a 1 × 1 convolution (for dimensionality reduction,

from 256 to 128 channels)

• a 3 × 3 convolution

• a 1 × 1 convolution (for dimensionality enlarge-

ment, back to 256)

In discussed neural network architecture, 7 × 7 con-

volutions with strides of (2, 2) are executed on the in-

put images, 2 × 2 max-poolings with strides of (2, 2)

are executed for downsampling, whereas the nearest

neighbor is utilized for upsampling the feature maps

by a factor equal to 2. A characteristic feature of this

architecture is that before each pooling, the current

feature map is branched off as a main branch and a

minor branch with three basic building blocks. Such

a minor branch is upsampled to the original size and

then added to the main branch. After every pool-

ing, three basic building blocks are added. The fea-

ture maps between each basic building block have

256 channels. In the original architecture, two hour-

glass blocks were stacked and an intermediate loss has

been placed between them and utilized as a compo-

nent in the complete loss. The network ended with

two 1 ×1 convolutions responsible for calculating the

heatmaps. The training of such a hourglass neural

network on MPII dataset took about three days on a

12GB NVIDIA TitanX GPU.

Figure 1 depicts the architecture of the hourglass

neural network that has been designed for determin-

ing the object keypoints. The neural network operates

on RGB images of size 256 × 256 and delivers 2D lo-

cations of eight object points, where each of them is

represented by a heatmap on a separate channel. It

consists of two hourglass blocks, see two rectangles

with dotted lines.

Each basic residual block, see read block on

Fig. 1, consists of a branch with three convolutions

(1 × 1, 3 × 3 and 1 × 1) that are followed by batch

normalizations, and a direct connection to calculate

the residual. The feature map that is fed to the ﬁrst

hourglass is determined by a residual block, which

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

576

Figure 1: Architecture of neural network for detection of

object keypoints.

is similar to a basic block except that instead of di-

rect connection a 1 × 1 convolution is utilized in or-

der to calculate the residual. The feature map that is

fed to mentioned above residual block is determined

by a block consisting of 1× 1 convolution, batch nor-

malization, basic residual block, max pooling, and

the basic residual block. The ﬁrst hourglass block is

followed by a residual block with 1 × 1 convolution

followed by 3 × 3 convolution in the ﬁrst branch and

1 × 1 convolution in the second one.

The feature maps determined by both hourglass

blocks are utilized in calculating the loss. The mean

squared error has been used in the loss function

comparing the predicted heatmaps to a ground-truth

heatmaps with 2D gaussians centered at the object

keypoints. The neural network detects eight ﬁducial

keypoints that are represented by heatmaps on sepa-

rate output maps. The variance of 2D gaussians rep-

resenting locations of ﬁducial points in the images

from the training subset has been set to ﬁve pixels.

The neural network has been trained using RMSprop

optimizer with learning rate set to 1e-6. It has been

trained in 400 epochs and batch size set to 32.

2.3 Algorithm for 6D Object Pose

Tracking

The algorithm operates on sequences of RGB images

that are acquired by a calibrated camera. For ev-

ery object of interest a 3D sparse object model has

been prepared in advance. Every 3D model con-

sists of eight 3D locations that correspond to ﬁdu-

cial keypoins of the object and which are detected

by the neural network. On every image, eight ﬁdu-

cial objects points are determined using the hourglass

neural network, which has been discussed in Subsec-

tion 2.2. The positions of ﬁducial points on the ob-

jects were selected manually. Given the ground-truth

data the 3D positions of the ﬁducial points have been

determined afterwards. Using the parameters of the

calibrated camera they were then projected onto the

image plane. Every keypoint has been represented

by zero-mean normal distribution of pixel intensities,

centered on it and stored in a separate image. The ob-

ject keypoints have been stored in multidimensional

images with number of channels equal to number of

keypoints. Using the ground-truth data the 3D points

have been projected to image plane to determine a

window surrounding the object to cut the subimage

with object centered on it. The coordinates of sub-

windows were also used to cut subimages from the

multidimensional image, which were then resized to

64 × 64, see also output shape on Fig. 1.

During 3D object pose tracking, given the object

pose determined in the previous frame, a subimage

surrounding the object is determined and then scaled

to size of 256 × 256. Such an image is then fed

to hourglass neural network that determines the key-

points and represents them as heatmaps on separate

images of size 64 × 64. 2D locations of the keypoints

on such images are determined through seeking for

maximas in the heatmaps. The 2D locations of the

keypoints representing the object in current and the

previous frame were then fed to a Siamese neural

network (Majcher and Kwolek, 2021) to predict the

3D object pose, i.e. to calculate the 3D translation

and rotation of the object in the current frame. The

quaternion particle ﬁlter, which is outlined in Sub-

section 2.1, consisting of 200 particles has been em-

ployed to achieve 3D object pose tracking. A subset

of the particles without the particle with the small-

est weight is resampled and then each particle is pre-

Pose Guided Feature Learning for 3D Object Tracking on RGB Videos

577

dicted according to probabilistic motion model, dis-

cussed in Subsection 2.1. A priori probability distri-

bution determined in such a way is extended about

particle with pose determined by the Siamese neural

network. Given a particle state, the 3D keypoints are

projected onto the image. At keypoint coordinates,

the values of heatmaps are determined and then aver-

aged. Such averaged values have then been utilized

to calculate the values of particle weights. The likeli-

hood of the particle s can be expressed in the follow-

ing manner:

p(y|x = s) = e

−λ



d(s)−d

min

max

−d

min



(7)

where the mean distance d has been computed di-

rectly on the basis of the heatmap values: d(s) =

1.0−

∑

, where d

is a value given by the heatmap

map for the keypoint i projected onto the image plane,

whereas N is equal to eight and λ was determined ex-

perimentally.

3 EXPERIMENTAL RESULTS

At the beginning of this Section we discuss the eval-

uation metric for 6D pose estimation. Afterwards, we

present experimental results.

3.1 Evaluation Metric for 6D Pose

Estimation

We evaluated the quality of 6-DoF object pose esti-

mation using ADD score (Average Distance of Model

Points) (Hinterstoisser et al., 2013). ADD is deﬁned

as average Euclidean distance between model vertices

transformed using the estimated pose and the ground

truth pose. It is deﬁned as follows:

ADD = avg

x∈M

||(Rx + t) − (

Rx +

t)||

(8)

where M is a set of 3D object model points, t and R

are the translation and rotation of a ground truth trans-

formation, respectively, whereas

t and

R correspond

to those of the estimated transformation. This means

that it expresses the average distance between the 3D

points transformed using the estimated pose and those

obtained with the ground-truth one. The pose is con-

sidered to be correct if average distance e is less than

d, where d is the diameter (i.e., the largest distance

between vertices) of M and k

is a pre-deﬁned thresh-

old (normally it is set to ten percent).

3.2 Evaluation of 3D Object Pose

Tracking

We evaluated our algorithm on a freely available OPT

benchmark dataset (Wu et al., 2017). It is a large 6-

DOF object pose tracking dataset that consists of 552

real-world image sequences. It includes RGB video

recordings of tracked objects, their 3D models, and

true poses. The dataset contains six models of vari-

ous geometric complexity. Object movement patterns

are diverse and the most natural scenario is FreeMo-

tion scenario in which the movements are in arbitrary

directions. As the OPT dataset does not contain the

object keypoints, we added eight keypoint locations

on each image from the FreeMotion scenario.

Table 1 presents root-mean-square errors (RMSE)

for 2D keypoints locations, which were obtained on

images from FreeMotion scenario of the OPT dataset.

It shows errors that were obtained for the four camera

views. In discussed table the RMSE errors achieved

by the hourglass neural network are compared with

the RMSE errors achieved by a simple neural net-

work. The simple neural network consisted of two

blocks with 32 and 64 3 × 3 2D convolutional ﬁl-

ters, followed by 2 × 2 max pool and batch normal-

ization, which in turn were followed by three blocks

with 3 × 3 2D convolutional ﬁlters and batch normal-

ization, with 128, 256, and 512 ﬁlters each. On every

image a rectangle of size 128× 128 with the object in

its center has been cropped and then stored for evalu-

ation of the precision of determining the 2D locations

of the keypoints. As we can observe, the hourglass

architecture permits achieving considerably smaller

RMSE errors in comparison to errors achieved by the

simple network.

Table 1: RMSE achieved on the OPT dataset by our network

for ﬁducial keypoints estimation.

Left Right Back Front

Iron. (simple) 15.92 12.78 9.53 7.83

Iron. (hourglass) 2.26 2.70 0.65 0.66

House (simple) 10.92 11.59 14.57 16.60

House (hourglass) 4.24 3.22 3.35 2.05

Bike (simple) 15.45 14.69 6.68 9.42

Bike (hourglass) 2.14 2.39 0.93 2.74

Jet (simple) 10.40 14.70 16.39 19.50

Jet (hourglass) 2.32 1.10 4.78 8.85

Soda (simple) 10.63 8.77 19.35 2.61

Soda (hourglass) 4.91 0.65 5.06 1.83

Chest (simple) 18.42 21.67 17.26 14.80

Chest (hourglass) 9.06 10.83 3.80 4.84

Table 2 contains ADD scores that have been

achieved by our algorithm on the OPT benchmark

dataset in the FreeMotion scenario. All tracking

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

578

scores presented below are averages of three indepen-

dent runs of the algorithm with unlike initializations.

As we can observe, the average 10% ADDs are close

or better than 60%, except of the soda object, c.f. re-

sults in penultimate row in the discussed table.

Table 2: ADD scores [%] achieved on the OPT dataset by

our network, with PF-based object pose tracking.

ADD [%] Iron. House Bike Jet Soda Chest

beh., ADD 10% 81 80 62 81 35 25

beh., ADD 20% 99 99 90 95 43 29

left, ADD 10%

58 74 77 59 58 54

left, ADD 20% 93 95 96 81 93 89

right, ADD 10% 53 66 78 69 46 74

right, ADD 20% 84 89 98 78 96 96

front, ADD 10% 80 86 57 49 56 79

front, ADD 20% 99 100 89 77 84 96

Avg., ADD 10% 68 77 69 65 49 58

Avg., ADD 20% 94 96 93 83 79 78

The ADD scores presented in Tab. 3 have been

achieved by algorithm with a pose reﬁnement. The

pose reﬁnement has been realized by a Levenberg-

Marguardt (LM) algorithm. The pose represented by

the best particle has been used to initialize staring vec-

tor from which the LM optimization is run. Finally,

we combined the set of propagated particles with the

optimized particle, i.e. with pose determined in LM-

based object pose reﬁnement. Comparing the ADD

scores achieved by the discussed algorithm against re-

sults presented in Tab. 2, we can observe that LM-

based pose reﬁnement permits achieving better re-

sults. As we can see, for ADD 10% all ADD scores

are better, except for the ADD score achieved for the

soda object.

Table 3: ADD scores [%] achieved on the OPT dataset by

our network, with PF-based object pose tracking, and LM-

based pose reﬁnement.

ADD [%] Iron. House Bike Jet Soda Chest

beh., ADD 10% 90 81 70 87 40 36

beh., ADD 20% 99 99 97 96 44 41

left, ADD 10% 68 74 82 64 59 60

left, ADD 20% 98 99 99 84 87 90

right, ADD 10% 64 71 89 76 32 70

right, ADD 20% 91 99 100 83 97 97

front, ADD 10% 81 86 59 65 63 83

front, ADD 20% 97 98 92 91 79 97

Avg., ADD 10% 72 78 75 73 49 62

Avg., ADD 20% 92 98 97 88 77 81

Table 4 compares results achieved by our algo-

rithm, where in the observation model the matching

was based on keypoints and heatmaps, and for com-

parison the observation model was based on object

segmentation and object rendering as in (Majcher and

Kwolek, 2021). As we can observe, none of the dis-

cussed algorithms obtains statistically better results.

However, it is worth noting that the observation model

based on keypoints and heatmaps is much simpler and

easier in implementation. Moreover, signiﬁcant gains

in tracking speed are expected to be achieved due

to rapid progress in hardware dedicated to executing

neural networks as well as progress in compression of

models of the neural networks.

Table 5 contains AUC scores achieved by recent

methods in 6D pose tracking of six objects in the

FreeMotion scenario. As we can observe, our algo-

rithm attains better results than results achieved by

PWP3D, UDP, and ElasticFusion. In comparison to

results attained by algorithm (Tjaden et al., 2019), re-

sults achieved by our algorithm are also better. How-

ever, it is worth noting that the discussed results

are averages from all scenarios, including translation,

zoom, in-plane-rotation, out-of-plane rotation, ﬂash-

ing light, moving light, i.e. scenarios in which the

errors are usually smaller than in the challenging free

motion scenario. Moreover, the discussed method de-

livers a single guess of each object’s pose, whereas

our algorithm outputs best poses together with prob-

ability distributions. The AUC scores by our algo-

rithm are noticeably better than results achieved in

(Majcher and Kwolek, 2021). Owing to using more

advanced neural network for object keypoints detec-

tion the whole algorithm for 6D object pose tracking

has been considerably simpliﬁed.

Figure 2 depicts ADD scores over time on se-

quences of images, which were achieved by our net-

work and PnP, and our network, PF and LM-based

object pose reﬁnement. As we can observe, our algo-

rithm permits achieving far better tracking of the 6D

object pose on sequences of RGB images. The PnP

tend to lose object pose after some time in image se-

quences.

Table 6 presents running times that were achieved

on Jetson AGX Xavier board and a PC equipped with

Intel Core i5-10400F and GeForce RTX 2060. At the

moment, due to unoptimized implementation the run-

ning time is longer on the Jetson, but it is expected

that it will be shortened. The complete system for 6D

pose estimation has been implemented in Python lan-

guage with experiments performed using Keras.

4 CONCLUSIONS

In this work, we presented an algorithm for 3D ob-

ject pose tracking in RGB images. It employs pairs

of objects keypoints to predict rotation represented

by quaternion, as well as translation with the corre-

sponding delta translation. A single Siamese neural

network for a set of objects is trained on keypoints

from current and previous frame in order to predict

Pose Guided Feature Learning for 3D Object Tracking on RGB Videos

579

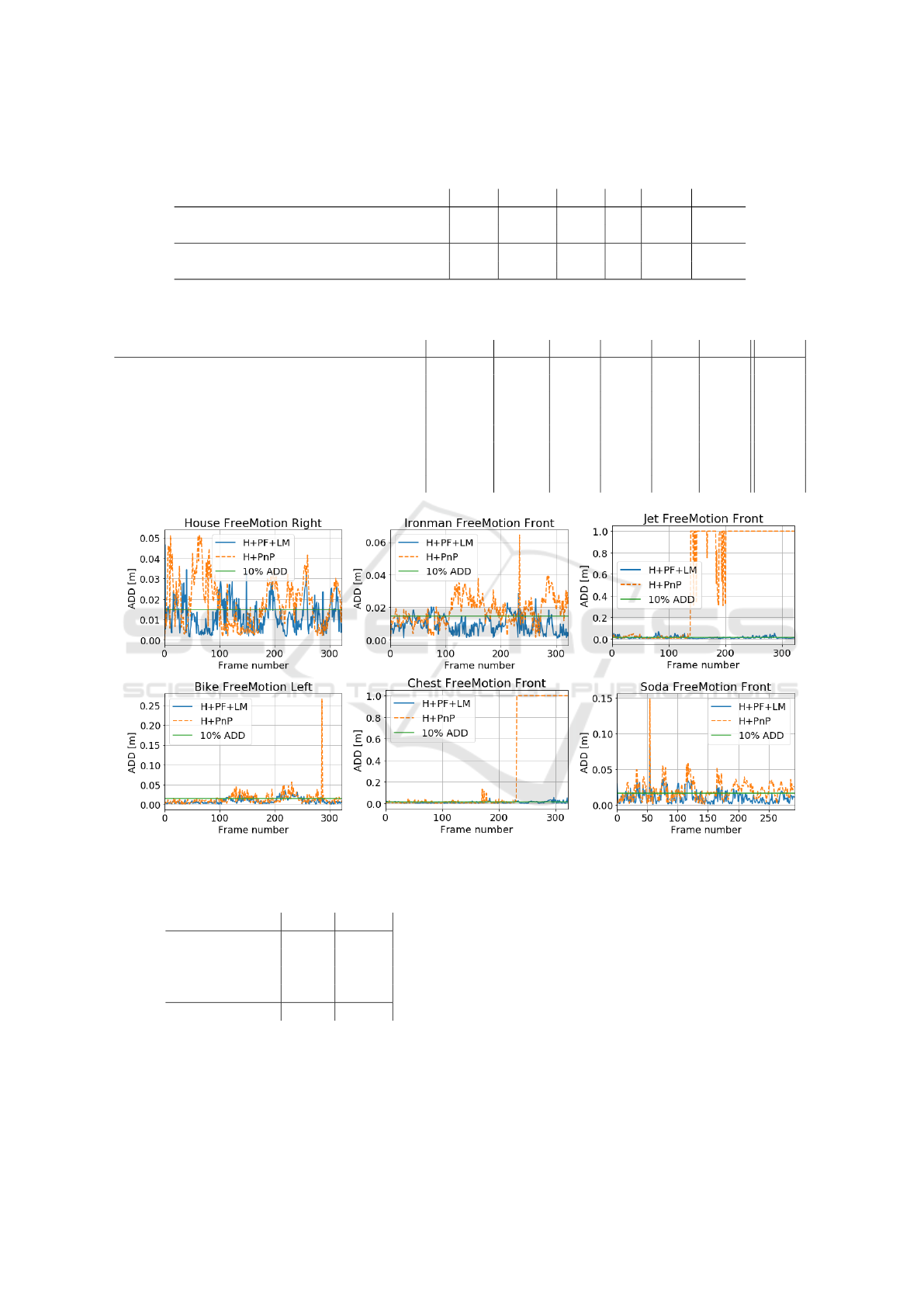
Table 4: ADD scores [%] achieved on the OPT dataset by our algorithm using keypoints and object rendering, as in (Majcher

and Kwolek, 2021).

Avg. ADD [%] Iron. House Bike Jet Soda Chest

object seg. and rend., 10% 71 67 67 66 49 58

object seg. and rend., 20% 93 79 91 85 74 85

keypoints and heatmaps (our), ADD 10% 72 78 75 73 49 62

keypoints and heatmaps (our), ADD 20% 92 98 97 88 77 81

Table 5: AUC scores achieved on OPT dataset in FreeMotion scenario (Wu et al., 2017), compared with AUC scores achieved

by recent methods.

Ironman House Bike Jet Soda Chest Avg.

PWP3D (all sc.) (Prisacariu and Reid, 2012) 3.92 3.58 5.36 5.81 5.87 5.55 5.02

UDP (all sc.) (Brachmann et al., 2016) 5.25 5.97 6.10 2.34 8.49 6.79 5.82

ElasticFusion (all sc.) (Whelan et al., 2016) 1.69 2.70 1.57 1.86 1.90 1.53 1.88

Reg. G-N. (all sc.) (Tjaden et al., 2019) 11.99 10.15 11.90 13.22 8.86 11.76 11.31

DQPP (FreeMotion) (Majcher and Kwolek, 2021) 10.32 13.27 11.88 10.33 8.90 7.60 10.38

Hourglass, LM (FreeMotion) 7.89 7.87 11.18 6.59 8.14 6.48 8.02

Hourglass, PF (w/o LM) (FreeMotion) 11.44 12.90 12.04 10.97 8.78 10.14 11.04

Our method (FreeMotion) 12.10 13.08 13.09 12.04 8.89 10.68 11.58

Figure 2: ADD scores over time on sequences of images, obtained by our network and PnP, and our network, PF and LM-based

pose reﬁnement (plots best viewed in color).

Table 6: Running times [sec.].

PC Jetson

Hourglass 0.050 0.020

Siamese 0.030 0.007

PF 0.053 0.130

Other functions 0.017 0.023

Total 0.150 0.180

the 3D object pose. A keypoint-based pose hypoth-

esis is injected into the probability distribution that

is recursively updated in a Bayesian framework. We

demonstrated experimentally that keypoint locations

can be determined with sufﬁcient precision by a single

hourglass neural network for a set of objects of inter-

est. The observation model of Bayesian ﬁlter has been

simpliﬁed without a noticeable drop in pose tracking

accuracy. In contrast to recent approaches, the al-

gorithm delivers the probability distribution of object

poses instead of a single object pose guess. LM-based

pose reﬁnement permits achieving better results. The

algorithm runs in real-time both on a PC and a Jetson

AGX Xavier. In future work we are planning to in-

vestigate the performance of the algorithm in scenar-

ios with partial occlusions, including conﬁgurations

of the algorithm with and without object rendering,

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

580

taking into account the rendering capabilities of Jet-

son AGX Xavier.

ACKNOWLEDGEMENTS

This work was supported by Polish National

Science Center (NCN) under a research grant

2017/27/B/ST6/01743.

REFERENCES

Brachmann, E., Michel, F., Krull, A., Yang, M., Gumhold,

S., and Rother, C. (2016). Uncertainty-driven 6D pose

estimation of objects and scenes from a single RGB

image. In CVPR, pages 3364–3372.

Brachmann, E. and Rother, C. (2019). Neural-guided

RANSAC: Learning where to sample model hypothe-

ses. In IEEE/CVF Int. Conf. on Computer Vision

(ICCV), pages 4321–4330.

Chen, W., Jia, X., Chang, H. J., Duan, J., Shen, L., and

Leonardis, A. (2021). FS-Net: Fast shape-based net-

work for category-level 6D object pose estimation

with decoupled rotation mechanism. In IEEE Conf. on

Comp. Vision and Pattern Rec., CVPR, pages 1581–

1590. Comp. Vision Foundation / IEEE.

Egger, B., Sch

onborn, S., Schneider, A., Kortylewski, A.,

Morel-Forster, A., Blumer, C., and Vetter, T. (2018).

Occlusion-aware 3D morphable models and an illumi-

nation prior for face image analysis. Int. J. Comput.

Vision, 126(12):1269–1287.

Fan, Z., Zhu, Y., He, Y., Sun, Q., Liu, H., and He, J.

(2021). Deep learning on monocular object pose

detection and tracking: A comprehensive overview.

arXiv 2105.14291.

Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski,

G., Konolige, K., and Navab, N. (2013). Model based

training, detection and pose estimation of texture-less

3D objects in heavily cluttered scenes. In Computer

Vision – ACCV 2012, pages 548–562. Springer.

Hu, Y., Hugonot, J., Fua, P., and Salzmann, M. (2019).

Segmentation-driven 6D object pose estimation. In

IEEE Conf. on Computer Vision and Pattern Rec.,

CVPR, pages 3385–3394.

Kaskman, R., Zakharov, S., Shugurov, I., and Ilic, S.

(2019). HomebrewedDB: RGB-D dataset for 6D pose

estimation of 3D objects. In IEEE Int. Conf. on Com-

puter Vision Workshop (ICCVW), pages 2767–2776.

Kehl, W., Manhardt, F., Tombari, F., Ilic, S., and Navab, N.

(2017). SSD-6D: Making RGB-Based 3D Detection

and 6D Pose Estimation Great Again. In IEEE Int.

Conf. on Computer Vision, pages 1530–1538.

Kutschireiter, A., Surace, C., Sprekeler, H., and Pﬁster, J.-P.

(2017). Nonlinear Bayesian ﬁltering and learning: A

neuronal dynamics for perception. Scientiﬁc Reports,

7(1).

Majcher, M. and Kwolek, B. (2021). Deep quaternion pose

proposals for 6D object pose tracking. In Proceed-

ings of the IEEE/CVF Int. Conf. on Computer Vision

(ICCV) Workshops, pages 243–251.

Manhardt, F., Wang, G., Busam, B., Nickel, M., Meier, S.,

Minciullo, L., Ji, X., and Navab, N. (2020). CPS++:

Improving class-level 6D pose and shape estimation

from monocular images with self-supervised learning.

arXiv 2003.05848.

Newell, A., Yang, K., and Deng, J. (2016). Stacked hour-

glass networks for human pose estimation. In ECCV,

pages 483–499. Springer.

Pavlakos, G., Zhou, X., Chan, A., Derpanis, K. G., and

Daniilidis, K. (2017). 6-DoF object pose from seman-

tic keypoints. In IEEE Int. Conf. on Robotics and Au-

tomation (ICRA), pages 2011–2018.

Peng, S., Liu, Y., Huang, Q., Zhou, X., and Bao, H. (2019).

PVNet: Pixel-Wise Voting Network for 6DoF Pose

Estimation. In IEEE Conf. on Comp. Vision and Patt.

Rec., pages 4556–4565.

Prisacariu, V. A. and Reid, I. D. (2012). PWP3D: Real-

Time Segmentation and Tracking of 3D Objects. Int.

J. Comput. Vision, 98(3):335–354.

Rad, M. and Lepetit, V. (2017). BB8: A scalable, accurate,

robust to partial occlusion method for predicting the

3D poses of challenging objects without using depth.

In IEEE Int. Conf. on Comp. Vision, pages 3848–3856.

Tekin, B., Sinha, S. N., and Fua, P. (2018). Real-time

seamless single shot 6D object pose prediction. In

IEEE/CVF Conf. on Comp. Vision and Pattern Rec.

(CVPR), pages 292–301. IEEE Comp. Society.

Tjaden, H., Schwanecke, U., Sch

omer, E., and Cremers, D.

(2019). A region-based Gauss-Newton approach to

real-time monocular multiple object tracking. IEEE

Trans. on PAMI, 41(8):1797–1812.

Tremblay, J., To, T., Sundaralingam, B., Xiang, Y., Fox, D.,

and Birchﬁeld, S. (2018). Deep object pose estimation

for semantic robotic grasping of household objects. In

Proc. 2nd Conf. on Robot Learn., volume 87 of Proc.

of Machine Learning Research, pages 306–316.

Wang, Z., Li, W., Kao, Y., Zou, D., Wang, Q., Ahn, M., and

Hong, S. (2018). HCR-Net: A hybrid of classiﬁcation

and regression network for object pose estimation. IJ-

CAI’18, pages 1014–1020. AAAI Press.

Whelan, T., Salas-Moreno, R. F., Glocker, B., Davison,

A. J., and Leutenegger, S. (2016). ElasticFusion. Int.

J. Rob. Res., 35(14):1697–1716.

Wu, P., Lee, Y., Tseng, H., Ho, H., Yang, M., and Chien,

S. (2017). A benchmark dataset for 6DoF object pose

tracking. In IEEE Int. Symp. on Mixed and Aug. Real-

ity, pages 186–191.

Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).

PoseCNN: A Convolutional Neural Network for 6D

Object Pose Estimation in Cluttered Scenes. In

IEEE/RSJ Int. Conf. on Intel. Robots and Systems.

Zakharov, S., Shugurov, I., and Ilic, S. (2019). DPOD: 6D

pose object detector and reﬁner. In IEEE/CVF Int.

Conf. on Computer Vision (ICCV), pages 1941–1950.

IEEE Computer Society.

Pose Guided Feature Learning for 3D Object Tracking on RGB Videos

581