Discovery of Effective Spectrum for Classifying iPS Cells

Taken with CARS Microscope

Ryouichi Furukawa

, Yohei Hayashi

, Hideaki Kano

Junichi Matsumoto

, Shoichi Honda

and Kazuhiro Hotta

Meijo University, Nagoya-shi, Japan

RIKEN, Tsukuba-shi, Japan

Department of Chemistry, Faculty of Science, Kyushu University, Fukuoka-shi, Japan

KATAOKA CORPORATION, Kyoto-shi, Japan

Keywords: CARS Microscope, iPS Cells, Effective Spectrum, Automatic Discovery.

Abstract: There is a technique using the CARS (Coherent Anti-Stokes Raman Scattering) microscope to identify iPS

cells. CARS microscope can visualize the different molecular structures of iPS cells in each spectrum, so it is

possible to identify iPS cells without destroying them. However, the information on molecules in the spectrum

obtained by the CARS microscope is so diverse that it takes a great deal of time and effort to identify them.

We propose a method to automatically identify the spectrum, which is effective for iPS cell identification,

thereby reducing the time and effort required for identification using the CARS microscope. In this paper, we

propose a network that handles multi-resolution information in parallel to learn both image classification and

segmentation simultaneously. Moreover, the effective spectrum for classifying iPS cells are discovered by

using the network gradients and the F-measure for cell segmentation. By the experiments on four kinds of iPS

cells, we confirmed that the accuracy of the proposed method for classifying iPS cells achieved 99%.

Furthermore, the effective spectrum for each iPS cell could be automatically identified.

1 INTRODUCTION

iPS cells (Takahashi et al., 2006) are capable of

transforming into almost any types of cells, and

regenerative medicine research (Hideyuki et al.,

2019) using their characteristics is actively

conducted. To use iPS cells for regenerative medicine,

it is necessary to transform them into other cell types

(called “differentiation”). However, because of the

variability in the efficiency and direction of

differentiation of iPS cells into the other cells, when

iPS cells are differentiated from iPS cells, cell types

other than the intended ones or cells that have not

been fully differentiated may be mixed in.

Furthermore, when cells differentiated from iPS cells

are transplanted into an organism, it is known that

tumors can be formed if undifferentiated iPS cells are

mixed in.

There is a method using CARS (Coherent Anti-

Stokes Raman Scattering) microscope (Cheng et al.,

2004) to identify iPS cells and their differentiated

cells. CARS (Begley et al., 1974) is a phenomenon in

which two different spectra of light are irradiated on

a material, and light with a spectrum different from

both is generated. CARS microscope allows us to

visualize the molecular structure of the cell in each

spectrum. Therefore, CARS microscopy makes it

possible to identify iPS cells without destroying

(killing) cells. However, the information on

molecules in the spectrum obtained by the CARS

microscopy is so diverse that it takes a great deal of

time and effort to identify them. Therefore, it reduces

the time and effort required for identification using

the CARS microscope by automatically identifying

the spectra that are effective for iPS cell

identification. We perform automatic classification

using CNN from spectrum images obtained by the

CARS microscope. Furthermore, from the results of

the classification, we discover the effective spectrum

for classifying each iPS cell.

There is a method using Grad-CAM (Selvaraju et

al., 2017) to identify the spectrum that is effective for

identification. By using Grad-CAM, it is possible to

identify the effective spectrum as the one with a large

importance value in the feature maps (Takeshi et al.,

228

Furukawa, R., Hayashi, Y., Kano, H., Matsumoto, J., Honda, S. and Hotta, K.

Discovery of Effective Spectrum for Classifying iPS Cells Taken with CARS Microscope.

DOI: 10.5220/0010900200003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 4: BIOSIGNALS, pages 228-235

ISBN: 978-989-758-552-4; ISSN: 2184-4305

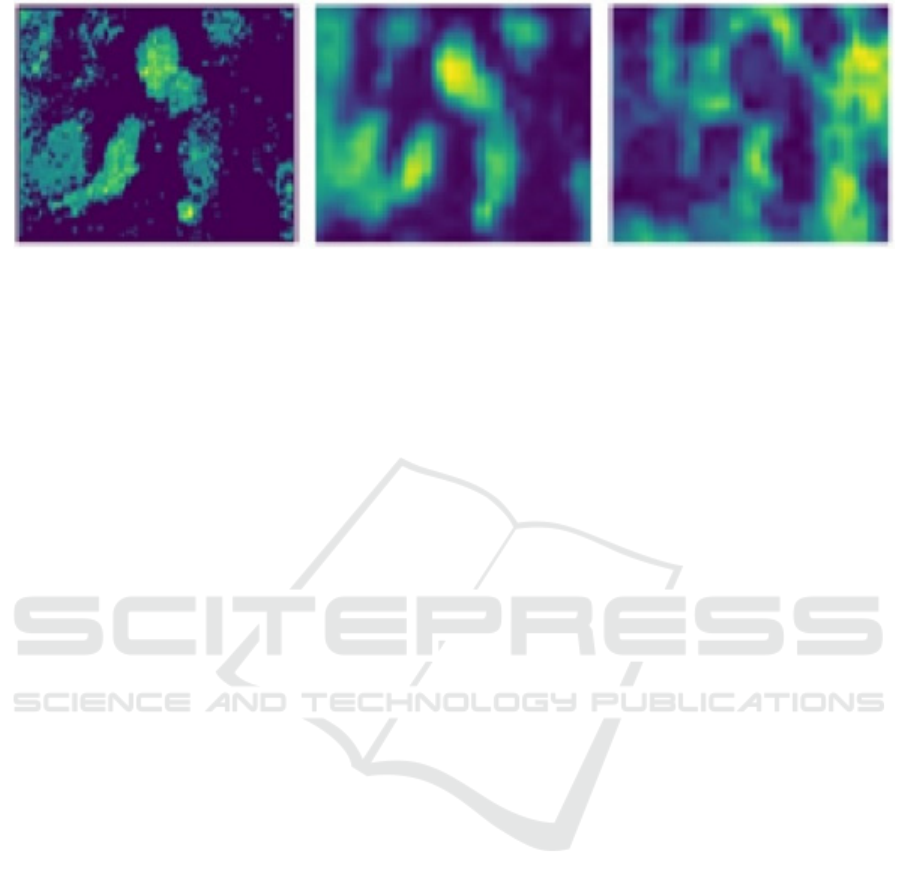
(a) (b) (c)

Figure 1: Example of visualization results for the portion of each spectrum that was identified as effective for classification.

(a) Visualization of the location of cells in the input image. (b) Example of a visualization result in which cells are captured

by the portion that is considered effective for classification. (c) Example of a visualization result in which cells are not

captured by the portion that is considered effective for identification.

2019). However, as shown in Figure 1, this method

judges an object to be effective even when the

effective spectrum for classification does not capture

the cells such as a culture medium.

We proposed the automatic detection method of

the effective spectrum shown in Figure 2 to solve the

shortcomings of the Grad-CAM based effective

spectrum identification. The multi-scale network

learns by handling feature maps with multiple

resolutions in parallel. The effective spectrum

calculation module uses the gradients like Grad-CAM

to calculate the important feature map and then

multiplies it by the F-measure for cell segmentation

obtained from the multi-scale network. By

multiplying F-measures, we can reduce the

importance of the spectrum that does not capture

cells.

In experiments, we classify four types of iPS cells

using images captured by the CARS microscope. We

also identify the effective spectrum from the

classification results. As a result, we were able to

successfully classify iPS cells with 99% accuracy and

discover class-specific effective spectrum.

This paper is organized as follows. Section 2

describes the related works. The details of the

proposed are presented in section 3. Section 4 shows

experimental results. Finally, conclusion and future

works are described in section 5.

2 RELATED WORKS

2.1 Identification of iPS Cells using

CARS Microscope

Researches on the application of iPS cells to

regenerative medicine are actively conducted. A

method for identifying high-quality iPS cells is to use

the CARS microscope (Michiel et al., 2007). CARS

microscope utilizes the phenomenon of CARS which

is the generation of light with a spectrum different

from that of either light when two lights with different

spectra are incident on a material. CARS microscope

allows us to visualize the molecular structure of iPS

cells in a non-destructive, non-invasive, non-staining,

and non-labelling manner. Thus, we can identify the

cells in their living state. However, the spectrum

obtained by the CARS microscope contains a variety

of molecular information, and it is very costly to

obtain all the molecular information. Therefore, we

reduce the cost by discovering the effective spectrum

for classifying cells. In this paper, we propose a

classification method of iPS cells using the CNN

which has a structure like the HR-net (Saad et al.,

2017), and an effective spectrum for classifying iPS

cells is discovered automatically.

2.2 Effective Spectrum Discovery using

Grad-CAM

There is a method for discovering the effective

spectrum for classification by using Grad-CAM

(Takeshi et al., 2019). This method identifies

effective spectrum by comparing the average of the

gradients of the convolutional layers computed in the

same way as Grad-CAM for each feature map.

However, in this method, the spectrum may be judged

to be effective even when the result is shown in Figure

1(c). In other words, when the gradient of a

convolutional layer is computed for the input cell

image and the gradient of non-cell pixels shows a

large value, this spectrum is erroneously judged to be

effective.

Discovery of Effective Spectrum for Classifying iPS Cells Taken with CARS Microscope

229

Figure 2: Overview of the proposed method. It consists of a multi-scale network and an effective spectrum calculation module,

and it identifies the effective spectrum for classifying the input cell by the magnitude of the final output value.

In this paper, we use segmentation (Long et al.,

2015) to solve this problem. Segmentation becomes

more accurate as the per-pixel accuracy improves.

Therefore, when the cell locations are recognized

more accurately, the F-measure becomes large. When

cell segmentation does not work well, the F-measure

becomes small. By multiplying the F- measure for

segmentation with the gradients of feature maps, it is

possible to suppress the importance values when the

gradients of non-cell pixels are large, and we discover

effective spectrum correctly. Therefore, by using the

result of cell segmentation, we can prevent the

example as shown in Figure 1(c).

3 PROPOSED METHOD

The proposed effective spectrum identification

network shown in Figure 2 consists of a multi-scale

network shown in Figure 3 and an effective spectrum

calculation module. Section 3.1 describes the multi-

scale network. Section 3.2 describes the effective

spectrum calculation module.

3.1 Multi-scale Network

The purpose of the multiscale network is to learn the

features while focusing on the location of cells. Multi-

scale networks have two characteristics. The first one

is the network structure used to learn by handling the

features of multiple resolutions in parallel. The

second one is the skip connection to compensate for

the information in the input spectrum.

The structure of the multiscale network is shown

in Figure 3. The reason for training multiple

resolutions in parallel (Sun et al., 2019) is to

efficiently learn the classification and segmentation at

the same time. Segmentation is the task that class

labels are assigned to each pixel in an image, and it is

possible to learn cell location information by

incorporating segmentation learning. Therefore, we

expected that the network would learn to use much

information of cells during classification because it

would understand the location of the cells better than

the case without segmentation learning. The

multiscale network used convolution with a kernel

size of 3 with stride 2 to reduce the resolution, and

bilinear interpolation to increase the resolution. In the

multiscale network, depth wise convolution was

applied to only the first layer, and normal convolution

was applied to the remaining layers. To perform

image classification, all feature maps of the input

image are aggregated into a feature map with a

reduced resolution of 1∕4. To perform segmentation,

all feature maps are aggregated into a feature map of

the same size as the input image. We also introduce

attention in the channel direction during training to

make it easier to identify the spectrum that is effective

for classification.

Multi-scale networks used convolution to extract

features. The convolution calculates the output of one

channel by multiplying all the input channels by their

weights. Since the information of all spectra is mixed,

it is impossible to identify effective spectrum from

the feature maps. To solve this problem, we used the

skip connection like ResNet (He et al., 2016), and

added the input features to the output feature maps of

the multi-scale network. By using the skip

connection, it is possible to compensate the original

spectrum for the output features and identify which

spectrum is effective. To match the size of the input

image and the output feature maps from the multi-

scale network, we used average pooling with filter

size 4 and stride 4.

3.2 Effective Spectrum Calculation

Module

The effective spectrum calculation module identifies

the effective spectrum for classification from the

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

230

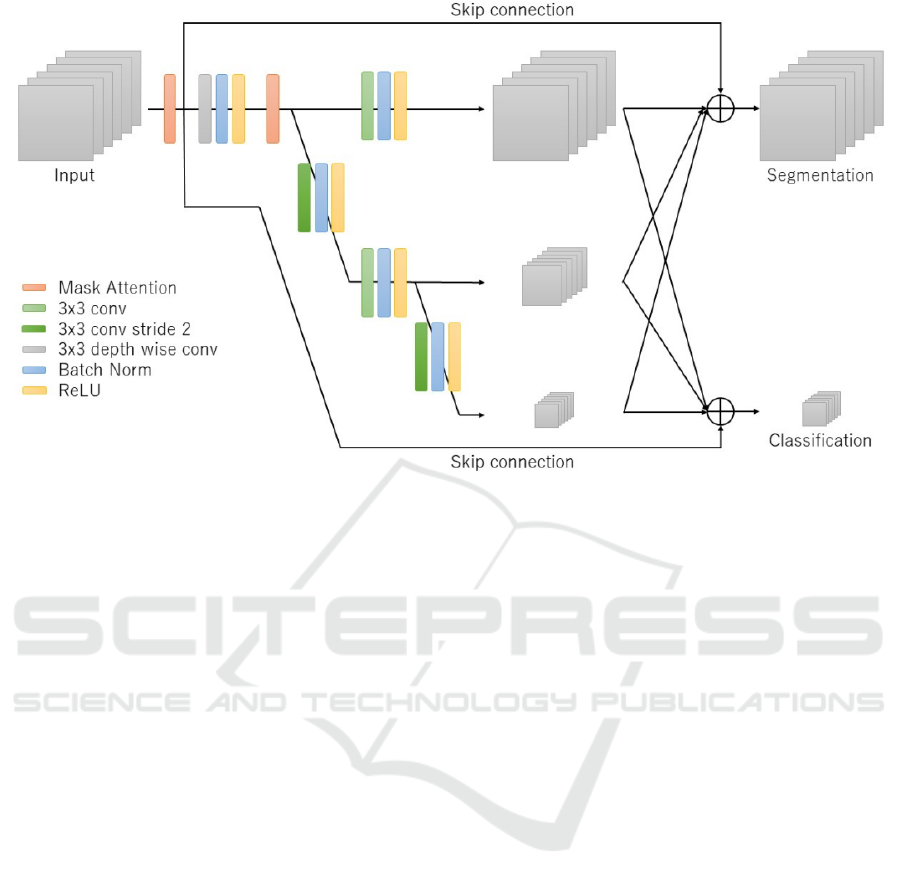
Figure 3: Overview of multi-scale networks.

feature maps in the multi-scale network. This module

can identify the effective spectrum while suppressing

the spectrum that does not capture cells as shown in

Figure 1(c). The module consists of the preparation of

keymaps and identification of the effective spectrum.

The keymaps indicate the importance of each

spectrum. The preparation of a keymap is performed

in the following three steps. First, we obtain the final

convolutional layer with the lowest resolution in the

multi-scale network. Second, we calculate the

gradient of the convolutional layer for the correct

class. Third, by multiplying the calculated gradient

value by the feature map, a keymap is created that

identifies the important areas for identification. By

multiplying the feature map by the gradient value, the

keymap has larger values for important pixels for

classification.

Identification of the effective spectrum is

performed in the following three steps. First, we

obtain the feature maps with the highest resolution in

the multi-scale network and evaluate whether the cell

locations are segmented well by using the F-measure

or not. Second, the keymaps for each spectrum are

multiplied by the F-measure for each spectrum. The

effective spectrum is identified by the magnitude of

the multiplied values. By multiplying the F-measure,

the spectrum that does not capture cells is suppressed,

and the shortcomings of the existing methods are

improved.

The creation of the segmentation labels required

to learn segmentation in section 3.1 and to obtain the

F- measure in section 3.2 is described in section 4.2.

4 EXPERIMENTS

In this section, we show the experimental results.

Section 4.1 describes the dataset and augmentation

used in this study. Section 4.2 gives the overview of

experiments. Section 4.3 presents the results of

evaluation experiments.

4.1 Dataset and Experimental Setup

The experiments were conducted using multi-

spectrum images of iPS cells captured by the CARS

microscope. The classes in the dataset consist of four

classes; ectoderm (ECT), mesoderm (MES),

endoderm (END), and undifferentiated (UND). The

total number of data for each class is 100; 25 for ECT,

25 for END, 25 for MES, and 25 for UND. These data

were originally from the same cell line and were

imaged after 1 week of incubation under different

culture conditions. The number of spectra visualized

per sample was 609, and the size of each image was

70x110 pixels. Due to the small number of images,

we use 5-hold cross-validation. We use 80 images for

training and 20 images for validation.

Data augmentation is proven to be an efficient

technique to improve the overall model performance.

In our experiments, data augmentation was used to

improve the performance of the multiscale network.

Discovery of Effective Spectrum for Classifying iPS Cells Taken with CARS Microscope

231

Table 1: The overview of experiments.

Processes

Ⅰ Create a simplified segmentation label

Ⅱ Learning Multiscale Networks

Ⅲ Back propagation of the final convolutional

layer using a trained multiscale network

Ⅳ Multiply the gradient by the convolutional layer

of the final layer

Ⅴ Calculating F-measure from high-resolution

feature maps of multiscale networks

Ⅵ Multiply the results of IV and V

Ⅶ Sum up the results for each class

In training, we performed random horizontal and

vertical flipping after random cropping of the image

to a size of 64 x 64 pixels. In validation, the image

size was changed to 72 x 112 by zero padding to make

the calculation easier.

We used the Pytorch library and trained the

network with Adam for 100 epochs. The base

learning rate (lr_base) was set to 0.01, and when there

were 50 epochs, the learning rate was set to 0.001 and

the network was trained. We use a batch size of 40

and a momentum of 0.9. The loss function is a

combination of Cross entropy loss during training for

discrimination and Dice loss during training for

segmentation.

4.2 Overview of Experiments

In this section, we describe the flow of experiments.

The overview is given in Table 1. A simplified label

for segmentation is created by summing all 609

spectra and then binarizing Otsu’s method (Otsu,

1979) because it is only necessary to distinguish cells

from the background. The network is trained in Table

1, II to create a model to identify iPS cells. All

operations below III in Table 1 are performed using

the trained model. Table 1 VII sums up the results of

the 5-fold cross-validation up to Table 1 VI. Cells that

are misclassified by the multiscale network is

excluded from the calculation.

4.3 Experimental Results

We conducted experiments on the dataset obtained by

the CARS microscope, and the classification results

of the four kinds of iPS cells are shown in Table 2.

We compared the accuracy of the network with and

without multiple resolutions. The network without

multiple resolutions is a standard CNN that classifies

the cells with only feature maps of low-resolution.

Table 2 demonstrated the effectiveness of usage of a

multi-scale network structure. This result suggests

Table 2: Comparison results. “Single” shows the result

without using multiple resolutions, and “Multi” shows the

result with multiple resolutions.

Acc

(

)

ECT END MES UND Mean

Sin

le 92 100 96 96 96

Multi 96 100 100 100 99

Table 3: Confusion matrix of the multiscale network.

Label

ECT END MES UND

ECT 24 0 0 0

END 1 25 0 0

MES 0 0 25 0

UND 0 0 0 25

that it is more effective to learn the feature maps while

retaining location information.

We compared the results of identifying effective

spectrum by the proposed method and

the conventional method using Grad-CAM. Figure 4

shows the importance of each class of iPS cells for the

proposed method and Figure 5 shows the importance

of each spectrum for the conventional method. Figure

4 demonstrated that the spectrum around 850𝑐𝑚



1200 𝑐𝑚



, and 1750 𝑐𝑚



for ectoderm (ECT),

1800𝑐𝑚



and later for mesoderm (MES), 1300𝑐𝑚



and 1500𝑐𝑚



for endoderm (END), and the first half

of the spectrum around 750𝑐𝑚



for undifferentiated

(UND) are effective for classification. When we

compare Figure 4 with Figure 5, the proposed method

makes it easier to identify the differences in the

effective spectrum of each cell.

Figure 6 showed the feature maps that correspond

to top five effective spectra discovered by the

proposed method and the conventional method

(Takeshi et al., 2019). As the result of the

conventional method, the feature maps that non-cells

have high value were ranked high. On the other hand,

in the case of the proposed method, only the feature

maps that captured cells were ranked high. This result

demonstrated the effectiveness of our method using

both the F-measure for segmentation and the

gradients of feature maps. However, the results in

Figure 4 showed that the ECT and END classes have

similar values when the importance of the spectrum

is not high. This may show that the features of ECT

and END classes are more similar than those of the

other two classes, and the ECT class is misclassified

as END class in Table 3.

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

232

(a)

(b)

(c)

(d)

Figure 4: The importance of each class of iPS cells by the proposed method. The result is the sum of all values from samples

in each class. The vertical axis of the figure shows the total importance value, and the horizontal axis shows the spectrum

(𝑐𝑚



). (a) Results from of cells in the ectoderm (b) Results of cells in the mesoderm (c) Results of cells in the endoderm (d)

Results of undifferentiated cells.

5 CONCLUSION

In this paper, we propose the multi-scale network for

classifying iPS cells from the CARS microscopy

images. Effective spectrum is identified by

multiplying the F-measure based on cell

segmentation and the importance based on gradients

of feature maps. By using the proposed method, we

were able to identify the effective spectrum for the

classification of four kinds of iPS cells. This result

means that it is possible to suggest the molecular

information that characterizes each cell type from the

imaging data of the CARS microscope without any

prior information or prejudice. In the future, we

would like to make it possible to obtain similar results

when there are multiple iPS cells in an image.

ACKNOWLEDGMENTS

This work was supported by the SAPOIN

“Development of non-staining and non-invasive cell

characterization technology”.

REFERENCES

Takahashi Kazutoshi, and Shinya Yamanaka. "Induction of

pluripotent stem cells from mouse embryonic and adult

fibroblast cultures by defined factors." cell 126.4,

pp.663-676, 2006

Hideyuki Okano and Shinya Yamanaka. “iPS cell

technologies: significance and applications to CNS

regeneration and disease.” Molecular brain, 7.1, pp.1–

12, 2014.

Ji-Xin Cheng and X Sunney Xie. “Coherent anti-stokes

raman scattering microscopy: instrumentation, theory,

and applications.” The Journal of Physical Chemistry

B, 108.3, pp.827–840, 2004.

Discovery of Effective Spectrum for Classifying iPS Cells Taken with CARS Microscope

233

(a)

(b)

(c)

(

)

Figure 5: The importance of each class of iPS cells by the conventional method. The result is the sum of all values from

samples in each class. The vertical axis of the figure shows the total importance value, and the horizontal axis shows the

spectrum (𝑐𝑚



). (a) Results from of cells in the ectoderm (b) Results of cells in the mesoderm (c) Results of cells in the

endoderm (d) Results of undifferentiated cells.

Figure 6: Visualization results of the top five important spectrum. The left column shows the input image, the top row shows

the results by conventional method, and the bottom row shows the results by the proposed method. From left to right images

shows the feature maps with the first to the fifth important spectrum.

Michiel Müler and Andreas Zumbusch. “Coherent anti-

stokes raman scattering microscopy.” ChemPhysChem,

8.15, pp.2156–2170, 2007.

Begley, R. F., A. B. Harvey, and Robert L. Byer. "Coherent

anti‐Stokes Raman spectroscopy." Applied Physics

Letters 25.7, pp.387-390, 1974.

Saad Albawi, Tareq Abed Mohammed, and Saad Al-Zawi.

“Understanding of a convolutional neural network.” In

2017 International Conference on Engineering and

Technology (ICET), pp.1–6, 2017.

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

234

Ramprasaath R. Selvaraju, Michael Cogswell, Abhishek

Das, Ramakrishna Vedantam, Devi Parikh. “Grad-cam:

Visual explanations from deep networks via gradient-

based localization.” In Proceedings of the IEEE

international conference on computer vision, pp. 618–

626, 2017.

Takeshi Uemori, Atsushi Ito, Yusuke Moriuchi, Alexander

Gatto, and Jun Murayama. “Skin-based identification

from multispectral image data using cnns.” In

Proceedings of the IEEE/CVF Conference on

Computer Vision and Pattern Recognition, pp.12349–

12358, 2019.

Sun, Ke., Xiao, Bin., Liu, Dong., and Wang, Jingdong.

“Deep highresolution representation learning for

human pose estimation.” In Proceedings of the IEEE

conference on Computer Vision and Pattern

Recognition, pp. 5693-5703, 2019.

He, Kaiming., Zhang, Xiangyu., Ren, Shaoqing., and Sun,

Jian. “Deep residual learning for image recognition.” In

Proceedings of the IEEE conference on computer vision

and pattern recognition, p. 770-778, 2016.

Long, Jonathan, Evan Shelhamer, and Trevor Darrell.

"Fully convolutional networks for semantic

segmentation." Proceedings of the IEEE conference on

computer vision and pattern recognition, pp. 3431-

3440, 2015.

Otsu, Nobuyuki. "A threshold selection method from gray-

level histograms." IEEE transactions on systems, man,

and cybernetics 9.1, pp.62-66, 1979.

Discovery of Effective Spectrum for Classifying iPS Cells Taken with CARS Microscope

235