Geometry Compression of Triangle Meshes using a Reference Shape

Eli

ska Mourycov

and Libor V

Department of Computer Science and Engineering, University of West Bohemia, Univerzitn

ı 8, Plze

n, Czech Republic

Keywords:

Compression, Triangle Mesh, Encoding, Geometry.

Abstract:

Triangle mesh compression is an established area, however, some of its special cases are yet to be investigated.

This paper deals with lossy geometry compression of manifold triangle meshes based on the EdgeBreaker al-

gorithm using a reference shape known to both the encoder and the decoder. It is assumed that the shape of

the reference object is similar to the shape of the mesh to be encoded. The predictions of vertices positions

are done extrinsically, i.e. outside the reference shape, and then orthogonally projected onto its surface. The

corrections are encoded by two integer numbers, denoting the layer order and an index of a hexagon in a hexag-

onal grid generated on the surface of the reference shape centered at the prediction point. The availability of

a reference mesh results in a smaller bitrate needed for comparable error when compared to a state of the art

static mesh compression algorithm using weighted parallelogram prediction.

1 INTRODUCTION

While triangle mesh compression is a mature ﬁeld

with numerous applications, there are still certain spe-

cial cases that remain unexplored. One particular

open question is how to efﬁciently exploit a shape ref-

erence that is available at both the encoder and the

decoder. This scenario occurs in practical applica-

tions, such as quality check scanning or compression

of time-varying meshes.

In quality check scanning, certain item is being

produced and 3D scanned at the end of a production

line in order to verify its quality. Apart from direct

analysis, the scans are commonly saved for further

processing/reference, which may be costly with high

volume production. At the same time, most of the

scans represent a very similar shape, and in most prac-

tical cases, even a perfect shape reference is available

in the form of a CAD model of the produced item.

A similar situation occurs when encoding a se-

quence of meshes representing an animation, i.e.

a continuous deformation of a certain shape. When

animations are created artiﬁcially, the frames usually

share connectivity (dynamic mesh), and such data can

be compressed very efﬁciently even when the anima-

tion structure (bone rig or similar) is unknown (Chen

et al., 2018). When scanning a real world dynamic

scene, on the other hand, a series of meshes with

https://orcid.org/0000-0001-9379-4097

https://orcid.org/0000-0002-0213-3769

varying connectivity (time-varying mesh) is often ob-

tained, making the need for efﬁcient storage more

acute, yet at the same time making the actual com-

pression much more difﬁcult. One way to deal with

the problem is to compress the frames sequentially,

using each previous frame (possibly warped in a cer-

tain way) as a reference for compression of each fol-

lowing frame.

The problem at hand is therefore as follows:

a coder and a decoder share a shape, represented as

a triangle mesh, denoted reference mesh. The task is

to transmit another shape, again represented by a tri-

angle mesh, from the encoder to the decoder. This

input mesh has a shape that is very similar to the

reference shape, however, it has a completely differ-

ent tessellation, and possibly even different topology

(genus). The objective is to encode the input mesh

using as few bits as possible, using the shared knowl-

edge of the actual shape that is being transmitted.

At ﬁrst sight, this may look like a low hanging

fruit: information that is available at a decoder can be

omitted from the transmission, providing an improved

compression performance. It may even seem that the

decoder already has all the information it needs, since

it has the shape available, however, additional infor-

mation is certainly needed, since the mesh represen-

tation captures not only the shape of the model, but

also its sampling, i.e. tessellation, since in our sce-

nario, we wish to preserve the connectivity of the in-

put mesh. How much of the bitrate commonly used

268

Mourycová, E. and Váša, L.

Geometry Compression of Triangle Meshes using a Reference Shape.

DOI: 10.5220/0010901100003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

268-277

ISBN: 978-989-758-555-5; ISSN: 2184-4321

for encoding a triangle mesh is spent on the actual

shape, and how much is spent on capturing the partic-

ular tessellation, is generally not known, and attempt-

ing to fruitfully exploit the shape reference in order

to reduce the data rate with respect to no-reference

encoder turns out to be a surprisingly difﬁcult task.

We present an algorithm based on traversing the

input mesh and predicting vertex positions one by

one. In order to make the prediction, we use the ref-

erence mesh. Our algorithm works with projections

of predicted and encoded vertices onto the surface of

the reference mesh. The difference between the pre-

diction and the actual position (also known as correc-

tion) is encoded intrinsically, restricting the possible

locations to the 2D reference surface and, most im-

portantly, using only two coordinates. Finally, rather

than using a rectangular grid in order to quantize the

coordinates, we use a hexagonal grid that has better

properties in terms of quantization error.

The rest of the paper is structured as follows:

Section 3 describes the overall process of encoding

a mesh, including requirements imposed on the input

shapes and steps taken to preprocess the data. Sec-

tion 4 then in detail describes three relatively indepen-

dent modules used for the assembly of the encoding

algorithm. Section 5 is devoted to the evaluation of

the performance of the proposed method and its com-

parison with an alternative static mesh encoder.

2 RELATED WORK

Compression of polygonal meshes, and of triangle

meshes in particular, is a ﬁeld that has been actively

studied for several decades. The problem can be fur-

ther split to compression of connectivity, which is al-

ways understood as lossless, and compression of ge-

ometry (vertex positions), where mostly lossy algo-

rithms are employed, sacriﬁcing reconstruction preci-

sion in order to achieve a more efﬁcient compression.

For connectivity compression, it is known that as-

suming that every possible triangulation is equally

probable, at least 3.245 bits per vertex (bpv) are

needed in the limit for genus 0 triangle meshes (Tutte,

1962). A guarantee of 4 bpv is provided by the Edge-

Breaker algorithm (Rossignac, 1999), which can be

further improved by employing a more efﬁcient en-

tropy coding. Further improvement is achieved by

valence based encoders (Alliez and Desbrun, 2001),

assuming that regular connectivities with vertex va-

lences close to 6 are more probable than others, reach-

ing data rates of 1-2 bpv for common datasets.

For geometry compression, the most common ap-

proach that complements the EdgeBreaker connectiv-

ity coder well is the parallelogram prediction (Touma

and Gotsman, 1998). Whenever a new vertex is en-

countered during the EdgeBreaker traversal, its po-

sition is predicted by forming a parallelogram from

a known neighbouring triangle. Next, rather than en-

coding the quantized coordinate, only a correction

vector which represents the difference between the ac-

tual and predicted position is stored reaching a lower

entropy and thus a lower bitrate.

This approach has been further improved by en-

coding the geometry in a separate pass, when the full

connectivity is known to both the encoder and the de-

coder. This allows adjusting the shape of the paral-

lelogram stencil according to the degrees of vertices

involved in the prediction (V

sa and Brunnett, 2013).

Other approaches to geometry encoding have been

proposed as well, building on concepts such as ex-

pressing the geometry in delta coordinates (Sorkine

et al., 2003), known as high-pass coding (HPC) or ex-

pressing the shape in the frequency domain (Valette

and Prost, 2004). These often lead to different char-

acter of introduced distortion, targeting at percep-

tual quality metrics (Corsini et al., 2013). Recently,

a modiﬁcation of the HPC has been proposed, which

allows achieving competitive results in terms of both

traditional error metrics, such as mean squared error

or Hausdorff distance, as well as perceptual metrics

sa and Dvo

ak, 2018).

Finally, a range of algorithms has been proposed

aiming at various particular desirable properties of

mesh transmission, such as the possibility of partial

decoding (Hoppe, 1996), encoding of mesh sequences

of shared connectivity (Chen et al., 2018) or joint en-

coding of meshes with color or texture information

(Caillaud et al., 2016). Our paper ﬁts into this last

category, focusing on a special case scenario when

a reference mesh is available.

The proposed compression procedure builds sub-

stantially on the concept of traversal based encod-

ing used by the EdgeBreaker algorithm (Rossignac,

1999). We give a short overview of the algorithm

in order to provide reference for the later exposition.

The EdgeBreaker algorithm starts with a single tri-

angle, which is selected by the encoder and assumed

at the decoder. Then the main loop follows, where in

each iteration, the processed part of the mesh (a single

triangle at the beginning, a larger subset of triangles

in later stages) is expanded by one triangle. The tri-

angle is attached to an implicitly selected border edge

of the processed part of the mesh, known as gate. It

therefore consists of two known vertices and a third,

possibly unknown tip vertex.

The data stream must indicate the status of the tip

vertex. If it is a new vertex, not yet known to the

Geometry Compression of Triangle Meshes using a Reference Shape

269

decoder, then a symbol “C” is emitted, possibly fol-

lowed by data identifying its 3D position. If the tip

vertex is already known to the decoder, then the data

stream must uniquely identify it. It is either directly

to the left on the border of the known portion of the

mesh (identiﬁed by the “L” symbol), or directly to the

right (“R” symbol), or possibly both (an ending trian-

gle ﬁlling a triangle sized ﬁnal hole, symbol “E”), or

none of the above, i.e. some other vertex somewhere

on the border of the already known part of the mesh

(symbol “S”). Rossignac has shown that by carefully

analyzing the following symbols in the data stream,

the particular position of the vertex in this situation

can be derived by the decoder without additional in-

formation. In summary, the connectivity is encoded

by a sequence of symbols from the CLERS alphabet,

one for each triangle.

3 ALGORITHM DESCRIPTION

This section describes the steps to encode (compress)

the input mesh. The algorithm works under the

assumption that both the encoder and the decoder

posses the same reference mesh, whose shape is sim-

ilar to that of the input mesh. However, the sampling

of the surfaces can be completely different.

3.1 Input Data

There are certain conditions that both the input and

the reference mesh must meet, in particular:

• both meshes must be manifold,

• all triangles in both meshes must be equally ori-

ented, i.e. all clockwise or all counterclockwise,

• the meshes cannot contain degenerate triangles,

i.e. triangles with zero area.

3.2 Preprocessing

Before the encoding algorithm is launched, two pre-

processing steps are done - a Bounding Volume Hier-

archy (BVH) tree for the reference mesh (as described

in section 4.2.4) is built, and the neighbors for each

triangle in both the input and the reference mesh are

found and stored.

The neighbors of each triangle are stored in a hash

table, where the keys are oriented edges, i.e. struc-

tures which keep the index of the start vertex and the

index of the end vertex. The hash table is ﬁlled by

iterating through all triangles of the mesh and adding

all three edges as keys with the same value - the cur-

rent triangle.

3.3 Encoding

To start encoding the mesh, the ﬁrst triangle of the

input mesh is projected onto the surface of the refer-

ence mesh (using orthogonal projection described in

section 4.2.4). The vertices of the projected triangle

are updated to match the projected positions.

The encoding algorithm then follows the steps of

the EdgeBreaker algorithm, traversing the connectiv-

ity of the input mesh. If the code “C” is encountered

during the EdgeBreaker algorithm, i.e. the next vertex

behind a prediction gate has not been conquered, then

the encoder does the following steps:

1. project the tip vertex from the input mesh onto the

reference mesh,

2. evaluate the prediction (see subsection 4.1 for de-

tails on how predictions are made),

3. construct the correction by generating a hexago-

nal grid on the reference surface and ﬁnding the

hexagon centre nearest to the projected tip,

4. replace the tip vertex position in the input mesh

by the nearest hexagon centre (in order to keep

the encoder in sync with the decoder for following

predictions),

5. save the correction (i.e. identiﬁcation of the near-

est hexagon) into the data stream - two values are

needed, the layer order and the index in the layer,

as will be described in more detail later.

The connectivity of the encoded mesh stays the

same as in the input mesh.

There are two sources of precision loss in the pro-

cedure: ﬁrst, the difference between the actual vertex

position and its projection onto the reference mesh is

neglected and not rectiﬁed in the decoder. This can

be ﬁxed using an additional correction layer, however,

we choose not to include such correction in order to

evaluate the algorithm assuming that this error is neg-

ligible. The other source of distortion is the quanti-

zation by the hexagon grid on the reference surface.

This error can be controlled by adjusting the hexagon

edge length.

4 MODULES

This section describes in detail parts of the algorithm

which are then used for the mesh compression.

4.1 Prediction of the Vertex Position

The predictions are made using an extrinsic parallel-

ogram prediction (see Fig. 1).

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

270

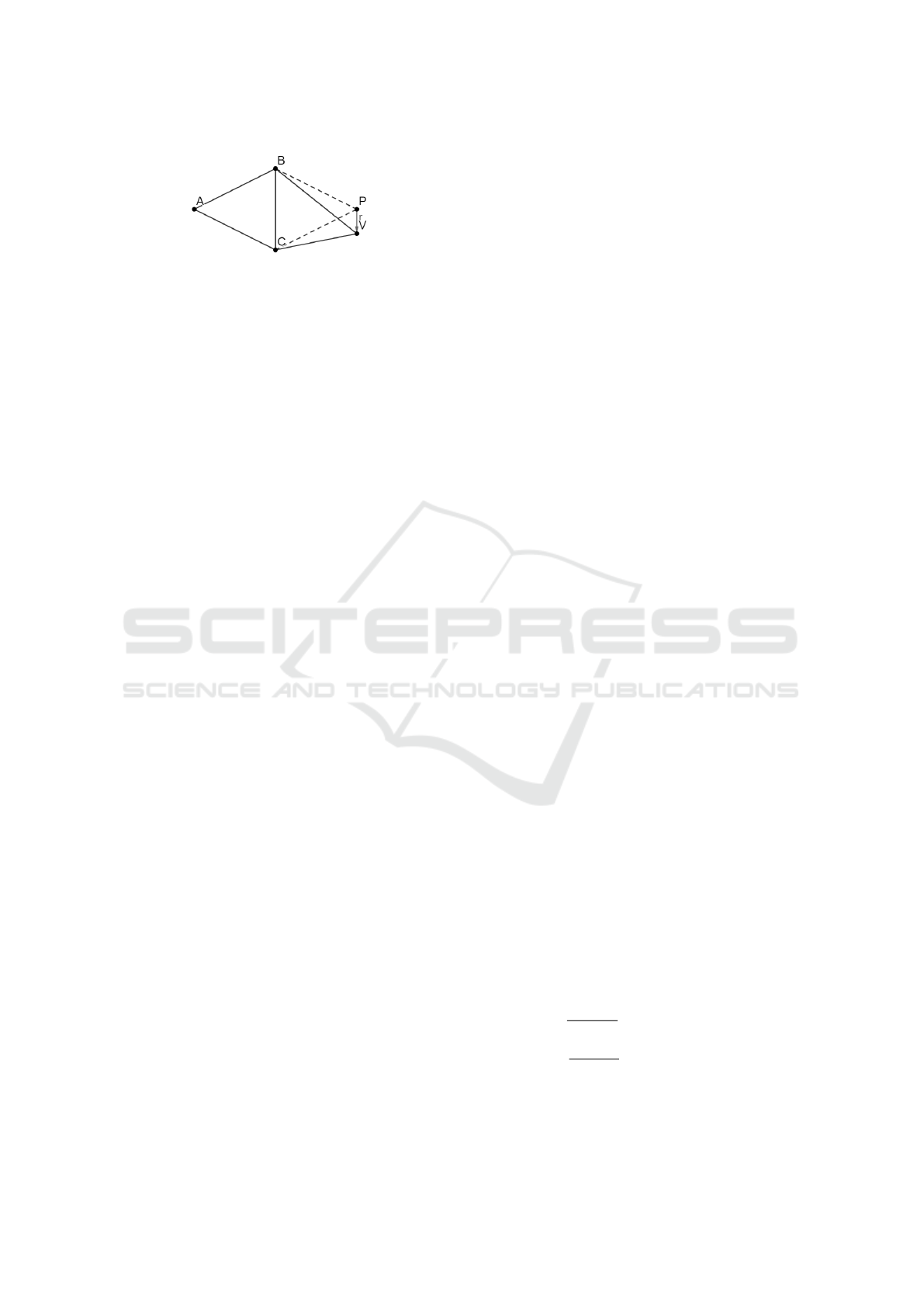
Figure 1: Paralellogram prediction.

In Fig. 1, point A is a vertex known to both en-

coder and decoder, points B and C form the current

gate in the EdgeBreaker procedure, point P is the pre-

dicted point, point V is the actual (projected in step 1.)

position of the point and vector~r is the correction vec-

tor (encoded by the hexagon layer and index).

Point P is acquired as P = B +C −A. Such point

does not always lie on the surface of the reference

mesh, therefore it is projected onto it - hence the term

extrinsic prediction.

4.2 Orthogonal Projection of Points

onto the Surface

Another required component of the solution is

a means of orthogonally projecting points onto the

surface of a mesh. This is used for projecting vertices

of the input mesh onto the surface of the reference

mesh and acquiring projections of the predictions of

the vertices of the input mesh.

To avoid a brute force approach, i.e. iterating through

all of the triangles of the reference mesh and check-

ing which is the closest one to the given query point,

a BVH tree is constructed.

4.2.1 Building a BVH Tree

The tree is built as a binary tree. Each node of the

tree holds a list of triangles it contains, references to

its parent, children and their bounding box. The con-

struction steps are:

1. Create a queue of tree nodes and enqueue the root

node.

• The root node contains all triangles in the mesh,

its bounding box is the same as that of the

whole mesh and it has no parent.

2. If the queue is empty, then break.

3. Dequeue a node into currNode

4. If currNode is not a leaf node, create its two chil-

dren.

• See subsection 4.2.2 for details.

5. Enqueue both children and go to 2.

4.2.2 Creating Children of a Tree Node

Children of a node are created by splitting the par-

ent’s bounding box along its longest side. The par-

ent’s list of triangles is sorted by the x,y or z posi-

tion of the triangles’ centroids (depending on which

side of the bounding box was the longest). The ﬁrst

half of the sorted triangles is assigned to the ﬁrst child

and the second half to the second child. New (sub-

)bounding boxes are calculated for both children. If

the children’s triangle count is less than 3, then they

are marked as leaf nodes.

4.2.3 Using the BVH Tree for Orthogonal

Projection

Using the tree to locate the nearest triangle to a given

query point is done as follows:

1. Start in the root node of the tree

2. Go to the child node whose bounding box centre

is closer to the query point

3. When a leaf node is reached, distances to its trian-

gles are evaluated and the minimum saved as d

• See section 4.2.4 for details on projecting

a point into a triangle

4. Traverse upwards from the leaf node and consider

whether a different (unvisited) branch needs to be

visited

• a branch does not need to be visited if the query

point lies farther than d from its bounding box

5. If a leaf node is reached again, d is updated if

a closer triangle is found

6. Continue until reaching the root node

7. Return the closest found triangle (with distance d

from the query point)

4.2.4 Projection of a Point into a Triangle

Projecting the query point into a triangle is done by

ﬁrst projecting the point onto the plane of the triangle:

~u = V

−V

,~v = V

−V

~n =~u ×~v

~w = Q −V

γ =

~u ×~w ·~n

~n ·~n

β =

~w ×~v ·~n

~n ·~n

α = 1 −γ −β,

Geometry Compression of Triangle Meshes using a Reference Shape

271

where V

, V

and V

are the vertices of the triangle

and Q is the query point to be projected. γ,β,α are

the barycentric coordinates of the projected point with

respect to the given triangle. If

β < 0 ∨ γ < 0 ∨β + γ > 1, (1)

then the projected point is outside of the triangle. In

this case we project the point onto the edges:

~ev = V

−V

(i+1)%3

~vv = P −V

C = P −V

~ev ·~vv

~ev ·~ev

~ev,

where V

is one of the vertices of the triangle, P is the

point projected onto the plane given by the triangle

and C is the point projected onto a line given by one

of the edges.

If C lies between the two vertices of the triangle

which deﬁned the line, then the distance between P

and C is computed and saved as d. d is updated if

a smaller distance is found.

After all edges are checked, distances to the trian-

gles vertices are computed individually and d is up-

dated if necessary. A point on the triangle with found

minimal distance d is ﬁnally returned.

4.3 Straight Walk on the Surface

The last of the required components of the algorithm

is a method for moving along a geodesic line on the

surface of a mesh from a starting point in a given di-

rection, until a desired distance is reached. This part

of the solution is used for the hexagonal grid genera-

tion on the surface of the reference mesh.

The starting point of the walk is described in barycen-

tric coordinates. For storing the barycentric coordi-

nates, we only need two values. The conversion from

barycentric to cartesian coordinates is done using the

following formulas:

cPt

= V

+ bPt

−V

) + bPt

−V

)

cPt

= V

+ bPt

−V

) + bPt

−V

)

cPt

= V

+ bPt

−V

) + bPt

−V

where cPt is a 3D point in cartesian coordinates, bPt

is the barycentric point to convert to cartesian coordi-

nates and V

are the vertices of the triangle in

which the barycentric point lies.

4.3.1 Determining the Walking Direction

This algorithm works with a direction in the coor-

dinate system of the triangle in which it is currently

operating (analogically to barycentric coordinates of

a point).

For conversion from triangle to cartesian direction

coordinates, following formulas are used:

cDir

= tDir

−V

) +tDir

−V

)

cDir

= tDir

−V

) +tDir

−V

)

cDir

= tDir

−V

) +tDir

−V

where cDir is a direction (vector) in cartesian coor-

dinates, tDir is the direction in the triangle coordi-

nate system to convert to cartesian coordinates and

are the vertices of the triangle in which the

direction is speciﬁed.

4.3.2 Finding the Intersected Edge

Next, an edge which will be intersected by walking

straight to the border of the current triangle is found.

This is done by calculating signed distances to all the

edges using the triangle coordinate system direction.

The distances are computed as follows:

(

−bPt

tDir

, if tDir

6= 0

−1, otherwise

(

1−bPt

−bPt

tDir

+tDir

, if tDir

+tDir

6= 0

−1, otherwise

(

−bPt

tDir

, if tDir

6= 0

−1, otherwise,

where d

is the signed distance to the edge between

vertices V

and V

, d

is the signed distance to the

edge between vertices V

and V

and d

is the signed

distance to the edge between vertices V

and V

The smallest positive distance is found and the

edge of this distance is identiﬁed as the edge to be

intersected. If no edge was found, we check whether

a vertex was hit by walking.

A barycentric point lies on a vertex of a triangle if

bPt

= 0 ∧ bPt

= 0 ∨

bPt

= 1 ∧ bPt

= 0 ∨

bPt

= 0 ∧ bPt

= 1

Next, we move towards the found edge or vertex. We

check if the traveled distance is greater or equal to the

desired distance. If it is, we calculate how much far-

ther we have walked compared to the desired distance

(because we end each iteration on an edge or vertex)

and we move back by the calculated difference vector

to the result point.

Otherwise, if not enough distance was traveled,

we rotate the walking direction (vector) over the in-

tersected edge or vertex.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

272

4.3.3 Rotating the Vector

Rotating the walking direction when an edge to ro-

tate over was found is done as follows: The vector

is rotated over the edge using the Rodrigues’ rotation

formula in a form allowing rotating a vector about an

axis by a given angle (Liang, 2018).

rot

=~vcos(θ) + (~n ×~v)sin(θ) +~n(~n ·~v)(1 −cos(θ)),

where~v is a vector in R

, ~n is a unit vector describing

an axis of rotation about which ~v rotates by an angle

θ and ~v

rot

is the rotated vector~v.

We select~n as the cross product of the current and

the neighbouring triangles (the one that shares the in-

tersected edge with the current triangle) normals. We

don’t calculate the angle θ directly, we obtain the sine

of the desired rotation angle as the length of~n (before

it is normalized) and the cosine of the angle as the dot

product of the current and the neighbouring triangle’s

normals.

Figure 2: Illustration of angle computation after vertex hit.

Fig. 2 illustrates the calculation of the angle to go

round a vertex to continue the walk after a vertex was

hit. We set:

β =

∑

i=0

,γ =

, (2)

where n is the number of triangles incident with the

hit vertex. In general β 6= 2π.

The steps of the algorithm are:

1. Calculate γ =

∑

i=0

2. Calculate δ

3. Go counterclockwise through the fan of triangles

incident with the hit vertex until kth triangle such

that δ

∑

i=1

< γ < δ

∑

k+1

i=1

4. Calculate δ

= γ −δ

−

∑

i=1

5. Continue walking from the hit vertex to (k + 1)th

triangle at angle δ

After the rotation, we switch to the new triangle

and continue with the next iteration.

4.3.4 Summary

To summarize, the straight walk algorithm consists of

the following steps:

1. Get the initial direction in which to walk

2. Find the edge which will be intersected by the

walk

3. Check if a vertex was hit

4. Check if desired distance was traveled

• If (more than) enough distance traveled, back-

track and return result point. End.

5. Rotate the walk direction (vector) over the inter-

sected edge or vertex

6. Switch to the next triangle

7. Go to 2.

4.4 Hexagonal Grid Generation on the

Surface

Hexagonal grid is used for encoding the correction

vector as two integer numbers - layer index and an

index of a given hexagon within the speciﬁed layer.

When a prediction is made, this part of the algorithm

generates a hexagonal grid on the surface of the ref-

erence mesh (using the walking module described in

section 4.3) from the prediction point and ﬁnds the

hexagon with centre closest to the projected point.

Note that rather than generating the actual

hexagons, the algorithm only generates their cen-

tres by walking a certain distance in a certain direc-

tion from the prediction point. Layer index 0 is re-

served for the hexagon centered at the prediction. The

hexagons in each layer are indexed clockwise.

For determining the distance to travel to a given

hexagon centre, cube coordinates are used (see

Fig. 3). Cube coordinates assign a virtual 3D point to

the centre of each hexagon. This 3D point can be un-

derstood as a vector going from point [0,0, 0] (i.e. the

hexagon in layer 0) to said point. This vector is then

multiplied by the user speciﬁed distance between two

centres of two neighbouring hexagons.

The direction in which the centre of the ﬁrst

hexagon of layer 1 lies is selected as ~v = V

−V

where V

is the ﬁrst vertex of the triangle in which

the grid generation starts and V

is the second vertex

of said triangle.

The user must specify the distance between two

centres of two neighbouring hexagons hexSize. From

hexSize we can calculate the distance between the

centre of a hex and its vertex and mark it as

Geometry Compression of Triangle Meshes using a Reference Shape

273

(a) Cube (b) Cube coordinates

for hexagonal grid

Figure 3: Cube coordinates for hexagonal grid.

centPeakDist:

triHeight =

(hexSize)

−(

hexSize

)

centPeakDist = (

2 ·triHeight

) ·

√

The user also speciﬁes the maximum number of lay-

ers to be generated (maxLayers).

The used approach for determining the closest

hexagon to the end point works as follows:

1. Get the default direction vector as~v = V

−V

2. Calculate centPeakDist

3. Calculate distance from the starting point to the

end point and save as d, set i = 1

4. Generate cube coordinates for hexagons in layer i

5. Generate hexagons in layer i. Use the cube coor-

dinates to get the distance of each hexagon from

the starting point (centre of the central hexagon)

• For each hexagon in the current layer, check if

its centre is closer to the end point than d, if it

is, update d

• If d < centPeakDist, return this hexagon as the

closest one. End.

6. Increment the angle of direction by 60/i

7. If i > maxLayers, return hexagon of distance d.

End.

8. Increment i and go to 4.

5 EVALUATION

The experiments to verify the functionality of the

algorithm were carried out on ﬁve different data

sets (meshes), each with ﬁve different hexagon sizes

and three different reference meshes. The results

were compared to the performance of a reference

implementation of the EdgeBreaker algorithm with

weighted parallelogram prediction (V

sa and Brun-

nett, 2013).

See the input meshes in section 5.1. The dif-

ferent types of reference meshes will be presented

in the following sections. Five different hexagon

sizes were selected as hexSizeX = length/X , where

X ∈ {1,1.5,2,2.5,3} and length is the length of

the ﬁrst edge of the ﬁrst triangle of the input mesh

and hexSizeX is the distance between two adjacent

hexagons’ centres.

5.1 Input Meshes

Fig. 4 shows the input meshes (meshes to be encoded)

which were used for the experiments.

(a) Mesh 1:

Lion

(b) Mesh 2:

Person

Homer

(d) Mesh 4:

Bunny

(e) Mesh 5:

Samba

Figure 4: Input meshes.

Note: This section contains charts showing the dis-

tribution of layer numbers and their occurrences. The

layers (denoted on the x axis) are sorted by their num-

ber in ascending order. The maximum layers allowed

to be generated for these experiments was 500. Only

those layers which appeared at least once are visible

in the chart.

For every encoded mesh, MSE was computed as

well as bits per vertex (bpv) of the hexagon layers

and index lists using arithmetic coding, see subsec-

tion 5.2. Experiments on the input meshes were per-

formed with unsuitable, good and very good reference

meshes.

By unsuitable reference, we mean such a mesh

whose surface is not very similar to the surface of the

input mesh. These reference meshes were acquired by

running ten iterations of HC Laplacian Smoothing on

the input meshes using the MeshLab software. Fig. 5

shows a typical result achieved by encoding the Lion

mesh using an unsuitable reference mesh.

Good reference meshes were acquired by running

two iterations of HC Laplacian Smoothing on the in-

put meshes using the MeshLab software. Fig. 6 shows

a typical results achieved by encoding the Person

mesh using a good reference mesh.

Very good reference meshes were acquired by

running one iteration of Isotropic Explicit Remesh-

ing on the input meshes using the MeshLab software.

Fig. 7 shows a typical results achieved by encoding

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

274

(a) Reference mesh (b) Decoded mesh

Figure 5: Lion mesh encoded using an unsuitable reference

mesh and hexSize2.

the Homer mesh using a very good reference mesh.

5.2 Mean Squared Error and BPV Data

This subsection contains information about the calcu-

lated MSE and bpv for each mesh. The data is shown

in Figures 8, 9, 10, 11 and 12. The results were

compared with the performance of the EdgeBreaker

algorithm with weighted parallelogram prediction.

The shown BPV is needed for encoding only the

geometry of the objects, the bitrate needed for en-

coding the connectivity is not taken into account, as

it is the same in both cases. The data shows that

our method is able to outperform the state of the art

algorithm, especially at very low bitrates, provided

that a good or very good reference mesh is available.

At higher bitrates, the proposed algorithm results in

a higher distortion, likely caused by projection on the

reference surface.

Although one could expect a more substantial im-

provement of coding efﬁciency, arguing that the shape

is actually known at the decoder, we believe that the

results in fact match a reasonable expectation. In-

tuitively, when a shape is fully unknown, there are

three degrees of freedom associated with each vertex.

When the shape is known and it is only the tessella-

tion that makes up the transmitted information, there

are still two degrees of freedom associated with each

vertex. If all degrees of freedom had the same statis-

tical properties, one could expect to save at most one

third of the data rate when a perfect shape reference

is available at the decoder.

(a) Reference

mesh

(b) Decoded

mesh

Figure 6: Person mesh encoded using a good reference

mesh and hexSize2.

(a) Reference

mesh

(b) Decoded

mesh

Figure 7: Homer mesh encoded using a very good reference

mesh and hexSize2.

Geometry Compression of Triangle Meshes using a Reference Shape

275

In practice, naturally, this assumption does not

hold. The tangential degrees of freedom may have

a different distribution than the original 3D coordi-

nates. On an abstract level, the key property is the ra-

tio of information entropy held by the tessellation (de-

pending on tessellation regularity in particular) and

the information entropy held by the shape itself (re-

lated mainly to the sampling density). It is for these

reasons that the practical results vary, as conﬁrmed by

the presented experiments. Since the algorithm pro-

vides a performance improvement even when the ref-

erence mesh does not fully match the encoded shape,

we conclude that it works correctly.

BPV

MSE

0.001

0.005

0.01

0.05

0.1

4.0 4.5 5.0 5.5 6.0

Edgebreaker

Unsuitable

Good

Very Good

Figure 8: Performance comparison on the Lion mesh.

BPV

MSE

0.000001

0.000005

0.00001

0.00005

0.0001

0.0005

3.5 4.0 4.5 5.0 5.5 6.0

Edgebreaker

Unsuitable

Good

Very Good

Figure 9: Performance comparison on the Person mesh.

BPV

MSE

0.0001

0.001

0.01

0.1

4 6 8 10

Edgebreaker

Unsuitable

Good

Very Good

Figure 10: Performance comparison on the Homer mesh.

BPV

MSE

1.0E-07

1.0E-06

1.0E-05

1.0E-04

3.5 4.0 4.5 5.0

Edgebreaker

Unsuitable

Good

Very Good

Figure 11: Performance comparison on the Bunny mesh.

BPV

MSE

0.001

0.005

0.01

0.05

4 5 6 7 8

Edgebreaker

Unsuitable

Good

Very Good

Figure 12: Performance comparison on the Samba mesh.

6 CONCLUSIONS

We have presented a compression algorithm for tri-

angle meshes that uses a reference mesh of similar

shape to reduce the required data rate. Although the

reference shape undoubtedly provides quite a lot of

information about the input mesh, exploiting it turns

out to be a non-trivial task, since the particular choice

of sampling of the shape represents a major portion

of the data needed for deﬁning a triangle mesh. The

results, however, demonstrate that our algorithm suc-

ceeds at this task using a novel combination of intrin-

sic encoding and hexagonal grid quantization.

In the current state, the algorithm is only practi-

cal for ofﬂine encoding, since the encoding is sub-

stantially slower than the decoding, because of the

exhaustive search for closest hexagon centre. This

does not eliminate all practical scenarios, because of-

ten meshes are indeed encoded ofﬂine and stored for

later processing, and the limiting factors are transmis-

sion time (which is improved due to better compres-

sion efﬁciency), and decoding time, which is much

faster than the encoding.

In the future, we would like to investigate a more

efﬁcient means of ﬁnding the nearest hexagon centre.

We have already performed experiments with a vari-

ant of walking algorithm with promising results, more

tests are, however, still needed.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

276

Also, we would like to explore possibilities of bet-

ter mapping of local quantization areas to the curved

surface of the reference mesh. It is well known that

hyperbolic vertices, i.e. vertices with sum of inci-

dent angles larger than 2π, compromise the bijectivity

of the exponential map, creating a certain ”shadow”

which cannot be reached by walking along a straight

line. Overcoming this problem could lead to a further

reduction of the data rate.

Finally, in the future we would like to perform

experiments with an additional correction layer rec-

tifying the projection error and making it possible to

reach an arbitrary coding precision. We believe that

this way we could use our approach to obtain a data

rate advantage that propagates even to higher data

rates/lower reconstruction errors, since even the com-

peting algorithms are only able to predict the vertex

positions up to a certain precision, and additional pre-

cision is encoded at the cost/entropy of a fully random

data source.

ACKNOWLEDGEMENTS

This work was supported by the project 20-02154S

of the Czech Science Foundation. Eli

ska Mourycov

was partially supported by the University speciﬁc re-

search project SGS-2019-016 Synthesis and Analysis

of Geometric and Computing Models. The authors

thank Diego Gadler from AXYZ Design, S.R.L. for

providing the test data.

REFERENCES

Alliez, P. and Desbrun, M. (2001). Valence-Driven Connec-

tivity Encoding for 3D Meshes. Computer Graphics

Forum.

Caillaud, F., Vidal, V., Dupont, F., and Lavou

e, G. (2016).

Progressive compression of arbitrary textured meshes.

Computer Graphics Forum, 35(7):475–484.

Chen, C., Xia, Q., Li, S., Qin, H., and Hao, A. (2018). High-

ﬁdelity compression of dynamic meshes with ﬁne

details using piece-wise manifold harmonic bases.

In Proceedings of Computer Graphics International

2018, CGI 2018, page 23–32, New York, NY, USA.

Association for Computing Machinery.

Corsini, M., Larabi, M. C., Lavou

e, G., Pet

ık, O., V

sa, L.,

and Wang, K. (2013). Perceptual Metrics for Static

and Dynamic Triangle Meshes. Computer Graphics

Forum.

Hoppe, H. (1996). Progressive meshes. In Proceedings

of the 23rd Annual Conference on Computer Graph-

ics and Interactive Techniques, SIGGRAPH ’96, page

99–108, New York, NY, USA. Association for Com-

puting Machinery.

Liang, K. K. (2018). Efﬁcient conversion from rotating ma-

trix to rotation axis and angle by extending rodrigues’

formula.

Rossignac, J. (1999). Edgebreaker: Connectivity compres-

sion for triangle meshes. IEEE Transactions on Visu-

alization and Computer Graphics, 5(1):47–61.

Sorkine, O., Cohen-Or, D., and Toldeo, S. (2003). High-

pass quantization for mesh encoding. In Proc. of Euro-

graphics Symposium on Geometry Processing, pages

42–51, Aachen, Germany. Eurographics Association.

Touma, C. and Gotsman, C. (1998). Triangle mesh com-

pression. In Graphics Interface, pages 26–34.

Tutte, W. T. (1962). A census of planar triangulations.

Canadian Journal of Mathematics, 14:21–38.

sa, L. and Brunnett, G. (2013). Exploiting connectiv-

ity to improve the tangential part of geometry predic-

tion. IEEE Transactions on Visualization and Com-

puter Graphics, 19:1467–1475.

sa, L. and Dvo

ak, J. (2018). Error Propagation Control

in Laplacian Mesh Compression. Computer Graphics

Forum.

Valette, S. and Prost, R. (2004). Wavelet-based progressive

compression scheme for triangle meshes: Wavemesh.

IEEE Trans. Vis. Comput. Graph., 10(2):123–129.

Geometry Compression of Triangle Meshes using a Reference Shape

277