
Vehicle Pair Activity Classification using QTC and Long Short Term
Memory Neural Network
Rahulan Radhakrishnan
a
and Alaa Alzoubi
b
School of Computing, The University of Buckingham, Buckingham, U.K.
Keywords:
Vehicle Activity Classification, Qualitative Trajectory Calculus, Long-Short Term Memory Neural Network,
Automatic LSTM Architecture Design, Bayesian Optimisation.
Abstract:
The automated recognition of vehicle interaction is crucial for self-driving, collision avoidance and secu-
rity surveillance applications. In this paper, we present a novel Long-Short Term Memory Neural Network
(LSTM) based method for vehicle trajectory classification. We use Qualitative Trajectory Calculus (QTC) to
represent the relative motion between a pair of vehicles. The spatio-temporal features of the interacting vehi-
cles are captured as a sequence of QTC states and then encoded using one hot vector representation. Then,
we develop an LSTM network to classify QTC trajectories that represent vehicle pairwise activities. Most of
the high performing LSTM models are manually designed and require expertise in hyperparameter configu-
ration. We adapt Bayesian Optimisation method to find an optimal LSTM architecture for classifying QTC
trajectories of vehicle interaction. We evaluated our method on three different datasets comprising 7257 tra-
jectories of 9 unique vehicle activities in different traffic scenarios. We demonstrate that our proposed method
outperforms the state-of-the-art techniques. Further, we evaluated our approach with a combined dataset of
the three datasets and achieved an error rate of no more than 1.79%. Though, our work mainly focuses on
vehicle trajectories, the proposed method is generic and can be used on pairwise analysis of other interacting
objects.
1 INTRODUCTION
Analysing the interaction between vehicles is imper-
ative in safety critical tasks such as autonomous ve-
hicle driving. Dangerous road events such as vehi-
cle overtaking and collisions can be avoided if the
behaviours of the surrounding vehicles are captured
accurately. Vehicle activity recognition task aims
to classify the actions of one or more vehicles by
analysing their temporal sequence of observations.
Potential collisions can be avoided or minimised by
recognising the behaviour that a vehicle is in (or about
to enter) beforehand (Ohn-Bar and Trivedi, 2016). A
vehicle can have complex motion behaviours either
on its own (single activity) or with another vehicle
(pair or group activity) (Ni et al., 2009) or with sta-
tionary obstacles (e.g. stalled vehicles). In the context
of activity classification task, two key approaches for
trajectory representation have been presented: quan-
titative and qualitative methods. Numerous studies
have been conducted using quantitative method where
a
https://orcid.org/0000-0002-4113-3710
b
https://orcid.org/0000-0003-1167-170X
real values of the features are directly used to rep-
resent the trajectories (Khosroshahi et al., 2016; Lin
et al., 2013; Deo et al., 2018). On the other hand,
qualitative methods have shown high performance for
activity classification applications such as vehicle tra-
jectory analysis (AlZoubi et al., 2017; AlZoubi and
Nam, 2019). It has motivated the researchers to inves-
tigate qualitative representations with deep learning
methods for vehicle trajectory analysis. Qualitative
methods (e.g. QTC (Van de Weghe, 2004)) abstract
the real values of the trajectories, use symbolic rep-
resentation, are computationally less expensive, and
more human understandable than quantitative meth-
ods.
Many previous studies on both single and multi-
ple vehicle activity classification and prediction have
deployed different techniques such as Bayesian Net-
works (Lef
`
evre et al., 2011) and Hidden Markov
Models (Berndt and Dietmayer, 2009; Deo et al.,
2018; Framing et al., 2018). However, the emergence
of LSTM as a powerful method to handle temporal
data with long term dependencies has increased the
interest on using such technique for vehicle activity
236
Radhakrishnan, R. and Alzoubi, A.
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network.
DOI: 10.5220/0010903500003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
236-247
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Our Proposed Method.
classification task. Recently, few studies have been
proposed on using a manually designed LSTM with
quantitative methods to classify multiple vehicles ac-
tivities (Khosroshahi et al., 2016). However, incor-
porating qualitative features with LSTM for vehicle
activity analysis still remains to be an open investiga-
tion area. On the other hand, the manual design of
LSTM architectures has several limitations: 1) trial-
and-error approach is time-consuming and requires
architectural domain expertise; 2) this might result in
building an architecture that is limited to the expert
previous knowledge; and 3) error prone. In addition,
LSTM architecture has a complex structure including
gates and memory cells to store long term dependen-
cies of sequential data. Thus, it requires a methodi-
cal way of tuning its hyperparameters to get the op-
timal architecture rather than using manual designing
or brute force methods such as Grid Search and Ran-
dom Search. Bayesian Optimisation has been used
for optimising LSTM networks in applications such
as image caption generation (Snoek et al., 2015) and
forecasting (Yang et al., 2019). Such optimiser can be
adapted to design the LSTM architectures for vehicle
trajectory classification task.
In this paper, we present our method for vehicle
pair activity classification based on QTC and LSTM.
Our method consists of three main stages, initially
we deploy QTC to represent the relative motion be-
tween the vehicles symbolically. Then, we transform
this representation into a two-dimensional matrix us-
ing one-hot vectors. In the second stage, we em-
ploy Bayesian Optimisation approach to search for a
generic optimal Bi-LSTM architecture (to which we
refer as LSTM in this paper) for vehicle activity clas-
sification. Both model accuracy and complexity were
used as criteria in our architecture selection policy.
Finally, the optimal LSTM architecture was used to
build LSTM model (called VNet) for vehicle pair ac-
tivity recognition. Our approach was evaluated with
three publicly available datasets of vehicle interac-
tion. The results show that our proposed method out-
performs all the existing methods. Figure 1 shows an
overview of the main components of our method. Our
approach is the first to use QTC with LSTM for pair-
wise vehicle activity classification.
The key contributions of this paper include: (1)
We propose a new method for pair-wise vehicle ac-
tivity classification based on QTC and LSTM net-
work; (2) We adopt Bayesian Optimisation method to
find an optimal LSTM architecture for vehicle activ-
ity classification with less human intervention in the
architectural and modelling design, and low risk of
model generalisation error; (3) we evidence the over-
all generality of our method with evaluations on three
vehicle interaction datasets. We show experimentally
that our proposed VNet model outperforms existing
state-of-the-art methods such as (AlZoubi and Nam,
2019; AlZoubi et al., 2017; Lin et al., 2013; Lin et al.,
2010; Ni et al., 2009; Zhou et al., 2008).
2 BACKGROUND AND
LITERATURE REVIEW
2.1 Qualitative Trajectory Calculus
Qualitative Trajectory Calculus (QTC) is a method to
represent an interaction between two moving objects
in a symbolic way (Van de Weghe, 2004). QTC con-
sists of six codes representing four features of a rel-
ative interaction: distance (C1,C2), speed (C3), side
(C4,C5) and angle (C6). These codes are represented
using three symbols: “-”, “0” and “+”. Given the po-
sitions of two moving objects (O
1
and O
2
):
• C1: distance of O
1
with respect to O
2
: “-” indi-
cates decrease, “+” indicates increase, and “0” in-
dicates no change;
• C2: distance of O
2
with respect to O
1
;
• C3: relative speed of O
1
with respect to O
2
at time
t;
• C4: shifting of O
1
with respect to the reference
line Li that connects the two objects: “-” if it
moves to the left, “+” if it moves to the right, and
“0” if it moves along Li or stationary;
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network
237

• C5: shifting of O
2
with respect to Li;
• C6: the angles (e) between the velocity vectors of
the objects and vector Li: “-” if e
1
< e
2
, “+” if
e
1
> e
2
and “0” if e
1
= e
2
.
Two main variants of QTC have been proposed: Dou-
ble Cross QTC (QTC
C
- uses C1,C2,C3 and C4) and
Full QTC (QTC
Full
- uses all six codes). There are
81 (3
4
) possible states for QTC
C
to represent the in-
teraction in a trajectory. Even though there are 729
(3
6
) possible combinations of states for QTC
Full
, only
305 states are possible in real life interaction (Van de
Weghe, 2004). For example, one object cannot move
faster than the other object when both of them are
stationary (0, 0, 0, 0, +, 0). Lately, QTC has shown
to be outperforming the quantitative methods as an
adequate trajectory representation for vehicle activ-
ity analysis task (AlZoubi and Nam, 2019; AlZoubi
et al., 2017).
2.2 Long Short-Term Memory
Long Short-Term Memory (LSTM) is an architec-
ture used in the field of deep learning for classify-
ing and predicting time series data (Hochreiter and
Schmidhuber, 1997), and represents the state-of-the-
art method for analysing sequential data. LSTM cell
consists of a memory cell and three gates namely for-
get gate, input gate and output gate. This architec-
ture allows these cells to capture and store long term
dependencies in lengthy sequential data (Yu et al.,
2019). In recent years, deep learning neural net-
works, in particular LSTM networks, have showed
outstanding performance in a variety of sequential
data recognition and prediction applications such as
human trajectory prediction (Alahi et al., 2016; Xue
et al., 2018), time series forecasting and classification
(Siami-Namini et al., 2019; Karim et al., 2017), nat-
ural language modelling (Sundermeyer et al., 2012),
sequence labelling (Reimers and Gurevych, 2017)
and speech synthesis (Fan et al., 2014). Bidirec-
tional LSTM (Bi-LSTM) is a variant of LSTM which
contains two LSTM layers where one of them learns
the sequential data in forward direction and the other
learns it from the backward direction (Graves et al.,
2013). It performs better than its unidirectional vari-
ant since it gets access to both past and future infor-
mation simultaneously (Siami-Namini et al., 2019).
Thus, we use the bidirectional variant of the LSTM in
our approach. Developing LSTM classifiers for a spe-
cific task (or application) involves designing of net-
work architecture and training parameters. Two main
approaches are followed for LSTM architecture de-
signing: manually designed (or handcraft) architec-
tures and automatically searched architectures. How-
ever, manual designing of LSTM architecture of many
hyperparameters requires expertise and time. It might
result in complex architectures and increase the risk
of model overfitting.
2.3 Bayesian Optimisation
Deep learning methods (e.g. Deep Convolutional
Neural Networks and Long Short-Term Memory)
have exhibited high performance in image classifi-
cation and sequential data analysis for various ap-
plications. However, most of these CNNs and
LSTMs architectures have been designed and opti-
mized manually. On the other hand, Neural Archi-
tecture Search (NAS) and Hyperparameter Optimisa-
tion (HPO) are two different approaches to perform
architecture search and both have significant overlaps
(Elsken et al., 2019). NAS and advanced NAS (Effi-
cient Neural Architecture Search - ENAS) approaches
are mainly used to build architectures of DCNN for
image classification task. ENAS has shown to be
successful in different image classification tasks such
as medical image classification (Ahmed et al., 2020)
and object recognition in natural images (Pham et al.,
2018).
Bayesian Optimisation is one of the recent de-
velopment in optimising deep learning hyperparame-
ters including Deep Convolutional Neural Networks
(DCNN) and LSTM. Unlike ENAS, Bayesian Op-
timisation accounts for modelling-hyperparameters
(e.g. mini-batch size, number of epochs). Bayesian
Optimisation works under the principle of Bayes the-
orem using two key elements: Acquisition Function
and Surrogate Model. The acquisition function de-
termines the next point of the search by calculating
the utility of different points in the search space. Ex-
pected Improvement is a type of the acquisition func-
tion which considers both mean and variance of the
posterior model while selecting the next hyperparam-
eter setting (Frazier, 2018). It provides the blend of
both exploration and exploitation which ensures the
optimiser does not settle for a local optima (Gelbart
et al., 2014). The surrogate model updates itself after
each iteration by fitting the newly observed point of
the objective function using Gaussian Process. Few
attempts have been made to use this method to find
optimal LSTM architectures (Snoek et al., 2015; Yang
et al., 2019; Kaselimi et al., 2019). However, no
LSTMs have been designed and optimised automat-
ically for pair vehicle activity classification task.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
238

2.4 Vehicle Trajectory Analysis
Methods for vehicle trajectory analysis can be
grouped into three categories: single-vehicle activ-
ities (Khosroshahi et al., 2016; Zyner et al., 2018;
Altch
´
e and de La Fortelle, 2017), pair vehicle ac-
tivities (AlZoubi et al., 2017; AlZoubi. and Nam.,
2019; AlZoubi and Nam, 2019; Zhou et al., 2008),
and group vehicle activities (Deo and Trivedi, 2018;
Lin et al., 2013; Kim et al., 2017), and a review is pro-
vided in (Ahmed et al., 2018). The spatio-temporal
representation of motion information is the first step
in the trajectory analysis. Both quantitative (Khos-
roshahi et al., 2016; Lin et al., 2013; Deo et al., 2018)
and qualitative (AlZoubi et al., 2017; AlZoubi. and
Nam., 2019; AlZoubi and Nam, 2019) methods were
used to encode vehicle activities successfully. Khos-
roshahi et al. (Khosroshahi et al., 2016) and Philips et
al. (Phillips et al., 2017) presented manually designed
LSTM networks with quantitative features (linear and
angular changes) to classify single vehicle activities at
intersections. Both studies demonstrated the impor-
tance of finding the optimal LSTM hyperparameters
such as the number of LSTM layers and the number of
neurons per layer in achieving higher accuracy. Zyner
et al. conducted a similar study in maneuver classifi-
cation of single vehicle activities in an unsignalised
intersection using x,y position coordinates, heading
angle and speed as quantitative input features (Zyner
et al., 2018). Studies of Lin et al. (Lin et al., 2013)
and Deo et al. (Deo and Trivedi, 2018; Deo et al.,
2018) focus on classifying pair-wise vehicle activi-
ties. Lin et al. (Lin et al., 2013) used a surveillance
camera dataset and showed that their heat map repre-
sentation of vehicle trajectories can achieve a classi-
fication error rate as low as 4.2%. A Hidden Markov
Model (HMM) based classification method was de-
veloped by (Deo et al., 2018) using x, y ground plane
coordinates and instantaneous velocities in the x and
y directions as features to classify pair vehicle ma-
neuvers on a highway. Their HMM model achieved
a classification accuracy of 87.19%. The first method
on pair activity classification was presented by Zhou
et al. using causality and feedback ratio (Zhou et al.,
2008). However, it was developed for human pair ac-
tivity classification. They used Support Vector Ma-
chine (SVM) as their classifier and achieved 92.1%
accuracy in classifying human pair activities. This
method has also been used by Lin et al. (Lin et al.,
2013) for vehicle activity classification.
Unlike quantitative methods, only few studies
have been conducted on qualitative features for ve-
hicle trajectory analysis. Initial investigation on qual-
itative methods were conducted by (AlZoubi et al.,
2017). They deployed QTC as the qualitative fea-
ture extraction technique. AlZoubi et al. used the
Surveillance Camera dataset which was previously
used in the heat map based vehicle trajectory clas-
sification algorithm (Lin et al., 2013) and reduced
the classification error rate up to 3.44%. Hence,
showed that their QTC method outperforms the quan-
titative heat map method for classification of vehi-
cle trajectories. Further, they expanded their study
and developed a DCNN method (TrajNet) to clas-
sify QTC sequences and achieved a reduced classifi-
cation error rate of 1.16% from the same dataset (Al-
Zoubi and Nam, 2019). TrajNet maps the QTC tra-
jectory into image texture and uses transfer learning
with AlexNet CNN model for activity classification.
The same authors also developed a simulation dataset
with three classes including collision scenarios (Al-
Zoubi and Nam, 2019). However, none of the afore-
mentioned techniques have investigated the incorpo-
ration of QTC and LSTM to solve this problem. It is
worth mentioning that one attempt was made to use
both QTC and manually designed LSTM architecture
for gaming application (Panzner and Cimiano, 2016).
The architecture contains a single LSTM layer with
128 hidden units without any dropout. This study
showed the potential of using QTC with manually de-
signed LSTM. However, LSTM is yet to be used with
qualitative features such as QTC in the context of ve-
hicle trajectory analysis.
We adopt the quantitative methods (AlZoubi et al.,
2017; Lin et al., 2013; Lin et al., 2010; Ni et al., 2009;
Zhou et al., 2008) and the qualitative method (Al-
Zoubi and Nam, 2019) as benchmark techniques for
our study, against which we evaluate our work. In ad-
dition, we also compare the performance of the man-
ually designed LSTM architecture in (Panzner and
Cimiano, 2016) against our optimised LSTM archi-
tecture.
3 PROPOSED METHOD
The proposed method comprises of three main com-
ponents: 1) Representing pair-wise vehicle move-
ments as QTC trajectory sequences; 2) Searching for
optimal LSTM architecture using Bayesian Optimisa-
tion method; and 3) Developing LSTM model (VNet)
for classifying QTC trajectories of interacting vehi-
cles. Our method for classifying vehicle trajectories
involves generation of QTC trajectories, automatic
designing of LSTM architecture with optimised mod-
elling hyperparameters, learned from the data, and ac-
counts for significant differences in sequence length
and interaction complexity. As presented in Section 4,
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network
239

our method generalises across three different vehi-
cle interaction datasets, and enables us to consistently
outperform state-of-the-art vehicle pair-activity anal-
ysis methods.
3.1 QTC Trajectory Generation and
Representation
The 2D position coordinates x;y are used to represent
the relative motion between two vehicles, and encode
their interaction as a trajectory of QTC states. In this
study, we use both QTC
C
and QTC
Full
variants de-
rived directly using the vehicle centre position coor-
dinates.
Definition: Given two interacting vehicles with their
x; y position coordinates during the time interval t
1
to
t
k
, the trajectories of the two vehicles are defined as:
V 1
i
= {(x
1
, y
1
), ..., (x
t
, y
t
), ..., (x
k
, y
k
);
V 2
i
= {(x
0
1
, y
0
1
), ..., (x
0
t
, y
0
t
), ..., (x
0
k
, y
0
k
).
where (x
t
,y
t
) is the position coordinates of the first
interacting vehicle at time t, (x
0
t
,y
0
t
) is the position co-
ordinates of the second, and k is the total number of
time steps in the trajectories. The pair-wise trajec-
tory is defined as a sequence of corresponding QTC
states: T v
i
= {S
1
, ..., S
R
, ...S
N
}, where S
R
is the QTC
state representation of the relative movement of the
two vehicles between time t and t +1 in trajectory T v
i
and N is the number of QTC observations (N = k −1)
in T v
i
. Due to the limited computational resources,
we used QTC
C
variant for the architecture search and
modelling as described in Section 3.2, while QTC
Full
was only used for modelling.
QTC Trajectory to One Hot Vector Representa-
tion: The trajectory T v
i
is a time varying, one dimen-
sional sequence of QTC states and it is represented as
a sequence of characters Ch
i
= {Ch
1
, ...,Ch
R
, ...Ch
N
}
in a text format. This text format only provides the
presence of a QTC state (Character) at a particular
time. Thus, it loses the information of QTC states
which are absent in that time frame. To capture this
high level information, the QTC sequence of charac-
ters (Ch
i
) were translated into numerical format using
One Hot encoding without losing its location informa-
tion. Thus, the one hot vector representation of trajec-
tory T v
i
provides a 2D matrix (Mv
i
) of size (Q ∗ N);
where Q is the number of possible QTC states and
N is the number of observations in T v
i
. This matrix
is used as the sequential input for the LSTM model
presented in Section 3.2.
3.2 Vehicle Activity Classification
In this section, we present the formulation of our
LSTM architecture with QTC trajectories for vehicle
activity classification. Gaining inspiration from au-
tomatic network search, we aim to take advantage of
Bayesian Optimisation method which is a powerful
technique to optimise deep learning hyperparameters.
First, we define an LSTM backbone architecture and
targeted hyperparameter search space. Then, we em-
ploy Bayesian Optimisation to find the optimal archi-
tecture and training parameters for accurate vehicle
activity classification.
3.2.1 Backbone Architecture Design and Search
Space
Bayesian Optimisation requires a definition of ini-
tial backbone architecture and the trainable hyper-
parameters. We designed a backbone architecture
consisting six layers: Sequence Input Layer (SI),
Bi-directional LSTM Layer (LST M), Dropout Layer
(DL), Fully Connected Layer (FL), SoftMax Layer
(SM), and Classification Layer (OL) in sequential or-
der as shown in Figure 2. Based on the pair-wise
vehicle trajectory representation (one hot vector) in
Section 3.1, an input layer was defined with size
(Q∗N). This was followed by L number of (Bi-LSTM
+ Dropout) Layer Pairs where m is the number of hid-
den units of the Bi-LSTM Layer and p is the dropout
percentage of the dropout layer. Values of L, m and
p were determined by the Bayesian Optimisation al-
gorithm. Our method identify the values of m and p
for each L (i.e. if we have two layers L = 2, m and p
values of each layer are estimated: (m
1
,m
2
), (p
1
,p
2
)).
Then, a fully connected layer was added based on the
number of vehicle activity classes C in the dataset. Fi-
nally, a softmax layer and classification output layer
were incorporated to match the number of classes C.
The softmax layer produces a probability distribution
over all the class labels. The output of the softmax
layer is passed to a classification layer which com-
putes the cross-entropy loss of each class to measure
the performance of the classification.
The selection of suitable hyperparameter search
space for building LSTM network plays a major role
in the model performance. We defined six hyper-
parameters for tuning our LSTM for vehicle trajec-
tory classification. The search space boundaries of
the identified optimisable hyperparameters are: L
= {1, 2, 3}, m = [8 − 512], p = {0, 25, 50, 75}%,
Epochs (E po) = [1 − 400], Minibatch Size (MB)
= {2, 4, 8, 16}, Optimiser (Opt) = {SGDM, Adam,
RMSprop}. The search space (values, boundaries and
categories) of the above mentioned hyperparamters
were selected based on two criteria: the best perform-
ing hyperparameters of previous studies (Reimers and
Gurevych, 2017) and suitability for our vehicle’s ac-
tivity classification task.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
240

Figure 2: Proposed LSTM Backbone Architecture.
3.2.2 Automatic Architecture Search
Given the backbone architecture and the search space
hyperparameters h, we use Bayesian Optimisation
method to find the optimal values of L, m, p, E po, MB,
and Opt. Thus, h = {h
1
, ..., h
j
, ..., h
z
} where h
j
is
the value of optimisable hyperparameter j in hyper-
parameter setting h and z is the total number of hy-
perparameters that are being optimised (in this case
z = 6). Firstly, we define the objective function f (h)
which we want the Bayesian Optimiser to minimize.
The objective function, f (h) is defined as the classi-
fication error rate of the test set when modelling the
backbone architecture with hyperparameter setting h:
f (h) = Classification Error(h) (1)
Number of seed points (r) that the Bayesian Opti-
miser uses to create the surrogate model was set to
4 and the number of search iterations was selected as
30. Those values were selected empirically. Num-
ber of seed points defines the number of points that
the Bayesian Optimiser examines before starting the
search process. Bayesian Optimiser uses those 4 seed
points to build the surrogate model and then iterates
30 times to select the optimal architecture. Initially,
Bayesian Optimiser randomly selects 4 sets of hy-
perparameter settings as the initial seed points and
models the backbone architecture using each of those
four settings. Then, it calculates the test error rate of
those four models to create the surrogate model G(h).
Gaussian Process Model (Regression) is used to con-
struct the surrogate model. After creating the surro-
gate model, Bayesian Optimiser selects a new hyper-
parameter setting using an acquisition function. We
use the acquisition function Expected Improvement
EI(h) which selects the next hyperparameter setting
as the one that has the highest expected improvement
over the current best observed point (lowest classifi-
cation error) of the objective function. The Expected
Improvement for hyperparameter setting h is,
EI(h) = E(max( f
∗
(h) − G(h), 0)) (2)
where G(h) is the current posterior distribution of the
surrogate model and f
∗
(h) is best observed point of
Algorithm 1: Bayesian Optimisation.
Input: Hyperparameter Seach Space h
Input: Objective Function f (h)
Input: Max No of Evaluation n
max
Input: Initial Seed Points r
Output: Optimal hyperparameter setting h
∗
Output: Classification Error of Optimal hyperpa-
rameter setting d
∗
Select: initial hyperparameter settings h
0
∈ h for r
number of points
Evaluate: the initial classification error d
0
= f (h
0
)
Set h
∗
= h
0
and d
∗
= d
0
for n = 1 to n
max
do
Select: a new hyperparameter configuration h
n
∈ h
by optimising the acquisition function D(h
n
)
h
n
= argmax(D(h
n
))
where,
D(h
n
) = EI(h
n
) = E(max( f
∗
(h) − G(h
n
), 0))
Evaluate: f for h
n
to obtain the classification error
d
n
= f (h
n
) for hyperparameter setting h
n
Update: the surrogate model
if d
n
<d
∗
then h
∗
= h
n
and d
∗
= d
n
end if
end for
Output: h
∗
and d
∗
the objective function so far. The h which maximizes
the acquisition function is evaluated next and the sur-
rogate model gets updated with this newly evaluated
point. This process repeats until a fixed number of it-
erations (n
max
= 30 iterations). Algorithm 1 elaborates
this process in detail.
3.2.3 Optimal Architecture Selection and
Modelling
We used two real-world datasets to identify a generic
optimal architecture for vehicle activity classification.
As described in Section 4, each vehicle trajectory
dataset was split into 5 groups (5-folds cross vali-
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network
241

dation). The selection of the optimal architecture
was carried out under two stages: initially within
the dataset and then between the datasets. In the
first stage, we generated 150 LSTM architectures per
dataset (i.e. 30 architectures per fold) using Bayesian
Optimisation. We defined two selection criteria: 1)
low classification error; and 2) low architecture com-
plexity. First, from each dataset, the architectures
which provide the lowest classification error on the
test set were selected from each fold. Then, the best
architecture of each fold was selected by comparing
their complexities. Complexity of the architecture is
determined by the total number of trainable param-
eters (T.P). Our proposed architecture consists train-
able parameters from Bi-LSTM layer and Fully Con-
nected layer which can be calculated using equation
3.
T.P = 2(4m(Q + m + 1)) +C(2m + 1) (3)
where 4 represents the 4 activation function unit equa-
tions of the LSTM cell and 2 represents the Bi-LSTM
variant of the LSTM. The first stage of selection re-
sults in the best 5 architectures from each dataset. In
the second stage, we compare the similarities of the
best architectures between the datasets. We use a sim-
ple similarity measure which is determined by how
identical (or similar) the values of hyperparameters
(L, m and p) are between two architectures from the
two datasets. Using this similarity measure, we iden-
tify a generic optimal architecture suitable for vehicle
activities observed from different settings. Our moti-
vation behind this approach of searching for optimal
architectures from two datasets separately was identi-
fying one generic architecture applicable for different
vehicle activity datasets as illustrated in Section 4.
Given the one hot vector representation of pair vehi-
cle trajectories and the optimal architecture, we build
VNet models for different activity classification. The
fully connected layer of the optimal architecture was
updated according to the number of classes C in the
dataset.
Figure 3: Example of Moving Vehicles Captured from a
Drone Camera for HighD Dataset (Krajewski et al., 2018).
Figure 4: Example Pair-wise Manoeuvres of HighD dataset
(Krajewski et al., 2018).
4 DATASETS AND
EXPERIMENTS
This section presents three publicly available vehi-
cle interaction datasets and comparative experiments
to evaluate the effectiveness of our method. All ex-
periments were conducted on an Intel Core i7 lap-
top, CPU@1.80GHz with 8.0GB RAM. All three
datasets were captured in different settings and con-
sist of different types of vehicle interactions. Fur-
ther, we developed a challenging fourth dataset which
combined all three datasets to evaluate our generic
LSTM model. Finally, we evaluated an existing man-
ually designed LSTM developed for QTC to deter-
mine the importance of incorporating automatic op-
timisation of LSTM architecture for vehicles activity
analysis domain.
Dataset 1: Highway Drone Dataset: Highway
Drone (HighD) Dataset is a dataset of vehicle trajec-
tories recorded using a drone (Krajewski et al., 2018).
Figure 3 shows the placement of the drone camera in
the data collection region. The dataset consists tra-
jectories of more than 110,500 vehicles with their x, y
position coordinates at each timestamp. Five unique
vehicle pair activities (Follow, Precede, Left Over-
take, Left Overtake (Complex) and Right Overtake)
were extracted from the dataset as illustrated in Fig-
ure 4. Follow and Precede are defined as Eco vehi-
cle is followed or preceded by another vehicle. Simi-
larly, Left Overtake and Right Overtake are annotated
as Eco vehicle is overtaken by another vehicle on the
left or right lane. Left Overtake (Complex) is a com-
bination of two behaviours. Initially, the Eco vehicle
is followed by another vehicle on the same lane and
then it is successfully overtaken by that vehicle using
the left lane. 6805 trajectories (1361 trajectories per
class) were selected from the dataset in order to avoid
imbalance between the classes and due to the limited
computational resource to model the LSTM network.
The dataset has sequences in varying lengths from 11-
1911 timesteps. Among the 6805 trajectories, 500
(100 trajectories per class) were used for searching
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
242

Figure 5: Example Pair-wise Manoeuvres of Traffic Dataset (Lin et al., 2013).
Figure 6: Example Pair-wise Manoeuvres of VOI dataset
(Alzoubi and Nam, 2018).
the optimal architecture. On the other hand, 5000 tra-
jectories were selected from the 6805 and used for
modelling, and the remaining 1805 trajectories were
kept unseen for external testing.
Dataset 2: Traffic Dataset: The traffic dataset was
generated by extracting position coordinates of vehi-
cles from 20 surveillance videos (Lin et al., 2013).
The videos are recorded from a road junction using
different surveillance cameras as shown in figure 5.
The dataset contains 175 trajectories of pair vehicles
in the form of x, y positions where each trajectory has
a length of 20 time steps. It has five unique vehicle
pair activities namely Turn, Follow, Pass, Overtake
and Both Turn as shown in Figure 5, and each activity
has 35 trajectories in the dataset.
Dataset 3: Vehicle Obstacle Interaction Dataset:
Vehicle Obstacle Interaction (VOI) dataset is obtained
through a simulation environment, and it mainly
focuses on close proximity manoeuvrings and rare
events for which there are not enough real-life data
such as crash (AlZoubi. and Nam., 2019). The dataset
contains 277 pair vehicle trajectories, in the form of
x, y positions, representing three classes which are
Left Pass (104 trajectories), Right Pass (106 trajec-
tories) and Crash (67 trajectories) as shown in Figure
6. The pair trajectories has lengths ranging from 10
to 71 time steps. Left Pass and Right Pass are defined
as vehicle successfully passing an obstacle on the left
or right, respectively. Crash is defined as the collision
of moving vehicle with an obstacle.
Dataset 4: Combined Dataset: Combined dataset is
constructed by combining the three above mentioned
datasets with careful consideration in preserving their
ground truths while merging and splitting the com-
mon classes. Thus, this fourth dataset contains 952
trajectories with 9 classes: Follow (135), Left Pass
(138), Right Pass (107), Turn (35), Both Turn (35),
Crash (67), Preceding (100), Right Overtake (135)
and Left Overtake (200). The definition of this classes
remains the same as their original.
4.1 LSTM Architecture Optimisation
To find the optimal hyperparameters of our proposed
backbone LSTM architecture, we perform Bayesian
Optimisation on the two real world datasets (High-
way Drone and Traffic datasets). Firstly, both datasets
were divided into 5 non-overlapping folds of train-
ing and testing (5-fold cross validation protocol). In
addition, the optimisable hyperparameters and their
search space (Section 3.2.1) were provided as input
for the optimiser. The error rate of the test set of
each fold has been determined as the objective func-
tion. 150 search iterations (30 iterations per fold)
were performed individually on both datasets. Our
selection method (Section 3.2.3) was used to iden-
tify the optimal and generic architecture. The ar-
chitectures with the lowest testing error rate in each
fold were selected. HighD Dataset provided 47 archi-
tectures with highest testing accuracy. On the other
hand, the Traffic dataset provided only 6 architectures
with highest testing accuracy. Since there were nu-
merous architectures that achieved the highest fold
wise accuracy, we compared their architecture com-
plexity to select the best one from each fold. The
summary of the best models of HighD and Traffic
datasets from each fold are presented in Table 1. The
selected architectures of Models 2, 3 and 4 provided
the best classification accuracy and the best class wise
standard deviation among the five models of HighD
dataset. Model 2 provided the best accuracy (93.88%)
for Traffic dataset. Our aim was to find a single op-
timal architecture for vehicle activity classification
from both datasets. Thus, we compared the similar-
ities of the best performing architectures of both the
datasets. Model 2 of both datasets have produced ex-
actly the same LSTM architecture with slight differ-
ences in the mini batch size and number of epochs.
Those two architectures share the same L, m and p
hyperparameters. Therefore, we selected this archi-
tecture as our generic optimal architecture. We used
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network
243

Table 1: Summary of the Best Performing Architectures: D.S - Dataset, Arc - Architecture Acc - Accuracy, S.D - Class-wise
Standard Deviation, T.Par - Trainable Parameters, Opt - Optimiser, L - Number of (Bi-LSTM + Dropout) Layer Pairs, m -
Number of Hidden Units, p - Dropout Percentage, MB - Mini Batch Size, Epo - Number of Epochs.
D.S Arc Acc(%) S.D T.Par Opt L m p MB Epo
HighD
1 99.00 2.24 9149 RMSprop 1 12 25% 8 23
2 100.00 0.00 93097 sgdm 1 74 50% 8 232
3 100.00 0.00 184909 adam 1 116 0% 8 381
4 100.00 0.00 36865 sgdm 1 38 50% 8 165
5 99.00 2.24 23819 sgdm 1 27 0% 16 379
Traffic
1 91.84 11.25 35749 sgdm 1 37 25% 8 283
2 93.88 11.25 93395 sgdm 1 74 50% 4 376
3 89.80 10.81 28465 sgdm 1 31 75% 4 372
4 91.84 11.25 187909 sgdm 1 117 75% 8 395
5 85.71 31.94 5879 sgdm 1 8 50% 8 69
the modelling-hyperparameters (E po, MB and Opt)
of Model 2 of HighD dataset to model our VNet clas-
sification models since HighD dataset is more chal-
lenging and 25 times larger than the Traffic dataset
and it has a trajectory length range from 11-1911.
4.2 Evaluation of the Optimal
Architecture
In this section, we evaluated the selected optimal ar-
chitecture (Section 4.1) using all three datasets as well
as the combined dataset. To determine the classifi-
cation error rates using our method, we used 5-fold
cross validation. On each iteration, we split the one
hot vector representation of the trajectories extracted
from the dataset into training and testing sets at ratio
of 80% to 20%, for each class. The training sets were
used to parametrise our LSTM network. The test set
was then classified by our trained VNet models.
4.2.1 Classification of Highway Drone Dataset
Using the one hot vector representations of the 5000
trajectories extracted from HighD dataset, the VNet
model was able to classify the HighD dataset with
an average accuracy of 99.80% (std=0.35%) on the
5 folds during the modelling. We evaluated the
model using both QTC
C
and QTC
Full
and it achieved
the same results. Further, we tested the 5 trained
VNet models on the 1805 trajectories of unseen
dataset, achieving an average accuracy of 99.87%
(std=0.29%). Even though only 10% of the whole
dataset was used to find the optimal architecture, our
VNet models maintained a high performance and gen-
eralised on unseen datasets. It also shows the power
of QTC in representing pair activity trajectories. For
comparative purposes, we have used the DCNN-QTC
(‘TrajNet’) (AlZoubi and Nam, 2019) as a benchmark
qualitative method, which has itself been shown to
outperform other qualitative and quantitative methods
(AlZoubi et al., 2017; Lin et al., 2013; Lin et al., 2010;
Ni et al., 2009; Zhou et al., 2008). Using the same
HighD dataset split, our VNet achieved a higher accu-
racy against TrajNet which achieved an average accu-
racy of 98.60% on 5-fold cross validation and 98.98%
on unseen test set. The difference in accuracy of our
VNet model and TrajNet is 1.2% in 5-fold modelling.
However, this 1.2% accounts for 60 trajectories in the
HighD dataset. Our VNet model was able to correctly
classify 60 more trajectories than TrajNet. Especially,
VNet performs better than TrajNet when classifying
simple and complex activities of similar behaviours
(Left Overtake and Left Overtake Complex) (Table 2).
Thus, it shows the superiority of our model statisti-
cally in such critical application. Further, our method
shows relatively high consistency among the 5 models
by providing lower standard deviation in both mod-
elling and external testing. Table 2 shows the perfor-
mance of both VNet and TrajNet on the internal and
unseen HighD datasets.
Table 2: Comparison between Our Proposed Method with
State-of-the-art TrajNet Method on HighD Dataset: Ave.
Acc. - Average Accuracy, S.D - Standard Deviation.
Model
Modelling External Testing
VNet Trajnet VNet Trajnet
Follow 99.80% 98.00% 100% 99.34%
Left
Overtake
100% 97.00% 100% 97.40%
Left
Overtake
Complex
99.20% 98.00% 99.36% 98.44%
Preceding 100% 100% 100% 99.90%
Right
Overtake
100% 100% 100% 99.76%
Ave Acc. 99.80% 98.60% 99.87% 98.98%
S.D 0.35% 1.34% 0.29% 1.05%
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
244
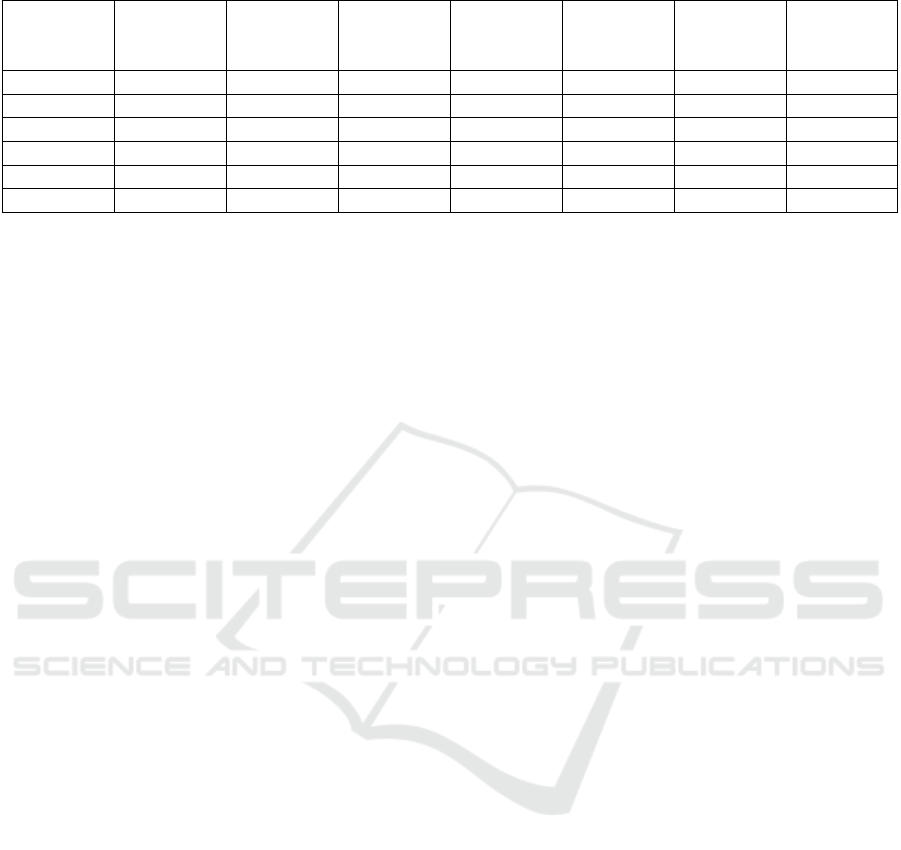
Table 3: Average Classification Accuracy of Different Algorithms on the Traffic Dataset.
Type VNet (AlZoubi
and Nam,
2019)
(AlZoubi
et al.,
2017)
(Lin et al.,
2013)
(Zhou
et al.,
2008)
(Ni et al.,
2009)
(Lin et al.,
2010)
Turn 100% 97.10% 97.10% 97.10% 98.00% 83.10% 89.30%
Follow 100% 100% 94.30% 88.60% 77.10% 61.90% 84.60%
Pass 100% 100% 100% 100% 88.30% 82.40% 84.50%
Bothturn 97.14% 100% 97.10% 97.10% 98.80% 97.10% 95.80%
Overtake 97.14% 97.10% 94.30% 94.30% 52.90% 38.30% 63.40%
Ave. Acc. 98.86% 98.84% 96.56% 95.42% 83.02% 72.76% 83.52%
4.2.2 Classification of Traffic Dataset
We have conducted similar classification experiments
using the traffic activity dataset presented in (Lin
et al., 2013). The optimal architecture was evaluated
using 5-folds cross validation using both QTC
C
and
QTC
Full
and the model achieved an average accuracy
of 98.86% (std=1.56%). 5-folds cross validation pro-
tocol guarantees that every trajectory in the dataset is
tested at least once. Table 3 shows the performance
comparison of our VNet against state-of-the-art ap-
proaches on this dataset (AlZoubi and Nam, 2019; Al-
Zoubi et al., 2017; Lin et al., 2013; Lin et al., 2010; Ni
et al., 2009; Zhou et al., 2008). Our method outper-
formed all six quantitative and qualitative methods by
achieving the lowest classification error rate of 1.14%.
4.2.3 Classification of VOI Dataset
Classifying very dangerous vehicle interactions is
crucial for collision avoidance and security surveil-
lance applications. Therefore, to gain traction as
a mainstream analysis technique, we evaluated our
method on the publicly available VOI dataset (Al-
zoubi and Nam, 2018) of crash behaviours. Using
5-folds cross validation, our VNet model achieved a
high average accuracy with 0% error rate which is
similar to TrajNet (AlZoubi and Nam, 2019). Both
QTC
C
and QTC
Full
achieved the same results. De-
spite the optimal architecture was designed from dif-
ferent vehicle datasets, our VNet generalized and
achieved a high performance on the VOI dataset.
4.2.4 Classification of Combined Dataset
Our main motivation is a generic supervised analy-
sis for vehicle interactions. The combined dataset is
challenging, as it contains simple and compound ac-
tivities and with various lengths. We split the 952 tra-
jectories into training and testing sets at ratio of 80%
to 20%, for each class. The training sets were used to
parametrise our network and the test set was then clas-
sified by our trained VNet model. Our VNet achieved
an average accuracy of 98.21% on the 5 folds which
shows how well our optimal architecture is gener-
alised across different and challenging datasets. For
comparative purposes, we have used TrajNet (Al-
Zoubi and Nam, 2019) as a benchmark qualitative
method. Using the same 5-fold split, our VNet model
outperforms TrajNet (Accuracy = 98.10%). Similar
to Experiment 4.2.1, TrajNet struggles to distinguish
between similar activities of the same side such as
(Left Overtake, Left Pass) and (Right Overtake, Right
Pass). VNet clearly outperforms TrajNet in those four
activities by classifying them with an average accu-
racy of 99.52% compared to TrajNet’s 98.24%. Thus,
both Experiment 4.2.1 and 4.2.4 show that VNet per-
forms better than TrajNet in distinguishing closely
matched behaviours such as Left Overtake, Left Over-
take Complex and Left Pass.
4.2.5 Manual vs Automatic LSTM Architecture
Design
Sections 4.2.1 - 4.2.4 have shown that our method out-
performed existing quantitative and qualitative meth-
ods evaluated on different and challenging datasets.
To the best of our knowledge, no existing LSTM ar-
chitecture has been designed (manually or automat-
ically) for vehicle pair activity classification. In or-
der to evaluate the performance of our auto-optimised
LSTM architecture, we used the manually designed
LSTM architecture developed for QTC features in
(Panzner and Cimiano, 2016) as a benchmark.
Using the same evaluation protocol, the models
of manually designed architecture achieved average
accuracies of 89.12%, 72%, 21.30%, and 26.79% on
VOI, Traffic, HighD, and Combined datasets, respec-
tively. The low performance of these models is a re-
sults of poor LSTM architecture design. This shows
that careful architecture design and parameter selec-
tion is very crucial for a successful vehicle activity
classification model. Table 4 shows the results of
the model (Panzner and Cimiano, 2016) compared
against state-of-the-art TrajNet (AlZoubi and Nam,
2019) model and our VNet model. Our VNet model
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network
245

Table 4: Average Classification Accuracy of Manually De-
signed LSTM (Handcrafted) (Panzner and Cimiano, 2016),
TrajNet (AlZoubi and Nam, 2019) and Our VNet across all
the datasets: H.LSTM - Handcrafted LSTM, Comb. - Com-
bined Dataset.
Method HighD Traffic VOI Comb.
H. LSTM 21.30% 72.00% 89.12% 26.79%
TrajNet 98.60% 98.84% 100% 98.10%
VNet 99.80% 98.86% 100% 98.21%
outperforms existing methods including the manually
optimised LSTM across all the datasets.
5 CONCLUSION
In this paper, we proposed a novel method for vehi-
cle activity classification using QTC and LSTM. We
used a qualitative feature representation method QTC
to represent the relative motion between two objects.
We then encoded the QTC sequences into a two-
dimensional matrix using one-hot vectors. Our results
show how efficiently our representation has abstracted
the features from real valued trajectories. Subse-
quently, we presented a method to efficiently find an
optimal LSTM architecture using Bayesian Optimi-
sation for accurate analysis of vehicle activities. Our
contribution is not only restricted to producing an op-
timal architecture for vehicle activity classification.
We also have presented a way to select the optimal
architecture for LSTM using Bayesian Optimization.
Thus, the approach can be used for other activity
classification applications as well. Our method has
been evaluated on three completely different datasets
recorded from different types of sources: a static cam-
era, a drone camera and a simulator. We compared
our method against the state-of-the-art qualitative (Al-
Zoubi and Nam, 2019; AlZoubi et al., 2017) and
quantitative (Lin et al., 2013; Zhou et al., 2008; Ni
et al., 2009; Lin et al., 2010) methods. The results
of the combined dataset (98.21% accuracy) evidently
show that our approach is a generalised solution for
vehicle activity classification.
Future self-driving technologies can be benefited
with our approach to tackle path planning and safety
related issues. Intrigued by the results, we intend to
extend our work by investigating on quantitative fea-
tures to use with our auto-optimised LSTM. It will lay
the foundation to evaluate both qualitative and quan-
titative approaches with deep neural networks under
the same experimental framework. We evaluated our
method on a large dataset (HighD) with 6805 tra-
jectories, however, both Traffic (175) and VOI (277)
datasets are relatively small. Trajectories of Traffic
dataset (Lin et al., 2013) are also limited to a fixed
length of 20 timesteps. Further, other potential inter-
actions such as chasing, collision of two moving vehi-
cles are not present in the datasets we have. Thus, we
hope to include these kinds of interactions in future.
In addition, we also plan to evaluate other sequential
modeling methods such as transformers, causal and
dilated convolutional neural networks.
REFERENCES
Ahmed, M., Du, H., and AlZoubi, A. (2020). An enas
based approach for constructing deep learning models
for breast cancer recognition from ultrasound images.
arXiv preprint arXiv:2005.13695.
Ahmed, S. A., Dogra, D. P., Kar, S., and Roy, P. P.
(2018). Trajectory-based surveillance analysis: A sur-
vey. IEEE Transactions on Circuits and Systems for
Video Technology, 29(7):1985–1997.
Alahi, A., Goel, K., Ramanathan, V., Robicquet, A., Fei-
Fei, L., and Savarese, S. (2016). Social lstm: Human
trajectory prediction in crowded spaces. In Proceed-
ings of the IEEE conference on computer vision and
pattern recognition, pages 961–971.
Altch
´
e, F. and de La Fortelle, A. (2017). An lstm network
for highway trajectory prediction. In 2017 IEEE 20th
International Conference on Intelligent Transporta-
tion Systems (ITSC), pages 353–359.
AlZoubi, A., Al-Diri, B., Pike, T., Kleinhappel, T., and
Dickinson, P. (2017). Pair-activity analysis from video
using qualitative trajectory calculus. IEEE Transac-
tions on Circuits and Systems for Video Technology,
28(8):1850–1863.
Alzoubi, A. and Nam, D. (2018). Vehicle Obstacle Interac-
tion Dataset (VOIDataset).
AlZoubi, A. and Nam, D. (2019). Vehicle activity recogni-
tion using dcnn. In International Joint Conference on
Computer Vision, Imaging and Computer Graphics,
pages 566–588. Springer.
AlZoubi., A. and Nam., D. (2019). Vehicle activity recogni-
tion using mapped qtc trajectories. In Proceedings of
the 14th International Joint Conference on Computer
Vision, Imaging and Computer Graphics Theory and
Applications - Volume 5: VISAPP,, pages 27–38. IN-
STICC, SciTePress.
Berndt, H. and Dietmayer, K. (2009). Driver intention in-
ference with vehicle onboard sensors. In 2009 IEEE
international conference on vehicular electronics and
safety (ICVES), pages 102–107. IEEE.
Deo, N., Rangesh, A., and Trivedi, M. M. (2018). How
would surround vehicles move? a unified framework
for maneuver classification and motion prediction.
IEEE Transactions on Intelligent Vehicles, 3(2):129–
140.
Deo, N. and Trivedi, M. M. (2018). Multi-modal trajec-
tory prediction of surrounding vehicles with maneuver
based lstms. In 2018 IEEE Intelligent Vehicles Sym-
posium (IV), pages 1179–1184. IEEE.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
246

Elsken, T., Metzen, J. H., and Hutter, F. (2019). Neural
architecture search: A survey. The Journal of Machine
Learning Research, 20(1):1997–2017.
Fan, Y., Qian, Y., Xie, F.-L., and Soong, F. K. (2014). Tts
synthesis with bidirectional lstm based recurrent neu-
ral networks. In Fifteenth annual conference of the
international speech communication association.
Framing, C.-E., Heßeler, F.-J., and Abel, D. (2018).
Infrastructure-based vehicle maneuver estimation
with intersection-specific models. In 2018 26th
Mediterranean Conference on Control and Automa-
tion (MED), pages 253–258. IEEE.
Frazier, P. I. (2018). A tutorial on bayesian optimization.
Gelbart, M. A., Snoek, J., and Adams, R. P. (2014).
Bayesian optimization with unknown constraints.
Graves, A., Mohamed, A.-r., and Hinton, G. (2013). Speech
recognition with deep recurrent neural networks. In
2013 IEEE international conference on acoustics,
speech and signal processing, pages 6645–6649. Ieee.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural computation, 9(8):1735–1780.
Karim, F., Majumdar, S., Darabi, H., and Chen, S. (2017).
Lstm fully convolutional networks for time series clas-
sification. IEEE access, 6:1662–1669.
Kaselimi, M., Doulamis, N., Doulamis, A., Voulodimos, A.,
and Protopapadakis, E. (2019). Bayesian-optimized
bidirectional lstm regression model for non-intrusive
load monitoring. In ICASSP 2019-2019 IEEE Inter-
national Conference on Acoustics, Speech and Signal
Processing (ICASSP), pages 2747–2751. IEEE.
Khosroshahi, A., Ohn-Bar, E., and Trivedi, M. M. (2016).
Surround vehicles trajectory analysis with recur-
rent neural networks. In 2016 IEEE 19th Interna-
tional Conference on Intelligent Transportation Sys-
tems (ITSC), pages 2267–2272. IEEE.
Kim, B., Kang, C. M., Kim, J., Lee, S. H., Chung, C. C.,
and Choi, J. W. (2017). Probabilistic vehicle trajec-
tory prediction over occupancy grid map via recurrent
neural network. In 2017 IEEE 20th International Con-
ference on Intelligent Transportation Systems (ITSC),
pages 399–404.
Krajewski, R., Bock, J., Kloeker, L., and Eckstein, L.
(2018). The highd dataset: A drone dataset of nat-
uralistic vehicle trajectories on german highways for
validation of highly automated driving systems. In
2018 IEEE 21st International Conference on Intelli-
gent Transportation Systems (ITSC).
Lef
`
evre, S., Laugier, C., and Iba
˜
nez-Guzm
´
an, J. (2011). Ex-
ploiting map information for driver intention estima-
tion at road intersections. In 2011 IEEE Intelligent
Vehicles Symposium (IV), pages 583–588. IEEE.
Lin, W., Chu, H., Wu, J., Sheng, B., and Chen, Z. (2013). A
heat-map-based algorithm for recognizing group ac-
tivities in videos. IEEE Transactions on Circuits and
Systems for Video Technology, 23(11):1980–1992.
Lin, W., Sun, M.-T., Poovendran, R., and Zhang, Z. (2010).
Group event detection with a varying number of group
members for video surveillance. IEEE Transac-
tions on Circuits and Systems for Video Technology,
20(8):1057–1067.
Ni, B., Yan, S., and Kassim, A. (2009). Recognizing hu-
man group activities with localized causalities. In
2009 IEEE Conference on Computer Vision and Pat-
tern Recognition, pages 1470–1477. IEEE.
Ohn-Bar, E. and Trivedi, M. M. (2016). Looking at hu-
mans in the age of self-driving and highly automated
vehicles. IEEE Transactions on Intelligent Vehicles,
1(1):90–104.
Panzner, M. and Cimiano, P. (2016). Comparing hidden
markov models and long short term memory neural
networks for learning action representations. In Inter-
national Workshop on Machine Learning, Optimiza-
tion, and Big Data, pages 94–105. Springer.
Pham, H., Guan, M., Zoph, B., Le, Q., and Dean, J.
(2018). Efficient neural architecture search via param-
eters sharing. In International Conference on Machine
Learning, pages 4095–4104. PMLR.
Phillips, D. J., Wheeler, T. A., and Kochenderfer, M. J.
(2017). Generalizable intention prediction of human
drivers at intersections. In 2017 IEEE Intelligent Ve-
hicles Symposium (IV), pages 1665–1670.
Reimers, N. and Gurevych, I. (2017). Optimal hyperpa-
rameters for deep lstm-networks for sequence labeling
tasks. arXiv preprint arXiv:1707.06799.
Siami-Namini, S., Tavakoli, N., and Namin, A. S. (2019).
The performance of lstm and bilstm in forecasting
time series. In 2019 IEEE International Conference
on Big Data (Big Data), pages 3285–3292. IEEE.
Snoek, J., Rippel, O., Swersky, K., Kiros, R., Satish, N.,
Sundaram, N., Patwary, M., Prabhat, M., and Adams,
R. (2015). Scalable bayesian optimization using deep
neural networks. In International conference on ma-
chine learning, pages 2171–2180. PMLR.
Sundermeyer, M., Schl
¨
uter, R., and Ney, H. (2012). Lstm
neural networks for language modeling. In Thirteenth
annual conference of the international speech commu-
nication association.
Van de Weghe, N. (2004). Representing and reasoning
about moving objects: A qualitative approach. PhD
thesis, Ghent University.
Xue, H., Huynh, D. Q., and Reynolds, M. (2018). Ss-
lstm: A hierarchical lstm model for pedestrian tra-
jectory prediction. In 2018 IEEE Winter Conference
on Applications of Computer Vision (WACV), pages
1186–1194. IEEE.
Yang, T., Li, B., and Xun, Q. (2019). Lstm-attention-
embedding model-based day-ahead prediction of pho-
tovoltaic power output using bayesian optimization.
IEEE Access, 7:171471–171484.
Yu, Y., Si, X., Hu, C., and Zhang, J. (2019). A review of
recurrent neural networks: Lstm cells and network ar-
chitectures. Neural computation, 31(7):1235–1270.
Zhou, Y., Yan, S., and Huang, T. S. (2008). Pair-activity
classification by bi-trajectories analysis. In 2008 IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 1–8. IEEE.
Zyner, A., Worrall, S., and Nebot, E. (2018). A recurrent
neural network solution for predicting driver intention
at unsignalized intersections. IEEE Robotics and Au-
tomation Letters, 3(3):1759–1764.
Vehicle Pair Activity Classification using QTC and Long Short Term Memory Neural Network
247
