
Detecting Anomalies Reliably in Long-term Surveillance Systems
Jinsong Liu
a
, Ivan Nikolov
b
, Mark P. Philipsen
c
and Thomas B. Moeslund
d
Visual Analysis and Perception Laboratory, CREATE, Aalborg University, 9000 Aalborg, Denmark
Keywords:
Surveillance, Anomaly Detection, Autoencoder, Long-term, Weighted Reconstruction Error, Background
Estimation.
Abstract:
In surveillance systems, detecting anomalous events like emergencies or potentially dangerous incidents by
manual labor is an expensive task. To improve this, anomaly detection automatically by computer vision
relying on the reconstruction error of an autoencoder (AE) is extensively studied. However, these detection
methods are often studied in benchmark datasets with relatively short time duration — a few minutes or
hours. This is different from long-term applications where time-induced environmental changes impose an
additional influence on the reconstruction error. To reduce this effect, we propose a weighted reconstruction
error for anomaly detection in long-term conditions, which separates the foreground from the background and
gives them different weights in calculating the error, so that extra attention is paid on human-related regions.
Compared with the conventional reconstruction error where each pixel contributes the same, the proposed
method increases the anomaly detection rate by more than twice with three kinds of AEs (a variational AE,
a memory-guided AE, and a classical AE) running on long-term (three months) thermal datasets, proving the
effectiveness of the method.
1 INTRODUCTION
For a safer daily life, round-the-clock surveillance
systems have been installed in some private and pub-
lic places. Generally they are manually operated,
which is expensive. Therefore, an automatic tool to
help find emergencies or potentially dangerous inci-
dents that require extra attention is in dire needed.
From the perspective of computer vision, such a
tool can be realized using either supervised or un-
supervised learning. Supervised learning needs a
large amount of annotated data illustrating what the
emergencies or potentially dangerous incidents look
like. This is too expensive as collecting enough data
of rarely-occurring incidents is time consuming and
even unfeasible. On the contrary, unsupervised learn-
ing greatly lowers the cost, making it more preferred
in this task.
This unsupervised solution is often realized
by anomaly detection via an autoencoder (AE),
which treats these rarely-happening emergencies and
potentially dangerous incidents as anomalies but
a
https://orcid.org/0000-0002-5231-6950
b
https://orcid.org/0000-0002-4952-8848
c
https://orcid.org/0000-0002-9212-2544
d
https://orcid.org/0000-0001-7584-5209
(a) August (b) January
(c) February (d) April
Figure 1: Example images from different months. All show
normal activity but with significant differences due to the
seasons.
frequently-occurring incidents as normal. In general,
an anomaly is deviating from a normal in many as-
pects. An AE trained with only normal data can re-
construct similar normal patterns with minimal errors,
but struggles with abnormal patterns. Hence the dif-
ference between the input and the reconstructed out-
Liu, J., Nikolov, I., Philipsen, M. and Moeslund, T.
Detecting Anomalies Reliably in Long-term Surveillance Systems.
DOI: 10.5220/0010907000003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
999-1009
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
999

put, usually in the form of mean square error (MSE),
has the ability to measure the input’s deviation from
the normal data. Input with the MSE larger than a
predefined threshold is detected as an anomaly.
This detection strategy works with an assumption
that the concept of what is normal is constant. Bench-
mark datasets on which existing anomaly detection
solutions are evaluated satisfy this assumption, be-
cause they are relatively short in time duration. How-
ever, in real life a surveillance system will be run-
ning for months and hence the normal pattern will
inevitably drift. This can be illustrated in Figure 1
where all these four harbor front scenes are normal
in terms of human activities, but the obvious changes
across time in contrast, illumination, water ripples,
and other environmental aspects make them different
from what has been defined as normal in the training
phase. This time-induced drift has a large influence
on the reconstruction error and thus the anomaly de-
tection is not reliable any more. This phenomenon
raises an open research question — how to detect
anomalies reliably in long-term surveillance systems.
To this end, we propose a weighted reconstruc-
tion error method that uses different weights for
foreground pixels and background pixels in calculat-
ing the error, for which five background estimation
(foreground extraction) methods are implemented and
evaluated. In this way, the influence of the time-
induced drift on the reconstruction error is reduced
and hence anomaly detection is more reliable.
By applying the proposed method to long-term
datasets spanning three months (August 2020, Jan-
uary 2021, April 2021) collected from a real-world
harbor front surveillance system, the experimental re-
sults show that the weighted reconstruction error in-
creases the anomaly detection rate by at least twice
than that with the conventional reconstruction error,
for all the three kinds of AEs (a variational AE, a
memory-guided AE, and a classical AE), proving the
effectiveness of the method.
The datasets and code are published on GitHub —
https://github.com/JinsongCV/Weighted-MSE, mak-
ing the integration of the weighted reconstruction er-
ror and the comparison between before and after re-
sults much easier.
2 RELATED WORK
Existing work on anomaly detection (Hasan et al.,
2016; Chong and Tay, 2017; Fu et al., 2018; Yue et al.,
2019; Nguyen and Meunier, 2019; Song et al., 2019;
Gong et al., 2019; Deepak et al., 2020; Tsai and Jen,
2021; Liu et al., 2021b) is usually AE-based.
Table 1: Time duration (hours) of benchmark datasets for
anomaly detection.
Avenue ShanghaiTec UCSD UMN Subway
0.5 3.6 3.1 0.07 2.3
Though some attempts are made to improve the
anomaly detection performance, for example incor-
porating temporal information (Fu et al., 2018; Yue
et al., 2019; Nguyen and Meunier, 2019), introducing
a generative adversarial network (GAN) to differen-
tiate reconstructions from inputs (Song et al., 2019),
using both the memorized features of the training set
and the input’s features to do reconstruction (Gong
et al., 2019; Park et al., 2020), and so on, these meth-
ods are only studies on benchmark datasets — Avenue
(Lu et al., 2013), ShanghaiTech (Luo et al., 2017),
UCSD (Mahadevan et al., 2010), UMN (Mehran
et al., 2009), and Subway (Adam et al., 2008)), which
have an imperfection in common — a short duration
of a few minutes or hours (shown in Table 1) (Pranav
et al., 2020; Nikolov et al., 2021). Therefore, gener-
alizing the existing work evaluated on such datasets
to a long-term application in real life can be problem-
atic, considering the extra time-induced changes. For
example, the illumination and contrast vary from the
shifts in day and night, weather, seasons, etc. This en-
vironmental drift imposes an additional variation on
the reconstruction error and thus makes it not solely
correlated to human activities that are responsible for
most anomalies.
This challenge inspires us to focus more on fore-
ground regions where anomalies are assumed in when
calculating the reconstruction error, to eliminate the
influence of the time-induced environmental drift,
which is exactly the proposed weighted reconstruc-
tion error does.
A similar solution to ours is the object-centric
AE (Ionescu et al., 2019; Georgescu et al., 2020)
that takes the pre-detected object region instead of
the full image as the input. Despite the similarity,
there are four distinctions. (i) The goals are differ-
ent. Their work expects to generalize an AE trained
on one scene to another scene without further finetun-
ing, while our method targets to reduce the effect of
the environmental drift in long-term surveillance sys-
tems. (ii) Our method still reconstructs the full image
instead of only object regions, because the location of
an object relative to the background is important, for
example, a drowning accident only happens in the wa-
ter area. (iii) Our method is much more flexible like a
post-processing module and thus easily incorporated
to any framework. (iv) Our method treating fore-
ground and background regions separately also pro-
vides an ability to investigate environmental anoma-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
1000

lies like a sudden contrast change due to an extreme
weather event.
3 METHODS
This paper proposes a weighted reconstruction error
for anomaly detection illustrated by the diagram in
Figure 2.
In it, the red flow indicates the conventional
anomaly detection scheme where the reconstruction
error (in the form of MSE) is directly calculated from
the input and the reconstructed output with each pixel
contributes the same. This calculation also considers
the time-induced environmental drift as part of the re-
construction error, and thus for input spanning a long
time period the MSE curve will fluctuate greatly. This
is very dangerous as a real anomaly will be ignored, if
its MSE value is lower than other fluctuated MSE val-
ues of normal inputs. Such a phenomenon is shown in
the upper MSE curve where normal inputs with drift
have larger MSE values than the threshold (the red
dashed line), not only introducing false positives but
also missing the real anomaly.
In contrast, the green flow in the diagram in-
dicates the proposed weighted reconstruction error-
based anomaly detection scheme. Additional back-
ground estimators or object-centric foreground ex-
tractors can segment an input into foreground region
and background region. This information together
with the input and the reconstruction are used to cal-
culate the reconstruction error where the foreground
pixels and background pixels are assigned different
weights, so that the error focuses more on the region
where anomalies usually happen and thus the effect
of the environmental drift is reduced. In this way,
the weighted MSE curve will be much more smoother
for normal inputs but generates a peak if an anomaly
comes in, like the lower W-MSE curve shows. An-
other thing to be mentioned is that both the red flow
scheme and the proposed green flow scheme are indi-
cating the inference phase — anomaly detection.
3.1 Autoencoder
Following what is customary, we use an AE to de-
tect anomalies by finding frames with the largest re-
construction errors. Three AEs are applied. The
first is a variational AE — VQVAE2 (Razavi et al.,
2019) whose encoder compresses the input into multi-
scale quantized latent maps for the decoder to process.
The second is a memory-guided AE — MNAD (Park
et al., 2020) that uses a concatenated latent space (of
the naive latent space from the encoder output and
the typical features stored in a memory module con-
structed from training) to reconstruct the input. An
anomaly is measured by not only the reconstruction
error but also the distance between the encoder out-
put and the nearest memorized features. The third is
a classical AE (CAE) designed by us, which is with-
out any advanced processing of the latent space. This
CAE uses eleven convolution layers and five pooling
layers to downsize the input (384 × 288 × 1) into a
compressed feature tensor (10 × 7 × 64), and another
six transposed convolution layers and five convolu-
tion layers to transform the latent feature space into
the reconstructed output. Detailed implementations
are shared on GitHub.
3.2 Background Estimation
As mentioned before, the method is characteristic of
foreground regions and background regions contribut-
ing differently to the weighted reconstruction error.
Therefore, separating the background from the fore-
ground is the key. To achieve this we test out two
pipelines, one using classical statistical methods to es-
timate the background, the other one using the result
of a human detector as the foreground and everything
else as the background.
In section 4, we will test all the methods of the
two pipelines and determine which is the best method
or the best combination of a few methods to separate
the foreground from the background, so that the drift
can be removed effectively for improving the anomaly
detection rate.
3.2.1 Statistical Background Estimation
This pipeline is composed of classical statistical ap-
proaches instead of deep learning segmentation meth-
ods (Babaee et al., 2018; Akilan et al., 2019) to min-
imize the complexity. Also this avoids the high price
of supervised segmentation concerning pixel-level an-
notations. In our harbor front scenario, the objects
in the foreground vary significantly — humans from
a single one to groups, vehicles, bicycles, and oth-
ers. These variations cause extra difficulties and man-
power in pixel-level annotations if a deep model is
chosen. The four classical background estimators are
as follows:
• Mixture of Gaussians (MOG2) (Zivkovic, 2004)
— using Gaussian mixture probability density to
continuously model the background.
• Mixture of Gaussians using K-nearest neighbours
(KNN) (Zivkovic and Van Der Heijden, 2006) —
an extension of the MOG2 method by implement-
Detecting Anomalies Reliably in Long-term Surveillance Systems
1001

Input
time
MSE
time
W-MSE
Autoencoder
Background Estimators
Object-centric Foreground
Extractors
R
econstruction
Anomaly
Figure 2: Diagram of the proposed method.
ing a K-nearest neighbours algorithm on top for a
more robust kernel density estimation.
• Image difference with arithmetic mean (ID
a
) —
the difference between the current image and the
previous one is processed by adaptive threshold-
ing to get the background mask. ID
a
uses an arith-
metic mean weight — each pixel in the neigh-
borhood contributes equally to compute the local
threshold.
• Image difference with Gaussian mean (ID
g
) — the
same principle with ID
a
, but with a different adap-
tive thresholding strategy. ID
g
uses a Gaussian
mean weight — pixels in the neighborhood far-
ther away from the center contribute less to the
local threshold computing.
To do background estimation, all the four methods
need the neighbouring images of the current frame.
For the MOG2 and KNN methods, the number of
neighbouring images is heuristically set to 20, as it
has been shown that more frames are better at mod-
eling the background. For the ID
a
and ID
g
methods,
only one previous image is used.
Once a mask is acquired from any of the four
methods, it goes through a post-processing procedure
— a morphological closing with a structuring element
of size 7 × 7 followed by an opening with an ele-
ment of size 3 × 3. This step serves to remove small
noise particles. Finally, the moving elements in the
background like the water, ropes, and masts are re-
moved from the mask by prior knowledge of their lo-
cations. The resulting mask will have foreground pix-
els with large grayscale values approaching 255 and
background pixels with small values near 0. All of
these procedures are implemented from the OpenCV
library (Bradski, 2000).
3.2.2 Object-centric Foreground Extraction
Besides the above four classical approaches, we test
another method — object-centric foreground extrac-
tion, provided that there is a well-trained human de-
tector at hand and human activities are the targets.
The detector we use is YOLOv5 (Ultralytics, 2020;
Liu et al., 2021a), with which each person is repre-
sented by a rectangle in the mask. The pixels in the
rectangle has a same grayscale value — the person’s
detection confidence multiplied by 255, while pixels
in other regions are with the value 0.
As a whole, these five versions of masks explicitly
locate foreground areas with very large grayscale val-
ues, so for a clear reference the subsequent contents
will call such a mask foreground map. Figure 3 shows
one input image and the results from the five methods.
3.3 Weighted Reconstruction Error
First to be noted is that this paper goes with the con-
vention and thus opts for the MSE to measure the dif-
ference between the input and the reconstructed out-
put, so the following contents will directly use MSE to
represent the difference without further explanation.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
1002

(a) Input (b) MOG2 (c) KNN (d) ID
a
(e) ID
g
(f) YOLOv5
Figure 3: An input thermal image and the outputs from the five implemented background estimation (foreground extraction)
methods.
As long as there is a foreground map M locating
foreground pixels P
f g
, any weighted MSE is possible
by giving P
f g
and background pixels P
bg
arbitrarily-
defined weights for a specific task.
For an input I with size H ×W and its correspond-
ing reconstruction R, a general weighted MSE
w
is:
MSE
w
=
∑
H
i=1
∑
W
j=1
(I
i j
·
¯
M
i j
− R
i j
·
¯
M
i j
)
2
H ×W
(1)
where
¯
M
i j
is the value of the weight map
¯
M at pixel
(i, j).
¯
M is calculated using Equation 2.
¯
M =
w
f g
× M + w
bg
× (255 − M)
255
(2)
where w
f g
and w
bg
are normalized weights for P
f g
and P
bg
, respectively; as an 8-bit image, 255 − M is
the “inverse” operation of M, explicitly locating P
bg
;
therefore
¯
M is the final weight map normalized to 0-1
for calculating weighted MSE in Equation 1.
Setting w
f g
as 1 and w
bg
as 0 is the special case of
the MSE only considering P
f g
. Likewise, setting w
f g
as 0 and w
bg
as 1 is the MSE only looking at P
bg
.
A more general case is a weighted MSE
w
com-
bining foreground maps (e.g., M
1
, M
2
) from several
background estimators (foreground extractors).
MSE
w
=
∑
H
i=1
∑
W
j=1
(I
i j
·
¯
M
i j
− R
i j
·
¯
M
i j
)
2
H ×W
(3)
¯
M = w
1
×
¯
M
1
+ w
2
×
¯
M
2
(4)
¯
M
1
=
w
f g
1
× M
1
+ w
bg
1
× (255 − M
1
)
255
(5)
¯
M
2
=
w
f g
2
× M
2
+ w
bg
2
× (255 − M
2
)
255
(6)
where,
¯
M
1
is the weight map from M
1
with w
f g
1
and
w
bg
1
as normalized weights for P
f g
and P
bg
in M
1
;
¯
M
2
is the weight map from M
2
with w
f g
2
and w
bg
2
as nor-
malized weights for P
f g
and P
bg
in M
2
;
¯
M is the final
weight map combining
¯
M
1
with weight w
1
and
¯
M
2
with weight w
2
; the resulting MSE
w
is the weighted
MSE considering foreground maps from two meth-
ods.
4 EXPERIMENTS
4.1 Dataset Information
Two datasets collected from a long-term harbor front
surveillance system are used to investigate the pro-
posed weighted MSE on anomaly detection.
One dataset called 300Ver has 300 images with
every 100 sampled from August 2020, January 2021,
and April 2021, making itself a dataset spanning 76
days. This dataset is a subset of a larger one covering
8-month and publicly available as part of the publica-
tion (Nikolov et al., 2021). The sampling protocol for
300Ver is also given in (Nikolov et al., 2021) which
uses the temperature as a basis to construct datasets
covering cold, warm, and in-between months.
The other dataset called 3515Ver is also a subset
of the dataset from (Nikolov et al., 2021), and has
3515 images intensively sampled with a frame rate of
0.5fps from 15 pm to 18 pm from 14-16 August 2020,
14-16 January 2021, and 14-16 April 2021. This sam-
pling protocol comes from three strategies. (i) Em-
pirically 15 pm to 18 pm is the time period when
there are most people present in view. (ii) Three days
from each month not only guarantee the data diversity
across time but also limit the amount of the dataset for
better visualization in section 4.3.3. (iii) 0.5fps limits
the amount of 3515Ver, at the same time keeping the
information continuity between neighboring frames.
In 300Ver persons are annotated with bounding
boxes. Therefore, six foreground maps from MOG2,
KNN, ID
a
, ID
g
, YOLOv5, and ground truth (GT), are
prepared for each image. The 3515Ver dataset has
no such annotations, so only five kinds of foreground
maps are calculated.
First the 300Ver dataset is used and the related
experiments are in sections 4.3.1 and 4.3.2. The
3515Ver dataset is then used to verify what has been
found on 300Ver and the related contents are in sec-
tion 4.3.3. There are three reasons why we do ex-
periments on both datasets. (i) 300Ver covers 76 days
with less images while 3515Ver have more images but
only covering 9 days; these two datasets compensate
for each other, making the experiments consider both
Detecting Anomalies Reliably in Long-term Surveillance Systems
1003

a long-term duration and a large amount of images.
(ii) This separation of two datasets avoids the prob-
lem that if all the images are sampled intensively from
the 76 days, the resultant 30000 images will make the
visualization of drawing the MSE values of them into
one curve (like the curve in the following contents)
extremely difficult. (iii) Annotating a small dataset
(300Ver) is much easier to provide a very accurate
foreground extraction, based on which the findings of
section 4.3.1 will be more convincing.
4.2 Implementation Details
Both VQVAE2 and MNAD are trained with 4000 im-
ages and validated with 1000 images. CAE is trained
with 15000 images and validated with 5000 images
due to its naive function compared with the other two.
VQVAE2 is trained with a batch size of 32 and a
learning rate of 0.0001. MNAD is trained with a batch
size of 32, a learning rate of 0.0002, and a value of 0.1
for the weight of the feature separateness and com-
pactness loss. CAE is trained with a batch size of 16
and a learning rate of 0.0003. The training phases stop
at the 100th epoch, the 100th epoch, and the 200th
epoch for VQVAE2, MNAD, and CAE, respectively,
at which the networks are converged with the train-
ing losses not decreasing any more. All these training
and validation sets are sampled from February 2021 to
not only avoid the overlapping with the three-month
datasets this paper uses but also enhance the effect of
the time-induced drift that we want to address. A kind
reminder is that the following experiments are done
with all these three AEs but we usually only show re-
lated visualizations of VQVAE2 to avoid the repeat of
similar results.
The YOLOv5 detector uses a pretrained model
from (Liu et al., 2021a) and the training set has no
overlapping with the images we use in this paper.
4.3 Weighted MSE
4.3.1 Weighted MSE Curves
To simplify the work and directly answer the ques-
tion how the conventional MSE and weighted MSE
behave for long-term datasets, according to Equation
1 and Equation 2, the MSE investigated will consider
three situations: the foreground only, the background
only, and the full image where each pixel contributes
the same as the convention, which are represented as
MSE
f g
, MSE
bg
, MSE
cvt
, respectively. These repre-
sentations will be used in all the following contents.
Therefore, for each AE with 300Ver as input, six
kinds of foreground maps produce six MSE
f g
curves
and six MSE
bg
curves describing the weighted MSE
changes across time; likewise, one MSE
cvt
curve can
be drawn to describe the conventional MSE changes
across time.
For a better comparison, Figure 4 shows the above
mentioned 13 MSE curves, produced by the VQVAE2
model. This visualization (of showing multiple curves
in one chart) is achieved with a critical pre-processing
module before plotting: first the original MSE val-
ues are smoothed by a mean filter with its kernel size
as 10; then the smoothed values are normalized be-
tween 0 and 1; after normalization the curves are
overlapped with each other, so a further translation is
done for each curve by adding an extra value. In this
way, the ranges of curves of MOG2, KNN, ID
a
, ID
g
,
YOLOv5, and GT are [2.5, 3.5], [2.0, 3.0], [1.5, 2.5],
[1.0, 2.0], [0.5, 1.5], [0, 1], respectively; the range of
the conventional MSE curve is [3.0, 4.0].
From Figure 4 several observations are found. (i)
The six MSE
f g
curves in (a) have totally different
trends with the trends of MSE
bg
curves in (b), which
is reasonable as the image regions they look at are
not the same. (ii) The MSE
cvt
curve in (b) has al-
most exactly same trend with that of the six MSE
bg
curves in (b), but largely deviates from the trends of
MSE
f g
curves in (a), proving that on 300Ver the con-
ventional MSE (where each pixel in the full image
contributes the same) cannot represent what happens
in the foreground region and thus have no ability to
do anomaly detection reliably. (iii) Though the six
MSE
f g
curves in (a) are diverse, they share a similar
trend to some extent especially between the MSE
f g
curve of YOLOv5 and the MSE
f g
curve of GT. This
reflects that they have the ability to represent the fore-
ground changes along with time but also have their
own focuses shown by distinct peaks due to the meth-
ods’ differences. The MSE
f g
curve of YOLOv5 and
the MSE
f g
curve of GT are bounding box-based fo-
cusing only on persons, therefore a larger similarity
is found between them. (iv) The trends of all the
MSE
bg
curves and the MSE
cvt
curve in (b) are U-
shape, revealing the influence of the drift across time
on the MSE as mentioned before. However, the U-
shape trend is not shown in foreground MSE curves in
(a), indicating that the time-induced effect influences
background regions higher than foreground regions.
Hence researches on long-term datasets (applications)
need separate analysis on them.
In addition to this, experiments done with MNAD
and CAE also get similar results that all support the
above findings. As a whole, this part confirms that in
long-term datasets (applications) with time-induced
drift, the conventional MSE (where each pixel con-
tributes the same) is not suitable to describe the fore-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
1004
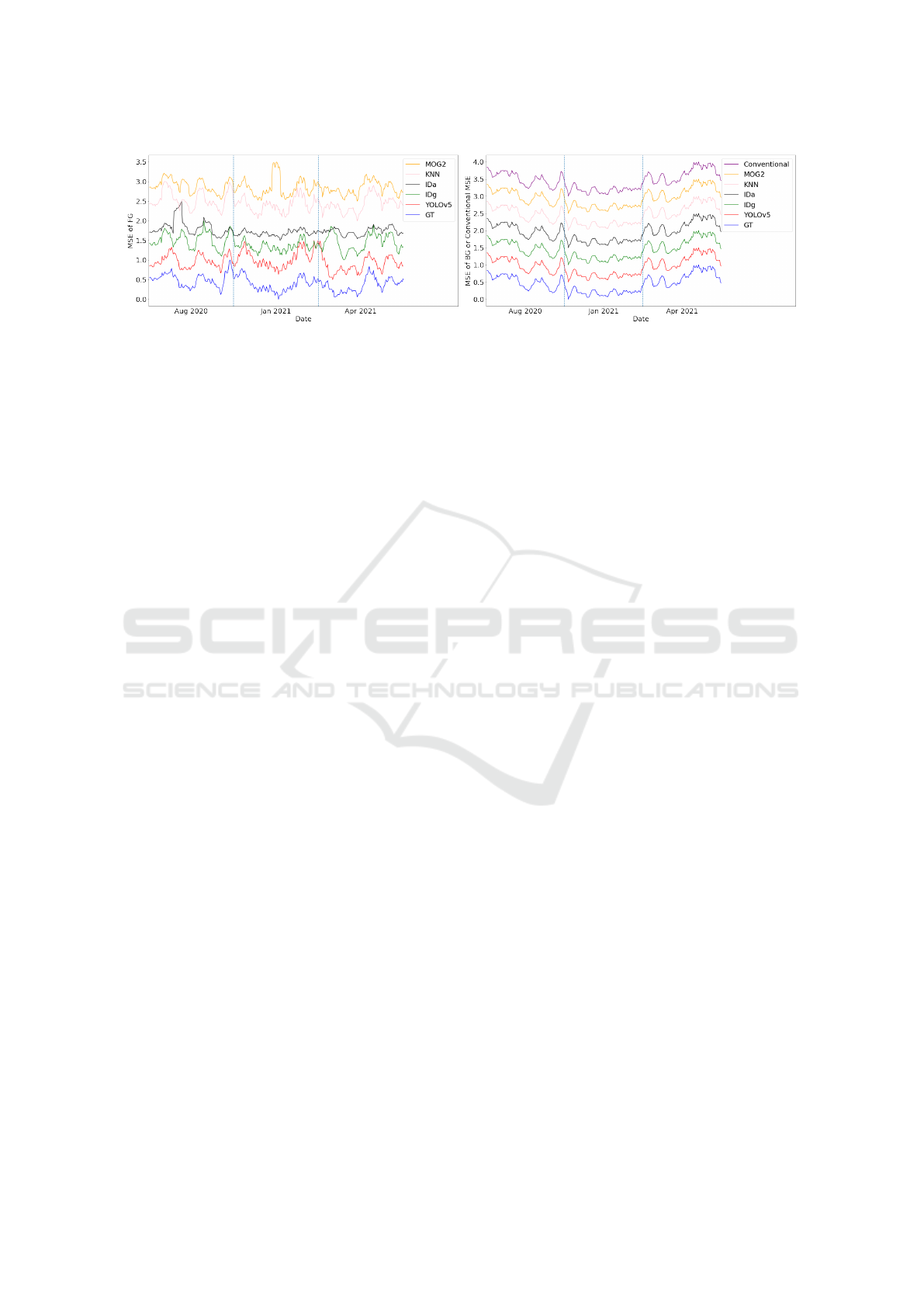
(a) MSE
f g
(b) MSE
bg
and MSE
cvt
Figure 4: MSE (after smoothing, normalization, and translation) curves across time from VQVAE2 on 300Ver. The vertical
azure dashed lines are used to separate different months.
ground information, not to mention a further step —
detecting anomalies.
4.3.2 Weighted MSE for Anomaly Detection
This section will test whether the proposed weighted
MSE performs better in anomaly detection. Since
there are no specified anomalies in the dataset, and
detecting specific anomalies is not the focus of this
work, we decide to use a strategy that maximizes
the difference between an anomaly and a normal im-
age, to better focus on the main research problem —
how to do anomaly detection reliably in long-term
datasets.
To realize this, we synthesize anomalies by over-
lapping “black-white-pixel” patterns (that the three
AEs have never seen) on the person regions of some
images. But it seems that such patterns overlapped
on only person regions will give the YOLOv5-based
foreground map a biased advantage. Hence, to eval-
uate the five kinds of foreground maps more fairly,
four shapes (rectangle, square, circle, and ellipse)
of the “black-white-pixel” pattern are considered for
the reason that the detector-based map has no round-
cornered foregrounds but the other four kinds of
maps have. We admit this four-shape strategy can-
not totally remove the bias on the YOLOv5-generated
map, but if we put the “black-white-pixel” pattern
on other foreground regions where there are no peo-
ple, a greater bias will be given to other statistical
background estimators because YOLOv5 only pre-
dicts human regions. Therefore, this four-shape strat-
egy should be the best solution to treat these five kinds
of foreground maps equally.
Accordingly, on the premise of having at least
one person in each synthesized anomalous image, 21
rectangle-shaped anomalies (the 1st, 11st, 21st, ...,
281st images of 300ver), 21 square-shaped anoma-
lies (the 3rd, 13rd, ..., 293rd images of 300ver), 20
circle-shaped anomalies (the 2nd, 12nd, ..., 282nd im-
ages of 300ver), and 16 ellipse-shaped anomalies (the
4th, 14th, ..., 284th images of 300ver) are synthesized.
In each of them the annotated GT person regions are
randomly chosen to be overlapped with “black-white-
pixel” patterns. Examples of the synthesized anoma-
lies are shown in Figure 5.
First, the rectangle-shaped anomalies are used to
test the anomaly detection rate. Accordingly, in Fig-
ure 6, six MSE curves (five MSE
f g
curves and one
MSE
cvt
curve) of VQVAE2 are drawn in color blue,
and the anomalies are located with orange peaks.
Each sub-figure caption has the same meaning with
what has been used in section 4.3.1.
From Figure 6, the large percentage of overlap-
ping between orange peaks and blue peaks in (a)-(e)
proves the usefulness of the proposed weighted MSE
in anomaly detection. This also happens in the exper-
iments of VQVAE2 on 300Ver but with anomalies in
the other three shapes. Specifically, among the images
of the largest 30 (10% of the dataset) MSE values of
each curve, the number of anomalies is listed in Table
2. From the table, the weighted MSE using any fore-
ground map has a way high detection rate than the
conventional MSE.
When taking multiple foreground maps from dif-
ferent methods into consideration, the top two results
in Table 2 — YOLOv5 and KNN, inspire us to com-
bine their foreground maps by applying Equation 3-6
in which w
1
(namely w
Y OLOv5
) and w
2
(namely w
KNN
)
are 0.52 and 0.48, respectively as the normalized val-
ues of 78.21% and 71.79%. To be noted is that any
combination is possible no matter whether a super-
vised human detector is available.
To avoid being one-sided, we do further experi-
ments with MNAD and CAE on 300Ver in a way of
using rectangle-shaped anomalies and the foreground
map combining YOLOv5 and KNN. By using the
weighted MSE instead of the conventional MSE, the
detection rate increases from 9.52% to 66.67% for
MNAD and from 4.76% to 66.67% for CAE.
Detecting Anomalies Reliably in Long-term Surveillance Systems
1005
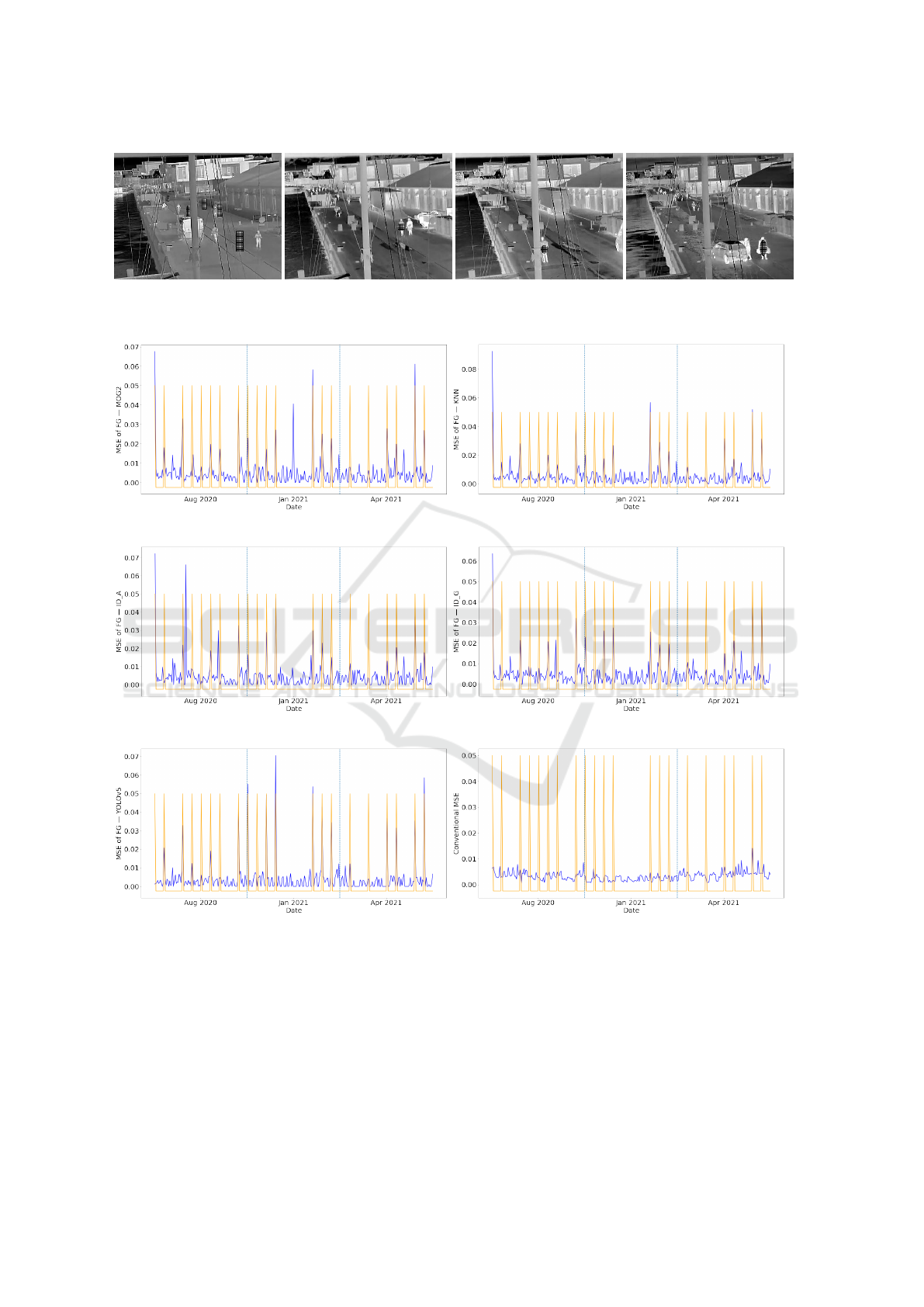
(a) Rectangle (b) Square (c) Circle (d) Ellipse
Figure 5: Examples of anomalies with “black-white-pixel” patterns in four different shapes.
(a) MSE
f g
of MOG2 (b) MSE
f g
of KNN
(c) MSE
f g
of ID
a
(d) MSE
f g
of ID
g
(e) MSE
f g
of YOLOv5 (f) MSE
cvt
Figure 6: After introducing rectangle-shaped anomalies, MSE curves across time from VQVAE2 on the 300Ver dataset. The
blue curves describe the MSE changes, and the orange peaks indicate the locations of anomalies. The vertical azure dashed
lines are used to separate different months.
As a whole, the proposed weighted MSE im-
proves anomaly detection rate markedly on 300Ver —
VQVAE2 (2.68 times-3.21 times), MNAD (7 times),
CAE (14 times), verifying that this strategy is worth
being incorporated in datasets or applications span-
ning a long time period.
4.3.3 Extended Experiments
The extended experiments on 3515Ver use rectangle-
shaped “black-white-pixel” patterns overlapping on
the persons who are near the horizontal edge of the
water to simulate the anomalies. The resultant 60
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
1006
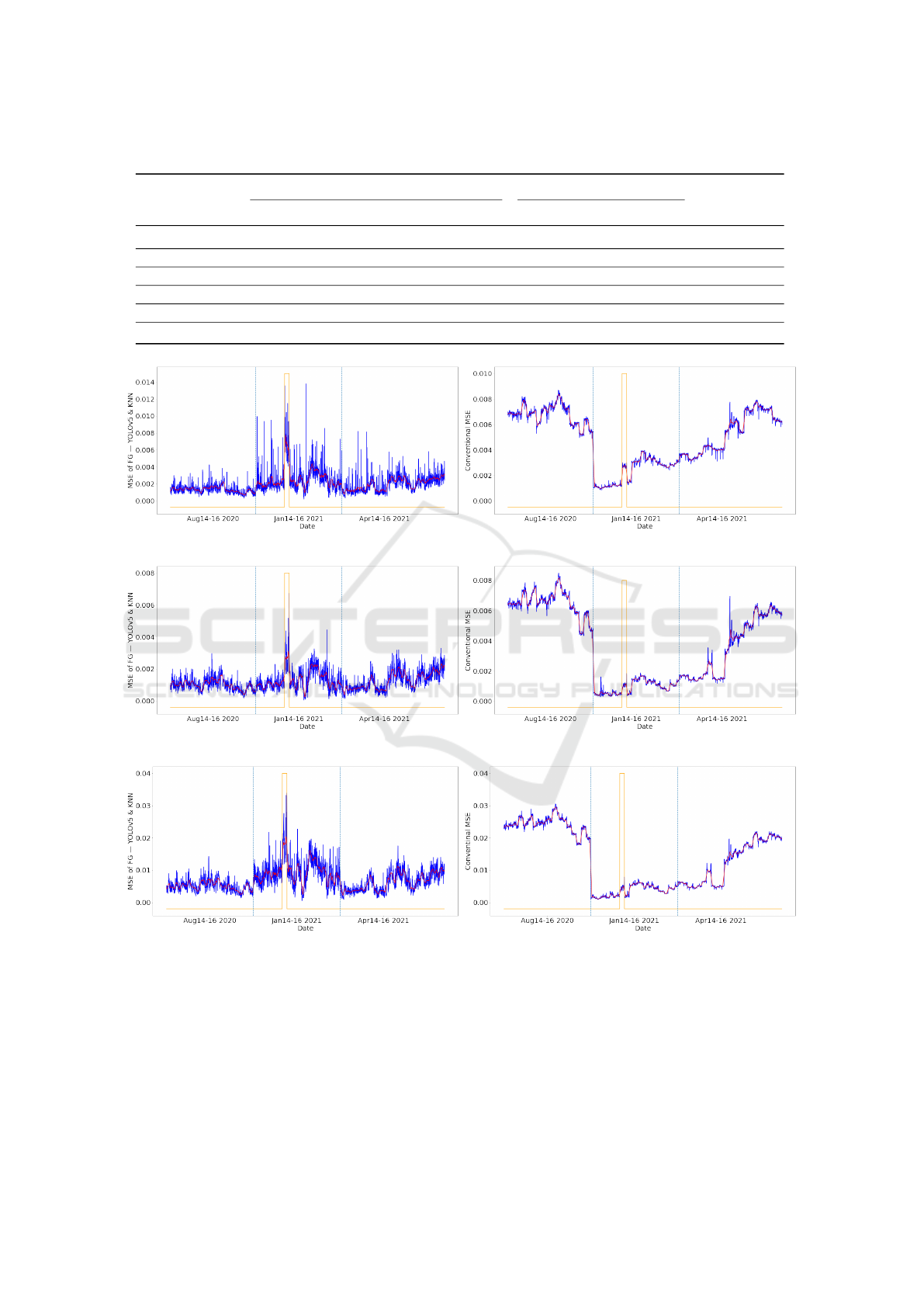
Table 2: Anomaly detection results of weighted MSE and conventional MSE.
Statistical Background Object-centric Foreground
Conventional
MOG2 KNN ID
a
ID
g
YOLOv5
Rectangle (21) 16 17 15 15 16 4
Square (21) 13 14 12 13 15 7
Circle (20) 11 13 10 10 16 4
Ellipse (16) 14 12 14 13 14 4
Sum (78) 54 56 51 51 61 19
Detection Rate 69.23% 71.79% 65.38% 65.38% 78.21% 24.36%
(a) VQVAE2: MSE
f g
of M
Y OLOv5&KNN
(b) VQVAE2: MSE
cvt
(c) MNAD: MSE
f g
of M
Y OLOv5&KNN
(d) MNAD: MSE
cvt
(e) CAE: MSE
f g
of M
Y OLOv5&KNN
(f) CAE: MSE
cvt
Figure 7: MSE curves of VQVAE2, MNAD, and CAE on 3515Ver with synthesized rectangle-shaped anomalies. The curve
of absolute MSE values is in blue. The curve of the smoothed values are in red. The anomalies are located with orange peaks.
The vertical azure dashed lines are used to separate different months.
synthesized anomalies are consecutive frames and
the persons overlapped with the abnormal pattern are
fixed individuals. This increases the authenticity of
the simulated anomalies — in real life an anomaly
usually persists through multiple frames and involves
fixed persons.
Figure 7 gives the MSE curves of the three AEs
on 3515Ver with synthesized anomalies, in which
the curves of absolute MSE values are in blue and
the smoothed ones are in red, and the anomalies
Detecting Anomalies Reliably in Long-term Surveillance Systems
1007

are located with orange peaks. In Figure 7, by
using the weighted MSE with the foreground map
M
Y OLOv5&KNN
combining YOLOv5 and KNN, the as-
cending peaks in (a), (c), and (e) accurately detect the
anomalies, yet the conventional MSE curves in (b),
(d), and (f) are entirely dominated by time-induced
influences for example the fall of a cliff due to the
seasonal transition between August 2020 and January
2021. We therefore believe that the extended experi-
ments on a much larger dataset also prove the effec-
tiveness of the proposed weighted MSE in anomaly
detection.
5 CONCLUSIONS
This paper proposes a weighted reconstruction er-
ror in autoencoder-based anomaly detection for long-
term surveillance systems. The method aims to make
the calculated error more focused on the region where
anomalies are assumed in and thus reduces the influ-
ence of time-induced environmental drift.
We apply three selected autoencoders to three-
month datasets to test the anomaly detection per-
formance. With synthesized anomalies, the autoen-
coder with proposed weighted reconstruction error al-
ways gets a much higher detection rate (more than
twice) than the conventional reconstruction error ver-
sion where each pixel contributes the same, which
proves the usefulness of the proposed strategy.
This method is implemented as a flexible module,
therefore we expect it can be integrated into and veri-
fied by more frameworks. Besides, as a study at har-
bor fronts, in the future we will use this method to de-
tect emergencies and potentially dangerous incidents
like traffic accidents, drowning accidents, crowds in
coronavirus days, etc., so that timely controls or res-
cues by polices, safeguards, and other professionals
can be provided for a safer life.
ACKNOWLEDGEMENTS
This work is funded by TrygFonden as part of the
project Safe Harbor.
REFERENCES
Adam, A., Rivlin, E., Shimshoni, I., and Reinitz, D. (2008).
Robust real-time unusual event detection using mul-
tiple fixed-location monitors. IEEE transactions on
pattern analysis and machine intelligence, 30(3):555–
560.
Akilan, T., Wu, Q. J., Safaei, A., Huo, J., and Yang, Y.
(2019). A 3d cnn-lstm-based image-to-image fore-
ground segmentation. IEEE Transactions on Intelli-
gent Transportation Systems, 21(3):959–971.
Babaee, M., Dinh, D. T., and Rigoll, G. (2018). A deep con-
volutional neural network for video sequence back-
ground subtraction. Pattern Recognition, 76:635–649.
Bradski, G. (2000). The OpenCV Library. Dr. Dobb’s Jour-
nal of Software Tools.
Chong, Y. S. and Tay, Y. H. (2017). Abnormal event detec-
tion in videos using spatiotemporal autoencoder. In
International Symposium on Neural Networks, pages
189–196. Springer.
Deepak, K., Chandrakala, S., and Mohan, C. K. (2020).
Residual spatiotemporal autoencoder for unsuper-
vised video anomaly detection. Signal, Image and
Video Processing, pages 1–8.
Fu, J., Fan, W., and Bouguila, N. (2018). A novel approach
for anomaly event detection in videos based on au-
toencoders and se networks. In 2018 9th International
Symposium on Signal, Image, Video and Communica-
tions (ISIVC), pages 179–184. IEEE.
Georgescu, M.-I., Tudor Ionescu, R., Shahbaz Khan, F.,
Popescu, M., and Shah, M. (2020). A scene-agnostic
framework with adversarial training for abnormal
event detection in video. arXiv e-prints, pages arXiv–
2008.
Gong, D., Liu, L., Le, V., Saha, B., Mansour, M. R.,
Venkatesh, S., and Hengel, A. v. d. (2019). Memoriz-
ing normality to detect anomaly: Memory-augmented
deep autoencoder for unsupervised anomaly detec-
tion. In Proceedings of the IEEE/CVF International
Conference on Computer Vision, pages 1705–1714.
Hasan, M., Choi, J., Neumann, J., Roy-Chowdhury, A. K.,
and Davis, L. S. (2016). Learning temporal regularity
in video sequences. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition,
pages 733–742.
Ionescu, R. T., Khan, F. S., Georgescu, M.-I., and Shao,
L. (2019). Object-centric auto-encoders and dummy
anomalies for abnormal event detection in video. In
Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 7842–
7851.
Liu, J., Philipsen, M. P., and Moeslund, T. B. (2021a). Su-
pervised versus self-supervised assistant for surveil-
lance of harbor fronts. In VISIGRAPP (5: VISAPP),
pages 610–617.
Liu, J., Song, K., Feng, M., Yan, Y., Tu, Z., and Zhu,
L. (2021b). Semi-supervised anomaly detection
with dual prototypes autoencoder for industrial sur-
face inspection. Optics and Lasers in Engineering,
136:106324.
Lu, C., Shi, J., and Jia, J. (2013). Abnormal event detection
at 150 fps in matlab. In Proceedings of the IEEE inter-
national conference on computer vision, pages 2720–
2727.
Luo, W., Liu, W., and Gao, S. (2017). In Proceedings of the
IEEE International Conference on Computer Vision,
pages 341–349.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
1008

Mahadevan, V., Li, W., Bhalodia, V., and Vasconcelos, N.
(2010). Anomaly detection in crowded scenes. In
2010 IEEE Computer Society Conference on Com-
puter Vision and Pattern Recognition, pages 1975–
1981. IEEE.
Mehran, R., Oyama, A., and Shah, M. (2009). Abnormal
crowd behavior detection using social force model. In
2009 IEEE Conference on Computer Vision and Pat-
tern Recognition, pages 935–942. IEEE.
Nguyen, T.-N. and Meunier, J. (2019). Anomaly detection
in video sequence with appearance-motion correspon-
dence. In Proceedings of the IEEE International Con-
ference on Computer Vision, pages 1273–1283.
Nikolov, I. A., Philipsen, M. P., Liu, J., Dueholm, J. V.,
Johansen, A. S., Nasrollahi, K., and Moeslund, T. B.
(2021). Seasons in drift: A long-term thermal imaging
dataset for studying concept drift. In Thirty-fifth Con-
ference on Neural Information Processing Systems.
Park, H., Noh, J., and Ham, B. (2020). Learning memory-
guided normality for anomaly detection. In Proceed-
ings of the IEEE/CVF Conference on Computer Vision
and Pattern Recognition, pages 14372–14381.
Pranav, M., Zhenggang, L., et al. (2020). A day on campus-
an anomaly detection dataset for events in a single
camera. In Proceedings of the Asian Conference on
Computer Vision.
Razavi, A., van den Oord, A., and Vinyals, O. (2019). Gen-
erating diverse high-fidelity images with vq-vae-2. In
Advances in neural information processing systems,
pages 14866–14876.
Song, H., Sun, C., Wu, X., Chen, M., and Jia, Y. (2019).
Learning normal patterns via adversarial attention-
based autoencoder for abnormal event detection in
videos. IEEE Transactions on Multimedia.
Tsai, D.-M. and Jen, P.-H. (2021). Autoencoder-based
anomaly detection for surface defect inspection. Ad-
vanced Engineering Informatics, 48:101272.
Ultralytics (2020). Yolov5. last accessed: October 25, 2021.
Yue, H., Wang, S., Wei, J., and Zhao, Y. (2019). Abnormal
events detection method for surveillance video using
an improved autoencoder with multi-modal input. In
Optoelectronic Imaging and Multimedia Technology
VI, volume 11187, page 111870U. International Soci-
ety for Optics and Photonics.
Zivkovic, Z. (2004). Improved adaptive gaussian mixture
model for background subtraction. In Proceedings of
the 17th International Conference on Pattern Recog-
nition, 2004. ICPR 2004., volume 2, pages 28–31.
IEEE.
Zivkovic, Z. and Van Der Heijden, F. (2006). Efficient adap-
tive density estimation per image pixel for the task of
background subtraction. Pattern recognition letters,
27(7):773–780.
Detecting Anomalies Reliably in Long-term Surveillance Systems
1009
